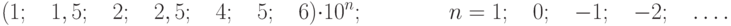Определение погрешности измерения на электроизмерительных приборах. Класс точности прибора
Следует помнить,
что никакое измерение, т.е. сравнение с
эталонной величиной, не может быть
выполнено абсолютно точно. Результат
измерения всегда содержит некоторую
ошибку. Кроме того, надо учесть, что
измерение проводится не путем сравнения
с самим эталоном, а с помощью измерительного
прибора (который при поверке был сравнен
с эталоном). Очевидно, что, измеряя с
помощью этого измерительного прибора,
мы не можем сделать ошибки меньшей, чем
та, которая определяется погрешностью
измерительного устройства.
Разность между
показаниями прибора и действительным
значением измеряемой величины называется
абсолютной погрешностью А.
|
А |
(1) |
Отношение
абсолютной погрешности к действительному
значению измеряемой величины, выраженное
в процентах, называется относительной
погрешностью:
|
|
(2) |
Приведенные
определения относительной и абсолютной
погрешности не дают возможности узнать
их величину, так как действительное
значение измеряемой величины нам
неизвестно. Определить величины
погрешностей при электрических измерениях
становится возможным, если известен
класс
точности
прибора (КЛ
Т).
Он дает предельную абсолютную погрешность,
выраженную в процентах от номинального
показания прибора (максимального при
данном пределе измерения) АНОМ:
|
КЛ |
(3) |
Класс
точности указан на шкале прибора (рис.
6).
Зная класс точности
прибора, можно легко определить абсолютную
погрешность измерения А:
|
А |
(4) |
Например,
для катушки сопротивления в 1000 Ом класса
точности 0,05 абсолютная погрешность:
|
А |
Относительную
погрешность также можно вычислить через
класс точности прибора. По определению
относительная
погрешность:
|
|
(5) |
Учитывая,
что действительное значение измеряемой
величины АДЕЙСТ
и показания прибора АИЗМ
примерно равны (АДЕЙСТ
АИЗМ),
и, используя формулу (4), получаем:
|
|
(6) |
Видно,
что относительная погрешность измерений
будет тем меньше, чем ближе снимаемые
показания к номинальному значению для
данного прибора, т.е. к концу
шкалы.
Следовательно, при работе с многопредельными
ЭИП нужно так выбирать предел измерения
прибора, чтобы показания считывались
со второй половины шкалы. Следует
помнить, что номинальное значение
многопредельного ЭИП определяется
положением, в котором стоит переключатель
пределов при данном измерении.
При работе с
многопредельными приборами нужно
внимательно рассчитывать цену одного
деления шкалы ЦД. Под делением
следует понимать не разность между
штрихами, а разность между ними в
соответствии с оцифровкой шкалы. Цена
деления равномерной шкалы равна
отношению номинального значения
показания прибора (предела измерения)
к общему числу делений N
на шкале прибора: ЦД =
.
Численное значение измеряемой величины
АИЗМ равно цене деления ЦД,
умноженной на измеренное число делений
NИЗМ
по шкале:
|
АИЗМ |
(7) |
Рассмотрим
примеры определения погрешностей для
многопредельных ЭИП.
|
Пример 1. |
||||
|
Переключатель измерения |
→ |
|
← ← |
Шкала
Класс |
|
Рис. 6. |
На рис. 6 изображен
многопредельный вольтметр. Вычислить
абсолютную и относительную погрешности
определения напряжения. Класс точности
вольтметра 0,5.
Номинальное
значение напряжения 300 В (определяется
положением переключателя пределов
напряжения).
Цена деления
данного предела измерения ЦД ==
2 В/дел.
Измеренное значение
напряжения UИЗМ = 2 В/дел.·75
дел. = 150 В.
Абсолютная
погрешность измерения U
=
= 1,5 (В).
Относительная
погрешность измерения 0
=
= 1,0%.
Пример 2
Рис. 7.
На рис. 7 изображен
тот же многопредельный вольтметр при
другом положении переключателя пределов
измерений. Вычислить абсолютную и
относительную погрешности определения
напряжения.
Номинальное
значение напряжения 150 В.
Цена деления
данного предела измерения ЦД =
150 В / 150 дел. =
1 В/дел.
Измеренное значение
напряжения UИЗМ = 1 В/дел.×150
дел. =
150 В.
Абсолютная
погрешность измерения U
=
= 0,75 (В).
Относительная
погрешность измерения 0
=
= 0,5%.
Таким образом,
выбор наиболее подходящего предела
измерения приводит к уменьшению как
абсолютной, так и относительной
погрешности.
Масштабные
измерительные преобразователи (МИП)
При необходимости
измерения токов и напряжений, превышающих
верхний предел измерения используемого
прибора, используются МИПы.
Для приборов
постоянного тока в качестве МИП
используются шунты и добавочные
сопротивления. Для приборов переменного
тока – добавочные резисторы (для
напряжений до 30 кВ и частот от 10 Гц до
20 кГц) и измерительные трансформаторы
тока и напряжения.
Расчет шунта к
амперметру
При измерении тока
амперметр включается последовательно
с нагрузкой. Если амперметром требуется
измерить ток, превышающий верхний предел
измерения, то параллельно амперметру
включается шунт с сопротивлением RШ
(рис. 8). Шунт представляет собой
толстую константановую или манганиновую
пластину. Применение этих сплавов для
изготовления шунтов связано с тем, что
их сопротивление слабо зависит от
температуры.
Рис. 8.
На рис. 8 показана
схема подключения шунта RШ к
амперметру. RА – внутреннее
сопротивление амперметра, которое мало
по сравнению с сопротивлением нагрузки
RН для того, чтобы включение
амперметра последовательно с нагрузкой
не приводило к существенным изменениям
тока в цепи нагрузки. I – ток через
сопротивление нагрузки RН; IШ
– ток через шунт с сопротивлением RШ;
IА – ток через амперметр с
сопротивлением RА.
По первому правилу
Кирхгофа алгебраическая сумма токов
в узле равна нулю:
I =
IА
+ IШ
и, следовательно,
IШ = I
– IА.
Падение напряжения
между точками а и b:
Uаb
= IА·RА
= IШ·RШ.
Таким образом, для
того, чтобы с помощью данного амперметра
измерить ток I, сопротивление шунта
должно быть
|
RШ |
(8) |
где
I/IA
= n
– коэффициент
шунтирования,
показывающий, во сколько раз расширяется
предел измерения амперметра при
подключении шунта.
Фактический ток
в цепи определяется произведением
показаний прибора и множителя n.
Рис. 9.
Реальный шунт
(рис. 9) должен иметь четыре контакта: к
двум из них подключается прибор, а к
двум другим – соединительные провода
электрической цепи.
Пример 3.
Рассчитать шунт
к миллиамперметру на 10 mА с внутренним
сопротивлением 500 Ом, если надо измерить
ток 10 А.
Воспользуемся
формулой (8):
Соседние файлы в папке Переменный ток
- #
- #
- #
- #
- #
- #
Систематические погрешности (ошибки) обычно остаются постоянными на протяжении всей серии измерений. Например, при переключении шкалы вольтметра с одного предела на другой меняется его внутреннее сопротивление, что может внести в последующие измерения систематическую погрешность.
Систематические погрешности надо стараться отслеживать и учитывать, корректируя полученные результаты, т.е. исправляя их на необходимую величину. Однако обнаружение систематических погрешностей требует, как правило, дополнительных более точных или альтернативных экспериментов, проведение которых невозможно в рамках лабораторных работ. В этих случаях достаточно указать возможный источник ошибок.
Все остальные погрешности являются случайными.
Промахи — грубые ошибки, обычно они связаны с неправильным отсчетом по шкале прибора, нарушением условий эксперимента и т.д. Их надо отбросить. В сомнительных случаях вопрос о том, является ли данный результат промахом, решают с помощью повторного, если возможно, более точного эксперимента или привлекая математические методы обработки полученных результатов, изучение которых лежит за рамками излагаемого элементарного анализа оценки погрешностей.
Приборные погрешности определяются двумя факторами:
1. классом точности прибора, связанным с его устройством – элементной базой и принципом действия.
Абсолютная погрешность через класс точности оценивается следующим образом:
(Dx) к.т.= (g/100)A,
где g — класс точности в %, указанный на панели прибора,
А= Аmax – предел измерения для стрелочных приборов, либо А есть текущее значение для магазинов сопротивления, индуктивности, емкости;
2. ценой делений шкалы прибора:
(Dx) ц.д.= h,
где h – цена деления шкалы прибора, т.е. расстояние между ближайшими штрихами шкалы, выраженное в соответствующих единицах измерения.
Погрешности разброса возникают вследствие различия экспериментальных значений при многократном повторении измерений одной и той же величины. Простейший способ определения (Dх)р дает метод Корнфельда, который предписывает следующий образ действий, если физическая величина х измерена n раз:
1) имея х1 , …,хn – значений измеряемой величины х, выбираем из хmax и хmin и находим среднее значение х:
;
2) находим абсолютную погрешность Dxр =
3) Записываем результат в виде: с
, где a — доверительная вероятность того, что истинное значение измеренной величины находится на отрезке
.
Доверительная вероятность определяет собой долю средних значений х, полученных в аналогичных сериях измерений, попадающих в доверительный интервал. (Эта формула доказывается в теории ошибок.)
Недостатком метода Корнфельда является то обстоятельство, что вероятность приводимого результата определяется исключительно количеством n проведенных измерений и не может быть изменена посредством увеличения или уменьшения доверительного интервала ± Dх. Такую возможность предусматривает несколько более сложный метод расчета погрешностей Стьюдента [2,3,7]. Последовательность расчета погрешностей этим методом такова:
1) Вы измерили и получили несколько i = 1,…,m значений случайной
величины i. Сначала исключаем промахи, то есть заведомо неверные
результаты.
2) По оставшимся n значениям определяем среднее значение величины :
.gif)
3) Определяем среднеквадратичную погрешность среднего значения :

i
4) Задаемся доверительной вероятностью a. По таблице коэффициентов
Стьюдента (Приложение 1) определяем по известному значению
числа измерений n и доверительной вероятности a коэффициент
Стьюдента tan.
5) Определяем погрешность среднего значения величины (доверительный интервал)
D= tan s<X>
6) Записываем результат
= (
± D
) с указанием доверительной вероятности a.
В научных статьях обычно приводят доверительный интервал
D = s<X>,
соответствующий доверительной вероятности α =0,7. Такой интервал называется стандартным, при его использовании часто значение доверительной погрешности не приводят. Использование метода Стьюдента является необходимым, когда требуется знать значение физических параметров с заданной доверительной вероятностью (как в ряде лабораторных работ). На практике доверительная вероятность погрешности разброса выбирается в соответствии с доверительной вероятностью, соответствующей классу точности измерительного прибора.
Для большинства исследований, в которых не выдвигается жестких требований к вероятности полученных результатов, метод Корнфельда является вполне приемлемым.
В теории ошибок показывается, что результирующая погрешность , если все эти погрешности рассчитаны для одной и той же доверительной вероятности. На практике, т.к. суммарная погрешность округляется до одной значащей цифры, достаточно выбрать максимальную из трех вычисленных погрешностей, и если она в 3 или более раз превосходит остальные, принять ее за погрешность измеренной величины, при этом фактор, с которым связана эта погрешность и будет в данном случае определять собой точность (а вернее — погрешность) эксперимента (подробнее см. в работе [1]).
-
- Жалоба
- Поделиться
Связь класса точности и абсолютной погрешности? Объясните пожалуйста формулами.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Специалисты
- Специалисты
-
- Жалоба
- Поделиться
Связь класса точности и абсолютной погрешности? Объясните пожалуйста формулами.
Вы смотрели ГОСТ 8.401-80? В нём есть все нужные Вам формулы…
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- 3 месяца спустя…
-
- Жалоба
- Поделиться
Связь класса точности и абсолютной погрешности? Объясните пожалуйста формулами.
Класс точности средства измерения умножаем на предел измерений, делим на 100 %, получаем предел допускаемой погрешности СИ.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Связь класса точности и абсолютной погрешности? Объясните пожалуйста формулами.
Класс точности средства измерения умножаем на предел измерений, делим на 100 %, получаем предел допускаемой погрешности СИ.
Классы точности бывают трех типов.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- 1 месяц спустя…
-
- Жалоба
- Поделиться
Связь класса точности и абсолютной погрешности? Объясните пожалуйста формулами.
Класс точности средства измерения умножаем на предел измерений, делим на 100 %, получаем предел допускаемой погрешности СИ.
По этой формуле вообщето сегда получается 1.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Связь класса точности и абсолютной погрешности? Объясните пожалуйста формулами.
Класс точности средства измерения умножаем на предел измерений, делим на 100 %, получаем предел допускаемой погрешности СИ.
По этой формуле вообщето сегда получается 1.
В зависимости от исходных данных (класс точности и предел измерений (а фактически — разность между максимальным и минимальным значением измерительного диапазона) может всё что угодно получиться.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Ну например у меня МП-100 кл.точночти 1,5. предел измерений 1,6МПа. И получается 1,5*1,6/100% и получается 1. И всегда получается 1.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Ну например у меня МП-100 кл.точночти 1,5. предел измерений 1,6МПа. И получается 1,5*1,6/100% и получается 1. И всегда получается 1.
А не 0,024 МПа?
Класс точности 1,5 говорит о том, что предел допускаемой основной погрешности +/-1,5% от ВПИ.
Изменено 22 Июля 2011 пользователем Orlangur
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
нет,у меня манометр ТМ100 поверенный кл.точности 1,5 вот я им всё и поверяю..не знаю можно конечно так или нет..)
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
нет,у меня манометр ТМ100 поверенный кл.точности 1,5 вот я им всё и поверяю..не знаю можно конечно так или нет..)
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Специалисты
- Специалисты
-
- Жалоба
- Поделиться
нет,у меня манометр ТМ100 поверенный кл.точности 1,5 вот я им всё и поверяю..не знаю можно конечно так или нет..)
И много приборов Вы поверили?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
нет,у меня манометр ТМ100 поверенный кл.точности 1,5 вот я им всё и поверяю..не знаю можно конечно так или нет..)
И много приборов Вы поверили?
Походу я так понял нельзя так?))
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Специалисты
- Специалисты
-
- Жалоба
- Поделиться
Походу я так понял нельзя так?))
Что-то сомневаюсь, чтобы в качестве средств поверки был указан манометр класса точности 1,5…
Какие приборы Вы поверили? По какой методике поверки? Какие в ней приведены требования к средствам поверки?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
да просто помпа ручная с двумя выходами. На один поверенный вот это манометр на другой поверяемый..и всё. Правда инспектор должен только в понедельник приехать принимать поверку..а что не примет думаете?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Специалисты
- Специалисты
-
- Жалоба
- Поделиться
Всё быть может, но с таким «эталоном» не должен… Как понимаю, и кондиционера у Вас нет — стало быть, и условия поверки у Вас не будут выдержаны — жарковато сейчас…
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
да просто помпа ручная с двумя выходами. На один поверенный вот это манометр на другой поверяемый..и всё. Правда инспектор должен только в понедельник приехать принимать поверку..а что не примет думаете?
судя по тому, что Вы ранее описали, не примет… Открывайте методику поверки и читайте — какие СИ заложены в качестве средств поверки Ваших приборов и следуйте ей (можно использовать не только конкретные модели, но и аналоги, при условии выполнения требований МП). Посмотрите, например, МИ 2124-90, возможно — это Ваш случай. И еще момент — какая помпа у Вас (стационарная или нет, т.к. стрелочные манометры должны устанавливаться в определенном положении при поверке, а с той, которая держится в руках при накачке, это проблематично).
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
нет,у меня манометр ТМ100 поверенный кл.точности 1,5 вот я им всё и поверяю..не знаю можно конечно так или нет..)
Поверять МП-100 с помощью ТМ-100…
Всё быть может, но с таким «эталоном» не должен… Как понимаю, и кондиционера у Вас нет — стало быть, и условия поверки у Вас не будут выдержаны — жарковато сейчас…
Где как, где как Александр Александрович.
Изменено 22 Июля 2011 пользователем Orlangur
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Специалисты
- Специалисты
-
- Жалоба
- Поделиться
Где как, где как Александр Александрович.
У нас пока 29 в тени, в Астрахани 33, а у Вас, Сергей Иванович, в Норильске 9 (и даже с плюсом )
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
да просто помпа ручная с двумя выходами. На один поверенный вот это манометр на другой поверяемый..и всё. Правда инспектор должен только в понедельник приехать принимать поверку..а что не примет думаете?
судя по тому, что Вы ранее описали, не примет…
Открывайте методику поверки и читайте — какие СИ заложены в качестве средств поверки Ваших приборов и следуйте ей (можно использовать не только конкретные модели, но и аналоги, при условии выполнения требований МП). Посмотрите, например, МИ 2124-90, возможно — это Ваш случай. И еще момент — какая помпа у Вас (стационарная или нет, т.к. стрелочные манометры должны устанавливаться в определенном положении при поверке, а с той, которая держится в руках при накачке, это проблематично).
Где мне взять эти методики где сказанно какие СИ заложены в качестве поверки???(
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
У нас пока 29 в тени, в Астрахани 33, а у Вас, Сергей Иванович, в Норильске 9 (и даже с плюсом
)
Угу, я вот то же думаю, не пора ли пуховик из шкафа доставать.
С полностью задраенными окнами и дверями, к обеду температура в лаборатории поднимается до +22, это максимум что удаётся добиться если не включать обогреватели.
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Ещё вопрос..у нас есть акредитованная лаборатория с оборудованием. Хотели заняться поверкой сигнализаторов загазованности но для этого обязательно нужно приглашать после настройки гос.поверителя из ЦСМ т.к. он говорит что сигнализаторы загазованности может поврять только гос.поверитель и выдавать свидетельство о поверке. Так ли это? и есть ли список СИ которые могут поверять просто акредитованные фирмы без участия ЦСМ с выдачей своих заключений и со своими штампами лаборатории?
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Здравствуйте! Помогите разобраться!
Есть два СИ. У одного в характеристиках стоит «Precision: 0,5% of reading», а у второго «Погрешность измерения: 2% от диапазона измерения». Как можно сравнить эти СИ по точности измерений. Нигде не смогу найти соотношений этих характеристик, только в книги «Метрология» Кузнецова, Исаев, Шайко написано про точность (не про прецизионность) «Значение точности иногда определяют величиной, обратной модулю относительной погрешности». Возможно неверно поставлена задача, и сравнение СИ не возможно…
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
- Специалисты
- Специалисты
-
- Жалоба
- Поделиться
Здравствуйте! Помогите разобраться!
Есть два СИ. У одного в характеристиках стоит «Precision: 0,5% of reading», а у второго «Погрешность измерения: 2% от диапазона измерения». Как можно сравнить эти СИ по точности измерений. Нигде не смогу найти соотношений этих характеристик, только в книги «Метрология» Кузнецова, Исаев, Шайко написано про точность (не про прецизионность) «Значение точности иногда определяют величиной, обратной модулю относительной погрешности». Возможно неверно поставлена задача, и сравнение СИ не возможно…
У первого СИ нормирована относительная погрешность, а у второго — приведённая…
При одинаковых диапазонах измерений первое СИ точнее…
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
-
- Жалоба
- Поделиться
Странно, но1,5*1,6/100% = 0,024МПа. Откуда единица получается?
Изменено 29 Июля 2011 пользователем Лилу
- Цитата
Ссылка на комментарий
Поделиться на других сайтах
Для получения количественной информации о физических величинах применяются средства измерения (СИ) — приборы различной степени сложности, от простейшей линейки до современных цифровых осциллографов и электронных микроскопов. При этом ни один из существующих приборов объективно нельзя признать идеально точным. Измеренная величина всегда разнится с истинным значением на некоторую ошибку — погрешность, обусловленную параметрами самого прибора и измерительными условиями (температура, влажность, давление).
- Определение класса точности
- Сколько КТ существует и как они обозначаются
- Какой ГОСТ систематизирует понятие точности применительно к измерительным приборам?
- Как определить КТ электроизмерительного прибора
- Для чего нужна поверка приборов
- На всякий случай о другом «классе точности»
- Заключение
Производители СИ стремятся добиться максимально возможной точности для так называемых прецизионных (научных) приборов. Для многих сфер применения вполне допустимый контроль величин с точностью, не превышающей разумные для данной области пределы. Предсказуемая величина погрешности задаётся с помощью такого параметра, как класс точности (КТ).
Определение класса точности
Поскольку регистрация физической величины не может быть произведена с абсолютной точностью, то, следовательно, любое проведённое измерение содержит некую погрешность. Иногда в этом контексте используется термин «ошибка измерения», который говорит не о неправильном результате измерения, а лишь о наличии погрешности. Различают три вида числовых погрешностей
1. Абсолютная погрешность: Δ=хд-хизм, где:
- хд — действительное (истинное) значение измеряемой величины;
- хизм — измеренное значение.
2. Относительная погрешность: δ=(Δ/хд)*100%.
3. Приведённая погрешность: γ=(Δ/хн)*100%, где хн — нормирующее значение, равное диапазону измерения СИ, то есть измерительной шкале.
Когда в процессе измерений задействовано несколько приборов, то определяется обобщенная (совокупная) характеристика. Все погрешности, выраженные в одних единицах, суммируются.
В зависимости от условий эксплуатации погрешность может быть основной и дополнительной:
- Основная погрешность — это погрешность СИ при нормальных условиях, которые соответствуют ГОСТ 8.395-80 «Нормальные условия измерений при поверке».
- Дополнительная погрешность — это добавочная погрешность СИ, возникающая вследствие выхода за нормативные пределы, установленные данным стандартом. Например, могут быть превышены пределы допустимой температуры окружающей среды, влажности воздуха, атмосферного давления, частоты и напряжения питающей сети.
Общая погрешность прибора зависит от длительности и условий эксплуатации, а поскольку её величина в каждом данном измерении неизвестна, то изготовитель обычно указывают диапазон (–θх, +θх) возможных значений погрешности прибора или полосу погрешностей, которую определяют экспериментально не для конкретного прибора, а для партии приборов данной серии. Границу θх полосы погрешностей прибора называют нормированным значением приборной погрешности или пределом допускаемой погрешности данного СИ.
Точность СИ — свойство устройства обеспечивать измерения с минимальной погрешностью (близкой к нулю). В качестве единого, обобщённого параметра для СИ введено понятие КТ, обусловленное пределами допускаемых основной и дополнительной погрешностей, а также прочими свойствами прибора, от которых зависит его точность.
КТ прибора — это число, соответствующее максимально допустимой нормами погрешности. КТ выражается в процентах от верхнего предела измерительной шкалы устройства.
Сколько КТ существует и как они обозначаются
В соответствии с ГОСТ 8.401-80, КТ обозначаются буквой латинского алфавита в сочетании с числовым (цифровым) индексом. Чем меньше число и выше место в алфавите латинской буквы, тем больше значение КТ. Обозначение КТ наносится на прибор в виде числа, вписанного в окружность, указывающего на величину разброса (плюс-минус) погрешностей измерений в процентах. Например, число 1,6 означает относительную погрешность ±1,6%. Если дополнительно имеется пиктограмма в виде «галки», то это означает, что весь диапазон шкалы необходимо применять для определения погрешности.
Далее идут следующие классы:
- 0,1 и 0,2 — самые высокие (прецизионные) классы для научных приборов;
- 0,5 и 0,6 — для бытовых устройств средней ценовой категории;
- 1,5 и 2,5 — для приборов с пониженной точностью измерения;
- В случае отсутствия на шкале прибора информации о КТ абсолютную погрешность приравнивают к половине наименьшего деления шкалы.
На высокоточных приборах маркер КТ может отсутствовать. Идентификация точности подобных устройств выполняется особыми знаками.
Какой ГОСТ систематизирует понятие точности применительно к измерительным приборам?
Основным нормативным актом, устанавливающим понятие КТ, является ГОСТ 8.401-80 «Классы точности средств измерения. Общие требования». Несмотря на то что нормативный акт был введён в действие в СССР в прошлом веке, его действие было подтверждено переизданием в октябре 2010 г. без каких-либо поправок. Это говорит о том, что базовые принципы и понятия сохранили свою актуальность.
В стандарте сформулированы общие положения ранжирования СИ на точностные классы, методики нормирования метрологических параметров и обозначения КТ:
- Если СИ, предназначенное для фиксации только одной физической величины, имеет два или более диапазона измерений, то ему может присваиваться два и более КТ.
- Если с помощью СИ может измеряться две или более физические величины (например, ток и напряжение), то могут быть присвоены различные КТ для каждой измеряемой величины.
- СИ должны соответствовать требованиям к метрологическим характеристикам, полученным при присвоении им КТ как при приёмке их на производстве, так и в процессе последующей эксплуатации.
- КТ присваиваются СИ после проведения государственных испытаний.
Как определить КТ электроизмерительного прибора
Для определения КТ прибора необходимо осмотреть корпус прибора и инструкцию, где обнаружится число, вписанное в окружность, например, 2. Это означает, что относительная погрешность прибора составляет ±2,0%. КТ нанесён на корпус или шкалу устройства. Если обозначение отсутствует, то это означает, что КТ превышает 4%.
Для чего нужна поверка приборов
КТ позволяет установить диапазон, в котором находится погрешность данного прибора. Величина диапазона погрешности не является константой и в силу различных причин (например, износа отдельных деталей прибора) может увеличиваться, что приводит к недостоверным результатам измерений. Для предотвращения таких ошибок введена процедура периодической поверки приборов.
Для организации процесса поверки должны быть обеспечены климатические условия, близкие к идеальным. Как правило, поверка проводится государственными метрологическими службами или в метрологических отделах предприятий, изготовивших данный прибор.
Различают первичную и периодическую поверки:
- Первичная проводится сразу после изготовления прибора с выдачей соответствующего сертификата.
- Периодическая поверка проводится, как правило, не реже одного раза в год. Для высокоточных (прецизионных) СИ могут устанавливаться меньшие межповерочные сроки.
Для популярных нынче бытовых счетчиков учёта электроэнергии и воды сроки поверки существенно больше:
- На холодную воду — раз в 6 лет.
- На горячую воду — раз в 4 года.
- На электросчётчики в зависимости от модели срок поверки может превышать 10 лет.
На всякий случай о другом «классе точности»
Следует упомянуть, что понятие КТ точности используется также в области, связанной с качеством поверхности металла после обработки на токарных, фрезерных и других станках. Несмотря на одинаковое словосочетание, речь идёт о таких характеристиках, как степень шероховатости, категории чистоты обработки металлов. Если поисковики в интернете будут выдавать ссылки на обе темы, то это не более, чем «однофамильцы».
Заключение
КТ СИ позволяет осуществить оптимальный выбор прибора для решения конкретной задачи. Для проведения лабораторных, научных измерений понадобится аппаратура самой высокой или прецизионной точности. Хороший уровень точности электросчётчика поможет контролировать потребление энергии, не переплачивая лишних средств. Для проведения простых электромонтажных работ, связанных с контролем качества монтажа, наличия заземления, измерений напряжений и токов в жилом помещении, вполне сгодится бюджетный мультиметр с невысоким КТ.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 2 чел.
Средний рейтинг: 3 из 5.
Аннотация: Рассмотрим подробный порядок операций, выполняемых при обработке результатов измерений. Содержание всех описываемых действий рассмотрено в предыдущих разделах. Проводимые расчеты основываются на предположении о нормальном распределении погрешностей, когда систематические погрешности уже учтены на предыдущих этапах работы с экспериментальными данными.
Нормирование погрешностей средств измерений
Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.
Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.
Обычно нормирующее значение принимают равным:
- большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
- сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
- длине шкалы или её части, соответствующей диапазону измерения, если шкала существенно неравномерна (например, у омметра);
- номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
- модулю разности пределов измерений, если принята шкала с условным нулём (например, для температуры), и т.д.
Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.
Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.
Указанное нормирование является гарантией взаимозаменяемости средств измерений.
Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.
Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.
Подход к нормированию погрешностей средств измерений заключается в следующем:
- в качестве норм указывают пределы допускаемых погрешностей, включающие в себя и систематические, и случайные составляющие;
- порознь нормируют все свойства средств измерений, влияющие на их точность.
Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.
Классы точности средств измерений
Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401–80.
Пределы допускаемой основной погрешности, определяемые классом точности, – это интервал, в котором находится значение основной погрешности СИ.
Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.
Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.
Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: 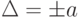
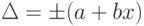
a, b – положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей.
В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, «Класс точности М», а на приборе – буквой «М». Для обозначения используются прописные буквы латинского алфавита или римские цифры, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Пределы допускаемой приведенной основной погрешности определяются по формуле 

Нормирующее значение xN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, равно модулю разности пределов измерений.
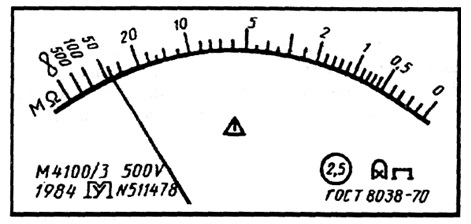
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка 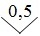
Рис.
3.1.
Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой
В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).
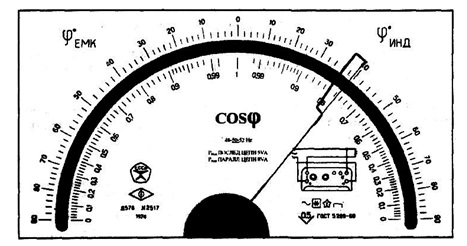
Рис.
3.2.
Лицевая панель амперметра класса точности 1,5 с равномерной шкалой
В том случае если абсолютная погрешность задается формулой 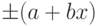
![delta=Delta/x=pm[c+d(|x_{k}/x|-1)]](https://intuit.ru/sites/default/files/tex_cache/3898a996678dab895193a1773d11ffc8.png) |
( 3.1) |
где с, d – отвлеченные положительные числа, выбираемые из ряда: 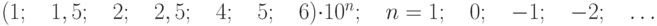
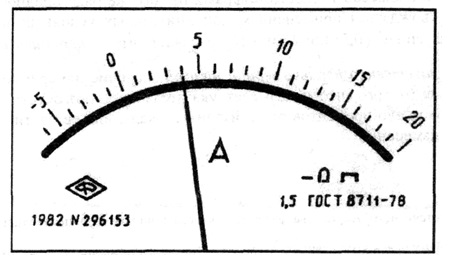
Рис.
3.3.
Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой
Пределы допускаемой относительной основной погрешности определяются по формуле 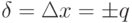
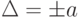
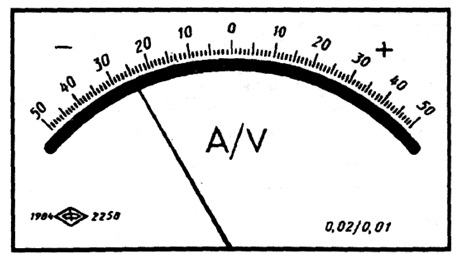
Рис.
3.4.
Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой
В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.
Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.
Контрольные вопросы
- Поясните, что такое класс точности СИ.
- Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
- Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений.
- Как нормируются приборы по классам точности?
- Какие метрологические характеристики описывают погрешность средств измерений?
- Как осуществляется нормирование метрологических характеристик средств измерений?