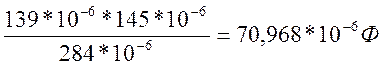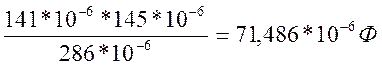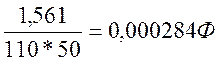Лабораторная работа № 1.
Расчет погрешностей емкости с помощью коэффициента Стьюдента.
Расчет погрешности измерения мощности и сопротивления
Цели занятия:
-
Общеобразовательная – Умение решать задачи по теме погрешности.
-
Развивающая — Углубление знаний .
-
Воспитательная – Проверить сформированность качеств знаний.
Теоретическая часть
Отклонение результата измерения от истинного измеряемой величины называют погрешностью измерения.
Абсолютная погрешность измерения ΔА равна разности между результатом измерения Ах и истинным значением измеренной величины А:
ΔА = Ах – А (1)
Действительная относительная погрешность представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины, выраженное в процентах:
(2)
Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению исследуемой величины,
т .е. к показанию прибора
(3)
Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к максимальному значению измерительного прибора
(4)
Для приборов с двухсторонней шкалой Амакс определяется как сумма абсолютных величин положительного и отрицательного пределов измерения.
Если шкала начинается не с нуля, а с какого-то минимального значения, то Амакс равно разности между конечным и начальным значениями шкалы.
Случайными называются погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности нельзя исключить опытным путем, т. к. они возникают случайно. Для того, чтобы исключить случайные погрешности производят неоднократные измерения и определяют среднее арифметическое из полученных значений, определяемое как
,
где а1, а2, …, аn – результаты отдельных измерений;
n – число измерений.
Для оценки точности результата измерений необходимо знать закон распределения случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдения Р:
где Р1 = а1 – Аср; Р2 = а2 – Аср; Рn = аn – Аср.
Этот способ определения доверительных интервалов справедлив толко для больших количеств измерений (20-30). Для небольшого количества измерений для определения доверительного интервала нужно пользоваться коэффициентами Стьюдента tn, которые зависят от задаваемой доверительной вероятности Р и количества измерений n.
Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат измерения можно записать так:
А = Аср tn
Контрольное задание
Задача 1. Для уменьшения влияния случайных погрешностей на результат измерения, емкость конденсатора С измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные погрешности имеют нормальный закон распределения, определить на основании заданного количества измерения (табл. 1, табл. 2):
-
Действительное значение измеряемой емкости;
-
Среднюю квадратическую и максимальную погрешности однократного измерения;
-
Доверительный интервал для результата измерения при доверительной вероятности Рд (табл.3).
-
Имеется ли систематическая составляющая в погрешности измерения емкости и с какой доверительной вероятностью ее можно оценить, если принять в качестве действительного значения емкости значения Сср (таб.1, таб.2).
Таблица 1
|
№№из мере ния |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
С, пФ |
2430 |
2440 |
2435 |
2438 |
2439 |
2441 |
2438 |
2440 |
2441 |
2439 |
|
№№из мере ния |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
С, пФ |
2500 |
2564 |
2550 |
2480 |
2450 |
2528 |
2440 |
2556 |
2562 |
2550 |
Таблица 2
|
№ вари анта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
№№из мере ния |
1-3 |
6-10 |
2-6 |
1-4 |
2-8 |
2-4 |
7-9 |
4-7 |
3-5 |
5-7 |
|
С0, пФ |
2428 |
2429 |
2430 |
2432 |
2436 |
2424 |
2440 |
2441 |
2440 |
2442 |
|
Рд |
0,89 |
0,9 |
0,99 |
0,95 |
0,85 |
0,94 |
0,97 |
0,9 |
0,96 |
0,98 |
|
№ вари анта |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
№№из мере ния |
11-14 |
12-15 |
16-19 |
13-16 |
14-17 |
17-20 |
15-18 |
11-13 |
12-16 |
15-20 |
Примечание. Количество и номера наблюдений значений емкости для каждого варианта определяются данными таблицы 1 и 2, например для варианта 1 следует взять результаты измерений 1-3 табл.2.
Указания к решению
-
Для удобства выполнения и проверки расчетов по заданию целесообразно представить промежуточное вычисление в виде таблицы
Таблица 3
|
№№ пп |
№№ наблюдения |
Сi, пФ |
Сi – Cср, пФ |
(Сi – Cср)2, пФ |
|
1 2 3 4 |
||||
|
Сумма Сi, пФ |
Сумма Сi – Cср, пФ |
Сумма (Сi – Cср)2, пФ |
-
Далее определить среднеквадратическую погрешность :
-
По таблице (4) определить коэффициент Стьюдента.
-
В конце решения следует записать окончательный (с учетом округления) результат измерения в требуемой форме, например: С = 1231
12 пФ, Р
Задание 2.. Используя формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей измерения мощности и сопротивления. Расчет выполняется в соответствии с вариантами указанными в задании.
Задача 1. Для определения сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены напряжение и ток. Зная основные параметры измерительных приборов (амперметра и вольтметра), определить ошибку косвенных измерений мощности и сопротивления.
Пример. Определить абсолютную и относительную погрешности измерения мощности, выделяемой на резисторе, если известны показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности КА = 1,0, номинальное значение шкалы 10 МА, показания 6 МА.
Решение:
-
Определяем мощность Р = U * I ( Вт)
-
Абсолютная ошибка измерения напряжения, В
-
Абсолютная ошибка измерения тока, М А
-
В соответствии с таблицей абсолютная ошибка измерения мощности, Вт
Относительная ошибка
-
Формула для сопротивления R = U / I
-
-
Относительная погрешность
Примечание:
-
Для вычисления погрешностей измерения мощности используются формулы 1,2,3,4,
-
Для вычисления погрешностей измерения сопротивления используются формулы 2,3,5,6,7.
Формулы для выполнения контрольной работы и письменного экзамена по предмету «Электрические измерения»
1.Абсолютная погрешность измерения
ΔА = Ах – А
2. Действительная относительная погрешность
3 Номинальная относительная погрешность
4.Приведенная относительная погрешность
-
Сопротивление шунта
RШ = RА / Р-1 (Ом)
6 .Добавочное сопротивление
RДОБ = RV * ( Р-1) (Ом)
-
Коэффициент трансформации по току:
Кi = I 1/ I2
8 Коэффициент трансформации по напряжению:
КU = U 1 /U2
9. Ток сети:
IC = Ki * I (А)
-
Напряжение сети:
UC = KU* U (В)
-
Активная мощность сети:
PC = Ki * KU *P (Вт)
-
Реактивная мощность сети :
Q = U*I* sinφ (Вар)
-
Полная мощность сети:
S = U*I (ВА)
14. Полное сопротивление сети :
ZC = UC/ IC (Ом)
15 Коэффициент мощности:
Cosφ = PC / SC
-
Номинальная постоянная счетчика:
СНОМ = W НОМ/ NНОМ (Вт*с/об)
-
Действительная постоянная счетчика:
С = (U*I*t / N) (Вт*с/об)
18 Поправочный коэффициент:
К= С / СНОМ
-
Относительная погрешность счетчика
Β = [(СНОМ – С) /CНОМ] * 100%
ОПРЕДЕЛЕНИЕ
ЕМКОСТИ КОНДЕНСАТОРА
Цель работы
Целью
данной работы является изучение законов
электростатики и одного из методов
измерения емкости конденсатора.
Краткая теория
Конденсатором
называется система, состоящая из двух
проводников, разделенных слоем
диэлектрика, в которой обеспечивается
сильная электрическая связь между
накопленными на этих проводниках
зарядами. Проводники, образующие
конденсатор, называются обкладками. В
зависимости от формы обкладок конденсаторы
бывают сферические, цилиндрические,
плоские. За заряд конденсатора принимается
заряд одной обкладки, взятый по абсолютной
величине.
Емкостью
конденсатора
называется скалярная физическая
величина, характеризующая способность
конденсатора накапливать электрический
заряд и численно равная заряду, который
должен быть перенесен с одной обкладки
конденсатора на другую, чтобы разность
потенциалов между ними изменилась на
единицу.
.
(2.03.1)
Емкость конденсатора
зависит от формы и размеров его обкладок,
диэлектрической проницаемости материала
диэлектрика и не зависит от свойств
проводников, из которых изготовлены
обкладки. Единицей измерения электрической
емкости в системе СИ является фарад
(Ф = Кл/В).
Емкость конденсатора
может быть измерена различными методами.
В данной работе использован метод,
основанный на измерении накопленного
конденсатором заряда. При этом емкость
рассчитывается в соответствии с
определением (2.03.1).
Д
ля
определения емкости неизвестного
конденсатора Cx
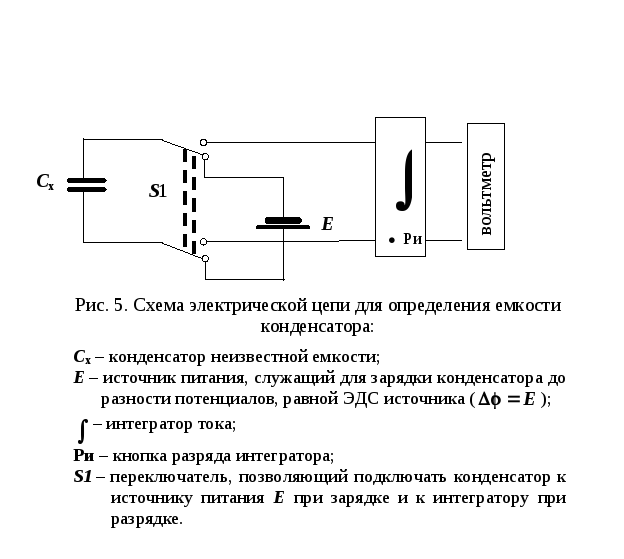
собирают цепь по рис. 5.
При подключении
к источнику питания конденсатор
заряжается. Заряд, накапливаемый на
обкладках конденсатора, при неизменном
значении разности потенциалов
пропорционален его емкости. В стационарном
состоянии разность потенциалов равна
ЭДС источника E.
. (2.03.2)
При разрядке
конденсатора в цепи протекает убывающий
во времени электрический ток. По
определению, сила тока
. (2.03.3)
Нас интересует
заряд Q,
т. е. необходимо вычислить
.
Для этого служит
электронное устройство, называемое
интегратором.
При подключении
заряженного конденсатора к интегратору,
который в свою очередь подключен к
вольтметру, в цепи интегратора протекает
ток. Напряжение на выходе интегратора
пропорционально интегралу от силы тока
на его входе, т. е. заряду:
,
(2.03.4)
где b – постоянная
интегратора (она неизвестна).
Напряжение Ux
измеряется цифровым вольтметром.
Сопоставляя формулы (2.03.2) и (2.03.4), получаем:
. (2.03.5)
В полученном
выражении постоянная интегратора b
и разность
потенциалов на конденсаторе E
являются неизвестными. Поэтому только
на основании (2.03.5) определить Cx
оказывается невозможным. Для того, чтобы
избежать определения величин b
и Е,
в данной
работе применяется хорошо известный
метод калибровки. Включим вместо
конденсатора Cx
конденсатор с известной емкостью C1
и проведем аналогичные измерения. При
этом на выходе интегратора получим
отсчет U1
и по аналогии с (2.03.5) запишем:
.
(2.03.6)
Разделив друг на
друга равенства (2.03.5) и (2.03.6), получим
, (2.03.7)
где Ux
и U1 – показания
вольтметра при разряде неизвестного и
известного конденсаторов соответственно
(максимальные значения показаний на
индикаторном табло вольтметра); C1
емкость известного конденсатора.
Выполнение работы
Необходимые
приборы:
конденсатор с известной емкостью
(С1 = 4700 пФ ± 10 %);
конденсатор с неизвестной емкостью Cx,
которая определяется в данной работе;
источник постоянного тока с эдс E;
переключатель; интегратор; цифровой
вольтметр. Все элементы схемы, кроме
вольтметра, смонтированы внутри
лабораторного стенда.
Схема
экспериментальной установки для
определения емкости конденсатора
показана на рис. 6 и на панели лабораторного
стенда.
Порядок выполнения
работы
-
Подготовьте
цифровой вольтметр к работе согласно
инструкции по эксплуатации, находящейся
на лабораторном столе. -
Подготовьте схему
для измерения емкости неизвестного
конденсатора Cx,
для чего гибкими перемычками попарно
соедините клеммы 1 и 3, 5 и 7, 6 и 8, а выходные
клеммы интегратора 9 и 10 соедините с
входом вольтметра (см. рис. 6). -
Включите лабораторный
стенд тумблером, расположенным в левой
части передней стенки. -
П
ереключателем
S1
конденсатор Cx
подключается к источнику E
(в верхнем положении) и заряжается
(время полной зарядки конденсатора ~10
с). -
Интегратор
разряжается нажатием кнопки Ри.
Кнопка Ри
на интеграторе предназначена для его
принудительного разряда и подготовки
прибора к новому измерению. -
Затем переключателем
S1
неизвестный конденсатор подключается
к интегратору (в нижнем положении).
Поскольку используемый в данной работе
интегратор не является идеальным,
происходит его самопроизвольный разряд
по окончании процесса интегрирования.
Поэтому в качестве Ux
следует принимать максимальное значение
показаний на табло вольтметра. Показание
Ux
на табло вольтметра записывается в
табл. 3.1. -
Измерения показаний
вольтметра при разрядке неизвестного
конденсатора проводят 5 раз. -
После этого клеммы
1 и 3 размыкаются, а клеммы 2 и 4 замыкаются
(см. рис. 6). При этом вместо неизвестного
конденсатора в цепь включается
конденсатор с известной емкостью C1.
С ним проводят пять измерений, согласно
вышеописанному порядку. Результаты
также записываются в табл. 3.1. -
Конденсаторы CX
и C1
соединяются параллельно путем добавления
перемычки между клеммами 1 и 3. Проводится
пять измерений для цепи из двух
параллельно соединенных конденсаторов. -
Конденсаторы
CX
и C1
соединяются
последовательно, для чего удаляют
перемычки 1 — 3, 2 — 4 и устанавливают
перемычку между клеммами 2 и 3. Проводятся
пять измерений для цепи из двух
последовательно соединенных конденсаторов.
Все результаты также записываются в
табл. 3.1.
Таблица
3.1
Результаты измерений
|
Номер опыта |
Неизвестная емкость Cx |
Известная емкость |
Параллельное |
Последовательное |
||||
|
Ux, В |
Ux, В |
U1, В |
U1, В |
Uпар, В |
Uпар, |
Uпос, В |
Uпос, В |
|
|
1 |
||||||||
|
2 |
||||||||
|
3 |
||||||||
|
4 |
||||||||
|
5 |
||||||||
|
Средние значения |
|
|
|
|
|
|
|
|
Определяются
средние значения показаний вольтметра
Ux,
U1,
Uпар,
Uпос.
По этим средним значениям вычисляются
опытные значения величин емкостей.
; (2.03.8)
;
(2.03.9)
.
(2.03.10)
Теоретическое
значение емкости параллельного cоединения
конденсаторов вычисляется следующим
образом:
. (2.03.11)
Емкость
последовательного соединения конденсаторов
рассчитывается по следующей формуле:
, (2.03.12)
из которой следует
расчетная формула для вычисления емкости
последовательного соединения
конденсаторов:
. (2.03.13)
Используя
значение
,
рассчитанное по формуле (2.03.8), вычислите
по формулам (2.03.12) и (2.03.13) значения
емкостей параллельного и последовательного
соединений конденсаторов. Результат
расчетов сравните с экспериментальными
значениями, определенными по формулам
(2.03.9) и (2.03.10).
Вычисление
погрешностей
Средние относительные
погрешности емкостей вычисляются по
формулам:
; (2.03.14)
; (2.03.15)
.
(2.03.16)
Средние абсолютные
погрешности емкостей:
; (2.03.17)
;
(2.03.18)
.
(2.03.19)
Окончательные
результаты измерения емкостей
конденсаторов записывается в виде:
; (2.03.20)
;
(2.03.21)
. (2.03.22)
Сравните
значения емкостей параллельного и
последовательного соединений
конденсаторов, полученные опытным
путем, и рассчитанные по теоретическим
формулам (2.03.11) и (2.03.13). Если разница
между теоретическими и опытными
значениями емкостей параллельного и
последовательного соединения конденсаторов
не превышает соответствующей абсолютной
погрешности, можно считать, что данный
метод удовлетворительно обеспечивает
проведение измерений емкостей.
КОНТРОЛЬНЫЕ
ВОПРОСЫ
-
Дайте определение
емкости конденсатора. -
Объясните по
схеме цепи назначение используемых
приборов. -
Подробно объясните
принцип определения емкости в данной
работе. -
Выведите расчетные
формулы для определения емкостей Cx,
Cпар,
Cпос. -
Каковы единицы
измерения емкости? -
Изобразите схемы
параллельного и последовательного
соединений конденсаторов. Запишите
формулы для результирующих емкостей. -
Выведите формулы
для расчета погрешностей Cx,
Cпар,
Cпос.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Иродов И.Е. Основные законы
электромагнетизма. М.: Высшая школа,
1983. 51 – 54 с.
Калашников С. Г. Электричество. М.:
Наука, 1970. 77 – 91с.
Савельев И. В. Курс общей физики. Т
2. М.: Наука, 1982. 87 – 89 с.
Физический практикум. Электричество
и оптика /Под ред. В. И. Ивероновой. М.:
Наука, 1968. 815 с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эти погрешности значительно меньше случайных, в чем можно убедиться после обработки экспериментальных данных, и поэтому имиможно пренебречь.Случайные погрешности. Разброс результатов повторных измерений величины U (табл. 3)указывает на их случайный характер. Причины, приводящие к такому разбросу, могутбыть разные. Длительность времени зарядки или разрядки складывается из следующего:а) длительности замкнутого состояния контактов кнопки «Запуск»; б) времени срабатывания реле; в) постоянной времени R3C1 цепи электронной схемы блока управления.Длительность замкнутого состояния контактов кнопки «Запуск» зависит от реакции экспериментатора, которая от опыта к опыту оказывается различной. Время срабатыванияреле имеет разброс, например, в силу колебания напряжения питания его обмотки и т.п.Значение постоянной времени R3C1 цепи блока управления может иметь разброс из-за изменений сопротивления R3 и емкости C1, вызванных колебанием температуры.Таким образом, погрешность измерения напряжения на конденсаторе носит в основномслучайный характер.2.
Оценить случайную погрешность единичного измерения напряжения на конденсаторе.Используя данные табл. 3, вычислить среднюю квадратическую погрешность единичногоизмерения ‘σU =1(U i − U )2 ,ån −1 iгде n — число измерений напряжения, соответствующего первой точке на кривой зарядкиконденсатора.Будем считать, что средние квадратические погрешности единичных измерений всех остальных точек кривой зарядки и разрядки не превышают найденной погрешности для первой точки, так как измерения проводятся тем же методом, с помощью того же вольтметраи тем же экспериментатором.3. Построить графики U=f(t) зарядки и разрядки конденсатора на миллиметровой бумаге водной системе координатных осей. На обоих графиках для первой экспериментальнойточки указать погрешность единичного измерения при помощи отрезка, длина которого ввыбранном масштабе равна 2σU .
Графическим способом определить постоянную времени цепи зарядки τЗАР и разрядки τРАЗ , Найденные значения внести в табл. 1 и 2.4. Проверить, является ли полученные экспериментально зависимости U=f(t) экспоненциальными, т.е. соответствуют ли они уравнениям (5) и (10), Для решения поставленной задачи — проверки соответствия наблюдаемой нелинейной зависимости теоретической поступают так. Строят график зависимости между измеряемыми величинами в функциональном масштабе, выбранном так, что теоретическая зависимость в этом масштабе имеетвид прямой линии. Если построенный график также представляет прямую линии, то наблюдаемая функциональная зависимость соответствует теоретической.Уравнения (5) и (10) эквивалентны уравнениям (4) и (9).
Эти уравнения являются уравнениями прямых линий в системе координат, в которой по оси ординат откладывается либоln(ε-U), либо lnU, а по оси абсцисс — время t . Наклон этих прямых определяется постоянной времени τ цепи зарядки и разрядки. Действительно, tgα = -1/τ где α — угол наклона.Указанные графики рекомендуется строить на специальной бумаге с полулогарифмической координатной сеткой, которая имеет по оси абсцисс линейный масштаб, а по оси ординат — логарифмический, причем отрезки, откладываемые по этой оси, пропорциональнынатуральному логарифму измеряемой величины, но указываемые цифры соответствуютсамой величине. На графиках, для всех экспериментальных точек, указать погрешностьединичного измерения, как указано в п.3.
Если полулогарифмической бумаги нет, то графики нужно построить на обычной миллиметровой бумаге, предварительно вычисливln(ε-Ui ) и lnUi . На основании построенных графиков сделать заключение о соответствииэкспериментальных зависимостей теоретическим и записать его в тетрадь.5. Определить значения τЗАР и τРАЗ по формуламtК − tНtК − tН(А)τ ЗАР =;,τ ЗАР =ln(ε − U Н ) − ln(ε − U К )ln U − ln UНКгде (tН , ln(ε-UН)), (tК , ln(ε-UК)) и (tН , lnUН), (tК , lnUК) – координаты первой и последнейточек соответственно на графике ln(ε-U)=f(t) зарядки и графике lnU=f(t) разрядки конденсатора.
Полученные значения сравнить с п. 3.6. Графически оценить случайную погрешность ∆τ измерения τЗАР и τРАЗ . Для этого провести относительно экспериментальных точек две прямые с максимально и минимальновозможным наклоном к оси времени (рис. б). По построенным прямым, используя формулы (А), найти максимальное τMAX и минимальное τMIN значения постоянной времени цепи.
Величину случайной погрешности ∆τ измерения постоянной времени цепи определитькак∆τ =τ MAX − τ MIN2Найденная таким способом погрешность является максимально возможной. Отметим, чтосуществуют аналитические методы проведения «наилучшей» прямой относительно экспериментальных точек и нахождения погрешности наклона (постоянной времени цепи) этойпрямой. К их числу, например, относится метод наименьших квадратов.U/В6.04.02.01.00.80.60.40.20.10102030405060t/cРис.67. Записать окончательный результат в видеτЗАР±∆τЗАР ; τРАЗ±∆τРАЗКОНТРОЛЬНЫЕ ВОПРОСЫ1.
Как называется величина RС ? Как графически ее найти? Какова размерность RС в системе СИ?2. Как меняется ток во времени при зарядке и разрядке конденсатора?3. Нарисовать вид зависимости от времени напряжения на конденсаторе при его разрядкес учетом того, что за время снятия показаний с вольтметра конденсатор частично разряжается.4. Какие виды ошибок обусловливают погрешность определения значения постояннойвремени цепи?5.
Показать на принципиальной электрической схеме лабораторной установки цепи зарядки и разрядки исследуемого конденсатора.6. Чем определяется продолжительность времени зарядки или разрядки конденсатора приоднократном нажатии на кнопку «Запуск»?7. Как графически проверить соответствие наблюдаемой функциональной связи величинтеоретически ожидаемой?ЛИТЕРАТУРА1.
Савельев И.В. Курс общей физики. Т.2. Электричество и магнетизм. Волны. Оптика:Учебное пособие для студентов втузов, М.: Наука, 1978. 480 с.2. Савельева А.И., Фетисов И.Н. Обработка результатов измерений при проведении физического эксперимента: Метод, указания ч лабораторной работе M-1 по курсу «Общая физика». — М.: МВТУ, 1984. 23 с..
ВНИМАНИЕ. В концесборки обязательно проверить,
чтобы провода от конденсатора ( батареи конденсаторов в целом ) соединялись с
клеммами 3 и 6 на стенде.
2.С помощью потенциометра ВУПа
установить на конденсаторе разность потенциалов Uи
измерить ее вольтметром. С целью уменьшения погрешности измерений значение
напряжения надо выбирать таким, чтобы стрелка вольтметра отклонялась более чем
на 2/3 его шкалы.
3.С помощью микроамперметра
измерить среднее значение силы тока < I>
.
4.Уменьшить напряжение до нуля.
5.Повторить п. 2, 3 , 4 десять
раз, каждый раз заново устанавливая на вольтметре напряжение U, и записатьполученные
значения силы тока в таблицу.
6.Руководствуясь требованиями
п.2 , установить на конденсаторе разность потенциалов Uотличную от U
, но значение которой тоже лежит
в последней трети шкалы вольтметра.
7.Выполнить операции
аналогичные п.3, 4, 5. Записать 10 полученных результатов в таблицу.
8.Вместо конденсатора Cвключить в схему конденсатор
Cи выполнить операции,
описанные в п.2, 3, 4, 5, 6, 7 при тех же значениях напряжений и занести
измеренные величины силы тока в таблицу.
9.Вместо C включить в схему батарею из
последовательно соединенных конденсаторов C иC
( т.е. C’ ); выполнить операции, описанные в п.2, 3, 4,
5, 6, 7, при тех же значениях напряжений Uи
U и занести измеренные величины
силы тока в таблицу.
10.Вместо батареи из
последовательно соединенных конденсаторов включить батарею из параллельно
соединенных конденсаторов ( C”).Выполнить операции, описанные п. 2, 3, 4, 5,
6, 7, при тех же значениях U, U
и
занести величины силы тока в таблицу.
4. Сводная
таблица результатов.
|
Разностьпотенциалов,В |
U |
U |
|||||||
|
Конденсаторы |
С |
С |
С |
С |
С |
С |
С |
С |
|
|
Сила тока,мА |
Nпп |
I |
I |
I |
I |
I |
I |
I |
I |
|
1 |
77 |
80 |
40 |
157 |
99 |
102 |
50 |
199 |
|
|
2 |
77 |
79 |
39 |
155 |
98 |
101 |
51 |
198 |
|
|
3 |
76 |
79 |
41 |
156 |
99 |
101 |
51 |
199 |
|
|
4 |
78 |
80 |
40 |
155 |
100 |
101 |
50 |
199 |
|
|
5 |
77 |
80 |
40 |
156 |
99 |
103 |
51 |
199 |
|
|
6 |
76 |
80 |
40 |
156 |
98 |
101 |
50 |
198 |
|
|
7 |
76 |
80 |
39 |
156 |
98 |
102 |
50 |
198 |
|
|
8 |
76 |
79 |
41 |
157 |
98 |
101 |
50 |
199 |
|
|
9 |
77 |
80 |
39 |
157 |
99 |
102 |
51 |
199 |
|
|
10 |
77 |
79 |
40 |
156 |
99 |
101 |
50 |
199 |
|
|
<I> |
0,767 |
0,796 |
0,399 |
1,561 |
0,987 |
1,015 |
0,504 |
1,987 |
|
|
S |
0,002 |
||||||||
|
I,A (по Стьюденту) |
0,00246 |
||||||||
|
I,A (приборная) |
0,01 |
||||||||
|
U,B |
3,75 |
||||||||
|
Электроемкость,Ф |
0,000139 |
0,000145 |
0,000073 |
0,000284 |
0,000141 |
0,000145 |
0,000071 |
0,000284 |
|
|
Емкость по формуле(3) |
70,968*10 |
284*10 |
71,486*10 |
286*10 |
5. Расчёт погрешностей измерений
(указать метод расчёта погрешностей).
1.По данным, полученным в
результате измерений, определить емкость конденсаторов C,C2 , C’, C”.

2.С помощью формул ( 3 ) рассчитать
значения C” и C’ и занести их в таблицу.
3.Оценить абсолютную
погрешность косвенных измерений емкости и сделать окончательную запись
результата в виде
1.Проработать содержание
методического указания по физике[3].
2.Вывести самостоятельно
формулу для расчета ошибки косвенных измерений и сравнить ее с формулой ( 4 ):
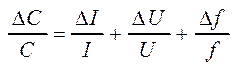
(4)
3.Рассчитать значения DI и DU
согласно указаниям [3], учитывая класс точности приборов.
4.Методом Стьюдента рассчитать
значение DI по данным полученным для большей емкости как при напряжении U , так и при напряжении U
.
5.Определить относительную
погрешность измерений для большей из емкостей как при напряжении Uтак и при U
. При этом
принять равным одному проценту.
6.Рассчитать абсолютную
погрешность измерений DC и сделать окончательную запись полученного
результата. По указанию преподавателя п. 4, 5, 6 могут выполняться и для другой
емкости.
7.С помощью формулы (3)
рассчитать емкости батарей конденсаторов и сравнить их со значениями,
полученными по формуле (2). Используя данные п.6, сделать выводы о величине
расхождений значений C’и C” , полученных различными способами.
6. Окончательные результаты:
U1: U2:
C,=0,000073 Ф
C,=0,0000471
Ф
С,,=0,000284 Ф С,,=0,000286
Ф
Подпись студента:
Лист – вкладыш
5. Расчёт погрешностей измерений (продолжение):
Абсолютная погрешность равна: С=0,000002
С =0,000002
Относительная погрешность равна:
I=1,23*
I=1,23*
7. Дополнительная страница
(для размещения таблиц, теоретического материала и дополнительных
сведений).
По формуле №3
А) С=
С=284*10Ф
Б) С=
С=286*10
По формуле №2:
А) С=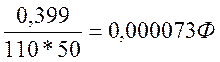
С=
Б) С= 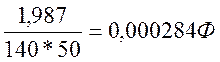
С=