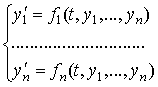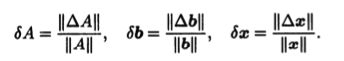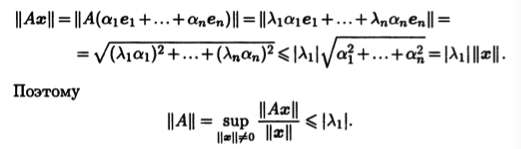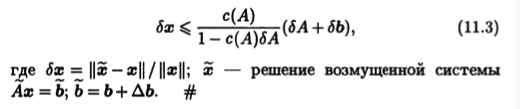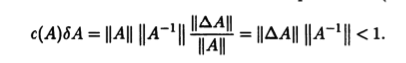1 ЭЛЕМЕНТЫ
ТЕОРИИ ПОГРЕШНОСТЕЙ
Во время решения
инженерных задач, в вычислительных устройствах, расчеты, как правило,
производятся над приближенными исходными данными. Поэтому главное грамотно
организовать вычисления, чтобы обеспечить заданную точность вычислений.
Погрешности вычислений
могут быть разбиты на следующие группы:
а) погрешности
модели – связанные с физическими допущениями, не контролируемые в
процессе численного решения;
б) погрешности
исходных данных – при измерениях;
в) погрешность
приближенного метода – возникает при численном решении задачи, где
точный оператор заменяется приближенным, требующим меньшего количества
операций. (Интеграл заменяют суммой, функцию многочленом и т.д.);
г) вычислительная
погрешность – в результате вынужденного округления чисел (количество
допустимых разрядов в ЭВМ).
Погрешности первых
двух видов относятся к неустранимым. Их учитывают при выборе метода решения.
В связи с этим
необходимо:
а) оценивать точность
результата по известной точности исходных данных;
б) определять точность
исходных данных, обеспечивающих заданную точность результата;
в) согласовывать точность
различных данных, чтобы не тратить время на один набор данных, если второй –
более груб;
г) строить алгоритм
вычислений так, чтобы обеспечить требуемую точность более рациональным путем.
1.1 АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ
ПОГРЕШНОСТЬ
Абсолютная
погрешностьприближенного числа а –
это число
, (1.1.1)
где А – точное значение
некоторой величины.
На практике чаще всего
пользуются предельной абсолютной погрешностью Δа.
, (1.1.2)
где Δа
– оценка сверху для Δ.
Основной характеристикой
точности будет являться относительная погрешность 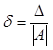
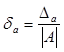
качество приближения, (безразмерная величина обычно измеряется в %).
1.2
ЗАПИСЬ ПРИБЛИЖЕННЫХ ЧИСЕЛ
Пусть приближенное число
записано в виде конечной дроби
а = αm·10 m + αm — 1·10 m – 1 + …+ αm – n + 1·10 m – n + 1(1.2.1)
где (αm ≠ 0) и αi = {0, 1… 9}.
Значащими цифраминазывают все цифры в записи числа, начиная с первой
ненулевой цифры слева. Например: а = 0,0503, b = 0,00630500. Значащую цифру
называют верной, если абсолютная погрешность числа не превосходит
единицы разряда, соответствующего этой цифре. В противном случае – цифра
считается сомнительной.
Например: Если а = 0,0503 и Δа
= 0,00002 или b = 0,00630500
и Δb = 0,000008. (В данном случае
подчеркнуты верные цифры).
Если исходное число имеет
несколько сомнительных чисел, то его надо предварительно округлить.
Правило округления: чтобы округлить число до n – значащих цифр, отбрасывают все его
цифры, стоящие после n – ой
значащей или (если это необходимо для сохранения разрядов) заменяют их нулями.
При этом:
а) если первое из
отбрасываемых чисел меньше 5, то оставшиеся десятичные знаки сохраняют без
изменений;
б) если больше 5, то к
последней сохраненной цифре добавляют 1.
в) если равно 5, то
возможны 2 случая:
1) после 5 идут ненулевые
цифры – последняя оставленная увеличивается на 1
2) если первая из
отброшенных 5 и далее идут нули, то последняя оставленная цифра увеличивается
на 1, если она нечетная и остается прежней, если она четная.
Например: b = 0,125168 ≈ 0,125; π = 3,14159265 ≈ 3,1416;
b = 0,125168 ≈ 0,13; с =
1,25000 ≈ 1,2 d = 1,3500 ≈
1,4.
Если приближенные числа
не носят окончательного характера, то следует сохранять в них одну или две
сомнительные цифры до окончания вычислений. При этом абсолютная погрешность меньше половины единицы
оставленного разряда.
≤ 0,5 · 10 m – n + 1 (1.2.2)
1.3
ПОГРЕШНОСТИ ФУНКЦИЙ
Пусть задана
дифференцируемая функция y = f(x1, x2, …xn), где каждый аргумент определяется с погрешностями Δхі. Тогда абсолютная погрешность
функции
Δy = │f(x1 + Δ x1; x2 + Δ x2; …; xn + Δ xn) — f(x1, x2, …xn)│. (1.3.1)
Если предположить, что Δхі → 0, то можно считать
Δ ≈ │df(x1, …xn)│= 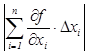
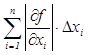
Отсюда определим верхнюю
границу для Δy.
Δy = 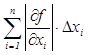
где Δхі – предельные абсолютные погрешности для
хі., а Δy – предельные абсолютные погрешности для y.
Тогда относительная
погрешность
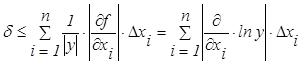
Поэтому предельная
относительная погрешность
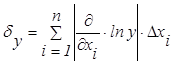
Пример. Найти предельные абсолютную и
относительную погрешности объема шара если
d = 3,7±0,05 см., а π ≈3,14.
Решение
Вычисляем первые частные
производные
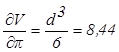
,
тогда =8,44×0,0016+21,5×0,05=1,088»1,1 (см3) тогда V ≈ 27,4 см3 ± 1,1 см3
и 
Применяя эти формулы
можно получить следующие правила вычисления погрешностей результата через
погрешности компонент:
а) предельная абсолютная
погрешность суммы или разности равна сумме предельных абсолютных погрешностей
слагаемых;
б) предельная
относительная погрешность не превосходит наибольшей из предельных относительных
погрешностей слагаемых;
в) предельная
относительная погрешность произведения и частного равна сумме предельных
относительных погрешностей компонент;
г) предельная
относительная погрешность n-ой
степени в n раз больше предельной относительной
погрешности данного числа (верно и для целых и для дробных n).
1.4
ОБРАТНАЯ ЗАДАЧА ТЕОРИИ ПОГРЕШНОСТЕЙ
Каковы должны быть
погрешности аргументов функции, чтобы абсолютная погрешность функции не
превышала заданной величины. Эта задача решается однозначно только для функции
одной переменной. y = f(x), тогда если f(x) – дифференцируема и f ´(x) ≠ 0, то 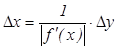
В случае нескольких
переменных нужно вводить дополнительные ограничения.
Например, принцип
равных влияний – предполагается, что в формуле (1.3.3) все слагаемые
равны и следовательно
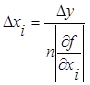
. (1.4.1)
Пример №1. С какой точностью нужно измерить
угол x в первой четверти, чтобы получить
значение sin x c пятью верными знаками (0° ≤ x ≤ 60°).
Решение: 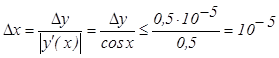
Пример №2.
Радиус основания цилиндра R ≈ 2 м. Н ≈ 3 м. – высота. С какой
точностью надо определить R и Н, чтобы его объем можно было
вычислить с точностью до 0,1 м3.
Решение: V = π R2H и ΔV = 0,1
м3. Для значений R = 2 м. Н = 3 м. π = 3,14 получим
приближенно:
.
На основании
«принципа равных влияний аргументов» (число аргументов n = 3) имеем:
.
2
МАТРИЦЫ
2.1
ОСНОВНЫЕ ДЕЙСТВИЯ МАД МАТРИЦАМИ:
а) Сложение (разность).
А ± В = [аij ± bij], (2.1.1)
причем А ±В = В ± А;
А ± 0 = 0 ± А = А.
Например: А = 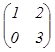
= 
б) Умножение на число.
α ∙А = А
∙ α = [α ∙ аij] (2.1.2)
Обусловленность матрицы. Погрешности.
Числа
обусловленности матрицы определяют
чувствительность решения системы
линейных уравнений к погрешностям
исходных данных. Следующие функции
позволяют найти числа обусловленности
матриц.
Значение
cond(X),
близкое к 1, указывает на хорошо
обусловленную матрицу;
Вернемся к анализу
формулы (4) для вариации решения x
-
Пусть матрица А
известна точно ()
и погрешность решения связана лишь с
погрешностьюправой части, тогда:
Из:
Перемножая
полученные неравенства, найдем:
Или
=M/m
— число
обусловленности матрицы А.
— всегда (в любой
норме), т.о. хорошо обусловленные матрицы
– это матрицы с малым
,
при этом относительная погрешность
решения мала.
-
Пусть известно
возмущение
матрицыА,
при условии, что правая часть f
задана точно.
Тогда:
Или
Таким
образом, чем больше число обусловленности,
тем чувствительнее система к округлениям.
Системы
с большим числом обусловленности
называют плохо
обусловленными.
В
случае СЛАУ 2-го порядка понятие
обусловленности матрицы допускает
наглядную
геометрическую интерпретацию.
Лекция №3
Метод
последовательного исключения
неизвестных – метод Гаусса.
Методы
решения систем линейных алгебраических
уравнений (СЛАУ):
1)
точные (прямые)
2)приближенные ( методы
последовательных
приближений.)
Прямые
методы
: метод Крамера, метод Гаусса и его
модификации: (метод главного элемента,
метод квадратного корня, метод отражений
и другие), метод ортогонализации. N
£
103.
Методы
последовательных приближений
(итерационные):
метод
простой итерации,
метод
Зейделя,
метод
релаксаций,
градиентные
методы и их модификации. N¸
106.
Рассмотрим
систему n
линейных алгебраических уравнений с
n неизвестными:
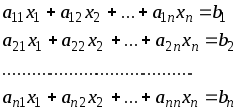
в
матричном виде: Ax
= b;
здесь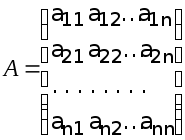
квадратная матрица размераn´n,
,
—
векторы n-го порядка.
В
индексной форме:
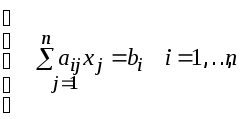
Система
линейных уравнений называется совместной,
если она имеет хотя бы одно решение, и
несовместной
(противоречивой), если она не имеет
решений.
Совместная
система называется определенной,
если она имеет единственное решение,
и неопределенной,
если более одного решения.
1. Схема единственного деления
Делим
первое уравнение этой системы на
коэффициент a11
¹
0
при
неизвестном х1
(ведущий
элемент).
Выполнения
условия a11¹
0
можно добиться всегда путем перестановки
уравнений системы.
(3) или
Исключаем
неизвестное х1
из остальных уравнений системы (для
этого достаточно из каждого уравнения
(i
=2,3,…,n)
вычесть уравнение (3), предварительно
умноженное на коэффициент при х1
, т.е. на a21,
a31
и т.д. ai1,
Например:
Обозначим
Преобразованные
уравнения будут иметь вид:
Здесь
обозначено
Матрица
системы имеет вид:
Вслед
за этим, оставив первое уравнение в
покое, над остальными уравнениями
системы совершим аналогичные
преобразования:
-
выберем
из их числа уравнение с ведущим элементом
a22(1) -
и
исключим с его помощью из остальных
уравнений неизвестное х2. -
Повторяя
этот процесс n
раз,
вместо системы (2) получим равносильную
ей систему с треугольной матрицей:
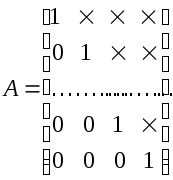
(4)
Матрицы
такого вида называются верхними
треугольными матрицами.
Из
системы (4) последовательно находятся
значения всех
неизвестных xn,
xn-1,
…, x1.
Таким
образом, процесс решения (1) по методу
Гаусса распадается на два этапа. Первый
этап, состоящий в последовательном
исключении неизвестных, называют прямым
ходом.
(число арифметических действий ¸
2N3/3)
Обратным
ходом.
(число арифметических действий ¸
N2)
Общие
формулы обратного хода имеют вид:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормы векторов и матриц абсолютная и относительная погрешности вектора
Нормы векторов и матриц. Обозначим через — точное решение системы, а через — приближенное решение системы. Для количественной характеристики вектора погрешности введем понятие нормы.
Нормой вектора называется число , удовлетворяющее трем аксиомам:
1) причем = 0 тогда и только тогда, когда = 0;
2) для любого вектора и любого числа ;
3) для любых векторов и .
Наиболее употребительными являются следующие три нормы:
, , .
Абсолютная и относительная погрешности вектора вводятся с помощью формул:
и .
Нормой матрицы называется величина . Введенная норма обладает свойствами, аналогичными свойствам нормы вектора:
1) причем = 0 тогда и только тогда, когда A = 0;
2) для любой матрицы A и любого числа ;
3) для любых матриц A и B;
4) .
Каждой из векторных норм соответствует своя подчиненная норма матрицы:
, , .
В оценках вместо нормы используется евклидова норма матрицы
, так как .
Абсолютная и относительная погрешности матрицы вводятся аналогично погрешностям вектора с помощью формул:
, .
ПРИМЕР 1. Вычисление норм вектора и матрицы.
ПРИМЕР 2. Вычисление норм матрицы.
Пусть рассматривается система линейных алгебраических уравнений
В матричной форме записи она имеет вид . Будем предполагать, что матрица системы задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво по входным данным.
Обусловленность задачи. Так же как и другие задачи, задача вычисления решения системы может быть как хорошо обусловленной, так и плохо обусловленной.
Теорема об оценке погрешности решения по погрешностям входных данных.
Пусть решение системы , а x* — решение системы A*x*=b*, тогда , где — относительное число обусловленности системы.
Если число обусловленности больше 10, то система является плохо обусловленной, так как возможен сильный рост погрешности результата.
ПРИМЕР 3. Оценка числа обусловленности и эксперимент.
Метод Гаусса. Рассмотрим метод Гаусса (схему единственного деления) решения системы уравнений. Прямой ход состоит из m-1 шагов исключения.
1 Шаг. Исключим неизвестное из уравнений с номерами i = 2,3. m. Предположим, что . Будем называть его ведущим элементом 1-го шага.
Найдем величины , i=2,3,. m , называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, . m vго уравнений системы первое уравнение, умноженное соответственно на . В результате 1-го шага получим эквивалентную систему уравнений:
Аналогично проводятся остальные шаги. Опишем очередной k-ый шаг. Предположим, что ведущий элемент . Вычислим множители к-го шага:, i=k+1. m и вычтем последовательно из (k+1)-го, . m v го уравнений системы k-ое уравнение, умноженное соответственно на
.После (m-1)-го шага исключения получим систему уравнений
,
матрица которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы находим . Подставляя найденное значение в предпоследнее уравнение, получим . Далее последовательно находим неизвестные .
LU разложение матрицы. Представим матрицу A в виде произведения нижней треугольной матрицы L и верхней треугольной U.
Введем в рассмотрение матрицы
и
Можно показать, что A = LU. Это и есть разложение матрицы на множители.
ПРИМЕР 4. Разложение матрицы A на множители.
ПРИМЕР 5. Решение системы уравнений с помощью LU — разложения матрицы.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Нормы векторов и матриц
Для исследования сходимости и точности численных итерационных методов решения задач линейной и нелинейной и нелинейной алгебры, в том числе итерационных методов решения СЛАУ и СНАУ, необходимо ввести понятие нормы векторов матриц.
Нормой вектора х = 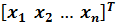
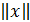
В n — мерной вещественном пространстве векторов x 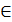
а) 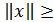
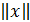
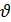
б) 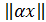
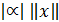
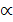
в) 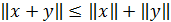
Нормой матрицы Аn+n(обозначается 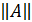
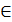
а) 
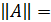

б) 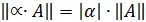
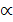
в) 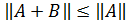
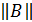
г) 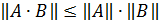
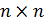
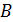
Нормы матриц и векторов, на которые матрицы действуют должны быть согласованы.
Норма матрицы А называется согласованной с нормой вектора х, на который действует матрица А; если выполняется неравенство
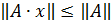
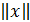
которое называется связью, осуществляющей согласование матрицы А с вектором х.
Наиболее употребительными являются следующие нормы векторов:
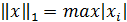
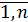
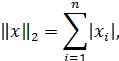
Согласованными с ними с помощью связи нормами матриц будут соответственно:
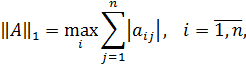
Где 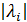
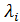
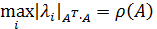
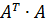
Основная и дополнительная литература по дисциплине.
Основная:
1. Формалев В.Ф., Ревизников Д.Л. Численные методы.-М.: Физматлит 2004-400с.
2. Пирумов У.Г. (редактор). Численные методы. Учебник и практикум. Бакалавр. Академический курс.-М.: Юрайт, 2014-422с.
3. Численные методы. Сборник задач. Под редакцией У.Г.Пирумова.-М.: Дрофа, 2007-144с.
Дополнительная:
4. Вержбицкий В.М. Численные методы. Три книги:
1) Линейная алгебра и нелинейные уравнения.
2) Математический анализ и ЛДУ.
3) Дифференциальные уравнения в частных производных.
5. Демидович Б.П., Марон И.А. Основы вычислительной математики.-М.: наука, 1966, — 664с.
Учебная литература к лекции 1:
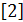
Дата добавления: 2016-03-04 ; просмотров: 2005 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Абсолютная и относительная погрешности вектора
Абсолютная и относительная погрешности вектора
Нормы векторов и матриц. Обозначим через — точное решение системы, а через — приближенное решение системы. Для количественной характеристики вектора погрешности введем понятие нормы.
Нормой вектора называется число , удовлетворяющее трем аксиомам:
1) причем = 0 тогда и только тогда, когда = 0;
2) для любого вектора и любого числа ;
3) для любых векторов и .
Наиболее употребительными являются следующие три нормы:
, , .
Абсолютная и относительная погрешности вектора вводятся с помощью формул:
и .
Нормой матрицы называется величина . Введенная норма обладает свойствами, аналогичными свойствам нормы вектора:
1) причем = 0 тогда и только тогда, когда A = 0;
2) для любой матрицы A и любого числа ;
3) для любых матриц A и B;
4) .
Каждой из векторных норм соответствует своя подчиненная норма матрицы:
, , .
В оценках вместо нормы используется евклидова норма матрицы
, так как .
Абсолютная и относительная погрешности матрицы вводятся аналогично погрешностям вектора с помощью формул:
, .
ПРИМЕР 1. Вычисление норм вектора и матрицы.
ПРИМЕР 2. Вычисление норм матрицы.
Пусть рассматривается система линейных алгебраических уравнений
В матричной форме записи она имеет вид . Будем предполагать, что матрица системы задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво по входным данным.
Обусловленность задачи. Так же как и другие задачи, задача вычисления решения системы может быть как хорошо обусловленной, так и плохо обусловленной.
Теорема об оценке погрешности решения по погрешностям входных данных.
Пусть решение системы , а x* — решение системы A*x*=b*, тогда , где — относительное число обусловленности системы.
Если число обусловленности больше 10, то система является плохо обусловленной, так как возможен сильный рост погрешности результата.
ПРИМЕР 3. Оценка числа обусловленности и эксперимент.
Метод Гаусса. Рассмотрим метод Гаусса (схему единственного деления) решения системы уравнений. Прямой ход состоит из m-1 шагов исключения.
1 Шаг. Исключим неизвестное из уравнений с номерами i = 2,3. m. Предположим, что . Будем называть его ведущим элементом 1-го шага.
Найдем величины , i=2,3,. m , называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, . m vго уравнений системы первое уравнение, умноженное соответственно на . В результате 1-го шага получим эквивалентную систему уравнений:
Аналогично проводятся остальные шаги. Опишем очередной k-ый шаг. Предположим, что ведущий элемент . Вычислим множители к-го шага:, i=k+1. m и вычтем последовательно из (k+1)-го, . m v го уравнений системы k-ое уравнение, умноженное соответственно на
.После (m-1)-го шага исключения получим систему уравнений
,
матрица которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы находим . Подставляя найденное значение в предпоследнее уравнение, получим . Далее последовательно находим неизвестные .
LU разложение матрицы. Представим матрицу A в виде произведения нижней треугольной матрицы L и верхней треугольной U.
Введем в рассмотрение матрицы
и
Можно показать, что A = LU. Это и есть разложение матрицы на множители.
ПРИМЕР 4. Разложение матрицы A на множители.
ПРИМЕР 5. Решение системы уравнений с помощью LU — разложения матрицы.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Норма вектора. Некоторые свойства векторных норм. Абсолютная и относительная погрешности. Сходимость.
Некоторым обобщением понятия длины вектора (оценкой величины вектора) является величина, называемая норма вектора. Функция
является нормой вектора, если она обладает следующими свойствами [112]:
Чтобы отличить одну норму от другой, используются индексы при двойной черте.
Полезный класс векторных норм — это п-нопмы. определяемые как
Наиболее важными из /?-норм являются 1. 2 и 00 ноомы:
— норма по модулю (частный случай (2.1.36) при р — 1);
— «евклидова» норма (частный случай (2.1.36) при р = 2);
— максимум модуля для элементов вектора (частный случай (2.1.36) при р—> со).
Очевидно, что евклидова норма ||3с|| = у](х,х) . Это соответствует естественному понятию длины вектора в двумерном и трехмерном пространстве. Единичным вектором по отношению к норме || • || называется вектор
х, удовлетворяющий равенству ||3с|| = 1.
Классический результат о «-нормах — неравенство Гелъдеоа
Очень важным частным случаем этого неравенства является неравенство Коши-Шварца:.
Все нормы в R» эквивалентны, т.е. для двух норм || • ||а и || • ||/; в R»
существуют положительные константы с, и с,, такие, что
для всех х из пространства R«. Например, для вектора х из R» имеем:
В вычислительной математике большую роль играет понятие «близости» двух векторов. Это соответствует понятию «расстояния», определяемому формулой
т.е. расстояние между векторами равно норме от их разности:
Оценка близости двух векторов используется для определения погрешности решения в итерационных методах.
Пусть вектор Т пространства R» есть аппроксимация к вектору х пространства R«. Для заданной векторной нормы || • || будем говорить, что
есть абсолютная погрешность Т, а при хфО формула
задает относительную погрешность х’.
Сходимость. Будем говорить, что последовательность векторов х‘, х 2 , х к , . сходится к вектору х, если
Отметим, что вследствие приведенных выше свойств векторных норм сходимость в а-норме влечет сходимость в Д-норме и наоборот.
Абсолютная и относительная погрешности 1 1
Главная > Документ
| Информация о документе |
| Дата добавления: |
| Размер: |
| Доступные форматы для скачивания: |
По свойству нормы (3.2)
|| A|| l = | A ( x ) k | || A ( x )|| l || A|| l || x || l .
Так как || x || l = 1 , выполняется равенство || A ( x )|| l = || A || l || x || l , т. е. l — норма минимальна.
Пусть при суммировании по столбцам максимальная сумма абсолютных величин элементов матрицы достигается в столбце с номером k
|| A || m =.
Координатный столбец образа базисного вектора e k равен k — му столбцу матрицы A , а
|| A ( e k )|| m = || A || m .
Так как || e k || m = 1 , m — норма минимальна.
Сферическая норма оператора не является минимальной. В евклидовом пространстве для любого вектора x
= ( A ( x ), A ( x )) = ( x , A T A ( x )) 0 .
Оператор B = A T A – самосопряженный и неотрицательный. Пусть Sp ( B ) = , s n, 1 >… > r 0. Собственные векторы оператора B , отвечающие различным собственным значениям, ортогональны. Любой вектор x V является линейной комбинацией собственных векторов
x = x 1 + … + x r , B ( x j ) = j x j , j =1, …, r .
= ( x , B ( x )) = 1 ( x 1 , x 1 ) + … + r ( x r , x r ) 1 (( x 1 , x 1 ) + … +( x r , x r )) = 1 ( x , x ).
Для ненулевого собственного вектора x 1 выполняется строгое равенство
= 1 (( x 1 , x 1 ).
Следовательно, минимальной нормой оператора в евклидовом пространстве является норма
|| A || s = ,
называемая спектральной. Здесь 1 – наибольшее собственное значение матрицы B = A T A . Характеристический многочлен матрицы B представим двумя выражениями
det ( B — E ) = ( — ) n + 1 ( — ) n-1 + … + n =
где d j – кратность собственного значения j . Коэффициент 1 называется следом матрицы B
1 = tr ( B ) = .
След матрицы выражается через собственные значения
1 1 = d 1 1 + … + d r r ( d 1 + … + d r ) 1 = n 1 .
,
(3.3) .
3.2 Пример. Найти сферическую и спектральную нормы матрицы
A = .
Решение: || A || n = = 9.
B = A T A = .
det ( B — E ) = = =
= ( 36 — )( 2 — 29 +132 ).
Наибольшее собственное значение равно 36 (сумма двух других равна 29 ). Итак, || A || s = 6.
Если матрица A – симметрическая, то собственные значения B равны квадратам собственных значений матрицы A и спектральная норма || A || s равна наибольшему по абсолютной величине собственному значению матрицы A .
3.3 Пример. Найти сферическую и спектральную нормы матрицы
A = .
Решение: Вычислим характеристический многочлен матрицы A
det ( A — E ) = =
= .
Итак, Sp ( A ) = . Следовательно, || A || s = 7 . Квадрат сферической нормы матрицы равен сумме квадратов ее собственных значений с учетом их кратности
|| A || n = 10,1.
Для норм операторов выполняются следующие свойства:
3.6 Предложение. У самосопряженного оператора l — и m -нормы совпадают.
Самосопряженный оператор имеет симметрическую матрицу.
3.7 Предложение. Любой элемент матрицы по абсолютной величине не превосходит любой ее нормы
a ij ||A||, i, j = 1, …, n.
Доказательство. Для l -, m -, n — норм утверждение очевидно из определения. Проверим утверждение для спектральной нормы. Согласно определению нормы оператора в евклидовом пространстве для базисного вектора e j имеем
|| A ( e j )|| n || A || s || e j || n .
Норма || e j || n = 1, а координатный столбец вектора A ( e j ) равен j — му столбцу матрицы A . Итак,
|| A ( e j )|| n = || A || s , j = 1, …, n ,
откуда следует доказываемое утверждение.
3.8 Предложение. Норма произведения операторов не превосходит произведения их норм
Доказательство. Для минимальных норм, используя теорему о наибольшем значении непрерывной функции на ограниченном замкнутом множестве, имеем
|| AB || =
.
Для n — нормы доказательство следует из неравенства Буняковского
.
Теория погрешностей в нормированном пространстве. Пусть в линейном нормированном пространстве V задан оператор A : V V . Перенесем основные понятия теории погрешностей на векторы и операторы.
3.9 Определение. Приближением вектора ( оператора ) называется вектор x ( оператор A ), близкий к точному x * ( A * ) и заменяющий его в вычислениях.
r x = x – x* ( R A = A – A* )
называется погрешностью вектора ( оператора ).
Предельной абсолютной погрешностью вектора ( оператора ) называется любое положительное число x ( A ) , удовлетворяющее условию
|| r x || x ( ||R A || A ).
Предельной относительной погрешностью вектора ( оператора ) называется любое положительное число x ( A ) , удовлетворяющее условию
|| r x || / || x *|| x ( || R A || / || A *|| A ).
Предельные погрешности зависят от определения нормы в векторном пространстве. Из определения предельной абсолютной погрешности имеем
|| x *|| = || x – ( x – x * )|| || x || + || r x || || x || + x ,
|| x || = || x * + ( x – x * )|| || x *|| + || r x || || x *|| + x ,
откуда получаем интервальную оценку
|| x || – x || x *|| || x || + x .
Аналогично выводится оценка для оператора
|| A|| – A || A*|| || A|| + A .
Следовательно, для вектора и оператора остаются справедливыми формулы (1.2), (1.3) и при малых погрешностях (1.4), при замене абсолютных величин на нормы.
3.4 Пример. В пространстве с n — нормой вычислен вектор
x = ( 2,97654; 0,01275; -4,00152 )
с предельной относительной погрешностью x = 10 -4 . Записать координаты вектора с сохранением одной сомнительной цифры.
Решение: || x || n = = 4,987 5 . По формуле (1.4)
x = || x || n x = 5 10 -4 . Погрешность координат вектора оценим согласно (3.2)
| x j – x j *| || r x || n x = 5 10 -4 .
x = ( 2,9765 5 10 -4 ; 0,0128 5 10 -4 ; -4,0015 5 10 -4 ).
3.5 Пример. Координаты вектора x вычислены с 4 верными знаками
x = ( 2,97654; 0,01275; -4,00152 ).
Найти предельную относительную погрешность вектора x в l -, m -, n — нормах.
Решение: Предельные абсолютные погрешности каждой из трех координат вектора x равны соответственно 10 -3 , 10 -5 , 10 -3 . Погрешность x находим по формуле (1.4):
в l — норме || x || l = 4,00152 4, || r x || l 10 –3 , x = ( 1 / 4 ) 10 –3 ;
в m — норме || x || m = 2,97654 + 0,01275 + 4,00152 = 6,9908 7,
|| r x || m 10 –3 + 10 –5 + 10 –3 2 10 –3 , x = ( 2 / 7 ) 10 –3 ;
в n- норме || x || n 5, || r x || n 10 –3 , x = ( / 5 ) 10 -3 .
3.6 Пример. Все элементы квадратной матрицы A вычислены с предельной абсолютной погрешностью . Найти предельную относительную погрешность A матрицы.
Решение: Найдем предельную абсолютную погрешность A матрицы. Из определения нормы вытекает, что в l -, m -, n — нормах A = n . Следовательно,
где в каждом случае используется соответствующая норма. Для спектральной нормы воспользуемся неравенством || R A || s || R A || n . Тогда формула останется справедливой и для спектральной нормы.
3.7 Пример. Все элементы квадратной матрицы A вычислены с предельной относительной погрешностью . Найти предельную относительную погрешность A матрицы.
Решение: По условию все элементы матрицы R A удовлетворяют условию | r ij | | a ij | . Тогда в l -, m -, n — нормах || R A || || A || и
Рассмотренная задача имеет прикладное значение. При переводе в двоичную систему счисления каждое число представляется t — разрядной двоичной дробью. Относительная погрешность представления числа = q –( t -1) / 1 . В двоичной системе q =2, 1 = 1. Отсюда вытекает, что предельная относительная погрешность матрицы при переводе в двоичную систему равна A = 2 –( t -1) .
Погрешность решения системы линейных уравнений. Выясним, как погрешности в матрице и свободном члене системы уравнений влияют на решение системы. Пусть точная система уравнений,
а при искажении матрицы и свободного члена погрешностями будет найдено приближенное решение системы
( A + R A )( x + r x ) = b + r b .
Разрешая уравнение для погрешности
A ( r x ) = r b — R A ( x + r x )
r x = A -1 ( r b ) — A -1 R A ( x + r x )
и после перехода к нормам
|| r x || || A -1 |||| r b || + || A -1 |||| R A || (|| x || + || r x ||).
Разделим правую и левую части неравенства на || x ||
|| r x || / || x || || A -1 |||| r b || / || x || + || A -1 |||| R A || ( 1 + || r x || / || x ||).
Из точного уравнения после перехода к нормам получим || b || || A || || x ||. Заменим в правой части || r b || / || b ||, || r x || / || x ||, || R A || / || A || на предельные относительные погрешности соответственно b , x , A . Тогда правая часть неравенства будет представлять предельную относительную погрешность решения
|| r x || / || x || || A -1 |||| A || b + || A -1 |||| A || A ( 1 + x ) = x .
Величина ( A ) = || A -1 |||| A || зависит от определения нормы и называется мерой обусловленности матрицы. Предельная относительная погрешность решения определяется формулой
(3.4) x = .
Особый интерес представляет спектральная мера обусловленности. Спектральная норма || A || s = определяется по наибольшему значению спектра матрицы B = A T A ,
Sp ( B ) = , 1 > …> r .
Спектр матрицы ( A -1 ) T A -1 = ( AA T ) -1 определяет || A -1 || s . Матрицы A T A и AA T имеют одинаковый спектр, а Sp (( AA T ) -1 ) = . Итак, в спектральной норме мера обусловленности матрицы s ( A ) = равна квадратному корню из отношения наибольшего и наименьшего собственных значений матрицы B = A T A . Для симметрической матрицы A мера обусловленности равна отношению наибольшего и наименьшего по абсолютным величинам собственных значений матрицы A . Из определения следует, что для любой матрицы s ( A ) 1.
3.8 Пример. Найти меру обусловленности матрицы
A = .
Решение: В примере 3.3 получен спектр симметрической матрицы A Sp ( A ) = . Значит, s ( A ) = 3,5.
3.9 Пример. Найти меру обусловленности матрицы
A = .
Решение: В примере 3.2 вычислен характеристический многочлен матрицы B = A T A
det ( B — E ) = ( 36 — )( 2 — 29 +132 ).
Наибольшее и наименьшее собственные значения равны 1 = 36, r = 264 / ( 29 + ).
s ( A ) = 2,52.
3.10 Пример. Оценить погрешность решения системы уравнений
при изменении правой части
и сравнить с реальной погрешностью.
Решение: Исходная система имеет решение x = ( 1, 0 ), измененная система – решение x = ( 0,9; 0,1 ). Погрешность решения r x = ( -0,1;0,1 ). В n — норме относительная погрешность || r x || / || x || = .
Вычислим меру обусловленности матрицы. Характеристический многочлен матрицы
A T A =
f ( ) = 2 – ( 10 –2 10 –3 +10 -6 ) + 10 –6
имеет корни 1 10 и 2 10 –7 . Значит, s ( A ) = 10 4 .
Погрешность правой части r b = ( -0; 10 -4 ). В n — норме b = . По формуле (3.4), полагая A = 0, получим предельную относительную погрешность решения x = , превышающую реальную в раз.
Вычисление спектральной нормы и меры обусловленности матрицы. У положительно определенной матрицы B = A T A имеем
Sp ( B ) = , 1 >… > r 0, r n.
Воспользуемся разложением произвольного вектора x в сумму взаимно ортогональных собственных векторов матрицы B
x = x 1 + … + x r , B ( x j ) = j x j , j = 1, …, r .
( B i ( x ), B i ( x )) = .
.
Зададим вектор y (0) произвольно и построим вычислительный процесс
z (i) = A ( y (i) ), y (i+1) = A T ( z (i) ) / | y (i) |.
Докажем, что y ( i ) = B i ( y (0) ) / | B i -1 ( y (0) )|. При i = 1 равенство верно. Индукция по i . Допустим, что равенство верно при i , и докажем, что оно верно при i +1.
y (i+1) = A T ( A ( y (i) )) / | y (i) | = B ( B i ( y (0) ) / | B i-1 ( y (0) )|) / | y (i) | = B i+1 ( y (0) ) / | B i ( y (0) )|.
.
У матрицы B = E – ( 1 / 1 ) B наибольшее значение спектра
max = 1 – r / 1 = 1 – .
Для вычисления max изменим вычислительный процесс следующим образом:
z (i) = A ( y (i) ), y (i+1) = ( y (i) – ( 1 / 1 ) A T ( z (i) )) / | y (i) |
при произвольном задании y (0) . В итоге двукратного умножения матрицы на вектор получим
y ( i +1) = ( E – ( 1 / 1 ) B )( y ( i ) / | y ( i ) |) = B ( y ( i ) / | y ( i ) |).
Следовательно, max . Спектральная норма матрицы вычисляется по формуле
(3.5) s ( A ) = .
§ 4 Системы линейных уравнений
Разложение квадратной матрицы в приизведение треугольных. Пусть дана система уравнений A ( x ) = b .
4.1 Теорема. Какова бы ни была квадратная матрица A с отличными от нуля угловыми минорами
a 11 0,
ее всегда можно разложить в произведение
где S и T соответственно левая и правая треугольные матрицы.
Доказательство. По условию теоремы s ik = 0 при k > i и t kj = 0 при k j . Тогда
a ij =.
Отсюда s 11 t 11 = a 11 , s ji = a j1 / t 11 , t 1j = a 1j / s 11 , j = 2, …, n;
s ii t ii = , s ji = () / t ii , t ij = () / s ii , j = i+1, …, n.
Итак, решение существует, если s ii 0 и t ii 0.
Допустим, что при некотором p получим s pp t pp = 0. В этом случае возможно разложение A p = S p T p , где A p , S p , T p – матрицы угловых миноров p — го порядка. Тогда
det ( A p ) = det ( S p ) det ( T p ) = = 0,
что противоречит условию теоремы.
Если фиксировать n диагональных элементов ( t ii = 1, i = 1, …, n ), то полученное решение будет единственным.
Метод Гаусса . Представим матрицу A произведением треугольных матриц и сведем задачу к решению двух систем
S ( y ) = b и T ( x ) = y .
Фиксируем диагональные элементы матрицы T , положив t ii = 1, i = 1, …, n . Столбец свободных членов b присоединим к матрице A , присвоив ему номер n +1 ( a i n +1 = b i ). Столбец y получим на месте ( n +1 )-го столбца матрицы T .
Решение системы S ( y ) = b составляет прямой ход метода Гаусса.
s i1 = a i1 , i = 1, …, n, t 1j = a 1j / a 11 , j = 2, …, n+1;
s ji = , j = i, …, n, t ij = () / s ii , j = i+1, …, n+1.
Обратный ход метода Гаусса состоит в решении системы T ( x ) = y . Координаты вектора y составляют ( n +1 )-й столбец матрицы T ( y i = t i n +1 ).
x n = y n / t nn , x i = y i – , i = n-1, …, 1.
Если один из угловых миноров матрицы A близок к нулю, метод Гаусса приводит к росту вычислительной погрешности.
4.1 Пример. Решить методом Гаусса систему линейных уравнений
при вычислении с тремя значащими цифрами.
Решение: Запишем расширенную матрицу системы. При прямом ходе метода Гаусса первую строку расширенной матрицы разделим на 10 -4 и вычтем из второй. Во второй строке появятся четырехзначные числа, которые необходимо округлить до трех знаков. На этом прямой ход закончен, матрица A приведена к треугольному виду.
обратный ход
Выполнив обратный ход, получим x 1 = 0, x 2 = 1. Решение системы с тремя верными знаками после запятой x 1 = 1, x 2 = 1. Итак, вычислительная погрешность существенно исказила результат. Потеря точности произошла при вычитании чисел с сильно различающимися порядками.
Метод Гаусса с выбором главного элемента позволяет исключить вычитание больших чисел. Главным называется наибольший по абсолютной величине коэффициент при неизвестных в ведущей строке расширенной матрицы. После деления на главный элемент коэффициенты при неизвестных в ведущей строке по абсолютной величине не больше единицы. При прямом ходе метода Гаусса ведущая строка умножается на элемент ниже расположенной строки и вычитается из нее. При этом в преобразуемой строке из каждого коэффициента вычитается число, не превышающее один из элементов этой строки. Порядок элементов существенно не изменяется. Однако, если вычитание ведущей строки ведет к уменьшению порядка всех коэффициентов при неизвестных, происходит потеря точности, связанная с вычитанием близких чисел. Поэтому процедура выбора главного элемента, усложняя метод, не гарантирует полностью от проблем с вычислительной погрешностью.
Метод квадратного корня . У положительно определенной матрицы A все угловые миноры положительны и являются доминирующими. Отпадает необходимость в поиске главного элемента. Симметрическая матрица A разлагается в произведение треугольных матриц A = ST , таких, что S = T T . Достаточно вычислять одну матрицу T . Метод Гаусса, адаптированный к линейным системам с положительно определенной матрицей, называется методом квадратного корня . Его реализация имеет вид ( s ij = t ji , a i n+1 = b i , t in+1 = y i )
t 11 = , t 1j =a ij / t 11 , j = 2, …, n+1;
t ii = , t ij = () / t ii , j = i+1, …, n+1.
http://helpiks.org/7-26161.html
http://b4.cooksy.ru/articles/absolyutnaya-i-otnositelnaya-pogreshnosti-vektora
Данный курс посвящен введению в вычислительную математику.
1. Теория погрешностей и машинная арифметика.
2. Решение нелинейных уравнений. Методы бисекций, простой итерации, Ньютона.
3. Решение нелинейных уравнений. Обусловленность задачи нахождения корня. Интервал неопределенности.
4. Решение систем линейных алгебраических уравнений. Нормы векторов и матриц. LU-разложение матрицы.
5. Решение систем линейных алгебраических уравнений прямыми методами.
6. Решение систем линейных алгебраических уравнений итерационными методами.
7. Приближение функций. Метод наименьших квадратов.
8. Приближение функций. Интерполяция.
9. Приближение функций. Сплайны.
10. Решение задачи Коши одношаговыми методами.
Наверх
1. Теория погрешностей и машинная арифметика.
Пусть — точное значение,
— приближенное значение некоторой величины.
Абсолютной погрешностью приближенного значения называется величина
.
Относительной погрешностью значения (при
0) называется величина
.
Так как, значение как правило неизвестно, чаще получают оценки погрешностей вида:
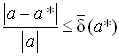
Величины и
называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.
Значащую цифру числа называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
Для оценки погрешностей арифметических операций следует использовать следующие утверждения:
Абсолютная погрешность алгебраической суммы (суммы или разности ) не превосходит суммы абсолютной погрешности слагаемых, т.е.
Если а и b — ненулевые числа одного знака, то справедливы неравенства
,
,
где ,
Для относительных погрешностей произведения и частного приближенных чисел верны оценки:
если и
, то
,
.
Пусть — дифференцируемая в области G функция переменных, вычисление которой производится при приближенно заданных значениях аргументов
. Тогда для абсолютной погрешности функции
справедлива следующая оценка

.
Здесь [x, x*] v отрезок, соединяющий точки x и x* =( )
Для относительной погрешности функции справедливо следующее приближенное равенство
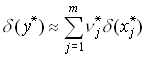
Наверх
2. Решение нелинейных уравнений. Методы бисекций, простой итерации, Ньютона.
Пусть рассматривается уравнение . Корнем уравнения называется значение
, при котором
. Корень
называется простым, если
, в противном случае корень называется кратным. Целое число m называется кратностью корня
, если
для k=1,2,3-,m-1 и
.
Постановка задачи вычисления приближенного значения корня с точностью : найти такое значения
, что
.
Решение задачи разбивается на два этапа: на первом этапе осуществляют локализацию корней, на втором этапе производят итерационное уточнение корней. На этапе локализации корней находят достаточно узкие отрезки ( или отрезок, если корень единственный), которые содержат один и только один корень уравнения . На втором этапе вычисляют приближенное значение корня с заданной точностью. Часто вместо отрезка локализации достаточно указать начальное приближение к корню.
Метод бисекции. Пусть [a,b] v отрезок локализации. Предположим, что функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков .
Алгоритм метода бисекции состоит в построении последовательности вложенных отрезков, на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Опишем один шаг итераций метода. Пусть на k-ом шаге найден отрезок такой, что
. Найдем середину отрезка
.gif)
, то
— корень и задача решена. Если нет, то из двух половин отрезка выбираем ту, на концах которой функция имеет противоположные знаки:
,
, если
,
, если
Критерий окончания итерационного процесса: если длина отрезка локализации меньше 2, то итерации прекращают и в качестве значения корня с заданной точностью принимают середину отрезка.
Теорема о сходимости метода бисекций. Пусть функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков .Тогда метод сходится и справедлива оценка погрешности :
Метод Ньютона (метод касательных) . Расчетная формула метода Ньютона имеет вид:
.gif)
есть точка пересечения с осью ОХ
касательной, проведенной к графику функции y=f(x) в точке .
Теорема о сходимости метода Ньютона. Пусть — простой корень уравнения
, в некоторой окрестности которого функция дважды непрерывно дифференцируема. Тогда найдется такая малая
— окрестность корня
, что при произвольном выборе начального приближения
из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка
, где
,
.
Критерий окончания итерационного процесса. При заданной точности >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство
.
Как указано в теореме, метод Ньютона обладает локальной сходимостью, то есть областью его сходимости является малая окрестность корня . Неудачный выбор может дать расходящуюся итерационную последовательность.
Метод простой итерации (метод последовательных повторений). Для применения метода простой итерации следует исходное уравнение преобразовать к виду, удобному для итерации
. Это преобразование можно выполнить различными способами. Функция
называется итерационной функцией. Расчетная формула метода простой итерации имеет вид:
.
Теорема о сходимости метода простой итерации. Пусть в некоторой — окрестности корня
функция
дифференцируема и удовлетворяет неравенству
, где
— постоянная . Тогда независимо от выбора начального приближения из указанной
— окрестности итерационная последовательность не выходит из этой окрестности, метод сходится
со скоростью геометрической последовательности и справедлива оценка погрешности: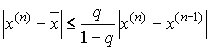
.
Критерий окончания итерационного процесса. При заданной точности >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство
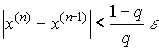
, то можно использовать более простой критерий окончания итераций:
.
Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду . Предположим дополнительно, что производная
знакопостоянна и
на отрезке [a,b]. Тогда при выборе итерационного параметра
метод сходится и значение
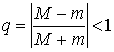
Наверх
3. Решение нелинейных уравнений. Обусловленность задачи нахождения корня. Интервал неопределенности.
Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым погрешностям входных данных.
Пусть установлено неравенство , где
— относительная погрешность входных данных, а
— относительная погрешность решения. Тогда
— называется абсолютным числом обусловленности задачи. Если же установлено неравенство
между относительными погрешностями данных и решения, то
называют относительным числом обусловленности задачи.
Обычно под числом обусловленности понимают относительное число обусловленности. Если
, то задачу называют плохо обусловленной.
Обусловленность задачи нахождения корня. Пусть v корень, подлежащий определению. Будем считать, что входными данными для задачи вычисления корня являются значения функции
. Так как
v вычисляется приближенно, то обозначим функцию, полученную в действительности через
. Предположим, что в малой окрестности корня выполняется неравенство:
. Для близких к
значений
справедливо равенство
, следовательно,
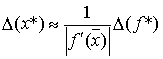

Интервал неопределенности корня. Если функция непрерывна, то найдется такая малая окрестность
корня
, имеющая радиус
, в которой выполнено неравенство
. Это означает, что
знак вычисленного значения
, вообще говоря не обязан совпадать со знаком
и, следовательно, становится невозможным определить, какое именно значение
из интервала
обращает функцию
в нуль. Этот интервал называется интервалом неопределенности корня. Очевидно, что радиус интервала неопределенности для простого корня равен
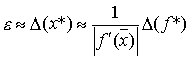

, а для кратного корня
.
Пусть . Корень уравнения простой и равен
= -0.34729635533861. Тогда
и
. Если
, то
. Это означает , что найти корень с точностью меньшей, чем радиус интервала неопределенности, не удастся.
Применение метода Ньютона для нахождения кратного корня. Метод Ньютона для случая кратного корня обладает лишь линейной скоростью сходимости. Чтобы сохранить квадратичную сходимость его модифицируют следующим образом:
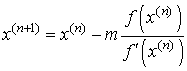
— кратность корня.
Как правило, значение v неизвестно. Используя метод Ньютона, можно узнать кратность корня. Для этого будем задавать значения
= 1,2,3 и вычислять значение корня с заданной точностью , одновременно подсчитывая количество итераций для каждого значения
. При некотором значении
число итераций будет минимальным. Это значение
и есть кратность корня.
Наверх
4. Решение систем линейных алгебраических уравнений. Нормы векторов и матриц. LU-разложение матрицы.
Нормы векторов и матриц. Обозначим через — точное решение системы, а через
— приближенное решение системы. Для количественной характеристики вектора погрешности
введем понятие нормы.
Нормой вектора называется число
, удовлетворяющее трем аксиомам:
1) причем
= 0 тогда и только тогда, когда
= 0;
2) для любого вектора
и любого числа
;
3) для любых векторов
и
.
Наиболее употребительными являются следующие три нормы:
,
.gif)
.
Абсолютная и относительная погрешности вектора вводятся с помощью формул:
и
.gif)
Нормой матрицы называется величина
.gif)
1) причем
= 0 тогда и только тогда, когда A = 0;
2) для любой матрицы A и любого числа
;
3) для любых матриц A и B;
4) .
Каждой из векторных норм соответствует своя подчиненная норма матрицы:
,
,
.
В оценках вместо нормы используется евклидова норма матрицы

.
Абсолютная и относительная погрешности матрицы вводятся аналогично погрешностям вектора с помощью формул:
,
.gif)
Пусть рассматривается система линейных алгебраических уравнений
.gif)
В матричной форме записи она имеет вид . Будем предполагать, что матрица системы
задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво по входным данным.
Обусловленность задачи. Так же как и другие задачи, задача вычисления решения системы может быть как хорошо обусловленной, так и плохо обусловленной.
Теорема об оценке погрешности решения по погрешностям входных данных.
Пусть решение системы , а x* — решение системы A*x*=b*, тогда
, где
— относительное число обусловленности системы.
Если число обусловленности больше 10, то система является плохо обусловленной, так как возможен сильный рост погрешности результата.
Метод Гаусса. Рассмотрим метод Гаусса (схему единственного деления) решения системы уравнений. Прямой ход состоит из m-1 шагов исключения.
1 Шаг. Исключим неизвестное из уравнений с номерами i = 2,3,..m. Предположим, что
. Будем называть его ведущим элементом 1-го шага.
Найдем величины , i=2,3,…m , называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …m vго уравнений системы первое уравнение, умноженное соответственно на
. В результате 1-го шага получим эквивалентную систему уравнений:
Аналогично проводятся остальные шаги. Опишем очередной k-ый шаг. Предположим, что ведущий элемент . Вычислим множители к-го шага:
, i=k+1,…m и вычтем последовательно из (k+1)-го, …m v го уравнений системы k-ое уравнение, умноженное соответственно на
.После (m-1)-го шага исключения получим систему уравнений
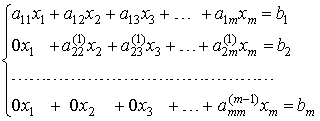
матрица которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы находим . Подставляя найденное значение
в предпоследнее уравнение, получим
. Далее последовательно находим неизвестные
.
LU разложение матрицы. Представим матрицу A в виде произведения нижней треугольной матрицы L и верхней треугольной U.
Введем в рассмотрение матрицы
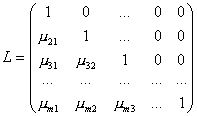
Можно показать, что A = LU. Это и есть разложение матрицы на множители.
Наверх
5. Решение систем линейных алгебраических уравнений прямыми методами.
Метод решения задачи называют прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций. Метод решения задачи называют итерационным, если в результате получают бесконечную последовательность приближений к решению. Если эта последовательность сходится к решению задачи, то говорят, что итерационный процесс сходится. К прямым методам решения относятся метод Гаусса и его модификации, метод Холецкого и метод прогонки.
В методе Гаусса для вычисления масштабирующих множителей требуется делить на ведущие элементы каждого шага. Если элемент равен нулю или близок к нулю, то возможен неконтролируемый рост погрешности.
Поэтому часто применяют модификации метода Гаусса, обладающие лучшими вычислительными свойствами.
Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). На k-ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент при неизвестной
в уравнениях с номерами i = k+1, … , m.Затем уравнение, соответствующее выбранному коэффициенту с номером
, меняют местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента
. После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.
Метод Холецкого. Если матрица системы является симметричной и положительно определенной, то для решения системы применяют метод Холецкого (метод квадратных корней). В основе метода лежит алгоритм специального LU-разложения матрицы A, в результате чего она приводится к виду A=. Если разложение получено, то как и в методе LU-разложения, решение системы сводится к последовательному решению двух систем с треугольными матрицами:
и
. Для нахождения коэффициентов матрицы L неизвестные коэффициенты матрицы
приравнивают соответствующим элементам матрицы A. Затем последовательно находят требуемые коэффициенты по формулам:
,
i = 2, 3, …, m,
,
i = 3, 4, …, m,
……………
i = k+1, … , m.
Метод прогонки.Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса — метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:
Преобразуем первое уравнение системы к виду , где
,
Подставим полученное выражение во второе уравнение системы и преобразуем его к виду и т.д. На i-ом шаге уравнение преобразуется к виду
, где
,
. На m-ом шаге подстановка в последнее уравнение выражения
дает возможность определить значение
:
. Значения остальных неизвестных находятся по формулам:
, i = m-1, m-2, …, 1.
Наверх
6. Решение систем линейных алгебраических уравнений итерационными методами.
Рассматривается система Ax = b.
Для применения итерационных методов система должна быть приведена к эквивалентному виду x=Bx+d. Затем выбирается начальное приближение к решению системы уравнений
и находится последовательность приближений к корню. Для сходимостиитерационного процесса достаточно, чтобы было выполнено условие
. Критерий окончания итераций зависит от применяемого итерационного метода.
Метод Якоби.
Самый простой способ приведения системы к виду удобному для итерации состоит в следующем: из первого уравнения системы выразим неизвестное x1, из второго уравнения системы выразим x2, и т. д. В результате получим систему уравнений с матрицей B, в которой на главной диагонали стоят нулевые элементы, а остальные элементы вычисляются по формулам:
,i, j = 1, 2, … n.
Компоненты вектора d вычисляются по формулам:
, i = 1, 2, … n.
Расчетная формула метода простой итерации имеет вид
,
или в покоординатной форме записи выглядит так:
, i = 1, 2, … m.
Критерий окончания итераций в методе Якоби имеет вид:
, где
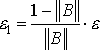
Если , то можно применять более простой критерий
окончания итераций
Метод Зейделя.
Метод можно рассматривать как модификацию метода Якоби. Основная идея состоит в том, что при вычислении очередного (n+1)-го приближения к неизвестному xi при i >1 используют уже найденные (n+1)-е приближения к неизвестным x1, x2, …, xi — 1, а не n-ое приближение, как в методе Якоби. Расчетная формула метода в покоординатной форме записи выглядит так:
,
i = 1, 2, … m.. Условия сходимости и критерий окончания итераций можно взять такими же как в методе Якоби.
Пусть матрица системы уравнений A — симметричная и положительно определенная. Тогда при любом выборе начального приближения метод Зейделя сходится. Дополнительных условий на малость нормы некоторой матрицы здесь не накладывается.
Метод простой итерации.
Если A — симметричная и положительно определенная матрица, то систему уравнений часто приводят к эквивалентному виду:
x = x — (Ax — b),
— итерационный параметр.
Расчетная формула метода простой итерации в этом случае имеет вид:
x (n+1) = x n — (Ax n — b).
Здесь B = E — A и параметр
> 0 выбирают так, чтобы по возможности сделать минимальной величину
.
Пусть и
— минимальное и максимальное собственные значения матрицы A. Оптимальным является выбор параметра
. В этом случае
принимает минимальное значение равное
.
Наверх
7. Приближение функций. Метод наименьших квадратов.
На практике часто возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате эксперимента. Часто вид эмпирической зависимости известен, но числовые параметры неизвестны.
Ниже рассматривается решение задачи приближения многочленами таблично заданной функции по методу наименьших квадратов и по методу интерполяции.
Постановка задачи приближения функции по методу наименьших квадратов. Пусть функция y=f(x) задана таблицей своих значений: , i=0,1,-n. Требуется найти многочлен фиксированной степени m, для которого среднеквадратичное отклонение (СКО)
.gif)
Так как многочлен определяется своими коэффициентами, то фактически нужно подобрать набор кофициентов
, минимизирующий функцию
.gif)
Используя необходимое условие экстремума, , k=0,1,-m получаем так называемую нормальную систему метода наименьших квадратов:
, k=0,1,-m.
Полученная система есть система алгебраических уравнений относительно неизвестных . Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.
Запишем нормальную систему наименьших квадратов для двух простых случаев: m=0 и m=2. При m=0 многочлен примет вид: . Для нахождения неизвестного коэффициента
имеем уравнение:
.gif)
есть среднее арифметическое значений функции в заданных точках.
Если же используется многочлен второй степени , то нормальная система уравнений примет вид:
Предположим, что функцию f можно с высокой точностью аппроксимировать многочленом некоторой степени m. Если эта степень заранее неизвестна, то возникает проблема выбора оптимальной степени аппроксимирующего многочлена в условиях, когда исходные данные
содержат случайные ошибки. Для решения этой задачи можно принять следующий алгоритм: для каждого m=0,1,2,.. вычисляется величина
.gif)
стабилизируется или начинает возрастать.
Определение параметров эмпирической зависимости. Часто из физических соображений следует, что зависимость между величинами хорошо описывается моделью вида
, где вид зависимости g известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров
из условия минимума функции:
.
Если зависимость от параметров нелинейна, то экстремум функции
ищут методами минимизации функций нескольких переменных.
Наверх
8. Приближение функций. Интерполяция.
Постановка задачи интерполяции функций.
Пусть функция y = f(x) задана таблицей своих значений:
, i=0,1,…n. Требуется найти многочлен степени n, такой, что значения функции и многочлена в точках таблицы совпадают:
, i=0,1,… n.
Справедлива теорема о существовании и единственности интерполяционного многочлена.
Одна из форм записи интерполяционного многочлена — многочлен Лагранжа:
, где
Многочлен представляет собой многочлен степени n , удовлетворяющий условию
.
Таким образом, степень многочлена равна n и при
в сумме обращаются в нуль все слагаемые, кроме слагаемого с номером
, равного
. Поэтому многочлен Лагранжа является интерполяционным.
Другая форма записи интерполяционного многочлена — интерполяционный многочлен Ньютона с разделенными разностями. Пусть функция f задана с произвольным шагом и
точки таблицы занумерованы в произвольном порядке. Величины
называют разделенными разностями первого порядка. Разделенные разности второго порядка определяются формулой:
.
Определение разделенной разности порядка таково:
.
Используя разделенные разности, интерполяционный многочлен Ньютона можно записать в следующем виде:
Величину называют погрешностью интерполяции или остаточным членом интерполяции.
Оценка погрешности интерполяции.
Если функция n+1 раз на отрезке [a,b] , содержащем узлы интерполяции , i=0,1,…n, то для погрешности интерполяции справедлива оценка:
. Здесь
,
.
Эта оценка показывает, что для достаточно гладкой функции при фиксированной степени интерполяционного многочлена погрешность интерполяции стремится к нулю не медленнее, чем величина, пропорциональная . Этот факт формулируют так: интерполяционный многочлен степени nаппроксимирует функцию с (n+1) порядком точности относительно
.
В практическом плане формула Ньютона обладает преимуществами перед формулой Лагранжа. Предположим, что в необходимо увеличить степень многочлена на единицу, добавив в таблицу еще один узел . При использовании формулы Лагранжа это приводит к необходимости вычислять каждое слагаемое заново. Для вычисления
достаточно добавить к
лишь очередное слагаемое:
. Если функция f достаточно гладкая, то справедливо приближенное равенство
. Это равенство можно использовать для практической оценки погрешности интерполяции :
.
Наверх
9. Приближение функций. Сплайны.
Глобальная и кусочно-полиномиальная интерполяция. Пусть функция f(x) интерполируется на отрезке [a,b]. Метод решения этой задачи с помощью единого многочлена для всего отрезка называют глобальной полиномиальной интерполяцией. В вычислительной практике такой поход применяется редко в силу различных причин. Одна из причин v необходимо задать стратегию выбора узлов при интерполяции функции f многочленами все возрастающей степени n.
Теорема Фабера. Какова бы ни была стратегия выбора узлов интерполяции, найдется непрерывная на отрезке [a,b] функция f, для которой при
. Таким образом, теорема Фабера отрицает существование единой для всех непрерывных функций стратегии выбора узлов. Проиллюстрируем сказанное примером.
Предположим, что выбираем равноотстоящие узлы, то есть , i = 0,1,…n, где
. Покажем, что для функции Рунге такая стратегия является неудачной.
На практике чаще используют кусочно-полиномиальную интерполяцию: исходный отрезок разбивается на части и на каждом отрезке малой длины исходная функция заменяется многочленом невысокой степени. Система Mathcad предоставляет возможность аппроксимации двумя важными классами функций: кусочно-линейной и сплайнами.
При кусочно-линейной интерполяции узловые точки соединяются отрезками прямых, то есть через каждые две точки ,
проводится полином первой степени.
Как видно из приведенного примера этот способ приближения также имеет недостаток: в точках «стыка» двух соседних многочленов производная, как правило, имеет разрыв.
Если исходная функция была гладкой и требуется, чтобы и аппроксимирующая функция была гладкой, то кусочно-полиномиальная интерполяция неприемлема. В этом случае применяют сплайны v специальным образом построенные гладкие кусочно-многочленные функции.
Интерполяция сплайнами. Пусть отрезок [a,b] разбит точками на n частичных отрезков . Сплайном степени m называется функция
, обладающая следующими свойствами:
1) функция непрерывна на отрезке [a,b] вместе со своими производными до некоторого порядка p.
2) на каждом частичном отрезке функция совпадает с некоторым алгебраическим многочленом
степени m.
Разность m-p между степенью сплайна и наивысшим порядком непрерывной на отрезке [a,b] производной называют дефектом сплайна. Кусочно-линейная функция является сплайном первой степени с дефектом, равным единице. Действительно, на отрезке [a,b] сама функция (нулевая производная) непрерывна. В то же время на каждом частичном отрезке
совпадает с некоторым многочленом первой степени.
Наиболее широкое распространение получили сплайны 3 степени (кубические сплайны) с дефектом равным 1 или 2. Система для осуществления сплайн-интерполяции кубическими полиномами предусматривает несколько встроенных функций. Одна из них рассмотрена в примере.
Погрешность приближения кубическими сплайнами. Пусть функция f имеет на отрезке [a,b] непрерывную производную четвертого порядка и . Тогда для интерполяционного кубического сплайна справедлива оценка погрешности:
.
Наверх
10. Решение задачи Коши одношаговыми методами.
Постановка задачи Коши для дифференциального уравнения первого порядка.
Пусть дано дифференциальное уравнение первого порядка . Требуется найти функцию
, удовлетворяющую при
дифференциальному уравнению и при
начальному условию
.
Теорема существования и единственности задачи Коши. Пусть функция определена и непрерывна на множестве точек
. Предположим также, что она удовлетворяет условию Липшица:
для всех
и произвольных
,
, где
— некоторая константа (постоянная Липшица). Тогда для каждого начального значения
существует единственное решение
задачи Коши, определенное на отрезке
.
Геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Заданием начального условия мы выделяем из семейства решений ту единственную кривую, которая проходит через фиксированную точку
Численное решение задачи Коши методом Эйлера.
Численное решение задачи Коши состоит в построении таблицы приближенных значений в точках
. Точки
,
называются узлами сетки, а величина
— шагом сетки. В основе построения дискретной задачи Коши лежит тот или иной способ замены дифференциального уравнения его дискретным аналогом. Простейший метод основан на замене левой части уравнения правой разностной производной:
. Разрешая уравнение относительно
, получаем расчетную формулу метода Эйлера:
,
.
Численный метод называется явным, если вычисление решения в следующей точке осуществляется по явной формуле. Метод называется одношаговым, если вычисление решения в следующей точке
производится с использованием только одного предыдущего значения
. Метод Эйлера является явным одношаговым методом.
Оценка погрешности метода Эйлера.
Локальной погрешностью метода называется величина . Найдем величину локальной погрешности метода Эйлера:
, при условии, что
. Другими словами
погрешность, которую допускает за один шаг метод, стартующий с точного решения. Глобальной погрешностью (или просто погрешностью) численного метода называют сеточную функцию
со значениями
в узлах. В качестве меры абсолютной погрешности метода примем величину
. Можно показать, что для явных одношаговых методов из того, что локальная погрешность имеет вид
следует, что
, где
и M — некоторые константы. Таким образом, метод Эйлера является методом первого порядка точности. Для нахождения решения задачи Коши с заданной точностью
требуется найти такое приближенное решение
, для которого величина глобальной погрешности
. Так как точное решение задачи неизвестно, погрешность оценивают с помощью правила Рунге.
Правило Рунге оценки погрешностей. Для практической оценки погрешности проводят вычисления с шагами h и h/2. За оценку погрешности решения, полученного с шагом h/2, принимают величину, равную 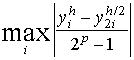
Модификации метода Эйлера.
Метод Эйлера обладает медленной сходимостью, поэтому чаще применяют методы более высокого порядка точности. Второй порядок точности по имеет усовершенствованный метод Эйлера :
. Этот метод имеет простую геометрическую интерпретацию. Метод Эйлера называют методом ломаных, так как интегральная кривая на отрезке
заменяется ломаной с угловым коэффициентом
. В усовершенствованном методе Эйлера интегральная кривая на отрезке
заменяется ломаной с угловым коэффициентом, вычисленным в средней точке отрезка
. Так как значение
в этой точке неизвестно, для его нахождения используют метод Эйлера с шагом
.
Еще одна модификация метода Эйлера второго порядка — метод Эйлера-Коши:
Решение систем дифференциальных уравнений методом Эйлера.
Пусть требуется решить нормальную систему дифференциальных уравнений:
с начальными условиями: ,
, …,
Эту систему в векторной форме можно записать в виде: ,
. Здесь
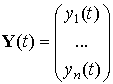

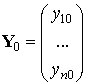
,
.
При решении любой математической задачи важную роль играет вопрос существования и единственности решения. Но положительный ответ на этот вопрос еще не гарантирует достоверности практических результатов, которые получены в результате решения математической задачи. Поясним это подробнее.
При постановке математической задачи, как правило, име-ются параметры, которые не фиксированы и могут принимать произвольные значения из некоторых интервалов. В качестве таких параметров могут рассматриваться данные измерений, результаты решения каких-то других задач, результаты экс-пертных оценок и т.п., которые задаются приближенно. Если при каждом допустимом наборе значений параметров (входных данных математической задачи) задача имеет решение, и притом единственное, то возникает зависимость решения от указанных параметров.
Результатом решения математической задачи является вычисление на основе входных данных некоторого набора числовых значений — выходных данных математической задачи. Как входные, так и выходные данные можно рассматривать в качестве элементов соответствующих нормированных пространств. Это позволяет сравнивать между собой различные варианты входных (выходных) данных и оценивать степень их близости, что приводит к понятию непрерывной зависимости решения задачи от входных данных.
Пусть х, x0 ∈ Rm представляют собой векторы входных данных некоторой математической задачи, а y, y0 ∈ Rm — со-ответствующие этим входным данным решения, или выходные данные. Скажем, что решение задачи непрерывно зависит от входных данных, если для любого x0 и для любого ε > 0 существует такое δ > 0, что при ||x — x0|| < δ имеем ||у — y0|| < ε, где ||·|| — некоторая норма в Rm.
Математическую задачу называют корректной или корректно поставленной, если ее решение существует, един-ственно и непрерывно зависит от входных данных. Бели одно из трех условий нарушается (решение неединственно, не существует или нарушается требование непрерывной зависимости от входных данных), то говорят о некорректной математической задаче.
Понятие корректной задачи легко конкретизировать для системы линейных алгебраических уравнений (СЛАУ) с невырожденной матрицей. Напомним, СЛАУ Ах = b с квадратной матрицей А порядка n имеет единственное решение тогда и только тогда, когда матрица А невырождена [III]. Входными данными задачи решения СЛАУ следует считать элементы ее матрицы и правые части уравнений.
Столбец неизвестных х и столбец правых частей b СЛАУ Ах = Ъ можно трактовать как векторы n-мерного линейного арифметического пространства Rn, в котором задана некоторая норма ||·||. Этой норме соответствует индуцированная норма матрицы, для которой будем использовать то же обозначение ||·||. Изменение входных данных означает, что наряду со СЛАУ Ах = b с решением надо рассмотреть другую возмущенную систему ~Ах = ~b с матрицей ~А = А + ΔА и столбцом правых частей b = b + Δb, которая отличается от исходной системы возмущением матрицы системы ΔА и возмущением столбца правых частей ΔЬ. Решением возмущенной системы будет некоторый столбец ~x, который отличается от х на столбец Δх = ~х — x, называемый возмущением решения. Величины ||ΔА||, ||Δb|| и ||Δx|| можно интерпретировать как абсолютные погрешности соответственно матрицы системы, правой части и решения, если компоненты исходной системы рассматривать как точные. При этом относительные погрешности будут выражаться формулами
Корректность задачи решения СЛАУ Ах = b с квадратной невырожденной матрицей заключается в том, что малым от-носительным погрешностям матрицы системы и правой части отвечает малая относительная погрешность решения системы. Чтобы показать, что это действительно так, нужно относительную погрешность решения оценить с помощью относительных погрешностей матрицы и правой части.
Определение 11.1. Для квадратной невырожденной матрицы А величину
c(A) = ||A||||A-1|| (11.1)
называют ее числом обусловленности.
Число обусловленности матрицы всегда положительно и зависит от заданной нормы матриц. Эта характеристика имеет следующие свойства.
Свойство 11.1. Для любой невырожденной матрицы А число ее обусловленности совпадает с числом обусловленности обратной матрицы А-1:
c(A) = c(A-1).
с(А-1) = ||A-1|| ||(A-1)-1|| = |A-1|| ||А|| = с(А).
Свойство 11.2. Бели норма матриц кольцевая, то с(АВ) ≤ с(А)с(B).
Согласно свойствам обратной матрицы, (АВ)-1 = B-1А-1, а согласно условию, что норма кольцевая, ||АВ|| ≤ ||А||||В||. Поэтому
с(АВ) = ||AB|| ||(AВ)-1| ≤ ||A|| ||В|| ||В-1|| ||А-1|| = (||A||||A-1||)(||В|||||B-1||)=с(А)с(В).
Свойство 11.3. Если матричная норма кольцевая, то с(А) ≥ 1 для любой невырожденной матрицы А.
Для единичной матрицы Е, согласно равенству ЕЕ = Е и свойству 11.2, получаем
с(Е) = с(ЕЕ) ≤ с(Е) с(Е).
Так как с(Е) > 0, то, сокращая в неравенстве на с(Е), имеем с(Е) ≥ 1.
Для невырожденной матрицы А существует обратная матрица A-1, при этом AA-1 = Е. Согласно свойствам 11.1 и 11.2, заключаем, что
1 ≤ с(Е) = с(АА-1) ≤ с(A) c(A-1) = (с(A))2.
Значит, с (А) ≥ 1, так как число обусловленности матрицы неотрицательное.
Свойство 11.4. Если ||·|| — спектральная норма, то число обусловленности симметрической матрицы А равно
с(А) = |λmax|/|λmin|,
где λmах, λmin — ее собственные значения, соответственно наибольшее и наименьшее по абсолютной величине.
Спектральная норма симметрической матрицы равна макси-мальной из абсолютных величин |λi| ее собственных значений. Действительно, если симметрическая матрица имеет порядок n, то в Rn существует ортонормированный базис е1,…, еn из ее собственных векторов. Пусть соответствующие им собствен-ные значения связаны неравенствами |λ1| ≥ |λ2| ≥ … ≥ |λn|. То
гда для любого вектора х = α1е1 +… + αnеn имеем
Но на самом деле в приведенном неравенстве должен стоять знак равенства, так как для х = е1 имеем
||Ax||/||x|| = ||λе1е1||/||е1|| = |λе1|
Отметим, что если λ — собственное значение невырожден-ной матрицы А, то λ-1 — собственное значение матрицы А-1, так как равенство Ах = λх, х ≠ 0, равносильно равенству А-1х = λ-1x. Кроме того, если А — симметрическая матрица, т.е. АT = А, то и А-1 — симметрическая матрица, так как (A-1)T = (АT)-1 = А-1 Поэтому, если λmах и λmin — соответственно наибольшее и наименьшее по абсолютной величине собственные значения матрицы А, то ||A|| = |λmах|, ||A-1|| = |λ-1min|. Следовательно, с(А) = ||А||||A-1|| = |λmax| |λ-1min|.
Число обусловленности матрицы А в значительной степени определяет чувствительность СЛАУ Ах = Ь к погрешностям в коэффициентах матрицы и в правых частях уравнений: чем больше это число, тем выше погрешность решения при данном уровне погрешностей входных данных. Эту связь показывает следующая теорема.
Теорема 11.1. Если матрица А невырождена и
||ΔA||<||A-1||-1 , (11.2)
где ||·|| — произвольная кольцевая норма матриц, то матрица ~А = А + ΔА тоже невырождена и верна следующая оценка для относительной погрешности решения
Замечание 11.1. Если выполняется неравенство (11.2), то
В этом случае в правой части неравенства (11.3) деления на нуль нет, и она положительная.
-
Линейные операции над векторами
-
Базис. Cкалярное произведение
-
Векторное и смешанное произведения векторов
-
Декартова система координат. прямая на плоскости
-
Плоскость в пространстве
-
Прямая в пространстве
-
Кривые второго порядка — I
-
Кривые второго порядка — II
-
Поверхности второго порядка
-
Матрицы и операции с ними
-
Обратная матрица
-
Ранг матрицы
-
Системы линейных алгебраических уравнений
-
Свойства решений однородных и неоднородных СЛАУ



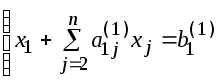
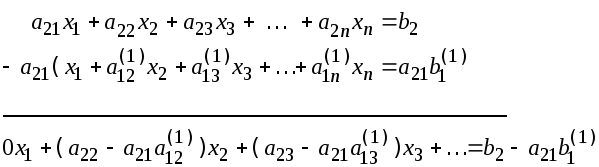

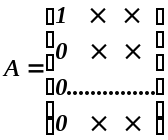
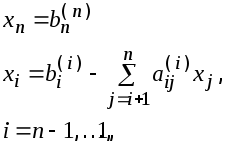
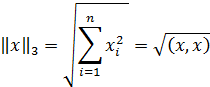
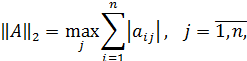
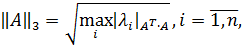
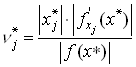


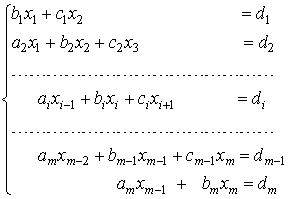
.gif)
.gif)