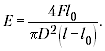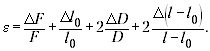И снова о погрешностях
Окончание. См. № 15/07
Д.А.ИВАШКИНА,
лицей г. Троицка, Московская обл.
aivashkin@mail.ru
И снова о погрешностях
4. Учёт случайных погрешностей при
прямых измерениях
Если, проведя одно и то же измерение
несколько раз, вы видите, что результат остаётся
одним и тем же, то случайные погрешности
эксперимента малы, их не следует учитывать. Но
если при повторении измерения получаются разные
значения, то следует взять среднее значение из
серии измерений:
где n – число измерений. Как
узнать, какова погрешность результата? Логично, и
ученики сами обычно предлагают это, определить
среднее отклонение результата от среднего
значения. Полученная величина носит название средней
арифметической ошибки: Она показывает, на сколько в
среднем каждое измеренное значение отклоняется
от среднего значения. Но эта величина слабо
зависит от количества проведённых измерений. В
чём же тогда смысл многократных измерений?
Для среднеквадратичной погрешности,
которая определяется немного сложнее:
есть простое правило: средняя
квадратичная погрешность среднего
арифметического равна средней квадратичной
погрешности отдельного результата, делённой на
корень квадратный из числа измерений: Из формулы ясно,
что с увеличением числа измерений случайная
погрешность среднего значения уменьшается.
Поэтому необходимо проводить столько измерений,
чтобы случайная погрешность стала меньше
значения систематической погрешности данного
измерения.
К сожалению, в лабораторных работах и
при любых других экспериментах в школе провести
достаточное количество измерений невозможно в
силу нехватки времени. Как поступать, может
решить сам учитель. На мой взгляд, для нахождения
средней арифметической погрешности среднего
значения можно использовать формулу,
аналогичную формуле для средней квадратичной
ошибки:
Хотя эта формула и неверна, она
помогает понять смысл проведения большого числа
измерений. Использоваться же она будет всего в
нескольких работах, и, следовательно, нет нужды
специально обучать нахождению погрешности
среднего значения. Зато, получив в этих работах
случайную погрешность меньше погрешности
систематической, ученик запомнит, что каждое
измерение следует производить несколько раз при
малейшем подозрении, что в данном эксперименте
имеется случайная погрешность. Как правило, уже
при пяти измерениях достигается необходимая
малость случайной погрешности по сравнению с
систематической.
5. Определение погрешности
результата косвенных измерений
К определению погрешности результата
косвенных измерений учащиеся готовы, на мой
взгляд, уже к 8-му классу. В зависимости от уровня
класса впервые метод границ [1, 12] можно
применить или в работе по сравнению количеств
теплоты при смешивании воды, или при нахождении
сопротивления проводника. Поясню на примерах.
-
Допустим, при нагревании холодной
воды в процессе смешивания мы имеем следующие
результаты измерений:
– температура холодной воды t1
= (16,0 ± 1,5) °С;
– температура смеси t = (43,0 ± 1,5) °С;
– объём холодной воды V1 = (80
± 2) мл = (80 ± 2) • 10–6 м3.
Получаем количество теплоты,
полученное холодной водой:
Q = 4190 Дж/(кг • °С) • 1000 кг/м3
• 80 • 10–6 м3 (43 – 16) °С = 9050,4 Дж.
(1)
Возникает вопрос: а какова погрешность
полученного значения? Другими словами, на
сколько мы можем ошибиться, если точные значения
не равны измеренным, а лежат где-то в интервале,
даваемом погрешностью? Например, начальная
температура воды может быть равна 16,5 °С, 17,0 °С и
т.д. Тогда вычисленное количество теплоты будет
меньше. Логично посмотреть, на сколько мы можем
ошибиться по максимуму. Максимальное количество
теплоты получится, если взять для всех
сомножителей максимальные значения, т.е. верхние
границы интервалов значений с погрешностью, для
уменьшаемого взять верхнюю границу значения, а
для вычитаемого – нижнюю:
Qв = 4190 Дж/(кг • °С) • 1000
кг/м3 • 82 • 10–6 м3 (44,5 – 14,5)°С = 10 307,4 Дж.
Аналогично вычисляем нижнюю границу
значения количества теплоты:
Qн = 4190 Дж/(кг • °С) • 1000
кг/м3 • 78 • 10–6 м3 (41,5 – 17,5) °С = 7843,68
Дж.
В данных пределах и лежит искомое
значение. Чтобы сравнивать методом интервалов
это значение с количеством теплоты, отданным
горячей водой, надо округлить значения верхней и
нижней границ. Лучше это сделать, оценив
абсолютную погрешность найденного значения
количества теплоты.
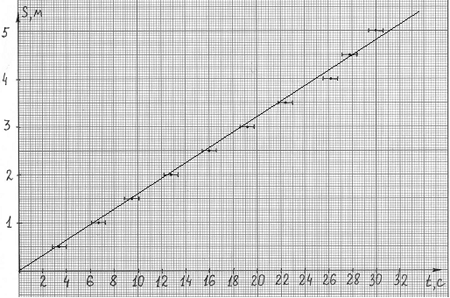
Рис. 2
Из рис. 2 видно, что
Найденное выше значение (1) близко к (3),
поэтому его не стоит находить ещё раз. А вот для
погрешности найдём с помощью (2):
(две
значащие цифры, т.к. первая «1»). Поэтому
количество теплоты, полученное холодной водой,
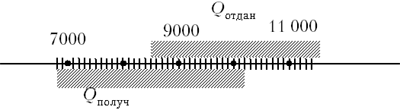
можно округлить: Qполуч = 9000 Дж ±
1200 Дж (т.е. между 7800 Дж и 10 200 Дж). Если количество
теплоты, отданное горячей водой, лежит между 8500
Дж и 11 500 Дж (Qотдан = 10 000 Дж ± 1500 Дж), то
можно видеть, что эти количества теплоты
совпадают в пределах погрешности эксперимента
(рис. 3).
Рис.3
-
Определение сопротивления резистора.
Пусть измеренные значения напряжения и силы тока
следующие:
– U = 2,60 В ± 0,15 В (инструментальная
погрешность 0,15 В; погрешность отсчёта может быть
взята равной 0,05 В, т.е. в 3 раза меньше
инструментальной, поэтому ею можно пренебречь);
– I = 1,2 А ± 0,1 А (инструментальная
погрешность 0,05 А, погрешность отсчёта 0,05 А).
Тогда для сопротивления получаем:
Но на самом резисторе написано: «2 ± 0,1 ». Получается, что
мы неверно определили сопротивление? Рассчитаем
погрешность нашего определения значения
сопротивления:
Uв = 2,75 В; Uн = 2,45 В; Iв
= 1,3 А, Iн = 1,1 А;
Полученное экспериментально значение
сопротивления R = (2,2 ± 0,3) Ом совпадает в
пределах погрешности со значением R = (2,0 ± 0,1)
Ом, указанным на резисторе.
С помощью метода границ можно вывести
и формулы для погрешности при обобщении темы
«Определение погрешности косвенных измерений»,
но уже в 9-м классе.
Определение погрешности разности. Пусть
А = В – С. Рассчитаем погрешность А в
общем виде:
Ав = Вв – Сн
= (В + В)
– (С – С)
= (В – С) + (В
+ С);
Ан = Вн – Св
= (В – В)
– (С + С)
= (В – С) – (В
+ С);
Полученное очень важно: в некоторых
работах в формулах для вычисления результата
встречается разность двух близких по значению
величин, что приводит к большой относительной
погрешности результата.
-
В cтарой работе «Определение модуля
Юнга резины» [11] удлинение резинового жгута
находилось как разность его результирующей и
начальной длин. Если условия опыта таковы, что
эта разность мала, например, составляет 1,5 см, то
относительная погрешность определения разности(погрешность
отсчёта взята гораздо меньше инструментальной
погрешности). Ясно, что такое измерение
использовать для определения модуля Юнга
нежелательно, – может получиться погрешность
больше 100%. Лучше увеличить нагрузку на жгут.
Аналогичная проблема возникает в работе
«Измерение ЭДС и внутреннего сопротивления
источника» [2] (одно сопротивление должно быть в
несколько раз больше другого) и др.
Определение погрешности частного
двух величин. Пусть Рассчитаем погрешность в общем виде:
Такую формулу трудно запоминать.
Поэтому найдём относительную погрешность
величины А:
Итак, относительная погрешность
частного равна сумме относительных погрешностей
величин, входящих в него. Такая же формула
получается и для относительной погрешности
произведения.
Важным я считаю не сам процесс расчёта
погрешности. Эти формулы дают мощный инструмент
для оценки обоснованности проведения
эксперимента. При их использовании легко
объяснить, при измерении какой из величин
следует увеличить точность, чтобы получить
лучший результат.
Рассмотрим формулу для нахождения
модуля Юнга:
Если воспользоваться для расчёта погрешности
результата методом границ, то неясным останется,
какая из величин в формуле вносит наибольшую
погрешность.
Для нахождения относительной
погрешности результата лучше воспользоваться
формулой:
При подстановке значений оказывается,
что слагаемое
даёт максимальный вклад в сумму, а остальные
слагаемые в несколько раз меньше, так что ими
можно пренебречь. Если l – l0 будет
невелико, то значение относительной погрешности
окажется очень большим, порой выше 100%. Какой
вывод сделают в таком случае ученики?
Такая ситуация – пример того, как
применение упрощённого способа вычисления
погрешностей может привести к большим ошибкам.
Конечно же, этот эксперимент совершенно
обоснован, с помощью него можно найти модуль
Юнга. Только следует выбрать те измерения, где l
– l0 достаточно велико, и не забыть
пренебречь малыми слагаемыми при расчёте
погрешности.
6. Определение коэффициента
прямой пропорциональности
В лабораторных работах нередко
встречается ситуация, когда необходимо по
графику определить коэффициент
пропорциональности в зависимости одной величины
от другой. И здесь в учебниках встречаются две
ситуации.
В работе «Определение модуля Юнга» [13]
после нахождения модуля Юнга для измерений с
тремя различными нагрузками учащимся
предлагается найти среднее арифметическое трёх
полученных значений. Такой подход ошибочен, т.к.
каждое значение получено с различными
систематическими погрешностями, т.е. с разной
степенью точности. Нельзя суммировать эти
значения «с одинаковым весом». При подобных
вычислениях в теории ошибок находится сумма этих
значений с разными коэффициентами.
Далее, в работе «Измерение жёсткости
пружины» [7] в аналогичной ситуации совершенно
справедливо отмечено, что, поскольку жёсткость
пружины в каждом из опытов получена при разных
условиях, среднее арифметическое этих значений
находить нельзя. И предлагается найти среднее
значение коэффициента жёсткости по графику как
коэффициент пропорциональности. Однако,
поскольку учащиеся не могут найти погрешность
найденного таким образом коэффициента
пропорциональности, предлагается взять в
качестве этой погрешности погрешность
наихудшего результата. Я считаю, что такой подход
не оправдан. Зачем брать погрешность самого
ненадёжного результата, если сам способ
нахождения коэффициента жёсткости из графика
применяется для того, чтобы определить этот
коэффициент наиболее точно? Думаю, авторы просто
не хотели заострять внимание на этом вопросе.
На мой взгляд, для определения
коэффициента пропорциональности по графику
можно предложить несколько вариантов.
Вариант 1. Самый простой, а потому
пригодный для младших классов. Отмечаем на
графике экспериментальные значения с указанием
погрешности. Обращаем внимание учащихся на то,
что если бы мы не нанесли погрешности на графики,
то провести прямую было бы затруднительно. В 7-м
классе достаточно просто отметить тот факт, что
зависимость между двумя величинами прямо
пропорциональна. Но если всё-таки необходимо
найти значение коэффициента пропорциональности,
можно обойтись без расчёта погрешности, отметив
только, что этот способ (многократные измерения
при различных условиях и построение графика)
используется именно для того, чтобы уменьшить
погрешность результата.
Вариант 2. Чертим прямую, находим
экспериментальную точку, которая лежит ближе
всего к прямой, и именно эту точку и считаем самой
точной. Остаётся вычислить результат для неё по
обычным формулам, рассчитав также и погрешность.
Вариант 3. Самый логичный. Пробуем
провести через точки вместе с их погрешностями
две прямые: с наибольшим и с наименьшим наклоном.
Значения коэффициентов для них и будут верхней и
нижней границами для результата. Зная границы,
рассчитываем среднее значение коэффициента и
погрешность. Данная погрешность неявно будет
содержать в себе как систематическую
погрешность экспериментально измеренных
величин, так и случайную погрешность определения
среднего, но уже с учётом точности каждого
результата. Этот вариант годится для
использования в экспериментах, когда
коэффициент должен быть оценён достаточно точно.
Но он достаточно сложен, поэтому не стоит его
использовать во всех случаях.
Вариант 4. Использование
встроенных программ в калькуляторах или готовых
компьютерных программ для вычисления
коэффициентов по методу наименьших квадратов.
Этот способ пригоден для практикума в старших
классах и/или в классах физматпрофиля. К
сожалению, в такие программы, как правило,
встроен метод наименьших квадратов, не
учитывающий погрешностей экспериментальных
точек. Применение имеет смысл в случаях, когда
погрешности всех точек практически одинаковы
или когда доминирующей является случайная
погрешность. Она и будет учтена.
Какой из этих вариантов выбрать, может
решать сам учитель. К счастью, таких работ
довольно мало. Продемонстрируем все эти варианты
на примере.
-
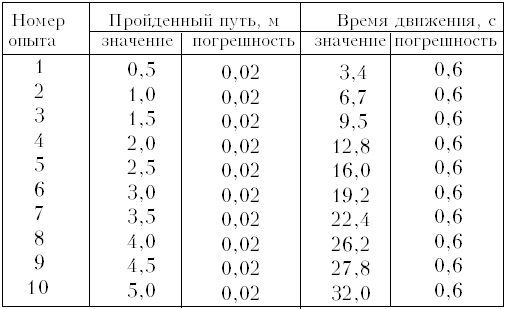
Возьмём данные эксперимента по
зависимости пути от времени равномерного
движения (машинка из конструктора с
электрическим приводом):
Действуя так, как описано в варианте 1,
строим график (рис. 4).
Рис. 4
Так как точек на графике много, можно с
уверенностью утверждать, что 8-я и 10-я точки
являются «выбросами», т.е. измерены небрежно.
Учитывая погрешность эксперимента, можно
провести прямую практически единственным
способом: соответствующая скорость 0,16 м/с. Если
воспользоваться методом наименьших квадратов
(например, встроенной функцией ЛИНЕЙН в
программе MicrosoftExcel), то для коэффициента мы
получим значение 0,158 ± 0,002 м/с (вариант 4).
Для варианта 2 подходит 3-я точка.
Скорость, вычисленная по данным для этой точки,
0,158 м/с. Рассчитаем погрешность: Так как относительная
погрешность пути мала по сравнению с
относительной погрешностью времени,
пренебрегаем ею. Абсолютная погрешность
результата: 0,063
• 0,158 = 0,010 м/с. То есть скорость, вычисленная в
варианте 2: (0,158 ± 0,010) м/с.
Из приведённого примера видно, что
значения коэффициента пропорциональности
получаются очень близкими. В этом примере
погрешности отдельных измерений были достаточно
малы, а точек, наоборот, было много. Рассмотрим
пример, когда погрешности, напротив, велики, а
количество опытов в силу объективных причин
мало.
-
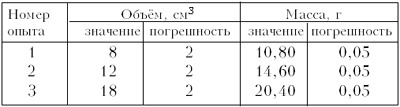
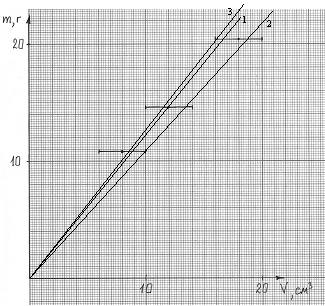
Найдём плотности пластмассы путём
измерения массы и объёмов тел.
В случае варианта 1 прямую проводим
так, чтобы количество точек над и под прямой было
одинаково (рис. 5), т.е. в данном случае – одна
сверху, одна снизу (прямая 1). Плотность в
этом случае равна 1,23 г/см3.
Рис. 5
В случае варианта 2 пригодна 2-я точка.
Для неё значение плотности (1,2 ± 0,2) г/см3.
Вариант 3: проведём прямые 2 и 3.
Для прямой 2 коэффициент пропорциональности
1,09 г/см3 является нижней границей
искомого значения плотности, а для прямой 3
(1,27 г/см3) – верхней. Полусумма этих
значений есть значение плотности (1,18 г/см3),
а полуразность – значение погрешности (0,09 г/см3).
Вариант 4 в данном случае менее
пригоден, т.к. не учитывает больших значений
погрешностей при измерении объёма с помощью
мерного цилиндра, но и в этом варианте плотность
(1,18 ± 0,05) г/см3.
Следует заметить, что в двух последних
примерах на графиках были обозначены только
погрешности вдоль горизонтальной оси, т.к.
погрешности значений второй переменной были
очень малы.
Послесловие
Научиться обрабатывать результаты
экспериментов учащиеся могут, лишь обрабатывая
результаты экспериментов. Это означает, что
помимо стандартного набора лабораторных работ
необходимо проводить много фронтальных и
демонстрационных экспериментов с обработкой
результатов. Это большая работа, и я хочу
пожелать успехов всем учителям, кто вступит на
этот путь или уже стоит на нём.
Литература
1. Анофрикова С.В., Стефанова Г.П.
Практическая методика преподавания физики.
Часть первая. – Астрахань: Издательство
Астраханского ГПИ, 1995.
2. Физика: Под ред. А.А.Пинского: Учебник
для 10 кл. школ и классов с угл. изучением физики. –
М.: Просвещение, 2002.
3. Попова О.Н. Обучение учащихся
выявлению устойчивых связей и отношений между
физическими величинами: Методическое пособие
для учителей физики. – Элиста: Элистинский лицей,
1998.
4. Анофрикова С.В. Азбука
учительской деятельности, иллюстрированная
примерами деятельности учителя физики. Ч. 1.
Разработка уроков. – М.: МПГУ, 2001.
5. Пёрышкин А.В. Физика-8. – М.:
Дрофа, 2004.
6. Громов С.В., Родина Н.А. Физика-8.
– М.: Просвещение, 2000.
7. Кикоин И.К., Кикоин А.К. Физика-10.
Механика. – М.: Просвещение, 2001.
8. Фронтальные лабораторные занятия по
физике в 7–11 классах общеобразовательных
учреждений. Книга для учителя: Под ред. В.А.Бурова,
Г.Г.Никифорова. – М.: Просвещение, Учебная
литература, 1996.
9. Зайдель А.Н. Элементарные оценки
ошибок измерений. – Л.: Наука, 1967.
10. Хорозов С.А. Работа над
ошибками: В кн. «Энциклопедия для детей», т. 16
«Физика», ч. 1 «Биография физики. Путешествие в
глубь материи. Механистическая картина мира». –
М.: Аванта+, 2000.
11. Мякишев Г.Я., Буховцев Б.Б., Сотский
Н.Н. Физика-10. – М.: Просвещение, 2004.
12. Кирик Л.А. Физика-9: Методические
материалы. – М.: Илекса, 2003.
13. Шахмаев Н.М., Шахмаев С.Н., Шодиев
Д.Ш. Физика-10. – М.: Просвещение, 1994.
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
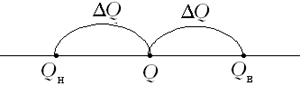
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})
Загрузить PDF
Загрузить PDF
При измерении чего-либо можно предположить, что есть некоторое «истинное значение», которое лежит в пределах диапазона значений, которые вы нашли. Для расчета более точной величины нужно взять результат измерения и оценить его при прибавлении или вычитании погрешности. Если вы хотите научиться находить такую погрешность, выполните следующие действия.
-
1
Выражайте погрешность правильно. Допустим, при измерении палки ее длина равна 4,2 см плюс-минус один миллиметр. Это означает, что палка примерно равна 4,2 см, но на самом деле может быть немного меньше или больше этого значения — с погрешностью до одного миллиметра.
- Запишите погрешность как: 4,2 см ± 0,1 см. Вы также можете переписать это как 4,2 см ± 1 мм, так как 0,1 см = 1 мм.
-
2
Всегда округляйте значения измерений до того же знака после запятой, что и в погрешности. Результаты измерений, которые учитывают погрешность, как правило, округляются до одной или двух значащих цифр. Наиболее важным моментом является то, что нужно округлить результаты до того же знака после запятой, что и в погрешности, чтобы сохранить соответствие.
- Если результат измерения 60 см, то и погрешность следует округлять до целого числа. Например, погрешность этого измерения может быть 60 см ± 2 см, но не 60 см ± 2,2 см.
- Если результат измерения 3,4 см, то погрешность округляется до 0,1 см. Например, погрешность этого измерения может быть 3,4 см ± 0,7 см, но не 3,4 см ± 1 см.
-
3
Найдите погрешность. Допустим, вы измеряете линейкой диаметр круглого шара. Это сложно, так как из-за кривизны шара будет трудно померить расстояние между двумя противоположными точками на его поверхности. Скажем, линейка может дать результат с точностью до 0,1 см, но это не значит, что вы можете измерить диаметр с той же точностью.[1]
- Изучите шар и линейку, чтобы получить представление о том, с какой точностью вы можете измерить диаметр. У стандартной линейки четко видна разметка по 0,5 см, но, возможно, вы сможете измерить диаметр с большей точностью, чем эта. Если вы думаете, что сможете измерить диаметр с точностью до 0,3 см, то погрешность в этом случае равна 0,3 см.
- Измерим диаметр шара. Допустим, вы получили результат около 7,6 см. Просто укажите результат измерения вместе с погрешностью. Диаметр шара составляет 7,6 см ± 0,3 см.
-
4
Рассчитайте погрешность измерения одного предмета из нескольких. Скажем, вам даны 10 компакт-дисков (CD), при этом размеры каждого одинаковы. Допустим, вы хотите найти толщину всего одного CD. Эта величина настолько мала, что погрешность практически невозможно вычислить. Тем не менее, чтобы вычислить толщину (и ее погрешность) одного CD, вы можете просто разделить результат измерения (и его погрешность) толщины всех 10 CD, сложенных вместе (один на другого), на общее количество CD.[2]
- Допустим, что точность измерения стопки CD с помощью линейки 0,2 см. Итак, ваша погрешность ± 0,2 см.
- Допустим, толщина всех CD равна 22 см.
- Теперь разделим результат измерения и погрешность на 10 (число всех CD). 22 см/10 = 2,2 см и 0,2 см/10 = 0,02 см. Это означает, что толщина одного компакт-диска 2,20 см ± 0,02 см.
-
5
Измерьте несколько раз. Для повышения точности измерений, будь то измерение длины или времени, замерьте искомую величину несколько раз. Вычисление среднего значения из полученных значений увеличит точность измерения и расчета погрешности.
Реклама
-
1
Проведите несколько измерений. Допустим, вы хотите найти, сколько времени падает мяч с высоты стола. Чтобы получить наилучшие результаты, измерьте время падения насколько раз, например, пять. Потом нужно найти среднее значение из пяти полученных значений измерений времени, а затем для наилучшего результата добавить или вычесть среднеквадратичное отклонение.[3]
- Допустим, в результате пяти измерений получены результаты: 0,43 с, 0,52 с, 0,35 с, 0,29 с и 0,49 с .
-
2
Найдите среднее арифметическое. Теперь найдите среднее арифметическое путем суммирования пяти различных результатов измерений и разделив результат на 5 (количество измерений). 0,43 + 0,52 + 0,35 + 0,29 + 0,49 = 2,08 с. 2,08 / 5 = 0,42 с. Среднее время 0,42 с.
-
3
Найдите дисперсию полученных значений. Для этого, во-первых, найдите разницу между каждой из пяти величин и средним арифметическим. Чтобы сделать это, вычтите из каждого результата 0,42 с.[4]
-
- 0,43 с — 0,42 с = 0,01 с
- 0,52 с — 0,42 с = 0,1 с
- 0,35 с — 0,42 с = -0,07 с
- 0,29 с — 0,42 с = -0,13 с
- 0,49 с — 0,42 с = 0,07 с
- Теперь сложите квадраты этих разниц: (0,01) 2 + (0,1) 2 + (-0,07) 2 + (-0,13) 2 + (0,07) 2 = 0,037 с.
- Найти среднее арифметическое этой суммы можно, разделив ее на 5: 0,037 / 5 = 0,0074 с.
-
-
4
Найдите среднеквадратичное отклонение. Чтобы найти среднеквадратичное отклонение, просто возьмите квадратный корень из среднего арифметического суммы квадратов. Квадратный корень из 0,0074 = 0,09 с, так что среднеквадратичное отклонение равно 0,09 с.[5]
-
5
Запишите окончательный ответ. Чтобы сделать это, запишите среднее значение всех измерений плюс-минус среднеквадратичное отклонение. Поскольку среднее значение всех измерений равно 0,42 с, а среднеквадратичное отклонение 0,09 с, то окончательный ответ 0,42 с ± 0,09 с.
Реклама
-
1
Сложение. Чтобы сложить величины с погрешностями, сложите отдельно величины и отдельно погрешности.[6]
- (5 см ± 0,2 см) + (3 см ± 0,1 см) =
- (5 см + 3 см) ± (0,2 см + 0,1 см) =
- 8 см ± 0,3 см
-
2
Вычитание. Чтобы вычесть величины с погрешностями, вычтите величины и сложите погрешности.[7]
- (10 см ± 0,4 см) — (3 см ± 0,2 см) =
- (10 см — 3 см) ± (0,4 см + 0,2 см) =
- 7 см ± 0,6 см
-
3
Умножение. Чтобы умножить величины с погрешностями, перемножьте величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности (в процентах).[8]
Рассчитать можно только относительную погрешность, а не абсолютную, как и в случае со сложением и вычитанием. Чтобы узнать относительную погрешность, разделите абсолютную погрешность на измеренное значение, затем умножьте на 100, чтобы выразить результат в процентах. Например:- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
Следовательно: - (6 см ± 0,2 см) х (4 см ± 0,3 см) = (6 см ± 3,3 % ) x (4 см ± 7,5 %)
- (6 см x 4 см) ± (3,3 + 7,5) =
- 24 см ± 10,8 % = 24 см ± 2,6 см
- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
-
4
Деление. Чтобы разделить величины с погрешностями, разделите величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности.[9]
- (10 см ± 0,6 см) ÷ (5 см ± 0,2 см) = (10 см ± 6 %) ÷ (5 см ± 4 %)
- (10 см ÷ 5 см) ± (6 % + 4 %) =
- 2 см ± 10 % = 2 см ± 0,2 см
-
5
Возведение в степень. Для того, чтобы возвести в степень величину с погрешностью, возведите величину в степень, а относительную погрешность умножьте на степень.[10]
- (2,0 см ± 1,0 см)3 =
- (2,0 см)3 ± (50 %) x 3 =
- 8,0 см3 ± 150 % или 8,0 см3 ±12 см3
Реклама
Советы
- Вы можете дать погрешность как для общего результата всех измерений, так и для каждого результата одного измерения в отдельности. Как правило, данные, полученные из нескольких измерений, менее достоверны, чем данные, полученные непосредственно из отдельных измерений.
Реклама
Предупреждения
- Точные науки никогда не работают с «истинными» величинами. Хотя правильное измерение, скорее всего, даст величину в пределах погрешности, нет никакой гарантии, что это будет так. Научные измерения допускают возможность ошибок.
- Погрешности, описанные здесь, применимы только для случаев нормального распределения (распределения Гаусса). Другие распределения вероятностей требуют других решений.
Реклама
Об этой статье
Эту страницу просматривали 105 033 раза.
Была ли эта статья полезной?
Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2197.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2197.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2197.
А какая ваша оценка?
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше 


Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 

- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения

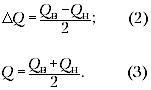
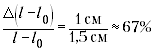 (погрешность
(погрешность