Определение радиуса кривизны линзы R, входящей в устройство колец Ньютона, а также оценка доверительного интервала и относительной погрешности в определении величины R
Страницы работы
Содержание работы
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
« ИНСТИТУТ ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА»СФУ
Лабораторная работа № 6
Определение радиуса кривизны линзы
с помощью колец Ньютона
Красноярск 2010 г.
Цель работы: Определение радиуса кривизны линзы R, входящей в устройство колец Ньютона, а также оценка доверительного интервала и относительной погрешности в определении величины R.
Оборудование: Оптическая скамья, осветитель, диафрагма, прибор Ньютона, линза-объектив, экран, светофильтр.
Кольца Ньютона наблюдаются в случае соприкосновении выпуклой поверхности плоско-выпуклой линзы малой кривизны с плоско-параллельной поверхностью. Воздушная прослойка между плоскостью и линзой имеет переменную толщину, разность хода интерферирующих их лучей зависит от толщины этой прослойки. Чем больше толщина воздушной прослойки, тем больше число наблюдаемых колец.
Кольца Ньютона могут наблюдаться в отраженном и проходящем свете.
В отраженном свете оптическая разность хода для колец Ньютона определяют, учитывая λ/2,условием:
,
В отраженном свете по условию образовании максимума:
,
Для минимумов в отраженном свете:
.
Так как на экране получаются увеличенные интерференционные кольца, то вначале надо рассчитать радиусы действительных колец:
,
Радиусы действительных колец рассчитывают для опыта с проходящим и отраженным светом. В первом случае берут радиусы колец определенного цвета, во втором – радиусы темных колец при условии, что в опыте с отраженным светом использовали фильтр того же цвета.
Радиус кривизны линзы, входящей в устройство колец Ньютона, определяется теоретически по формуле:
,
Так как практически трудно добиться идеального контакта сферической поверхности линзы и плоской пластинки в одной точке вследствие упругой деформации стекла и падения в место соприкосновения пылинки, то формулу использовать непосредственно нельзя: кольцу с номером m в действительности может соответствовать номер (m+p), где p – неизвестное целое число, одинаковое для всех колец. Для исключения числа p вычисление радиуса кривизны надо делать по разности квадратов радиуса двух колец:
.
Измеряем радиусы полученных колец:
; ; .
Вычисляем радиусы действительных колец по формуле:
,
где =155 мм=0,155 м; =445мм=0,445м.
;
;
;
После того как мы вычислили действительные радиусы колец, вычисляем радиус кривизны линзы по формуле:
,
Где =435 Нм=м,
;
;
.
Найдем среднее значение:
;
Найдем средне квадратичную погрешность:
;
Доверительный интервал найдем по формуле:
; ;
Найдем относительную погрешность:
.
Вывод: Мы определили радиусы кривизны линзы R, входящей в устройство колец Ньютона, а также оценили доверительный интервал и относительную погрешность в определении величины R.
Погрешности измерений, представление результатов эксперимента
п.1. Шкала измерительного прибора
Примеры шкал различных приборов:
п.2. Цена деления
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. |
Цена деления: begin triangle=frac\ triangle=frac<10-5><24+1>=frac15=0,2 c end
п.3. Виды измерений
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Определяется субъективным фактором, ошибками экспериментатора.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin triangle=frac= frac<1 text<см>><1+1>=0,5 text <см>end Инструментальная погрешность: begin d=frac<triangle><2>=frac<0,5><2>=0,25 text <см>end Истинное значение: (L_0=4 text<см>) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text <см>$$ Относительная погрешность: $$ delta=frac<0,25><4,00>cdot 100text<%>=6,25text<%>approx 6,3text <%>$$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin triangle=frac= frac<1 text<см>><9+1>=0,1 text <см>end Инструментальная погрешность: begin d=frac<triangle><2>=frac<0,1><2>=0,05 text <см>end Истинное значение: (L_0=4,15 text<см>) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text <см>$$ Относительная погрешность: $$ delta=frac<0,05><4,15>cdot 100text<%>approx 1,2text <%>$$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin m_0=frac<99,8+101,2+100,3><3>=frac<301,3><3>approx 100,4 text <г>end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end Находим среднее абсолютное отклонение: begin triangle_=frac<0,6+0,8+0,1><3>=frac<1,5><3>=0,5 text <(г)>end Мы видим, что полученное значение (triangle_) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin triangle m=maxleft<triangle_; dright>=maxleft<0,5; 0,05right> text <(г)>end Записываем результат: begin m=m_0pmtriangle m\ m=(100,4pm 0,5) text <(г)>end Относительная погрешность (с двумя значащими цифрами): begin delta_m=frac<0,5><100,4>cdot 100text<%>approx 0,050text <%>end
п.6. Представление результатов эксперимента
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac), мл |
| 1 | 20 | 40 | 4 | (frac<40-20><4+1>=4) |
| 2 | 100 | 200 | 4 | (frac<200-100><4+1>=20) |
| 3 | 15 | 30 | 4 | (frac<30-15><4+1>=3) |
| 4 | 200 | 400 | 4 | (frac<400-200><4+1>=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac<triangle><2>), мл |
Относительная погрешность (delta_V=frac<triangle V>cdot 100text<%>) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text<м>, x_2=(4,0pm 0,03) text <м>$$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin delta_1=frac<0,1><4,0>cdot 100text<%>=2,5text<%>\ delta_2=frac<0,03><4,0>cdot 100text<%>=0,75text <%>end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac<10><2>=5 (text<км/ч>), triangle v_2=frac<1><2>=0,5 (text<км/ч>) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text<км/ч>, v_2=(72pm 0,5) text <км/ч>$$ Скорость сближения равна сумме скоростей: $$ v_0=v_<10>+v_<20>, v_0=54+72=125 text <км/ч>$$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text <км/ч>$$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text <км/ч>$$ Относительная погрешность: $$ delta_v=frac<5,5><126,0>cdot 100text<%>approx 4,4text <%>$$ Ответ: (v=(126,0pm 5,5) text<км/ч>, delta_vapprox 4,4text<%>)
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac<0,1><2>=0,05 text<см>)
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text<см>, b=(60,10pm 0,05) text <см>$$ Относительные погрешности (не забываем про правила округления): begin delta_1=frac<0,05><90,20>cdot 100text<%>approx 0,0554text<%>approx uparrow 0,056text<%>\ delta_2=frac<0,05><60,10>cdot 100text<%>approx 0,0832text<%>approx uparrow 0,084text <%>end Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text<см>^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text<%>+0,084text<%>=0,140text<%>=0,14text <%>$$ Абсолютная погрешность: begin triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text<см>^2\ S=(5421,0pm 7,6) text<см>^2 end Ответ: (S=(5421,0pm 7,6) text<см>^2, delta_Sapprox 0,14text<%>)
Радиус круга равен 2см. Наидите погрешность допушенную при вычесления его площади,
Радиус круга равен 2см. Наидите погрешность допушенную при вычесления его площади, если погрешность при измерении длины радиуса одинакова: 1) 0,2см. 2) 0,1 ; 3)h
- Regina Marzjuk
- Алгебра 2018-12-14 22:34:38 18 2
Так как Sкр = пи*R^2 , то погрешность вычисления площади
В данном случае она соответственно одинакова:
1) Предельная относительная погрешность одинакова 0,2 / 2 = 0,1.
Условная погрешность вычисленной площади S круга одинакова
S/S = R/R + R/R = 0,1+0,1 = 0,2.
Тогда безусловная погрешность площади круга одинакова
S = 0,2S = 0,24 = 0,8
2) Предельная условная погрешность одинакова 0,1 / 2 = 0,05.
Условная погрешность вычисленной площади S круга одинакова
S/S = R/R + R/R = 0,05+0,05 = 0,1.
Тогда безусловная погрешность площади круга одинакова
S = 0,1S = 0,14 = 0,4
3) Предельная условная погрешность одинакова h/2.
Условная погрешность вычисленной площади S круга равна
S/S = R/R + R/R = h/2 + h/2 = h.
Тогда абсолютная погрешность площади круга равна
S = hS = h4 = 4h
http://reshator.com/sprav/fizika/7-klass/pogreshnosti-izmerenij-predstavlenie-rezultatov-eksperimenta/
http://obrazovalka.com/qa/algebra/40635-radius-kruga-raven-2sm-naidite-pogreshnost-dopushennuju-pri-vycheslenija-ego-ploshhadi-.html
Радиус круга равен 2см найдите погрешность допущеную при вычислении его площади если погрешность при измерении длины радиуса равна : 1.
0, 2см ; 2.
ДR ; 3.
0, 1см ; 4n.
Вопрос Радиус круга равен 2см найдите погрешность допущеную при вычислении его площади если погрешность при измерении длины радиуса равна : 1?, расположенный на этой странице сайта, относится к
категории Алгебра и соответствует программе для 10 — 11 классов. Если
ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска
похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему.
Для этого ключевые фразы введите в строку поиска, нажав на кнопку,
расположенную вверху страницы. Воспользуйтесь также подсказками посетителей,
оставившими комментарии под вопросом.
23
Содержание
-
Источники
погрешностей и их классификация
. …2 -
Приближенные
числа, их запись и действия над
ними………..3 -
Представление
чисел ЭВМ и связанные с ним погрешности..7 -
Погрешность метода
вычисления. Понятие об устойчивых
алгоритмах………………………………………………………………………….13
Контрольные вопросы
к лабораторной работе………………….
..16
Задания к лабораторной
работе………………………………………..
.17
Приложение
1………………………………………………………………….
.18
Список
литературы…………………………………………………………
..23
1.1
Источники
погрешностей и их классификация.
Анализ
ошибок (погрешностей) в численном
результате решения задачи должен
являться непременной частью любого
расчета, вне зависимости от того,
проводятся ли вычисления “вручную”
или при помощи ЭВМ. Погрешности решения
задач могут возникать вследствие
следующих причин:
1. Математическое
описание задачи является неточным, в
частности, неточно заданы исходные
данные.
2. Применяемый
метод решения задачи является приближенным,
например, получение результата требует
бесконечно большого числа арифметических
операций (или неприемлемо большого).
3. Используемый
инструмент для проведения вычислений
сам вносит погрешности. Например, при
выполнении вычислений на ЭВМ эта
погрешность возникает при вводе данных
в машину и при выполнении арифметических
операций.
В
соответствии с этой классификацией
погрешности называются следующим
образом: погрешность типа 1 — неустранимая
погрешность, типа 2 — погрешность метода
и типа 3 — вычислительная погрешность.
В
настоящей работе мы будем заниматься
оценкой погрешностей типа 1,2 и 3. Причем,
погрешность типа 1 мы будем рассматривать
только как погрешность задания исходных
данных, поскольку задача оценки качества
математической модели решается конкретной
наукой, поставляющей данную модель.
1.2
Приближенные числа, их запись и действия
над ними.
Пусть
х — точное (вообще говоря, неизвестное)
числовое значение некоторой величины;
х* — приближенное числовое значение этой
величины. Величина

приближенного числа х*, а величина
относительной погрешностью. Когда
точное значение числа х неизвестно,
будем выбирать в качестве абсолютной
и относительной погрешностей величиныи
,
которые называются предельными
погрешностями, соответственно абсолютной
и относительной.
Наиболее аккуратный
способ записи приближенного числа
должен указывать соответствующую ему
область неопределенности и, например,
может иметь вид:
,
т.е.
,
причем при
выписывании абсолютной погрешности не
рекомендуется удерживать более двух
значащих цифр, т.е. нужно производить
округление, оставив две значащие цифры.
При записи чисел
в большую таблицу указанная выше форма
записи будет громоздкой, потому можно
договорится представлять приближенное
число в таком виде, что по форме его
записи можно судить о погрешности. Такую
форму записи называют записью числа со
всеми верными цифрами. Подробно обсудим
ряд понятий, связанных с этим представлением
чисел.
Рассмотрим
представление (кодирование) чисел в
десятичной системе счисления на
конкретном примере:
Целое
число 123 имеет единицу разряда сотен,
двойку разряда десяток и тройку разряда
единиц. Любое число, в том числе и дробное,
представимо в виде суммы произведений
степеней десятки на цифры
{0,1,2,3,4,5,6,7,8,9}, причем числа, модуль которых
меньше 1 раскладываются по отрицательным
степеням десятки. В этом смысле любое
число
можно представить в виде:
где {
}
— цифры числа до десятичной точки, {}
— цифры числа после десятичной точки,— основание системы счисления. В нашем
случае,
но совершенно очевидно, чтоможет быть любым целым числом с
естественным ограничением.
При записи числа(мы сейчас отдельно не выделяем цифры
до и после десятичной точки), цифраназывается верной, если
.
Число х*, записанное со всеми верными
цифрами, выглядит следующим образом:
Иначе говоря, если
число х* записано со всеми верными
цифрами, то его погрешность не превосходит
единицы его младшего разряда. Приведем
примеры записи чисел с верными цифрами,
если задана абсолютная погрешность
числа
a)
б)
Пусть х* число
записано со всеми верными цифрами,
укажем его абсолютную погрешность:
a)
б)
Чтобы
показать, что абсолютная погрешность
числа 314000 не превышает 103,
(записать его со всеми верными цифрами),
его предварительно нормализуют (т.е.
записывают в виде 0.314000106)
и далее поступают аналогично рассмотренному
выше.
При выполнении
арифметических операций над приближенными
числами необходимо уметь оценивать
погрешности результата. Приведем правила
оценки погрешности для арифметических
операций:
a)
сложение и вычитание:
б) умножение и
деление:
Эти правила можно
сформулировать в следующем виде. При
сложении и вычитании приближенных чисел
предельная абсолютная погрешность
результата равна сумме абсолютных
погрешностей, а при умножении и делении
предельная относительная погрешность
результата равна сумме относительных
погрешностей.
Приведем
также правило приближенной оценки
погрешности значения функции
если заданы погрешности
Пример №1.
Радиус
круга измерен с точностью
Оценить погрешность расчета площади
круга.
Решение:
Площадь
круга
Абсолютную погрешность в вычислении
площади определим по формулеи относительную
Иногда
приходиться решать обратную задачу,
т.е. по заданной погрешности
функции
определить
погрешность x*. Как нетрудно видеть, эта
задача легко решается на основе
приведенной выше формулы.
Пример №2.
С
какой погрешностью следует измерять
радиус круга, чтобы погрешности вычисления
площади не превзошла
.
Решение:
В
предыдущем примере мы имели оценку
погрешности вычисления площади круга
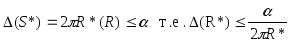
Задачи для
самостоятельного решения
-
Написать
число p
и число pn
в p-ичной
системе счисления. -
Составить таблицу
умножения и сложения для двоичной
системы счисления. -
Какие
из рациональных чисел могут быть точно
представлены конечными p-ичными
числами. -
Указать
какой-нибудь алгоритм деления p-ичных
чисел. -
Записать
числа
с
тремя верными цифрами и определить их
предельные абсолютные и относительные
погрешности. -
Сторона
квадрата приблизительно 1 м. С какой
точностью ее надо измерить, чтобы
погрешность определяемой площади
составила 1 см2. -
Корни
уравнения
, нужно получить с четырьмя верными
цифрами. С каким числом цифр необходимо
взять свободный член уравнения -
С
какой точностью необходимо измерить
диаметр шара
см, чтобы погрешность вычисления объема
составила 0,1 см3. -
Оценить пределы
применимости формулы линейной оценки
погрешности.
1.3
Представление чисел в ЭВМ и связанные
с ним погрешности.
Современные
ЭВМ оперируют с числами, представленными
в одной из приведенных ниже форм.
а) Форма с
фиксированной запятой.
Эта форма используется
для представления данных диапазон
изменения, которых, заранее известен.
Таковыми, могут являться денежные
величины 128 руб. 31 коп. (запятая у числа
12831 фиксирована на втором месте от левого
края числа). В этой форме обычно
представляются данные целого типа, хотя
в машинном представлении все числа
имеют модуль меньше единицы, число
знаков после запятой фиксировано и
число имеет следующий вид:
(3.1)
Здесь
— основание системы счисления,
—
целые, в пределах
,
t — длина разрядной сетки. Из формулы
(3.1) очевидно, что предельная абсолютная
погрешность представления числа есть,
если число имеет более чемзначащих цифр, и
в противном случае. Числа меньше, чем
представлены как ноль. При операциях
над числамимогут появиться числа
,
в этом случае (в зависимости от конкретной
реализации арифметики с фиксированной
запятой) может произойти аварийный
останов машины, обнуление результата
или число будет переписано в другой
форме.
б) Форма с плавающей
запятой.
Эта
форма используется для представления
данных диапазон изменения, которых
заранее неизвестен. Она является наиболее
распространенной формой представления
чисел в ЭВМ, при проведении научных
расчетов. При этом число, х представлено
в виде числа с фиксированной запятой
умноженного на масштабный множитель
(3.2)
где
— основание системы счисления;
— целые, в пределах
,
t — длина разрядной сетки. Наиболее
употребительны2,
10, 16. Типичные значения t=8, 16, 32, 64 и наиболее
распространен интервал показателя
масштабного множителя.
Числообычно называют показателем, а (
)-
мантиссой числа х (она, как правило,
задается в нормализованной форме т.е.).
Множество чисел с плавающей запятой,
которое мы будем обозначать F,
характеризуется следующими параметрами
:и
интервалом значений показателяМножество F чисел очевидно не является
бесконечным, Эти числа расположены
неравномерно, равномерность имеет место
только при фиксированном показателе.
Операции сложения и умножения чисел на
этом множестве очевидно коммутативны,
но не ассоциативны и не дистрибутивны.
Поскольку эти законы имеют основополагающее
значение для математического анализа,
то учет всех особенностей вычислений
на данном множестве чисел достаточно
сложен.
Рассмотрим
ряд простых примеров иллюстрирующих
возникновение погрешностей при операциях
с плавающей запятой. Операции сложения
и умножения, алгоритмы которых мы здесь
приведем, могут в деталях отличаться
от действительных, но эти различия, как
правило, можно игнорировать, говоря об
основных проблемах появления ошибок
связанных с вычислениями на ЭВМ. Из
формулы (3.2) следует, что предельная
относительная погрешность
представления числа х, не большие чем
,
т.е. корректная форма записи приближенного
числа х:
.
При сложении и
вычитании чисел с плавающей запятой
предварительно выравниваются порядки
чисел. Это означает, что мантисса меньшего
по абсолютной величине числа сдвигается
вправо на столько разрядов, сколько
необходимо, чтобы порядки стали
одинаковыми, а затем производится
сложение мантисс чисел. При умножении
и делении операции с мантиссами чисел
и их порядками производятся независимо.
Рассмотрим
пример сложения двух чисел на гипотетической
машине, в которой параметры арифметики
с плавающей запятой таковы:
Пусть имеем два числа:
После выравнивания
порядков получится следующий результат:
Во
втором числе цифры 2, 9 не могут быть
представлены в нашем множестве F и
поэтому будут утрачены. В результате
это скажется на абсолютной погрешности
суммы, а относительная погрешность
суммы по прежнему будет оцениваться
величиной
Более точное значение относительной
погрешности Е (машинное эпсилон), можно
определить в результате выполнения
программы, если мы определим Е, как
наименьшее число с плавающей запятой,
для которого еще имеет место неравенство:
Фрагмент
такой программы, которая дает значение
Е,
с точностью до некоторого множителя,
приведен в приложении 1. Там же приведены
программы, по которым можно определить
диапазон показателя порядка.
Задачи
для самостоятельного решения
-
Привести
примеры физических устройств, имеющих
p
устойчивых состояний. -
Предложить
какой-либо способ представления чисел
отличный от фиксированной и плавающей
запятой. Как при этом выполняются
операции над числами. -
Имеет ли место
неоднозначность представления каких-либо
чисел в форме с фиксированной и плавающей
запятой? -
Будет ли операция
умножения ассоциативной при каком-либо
способе округления? -
Будет ли операция
сложения ассоциативной при каком-либо
способе округления? -
Можно ли выбором
способа округления добиться выполнения
закона дистрибутивности? -
Привести примеры
возможных пар алгебраических операций
на ЭВМ, для которых выполняются законы
коммутативности, ассоциативности
и дистрибутивности. -
Для каких чисел
на ЭВМ операции сложения и умножения
с плавающей запятой выполняются
абсолютно точно? -
Выяснить, как
устроено округление на Вашей ЭВМ? -
Хорошо
известно, что ряд для
хорошо представляет экспоненту.
Предлагается найти (составив программу)
значениеи сравнить полученное значение со
значением, даваемым встроенной функцией. -
Найти
корни квадратного уравнения
Ответ проверить подстановкой решений
в уравнение. Объяснить полученный
результат. -
Для
функции Ф(х)=(т.н. интеграл вероятности или функция
Лапласа), вычислите ее значения для
х=0.5, 1.0, 5.0, 10.0 и сравните полученные
значения с данными таблицы. -
Будет ли десятичное
число 0.1 точно представимо в вашей
машине? Каково ближайшее число с
плавающей точкой среди чисел меньших
0.1? -
Вычислите
сумму ряда из задачи №12 для х=0, шаг 0.1
до 1 с ошибкой, не превышающей
.
-
Вычислить
сумму ряда
,
точностью 10-7. -
Дан круговой
сектор следующих размеров: АВ=2640;
АСВ=2640.5. Найти СМ, с точностью до 5
значащих цифр.
С

М
О
-
Составив программу,
определите параметры арифметики с
плавающей запятой для Вашей машины
(см. приложение 1). -
Определить
величину машинного нуля. (максимального
числа, представимого как ноль на ЭВМ). -
Построить графики
относительной и абсолютной погрешностей,
представления чисел с фиксированной
и плавающей запятой, как функцию величины
числа. -
Квадратное
уравнение
имеет два решения, даваемые формулой
.
Пусть арифметика с плавающей запятой
задана параметрами:,
получить решения, для случаев:
,
и произвести оценку
погрешности.
-
Рассмотрим
трехзначную десятичную плавающую
систему с усечением числа, имеющего
вид
,
гдеи
,
причем,
для.
Число нуль имеет единственное
представление.
Посредствоми
будем обозначать операции сложения и
умножения. Для всех чисел величиныи
определяются, как числа с плавающей
запятой, ближайшие ки
,
но не превосходящие их по модулю.
а) Сколько различных
чисел могут быть представлены абсолютно
точно?
б) Найдите примеры
чисел, показывающие, что нижеследующие
равенства, вообще говоря, неверны, даже
если результат принадлежит множеству
точно представимых чисел
в)
Найдите пример, в котором сумма
имеет относительную ошибку, по меньшей
мере, 50%.
1.4
Погрешность метода вычисления. Понятие
об устойчивых алгоритмах.
Для
некоторых задач
вычислительного характера удовлетворительную
точность, при решении ее на ЭВМ, нельзя
получить никаким алгоритмом, потому
что задача чувствительна к малым ошибкам,
допущенным в представлении данных и
возникающим при выполнении арифметических
операций. Эти задачи называются
неустойчивыми (некорретными). Задачи
такого типа в настоящей лабораторной
работе мы рассматривать не будем, это
самостоятельная и обширная тема, а будем
рассматривать только те задачи, в которых
путем изменения алгоритма решения можно
избежать накапливания погрешностей.
Будем
называть алгоритм решения задачи
устойчивым, если при его реализации
погрешности вычисления не накапливаются,
с ростом объема вычмслений. Приведем
пример неустойчивого алгоритма.
Рассмотрим расчет значений Еn
по рекуррентной
формуле
.
Эта формула возникает при вычислении
интеграла.
Как нетрудно видеть, величинаВычисления, проведённые на ЭВМ с
дают результаты из которых видно, что
величинастановится
отрицательной, уже для n=20.Заметим,
что единственная ошибка округления,
сделанная в приведенных вычислениях,
связана с ошибками представления,
предполагая, что арифметические операции
выполняются точно. Причину катастрофического
роста погрешности вычислениялегко установить, заметив, что
первоначальная ошибка впри вычислении
умножается на -2,
на -3 и т.д., т.е. при вычислении
эта ошибка умножается на огромное число
20!, и тем самым, ошибка в вычислениисоставит
Очевидно, что приведенный алгоритм
является неустойчивым. Рассмотрим,
каким образом его можно сделать
устойчивым. Для этого перепишем
рекуррентную формулу в виде:
Поскольку
последовательность
является монотонно убывающей, то в
качествеможно взять значение равное нулю, что
конечно вносит погрешность в результат
вычисления,
но эта погрешность будет уменьшаться
в результате деления на n и при вычислениивеличина ошибки, связанной с неточным
заданием, станет исчезающей малой и приведенный
алгоритм будет являться устойчивым.
Иванов Д.А.
1
Васильева А.А.
2
Абляз Т.Р.
2
1 ООО «ОПТЭК»
2 Пермский национальный исследовательский политехнический университет
Актуальность работы заключается в решении зависимости увеличения погрешности вычисления радиуса окружности от угла измеряемого сектора. Если не учитывать погрешности вычисления радиуса, могут возникнуть недочеты при контроле качества на производстве. Соответственно необходимо вычислять и учитывать данные погрешности. Также при вычислении погрешностей необходимо учитывать зависимость погрешности радиуса от угла. Тем самым данная тема является очень актуальной для решения данной задачи. Целью работы является определение зависимости увеличения погрешности вычисления радиуса окружности от угла измеряемого сектора.
угол сектора.
радиус окружности
погрешность
1. Абляз Т.Р. Метод контроля конических резьб для элементов бурильных колонн на координатно-измерительной машине / Т.Р. Абляз, О.А. Халтурин// Вестник Пермского государственного технического университета. Машиностроение, материаловедение. — 2012. — №1. — С. 85-91.
2. Брянкин С.Ю. Приоритетные направления метрологического обеспечения координатных методов измерений геометрических параметров деталей / С.Ю. Брянкин, В.Г. Лысенко, К.Ф. Федосов // Научно-практическая конференция «100 лет Российскому подводному флоту». — Северодвинск, 2006. — С. 115-119.
3. Брянкин С.Ю. Применение математического моделирования для оценки точности координатных измерений на координатно-измерительных машинах / С.Ю. Брянкин, В.Г. Лысенко, С.С. Голубев, К.Ф. Федосов // Научно-практическая конференция «100 лет Российскому подводному флоту». — Северодвинск, 2006. — С. 45-49.
4. Вержбицкий В. Основы численных методов : учебник для вузов. — М.:Высш.шк., 2005. — 840 с.
5. Выгодский М. Справочник по высшей математике. — М.: АСТ, 2008. — 992 с.
Данная работа предназначена для
математического обоснования увеличения погрешности измерения окружности при
уменьшении угла измеряемого сектора. На многих предприятиях присутствуют
детали, на которых задаются достаточно жесткие допуски на малых секторах
окружности, опираясь на определенный парк измерительной техники предприятия.
Вопросы повторяемости результатов (как одного из главных параметров при
измерении и изготовлении) при таких измерениях возникают при использовании
координатно-измерительных машин, которые рассчитывают погрешность, как указано
на чертеже, как диаметр или радиус и граница допуска от них. Это не совсем
правильный подход, с помощью геометрических вычислений ниже разберем причину
таких расчетов. Также этот вариант вычисления предлагается, как один из методов
теоретического определения величины погрешности измерения при уменьшении угла
сектора и доказательства необходимости другого подхода к измерению таких
поверхностей с помощью КИМ.
При вычислении центра окружности из
секторасведем к определению окружности из трех точек– две по краям сектора и
одну посередине сектора. Геометрическое вычисление центра в данном случае —
пересечение перпендикуляров, выходящих из середин отрезков, соединяющих эти три
точки. На рисунке 1 видно, как при малом угле сектора вырастает погрешность
вычисления радиуса Sб и Sм от погрешности касания машины S – погрешность касания 2S, потому что погрешность машины +- S. β – полный угол сектора, l – длина участка, на котором расположен
сектор – если сектор задан не углом, а радиусом и длиной участка[1; 2].
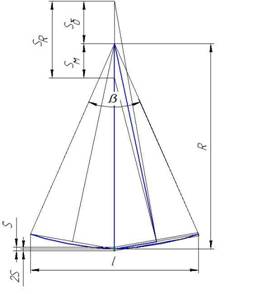
Рис.1.Погрешность вычисления радиуса:S – погрешность КИМ в
точке измерения; R – радиус окружности, м; SR – погрешность радиуса
окружности
Если сектор задан не углом, а радиусом и
длиной участка l – то вычисление угла сектора показано
на рисунке 2 (1).
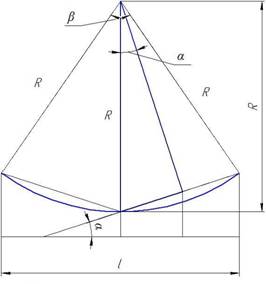
Рис.2. Вычисление угла сектора: β – полный угол
раскрытия; α=β – четверть угла
раскрытия (нужен для вычисления погрешности); l – длина участка, м; R – радиус, м
Исходя из рисунка 2с помощью тригонометрических
преобразований (1) выведем формулы для нахождения углов α и β (2):
(1)
(2)
Так как центральную точку изначально
взяли посередине, то вычисление центра окружности сводится к пересечению одного
из перпендикуляров (на рисунке 2 правого) отрезков с прямой, перпендикулярной
отрезку, соединяющему две крайние точки, и проходящей через центральную точку.
И дальнейшие вычисления будем проводить с этим прямоугольным треугольником[2-4].
На рис.3 выделяем этот треугольник для
более подробного рассмотрения,S – погрешность машины, Sб – погрешность в большую сторону, Sм – погрешность в меньшую сторону, то же
самое с углами.
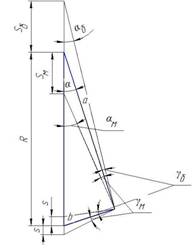
Рис.3.Вычисление погрешности с помощью прямоугольного
треугольника
Расчет погрешности в меньшую сторону
представлен на рис.4.
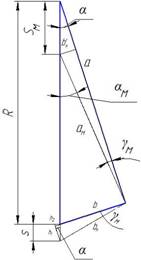
Рис.4. Расчет погрешности в меньшую сторону
Для того чтобы найти погрешность в
меньшую сторону, необходимо использовать формулу (6), опираясь на расчеты (5).
В формуле (6) неизвестным является угол погрешности (4), который можно вывести
через вычисления (3) [4-5].
Дано:R, ,
S
(3)
(4)
(5)
(6)
Расчет погрешности в большую сторону
представлен на рис.5.
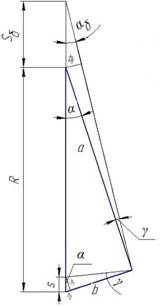
Рис.5. Расчет погрешности в большую сторону:R – радиус окружности,
м; α – четверть угла раскрытия; S – погрешность
измерения в точке; γ – угол погрешности
То же самое делаем для нахождения
погрешности в большую сторону. Находим формулу для погрешности (8). В данном
случае в формуле (8) неизвестной величиной является угол погрешности, который
можно найти по формуле (7)[4-5].
Дано:R, α, S
(7)
(8)
Так
как γ очень мал, то допустимо
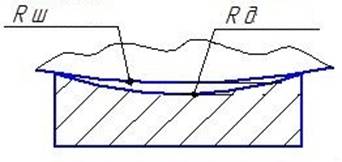
Рис.6.СравнениеR шаблона и R детали

Рис. 7. Отклонение от формы реального профиля. S- отклонение от формы
На рисунке 6 показана методика измерения
с помощью шаблона как одна из предполагаемых и в общем правильных методик
измерения таких секторов, что R детали совсем не равно R шаблона минус зазор, который
определяется подбором щупа.R детали совсем другой, и его нужно вычислять
– в данном случае такая методика измерения — это совсем не измерение радиуса
или диаметра -этот зазор показывает отклонение от формы на данном участке (рис.7).
Напрашивается вывод, что именно отклонение от формы надо указывать в таких
случаях, если бы не один подводный камень — отклонение от формы рассматривает
ТОЛЬКО форму и не учитывает размер, то есть форма может быть хорошей, а размер
совсем другим. В данном случае при использовании не шаблонов, а
координатно-измерительных машин рекомендуется использовать — отклонение формы заданного профиля(не
отклонение профиля продольного сечения – это совсем разные допуски) для
окружности и отклонение формы заданной поверхности для измерения сферической
поверхности. Такая же методика используется при измерении криволинейных
сечений, только тут номинальные точки находятся на секторе окружности.
Вывод
В данной работе было проведено решение
задачи по определению зависимости увеличения погрешности вычисления радиуса
окружности от угла измеряемого сектора. Решение данной задачи показало, что чем
меньшеугол
измеряемого сектора, тем больше будет погрешность радиуса или диаметра
окружности.
Рецензенты:
Беленький В.Я., д.т.н., проф., декан МТФ
ПНИПУ, г. Пермь;
Сиротенко Л.Д,,
д.т.н., проф., ПНИПУ, г. Пермь.
|
0 / 0 / 0 Регистрация: 05.06.2016 Сообщений: 72 |
|
|
1 |
|
Найти абсолютную и относительную погрешности при вычислении площади круга02.03.2017, 12:15. Показов 5511. Ответов 1
При измерении радиуса R круга с точностью до 0,5 см получилось 12 см. Найти абсолютную и относительную погрешности при вычислении площади круга.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
02.03.2017, 12:15 |
|
Ответы с готовыми решениями: Найти абсолютную и относительную погрешности выражения Найти абсолютную и относительную погрешности Найти абсолютную и относительную погрешности величины
1 |
|
3372 / 1896 / 570 Регистрация: 09.04.2015 Сообщений: 5,313 |
|
|
03.03.2017, 07:26 |
2 |
|
Сосчитай площадь круга для 11.5, 12.0, 12.5 см. И определи необходимые погрешности
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
03.03.2017, 07:26 |
|
Помогаю со студенческими работами здесь Вычислить значения функции и указать абсолютную и относительную погрешности результатов Определить абсолютную и относительную погрешности измерения и назначить класс точности Округлить число, определить абсолютную и относительную погрешности приближенного числа (C++ или Delphi) Найти относительную и абсолютную погрешность Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 2 |


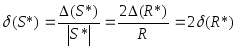




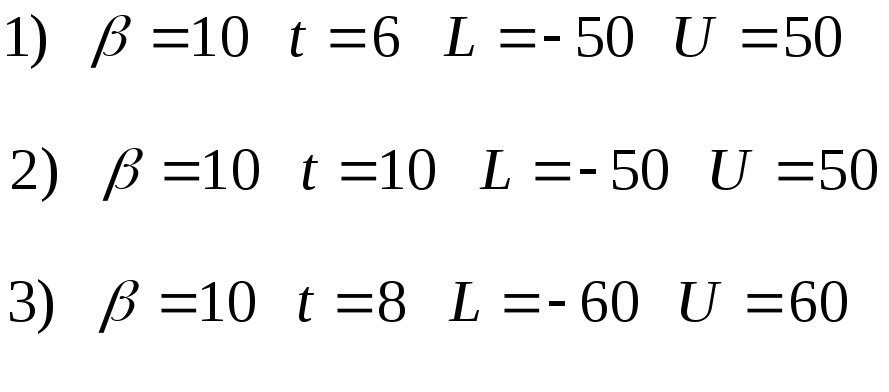 ,
,

 Округлить число, определить абсолютную и относительную погрешности приближенного числа
Округлить число, определить абсолютную и относительную погрешности приближенного числа