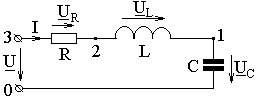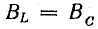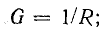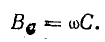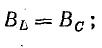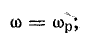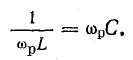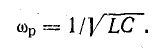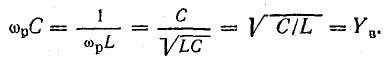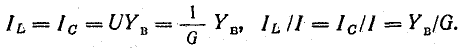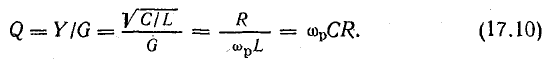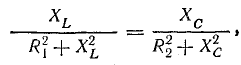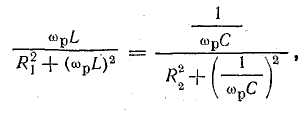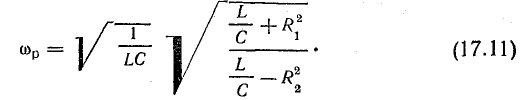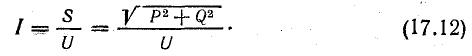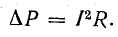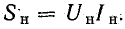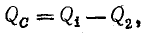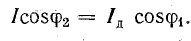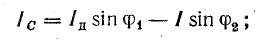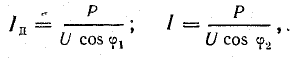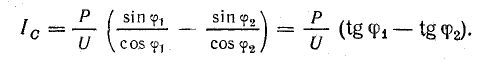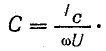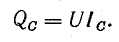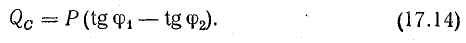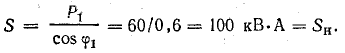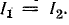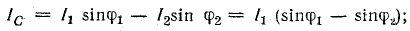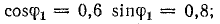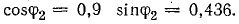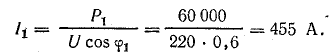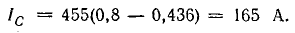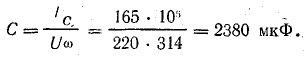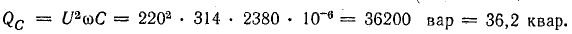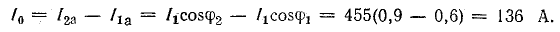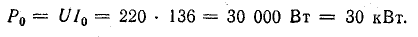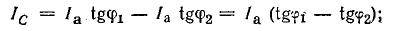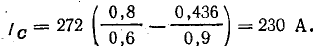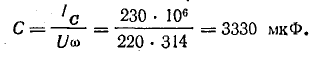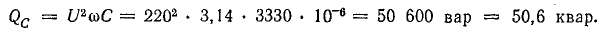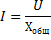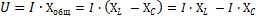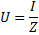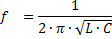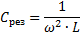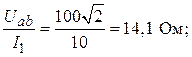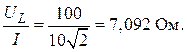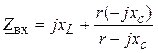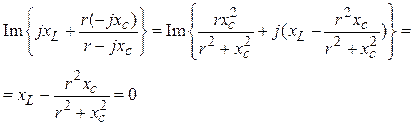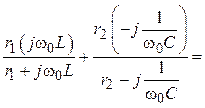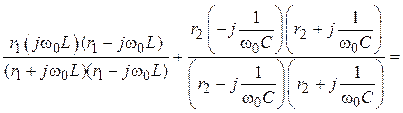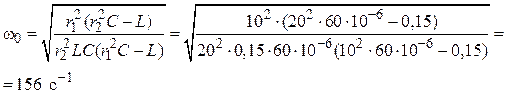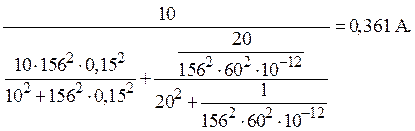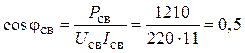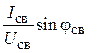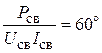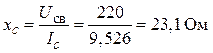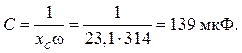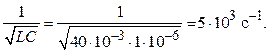-
Резонанс напряжений
Основные
соотношения для простейшей резонансной
цепи, состоящей из последовательно
соединенных R,
L, C —
элементов, приведены в табл. 3.1.
Таблица
3.1
|
Резонанс |
|
|
Условие X или при
|
|
|
Напряжения на реактивных
UL= |
Векторная
|
|
Резонансная |
|
|
Характеристическое сопротивление |
= |
|
Добротность |
|
|
Частотные I(), В
|
|
|
Полоса резонансной |
П |
|
Добротность |
П 0 |
ПРИМЕР
3.2.
Рассчитать параметры катушки R,
L резонансного
Q
— метра с заданным коэффициентом передачи
по напряжению К=500 на фиксированной
частоте 0
= 105
рад/с,
показанного на рис. 3.4. Значение емкости
С принять равной 1 нФ.

Рис.
3.4
РЕШЕНИЕ.
Резонансный Q
— метр без нагрузки можно рассматривать
как последовательный колебательный
контур с добротностью Q
= K =
= U2/U1
= 500. Поскольку
при резонансе напряжений в последовательном
контуре XL
= XC,
(см. табл. 3.1), то индуктивность катушки
должна составлять величину L
= 1/(20С)
или численно L
= 1/(101010-9)
= 0,1 Гн.
Активное
сопротивление катушки определится из
условия:
,
что дает:
Ом.
-
Резонанс токов
Основные
соотношения для параллельных контуров
без потерь и с потерями приведены в
табл. 3.2 и 3.3.
Таблица
3.2
|
Параллельный |
|
|
Условие где при |
|
|
Токи IL I |
Векторная
|
|
Резонансная |
Р |
|
Добротность |
Q |
|
Частотные характеристикам |
Таблица
3.3
|
Резонанс токов |
|
|
Условие
XL |
|
|
Токи в ветвях
|
Векторная
|
|
Резонансная |
где |
|
Добротность |
при Если Если |
ПРИМЕР
3.3. По известным показаниям амперметров
А1
и А2
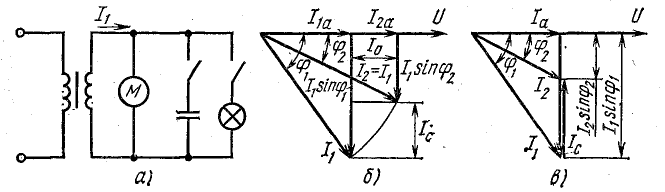
в цепи по рис. 3.5 а определить в режиме
резонанса показание амперметра А0
и добротность
контура Q,
если I1
= 5 A, I2
= 4 A.

а б
Рис.
3.5
РЕШЕНИЕ.
В цепи резонанс токов. Входной ток I0
должен
совпадать по фазе с входным напряжением
U.
Ток I1
должен отставать по фазе от напряжения
на угол 900,
а ток I2
опережать его на некоторый угол
(см. векторную диаграмму на рис. 3.5, б).
Поскольку
треугольник ОАВ — прямоугольный, то
.
Подставляя числовые
значения, найдем:
.
Добротность
параллельного контура (см. табл. 3):
Q
= XC/R
= I1/I0
= 4/3 = 1,33.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Резонанс токов:
При рассмотрении параллельного соединения катушки и конденсатора был отмечен случай равенства активной и реактивной проводимостей
Условия возникновения резонанса
Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте ωр, а
Режим электрической цепи при параллельном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивной и емкостной проводимостей, называют резонансом токов.
Сначала рассмотрим этот режим для схемы идеализированной цепи (рис. 17.6, а). В этой схеме параллельно резистору R включены идеальные катушки L и конденсатор С, потери энергии в которых не учитываются.
Рис. 17.6. К вопросу о резонансе токов
Реактивные проводимости зависят от частоты вынужденных колебаний. Для рассматриваемой схемы:
активная проводимость
реактивные проводимости
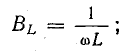
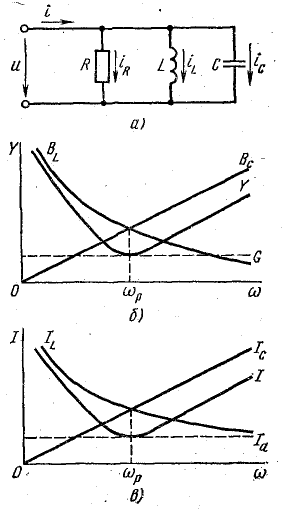
При резонансе токов
Отсюда определяют резонансную частоту:
Выражение для резонансной частоты в данном случае такое же, какое было получено при рассмотрении резонанса напряжений [см. формулу (17.8)] и для частоты собственных колебаний в контуре без потерь.
Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и С или изменением частоты источника энергии.
Резонансные кривые
На рис. 17.6, б показаны зависимости проводимостей от частоты. Полная проводимость цепи Y при резонансной частоте ωр оказывается наименьшей, равной активной проводимости G. При изменении частоты в обе стороны от резонансной полная проводимость увеличивается.
При заданном напряжении источника энергии ток в цепи пропорционален проводимости (рис. 17.6, в): 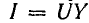
При резонансе токов отношение тока индуктивного или емкостного к току в неразветвленной части цепи равно отношению волновой проводимости 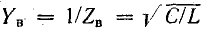
Реактивные проводимости при резонансе
Поэтому
Добротность контура
При параллельном соединении элементов качество резонансной цепи считается тем выше, чем больше отношение 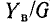
Чем меньше потери энергии в цепи (этому соответствует большая величина R), тем больше добротность.
Параметры реальных катушек и конденсаторов (R, L, С) измеряются и задаются в справочниках применительно к их схемам замещения с последовательным соединением активных и реактивных элементов (см. рис. 14.11, б).
Условие резонанса токов — равенство реактивных проводимостей обеих ветвей 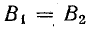
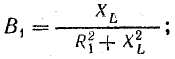
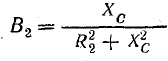
где R1 и R2 — активные сопротивления катушки и конденсатора с потерями.
Приравнивая реактивные проводимости, получим исходное уравнение для определения резонансной частоты
или
откуда
Из «того выражения видно, что резонансная частота зависит от активных сопротивлений катушки и конденсатора. Если потери энергии в катушке и конденсаторе малы (R1 и R2 малы) и ими можно пренебречь, для резонансной частоты получается выражение, найденное раньше для идеализированной цепи.
Компенсация реактивной мощности в электрических сетях с помощью конденсаторов
Было отмечено, что в электрической цепи переменного тока, в которой имеются катушка индуктивности и конденсатор, включенные последовательно или параллельно, общая реактивная мощность цепи всегда меньше, чем реактивная мощность каждого из элементов.
Благодаря взаимному обмену энергией между катушкой и конденсатором и рис. 14.5 источник частично или полностью освобождается от поставки реактивной энергии в цепь.
В этом случае говорят о компенсации реактивной мощности катушки реактивной мощностью конденсатора и наоборот (реактивные мощности QL и QС имеют противоположные знаки). Полная компенсация реактивной мощности имеет место при резонансе.
Компенсация реактивной мощности в электрических сетях имеет большое технико-экономическое значение. Далее кратко рассмотрены общие сведения по этому вопросу и принцип применения конденсаторов для компенсации реактивной мощности.
Реактивная мощность электрических установок
Энергетический процесс в катушке индуктивности, включенной в цепь переменного тока, характеризуется активной мощностью 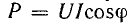
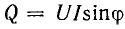
В электрической схеме замещения такая катушка представлена активным сопротивлением R и индуктивностью L, или активной проводимостью G и реактивной проводимостью Y.
В этом отношении катушке индуктивности подобны многочисленные устройства переменного тока: асинхронные двигатели, индукционные нагревательные установки, трансформаторы, воздушные линии и др.
Получая от генераторов электрическую энергию, эти устройства передают или преобразуют ее в другие виды энергии (активная мощность Р), т. е. выполняют те функции, для которых созданы.
Одновременно они обмениваются энергией с источниками (реактивная мощность Q), что является процессом хотя и нежелательным, но неизбежным, так как без магнитного поля и периодического накопления энергии в нем перечисленные устройства работать не могут.
Если реактивная мощность устройства не равна нулю, то отношение 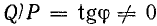
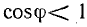
На каждом предприятии одновременно работают электродвигатели (их может быть десятки и сотни), трансформаторы и другие устройства. Чем больше их число и чем меньше их коэффициент мощности, тем больше общая реактивная мощность электрооборудования производственного участка, цеха, всего предприятия.
Величина общей реактивной мощности электрической установки или электрооборудования предприятия в целом зависит еще и от правильного выбора, степени загрузки электродвигателей, трансформаторов, от соблюдения правил эксплуатации электрооборудования.
Далее будет показано, что за счет реактивной мощности потребителей электрический ток в сетях оказывается больше, чем требуется по величине активной нагрузки. С этим связана одна из проблем проектирования и эксплуатации электрических сетей. При передаче электрической энергии, особенно на большие расстояния, из-за наличия индуктивных и емкостных сопротивлений в элементах сети переменного тока возникает также проблема поддержания заданного уровня напряжения на всех приемниках.
Для обеспечения оптимальной величины тока и требуемых величин напряжения в сети необходимо иметь оптимальный баланс реактивных мощностей (индуктивной и емкостной).
Влияние величины реактивной мощности на технико-экономические показатели электроустановок
Для выяснения влияния величины реактивной мощности на экономические показатели электротехнических установок рассмотрим приемник энергии (например, асинхронный электродвигатель), работающий с постоянной активной мощностью при постоянном напряжении в сети.
Ток в приемнике, а следовательно, и в проводах, соединяющих его с источником энергии, при этих условиях зависит от величины реактивной мощности Q:
Чем больше реактивная мощность приемника, тем больший ток должен быть в самом приемнике, в генераторе, соединительных проводах, трансформаторе и других элементах сети электроснабжения.
Мощность тепловых потерь, согласно закону Ленца — Джоуля, пропорциональна квадрату тока и сопротивлению проводов:
Очевидно, чем больше ток приемника, тем больше потери энергии во всех элементах электрической цепи.
Стоимость потерянной энергии входит в эксплуатационные расходы. Уменьшение реактивной мощности приемников ведет к уменьшению их токов, сокращению потерь энергии и эксплуатационных расходов.
Если электрическая установка спроектирована с относительно большей величиной реактивной мощности, то оборудование (коммутационная аппаратура, приборы контроля и т. д.) и провода необходимо выбрать на большие токи, чем при меньшей величине реактивной мощности.
Это значит, что оборудование должно быть установлено относительно больших размеров, а провода — большего сечения. Последнее повлечет за собой увеличение объема зданий, утяжеление фундаментов и опор и т. п.
Уменьшение реактивной мощности приемников энергии сокращает капитальные затраты.
Генераторы электрической энергии и трансформаторы характеризуются номинальной мощностью — произведением номинальных величин напряжения и тока:
Наиболее полное использование генераторов и трансформаторов соответствует режиму работы с номинальным током при номинальном напряжении (особые случаи, когда допускается некоторая перегрузка оборудования при эксплуатации, здесь не учитываются).
Величина активной мощности генератора равна активной мощности питающихся от него приемников.
Если реактивная мощность приемников равна нулю, то генератор может развивать активную мощность, равную его номинальной мощности , т. е. основная функция генератора — преобразование энергии — может быть выполнена наиболее полно, а первичный двигатель (например, турбина), также рассчитанный на номинальную мощность, будет работать с полной нагрузкой.
При наличии у приемников реактивной мощности активная мощность генератора меньше номинальной, хотя он работает при номинальных напряжении и токе. Таким образом, генератор и первичный двигатель по мощности недогружены, что приводит к снижению их коэффициента полезного действия.
Компенсация реактивной мощности
Из приведенных рассуждений следует, что реактивную мощность установок, потребляющих электрическую энергию, надо по возможности сокращать.
На практике это достигается путем правильного выбора мощности электродвигателей переменного токаи трансформаторов, рациональной эксплуатации их без недогрузки и работы вхолостую. Эти и некоторые другие меры уменьшения реактивной мощности, связанные с выбором и эксплуатацией электрооборудования, называют естественными.
В тех случаях, когда естественные меры не могут обеспечить оптимальной величины реактивной мощности установки, принимают искусственные меры для ее компенсации.
Одной из таких мер является включение параллельно к приемникам батареи конденсаторов.
Для определения мощности и емкости батареи конденсаторов должны быть известны величины напряжения сети U, реактивной мощности установки до компенсации (Q1) и после компенсации (Q2).
Можно установить батарею конденсаторов мощностью QC = Q1, тогда Q2 = 0. Полная компенсация реактивной мощности освобождает полностью сеть от реактивного тока.
Однако технико-экономические расчеты показывают, что полная компенсация в большинстве случаев не является оптимальным решением вопроса, так как компенсационное устройство оказывается более сложным и дорогим, чем при некоторой оптимальной величине реактивной мощности Q2, которую определяют на основе технико-экономического сопоставления вариантов (Определение оптимальной величины Q2, выбор вида компенсирующего устройства и места его установки в сети рассматриваются в специальных курсах).
Мощность батареи конденсаторов
а емкость
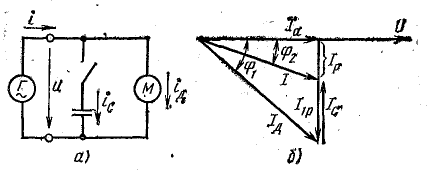
Рис. 17.7. К вопросу о компенсации реактивной мощности
Сущность компенсации реактивной мощности с помощью конденсаторов видна из векторной диаграммы (рис. 17.7, б), построенной для схемы (рис. 17.7, а), на которой параллельно приемнику, например асинхронному двигателю (группе двигателей), может быть включена конденсаторная батарея. До включения конденсаторов ток в подводящих проводах Iд отстает по фазе от напряжения на угол φ1. После включения батареи реактивная составляющая I1р тока двигателя частично компенсируется емкостным током IC, в связи с чем ток в подводящих проводах уменьшается до I, а угол сдвига фаз — до φ2 (в обменном энергетическом процессе между генератором и приемником участвует меньшее количество электромагнитной энергии).
Активная составляющая тока в проводах не изменяется, следовательно, по активной мощности режим цепи остается прежним:
Ток батареи конденсаторов имеет величину
где Р — активная мощность приемника (в данном случае двигателя);
Емкость батареи конденсаторов
Мощность батареи конденсаторов
Нетрудно заметить, что мощность конденсаторов можно найти, не подсчитывая тока IC:
Задача 17.7.
К трансформатору номинальной мощностью 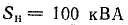
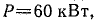
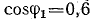
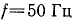
Определить емкость и мощность батареи конденсаторов и дополнительную осветительную нагрузку, которые нужно подключить к трансформатору так, чтобы реактивная мощность установки уменьшилась до величины, при которой коэффициент мощности 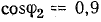
Определить емкость и мощность батареи конденсаторов в том случае, когда 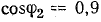
Решение. 1. В первоначальном режиме трансформатор был загружен до номинальной мощности
Дополнительную осветительную нагрузку можно присоединить только за счет разгрузки трансформатора от части реактивной мощности путем включения батареи конденсаторов.
Согласно условию задачи, трансформатор после компенсации части реактивной мощности остается полностью загруженным, следовательно, при неизменном напряжении ток трансформатора должен остаться прежним:
Рис. 17.8. К задаче 17.7
Из векторной диаграммы (рис. 17.8, б) следует выражение для тока конденсатора:
при
при
Ток установки до компенсации реактивной мощности
Ток батареи конденсаторов
Емкость батареи конденсаторов
Мощность батареи конденсаторов
Активный ток дополнительной осветительной нагрузки
Мощность осветительной нагрузки
2. При отсутствии дополнительной осветительной нагрузки необходимый ток в батарее конденсаторов (рис. 17.8, в)
Емкость батареи конденсаторов
Мощность батареи конденсаторов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле
- Электрические цепи синусоидального тока
- Соединение звездой и треугольником в трехфазных цепях
- Принцип действия асинхронного и синхронного двигателей
- Метод симметричных составляющих
- Цепи периодического несинусоидального тока
Что такое резонанс напряжений?
Резонансные явления наблюдаются в колебательных системах, когда частота собственных колебаний элементов системы совпадает с частотой внешних (вынужденных) колебательных процессов. Данное утверждение справедливо и для цепей с циркулирующим переменным током. В таких электрических цепях при наличии определённых условий возникает резонанс напряжений, что влияет на параметры тока. Явление резонанса в электротехнике может быть полезным или вредным, в зависимости от ситуации, в которой происходит процесс.
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.

Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Формула
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).

Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).


В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:

Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
Формулировка
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
В случае, если XL = Xc – справедливо равенство: ωL = 1/ωC , отсюда получаем:
Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Условия наступления
Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.
Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.
Источник
с помощью каких приборов и по каким признакам можно судить о наступлении режимов резонанса токов и резонанса напряжений?
РЕЗОНАНС НАПРЯЖЕНИЙ: Соединяешь ПОСЛЕДОВАТЕЛЬНО резистор (обычное сопротивление) , конденсатор переменной емкости, катушку индуктивности, амперметр и всю цепь подсоединяешь к источнику переменного напряжения (220 В, например) . Меняешь емкость конденсатора и одновременно наблюдаешь за показаниями амперметра. В тот момент, когда они будут МАКСИМАЛЬНЫ, в цепи получится резонанс напряжений.
РЕЗОНАНС ТОКОВ: Соединяешь ПАРАЛЛЕЛЬНО резистор, конденсатор переменной емкости, катушку индуктивности, а к ним последовательно амперметр и всю цепь подсоединяешь к источнику переменного напряжения. Меняешь емкость конденсатора и одновременно наблюдаешь за показаниями амперметра, который меряет общий ток, текущий через параллельно соединенные конденсатор, катушку и резистор. В тот момент, когда показания амперметра будут МИНИМАЛЬНЫ, в цепи получится резонанс токов.
Т. е. момент наступления ОБОИХ резонансов можно определить с помощью ОДНОГО-ЕДИНСТВЕННОГО АМПЕРМЕТРА! Главное — это правильно собрать цепь.
Далее можно куда-нибудь еще каких-нибудь дополнительных амперметров-вольтметров-осциллографов поподключать, но это будет уже более сложный вариант с НЕСКОЛЬКИМИ ИЗМЕРИТЕЛЬНЫМИ ПРИБОРАМИ.
при резонансе напряжение на контуре резко возрастает, и может превышать подводимое
Ток меряют Амперметром, Напряжение — Вольтметром.
Форму напряжения наблюдают на Осциллографе.
Источник
Резонанс напряжений
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
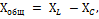
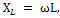
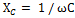
Применив к этой цепи закон Ома, получим:
Формулу эту можно преобразовать следующим образом:
В полученном равенстве I XL — действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а I ХС — действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
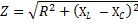
где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать:
Резонанс напряжений в цепи переменного тока
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Иначе говоря, от одновременного действия этих двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда XL = ХС или, что то же, когда ω L = 1 / ωС.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома I = U / R , где вместо Z теперь поставлено R.
Одновременно с этим действующие напряжения как на катушке UL = I XL так и на конденсаторе Uc = I ХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений .
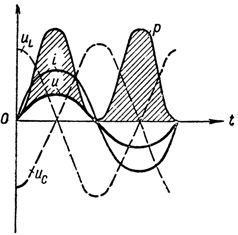
На рис. 1 приведены кривые напряжений, тока и мощности при резонансе напряжений в цепи.
График тока напряжений и мощности при резонансе напряжений
Следует твердо помнить, что сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ω L возрастет, а ХС = = 1 / ωС уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Действительно, в цепи с одной катушкой индуктивности происходит колебание энергии, т. е. периодический переход энергии из генератора в магнитное поле катушки. В цепи с конденсатором происходит то же самое, но за счет энергии электрического поля конденсатора. В цепи же с конденсатором и катушкой индуктивности при резонансе напряжений (XL = ХС) энергия, раз запасенная цепью, периодически переходит из катушки в конденсатор и обратно и на долю источника тока выпадает только расход энергии, необходимый для преодоления активного сопротивления цепи. Таким образом, обмен энергии происходит между конденсатором и катушкой почти без участия генератора.
Стоит только нарушить резонанс напряжений в цени, как энергия магнитного поля катушки станет не равной энергии электрического поля конденсатора, и в процессе обмена энергии между этими полями появится избыток энергии, который периодически будет то поступать из источника в цепь, то возвращаться ему обратно цепью.
Явление это очень сходно с тем, что происходит в часовом механизме. Маятник часов мог бы непрерывно колебаться и без помощи пружины (или груза в часах-ходиках), если бы не силы трения, тормозящие его движение.
Пружина же, сообщая маятнику в нужный момент часть своей энергии, помогает ему преодолеть силы трения, чем и достигается непрерывность колебаний.
Подобно этому и в электрической цепи, при явлении резонанса в ней, источник тока расходует свою энергию только на преодоление активного сопротивления цепи, тем самым поддерживая в ней колебательный процесс.
Итак, мы приходим к выводу, что цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему . Такая цепь получила название колебательного контура.
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:
Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений :
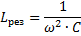
Таким образом, изменяя любую из этих трех величин ( f рез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
Пример полезного применения резонанса напряжений : входной контур приемника настраивается конденсатором переменной емкости (или вариометром) таким образом, что в нем возникает резонанс напряжений. Этим достигается необходимое для нормальной работы приемника большое повышение напряжения на катушке по сравнению с напряжением в цепи, созданным антенной.
Наряду с полезным использованием явления резонанса напряжений в электротехнике технике часто бывают случаи, когда резонанс напряжений вреден. Большое повышение напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Страницы работы
Содержание работы
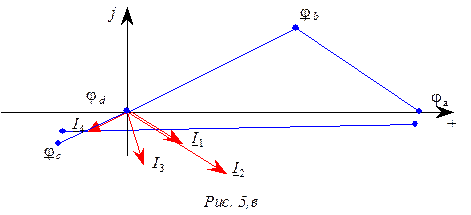
6. Топографическая диаграмма цепи в предположении, что
j d = 0 (рис. 5,в).
j b = j d + I2Z2
= 108 Ð 33,7º (B),
j c
= j d + I4Z4
= 36 Ð-146,3º (B),
j a = j b + I1Z1
= 130 (B).
VIII.
РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Основные
вопросы
1. Какой режим электрической цепи
называется резонанс-ным?
2. Условия резонанса напряжений.
3. Условия резонанса токов.
4. Резонансная частота последовательного
и параллельного резонансных контуров.
Литература
1. Зевеке Г.В., Ионкин П.А., Нетушил
Л.В., Страхов С.В.
Основы теории цепей. – М., 1989. – § 5.1, 5.2, 5.4 ,5.5, 5.7.
2. Бесонов Л. А. Теоретические основы электротехники.
– М., 1978. – § 3…25; 3…29.
Примеры
Задача 1
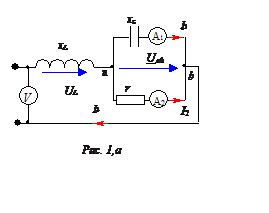
амперметры А1 и А2 показывают по 10 А, вольтметр на входе
цепи показывает 100 В. Входные ток и напряжение совпадают по фазе.
Определить входной ток I и параметры цепи r, xL, xC.
Решение
Вариант 1 (расчет с по-мощью векторной диа—граммы)
Векторная диаграмма рассматриваемой цепи, пред-ставленная на рис. 1,б,
построена в соответствии с
уравнениями
и
при условии
совпадения фаз Uвх и I.
Порядок построения векторной диаграммы следующий:
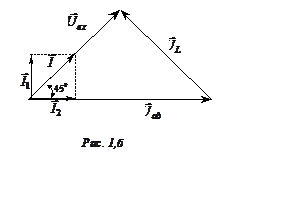
вектора ;
· вектор тока совпадает по направлению с вектором
, а вектор тока
опережает
его на угол, равный 90°;
· в силу того, что I1
=
= I2, входной ток цепи
,
а изображающий
его вектор , опережает напряжение
на 45°.
Вектор (длина его выбрана произвольно) суммируется
с вектором , опережающим вектор общего тока
на 90°, так, чтобы вектор входного напряжения
совпал с направлением вектора тока
.
Из диаграммы следует:
UL = U = 100 B;
Uав = = 100
B;
хc =
r = хc = 14,1 Ом;
хL =
Вариант 2
1. Из условия
резонанса
Im(Zвх)
= 0,
где
следует, что
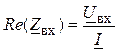
2. Из условия I1
= I2 вытекает, что
r = хc и (cм.
рис. 1,б).
3. Решая
совместно уравнения
и
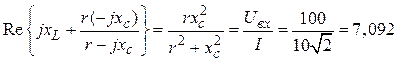
находим
xc
= r =
14,1 Ом, xL = 7,092 Ом.
Ответ: I = 14,1 A, r = 14,1 Ом, xL
=7,092 Ом, xC = 14,1 Ом.
Задача 2
К цепи (рис. 2) приложено напряжение U = 10 В.
r1 =10 Ом, r2 = 20 Ом, L
= 0,15 Гн, C = 60 мкФ.
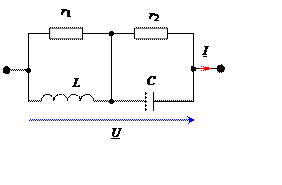
мощность при резонансной частоте.
Решение
1. Из
условия резонанса в цепи
Im(Zвх)
= Im(rвх + jxвх) = 0,
следует, что xвх
= 0.
2. Комплекс
входного сопротивления цепи:
Zвх =
=
=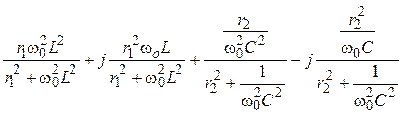
=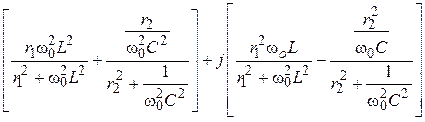
3. Определение резонансной частоты ω0.
хвх = 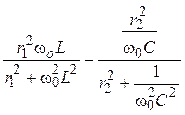
или
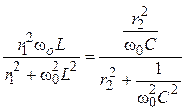
Преобразовав полученное тождество:
r12 ω02Lr22C2+r12L
= r12 r22C+r22
C ω02L,
получим
уравнение для определения частоты резонанса
ω02r22LC(r12C – L)
— r12(r22C – L)
= 0,
из которого
следует:
4. Определение входного тока:
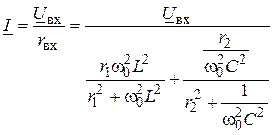
=
5. Определение активной мощности P0:
P0 = I2 rвх = 0,3612×27,7 = 3,61 Вт.
Ответ: I = 0,361 A, P0
= 3,61 Вт.
Задача 3
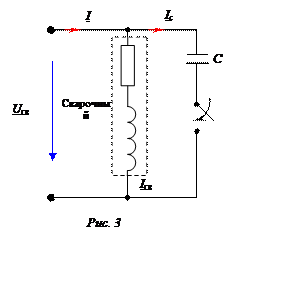
при напряжении сети
Uсв = 220 В и f = 50Гц
потребляет ток Iсв
= 11 А.
Определить емкость и мощность батареи конден-саторов,
которую необхо-димо включить параллельно сварочному аппарату (рис. 3), чтобы повысить коэф-фициент мощности (соsj) цепи до 1, а также ток, потребляемый
цепью после подключения батареи кон-денсаторов.
Решение
Вариант 1
1. Коэффициенту мощности, равному 1, соответствует режим резонанса токов в
цепи (рис. 3), условием которого является:
Im(Yвх) = Im(gвх
+ jbвх) = 0,
и, как
следствие
bвх = bLсв— bC =
0.
2. Заданные характеристики сварочного аппарата (Pсв, Uсв,
Iсв) позволяют определить его коэффициент мощности
и реактивную
проводимость
bLсв = Yсв sin jн = 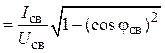
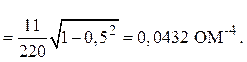
3. Требуемая
емкость определяется из условия резонанса
bc =wС
= bLсв = 0,0432 Ом-1.
В результате
C =
4. Мощность
батареи конденсаторов
Qc =
5. Входной ток цепи может быть определен с помощью первого закона Кирхгофа
I = ILсв
+ Ic.
В режиме резонанса токов реактивная составляющая тока сварочного аппарата
уравновешивается током батареи конденсаторов
= Ic,
поэтому входной
ток цепи определяется лишь активной составляющей тока сварочного аппарата:
I =
Ответ: С = 139 мкФ; QC = 2100 Вар; I
= 5,5 A.
Вариант 2 (расчет с помощью
векторной диаграммы).
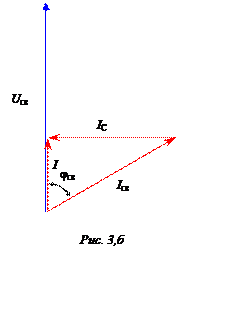
резонанса (совпадения по фазе входного напряжения и входного тока), представлена
на рис. 3,б. Диаграмма строится на основании первого закона Кирхгофа
.
Порядок построения диаграммы:
· в произвольном направлении строится вектор
входного напряжения ;
· в соответствующем масштабе строится вектор тока
сварочного агрегата , отстающий на угол
jсв = arccos
от
вектора входного напряжения;
·
к
концу вектора пристраивается вектор емкостного
тока , опережающий на прямой угол вектор
входного напряжения, причем длина вектора
емкостного тока принимается такой, чтобы вектор результирующего тока оказался в фазе с вектором
входного напряжения.
Диаграмма позволяет определить емкостный ток
IC = Iсвsinjсв = 11×sin 60° = 9,526 A,
и
вслед за этим найти сопротивление конденсатора
и
величину емкости, обеспечивающей резонанс,
Задача 4
В цепи, изображенной на рис. 4,а, ток амперметра А равен 0.
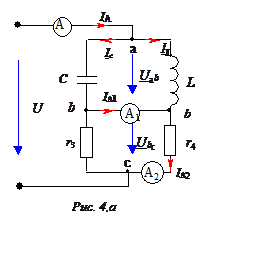
U = 240 B;
L = 40 мГн;
C =
1 мкФ.
Сопротивления амперметров равны 0.
Определить показания амперметров А2 и А1
(токи IA1 и IA2) .
Решение
1. Так как IА = 0, в цепи наблюдается резонанс токов на
участке аb. Векторная диаграмма для этого случая показана на рис. 4,б.
Из условия резонанса
bL0 – bC0 = 0
следует, что
частота резонанса
ω0 =
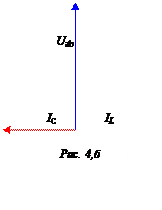
1. С учетом
того что
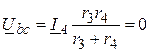
из уравнения по
второму закону Кирхгофа следует
Uab = U – Ubc
= U = 240 В.
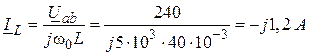
3. Так как
IA2 = 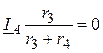
искомый ток через амперметр А1, как сле-
дует из первого
закона Кирхгофа для узла
«b»,
IA1 = IA2 – I2
= 0 – (-j1, 2) = + j1,2 A.
Ответ: IA1
= 1,2 A.
Задачи для самостоятельного решения
Задача 5
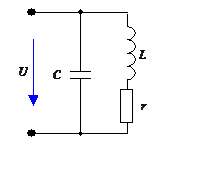
входной ток цепи в режиме резонанса, если
С = 58мкФ; U = 220 В; f = 50 Гц.
Расчет провести для случаев :
а) r =22 Ом, б) r = 0.
Ответ:
а) L1 = 0.139 Гн; Iвх =
10 А
б) L2 = 0.035 Гн, Iвх =
0.
Задача 6
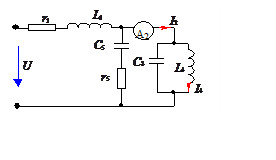
равно нулю. Чему равен ток I4, если U = 200 B; L1 = 0,2 Гн; r1
= 50 Ом, C3 = 10 мкФ; L4 = 0,1 Гн; C5
=5 мкФ;
r5 = 50 Ом.
Построить векторную диаграмму токов и напряжений.
Ответ: I4
= 4,12 A.
Задача 7
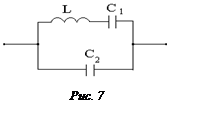
Гн;
С1 = 0,25 мкФ; С2 = 0,2 мкФ, активным
сопротивлением цепи пренебречь.
Ответ: 1. Резонанс токов при
ω1 = 3 ·104 (1/с);
2. Резонанс напряжений при
ω2 = 2 · 104(1/c).
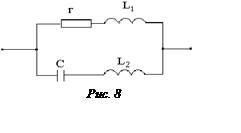
Задача 8
Определить индуктивность катушки L2, если резонанс токов в цепи
возникает при ω0 = 2·107 с-1.
Параметры цепи:
r =
20 Ом; L1 = 20 мГн; С = 6,25 мкФ.
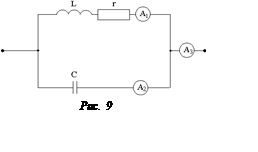
Задача 9
В цепи, изображенной на
рис. 9, имеет место резонанс токов. Амперметр А1 показывает
6 А, показание амперметра А3 составляет 3,6 А. Определить показание
А2.
Ответ: IА2 = 4,8 А.
Цепь находиться в состоянии резонанса Е = 40 В;
UL = 30 B; U12 = 50 B.
Мощность, потребляемая цепью, Р = 40 Вт.
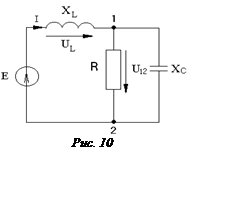
Ответ: R = 12,5 Ом; xL = 6 Ом; xC = 16,6 Ом.
Похожие материалы
- Практический курс теоретических основ электротехники: Методическое руководство (Разделы I-VI: Основные законы электрических цепей. Электрические цепи синусоидального тока)
- Расчет нелинейных электрических цепей с использованием замены реальных нелинейных элементов условно-нелинейными
- Расчет переходного процесса классическим и оперативным методами
Информация о работе
Тип:
Методические указания и пособия