Определение показателя адиабаты
Цель
работы:
познакомиться с адиабатическим процессом,
определить показатель адиабаты для
воздуха.
Оборудование:
баллон с клапанома, компрессор, манометр.
Теоретическое введение
Адиабатический
процесс – это
процесс, протекающий в термодинамической
системе без теплообмена с окружающей
средой. Термодинамической системой
является система, содержащая огромное
количество частиц. Например газ, число
молекул которого сравнимо с числом
Авагадро 6,02∙1023
1/моль. Хотя движение каждой частицы
подчиняется законам Ньютона, но их так
много, что состояние системы характеризуют
макроскопическими параметрами, такими
как давление
P,
объем V,
температура
T.
Согласно
первому началу термодинамики, являющемуся
законом сохранения энергии в
термодинамических процессах, теплота
Q,
подводимая к системе, расходуется на
совершение работы А
и на изменение внутренней энергии Δ
U
Q
= A
+
U.
(1)
В
применении к идеальному газу теплота,
подводимая к газу приводит к изменению
температуры:
,
где
= m/M
– количество газа, равное отношению
массы к массе одного моля, С
− молярная теплоемкость, зависящая от
вида процесса. Внутренняя энергия
идеального газа − это кинетическая
энергия всех молекул, она равна
,
гдеCv
– молярная
теплоемкость при изохорическом
нагревании. Работа элементарного
изменения объема силами давления равна
произведению давления на изменение
объема: dA=
PdV.
Для
адиабатического процесса, происходящего
без теплообмена (Q
= 0), работа совершается за счет изменения
внутренней энергии, A
= −
U.
При адиабатическом расширении работа
газа положительна, поэтому внутренняя
энергия и температура понижаются. При
сжатии – наоборот. Все
быстро протекающие процессы можно
достаточно точно считать адиабатическими.
Выведем
уравнение
адиабатического
процесса идеального газа. Для этого
применим уравнение первого начала
термодинамики для элементарного
адиабатического процесса
dA=
− dU,
которое
принимает
вид
РdV
=−
СvdT
. Применим еще одно уравнение, полученное
дифференцированием уравнения Менделеева
– Клапейрона (PV=νRT):
PdV
+VdP
=R
dT.
Исключая один из параметров, например,
температуру, получим соотношение для
двух других параметров
.
Интегрируя и потенцируя, получим
уравнение адиабаты черездавление
и объем: P
V
= const.
Аналогично
для других пар параметров:
T
V
-1
= const, P
-1
T—
= const.
(2)
Здесь
– показатель адиабаты, равный отношению
теплоемкостей газа при изобарическом
и изохорическом нагревании.
Получим формулу для показателя адиабаты
в молекулярно-кинетической теории.
Молярная теплоемкость по определению
это количество теплоты, необходимое
для нагревания одного моль вещества на
один Кельвин
.
При изохорическом нагревании теплота
расходуется на повышение внутренней
энергии.
Подставив теплоту, получим.
Тогда показатель адиабаты может быть
определен теоретически по формуле
.
(3)
Здесь
i
– число степеней свободы молекул газа.
Это число координат, достаточное для
определения положения молекулы в
пространстве или число составляющих
компонентов энергии молекулы. Например,
для одноатомной молекулы кинетическая
энергия может быть представлена как
сумма трех компонентов энергии,
соответствующих движению вдоль трех
осей координат, i
= 3. Для жесткой двухатомной молекулы
следует добавить еще два компонента
энергии вращательного движения, так
как энергия вращения относительно
третьей оси, проходящей через атомы,
отсутствует. Итак, для двухатомных
молекул i
= 5. Для воздуха как для двухатомного
газа теоретическое значение показателя
адиабаты будет равно
= 1,4.
Показатель
адиабаты можно определить экспериментально
методом Клемана – Дезорма. В баллон
нагнетают
воздух, сжимая до некоторого давления
Р1,
немного
больше
атмосферного.
При сжатии воздух несколько нагревается.
После установления теплового равновесия
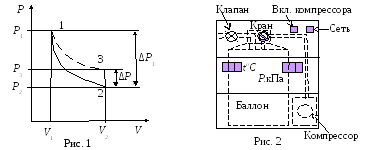
баллон на короткое время открывают.
В этом
процессе расширения 1–2 давление падает
до атмосферного Р2=Ратм,
а исследуемая масса газа, которая до
этого занимала часть объема баллона
V1,
расширяется, занимая весь баллон V2
(рис.1).
Процесс расширения воздуха (1−2) происходит
достаточно быстро, его можно считать
адиабатическим, происходящим по уравнению
(2)
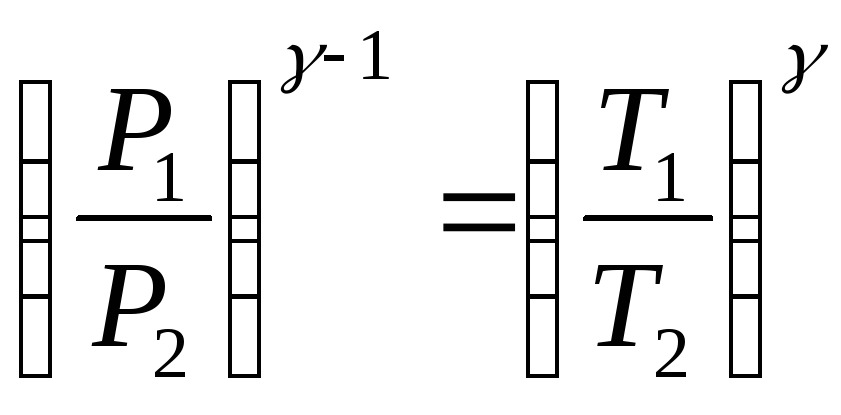
( 4)
В
адиабатическом процессе расширения
воздух охлаждается. После закрытия
клапана охлажденный воздух в баллоне
через стенки баллона нагревается до
температуры лаборатории Т
3
= Т1.
Это изохорический процесс 2–3
.
(5)
Решая совместно
уравнения (4) и (5), исключая температуры,
получим уравнение, связывающее давления:
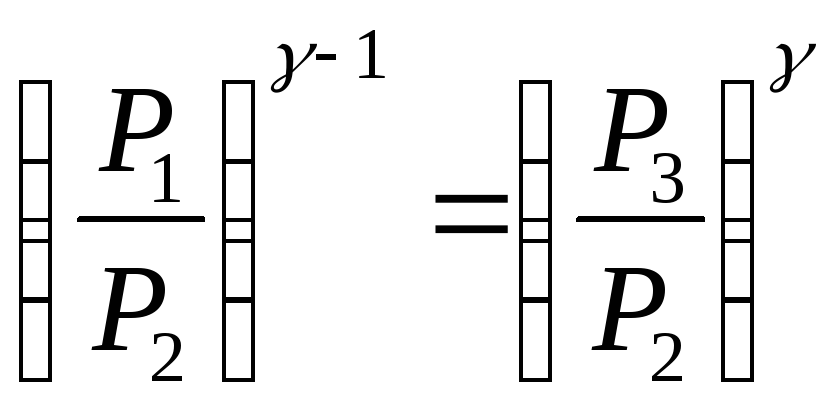
из которого следует определить показатель
адиабатыγ.
Датчик давления измеряет не абсолютное
давление, которое записано в уравнениях
процессов, а избыточное над атмосферным
давлением. То есть Р1
= ΔР1+
Р2,
и Р3
=
ΔР3+Р2.
Переходя к избыточным давлениям, получим
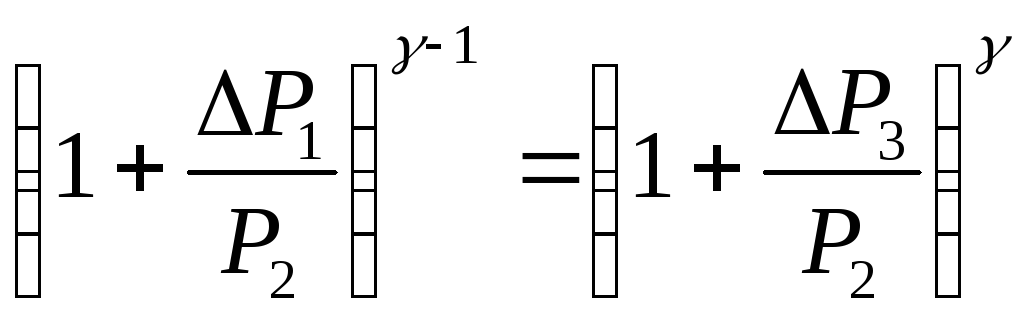
Избыточные давления невелики по
сравнению с атмосферным давлениемР2
. Разложим члены уравнения в ряд по
соотношению
.
После сокращения наР2
получим для показателя адиабаты расчетную
формулу
.
(6)
Лабораторная
установка
(рис.2) состоит из стеклянного баллона,
который сообщается с атмосферой через
клапан «Атмосфера». Воздух накачивается
в баллон компрессором при открытом
кране «К». После накачивания, во избежание
утечки воздуха, кран закрывают.
ВЫПОЛНЕНИЕ РАБОТЫ
1.
Включить установку в сеть 220 В.
Открыть
кран баллона. Включить компрессор,
накачать воздух до избыточного давления
в диапазоне 4 –11 кПа. Закрыть кран
баллона. Выждать 1,5 –2 мин, записать
величину давления ΔР1
в таблицу.
|
ΔР1, |
|||||
|
ΔР3, |
|||||
|
γ |
2. Повернуть клапан
«Атмосфера» до щелчка, клапан откроется
и захлопнется. Произойдет адиабатический
сброс воздуха с понижением температуры.
Следить за повышением давления в баллоне
по мере нагрева. Измерить наивысшее
давление ΔР3
после установления
теплового равновесия. Записать в таблицу.
Повторить
опыт не менее пяти раз, изменяя исходное
давление в диапазоне 3–11 кПа.
Выключить
установку.
3.
Произвести расчеты. Определить показатель
адиабаты в каждом опыте по формуле (6).
Записать в таблицу. Определить среднее
значение показателя адиабаты <γ>
4.
Оценить случайную погрешность измерения
по формуле для прямых измерений
.
(7)
5.
Записать результат в виде:
=
.
Р =
0,9. Сравнить результат с теоретическим
значением показателя адиабаты двухатомного
газа
теор
= 1,4.
Сделать
выводы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Показатели адиабаты: определение и процесс
При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.
Адиабатический процесс
Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:
- теплопроводность между внешней средой и системой по той или иной причине является низкой;
- скорость процесса велика, поэтому обмен теплом не успевает происходить.
В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.
Уравнение Пуассона для адиабаты идеального газа
Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.
Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:
Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.
В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:
Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.
Что такое показатель адиабаты?
Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом CP изобарную теплоемкость, а символом CV — изохорную. Тогда для γ справедливо равенство:
Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.
Теплоемкости CP и CV
Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:
Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.
Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:
Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.
Величина γ для газа идеального одноатомного
Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:
Откуда можно определить значение изохорной теплоемкости CV:
Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:
Из последних двух равенств следует значение показателя адиабаты:
Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.
Зависимость γ от числа степеней свободы
Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.
Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:
Тогда значение γ будет равно:
Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.
Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:
Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.
Показатель адиабаты для смеси газов
Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:
Где γi — это величина γ для i-го компонента.
Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.
Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи
Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.
Кратко об идеальном газе
Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:
Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.
Что это адиабатический процесс?
Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.
Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.
Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.
Уравнения Пуассона для адиабатического процесса
Первый закон термодинамики записывается в таком виде:
Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:
При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:
Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:
Где dV — малое изменение объема.
Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:
Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.
Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:
Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:
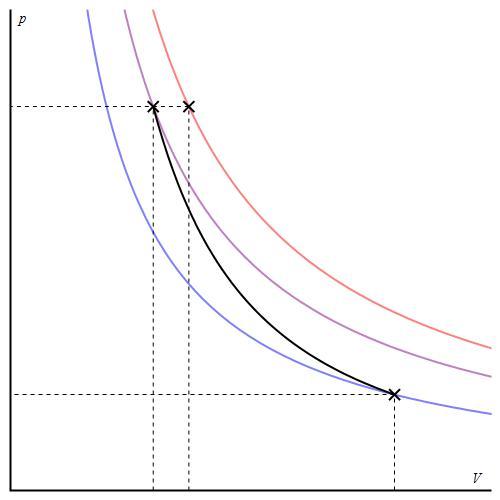
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.
Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.
Пример задачи
В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.
Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?
Для решения задачи следует использовать следующее уравнение адиабаты:
Его лучше записать в таком виде:
Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.
Новое в блогах
Физический смысл адиабатного процесса (Часть 1 — Давление газа)
1. Это первая часть статьи, которую я планирую написать и опубликовать. Вторая часть будет посвящена температуре, третья — экспериментальной проверке теоретических выводов.
2. Приношу свои извинения за не совсем адекватное написание формул. Всем, кого заинтересовала эта статья, могу выслать на мыло вариант в формате docx с нормально написанными формулами (мой адрес — [email protected])
3. Приглашаю к сотрудничеству по разработке основных положений электромагнитной теории теплоты всех желающих
4. Продолжение следует.
Хорошо известно, что при сжатии газа повышается его давление и его температура. Соответственно, при расширении газа температура и давление падают. Если при этом система (сжимаемый газ и ёмкость, в котором этот газ содержатся) не обменивается тепловой энергией друг с другом и с окружающим пространством, то такие процессы сжатия и расширения называются адиабатными (адиабатическими).
Современная теоретическая физика (статистическая физика, статистическая механика, физическая кинетика) до сих пор объясняет изменение давления и температуры газов работой, которая совершается над газами при их сжатии или которую совершает сам газ при расширении. См, например: ( http://ru.wikipedia.org/wiki/%C0%E4%E8%E0%E1%E0%F2%E8%F7%E5%F1%EA%E8%E9_%EF%F0%EE%F6%E5%F1%F1 )
Характер изменения величин давления и температуры газов при адиабатном процессе в современной теоретической физике считается потенциальной функцией, основанием которой является занимаемый газом определенной массой объём V , а показатель зависит от т.н. показателя адиабаты k :
k = C (p) /C (V) , где
Cp и CV — теплоёмкости газа при постоянном давлении и постоянном объёме, соответственно.
Для идеальных газов, с которыми так любит иметь дело современная теоретическая физика, теплоёмкости которых считаются постоянными, характер изменения давления и температуры определяется простейшими уравнениями:
p= const /V^ k =co nst V^ (- k ) ,
T= const/ V^ (k-1) =const V^ (1-k) , где
p – давление газа,
V – объем, занимаемый газом,
T – температура газа (абсолютная),
k – показатель адиабаты.
Тому же самому учат и все современные школьные учебники и курсы лекций по общей физике.
Современная теоретическая физика считает, что величина показателя адиабаты k равна 5/3 для одноатомных газов, 7/5 – для двухатомных и 4/3 – для трёхатомных газов. Изменение величины показателя адиабаты принято обосновывать количеством неких «степеней свободы» у газообразных молекул. Хотя абсолютно никакой логики и никакого физического смысла в попытке связать эти самые «степени свободы» с величиной показателя адиабаты нет.
Что же происходит при адиабатных процессах с газами согласно разрабатываемой мной электромагнитной теории теплоты (ЭТТ).
Согласно ЭТТ агрегатное состояние вещества определяется текущим распределением электронов атомов, входящих в состав молекулы. Существует три основным электронных уровня – газообразующий, в котором может находиться не более двух электронов, гидрогенный («жидкостной») и кристаллообразующий, в группах которых может содержаться максимум по 8 электронов. Таковы на сегодняшний день представления ЭТТ о строении атомов и молекул, сделанные на основе свойств элементов периодической таблицы Менделеева.
Молекула реального газа гелия (He), более всех других подходящего на роль «идеального» газа, представлена на рис. 1. Она имеет одноатомное молекулярное ядро, в состав которого входит два протона и два нейтрона, и два электрона, которые при нормальных условиях располагаются на газообразующем уровне – вращаясь по замысловатым траекториям вокруг молекулярного ядра, они создают вокруг него сферическое электронное «облако».
Рис. 1. Газообразная молекула He (гелия)
согласно электромагнитной теории теплоты.
Электроны, вращаясь вокруг молекулярного ядра, создают т.н. «электронное облако», которое индуцирует электрическое и магнитное поля. Эти поля, взаимодействуя с электрическими и магнитными полями, индуцируемыми электронами соседних молекул, и заставляют газообразные молекулы отталкиваться друг от друга, как одноимённые электрические заряды и одинаковые полюса магнитов. Эти силы отталкивания молекул друг от друга и приводят ко всем хорошо известным свойствам газов занимать весь предоставленный объём, рассеиваться в вакууме (космическом пространстве), обладать упругостью, создавать, вследствие действия силы притяжения к Земле, атмосферное давление, передавать давление в разных направлениях, например, звуковые волны и т.д. и т.п.
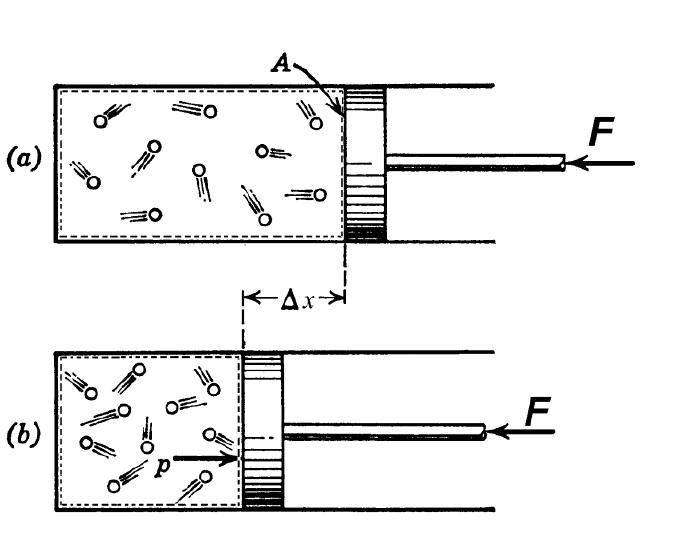
Предположим, мы имеем некий цилиндр с поршнем, наполненный молекулами «идеального» газа гелия (см. рис. 2 слева). Приложив к штоку поршня некоторую силу F , т.е. попросту надавив на поршень, мы уменьшили объём газа в n раз – например, как это показано на рис. 2 справа – вдвое.
Рис. 2. Адиабатное сжатие газа
согласно электромагнитной теории теплоты.
Вследствие сжатия газообразные молекулы гелия уплотнились, расстояния между молекулярными ядрами уменьшились. Соответственно, главные эквипотенциальные поверхности полей молекул сократились в размерах, – что наглядно изображено на рис. 2.
Кстати, рис. 2 наглядно отображает характер уплотнения молекул. Хотя сперва кажется, будто бы я просто-напросто не нарисовал половину молекул внутри цилиндра с поршнем. Присмотритесь внимательно – в каждом ряду молекул на рисунке справа – 9 штук, а слева – уже 11. Я не ошибся. При уменьшении объёма вдвое расстояние между молекулами уменьшается всего на одну пятую часть – см. рис. 3.
Рис. 3. Изменение соотношений длины ребра и площади грани куба
при уменьшении его объёма вдвое.
То есть, при уменьшении объёма в n раз расстояние между центрами газовых молекул сокращается в куб.корень из < n> раз.
Определим, в какой пропорции увеличиваются силы отталкивания между отдельными молекулами (см. рис. 4).
Рис. 4. Увеличение сил отталкивания между отдельными газовыми молекулами при сжатии газа.
Согласно закона Кулона, величина силы взаимодействия двух точечных зарядов прямо пропорциональна произведению модулей этих зарядов q 1 и q 2 и обратно пропорциональна квадрату расстояния R между ними:
k в данном случае – коэффициент пропорциональности.
Эта формула универсальна для всех известных полей – и для магнитного и для гравитационного. Для гравитационного поля, например, этой формулой описывается закон всемирного тяготения:
где γ — гравитационная постоянная, по сути – тот же самый коэффициент пропорциональности, а m 1 и m 2 – масса тел («гравитационный заряд»).
В нашем случае мы под обозначением q 1 и q 2 будем понимать условную сумму всех типов «зарядов», индуцирующих соответствующие поля – и электрического, и магнитного, и пытающегося им противостоять гравитационного (как известно, гравитационное поле создаёт лишь силы притяжения). Таким образом (см. рис. 4), до сжатия газа, отдельно взятые молекулы отталкивались друг от друга с силой:
а после сжатия – с силой:
Таким образом, при уменьшении объёма в n раз (специалисты в области двигателей внутреннего сгорания называют эту величину степенью сжатия) сила отталкивания между отдельными молекулами увеличится в:
Во сколько же раз в этом случае возрастёт давление газа? Чтобы правильно ответить на этот вопрос, вспомним, что же такое давление. Это величина усилия на единицу площади.
После сжатия, как мы определили, усилие каждой отдельной газовой молекулы на внутреннюю поверхность цилиндра увеличилось в <куб. кор из n>^ 2 раз. Но, помимо этого, увеличилось и количество молекул, оказывающих давление на ту же самую площадь внутренней поверхности цилиндра (см. рис. 5).
Рис. 5. При сжатии газа увеличивается количество молекул,
оказывающих давление на единицу площади.
Допустим, что если до сжатия на «единичную» площадь оказывало давление a× a молекул, то, как абсолютно очевидно, после сжатия газа в n раз число этих молекул стало <куб. кор. из n> a × <куб. кор. из n> a = <куб. кор. из n>^ 2 a^ 2 . То есть количество газовых молекул, оказывающих давление на «единичную» площадь, увеличилось в <куб. кор. из n>^ 2 раз.
Если количество молекул, оказывающих давление на единицу площади поверхности, увеличилось в <куб. кор из n>^ 2 раз, и сила давления каждой молекулы на поверхность тоже увеличилось в <куб. кор. из n>^ 2 раз, то давление газа при его сжатии в n раз увеличивается в <куб. кор. из n>^ 2 × <куб.кор. из n>^ 2 = <куб.кор. из n>^ 4 = n ^<4/ 3> раз.
Таким образом, используя простейшие математические операции и логику, мы получаем показатель адиабаты для одноатомных идеальных газов, равный 4/3.
Как видим, он не соответствует общепринятому на сегодня показателю адиабаты для идеальных одноатомных газов, равному 5/3. Значит, выводы поспешны и не соответствуют истине? Вовсе нет. Ответ на вопрос, какая теория – молекулярно-кинетическая или электромагнитная более адекватно и более точно описывает реальное состояние газовых сред, могут дать только натурные эксперименты. Дело в том, что результаты прямого измерения показателя адиабаты для инертных газов вовсе не соответствуют теоретическим выкладкам, полученным из количества степеней свободы.
http://1ku.ru/obrazovanie/58101-adiabaticheskij-process-i-uravnenija-adiabaty-dlja-idealnogo-gaza-primer-zadachi/
http://maxpark.com/community/191/content/1359586
Уравнение Пуассона для адиабатного процесса
Содержание:
- Описание адиабатного процесса
- Уравнение Пуассона
- Коэффициент Пуассона
- Применение уравнения в расчетах ДВС и холодильных установок
Описание адиабатного процесса
Определение
Адиабатный или адиабатический процесс – это процесс, который протекает с небольшой скоростью при отсутствии теплового обмена с окружающей средой.
Адиабатный процесс является разновидностью термодинамического процесса. Важными условиями его возникновения являются теплоизолированная система и условия, при которых полностью исключается теплообмен с окружающей средой. При проведении практических исследований Q = 0. По первому закону термодинамики требуется полный расход выполненной работы для изменения внутренней энергии системы:
(A=Delta U)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Такие результаты практически недостижимы при реальных условиях. Причина заключается в отсутствии идеальных теплоизоляционных материалов. Однако ученым удалось максимально приблизиться к созданию подходящих условий.
Например, благодаря применению оболочек, которые характеризуются низкими параметрами теплопроводности, создаются условия, как в термосе. Другим способом выступает достижение достаточно большой скорости протекания адиабатного процесса. В этом случае система обменивается теплом с окружающей средой в течение короткого промежутка времени, которым можно пренебречь при расчетах.
Уравнение Пуассона
При возникновении адиабатного процесса наблюдается одновременное изменение трех характеристик, которыми обладает газообразное вещество: V, p, Т. Величины зависят друг от друга, что выражается в уравнении Клапейрона-Менделеева. Корректно представить описание процесса можно, дополняя формулу уравнением Пуассона.
Формулировка отражает наличие зависимости между объемом и давлением газа. Исходя из первого принципа термодинамики, уравнение для адиабатного процесса в случае идеального газа будет выглядеть следующим образом:
(0 = CVDt + pdV)
Удаляя из уравнения выражение dT по уравнению Клапейрона-Менделеева, получается следующее равенство:
(pV = RT)
Таким образом:
(dT=frac{1}{R}left(pdV+V dp right))
В результате будет записана формула:
(frac{C_{V}}{R}left(pdV+V dp right)+pdV=0)
Исходя из уравнения Майера,
(R = CP – CV)
Необходимо подставить эту формулу, а также поделить числитель и знаменатель дроби перед скобками на (CV) и обозначить (CP/CV) – (gamma)
(frac{1}{gamma -1}left(pdV+V dp right)+pdV=0)
Можно сделать следующий вывод:
(V dp + gamma pdV=0)
Почленно поделив уравнение на произведение (pV), формула будет записана следующим образом:
(frac{dp}{p}+gamma frac{dV}{V}=0)
В результате интеграции данного уравнения получается следующее соотношение:
(ln p+gamma ln V=ln C)
где С является постоянной величиной интегрирования.
Если пропотенциировать последнюю формулу, то в итоге получается уравнение Пуссона:
(pVgamma =const)
Важно отметить, что (gamma) определяется природой газообразного вещества. К примеру, в случае воздуха (gamma=1,42).
Коэффициент Пуассона
Определение
Показатель адиабаты равен отношению теплоемкости в условиях постоянного давления к теплоемкости в условиях постоянного объема.
Показатель адиабаты по-другому называют коэффициентом Пуассона или фактором изоэнтропийного расширения. Для обозначения этой величины используют греческую букву γ (гамма) или κ (каппа). Такие специальные символы применимы для решения задач химических инженерных дисциплин. Если решается задача по теплотехнике, целесообразно изображать коэффициент Пуассона в виде латинской буквы k.
Показатель адиабаты рассчитывают из отношения между изобарной теплоемкостью газообразного вещества и его изохорной теплоемкостью. Формула имеет следующий вид:
(k=frac{C_{p}}{C_{V}})
В разных газах показатель адиабаты будет неодинаковым. Для идеального газообразного вещества коэффициент Пуассона составляет 5/3, для двухатомного – 7/3, для трехатомного – 4/3.
Применение уравнения в расчетах ДВС и холодильных установок
В условиях реальных газов имеют значения силы, которые возникают при взаимодействии молекул друг с другом. Для расчета показателя адиабаты исследованных газообразных веществ требуется проводить эксперименты. В 1819 году учеными Клеманом и Дезормом были предложены методики определения коэффициента Пуассона. Описание эксперимента:
- резервуар наполнили охлажденным газом;
- достижение давлением величины Р1;
- открытие крана;
- адиабатическое расширение газа;
- понижение давления до значения атмосферного РА;
- изохорное прогревание газообразного вещества до температуры окружающей среды;
- повышение давления в баллоне до Р2.
В этом случае показатель адиабаты будет иметь следующий вид:
(k=frac{P_{1}-P_{A}}{P_{1}- P_{2}})
После расчетов показатель адиабаты будет больше 1. Это объясняет постоянное возрастание температуры во время адиабатического сжатия идеального или реального газа. В случае расширения газообразного вещества, температурные показатели снижаются. Описанное явление носит название пневматического огнива. Это свойство адиабатического процесса применяют при конструировании двигателей, функционирующих на дизельном топливе. Горючая смесь в агрегате сжимается, находясь в специальном цилиндре, и воспламеняется под действием высокой температуры.
Уравнение Пуассона применимо не только для разработки двигателей внутреннего сгорания, но и активно применяется для осуществления расчетов в проектировании холодильного оборудования. Формула Пуассона позволяет с максимальной точностью описать равновесный адиабатный процесс, при условии которого состояния равновесия непрерывно сменяют друг друга. Если в реальных обстоятельствах открыть кран в баллоне, что приведет к адиабатному расширению газа, можно будет наблюдать нестационарный переходный процесс, сопровождающийся завихрениями газообразного вещества, которые со временем затухают по причине макроскопического трения.
Насколько полезной была для вас статья?
Рейтинг: 2.00 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.
Адиабатический процесс
Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:
- теплопроводность между внешней средой и системой по той или иной причине является низкой;
- скорость процесса велика, поэтому обмен теплом не успевает происходить.
В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.
Уравнение Пуассона для адиабаты идеального газа
Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.
Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:
dU = -P*dV.
Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.
В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:
P*Vγ = const.
Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.
Что такое показатель адиабаты?
Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом CP изобарную теплоемкость, а символом CV — изохорную. Тогда для γ справедливо равенство:
γ = CP/CV.
Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.
Теплоемкости CP и CV
Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:
dU = CV*dT.
Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.
Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:
CP*dT = CV*dT + P*dV.
Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.
Величина γ для газа идеального одноатомного
Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:
CP = CV + R.
Откуда можно определить значение изохорной теплоемкости CV:
γ = CP/CV;
CV = R/(γ-1).
Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:
CV = 3/2*R.
Из последних двух равенств следует значение показателя адиабаты:
3/2*R = R/(γ-1) =>
γ = 5/3 ≈ 1,67.
Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.
Зависимость γ от числа степеней свободы
Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.
Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:
CV = 5/2*R.
Тогда значение γ будет равно:
γ = 7/5 = 1,4.
Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.
Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:
γ = 4/3 ≈ 1,33.
Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.
Показатель адиабаты для смеси газов
Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:
γ = ∑i=1N(ai*γi).
Где γi — это величина γ для i-го компонента.
Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.
Иное название этого понятия — «коэффициент Пуассона»; о параметре, характеризующем упругие свойства материала, см. Коэффициент Пуассона.
| Термодинамика |
|---|
 |
| Статья является частью одноименной серии. |
| Начала термодинамики |
| Уравнение состояния |
| Термодинамические величины |
| Термодинамические потенциалы |
| Термодинамические циклы |
| Фазовые переходы |
| править |
| См. также «Физический портал» |
Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении (




Уравнение:
,
где
— теплоёмкость газа,
— удельная теплоёмкость (отношение теплоёмкости к единице массы) газа,
- индексы
и
обозначают условие постоянства давления или постоянства объёма, соответственно.
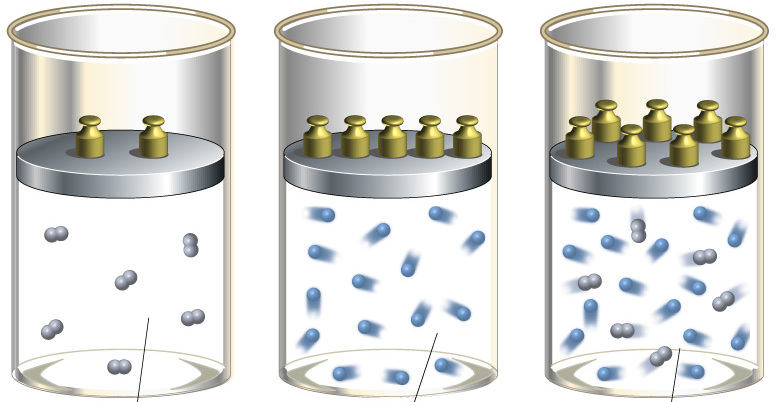
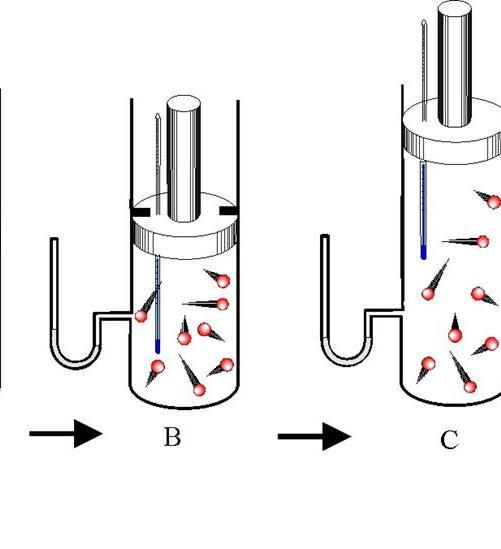
Для понимания этого соотношения можно рассмотреть следующий эксперимент:
Закрытый цилиндр с закреплённым неподвижно поршнем содержит воздух. Давление внутри равно давлению снаружи. Этот цилиндр нагревается до определённой, требуемой температуры. До тех пор, пока поршень закреплён в неподвижном состоянии, объём воздуха в цилиндре остаётся неизменным, в то время как температура и давление возрастают. Когда требуемая температура будет достигнута, нагревание прекращается. В этот момент поршень «освобождается» и, благодаря этому, начинает перемещаться под давлением воздуха в цилиндре без теплообмена с окружающей средой (воздух расширяется адиабатически). Совершая работу, воздух внутри цилиндра охлаждается ниже достигнутой ранее температуры. Чтобы вернуть воздух к состоянию, когда его температура опять достигнет упомянутого выше требуемого значения (при всё ещё «освобождённом» поршне) воздух необходимо нагреть. Для этого нагревания извне необходимо подвести примерно на 40 % (для двухатомного газа — воздуха) большее количество теплоты, чем было подведено при предыдущем нагревании (с закреплённым поршнем). В этом примере количество теплоты, подведённое к цилиндру с закреплённом поршне, пропорционально 

Другой путь для понимания разницы между 




| Показатели адиабаты для различных газов[2][3] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Темп. | Газ | γ | Темп. | Газ | γ | Темп. | Газ | γ | ||
| −181 °C | H2 | 1.597 | 200 °C | Сухой воздух | 1.398 | 20 °C | NO | 1.400 | ||
| −76 °C | 1.453 | 400 °C | 1.393 | 20 °C | N2O | 1.310 | ||||
| 20 °C | 1.410 | 1000 °C | 1.365 | −181 °C | N2 | 1.470 | ||||
| 100 °C | 1.404 | 2000 °C | 1.088 | 15 °C | 1.404 | |||||
| 400 °C | 1.387 | 0°C | CO2 | 1.310 | 20 °C | Cl2 | 1.340 | |||
| 1000 °C | 1.358 | 20 °C | 1.300 | −115 °C | CH4 | 1.410 | ||||
| 2000 °C | 1.318 | 100 °C | 1.281 | −74 °C | 1.350 | |||||
| 20 °C | He | 1.660 | 400 °C | 1.235 | 20 °C | 1.320 | ||||
| 20 °C | H2O | 1.330 | 1000 °C | 1.195 | 15 °C | NH3 | 1.310 | |||
| 100 °C | 1.324 | 20 °C | CO | 1.400 | 19 °C | Ne | 1.640 | |||
| 200 °C | 1.310 | −181 °C | O2 | 1.450 | 19 °C | Xe | 1.660 | |||
| −180 °C | Ar | 1.760 | −76 °C | 1.415 | 19 °C | Kr | 1.680 | |||
| 20 °C | 1.670 | 20 °C | 1.400 | 15 °C | SO2 | 1.290 | ||||
| 0°C | Сухой воздух | 1.403 | 100 °C | 1.399 | 360 °C | Hg | 1.670 | |||
| 20 °C | 1.400 | 200 °C | 1.397 | 15 °C | C2H6 | 1.220 | ||||
| 100 °C | 1.401 | 400 °C | 1.394 | 16 °C | C3H8 | 1.130 |
Содержание
- 1 Соотношения для идеального газа
- 1.1 Соотношения с использованием количества степеней свободы
- 2 Соотношения для реальных газов
- 3 Термодинамические выражения
- 4 Адиабатический процесс
- 5 Экспериментальное определение величины показателя адиабаты
- 6 См. также
- 7 Примечания
[править] Соотношения для идеального газа
Для идеального газа теплоёмкость не зависит от температуры. Соответственно, можно выразить энтальпию как 

С другой стороны, теплоёмкости могут быть выражены также через показатель адиабаты (

Может оказаться достаточно трудным найти информацию о табличных значениях 


где 
[править] Соотношения с использованием количества степеней свободы
Показатель адиабаты (

или
Таким образом, для одноатомного идеального газа (три степени свободы) показатель адиабаты равен:
,
в то время как для двуатомного идеального газа (пять степеней свободы) (при комнатной температуре):
.
Воздух на земле представляет собой в основном смесь двухатомных газов (около 78 % азота — N2, и около 21 % кислорода — O2), и при нормальных условиях его можно рассматривать как идеальный. Двухатомный газ имеет пять степеней свободы (три поступательных и две вращательных степени свободы; колебательная степень свободы не задействована, за исключением высоких температур). Как следствие, теоретически, показатель адиабаты для воздуха имеет величину:
.
Это хорошо согласуется с экспериментальными измерениями показателя адиабаты воздуха, которые приблизительно дают значение 1.403 (приведённое выше в таблице).
[править] Соотношения для реальных газов
По мере того, как температура возрастает, более высокоэнергетические вращательные и колебательные состояния становятся достижимыми для молекулярных газов, и таким образом, количество степеней свободы возрастает, и уменьшается показатель адиабаты 
Для реальных газов, как 






[править] Термодинамические выражения
Значения, полученные с помощью приближённых соотношений (в частности, 


Значения 

Вышеприведённые соотношения отражают подход, основанный на развитии строгих уравнений состояния (таких, как уравнение Пенга — Робинсона[en]), которые настолько хорошо согласуются с экспериментом, что для их применения требуется лишь незначительно развивать базу данных соотношений или значений 
[править] Адиабатический процесс
Для изоэнтропийного, квазистатического, обратимого адиабатного процесса, происходящего в простом сжимаемом идеальном газе:
где 

[править] Экспериментальное определение величины показателя адиабаты
Поскольку процессы, происходящие в небольших объёмах газа при прохождении звуковой волны, близки к адиабатическим[4], показатель адиабаты можно определить, измерив скорость звука в газе. В этом случае показатель адиабаты и скорость звука в газе будут связаны следующим выражением:
где 





Другим способом экспериментального определения величины показателя адиабаты является метод Клемана — Дезорма, который часто используется в учебных целях при выполнении лабораторных работ. Метод основан на изучении параметров некоторой массы газа, переходящей из одного состояния в другое двумя последовательными процессами: адиабатическим и изохорическим.[5]
Лабораторная установка включает стеклянный баллон, соединенный с манометром, краном и резиновой грушей. Груша служит для нагнетания воздуха в баллон. Специальный зажим предотвращает утечку воздуха из баллона. Манометр измеряет разность давлений внутри и вне баллона. Кран может выпускать воздух из баллона в атмосферу.
Пусть первоначально в баллоне было атмосферное давление и комнатная температура. Процесс выполнения работы можно условно разбить на два этапа, каждый из которых включает в себя адиабатный и изохорный процесс.
1-й этап:
При закрытом кране накачиваем в баллон небольшое количество воздуха и зажимаем шланг зажимом. При этом давление и температура в баллоне повысятся. Это адиабатный процесс. Со временем давление в баллоне начнет уменьшаться вследствие того, что газ в баллоне начнёт охлаждаться за счет теплообмена через стенки баллона. При этом давление будет уменьшаться при построянном объёме. Это изохорный процесс. Выждав, когда температура воздуха внутри баллона сравняется с температурой окружающего воздуха, запишем показания манометра 
2-ой этап:
Теперь откроем кран 3 на 1—2 секунды. Воздух в баллоне будет адиабатно расширяться до атмосферного давления. При этом температура в баллоне понизится. Затем кран закроем. Со временем давление в баллоне начнет увеличиваться вследствие того, что газ в баллоне начнет нагреваться за счет теплообмена через стенки баллона. При этом снова будет увеличиваться давление при постоянном объёме. Это изохорный процесс. Выждав, когда температура воздуха внутри баллона сравнится с температурой окружающего воздуха, запишем показание манометра 
Недостатком данного метода является то, что процессы быстрого расширения газа в ходе лабораторной работы не являются чисто адиабатическими ввиду теплообмена через стенку сосудов, а рассматриваемый газ заведомо не является идеальным. И хотя полученная в ходе лабораторной работы величина будет заведомо содержать методическую погрешность, всё же существуют различные способы её устранения, например, за счет учета времени расширения и количества подведенного за это время тепла.[6]
[править] См. также
- Теплоёмкость
- Удельная теплоёмкость
- Скорость звука
- Термодинамические уравнения (англ.)
- Термодинамика
- Объёмная теплоёмкость
[править] Примечания
- ↑ Fox, R., A. McDonald, P. Pritchard: Introduction to Fluid Mechanics 6th ed. Wiley
- ↑ White, Frank M.: Fluid Mechanics 4th ed. McGraw Hill
- ↑ Lange’s Handbook of Chemistry, 10th ed. page 1524
- ↑ Савельев2001, с. 30—32
- ↑ http://www.physdep.isu.ru/kosm/method/obsh/lab/2-8.pdf
- ↑ http://www.physchem.msu.ru/doc/12_molecular.PDF





 ,
, — теплоёмкость газа,
— теплоёмкость газа, — удельная теплоёмкость (отношение теплоёмкости к единице массы) газа,
— удельная теплоёмкость (отношение теплоёмкости к единице массы) газа, и
и  обозначают условие постоянства давления или постоянства объёма, соответственно.
обозначают условие постоянства давления или постоянства объёма, соответственно.


 или
или 
 ,
, .
. .
.


