Коэффициент асимметрии. Эксцесс распределения
Краткая теория
При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.
Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:
Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.
На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию
,
а кривая II – отрицательную (левостороннюю)
.
Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:
Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.
Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой — эксцессом.
Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:
Число 3 вычитается из отношения
потому, что для наиболее часто встречающегося
нормального распределения отношение
.
Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные — отрицательным
эксцессом.
Примеры решения задач
Задача 1
Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим расчетную
таблицу
Средняя:
Найдем моду — варианту, которой соответствует наибольшая частота.
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии Пирсона:
Коэффициент асимметрии можно найти по формуле:
Центральный момент
3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Центральный момент
4-го порядка:
Получаем:
Задача 2
Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.
Решение
Составим расчетную таблицу
Перейдем к условным вариантам
В качестве ложного нуля возьмем
3-ю варианту
0
Условные варианты вычислим по
формуле:
где
4
(разность между соседними вариантами)
Условный момент 1-го порядка:
Средняя:
Условный момент 2-го порядка:
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии можно найти
по формуле:
Условный момент 3-го порядка:
Центральный момент 3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Условный момент 4-го порядка:
Центральный момент 4-го порядка:
Получаем:
Распределение коммерческих банков по размеру активов характеризуется следующими данными:
| Размер активов, млн руб. | До 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 | 600 и более | Итого |
|---|---|---|---|---|---|---|---|
| Удельный вес банков, % к итогу | 8 | 25 | 52 | 7 | 5 | 3 | 100 |
Определите характеристики распределения:
а) среднюю;
б) моду;
в) среднее квадратическое отклонение;
г) коэффициент вариации;
д) коэффициент асимметрии и эксцесс.
Решение:
Данный интервальный вариационный ряд содержит открытые интервалы, которые предварительно необходимо закрыть. Для этого из величины верхней границы первого интервала надо вычесть величину второго интервала. Получим нижнюю границу первого интервала.
200 — 100 = 100.
Первый интервал: 100 — 200.
Теперь к нижней границе последнего интервала прибавляем величину предшествующего интервала:
600 + 100 = 700
Последний интервал: 600 — 700.
а) Определение средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения каждого интервала.
Так, например, дискретная величина х для первого интервала будет равна: (100 + 200) / 2 = 150.
Построим таблицу рассчётных данных:
Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной.
б) Определим моду.
Мода — это величина признака наиболее часто встречающегося в совокупности.
В интервальных рядах распределения с равными интервалами мода определяется по формуле:
где
хМо – начальное значение интервала, содержащего моду;
iМо – величина модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, предшествующего модальному,
fМо+1 – частота интервала, следующего за модальным.
Мода содержится в интервале от 300 до 400, так как у этого интервала наибоьшая частота
f = 52.
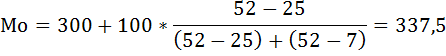
в) Найдём среднее квадратическое отклонение:
Значения размера активов в ряду распределения могут отличаться от среднего значения на 104,28 млн. руб.
Дисперсия будет равна:
σ2 = 10 875
г) Коэффициент вариации рассчитаем по формуле:
Совокупность однородна, так как коэффициент вариации не превышает 33%.
д) Рассчитаем показатель асимметрии через отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе, то есть
где μ3 — центральный момент третьего порядка, рассчитываемый по формуле:
μ3 = 88 275 000 / 100 = 882 750
As = 882 750 / 104,283 = 0,78
Так как величина показателя асимметрии положительна, следовательно, речь идёт о правосторонней асимметрии.
Полученный результат свидетельствует о наличии несущественной по величине и положительной по своему характеру асимметрии.
Далее рассчитаем показатель эксцесса (Еk). Наиболее точно он определяется по формуле с использованием центрального момента четвёртого порядка:
μ4 = 52 123 312 500 / 100 = 521 233 125
σ4 = 118 265 625
Ek = 521 233 125 / 118 265 625 – 3 = 4,41 — 3 = 1,41
Так как Ek > 0 распределение является островершинным.
58. Коэффициенты асимметрии и эксцесса.
Центральные
моменты распределения
Для дальнейшего изучения характера
вариации используются средние значения
разных степеней отклонений отдельных
величин признака от его средней
арифметической величины. Эти показатели
получили название центральных
моментов распределения порядка,
соответствующего степени, в которую
возводятся отклонения,
или просто моментов.
Показатели формы распределения
-
Асимметрия – Коэффициент
асимметрии
характеризует асимметричность
(«скошенность») распределения признака
в совокупности -
Эксцесс – Показатель эксцесса
представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения
Асимметрия распределения
-
При
=0
распределение считается нормальным. -
При
> 0 правосторонняя асимметрия. -
При
<0
левосторонняя асимметрия. -
Если асимметрия более 0,5, то независимо
от знака она считается значительной -
Если асимметрия меньше 0,25, то она
считается незначительной
|
Асимметрия |
|
|
является |
|
Расчет |
|
т.е. — нормированный |
Показатель Пирсона зависит от степени
асимметричности в средней части ряда
распределения, а показатель асимметрии,
основанный на моменте третьего порядка,
— от крайних значений признака.
Оценка существенности асимметрии
Для оценки существенности асимметрии
вычисляют показатель средней квадратической
ошибки коэффициента асимметрии
Если отношение
имеет значение больше 2, то это
свидетельствует о существенном характере
асимметрии
Эксцесс распределения
Показатель эксцесса
представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения, НО! График
распределения может выглядеть сколь
угодно крутым в зависимости от силы
вариации признака: чем слабее вариация,
тем круче кривая распределения при
данном масштабе. Не говоря уже о том,
что, изменяя масштабы по оси абсцисс и
по оси ординат, любое распределение
можно искусствен но сделать «крутым»
и «пологим». Чтобы показать, в чем состоит
эксцесс распределения, и правильно его
интерпретировать, нужно сравнить ряды
с одинаковой силой вариации (одной и
той же величиной σ) и разными показателями
эксцесса. Чтобы не смешать эксцесс с
асимметрией, все сравниваемые ряды
должны быть симметричными. Такое
сравнение изображено на рис.
Поскольку эксцесс нормального
распределения равен 3, показатель
эксцесса вычисляется по формуле
|
|
или |
где |
-
При
>0
– высоковершинный эксцесс распределения -
При
<0
– низковершинный эксцесс распределение -
При
=0 – нормальное распределение
Оценка существенности эксцесса
Для оценки существенности эксцесса
вычисляют показатель его средней
квадратической ошибки
Если отношение
имеет значение больше 3, то это
свидетельствует о существенном характере
эксцесса
Как интерпретировать асимметрию в статистике (с примерами)
17 авг. 2022 г.
читать 3 мин
В области статистики мы используем асимметрию для описания симметрии распределения.
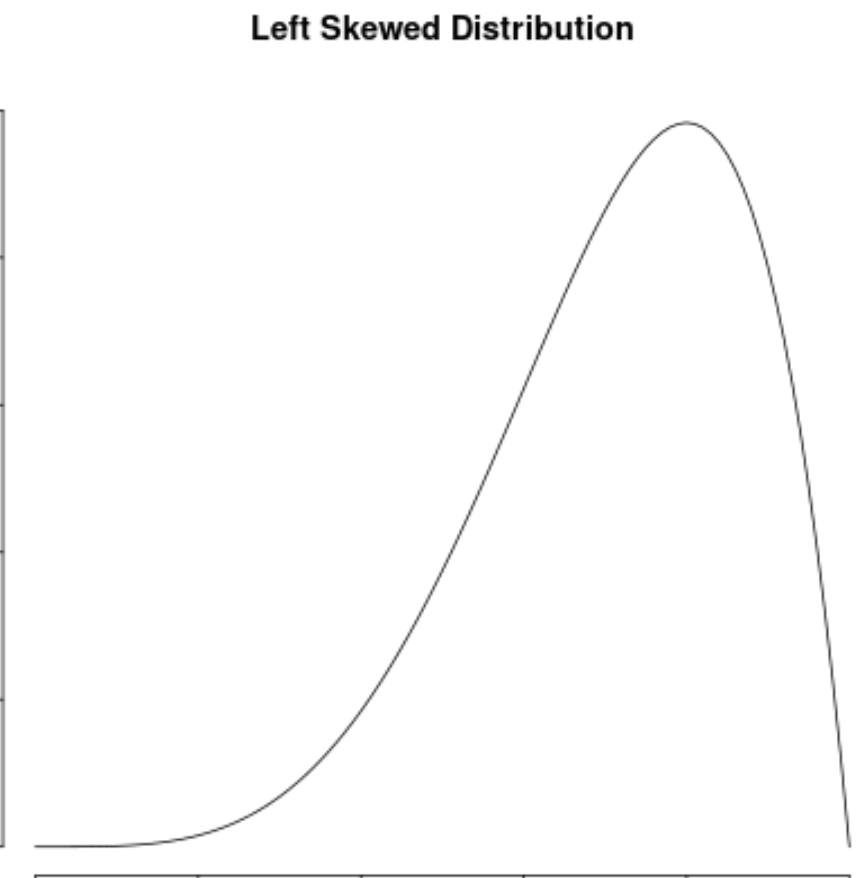
Мы говорим, что распределение значений данных асимметрично влево , если оно имеет «хвост» в левой части распределения:
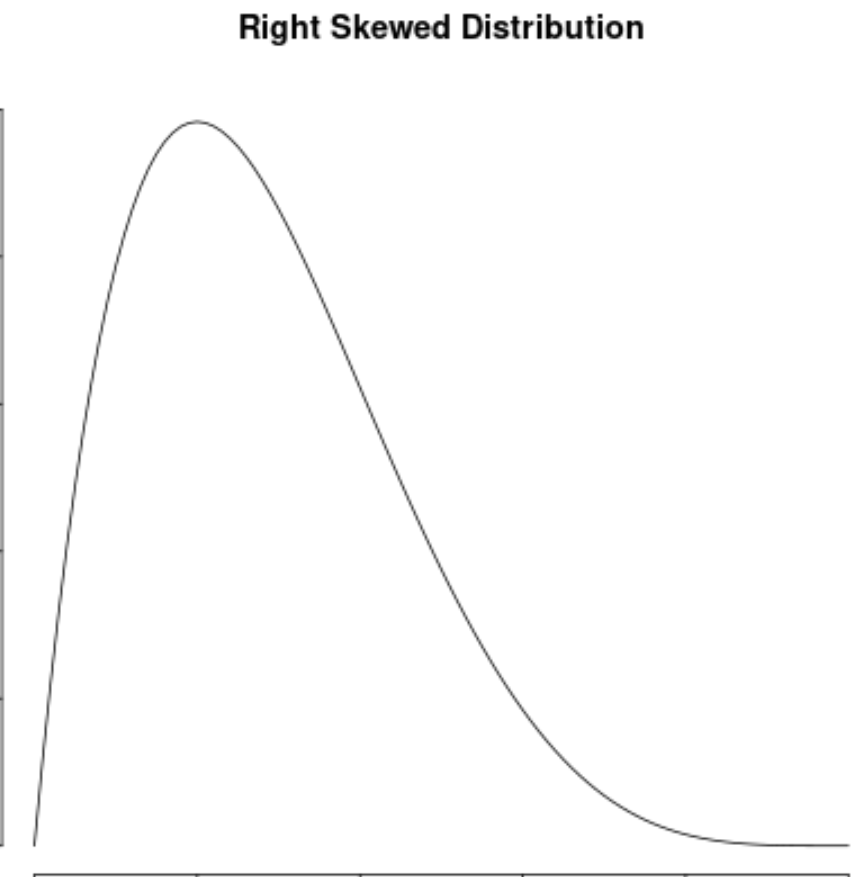
Мы говорим, что распределение скошено вправо , если оно имеет «хвост» в правой части распределения:
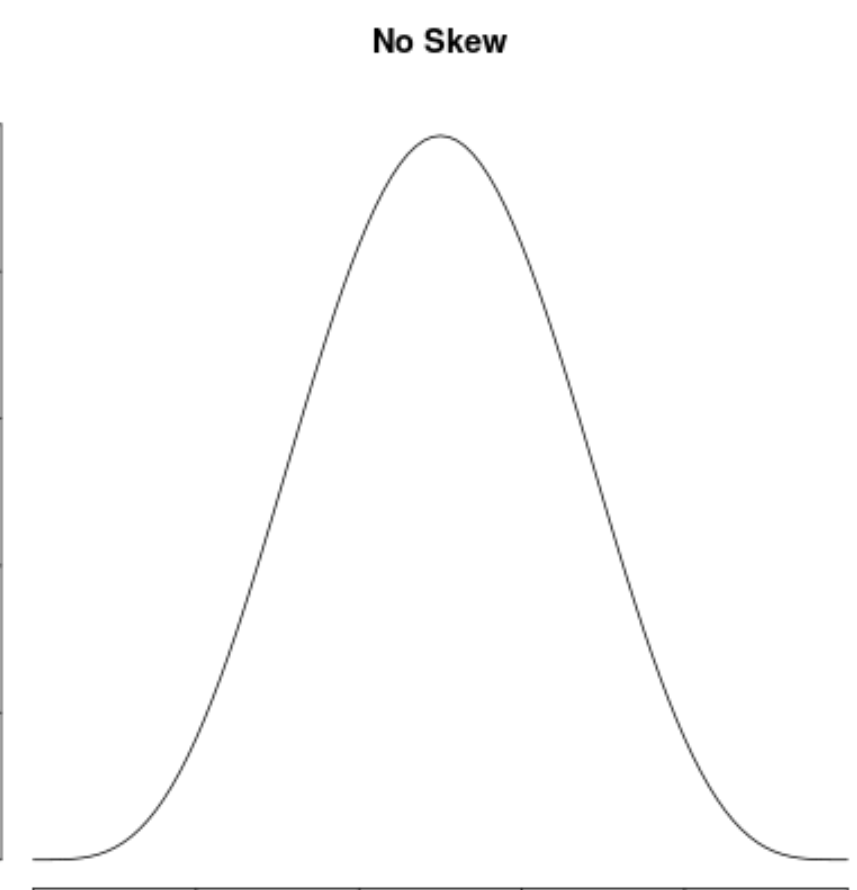
И мы говорим, что распределение не имеет перекоса , если оно симметрично с обеих сторон:
Как интерпретировать асимметрию
Значение асимметрии может варьироваться от отрицательной бесконечности до положительной бесконечности.
Вот как интерпретировать значения асимметрии:
- Отрицательное значение асимметрии указывает на то, что хвост находится в левой части распределения, которая простирается в сторону более отрицательных значений.
- Положительное значение асимметрии указывает на то, что хвост находится на правой стороне распределения, которая простирается в сторону более положительных значений.
- Нулевое значение указывает на то, что в распределении вообще нет асимметрии, что означает, что распределение совершенно симметрично.
В следующих примерах показано, как интерпретировать значения асимметрии на практике.
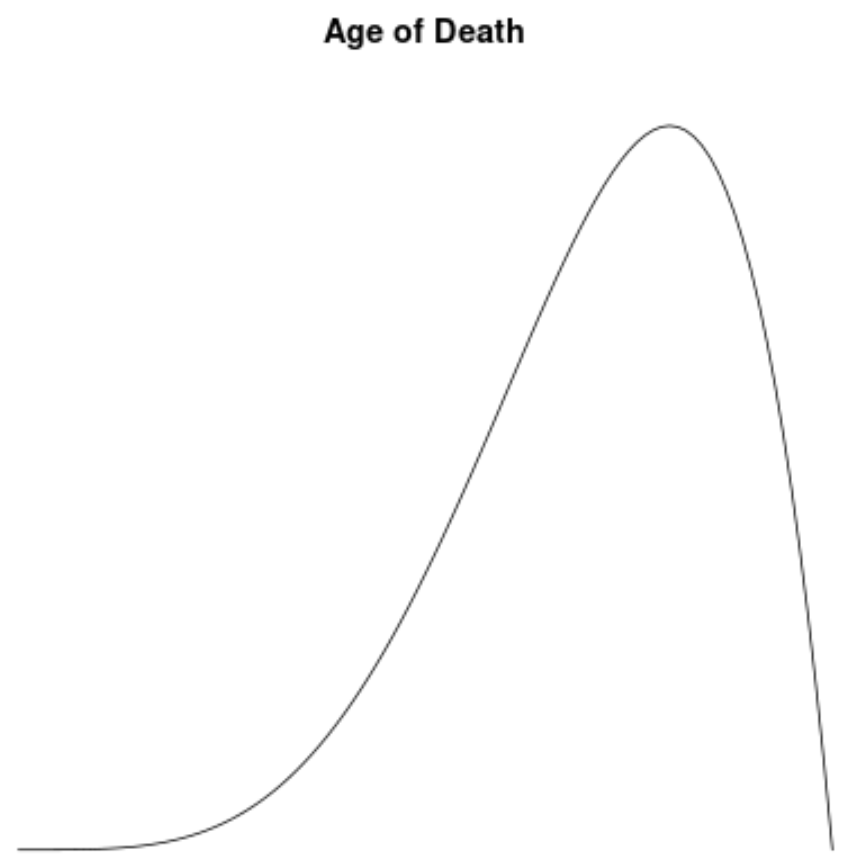
Пример 1: Распределение с асимметрией влево
Распределение возраста умерших в большинстве популяций асимметрично влево. Большинство людей доживает до 70–80 лет, и все меньше и меньше людей доживает до этого возраста.
Если бы мы создали график плотности , чтобы визуализировать распределение значений возраста смерти, он мог бы выглядеть примерно так:
Предположим, мы вычисляем асимметрию для этого распределения и обнаруживаем, что она равна -1,3225 .
Поскольку это значение отрицательное, мы интерпретируем это как означающее, что распределение смещено влево, что означает, что хвост распространяется на левую часть распределения.
Пример 2: Правостороннее распределение
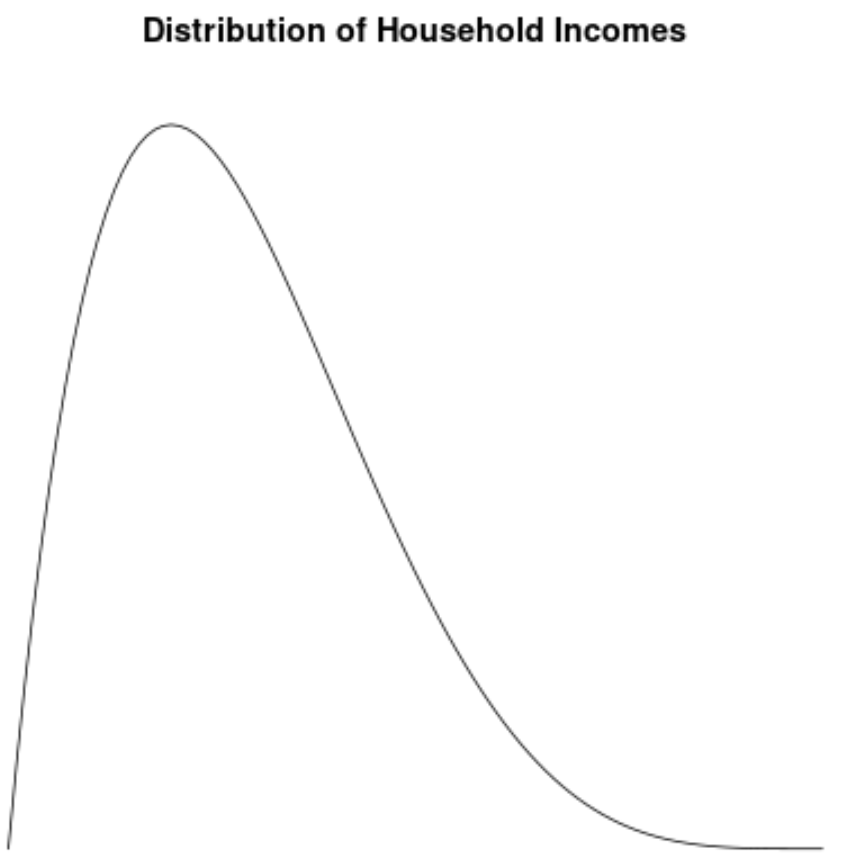
Распределение доходов домохозяйств в США смещено вправо: большинство домохозяйств зарабатывают от 30 до 70 тысяч долларов в год, но с длинным правым хвостом домохозяйств, которые зарабатывают гораздо больше.
Если бы мы создали график плотности, чтобы визуализировать распределение значений дохода домохозяйства, он мог бы выглядеть примерно так:
Предположим, мы вычисляем асимметрию для этого распределения и обнаруживаем, что она равна 2,0043 .
Поскольку это значение положительное, мы интерпретируем это как означающее, что распределение скошено вправо, что означает, что хвост распространяется на правую часть распределения.
Пример 3: Нет перекоса
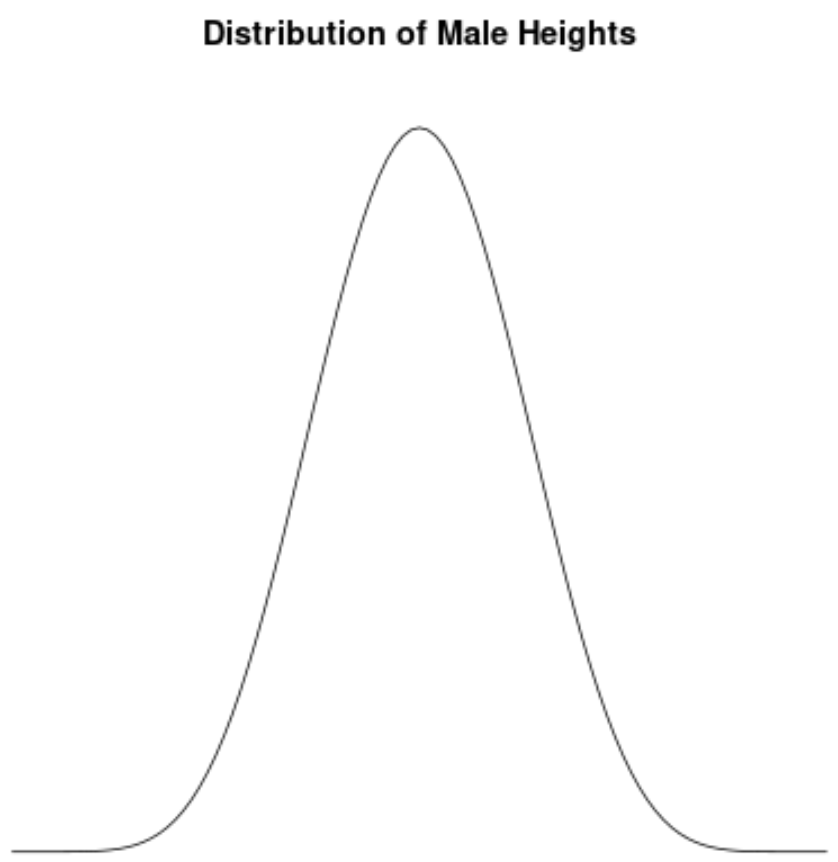
Высота самцов примерно нормально распределена и не имеет перекоса. Например, средний рост мужчины в США составляет примерно 69,1 дюйма. Распределение высоты примерно симметрично: некоторые из них ниже, а некоторые выше.
Если бы мы создали график плотности, чтобы визуализировать распределение роста мужчин в США, он мог бы выглядеть примерно так:
Предположим, мы вычисляем асимметрию для этого распределения и обнаруживаем, что она равна 0,0013 .
Поскольку это значение близко к нулю, мы интерпретируем это как означающее, что распределение практически не имеет перекоса, что означает, что хвосты с обеих сторон распределения примерно равны.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация об асимметрии в статистике:
5 примеров положительно асимметричных распределений
5 примеров распределения с отрицательным перекосом
Как рассчитать асимметрию в Excel
Как определить асимметрию в ящичковых диаграммах
The measure of skewness tells us the direction and the extent of skewness. In symmetrical distribution the mean, median, and mode are identical. the more the mean moves away from the mode, the larger the asymmetric or skewness.
Before learning let’s learn more about Mean, Median, and Mode first.
Mean
Mean is the average of the numbers in the data distribution, It is calculated by adding up all the values in the dataset and dividing the sum by the number of values in the dataset.
Mean= Sum of all values in Dataset / Total number of values
Example: Find the mean of a dataset of exam scores: 70, 80, 85, 90, and 95.
Solution:
Mean = (70 + 80 + 85 + 90 + 95) / 5 = 84
So the mean of this dataset is 84.
Median
When arranging all the data in order (ascending and descending) the comes in the middle of the data is called the median.
Median is the middle value of a dataset when the values are arranged in order from smallest to largest.
Examples for Odd Numbers in the Dataset
Example 1: Find the median of a dataset of exam scores: 70, 85, 80, 95, 90
Solution:
Firstly arrange all no. in order from smallest to largest: 70, 80, 85, 90, 95.
The mid value is 85. so, the median is 85.
Example 2: Find the median of a dataset: 5, 10, 15, 20, 25.
Solution:
Firstly arrange all no. in order from smallest to largest: 5, 10, 15, 20, 25.
The mid value is 15. so, the median is 15.
If there are an even number of values in the dataset, the median is calculated by taking the average of the two middle values.
Examples for Even Numbers in the Dataset
Example 1: Find the median of a dataset of exam scores: 70, 80, 85, 90.
Solution:
The median is calculated as (80 + 85) / 2 = 82.5
So the median of this dataset is 82.5.
Example 2: Find the median of a dataset: 2, 4, 6, 8, 10, 12.
Solution:
Firstly, we need to find the middle two numbers. So, 6, and 8 are mid values of the dataset
Median = (6 +
/ 2 = 7
So the median of this dataset is 7.
Mode
most frequently used number in data is called the mode of the data.
Example 1: We have a data set representing the number of pets owned by 10 people: 3, 1, 0, 2, 1, 1, 4, 2, 2, 1. Find the mode.
Solution:
So, the value that appears most frequently in the data set is 1. the value 1 appears four times. Therefore, the mode of this data set is 1.
Skewness Formula
The skewness formula is discussed in the image below,
Type of Skewness
Various types of skewness used in mathematics are,
- Positive Skewness
- Negative Skewness
- Zero Skewness
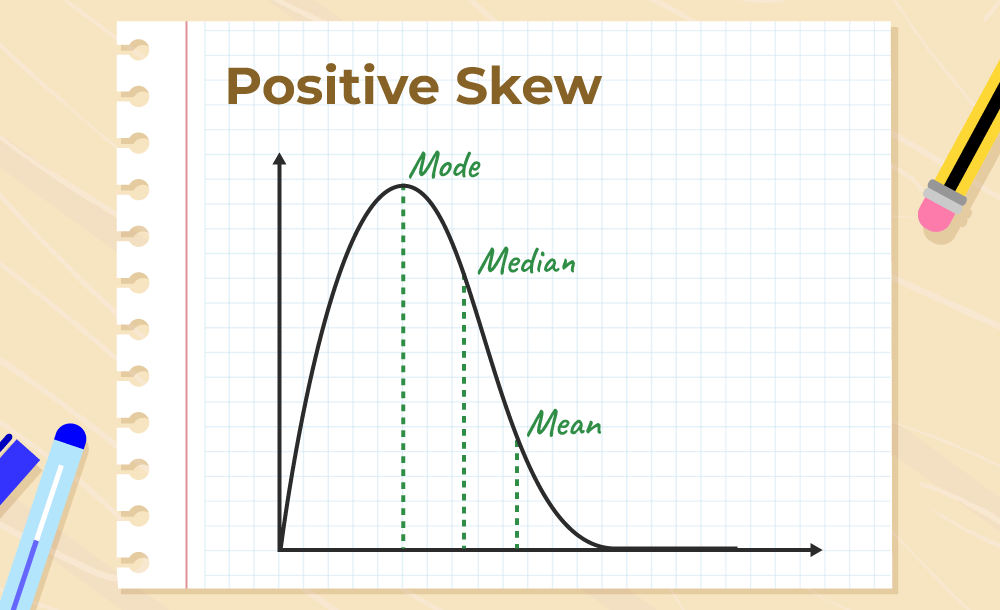
Positive Skewness
Positive Skewness means the tail on the right side of the distribution is longer. The mean and median will be greater than the mode.
Condition for positive skewness = Mean > Median >Mode
The positive curve of skewness is shown in the image below,
Let’s take an example of the income distribution where a few people earn very high incomes and the majority earn lower incomes. so, this is often positively skewed. Analyzing skewed data can provide valuable insights into the underlying causes and potential solutions or interventions.
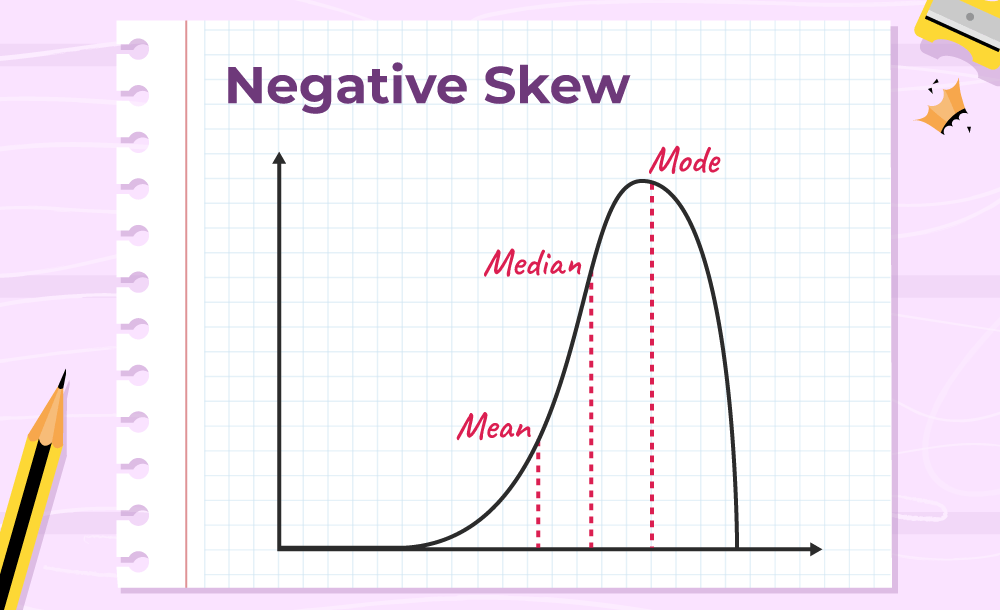
Negative Skewness
Negative Skewness means when the tail of the left side of the distribution is longer than the tail on the right side. The mean and median will be less than the mode.
Condition for negative skewness is Mode > Median > Mean
The curve shows negative skewness in the image below,
Let’s take an example of a match, during the match most of the players of a particular team scored runs above 50 and only a few of them scored below 10. In such a case, the data is generally represented with the help of a negatively skewed distribution. And this data is helpful to analyze the game’s performance.
Zero Skewness
It is also known as a “symmetric distribution”.It signifies that distribution of data is evenly distributed around the mean, with no long tails on either end of the distribution
Condition for zero skewness is Mean = Mode = Median
The curve for zero skews is shown in the image below,
Methods to Measure Skewness
Skewness can be measured using Karl Pearson’s Coefficient of Skewness.
Karl Pearson’s Co-efficient of Skewness
The formula for measuring Skewness using Karl Pearson’s Co-efficient is discussed below in the image,
Conditions
- Mean = Mode = Median, then the coefficient of skewness is zero for symmetrical distribution.
- Mean > Mode, then the coefficient of skewness will be positive.
- Mean < Mode, then the coefficient of skewness will be negative.
Karl person`s coefficient of skewness has a positive sign for the positively skewed and a negative sign for the negatively skewed.
Read More,
- Bayes’ Theorem
- Mean
Solved Examples on Skewness Formula
Example 1: Find the skewness for the given Data ( 2,4,6,6)
Solution:
Mean of Data = (2 + 4 + 6 + 6) / 4
= 18 / 4
= 4.5
Number of terms (n) = 4 (even)
Median of Data = {[n / 2]th + [n / 2 + 1]th}/2 term
= [(4 /2)th term + (4/2 +1)th term] / 2
= [2nd term + 3rd term] / 2
= [4+6]/2
= 10/2
Median of Data = 5
Mode of Data = Highest Frequency term = 6 (frequency 2)
S.D. = √[(2 – 5)2 + (4-5)2 + (6-5)2 + (6-5)2/4]
= √[(9 + 1 + 1 + 1)/4]
= √(3)
= 1.732
Skewness = 3(Mean – Median)/S.D.
By Applying Skewness Formula,
Skewness = 3(4.5 – 5)/1.732
= 3(-0.5)/ 1.732
Skewness = – 0.866
So, the skewness of these data is negative.
Example 2: A boy collects some rupees in a week as follows (25,28,26,30,40,50,40) and finds the skewness of the given Data in question with the help of the skewness formula.
Solution:
Mean of Data = (25+28+26+30+40+50+40) / 7
= 239 / 7
= 34.14
Number of terms (n) =7 (odd)
Arrange Data in ascending order = 25,26 ,28,30,40,40,50
The median of data is = 30
Mode of Data = Highest Frequency term = 40 (frequency 2)
S.D = √(1/7 – 1) x ((25 – 34.1429)2 + (28 – 34.1429)2 + (26 – 34.1429)2 + (30 – 34.1429)2 + (40 – 34.1429)2 +(534.1429)2 + (40 – 34.1429)2)
= √(1/6) x ((-9.1429)2 + (-6.1429)2 + (-8.1429)2 + (-4.1429)2 + (5.8571)2 + (15.8571)2 + (5.8571)2)
= √(0.1667) x ((83.5926) + (37.7352) + (66.3068) + (17.1636) + (34.3056) + (251.4476) + (34.3056))
= √(0.1667) x 524.8571
= √87.4762
. = 9.3529Skewness = 3(Mean – Median)/S.D.
By Applying Skewness Formula,
Skewness = 3(34.14 – 30)/9.3529
= 1.32
Skewness = 1.32
So skewness for these data is positive
Example 3: Attendance of all classes of a school are as follows find their skewness?
1st (35), 2nd(32), 3rd(38), 4th(39), 5th(43)
| Class Name | Number of students |
|---|---|
| 1 st | 35 |
| 2 nd | 32 |
| 3 rd | 38 |
| 4 th | 39 |
| 5 th | 45 |
Solution:
Mean of Data = (35 + 32 + 38 + 39 + 42)/5
= 186/5
= 37.2
Number of terms (n) = 5 (odd)
Arrange Data in ascending order = 32,35,38,39,42
Median of Data = 38
S.D. = √(1/5 – 1) x ((35 – 37.2)2 + (32 – 37.2)2 + (38 – 37.2)2 + (39 – 37.2)2 + (42 – 37.2)2)
= √(1/4) x ((-2.2)2 + (-5.2)2 + (0.8)2 + (1.8)2 + (4.8)2)
= √(0.25) x ((4.84) + (27.04) + (0.64) + (3.24) + (23.04))
= √(0.25) x 58.8
= √14.7
= 3.8341Skewness = ∑(yi – ymean) / (n – 1) x (sd)³
Skewness =((35 – 37.2)³ + (32 – 37.2)³ + (38 – 37.2)³ + (39 – 37.2)³ + (42 – 37.2)³) / (5 – 1)³ x 3.8341
Skewness = ((-2.2)³ + (-5.2)³ + (0.8)³ + (1.8)³ + (4.8)³ )/ (4)³ x 3.8341
Skewness =((-10.648) + (-140.608) + (0.512) + (5.832) + (110.592)) / 64 x 3.8341
Skewness =-34.32 / 245.3824
Skewness = -0.1522
So, the skewness of these data is negative.
FAQs on Skewness
Q1: Can skewness be zero?
Answer:
Yes, skewness can be zero. This occurs when the distribution is perfectly symmetrical. It is possible if there are an equal number of values on the left and right sides of the mean.
Q2: What does positive skewness mean?
Answer:
Positive skewness means the distribution is skewed to the right. There are more values on the right side of the mean than on the left side.
Condition for Positive Skewness = Mean > median >mode
Q3: What does negative skewness mean?
Answer:
Negative skewness means the distribution is skewed to the left. There are more values on the left side of the mean than on the right side.
Condition for negative skewness = Mode > median > mean
Q4: How is skewness used in finance and investment analysis?
Answer:
In finance and investment analysis, skewness is used to measure the degree of asymmetry in returns on investment. Skewed returns can have an impact on portfolio management and risk management strategies, and understanding the skewness of a particular investment can help investors to make better-informed decisions.
Q5: What is the formula for calculating skewness?
Answer:
The formula used to calculate Skewness is,
Skewness Formula= 3(Mean – Median)/S.D.
Q6: How is skewness used in hypothesis testing?
Answer:
Skewness is used in hypothesis testing to determine whether a sample of data is normally distributed or not. If the skewness value is close to zero, the data is likely to be normally distributed. If the skewness value is positive or negative, the data is likely to be skewed and may require non-parametric tests for hypothesis testing.

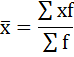
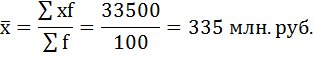
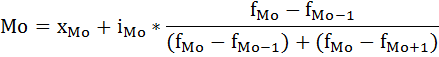
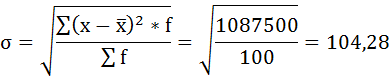
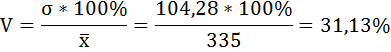
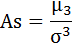
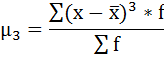
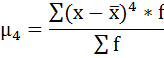
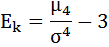




 / 2 = 7
/ 2 = 7