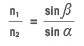Как найти показатель преломления если известен угол - Исправление недочетов и поиск решений вместе с Examum.ru

Преломление света.

Закон преломления (частный случай).
Обратимость световых лучей.
Закон преломления (общий случай).
Полное внутреннее отражение.
Разберем задачи ЕГЭ по теме: Преломление света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.

На границе раздела двух прозрачных сред наряду с отражением света наблюдается его преломление — свет, переходя в другую среду, меняет направление своего распространения.

Преломление светового луча происходит при его наклонном падении на поверхность раздела (правда, не всегда — читайте дальше про полное внутреннее отражение). Если же луч падает перпендикулярно поверхности, то преломления не будет — во второй среде луч сохранит своё направление и также пойдёт перпендикулярно поверхности.

к оглавлению ▴

Закон преломления (частный случай).

Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.

Предположим, что луч света, идущий в воздухе, наклонно падает на поверхность стекла, воды или какой-либо другой прозрачной среды. При переходе в среду луч преломляется, и его дальнейший ход показан на рис. 1.

Рис. 1. Преломление луча на границе «воздух–среда»

В точке падения проведён перпендикуляр (или, как ещё говорят, нормаль) к поверхности среды. Луч , как и раньше, называется падающим лучом, а угол alpha между падающим лучом и нормалью — углом падения. Луч — это преломлённый луч; угол beta между преломлённым лучом и нормалью к поверхности называется углом преломления.

Всякая прозрачная среда характеризуется величиной , которая называется показателем преломления этой среды. Показатели преломления различных сред можно найти в таблицах. Например, для стекла n=1,6 , а для воды n=1,33 . Вообще, у любой среды ; показатель преломления равен единице только в вакууме. У воздуха , поэтому для воздуха с достаточной точностью можно полагать в задачах n=1 (в оптике воздух не сильно отличается от вакуума).

Закон преломления (переход «воздух–среда»).

1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=n$ . (1)

Поскольку из соотношения (1) следует, что , то есть — угол преломления меньше угла падения. Запоминаем: переходя из воздуха в среду, луч после преломления идёт ближе к нормали.

Показатель преломления непосредственно связан со скоростью распространения света в данной среде. Эта скорость всегда меньше скорости света в вакууме: . И вот оказывается,что

$n=frac{displaystyle c }{displaystyle v }$ . (2)

Почему так получается, мы с вами поймём при изучении волновой оптики. А пока скомбинируем формулы . (1) и (2):

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle c }{displaystyle v }$ . (3)

Так как показатель преломления воздуха очень близок единице, мы можем считать, что скорость света в воздухе примерно равна скорости света в вакууме . Приняв это во внимание и глядя на формулу . (3), делаем вывод: отношение синуса угла падения к синусу угла преломления равно отношению скорости света в воздухе к скорости света в среде.

к оглавлению ▴

Обратимость световых лучей.

Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.

Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.

Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.

Рис. 2. Преломление луча на границе «среда–воздух»

Раз геометрическая картинка не изменилась, той же самой останется и формула (1): отношение синуса угла alpha к синусу угла beta по-прежнему равно показателю преломления среды. Правда, теперь углы поменялись ролями: угол beta стал углом падения, а угол alpha — углом преломления.

В любом случае, как бы ни шёл луч — из воздуха в среду или из среды в воздух — работает следующее простое правило. Берём два угла — угол падения и угол преломления; отношение синуса большего угла к синусу меньшего угла равно показателю преломления среды.

Теперь мы целиком подготовлены для того, чтобы обсудить закон преломления в самом общем случае.

к оглавлению ▴

Закон преломления (общий случай).

Пусть свет переходит из среды 1 с показателем преломления $n_{displaystyle 1}$ в среду 2 с показателем преломления $n_{displaystyle 2}$ . Среда с большим показателем преломления называется оптически более плотной; соответственно, среда с меньшим показателем преломления называется оптически менее плотной.

Переходя из оптически менее плотной среды в оптически более плотную, световой луч после преломления идёт ближе к нормали (рис. 3). В этом случае угол падения больше угла преломления: .

Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4). Здесь угол падения меньше угла преломления:

Оказывается, оба этих случая охватываются одной формулой — общим законом преломления, справедливым для любых двух прозрачных сред.

Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle n_{displaystyle 2}}{displaystyle n_{displaystyle 1}}$ . (4)

Нетрудно видеть, что сформулированный ранее закон преломления для перехода «воздух–среда» является частным случаем данного закона. В самом деле, полагая в формуле (4) $n_{displaystyle 1}=1, n_{displaystyle 2}=n$ , мы придём к формуле (1).

Вспомним теперь, что показатель преломления — это отношение скорости света в вакууме к скорости света в данной среде: $n_{displaystyle 1}=c/v_{displaystyle1}, n_{displaystyle 2}=c/v_{displaystyle2}$ . Подставляя это в (4), получим:

$frac{displaystyle sinalpha}{displaystyle sinbeta }=frac{displaystyle v_{displaystyle 1}}{displaystyle v_{displaystyle 2}}$ . (5)

Формула (5) естественным образом обобщает формулу (3). Отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде.

к оглавлению ▴

Полное внутреннее отражение.

При переходе световых лучей из оптически более плотной среды в оптически менее плотную наблюдается интересное явление — полное внутреннее отражение. Давайте разберёмся, что это такое.

Будем считать для определённости, что свет идёт из воды в воздух. Предположим, что в глубине водоёма находится точечный источник света , испускающий лучи во все стороны. Мы рассмотрим некоторые из этих лучей (рис. 5).

Рис. 5. Полное внутреннее отражение

Луч $SO_{displaystyle 1}$ падает на поверхность воды под наименьшим углом. Этот луч частично преломляется (луч $O_{displaystyle 1} A_{displaystyle 1}$ ) и частично отражается назад в воду (луч $O_{displaystyle 1} B_{displaystyle 1}$ ). Таким образом, часть энергии падающего луча передаётся преломлённому лучу, а оставшаяся часть энергии -отражённому лучу.

Угол падения луча $S O_{displaystyle 2}$ больше. Этот луч также разделяется на два луча — преломлённый и отражённый. Но энергия исходного луча распределяется между ними по-другому: преломлённый луч $O_{displaystyle 2} A_{displaystyle 2}$ будет тусклее, чем луч $O_{displaystyle 1} A_{displaystyle 1}$ (то есть получит меньшую долю энергии), а отражённый луч $O_{displaystyle 2} B_{displaystyle 2}$ — соответственно ярче, чем луч $O_{displaystyle 1} B_{displaystyle 1}$ (он получит большую долю энергии).

По мере увеличения угла падения прослеживается та же закономерность: всё большая доля энергии падающего луча достаётся отражённому лучу, и всё меньшая — преломлённому лучу. Преломлённый луч становится всё тусклее и тусклее, и в какой-то момент исчезает совсем!

Это исчезновение происходит при достижении угла падения $alpha _{0}$ , которому отвечает угол преломления $90^{circ}$ . В данной ситуации преломлённый луч должен был бы пойти параллельно поверхности воды, да идти уже нечему — вся энергия падающего луча целиком досталась отражённому лучу .

При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.

Описанное явление и есть полное внутреннее отражение. Вода не выпускает наружу лучи с углами падения, равными или превышающими некоторое значение $alpha _{0}$ — все такие лучи целиком отражаются назад в воду. Угол $alpha _{0}$ называется предельным углом полного отражения.

Величину $alpha _{0}$ легко найти из закона преломления. Имеем:

$frac{displaystyle sinalpha _{0}}{displaystyle sin90^{circ}}=frac{displaystyle 1}{displaystyle n}$ .

Но $sin90^{circ}=1$ , поэтому

$sinalpha _{0}=frac{displaystyle 1}{displaystyle n}$ ,

откуда

$alpha _{0}=arcsinfrac{displaystyle 1}{displaystyle n}$ .

Так, для воды предельный угол полного отражения равен:

$alpha _{0}=arcsinfrac{displaystyle 1}{1,33} approx 48,8^{circ}$ .

Явление полного внутреннего отражения вы легко можете наблюдать дома. Налейте воду в стакан, поднимите его и смотрите на поверхность воды чуть снизу сквозь стенку стакана. Вы увидите серебристый блеск поверхности — вследствие полного внутреннего отражения она ведёт себя подобно зеркалу.

Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.

к оглавлению ▴

Разберем задачи ЕГЭ по теме: Преломление света.

Задача 1. Нижняя грань AC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина $alpha = 30^{circ}$ . Луч света падает из воздуха на клин перпендикулярно грани AB, преломляется и выходит в воздух через ту же грань AB, но уэе под углом преломления $beta = 90^{circ}$ Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.

Дано:
$alpha = 30^{circ}$
$beta = 90^{circ}$
n-?
Решение. Решение задач по геометрической оптике необходимо начинать с построения чертежа (рисунка), моделирующего условия, описанные в тексте задачи.

Световой луч падает на прозрачный клин перпендикулярно стороне АВ (см.рис.1). В этом случае, световой луч не преломляется на границе раздела воздух-клин, так как угол падения равен 0, соответственно, угол преломления также равен 0. Следовательно, внутри клина световой луч попадает на нижнюю грань АС, которая представляет собой плоское зеркало. Согласно рис.1 величина угла $alpha_1=180^{circ}-(alpha+90^{circ})=90^{circ}-alpha.$

$alpha_1=90^{circ}-30^{circ}=60^{circ}.$

Тогда угол падения луча на плоское зеркало будет равен
$90^{circ}-alpha_1=90^{circ}-60^{circ}=30^{circ}.$

То есть угол падения равен $alpha=30^{circ}$ .
Согласно закону отражения света, угол падения светового луча равен углу отражения. В треугольнике МКО угол КОМ образован суммой двух углов α, поэтому он равен 60°. Тогда угол падения светового луча на грань АВ также будет равен $2alpha=60^{circ}$ (равенство накрест лежащих углов).
На следующем этапе задачи надо применить закон преломления света, так как луч переходит из одной среды в другую.
$frac{sin{2alpha}}{sinbeta}=frac{1}{n}$
При записи этой формулы учтено, что второй средой является воздух с показателем преломления равным 1, а первой средой является материал клина с показателем преломления n, который необходимо определить. Из последней формулы можно выразить и рассчитать n.

$n=frac{sinbeta}{sin2alpha}$

$n=frac{sin90^{circ}}{sin(2cdot 30^{circ})}=frac{sin90^{circ}}{sin60^{circ}}approx 1,15$

Ответ: 1,15

Задача 2. На тонкую собирающую линзу от удалённого источника падает пучок параллельных лучей (см. рисунок). Как изменится положение изображения источника, создаваемого линзой, если между линзой и её фокусом поставить
плоскопараллельную стеклянную пластинку с показателем преломления n (на рисунке положение пластинки отмечено пунктиром)? Ответ поясните, указав, какие физические закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной стеклянной пластинки.

Решение. Рассмотрим ход световых лучей от удаленного источника через линзу при отсутствии плоскопараллельной стеклянной пластинки (см.рис.1).

Луч 1-1ʹ проходит через оптический центр линзы и не преломляется. Луч 2-2ʹ идет через фокус и после прохождения через линзу, идет параллельно главной оптической оси. Пересечение этих двух лучей дает действительное изображение удаленного источника, которое расположено в фокальной плоскости линзы. Этот факт также можно доказать, используя формулу тонкой линзы.

$frac{1}{d}+frac{1}{f}=frac{1}{F} (1)$

Так как источник света расположен на расстоянии то $frac{1}{d}rightarrow 0.$

Тогда формула тонкой линзы (1) примет вид $frac{1}{f}=frac{1}{F},$ следовательно, f=F, т.е. изображение формируется в фокальной плоскости линзы.

Рассмотрим ход световых лучей через плоскопараллельную стеклянную пластинку. Для этого необходимо использовать закон преломления света.

Рис.2

Согласно рис.2 угол падения луча на пластину равен α. Закон преломления света на границе раздела воздух-пластинка имеет вид:

$frac{sinalpha}{sinbeta}=frac{n}{1}=n (1).$

Здесь учтено, что показатель преломления воздуха равен 1, а пластинки n.
При переходе светового луча из пластинки в воздух, закон преломления света будет иметь вид:

$frac{sinbeta}{singamma}=frac{1}{n} (2).$

В этом случае первой средой является пластинка с показателем преломления n, а второй средой будет воздух с показателем преломления равным 1.
Из (1) и (2) выразим и .

Так как правые части этих уравнений равны, то

Отсюда вытекает равенство углов . Следовательно, луч, падающий на стеклянную пластину, выходит из нее, оставаясь параллельным входящему лучу. Но при этом выходящий луч немного смещается вверх.

Исходя из этого можно сделать вывод, что изображение удаленного источника после прохождения через плоскопараллельную стеклянную пластину, не изменится. Из удаленного источника выходит бесконечное количество параллельных лучей, которые собираются в фокальной плоскости линзы.

Ответ: не изменится.

Задача 3. Ученик провел опыт по преломлению света, представленный на фотографии. Как изменится при уменьшении угла падения угол преломления светового пучка и скорость света, распространяющегося в стекле? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшиться
3) не изменится
Запишите в таблицу выбранные цифры для каждой величины. Цифры в ответе могут повторяться.

Угол преломления	Скорость света в стекле

Решение. Для ответа на первый вопрос задачи необходимо применить закон преломления света для границы раздела воздух-стекло.

$frac{sinalpha}{sinbeta}=frac{n}{1}=n.$

Показатель преломления стекла равен n, а воздуха 1.
При уменьшении угла падения α, будет уменьшаться и значение Так как показатель преломления стекла не изменяется, то значение sinbeta так же будет уменьшаться. Поэтому угол преломления уменьшится.

Для ответа на второй вопрос надо учесть, что скорость света в данной среде определяется значением показателя преломления $v_{cp}=frac{c}{n},$ где с – скорость света в вакууме, а n – показатель преломления среды (стекла). Так как эти обе величины не изменяются, то скорость света в стекле так же не изменяется.

Ответ: 23.

Задача 4. Чему равен синус предельного угла полного внутреннего отражения при переходе света из вещества с n_1=1,5 в вещество с n_2=1,2 ?

Решение.

Явление полного внутреннего отражения наблюдается при переходе светового луча из оптически более плотной среды в оптически менее плотную (см.рис.1). Источник света S должен находиться в среде с большим показателем преломления.

Для нахождения синуса угла полного внутреннего отражения необходимо воспользоваться законом преломления света.

$frac{sinalpha_{np}}{sinbeta}=frac{n_2}{n_1} (1)$

При полном внутреннем отражении преломленный луч скользит по границе раздела двух сред и угол преломления $beta=90^{circ}$ . С учетом того, что $sin90^{circ}=1$ уравнение (1) примет вид:

$sinalpha_{np}=frac{1,2}{1,5}=0,8$

$sinalpha_{np}=0,8$

Ответ: 0,8.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преломление света.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Данная
тема будет посвящена решению задач, связанных с таким явлением, как преломление
света.

Задача
1.
Луч света падает на стекло под углом 45º. Известно, что угол преломления
данного луча равен 20º. Постройте соответствующий чертёж, найдите
показатель преломления данного стекла и примерное значение скорости света в
нём.

ДАНО:

РЕШЕНИЕ

Закон
преломления света

Откуда
абсолютный показатель преломления

Также
абсолютный показатель преломления света равен

Тогда
скорость света в стекле равна

Задача
2.
Два разных стёкла (с показателями преломления 1,5 и 2,1) сложены вплотную друг
к другу. Может ли луч света, пройдя сквозь одно из стёкол, полностью отразиться
от второго?

ДАНО:

РЕШЕНИЕ

Закон
преломления света

Тогда

Как
известно, функция синуса принимает значения в пределах от минус 1 до 1,
поэтому, полученное уравнение не имеет решения. Это говорит о том, что нет
такого угла падения альфа, при котором луч света прошёл бы в одно стекло, но
полностью отразился от другого.

Ответ:
нет,
не может.

Задача
3.
В сосуде кубической форме лежит предмет, расположенный точно в центре дна. Глаз
наблюдателя расположен таким образом, что он видит нижний угол сосуда. Чтобы
наблюдатель мог увидеть предмет в сосуде, его заполняют некой жидкостью с
показателем преломления 1,7. Найдите минимальный уровень этой жидкости.

ДАНО:

РЕШЕНИЕ

Закон
преломления света

Ответ:
сосуд
нужно заполнить на 92%.

Задача
4.
Луч света выходит из некоторой среды в воздух таким образом, что угол падения
вдвое меньше угла преломления. Если угол падения увеличить на 10º, то он
достигнет своего предельного значения. Найдите показатель преломления данной
среды.

ДАНО:

РЕШЕНИЕ

Закон
преломления света

Предельный
угол полного отражения

Тогда

Левую
часть уравнения распишем, воспользовавшись формулой синуса суммы углов, а
правую часть уравнения распишем, воспользовавшись формулой синуса двойного
угла

Разделим
правую и левую части на cos a

Ответ:
1,88.

Задача
5.
Мальчик старается попасть палкой в предмет, находящийся на дне пруда глубиной 50
см. Точно прицелившись, он двигает палку под углом сорок 40º к поверхности
воды. На каком расстоянии от предмета палка ткнёт в дно пруда?

ДАНО:

СИ

РЕШЕНИЕ

Закон
преломления света

Ответ:
14
см.

Источник

Что такое показатель преломления?

Показатель преломления вещества — это отношение скоростей света (электромагнитных волн) в вакууме и в данной среде. Показатель преломления — безразмерная величина, которая зависит от температуры и длины волны света. Показатель преломления характеризует скорость распространения света в среде и рассчитывается по формуле:

n = c / v,

где:

n — показатель преломления;
c — скорость света в вакууме (или воздухе);
v — скорость света в среде (например, воде, оливковом масле и т. п.).

На этой странице приведена необходимая информация о методах измерения показателя преломления.

Узнайте больше о показателе преломления, его применении, способах измерения, а также о законе преломления света и многом другом.

Перейдите в один из следующих разделов, чтобы узнать больше о показателе преломления:

Преломление света: практический пример
Закон преломления света (закон Снеллиуса)
Полное внутреннее отражение и критический угол
Закон преломления света и устройство рефрактометра
Измерение показателя преломления: что измеряет рефрактометр?
Факторы, влияющие на величину показателя преломления
Показатель преломления: применение на практике
Абсолютный и относительный показатель преломления
Рекомендации по измерению показателя преломления
Совершенствуйте методику измерения показателя преломления
Приблизительные значения показателя преломления стандартных и эталонных веществ
Часто задаваемые вопросы

Преломление света: практический пример

Прежде чем углубиться в теоретическое обоснование показателя преломления, рассмотрим наглядный пример распространения света в различных средах.

На иллюстрации изображены три стакана с опущенными в них стеклянными палочками. Стаканы заполнены разными жидкостями:

Жидкость в стакане
1 Вода.
2 Вода и кедровое масло.
3 Кедровое масло.

Что мы видим в этих стаканах?

Показатель преломления воды (n = 1,333) ниже, чем стекла (n = 1,517). По этой причине стеклянную палочку видно в стакане 1 и отчасти — в стакане 2.

Зато у стеклянной палочки (n = 1,517) и кедрового масла (n = 1,516) показатели преломления почти одинаковые, поэтому кажется, что палочка при погружении в кедровое масло исчезает (частично в стакане 2 и полностью в стакане 3).

Закон преломления света (закон Снеллиуса)

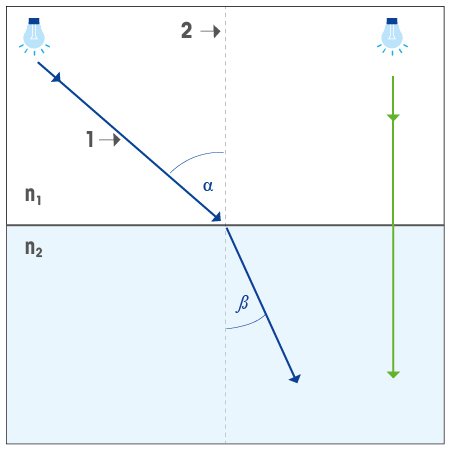
Закон преломления света, известный также как закон Снеллиуса, описывает взаимосвязь углов падения и преломления с показателями преломления граничащих сред. Как показано на иллюстрации, согласно этому закону отношение синуса угла падения α к синусу угла преломления β (и показателей преломления n₁ и n₂) — это величина, постоянная для двух данных сред:

n₁ sin α = n₂ sin ⁡β.

На иллюстрации показано, как отклоняется световой луч (1, синяя стрелка), проходящий под определенным углом из оптически менее плотной (n₁) в оптически более плотную среду (n₂), например из воздуха в воду.

Но когда луч проходит из одной среды в другую перпендикулярно границе раздела, никакого преломления не происходит (зеленая стрелка).

Согласно закону преломления света, отношение показателей преломления граничащих сред пропорционально отношению угла падения и угла преломления светового луча. То есть:

Полное внутреннее отражение и критический угол

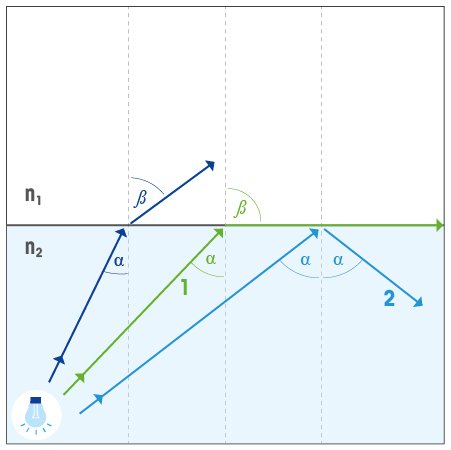
Полное внутреннее отражение возникает, когда весь свет, направленный из оптически более плотной среды в оптически менее плотную, отражается обратно в оптически более плотную среду. Для понимания этого явления рассмотрим иллюстрацию слева.

Синяя стрелка: луч света преломляется, проходя из оптически более плотной среды (n₂) в оптически менее плотную (n₁).

Угол падения α увеличивается (зеленая стрелка): когда угол падения α возрастает (1), он может достигнуть критической величины, после которой свет не проходит в оптически менее плотную среду (n₁), а отражается вдоль раздела двух сред. Такой угол падения называют критическим углом полного внутреннего отражения. Заметим, что при этом угол отражения β = 90°.

Угол падения больше критической величины: если угол падения превышает критическую величину, свет полностью отражается обратно в оптически более плотную среду (n₂). Это явление называют полным внутренним отражением (2).

Показатель преломления n1 рассчитывается по величине критического угла α, когда
β = 90° —> sin β = 1.

Внимание! Луч в случае 1 (зеленая стрелка) падает под критическим углом, а полное внутренне отражение происходит в случае 2 (голубая стрелка).

Закон преломления света и устройство рефрактометра

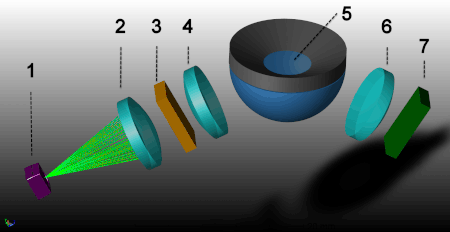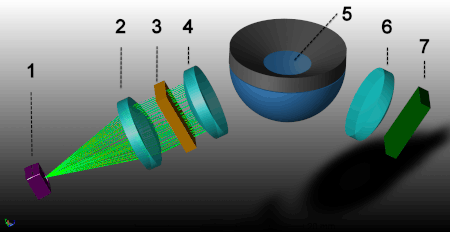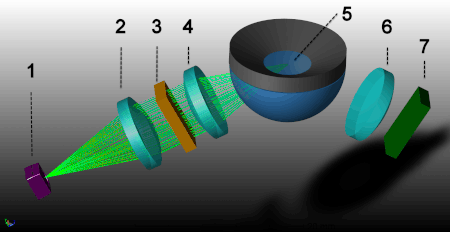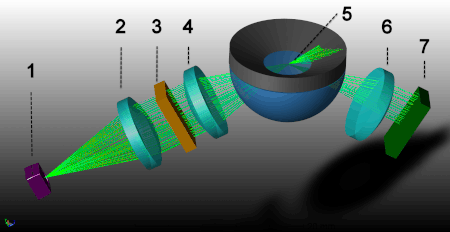
На основе описанного выше закона преломления света созданы рефрактометры — приборы для измерения показателя преломления жидкостей и высоковязких веществ.

На иллюстрации схематически показано устройство измерительной ячейки цифрового рефрактометра, в котором использован закон преломления света. Процедура измерения связана с полным внутренним отражением и критической величиной угла падения света. Принцип действия:

Источник света (1) — светодиод (LED). Луч света от светодиода проходит через поляризационный фильтр (2), интерференционный фильтр (3) и фокусирующие линзы (4), а затем через сапфировую призму (5) на образец.

Когда угол падения превышает критическую величину, отраженный свет попадает через линзу (6) на оптический датчик с зарядовой связью (7), который фиксирует критический угол. Кроме того, современные цифровые рефрактометры автоматически контролируют температуру на поверхности раздела призма/образец для повышения точности измерения.

Измерение показателя преломления: что измеряет рефрактометр?

Цифровой рефрактометр предназначен для измерения показателя преломления и связанных с ним характеристик жидкостей по методу полного внутреннего отражения. Процедура измерения автоматизирована, благодаря чему точность результатов не зависит от оператора. Измерение выполняется в течение нескольких секунд с высокой точностью на небольших образцах (объемом от 0,5 до 1 мл).

Также для измерения показателя преломления используются ручные рефрактометры, например оптический настольный рефрактометр Аббе или обычный переносной рефрактометр. Подробнее об их достоинствах и недостатках.

Факторы, влияющие на величину показателя преломления

Влияние температуры на измерение показателя преломления

Как зависит величина показателя преломления от температуры?

Сначала узнаем, как влияет температура на жидкости. С ростом температуры увеличивается пространство, которое занимают атомы, связанные между собой в одной молекуле. При нагревании усиливаются колебания атомов, атомы отодвигаются друг от друга раздвигаются, что приводит к снижению оптической плотности среды.

Как сказано выше, показатель преломления связан со скоростью распространения света в среде. Когда температура растет, оптическая плотность среды снижается, а скорость света в ней увеличивается, что приводит к небольшому изменению угла преломления. Другими словами, чем выше температура, тем меньше показатель преломления, как показано на графике ниже на примере воды.

Из графика видно, что температура образца существенно влияет на измеряемую величину. Это означает, что температуру следует точно измерять и по возможности регулировать.

Приборы старой конструкции, например рефрактометры Аббе, приходится помещать в жидкостный термостат. В большинстве современных цифровых рефрактометров температура оптической системы регулируется с помощью элемента Пельтье. Такая конструкция обеспечивает быстрое и точное измерение показателя преломления.

Влияние температуры на измерение показателя преломления

Влияние длины волны на измерение показателя преломления

Вследствие различной дисперсии света (дисперсионного соотношения) в разных веществах показатели преломления также почти всегда различаются в зависимости от длины волны света, используемого для измерения. Дисперсионное соотношение можно рассчитать следующим образом.

Мы знаем, что скорость распространения света в среде равна:

v = c/n,

где:
n — показатель преломления;
c — скорость света в вакууме (или воздухе);
v — скорость света в данной среде.

Длина волны в этой же среде:

λ = λ₀/n,

где: λ₀ — длина световой волны в вакууме (или воздухе).

Следовательно, величина показателя преломления (n) обратно пропорциональна как длине волны, так и скорости распространения света в среде. Это означает, что при большей длине волны показатель преломления уменьшается. Такое соотношение можно представить в виде уравнения:

v(λ) = c/n(λ).

В то же время для контроля качества в промышленности необходимо иметь определенную точную длину волны, чтобы сравнивать значения показателя преломления различных образцов, измеренные в одинаковых условиях.

Чаще всего в рефрактометрах используется желтая линия спектра натрия с длиной волны 589,3 нм. Желтая линия натрия уже давно используется для измерения показателя преломления. Это широко доступный, надежный и стабильный стандарт оптического излучения.

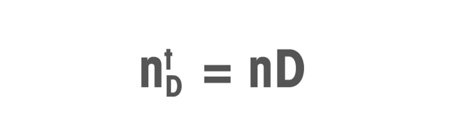
n = показатель преломления.

t = температура (°C).

D = желтая линия натрия.

Значение показателя преломления, измеренное по желтой линии натрия, обозначается символом nD.

Показатель преломления: применение на практике

Любой материал, который взаимодействует со светом, можно характеризовать показателем преломления. Во многих отраслях промышленности измерение показателя преломления используется для проверки чистоты и концентрации жидких, высоковязких и твердых образцов. Показатель преломления жидких и высоковязких материалов измеряется с высокой точностью (погрешность от ± 0,00002).

Кроме того, показатель преломления можно сопоставлять с широким диапазоном концентраций. Эту зависимость используют для анализа многих материалов в разных отраслях, например:

Производство пищевых продуктов и напитков: плотность (содержание сахара) по шкале Брикса для безалкогольных напитков или плотность виноградного сусла по шкале Эксле.
Химическая промышленность: температура замерзания (°C или °F), концентрация кислоты/щелочи, содержание органических растворителей или неорганических солей в объемных или весовых процентах.
Производство и клинические исследования лекарств: содержание перекиси или метилового спирта, концентрация различных веществ в моче.

В некоторых случаях измерение показателя преломления сочетают с измерением плотности, получая простой и эффективный метод контроля. Такой анализ можно полностью автоматизировать.

Требуется более подробная информация о показателях Брикса, Плато, Баллинга и Боме?

Наряду с плотностью по шкале Брикса, существуют другие сопоставимые единицы для измерения содержания сахарозы, например градусы Плато, Боме, Эксле и Баллинга. Узнайте больше об их различиях, применении, способах измерения и расчета.

Абсолютный и относительный показатель преломления

Абсолютный показатель преломления

Абсолютный показатель преломления рассчитывается относительно вакуума, в котором свет распространяется с максимально возможной скоростью 299 792 458 метров в секунду (скорость света). На практике воздух, которым мы дышим, также считается эталонной средой, хотя свет распространяется в нем с чуть меньшей скоростью (в 1,0003 раза медленнее, чем в вакууме).

Можно сказать, что абсолютный показатель преломления указывает, во сколько раз скорость света в вакууме (или воздухе) больше, чем в другой среде.

В качестве примера рассчитаем абсолютный показатель преломления воды, в которой, как известно, свет при 20 °C распространяется со скоростью 2,25 × 10⁸ м/с.

Получается, что в воде свет распространяется в 1,33333 раза медленнее, чем в вакууме (или воздухе).

Относительный показатель преломления

Относительный показатель преломления — это отношение скоростей распространения света в любых двух средах, кроме вакуума (или воздуха). Можно, например, измерить показатель преломления оливкового масла относительно показателя преломления воды. Однако в производственной практике пользоваться относительными величинами неудобно.

Совершенствуйте методику измерения показателя преломления

Есть важные правила, которые необходимо соблюдать, чтобы измерять показатель преломления более точно, независимо от того, работаете вы с химическими реактивами, пищевыми продуктами, напитками или другими материалами, которые могут быть и пастообразными, и жидкими. Необходимо уделить внимание следующим вопросам:

Как часто следует калибровать прибор?
Какой растворитель использовать для очистки измерительной ячейки и призмы?
Образец пастообразный или вязкий. Какой должна быть процедура его подготовки и измерения?

Ответы на эти вопросы напрямую влияют на качество результатов. Изучите интерактивную брошюру, посвященную основным проблемам измерения показателя преломления, градусов Брикса и плотности.

Приблизительные значения показателя преломления стандартных и эталонных веществ

Часто задаваемые вопросы

О чем говорит высокое значение показателя преломления?

Высокое значение показателя преломления означает, что лучи света распространяются в среде медленно. На практике высокий показатель преломления указывает на высокую концентрацию раствора.

Как примеси влияют на показатель преломления?

Влияние примесей на показатель преломления может быть двояким:

Если показатель преломления примеси выше показателя преломления среды: скорость света в среде уменьшается, и показатель преломления увеличивается.
Если показатель преломления примеси ниже показателя преломления среды: скорость света в среде увеличивается, и показатель преломления уменьшается.

Как твердые частицы влияют на показатель преломления?

Если жидкий образец содержит взвесь твердых частиц, рекомендуется после нанесения образца на предметный столик микроскопа подождать немного (например, 10 секунд), прежде чем приступить к измерению.

Можно ли с помощью рефрактометра измерять показатель преломления черных или цветных образцов?

Да, с помощью цифрового рефрактометра можно измерять показатель преломления темных, черных и окрашенных материалов.

Как показатель преломления можно использовать для идентификации веществ?

Показатель преломления удобно использовать для идентификации чистых образцов, поскольку каждое вещество имеет собственное значение этой величины. По измеренному значению показателя преломления можно, пользуясь справочником, определить соответствующее вещество. Кроме того, автоматические рефрактометры пересчитывают значение показателя преломления в единицы измерения концентрации (например, градусы Брикса, весовые или объемные проценты и т. д.).

Источник

Преломление света.

Закон преломления (частный случай).

Обратимость световых лучей.

Закон преломления (общий случай).

Полное внутреннее отражение.

Разберем задачи ЕГЭ по теме: Преломление света.

Что такое показатель преломления?

Преломление света: практический пример

Закон преломления света (закон Снеллиуса)

Полное внутреннее отражение и критический угол

Закон преломления света и устройство рефрактометра

Измерение показателя преломления: что измеряет рефрактометр?

Факторы, влияющие на величину показателя преломления

Влияние температуры на измерение показателя преломления

Влияние длины волны на измерение показателя преломления

Показатель преломления: применение на практике

Требуется более подробная информация о показателях Брикса, Плато, Баллинга и Боме?

Абсолютный и относительный показатель преломления

Абсолютный показатель преломления

Относительный показатель преломления

Рекомендации по измерению показателя преломления

Совершенствуйте методику измерения показателя преломления

Приблизительные значения показателя преломления стандартных и эталонных веществ

Часто задаваемые вопросы

О чем говорит высокое значение показателя преломления?

Как примеси влияют на показатель преломления?

Как твердые частицы влияют на показатель преломления?

Можно ли с помощью рефрактометра измерять показатель преломления черных или цветных образцов?

Как показатель преломления можно использовать для идентификации веществ?