Как найти полное сопротивление цепи содержащей - Исправление недочетов и поиск решений вместе с Examum.ru

Формулы

Советы

Об этой статье

Была ли эта статья полезной?

Что такое полное сопротивление цепи и как его правильно найти

Виды электрических сопротивлений

Определение эквивалентного сопротивления

Как определяется ПС при последовательном соединении емкостей и индуктивностей

Определение ПС при использовании параллельного соединения элементов

Видео по теме

Не совсем яблочко от яблоньки

Но что такое реактивное сопротивление?

Как измерить полное электрическое сопротивление

Расчет полного электрического сопротивления конденсатора

Расчет полного электрического сопротивления катушки индуктивности

Расчет полного электрического сопротивления цепи

Практическое применение полного электрического сопротивления

Формулы

Советы

Об этой статье

Была ли эта статья полезной?

Что такое полное сопротивление цепи и как его правильно найти

Виды электрических сопротивлений

Определение эквивалентного сопротивления

Как определяется ПС при последовательном соединении емкостей и индуктивностей

Определение ПС при использовании параллельного соединения элементов

Видео по теме

Не совсем яблочко от яблоньки

Но что такое реактивное сопротивление?

Как измерить полное электрическое сопротивление

Расчет полного электрического сопротивления конденсатора

Расчет полного электрического сопротивления катушки индуктивности

Расчет полного электрического сопротивления цепи

Практическое применение полного электрического сопротивления

Цепь с емкостью.

Полное сопротивление цепи переменного тока.

Мост rlc.

Отбросьте в сторону все ваши умные книги — мы займемся практикой.

Индуктивное реактивное сопротивление

Емкостное реактивное сопротивление

Отбросьте в сторону все ваши умные книги — мы займемся практикой.

Индуктивное реактивное сопротивление

Емкостное реактивное сопротивление

Загрузить PDF

Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.

Полное сопротивление Z = R или X_Lили X_C (если присутствует что-то одно)
Полное сопротивление (последовательное соединение) Z = √(R² + X²) (если присутствуют R и один тип X)
Полное сопротивление (последовательное соединение) Z = √(R² + (|X_L — X_C|)²) (если присутствуют R, X_L, X_C)
Полное сопротивление (любое соединение) = R + jX (j — мнимое число √(-1))
Сопротивление R = I / ΔV
Индуктивное сопротивление X_L = 2πƒL = ωL
Емкостное сопротивление X_C = ¹ / _2πƒL = ¹ / _ωL

1
Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:^[1]
- Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
- Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.
2
Сопротивление — это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R.^[2] Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете измерить сопротивление при помощи мультиметра.
- ΔV — это напряжение (разность потенциалов), измеряемое в вольтах (В).
- I — сила тока, измеряемая в амперах (А).
- R — это сопротивление, измеряемое в омах (Ом).
3
Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:
- Индуктивным сопротивлением X_C обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.^[3] Чем быстрее меняется направление тока, тем больше индуктивное сопротивление.
- Емкостным сопротивлением X_C обладают конденсаторы, которые накапливают электрический заряд. При изменении направления тока в цепи конденсатор неоднократно обнуляет и накапливает электрический заряд. Чем дольше конденсатор заряжается, тем больше емкостное сопротивление.^[4] Поэтому чем быстрее меняется направление тока, тем меньше емкостное сопротивление.
4
Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: X_L = 2πƒL, где L — индуктивность, измеряемая в генри (Гн).^[5]
- Индуктивность L зависит от количества витков в катушке индуктивности.^[6] Также вы можете измерить индуктивность.
- Если вы знакомы с единичной окружностью, то представьте, что один цикл переменного тока равен одному полному вращению этой окружности (на 2π радиан). Если умножить это значение на ƒ, которая измеряется в герцах (единиц в секунду), вы получите результат, измеряемый в радианах в секунду. Это единица измерения угловой скорости, которая обозначается через ω. Вы можете переписать формулу для вычисления индуктивного сопротивления так: X_L=ωL^[7]
5
Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: X_C = ¹ / _2πƒC.^[8] С — это емкость конденсатора, измеряемая в фарадах (Ф).
- Вы можете измерить электрическую емкость.
- Эту формулу можно переписать так: X_C = ¹ / _ωL (объяснения см. выше).
Реклама

1
Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.^[9]
- Если резисторы соединены последовательно, то полное сопротивление R = R₁ + R₂ + R₃…
- Если резисторы соединены параллельно, то полное сопротивление R = ¹ / _R₁ + ¹ / _R₂ + ¹ / _R₃ …
2
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:^[10]
- Последовательное соединение катушек: X_total = X_L1 + X_L2 + …
- Последовательное соединение конденсаторов: C_total = X_C1 + X_C2 + …
- Параллельное соединение катушек: X_total = 1 / (1/X_L1 + 1/X_L2 …)
- Параллельное соединение конденсаторов: C_total = 1 / (1/X_C1 + 1/X_C2 …)
3
Вычтите индуктивные и емкостные сопротивления, чтобы получить общее реактивное сопротивление. Так как при возрастании одного типа сопротивления другое уменьшается, то они, как правило, компенсируют друг друга. Чтобы найти общее реактивное сопротивление, вычтите меньшее сопротивление из большего.^[11]
- Или воспользуйтесь формулой: X_total = |X_C — X_L|
4
Вычислите импеданс по активному и реактивному сопротивлениям в последовательной цепи. Нельзя просто сложить эти величины, так как они меняются с течением времени, но достигают максимальных значений в разное время.^[12] Поэтому воспользуйтесь формулой:Z = √(R² + X²).^[13]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.^[14]^[15]
5
Вычислите импеданс по активному и реактивному сопротивлениям в параллельной цепи. В этом случае используются комплексные числа (это единственный способ вычислить полное сопротивление в параллельной цепи, в которой есть как активное, так и реактивное сопротивление).
- Z = R + jX, где j — мнимая единица: √(-1). Используйте j вместо i, чтобы не перепутать мнимую единицу (j) с силой тока (I).
- Складывать эти числа нельзя. Например, полное сопротивление может быть представлено так: 60 Ом + j120 Ом.
- Если у вас есть две последовательные цепи, то вы можете отдельно сложить натуральные числа и отдельно — комплексные. Например, если Z₁ = 60 Ом + j120 Ом, а к этой цепи последовательно подключен резистор с Z₂ = 20Ω, то Z_total = 80Ω + j120Ω.
Реклама

Общее сопротивление (активное и реактивное сопротивления) также может быть выражено через мнимое число.

Эту страницу просматривали 169 190 раз.

Источник

Содержание

1 Виды электрических сопротивлений
2 Определение эквивалентного сопротивления
3 Как определяется ПС при последовательном соединении емкостей и индуктивностей
4 Определение ПС при использовании параллельного соединения элементов
5 Видео по теме

Для начала нужно понять, что такое электрическое сопротивление. Это физическая величина, которая отражает противодействие движению электротока по схеме или же внутри проводника. Данная величина взаимосвязана с электронапряжением и силой электротока, что отражено в законе Ома, названном так по имени немецкого физика.

Формулировка закона Ома

Известно о двух видах электронапряжения — постоянном и переменном. В электроцепи постоянного тока присутствует исключительно активное электросопротивление. Таким является любое электросопротивление, поглощающее энергию. В этом случае найти полное сопротивление поможет формулировка закона Ома.

В электроцепях с переменным напряжением есть реактивное электросопротивление, то есть такое, которое энергию не поглощает. Оно делится на емкостное и индуктивное. В реальности не существует электроцепей только с каким-либо одним видом электросопротивления. Наряду с резисторами в них используются емкости и катушки индуктивности. Поэтому в электротехнике вводится такое понятие, как полное сопротивление цепи, представляющееся в виде векторной суммы всех электросопротивлений, присутствующих в данной цепи.

Классификация электроцепей переменного электротока

Величина реактивного электросопротивления зависит от частоты параметров используемой электросети. Формула, с помощью которой можно определить емкостное электросопротивление, выглядит так:

Определение емкостного сопротивления

Здесь ω — угловая частота. Она связана с частотой электросети f и определяется по формуле:

Значение угловой частоты

Индуктивное электросопротивление находим с помощью такого выражения:

Определение индуктивного электросопротивления

В формулах для определения емкостного и индуктивного электросопротивления используются определенные физические величины. Их обозначение и единицы измерения приводятся в таблице ниже. Само электросопротивление измеряется в омах.

Таблица физических величин

Чтобы вычислить полное сопротивление цепи Z, учитывающее все имеющиеся активные и реактивные составляющие, следует воспользоваться формулой:

Вычисление импеданса

В электросхеме может быть использовано несколько нагрузок одного вида, соединенных между собой последовательно или параллельно. В первом случае их электросопротивления складываются. Поэтому эквивалентное сопротивление будет тем больше, чем больше элементов соединено последовательно.

Электроцепь с последовательно соединенными активными проводниками

Если используется параллельное соединение проводников, расчет полного сопротивления цепи выполняется несколько иначе:

Определение эквивалентного электросопротивления при параллельном соединении

В данном случае эквивалентное сопротивление с увеличением количества используемых нагрузок будет уменьшаться. Такое явление можно наблюдать в повседневной жизни: чем больше к электросети подключено потребителей, тем меньшим будет значение эквивалентного электросопротивления и большим электроток нагрузки.

При наличии реактивной нагрузки в электроцепи будет наблюдаться опережение или отставание электротока от электронапряжения. При подключении индуктивной нагрузки электроток отстает от электронапряжения, а емкостной, наоборот, опережает. То есть, при подключении конденсатора к источнику переменного электротока он будет постоянно перезаряжаться с частотой, соответствующей частоте электросети. Электроток при этом будет увеличиваться раньше, чем электронапряжение. При подключении индуктивного контура наблюдается обратный результат.

Графическое изображение электрических величин при последовательно соединенных элементах электроцепи

Рассмотрим схему с использованием последовательно соединенных резистора и индуктивности.

Электросхема с использованием резистора и индуктивности соединенных последовательно

Для этого участка цепи результирующее электронапряжение в точках А и В можно определить достаточно простым способом — геометрическим сложением векторов U_L и U_R. Как видно из рисунка, результирующий вектор U_АВ — это гипотенуза треугольника. Следовательно, чтобы рассчитать ее, можно применить теорему Пифагора:

Определение результирующего электронапряжения

Если исходить из формулировки закона Ома, то электронапряжение — это произведение электросопротивления и силы электротока. Поскольку последний параметр во всех точках электроцепи имеет одинаковое значение, то квадрат ПС — это сумма квадратов электросопротивлений, называемых активными и реактивным:

Сумма квадратов электросопротивлений

Следовательно, полное сопротивление приведенной цепи Z определяется выражением:

Определение ПС

Кроме расчетов для определения ПС в цепи можно использовать еще и геометрический способ, являющийся построением треугольника, представленного на рисунке 11д. Его катеты — это активное и реактивное электросопротивление для участка цепи. Понятно, что стороны треугольника следует откладывать в одном масштабе.

Полное сопротивление цепи в рассматриваемом случае не будет исключительно активным или реактивным. В него входят обе составляющие. По этой причине угол сдвига по фазе между электротоком и электронапряжением может меняться от 0 до 90 градусов. К какому из этих предельных значений будет приближена величина φ, зависит от вида преобладающего электросопротивления. Если индуктивная составляющая превышает активную, φ стремится к 90 градусам, а преобладающая активная составляющая уменьшает его до нуля.

Теперь рассмотрим электроцепь с присутствующими в ней резистором и конденсатором, соединенными последовательно. Полное сопротивление цепи и в данном случае можно определить, используя построение треугольника.

Электросхема с последовательно соединенными резистором и конденсатором

Как можно увидеть из рисунка, треугольник сопротивлений, построенный для активно-емкостного участка цепи, развернут в другую сторону. Это связано с тем, что электроток в емкости опережает электронапряжение (в активно-индуктивной ветви электроток отстает от электронапряжения). Полное электрическое сопротивление цепи Z в данном случае будет равно:

Определение импеданса при использовании резистора и конденсатора в электроцепи

Если же в электроцепи присутствуют все виды электросопротивлений, то сначала следует найти реактивную составляющую, а потом уже и значение ПС или импеданса.

Электросхема с использованием разных видов электросопротивлений

Общее реактивное электросопротивление для данного участка цепи — это разница между индуктивной и емкостной составляющими, поскольку они по своему характеру являются противоположными друг другу.

Расчет общего реактивного электросопротивления

Полное сопротивление электрической цепи при наличии индуктивной и емкостной составляющей определяется по формуле:

Определение ПС при наличии индуктивности и емкости в электроцепи

Треугольник электросопротивлений при наличии индуктивной и емкостной составляющей показан на рисунке.

Немаловажно понимать, что если одно из электросопротивлений (емкостное или индуктивное) больше другого более, чем в десять раз, то составляющую с наименьшим значением можно оставить без внимания.

На рисунке ниже изображены графики электронапряжений и электротоков, присутствующих на нагрузках при параллельном соединении.

Графики электронапряжений и электротоков при параллельном соединении элементов электроцепи

Чтобы определить полное электрическое сопротивление цепи, включающей резистор и индуктивность или резистор и емкость, соединенные параллельно, необходимо в первую очередь найти проводимость каждой параллельной линии, затем общую проводимость этой цепи между точками А и В. На последнем этапе вычисляется ПС между А и В.

Пример электросхемы с параллельно соединенными элементами

Вычисляемое значение проводимости активного участка цепи равняется 1/R, индуктивного — 1/ ωL. Формула для определения полной проводимости выглядит так:

Полная проводимость участка электроцепи

Приводя к общему знаменателю выражение под знаком корня, получаем следующее выражение:

Формула после преобразования

Отсюда находим формулу для определения ПС для участка цепи с параллельно соединенными резистором и индуктивностью:

Определение ПС при параллельно соединенных элементах

Формула для вычисления ПС при использовании параллельного соединения резистора и емкости имеет такой вид:

Определение ПС при параллельном соединении резистора и емкости

В радиотехнике чаще всего используется параллельное соединение конденсатора и катушки индуктивности, например, в колебательном контуре. Поскольку катушка имеет и индуктивное, и активное сопротивление, то в индуктивную ветвь включается еще резистор.

Схема колебательного контура

Для определения ПС следует воспользоваться формулой:

Определение ПС колебательного контура

Учитывая то, что активное электросопротивление катушки значительно меньше индуктивного, формулу можно представить так:

Формула для расчета ПС колебательного контура

Значение индуктивности и емкости для колебательного контура принято выбирать так, чтобы соблюдалось условие:

Условие для колебательного контура

В данном случае для определения ПС колебательного контура получаем очень простую формулу:

Упрощенная формула для расчета ПС колебательного контура

С целью облегчения расчетов импеданса используют комплексные числа. Действительную часть такого числа представляет активное электросопротивление, а мнимую — реактивное.

Для последовательно соединенных радиоэлементов ПС в комплексном виде можно представить так:

Определение комплексного ПС

В тригонометрической интерпретации модулем комплексного числа является ПС, а аргументом — угол φ.

Треугольник сопротивлений

Следовательно, активную и реактивную составляющие ПС можно найти по формулам:

Определение составляющих ПС

При вычислении ПС или импеданса для параллельно соединенных элементов используют сумму проводимостей — величин, обратных электросопротивлениям.

Треугольник проводимостей

Комплексная проводимость является величиной, обратной комплексному электросопротивлению. Алгебраически она выражается так:

Определение комплексной проводимости

Вычисление импеданса является достаточно сложной задачей, поскольку используется большое количество формул, тригонометрических функций. Поэтому с целью облегчения расчетов можно воспользоваться онлайн калькулятором. Чтобы получить результат, понадобится лишь ввести значение частоты электротока, емкость конденсатора, индуктивность катушки, сопротивление резистора.

Источник

Отдельным видом задач или частью общей большой задачи является задачи на поиск полного (общего) сопротивления цепи постоянного тока.

Пусть дана цепь с заданными сопротивлениями $displaystyle {{R}_{1}}-{{R}_{7}}$ (рис. 1).

Рис. 1. Полное сопротивление цепи — 1

Проанализируем её: визуально выделяем участки цепи, на которых есть только последовательные или только параллельные соединения. Таких участка два, оба с параллельным подключением проводников, обозначим их $displaystyle {{R}_{02}}$ и $displaystyle {{R}_{02}}$ (рис. 2).

Рис. 2. Полное сопротивление цепи — 2

Найдём значения $displaystyle {{R}_{02}}$ и $displaystyle {{R}_{02}}$ , исходя из параллельности проводников: $displaystyle frac{1}{{{R}_{0}}}=sumlimits_{i}{frac{1}{{{R}_{i}}}}$ .

$displaystyle frac{1}{{{R}_{01}}}=frac{1}{{{R}_{1}}}+frac{1}{{{R}_{2}}}Rightarrow {{R}_{01}}=frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$ (1)

$displaystyle frac{1}{{{R}_{02}}}=frac{1}{{{R}_{4}}}+frac{1}{{{R}_{5}}}+frac{1}{{{R}_{6}}}Rightarrow {{R}_{02}}=frac{{{R}_{4}}{{R}_{5}}{{R}_{6}}}{{{R}_{4}}{{R}_{5}}+{{R}_{4}}{{R}_{6}}+{{R}_{5}}{{R}_{6}}}$ (2)

Введём обозначения и перерисуем получившуюся схему (рис. 3).

Рис. 3. Полное сопротивление цепи — 3

Проанализируем получившуюся цепь: в ней ряд сопротивлений подключены последовательно (рис. 4).

Рис. 4. Полное сопротивление цепи — 4

Найдём значение $displaystyle {{R}_{03}}$ , исходя из последовательности проводников: $displaystyle {{R}_{0}}=sumlimits_{i}{{{R}_{i}}}$ .

$displaystyle {{R}_{03}}={{R}_{01}}+{{R}_{3}}+{{R}_{02}}$ (3)

Введём обозначения и перерисуем получившуюся схему (рис. 5).

Рис. 5. Полное сопротивление цепи — 5

Тогда мы получили обычную параллельную цепь, общее значение сопротивление которой:

$displaystyle {{R}_{0}}=frac{{{R}_{7}}{{R}_{03}}}{{{R}_{7}}+{{R}_{03}}}$ (4)

Подставив (1) и (2) в (3), а получившееся значение в (4), получим искомый ответ. Делать это долго, поэтому мы делать это не будем. Получим ответ при условии:

$displaystyle {{R}_{1}}={{R}_{2}}={{R}_{3}}={{R}_{4}}={{R}_{5}}={{R}_{6}}={{R}_{7}}=R$ (5)

Тогда из (1) и (2):

$displaystyle {{R}_{01}}=frac{RR}{R+R}=frac{R}{2}$ (6)

$displaystyle {{R}_{02}}=frac{RRR}{RR+RR+RR}=frac{{{R}^{3}}}{3{{R}^{2}}}=frac{R}{3}$ (7)

Подставим получившиеся значения в (3):

$displaystyle {{R}_{03}}=frac{R}{2}+R+frac{R}{3}=frac{3R+6R+2R}{6}=frac{11R}{6}$ (8)

И последнее, подставим (8) в (4):

$displaystyle {{R}_{0}}=frac{{}^{11R}!!diagup!!{}_{6};R}{{}^{11R}!!diagup!!{}_{6};+R}=frac{11R}{17}$ (9)

Вывод: Пользуясь представленной логикой, можно найти полное сопротивление цепи любой сложности.

Источник

Обновлено: 7 июл. 2020 г.

Вы когда-либо пробовали разобраться, что такое полное электрическое сопротивление, которое еще называют импедансом? Если раньше вы уже успели окунуться в эту тему, то скорее всего, уже нахватались жаргонных словечек, таких как «фазовый вектор», «соотношения фаз» и даже «реактивное сопротивление». Какого черта, что все это значит?

Не все из нас по образованию инженеры-электрики. Некоторые в свободное время просто возятся с электроникой, но никогда не касаются строгих математических обоснований, которые вы изучали в университете. Однако это не означает, что отсутствие понимания, что такое полное электрическое сопротивление должно стать препятствием. Если вы планируете работать с электронными устройствами переменного тока, то вам нужно знать, что такое полное сопротивление, и как оно влияет на вашу электрическую цепь.

Давайте выясним это!

Лучший способ понять, что же такое полное электрическое сопротивление – это сравнить его с чем-то уже вам известным, скажем – «простым» сопротивлением. Так мы сможем дать исчерпывающее определение полного электрического сопротивления одной фразой:

Полное электрическое сопротивление – это вид сопротивления, зависящее от частоты.

Вот и всё. Сейчас вы можете остановиться и записать еще одно слово в ваш словарь инженера-электрика. Просто и понятно: полное электрическое сопротивление – вид сопротивления, которое зависит от рабочей частоты электрической цепи. Но, разумеется, это еще не всё.

Резисторы выполняют в цепи постоянного тока чрезвычайно простую работу. Они оказывают сопротивление току, протекающему через какой-либо металл, например медь. Вы добавляете резистор на 220 кОм в цепь постоянного тока, и получаете определенное уменьшение тока, который втекает в резистор с одной стороны, и вытекает из него с другой стороны. Резисторы, подобно другим чисто омическим компонентам электрической цепи, не думают о том, какую же частоту выдает источник тока. Они просто делают то, что должны делать – оказывают некое постоянное сопротивление току.

Но что произойдет, если вы начнете работать с электроникой с питанием от источника переменного тока? Источник переменного тока не просто дает 5 В для питания вашей схемы. Кроме нового источника тока вы получили новые переменные, с которыми необходимо считаться. Например, сюда входит заранее известная частота переменного тока в сети питания. В Соединенных Штатах Америки частота тока в электрической сети составляет 60 колебаний в секунду (60 Гц). За океаном, в Европе, частота тока в сети 50 Гц.

В отличие от постоянного тока (DC), график которого представляет собой

прямую линию, переменный ток (АС) колеблется с определенной частотой.

В итоге получается следующее: в электронных устройствах, использующих переменный ток, необходимы не только активные компоненты, такие как резисторы, задачей которых является оказание сопротивления электрическому току, также нужны компоненты, которые могут реагировать на изменения тока и частоты, например конденсаторы и катушки индуктивности. В противном случае электрическая схема не будет работать так, как задумывалось. Зная все это уже можно посчитать полное сопротивление, которое является старшим братом активного сопротивления. Полное электрическое сопротивление включает в себя и активное, и реактивное сопротивления. Это можно записать в виде выражения:

Полное сопротивление =
активное сопротивление + реактивное сопротивление

Реактивное сопротивление бывает двух видов в зависимости от используемого реактивного компонента. Сюда входит:

Оно встречается в цепях, где есть своего рода электромагниты, влияющие на магнитное поле электрической цепи. Еще их называют катушками индуктивности. Катушки индуктивности имеют низкое полное электрическое сопротивление на низких частотах и высокое полное электрическое сопротивление на высоких частотах.

Разные катушки индуктивности. Обратите внимание на общность

конструкции – медный провод намотан на магнит, образуя катушку.

Оно встречается там, где электрическое поле между двумя проводящими поверхностями вызывает накопление заряда. Такие устройства еще называют конденсаторами. Конденсаторы имеют высокое полное электрическое сопротивления на низких частотах и низкое полное сопротивление на высоких частотах.

Конденсаторы встречаются всех форм и размеров.

Соберем электрическую цепь переменного тока из резисторов, катушек индуктивности и конденсаторов. Теперь вы сможете не только оказывать сопротивление электрическому току, но и накапливать и высвобождать энергию. Если резисторы сохраняют постоянное сопротивление вне зависимости от изменяющихся условий, то сопротивление катушек индуктивности и конденсаторов изменяется в зависимости от частоты проходящего через них электрического сигнала. Когда конденсаторы и катушки индуктивности вместе оказывают сопротивление и накапливают/высвобождают энергию, тогда и говорят о полном электрическом сопротивлении.

Соединим все детали вместе в простую электрическую цепь. Взглянем на рисунок ниже: это цепь с источником питания постоянного тока. Ток течет через резистор. Весьма просто, верно? Чем больше сопротивление резистора в цепи, тем меньше будет ток.

Простая цепь постоянного тока с резистором

на 100 Ом для ограничения силы тока.

Что произойдет, если мы добавим в электрическую цепь источник питания переменного тока, катушку индуктивности и конденсатор? Теперь в цепи есть два дополнительных компонента, каждый из которых по своему оказывает сопротивление электрическому току. Как и резистор, они оба препятствуют прохождению электрического тока, при этом также воздействуют на ток. Если суммировать активное сопротивление резистора и активное и реактивное сопротивления конденсатора и катушки индуктивности, то получится полное электрическое сопротивление или импеданс.

В цепи переменного тока последовательно соединены резистор, катушка индуктивности и конденсатор

Постойте! Чтобы рассчитать полное электрическое сопротивления недостаточно просто сложить активные и реактивные сопротивления. Обычно в большинстве учебных пособий с этого момента начинается изобилие математических формул, поэтому дальше читайте не спеша.

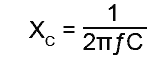
Чтобы найти полное электрическое сопротивление конденсатора, вы можете воспользоваться следующей формулой. В ней Xc – полное электрическое сопротивление, которое необходимо найти. Оно измеряется в Омах. Переменная f – это частота сигнала, проходящего через конденсатор, а C – емкость конденсатора.

Чтобы найти полное электрическое сопротивление катушки индуктивности, вы можете воспользоваться следующей формулой. В ней XL – полное электрическое сопротивление, которое необходимо найти. Оно измеряется, опять же, в Омах. Переменная f – это частота сигнала, проходящего через катушку индуктивности, а L – индуктивность.

Эти формулы правильны и прекрасны, если вы хотите рассчитать полное электрическое соединение отдельных компонентов электрической цепи, но что же делать, если нужно найти полное сопротивление всей цепи? Теперь все еще более усложняется.

Перед тем, как мы перейдем к нашей последней формуле, мы хотим предложить вашему вниманию калькулятор полного электрического сопротивления, который может упростить вам жизнь: Калькуляторы полного сопротивления от Keisan.

Чтобы выполнить расчет, вам необходимо обратиться за помощью к теореме Пифагора. Как мы уже рассказали выше, в цепях переменного тока действуют и активное, и реактивное сопротивления, вместе образуя полное электрическое сопротивление. Но простое суммирование активного и реактивного сопротивления не имеет смысла. Мы можем объяснить, почему это так, но тогда нам придется рассказать о премудростях фазовых векторов и о правилах работы с ними, а для этого понадобится отдельный блог.

Когда вы сталкиваетесь с расчетом полного электрического сопротивления всей цепи, вам может помочь то, что называется треугольником сопротивлений, который показан на рисунке ниже.

Треугольник сопротивлений упрощает расчет

полного электрического сопротивления цепи.

Наиболее важная часть этого треугольника – его гипотенуза, дает величину полного сопротивления цепи, которое представляет собой квадратный корень из суммы квадратов активного и реактивного сопротивлений. Если вы подставите их в данную формулу, то сможете найти полное сопротивление электрической цепи. В ней Z – это искомое полное электрическое сопротивление цепи, R – полное активное сопротивление, X – полное реактивное сопротивление.

Становится понятно, в конце концов, что после всех наших объяснений разобраться, что такое полное электрическое сопротивление, несложно, не так ли? Существуют десятки бесплатных калькуляторов, которые помогут вам выполнить расчеты. Что вам на самом деле нужно – это знать, что полное сопротивление работает так же, как активное сопротивление, ограничивая ток в цепи переменного тока.

Способность таких компонентов, как конденсаторы и катушки индуктивности реагировать на постоянные изменения переменного тока, делает их уникальными. Благодаря полному сопротивлению в вашей цепи можно организовать нечто похожее на электрический щит с защитными автоматами, которые реагируют на неожиданные скачки электричества, защищая от выгорания домашнюю электропроводку. Можно также сказать спасибо полному сопротивлению за то, что вы можете носить с собой ноутбук с полностью заряженным аккумулятором, не опасаясь его взрыва.

Когда дело доходит до работы с устройствами с питанием от источника переменного тока, будь то ноутбук или электрощит в вашем доме, стоит быть благодарным полному электрическому сопротивлению. И помните, полное электрическое сопротивление – это просто старший брат привычного активного сопротивления, который объединяет активное и реактивное сопротивления в одной простой формуле.

Источник

Цепь с емкостью.

Если
цепь переменного тока содержит
конденсатор, и на него подать переменное
напряжение
,
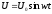
то сила тока в цепи будет изменяться в
соответствие с выражением:

где
С – емкость конденсатора.

Величина

(2)

играет
роль сопротивления и называется емкостным
сопротивлением цепи. В цепи с конденсатором
изменение силы тока опережает по фазе
изменение напряжения на
.

Полное сопротивление цепи переменного тока.

Полное
сопротивление цепи, обладающей активным
сопротивлением, емкостью и индуктивностью
может быть найдено по формуле:

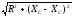
Величина

называется реактивным сопротивлением
цепи.

Мост rlc.

Электрическая
цепь, схема которой представлена на
рис. 1, называется мостом, это одна из
основных электрических измерительных
схем. На участке (СД) направление и
величина тока будут зависеть от
сопротивлений участков 1,2,3,4.

Рис. 2. Схема моста

Так как в схеме
моста проводники АСВ, АДВ соединены
параллельно и падение напряжения на
них одинаково, очевидно, всегда можно
найти точки С и Д, разность потенциалов
между которыми равна нулю, и, следовательно,
если соединить эти точки, в проводнике
СД тока не будет. В этом случае говорят,
что мост уравновешен или сбалансирован.

Применим для
уравновешенного моста правила Кирхгофа.
Допустим, участки 1,2,3,4 содержат активные
сопротивления. Если в участке СД ток
отсутствует, то в ветвях 1 и 2 сила тока
будет одинакова. То же самое можно
сказать о силе тока в ветвях 3 и 4. В этом
случае для контуров АСДА и ДСВД на
основании 2-го правила Кирхгофа можно
записать уравнения:

Из этих уравнений
получим:

Если одно из этих
сопротивлений, допустим,
,
неизвестно, то для его вычисления нужно
знать остальные три, или
,
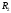
и отношение
.

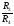
На этом основано
применение уравновешенного моста.
Обычно при определении неизвестного
сопротивления его включают на участке
1, на участке 2 включают эталонное
сопротивление, а проводник АДВ заменяют
реохордом и контакт Д делают подвижным.
Тогда отношение сопротивлений
можно
заменить отношением длин соответствующих
участков
.
Для установления факта уравновешивания
моста между точками С и Д в цепь включают
нулевой гальванометр, и подбирают такие
значения

и
,
чтобы при замыкании цепи гальванометра
его стрелка не отклонялась.

Если
мостовая схема используется в цепях
переменного тока, то аналогичным способом
можно определять неизвестную емкость
или индуктивность. Для этого на участке
1 включают элемент с неизвестным
номиналом, который нужно определить,
на участке 2 – эталонный элемент той же
природы (например, катушка с неизвестной
индуктивностью и эталонная катушка,
конденсатор с неизвестной емкостью и
эталонный конденсатор и т.д.), а на
участках 3,4 – реохорд. Измерение
неизвестного параметра также основано
на уравновешивании моста.

Если
на участках 1, 2 включены катушки
индуктивности, то для уравновешенного
моста:

;
используя формулу (1), получим:
.
Отсюда:

(3)

где
L_э -индуктивность
эталонной катушки, x
– длина плеча реохорда для уравновешенного
моста,

— полная длина реохорда.

Если
на участках 1,2 включены конденсаторы,
то для уравновешенного моста:

;
используя формулу (2), получим:
.
Отсюда:

(4)

где
С_э
– емкость эталонного конденсатора.

Если
на участках 1, 2 включены резисторы, то
для уравновешенного моста:

,
откуда:

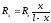
(5)

где
R_э
– сопротивление эталонного резистора.

Экспериментальная
установка

Установка
(рис.2) состоит из основного блока –
измерительного модуля с реохордом,
имеющего клеммы для подключения
дополнительных элементов, генератора
сигналов, наушников, набора катушек с
разными значениями индуктивности и
набора минимодулей с различными
значениями сопротивления и емкости.

Для
выполнения работы собирается электрическая
цепь в соответствии со схемой, изображенной
на верхней панели модуля. Для фиксации
уравновешивания моста используются
наушники (при уравновешивании громкость
звука минимальная), подключаемые в
специальное гнездо модуля. Параметры
эталонного элемента задаются преподавателем

Рис.2.
Установка для изучения моста RLC

Порядок
выполнения работы

Подключить
генератор к разъему на задней панели
модуля. Подключить наушники. Установить
в плечи моста минимодули с неизвестным
и эталонным сопротивлениями.
Установить на
генераторе параметры выходного сигнала:
вид сигнала: «Wave»
– синусоидальный (1), диапазон частот:
«Range»
– 5, после чего, нажав «Run»
установить поворотом «FADJ»,
значение частоты порядка 4600Гц-5000Гц,
поворотом «DADJ»
— амплитуду сигнала порядка 9,4В-9,6В.
Вращая ручку
реохорда, добиться минимальной громкости
звука в наушниках. Соответствующее
значение плеча реохорда х записать в
таблицу 1. Повторить описанные действия
5 раз.
Измерить длины и
диаметры эталонной и исследуемой
катушек. Занести данные измерений и
количество витков (указано на катушках)
в таблицу 2.
Установить в плечи
моста катушки с неизвестной и эталонной
индуктивностями.
Повторить действия,
описанные в п.3, данные измерений занести
в таблицу 1.
Установить в плечи
моста минимодули с неизвестной и
эталонной емкостями.
Повторить действия,
описанные в п.3, данные измерений занести
в таблицу 1. Указать в таблице значение
полной длины реохорда
.
Выключить генератор.
Отключить модуль от сети. Отсоединить
генератор, наушники и минимодули от
измерительного блока. Движок реохорда
поставить в начальное положение.

Таблица
1

Таблица
2

Катушка	N	D (см)	(см)
Эталонная
Исследуемая

Расчет индуктивности
катушки.

Для длинной катушки,
длина которой много больше ее диаметра,
индуктивность может быть найдена по
формуле:

(6)

где N
– общее число витков катушки,
—
ее длина, S
– площадь поперечного сечения,

— магнитная постоянная.

,
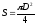
где D
– диаметр катушки.

Подставив в (6) S
и μ₀
, преобразуем формулу:

При условии, что
длина и диаметр катушки выражены в
метрах, индуктивность получим в генри
(Гн).

Если же длина
катушки, как в данной работе, сравнима
с ее диаметром, то следует использовать
более точную формулу для вычисления
индуктивности. Для однослойной катушки
она будет иметь вид:
.

(7)

Удобно длину и
диаметр катушки выражать в см, тогда
можно рассчитать индуктивность в мкГн,
приведя формулу (7) к виду:

(8)

В данной работе
не все катушки являются однослойными,
но, поскольку толщина намотки мала по
сравнению с диаметром катушек,
индуктивность можно вычислять, используя
формулу (8).

Обработка
результатов измерений

Используя данные
таблицы 1, посчитайте среднее значение
плеча х и его погрешность для каждого
эталонного элемента.
Рассчитайте
индуктивность эталонной катушки,
используя выражение (8) и данные таблицы
2.
Используя формулы
(3), (4), (5), найдите средние значения
неизвестных параметров: активного
сопротивления, емкости, индуктивности.
Рассчитайте
относительные и абсолютные погрешности
измерения сопротивления, индуктивности
и емкости:

,
;

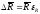
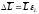
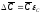
Сравните полученные
значения с действительными (активное
сопротивление и емкость можно измерить
с помощью цифрового мультиметра, а
индуктивность посчитать.).

Контрольные
вопросы

Нарисуйте схему
моста. В каком случае мост называется
уравновешенным? Для чего можно
использовать мостовые схемы?
Какие токи
называются квазистационарными? Что
называется эффективным значением силы
тока, как его найти?
Как найти индуктивное
и емкостное сопротивление цепи
переменного тока?
Как можно найти
полное сопротивление цепи переменного
тока?
Как записать закон
Ома для участка цепи с катушкой?
Сформулируйте и
запишите правила Кирхгофа.

ЛИТЕРАТУРА

1.Трофимова
Т.И. Курс физики. / Т.И. Трофимова. — М.:
Высшая школа, 2006-2009 г. г. – 544с.

2.
Савельев И.В. Курс физики. В 3-х томах.
Том 2. Электричество. Колебания и волны.
Волновая оптика. Изд. 3-е, стереотип. /
И.В. Савельев — М.: Лань, 2007. — 480 с.

3.
Грабовский Р. И. Курс физики / Р.И.
Грабовский — СПб: издательство «Лань»,
2012. – 608с.

4.
Зисман Г. А., Тодес О. М. Курс общей физики.
В 3-х томах. Том 2. Электричество и магнетизм
/ Г.А. Зисман, О.М. Тодес — СПб: «Лань»,
2007. — 352 c.

Концевой
титул

Учебное
издание

Составитель:

Плотникова
Ольга
Васильевна

Соседние файлы в папке 12-02-2015_08-16-01

Источник

R_э
=…Ом,
=…мм

L_э=…Гн,

=…мм

С_э=…мкФ,
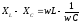
=…мм