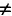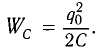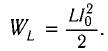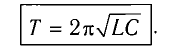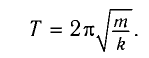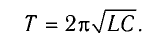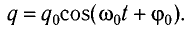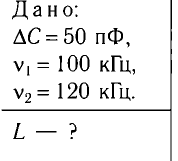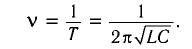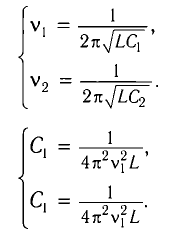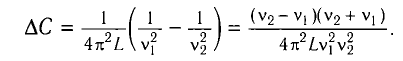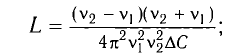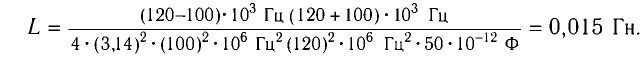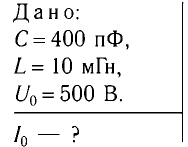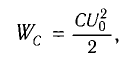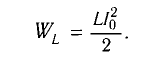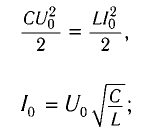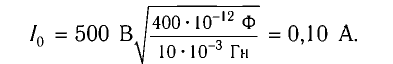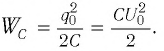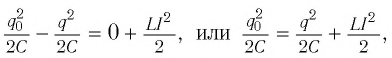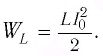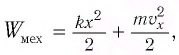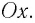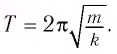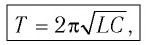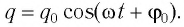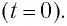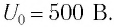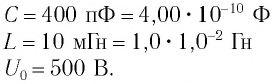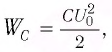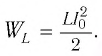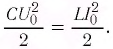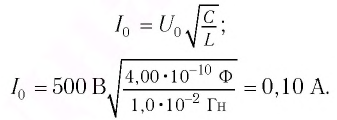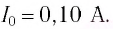Как найти полную энергию колебательного контура

Колебательный контур:

Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.

Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.

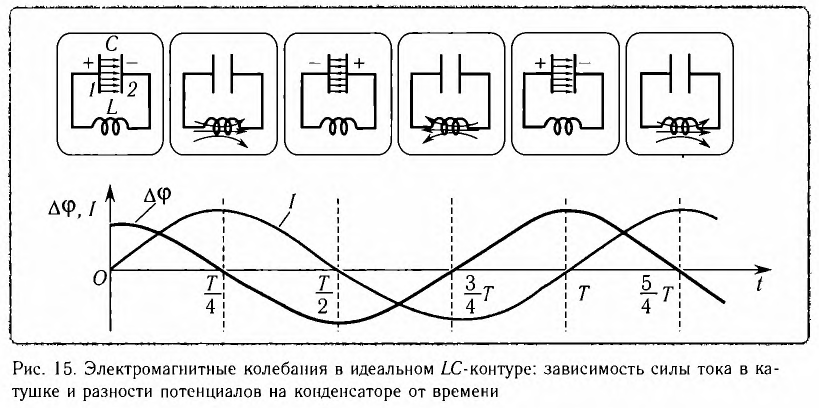
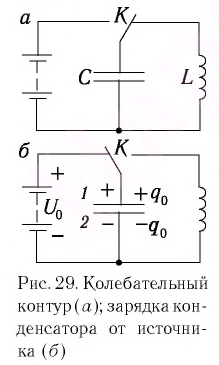
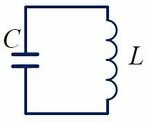
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.

В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R

Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +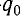, а на второй —. При этом конденсатор обладает энергией

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.

Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.

В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения . В соответствии с законом сохранения энергии первоначально запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:

После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.

Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения . При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно (см. рис. 15). Далее процесс повторится с той лишь разницей, что электрический ток будет проходить в противоположном направлении.

Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений и в различные моменты времени (см. рис. 15).

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:

Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

 (1)

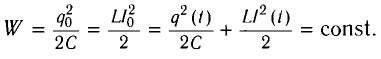
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.

Для пружинного маятника полная механическая энергия в любой момент времени    2 ,

(2)

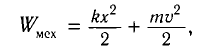
и период его колебаний

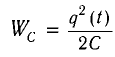
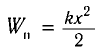
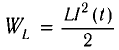
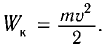
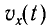
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора и потенциальной энергии упругой деформации пружины энергии магнитного поля катушки  и кинетической энергии груза Аналогом координаты x(t) при колебаниях в электрическом контуре является заряд конденсатора q(t), а аналогом проекции скорости груза служит сила тока I(t) в колебательном контуре.

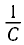
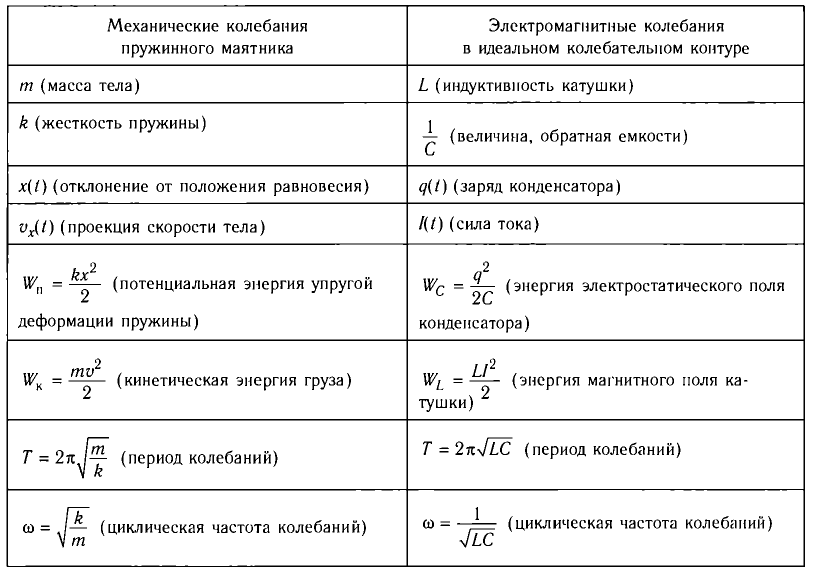
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на , тогда для периода свободных колебаний в LC-контуре получим формулу Томсона: 

Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Таблица 4

Сопоставление физических величин, характеризующих электромагнитные и механические колебания

Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:

Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.

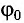
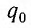
Для определения начальной фазы и амплитуды колебаний заряда необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени (t = 0).

Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.

Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.

Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.

Пример №1

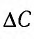
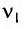
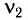
При изменении емкости конденсатора идеального LC-контура на = 50 пФ частота свободных электромагнитных колебаний в нем увеличилась с = 100 кГц до = 120 кГц. Определите индуктивность L контура.

Решение

Частота колебаний в контуре

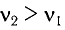
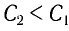
Поскольку частота колебаний в контуре увеличилась (), то электроемкость должна уменьшится, т. е. .

Из условия задачи получаем систему уравнений

Откуда 
 

Вычитая из первого уравнения второе, получаем

Откуда находим

Ответ: L = 0,015 Гн.

Пример №2

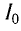
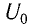
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока в контуре, если амплитудное значение напряжения на конденсаторе = 500 В.

Решение

Максимальная энергия электростатического поля конденсатора

а максимальная энергия магнитного поля катушки

Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 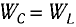, т. е.

откуда 

Ответ: .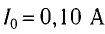

Колебательный контур и свободные электромагнитные колебания в контуре

Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.

Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.

Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.

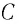
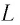
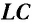
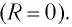
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью  и катушки (соленоида) индуктивностью  (рис. 29, а), называемую идеальным колебательным контуром или -контуром. Электрическое сопротивление идеального контура считают равным нулю  Следовательно, идеальный колебательный контур является упрощенной моделью реального колебательного контура.

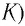
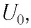
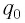
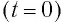
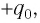
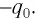
Подключив (при помощи ключа  источник тока, зарядим конденсатор до напряжения  сообщив ему заряд  (рис. 29, б). Следовательно, в начальный момент времени  конденсатор заряжен так, что на его обкладке 1 находится заряд  а на обкладке 2 — заряд  При этом электростатическое поле, создаваемое зарядами обкладок конденсатора, обладает энергией 

Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 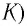 (рис. 30) он начнет разряжаться, так как под действием электрического поля, создаваемого зарядами на обкладках конденсатора, свободные электроны будут перемещаться по цепи от отрицательно заряженной обкладки к положительно заряженной. На рисунке 30 стрелкой показано начальное направление тока в электрической цепи.

Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 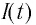 которого будет изменяться с течением времени (рис. 31, а). Но мгновенная разрядка конденсатора невозможна, так как изменение магнитного поля катушки, создаваемое нарастающим по модулю током, вызывает возникновение вихревого электрического поля. Действительно, в катушке индуктивности возникнет изменяющийся во времени магнитный поток, который вызовет появление ЭДС самоиндукции. Согласно правилу Ленца ЭДС самоиндукции стремится противодействовать вызвавшей ее причине, т. е. увеличению силы тока по модулю.

Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 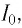 определяемого индуктивностью катушки и электроемкостью конденсатора (рис. 31, б).

При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):

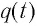
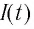
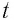
где  — мгновенное значение заряда конденсатора и  — сила тока в катушке в некоторый момент времени  после начала разрядки конденсатора.

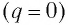
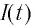
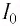
В момент полной разрядки конденсатора  сила тока в катушке  достигнет своего максимального по модулю значения  (см. рис. 31, б). В соответствии с законом сохранения энергии запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:

После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. 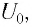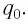Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения  но знак заряда на каждой обкладке оказывается противоположным знаку начального заряда. Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения  При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно. Далее процесс повторится с той лишь разницей, что электрический ток в ко туре будет проходить в противоположном направлении, что отражено на рисунке 31, а.

Таким образом, в идеальном 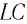-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.

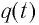
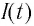
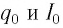
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд  конденсатора и сила тока  в катушке достигают своих максимальных значений  в различные момента времени (см. рис. 31 а, б).

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

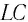
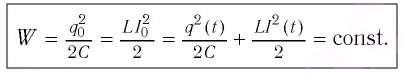
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального -контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство: 
 

Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:

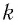
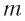
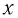
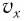
где  — жесткость пружины,  — масса груза,  — проекция смещения тела от положения равновесия,  — проекция его скорости на ось 

Период его колебаний:

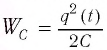
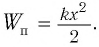
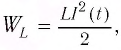
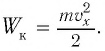
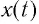
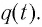
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора  является аналогом потенциальной энергии упругой деформации пружины  Соответственно, энергия магнитного поля катушки  которая обусловлена упорядоченным движением зарядов, является аналогом кинетической энергии груза  Следовательно, аналогом координаты  пружинного маятника при колебаниях в электрическом контуре является заряд конденсатора  Тогда, соответственно, аналогом проекции скорости груза будет сила тока в колебательном контуре, поскольку сила тока характеризует скорость изменения заряда конденсатора с течением времени.

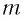
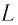
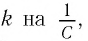
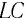
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу  на индуктивность  и жесткость  тогда для периода свободных колебаний в -контуре получим формулу:

которая называется формулой Томсона.

Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Для наблюдения и исследования электромагнитных колебаний применяют электронный осциллограф, на экране которого получают временную развертку колебаний (рис. 32).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:

Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.

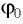
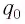
Для определения начальной фазы  и максимального заряда  необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени 

Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.

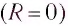
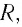
Полная энергия идеального колебательного контура  с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется. Реальный колебательный контур всегда имеет некоторое электрическое сопротивление  которое обусловлено сопротивлением катушки и соединительных проводов. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они будут происходить сколь угодно долго.

Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.

Пример решения задачи:

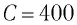
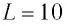
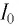
Идеальный колебательный контур состоит из конденсатора емкостью  пФ и катушки индуктивностью  мГн. Определите максимальное значение силы тока  в контуре, если максимальное значение напряжения на конденсаторе 
Дано:

Решение

Максимальная энергия электростатического поля конденсатора:

а максимальная энергия магнитного поля катушки:

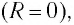
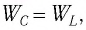
Так как контур идеальный  то его полная энергия сохраняется с течением времени. По закону сохранения энергии  т. е.

Отсюда

Ответ: 

Энергия колебательного контура складывается из энергии катушки и энергии конденсатора. Полная энергия контура считается постоянной, при отсутствии потерь энергии.

W — энергия, Дж (Джоуль)
L — индуктивность катушки, Гн (Генри)
C — электроемкость конденсатора, Ф (Фарад)
U — напряжение, В (Вольт)
I — сила тока, А (Ампер)



В процессе электромагнитных колебаний, в LC-контуре происходит непрерывный переход электрической энергии конденсатора в энергию магнитного поля катушки и обратно. Это можно сравнить с колебанием математического маятника, где аналогично происходит переход кинетической энергии маятника в потенциальную энергию.

Колебания напряжения на концах катушки, опережают по фазе колебания силы тока на ПИ/2.

Задача 51.
В идеальном колебательном контуре, максимальная энергия магнитного поля катушки равна 5мДж, емкость конденсатора 0,01 мкФ. Чему равен максимальный заряд на обкладках конденсатора.

Показать ответ

Колебательный контур

• Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

• Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур.

• Идеальный колебательный контур (LC-контур) — электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

(W=W_{e} + W_{m}, ; ; ; W_{e} =dfrac{Ccdot u^{2} }{2} = dfrac{q^{2} }{2C}, ; ; ; W_{m} =dfrac{Lcdot i^{2}}{2},)

где W_e — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, W_m — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.

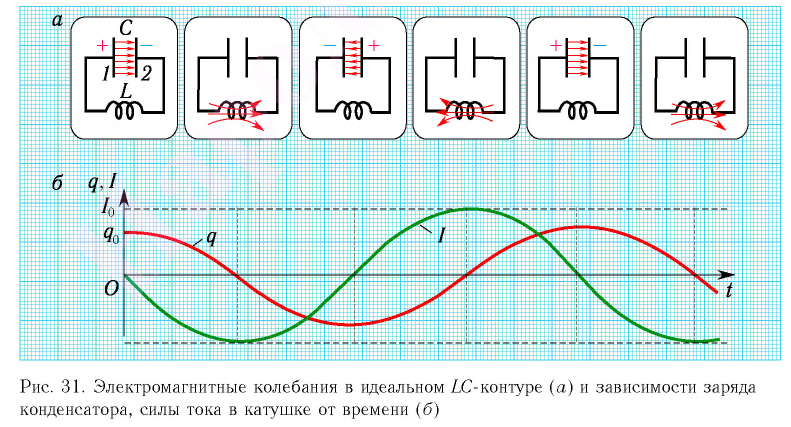
Процессы в колебательном контуре

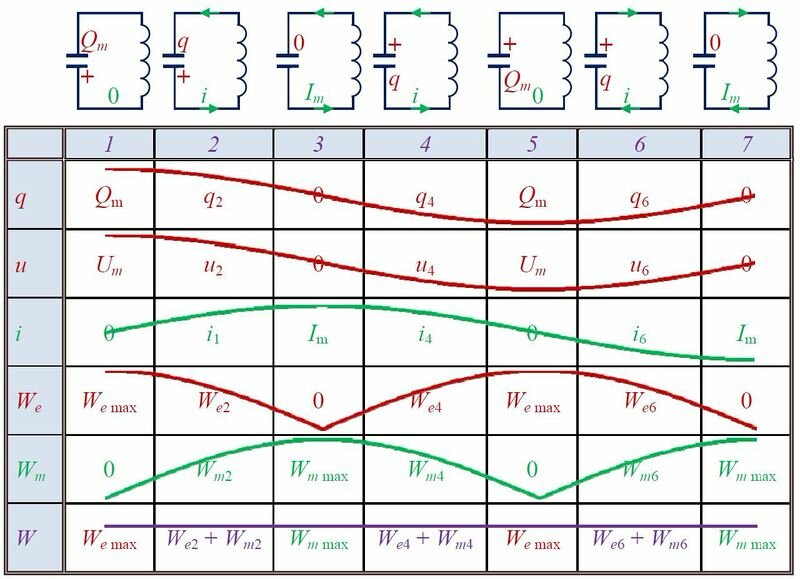
Рассмотрим процессы, которые возникают в колебательном контуре.

Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m (рис. 2, положение 1). С учетом уравнения (U_{m}=dfrac{Q_{m}}{C}) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2). Вместе с зарядом q будет уменьшаться и напряжение u (left(u = dfrac{q}{C} right).) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I_m (см. рис. 2, положение 3).

Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I_m (в положении 3) оказывается максимальным значением силы тока в контуре.

Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m) (см. рис. 2, положение 5).

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6)до нуля (см. рис. 2, положение 7). И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e (left(W_{e}=dfrac{q^{2}}{2C}=dfrac{C cdot u^{2}}{2} right),) а сила тока в катушке i — энергию магнитного поля Wm (left(W_{m}=dfrac{L cdot i^{2}}{2} right),) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Обозначения в таблице:

Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку в нем потерь энергии (нет сопротивления). Тогда

(W=W_{e, max } = W_{m, max } = W_{e2} + W_{m2} = W_{e4} +W_{m4} = …)

Свободные электромагнитные колебания

Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока i, заряда q и напряжения u, причем полная энергия контура при этом будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

• Свободные электромагнитные колебания в контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q и сила тока в катушке i достигают своих максимальных значений Q_m и I_m в различные моменты времени.

Свободные электромагнитные колебания в контуре происходят по гармоническому закону:

(q=Q_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; u=U_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; i=I_{m} cdot cos left(omega cdot t+varphi _{2} right).)

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в LC-контуре определяется по формуле Томсона:

(T=2pi cdot sqrt{Lcdot C}, ;;; omega =dfrac{1}{sqrt{Lcdot C}}.)

Сточки зрения механической аналогии, идеальному колебательному контурусоответствует пружинный маятник без трения, а реальному — с трением. Вследствиедействия сил трения колебания пружинного маятника затухают с течением времени.

*Вывод формулы Томсона

Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

(W=dfrac{Q_{m}^{2} }{2C} =dfrac{Lcdot I_{m}^{2} }{2} =dfrac{q^{2} }{2C} +dfrac{Lcdot i^{2} }{2} ={rm const}.)

Получим уравнение колебаний в LC-контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что

(W’=0, ;;; q’=i, ;;; i’=q»,)

получаем уравнение, описывающее свободные колебания в идеальном контуре:

Переписав его в виде:

(q»+omega ^{2} cdot q=0,)

замечаем, что это — уравнение гармонических колебаний с циклической частотой

(omega =dfrac{1}{sqrt{Lcdot C} }.)

Соответственно период рассматриваемых колебаний

(T=dfrac{2pi }{omega } =2pi cdot sqrt{Lcdot C}.)

Литература

1. Жилко, В.В. Физика: учеб. пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, Л.Г. Маркович. — Минск: Нар. Асвета, 2009. — С. 39-43.

Физика, 11 класс

Урок 7. Свободные и вынужденные электромагнитные колебания. Колебательный контур

Перечень вопросов, рассматриваемых на уроке:

1) электромагнитные колебания, колебательный контур;

2) универсальность основных закономерностей колебательных процессов для колебаний любой физической природы;

3) гармонические колебания;

4) физический смысл характеристик колебаний.

5) графики зависимости электрического заряда, силы тока и напряжения от времени при свободных электромагнитных колебаниях.

6) определение по графику характеристик колебаний;

7) аналогия между механическими и электромагнитными колебаниями.

формула Томсона.

Глоссарий по теме

Электромагнитными колебаниями называют периодические изменения со временем заряда, силы тока и напряжения.

Электромагнитные колебания бывают двух видов — свободные и вынужденные.

Свободными колебаниями называют колебания, возникающие в колебательной системе за счет первоначально сообщенной этой системе энергии.

Вынужденные электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения в цепи под действием переменной электродвижущей силы от внешнего источника.

Система, состоящая из конденсатора и катушки индуктивности, присоединенной к его обкладкам, называется колебательным контуром.

Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание.

Частота колебаний – число колебаний в единицу времени.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я.,Буховцев Б.Б.,Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 74 — 82.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа, 2009. – С. 126 – 128.

Основное содержание урока

Колебательным контуром называется система, состоящая из конденсатора и катушки, присоединенной к его обкладкам, в которой могут происходить свободные электромагнитные колебания

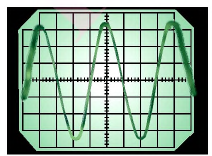
Электромагнитные колебания в контуре происходят с большой частотой и определять его характеристики без осциллографа невозможно.

Развертка получаемая на экране осциллографа схожа с той, что вычерчивает маятник с песочницей над движущимся листом бумаги при колебаниях математического маятника.

Чтобы в колебательном контуре возникли колебания, необходимо сообщить колебательному контуру энергию, зарядив конденсатор от источника тока.

Энергия, полученная конденсатором заключена в электрическом поле обкладок

где — заряд конденсатора, C – его электроемкость.

Между обкладками конденсатора возникает разность потенциалов .

При разрядке конденсатора энергия электрического поля превращается в энергию магнитного поля, определяемая по формуле

где – индуктивность катушки, – сила переменного тока.

Полная энергия колебательного контура равна

Когда конденсатор разрядится полностью, вся энергия электрического поля превращается в энергию магнитного поля. Когда сила тока и созданное им магнитное поле начинает уменьшаться, возникает ЭДС самоиндукции, стремящийся поддержать ток, и начинается перезарядка конденсатора. При свободных колебаниях через промежутки времени, равные периоду колебаний, состояние системы в точности повторяется. Полная энергия такой системы любой момент времени равно максимальной энергии электрического поля или максимальной энергии магнитного поля.

q, u и i — мгновенные значения заряда, напряжения и силы тока. При отсутствии сопротивления в контуре полная энергия электромагнитного поля не изменяется. Колебания затухающие, сопротивление катушки и проводников превращают энергию электромагнитного поля во внутреннюю энергию проводника.

Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями. Характер периодического изменения различных величин одинаков. При механических колебаниях периодически изменяются координата тела x и проекция его скорости , а при электромагнитных колебаниях изменяются заряд q конденсатора и сила тока i в цепи.

Индуктивность катушки L аналогична массе тела m, при колебаниях груза на пружине, кинетическая энергия тела , аналогична энергии магнитного поля тока .

Роль потенциальной энергии выполняет энергия заряда конденсатора:

Координата тела аналогична заряду конденсатора.

Полная энергия колебательного контура, в любой момент времени, равна сумме энергий магнитного и электрического полей:

Производная полной энергии по времени равна нулю при R = 0. Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей:

то есть

Знак « — » минус в этом выражении означает, что, когда энергия магнитного поля возрастает, энергия электрического поля убывает и наоборот. Физический смысл этого выражения заключается в том, что скорость изменения энергии магнитного поля равна по модулю и противоположна по направлению скорости изменения электрического поля.

Электрический заряд и сила тока, при свободных колебаниях с течением времени изменяются по закону синуса или косинуса, то есть совершают гармонические колебания.

Циклическая частота для свободных электрических колебаний:

Период свободных колебаний в контуре равен:

Формула Томсона.

Период свободных электрических колебаний в колебательном контуре зависит от индуктивности катушки и емкости конденсатора.

Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание.

Частотой колебаний называется величина, обратная периоду колебаний:

Частоту свободных колебаний называют собственной частотой колебательной системы.

Заряд конденсатора изменяется по гармоническому закону:

где – амплитуда колебаний заряда. Сила тока также совершает гармонические колебания:

где – амплитуда колебаний силы тока. Колебания силы тока опережают по фазе колебания заряда на .

Разбор типовых тренировочных заданий

Задача 1. Идеальный колебательный контур состоит из конденсатора ёмкостью 2 мкФ и катушки индуктивности. В контуре происходят свободные электромагнитные колебания. В таблице приведена зависимость энергии W, запасённой в конденсаторе идеального колебательного контура, от времени t.

t, нс	0	125	250	375	500	625	750	875	1000
W, мкДж	0	3,66	12,5	21,34	25,0	21,34	12,5	3,66	0,00

t, нс	1125	1250	1375	1500	1625	1750	1875	2000	2125
W, мкДж	3,66	12,5	21,34	25,0	21,34	12,50	3,66	0,00	3,66

На основании анализа этой таблицы выберите два верных утверждения.

1) Период электромагнитных колебаний в контуре равен 1 мкс.

2) Период электромагнитных колебаний в контуре равен 2 мкс.

3) Индуктивность катушки равна примерно 13 нГн.

4) Максимальное напряжение на конденсаторе равно 5 В.

5) Максимальное напряжение на конденсаторе равно 50 кВ.

Решение. При электромагнитных колебаниях в контуре происходит периодическое превращение энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно, при этом максимальная энергия, запасенная в катушке, равна максимальной энергии, запасенной в конденсаторе

Период колебаний конденсатора равен 1000 нс, но период электромагнитных колебаний в контуре в два раза больше и составляет 2000 нс = 2 мкс.

Утверждение 2 — верно, утверждение 1 — неверно.

Воспользуемся формулой Томсона и выразим индуктивность катушки:

Утверждение 3 — неверно.

Максимальное напряжение на конденсаторе равно

Значение находим из таблицы =25 мкДж

Утверждение 4 верно, 5 — неверно

2. Емкость конденсатора колебательного контура С=1мкФ, индуктивность катушки L=0,04 Гн, амплитуда колебаний напряжения U_m=100 В.

В данный момент времени напряжение на конденсаторе u=80 В. Найти:

1. амплитуду колебаний силы тока I_m;

2. полную энергию W;

3. энергию электрического поля W_эл;

4. энергию магнитного поля W_м;

5. мгновенное значение силы тока i.

Дано:

С=1 мкФ=0,000001Ф

L=0,04 Гн

U_m=100 В

u=80 В

Найти: I_m; W; W_эл; W_м; i.

Решение

Из закона сохранения энергии максимальные энергии конденсатора и катушки индуктивности равны

Откуда

Полная энергия равна

Энергия электрического поля в момент, когда напряжение на конденсаторе

Из закона сохранения энергии выразим :

Мгновенное значение силы тока выразим из формулы:

Теорема физики (формула) и словесная формулировка математической записи: полная энергия Е электромагнитных колебаний колебательного контура в каждый момент времени равна сумме энергии электрического поля в конденсаторе и энергии магнитного поля катушки индуктивности в этот момент времени. Полная энергия равна максимальной энергии электрического поля E_Cmax (в момент, когда энергия магнитного поля катушки равна нулю) и максимальной энергии магнитного поля катушки E_Lmax (в момент, когда энергия электрического поля равна нулю).

(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8% qacaWGfbGaeyypa0Jaamyra8aadaWgaaWcbaGaamitaiGac2gacaGG% HbGaaiiEaaqabaGcpeGaaiilaiaadweapaWaaSbaaSqaa8qacaWGmb% aapaqabaGcdaWgaaWcbaWdbiaad2gacaWGHbGaamiEaaWdaeqaaOWd% biabg2da98aadaWcaaqaaiaadYeacaWGXbWaa0baaSqaaiaaicdaae% aacaaIYaaaaOGaeqyYdC3aaWbaaSqabeaacaaIYaaaaaGcbaGaaGOm% aaaapeGaaiilaiaacckacaWGfbGaeyypa0Jaamyra8aadaWgaaWcba% Gaai4qaiGac2gacaGGHbGaaiiEaaqabaGcpeGaaiilaiaadweapaWa% aSbaaSqaaiaadoeaaeqaaOWaaSbaaSqaa8qacaWGTbGaamyyaiaadI% haa8aabeaak8qacqGH9aqppaWaaSaaaeaacaWGXbWaa0baaSqaaiaa% icdaaeaacaaIYaaaaaGcbaGaaGOmaiaadoeaaaaaaa!5E23!E = {E_{Lmax }},{E_L}_{max} = frac{{Lq_0^2{omega ^2}}}{2},E = {E_{Cmax }},{E_C}_{max} = frac{{q_0^2}}{{2C}})

Здесь L – индуктивность катушки, q₀ – максимальный заряд конденсатора, ω – круговая частота электромагнитных колебаний контура, С – емкость конденсатора.

Доказательство теоремы (вывод формулы): значение электрической энергии колебательного контура, в котором совершаются гармонические колебания, в любой момент времени t равно

E_С(t)=(frac{{q_0^2{{cos }^2}(omega t + {phi _0})}}{{2C}})

Магнитная энергия контура, совершающего гармонические колебания, в любой момент времени t равна 

E_L(t)=(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca% WGmbGaamyCamaaDaaaleaacaaIWaaabaGaaGOmaaaakiabeM8a3naa% CaaaleqabaGaaGOmaaaakiGacohacaGGPbGaaiOBamaaCaaaleqaba% GaaGOmaaaakiaacIcacqaHjpWDcaWG0bGaey4kaSIaeqy1dy2aaSba% aSqaaiaaicdaaeqaaOGaaiykaaqaaiaaikdaaaaaaa!487A!frac{{Lq_0^2{omega ^2}{{sin }^2}(omega t + {phi _0})}}{2})

В области гармонических колебаний, когда омическое сопротивление пренебрежимо мало (R=0), энергетических потерь нет, и заряд на обкладках восстанавливается через каждый период полностью. Магнитная энергия переходит в электрическую, и наоборот, электрическая в магнитную. По закону сохранения энергии полная энергия контура не изменяется и в любой момент времени равна сумме электрической и магнитной энергий. Найдем эту сумму:

Е=E_С+E_L=(frac{{q_0^2{{cos }^2}(omega t + {phi _0})}}{{2C}} + frac{{Lq_0^2{omega ^2}{{sin }^2}(omega t + {phi _0})}}{2})

Заменяя величину ({omega ^2})на ее значение во втором слагаемом ({omega ^2} = frac{1}{{LC}}), получим 

Е=(frac{{q_0^2{{cos }^2}(omega t + {phi _0})}}{{2C}} + frac{{q_0^2{{sin }^2}(omega t + {phi _0})}}{{2C}} = frac{{q_0^2}}{{2C}}({cos ^2}(omega t + {phi _0}) + {sin ^2}(omega t + {phi _0}))) 

Выражение в скобках равно единице, поэтому (% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyraiabg2% da9maalaaabaGaamyCamaaDaaaleaacaaIWaaabaGaaGOmaaaaaOqa% aiaaikdacaWGdbaaaaaa!3BFD!E = frac{{q_0^2}}{{2C}})

Максимального значения электрическая энергия достигает в те моменты времени, когда косинус фазы принимает значения, равные единице, поэтому E_Смах =(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca% WGXbWaa0baaSqaaiaaicdaaeaacaaIYaaaaaGcbaGaaGOmaiaadoea% aaaaaa!3A2D!frac{{q_0^2}}{{2C}})

Магнитная энергия достигает максимального значения в те моменты времени, когда синус фазы принимает значения, равные единице, поэтому E_Lмах=(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca% WGmbGaamyCamaaDaaaleaacaaIWaaabaGaaGOmaaaakiabeM8a3naa% CaaaleqabaGaaGOmaaaaaOqaaiaaikdaaaaaaa!3CF6!frac{{Lq_0^2{omega ^2}}}{2}), но (% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyYdC3aaW% baaSqabeaacaaIYaaaaOGaeyypa0ZaaSaaaeaacaaIXaaabaGaamit% aiaadoeaaaaaaa!3C20!{omega ^2} = frac{1}{{LC}}) и E_{Lмах=(% MathType!MTEF!2!1!+-% feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca% WGXbWaa0baaSqaaiaaicdaaeaacaaIYaaaaaGcbaGaaGOmaiaadoea% aaaaaa!3A2D!frac{{q_0^2}}{{2C}})}

Максимальная электрическая энергия электромагнитного колебания равна максимальной магнитной энергии. Сравнивая полученные значения с выражением для полной энергии, как и положено по закону сохранения энергии, имеем равенство полной энергии в любой момент времени максимальным значениям кинетической и потенциальной энергий. В те моменты времени, когда кинетическая энергия максимальна, потенциальная минимальна и наоборот, так один вид энергии периодически полностью без потерь переходит в другой.

Теорема доказана.

Условия выполнения: выполняется в области упругих растяжений пружины для случая, когда массой пружины пренебрегают по сравнению с массой подвеса. Кроме того, пренебрегают процессами затухания колебаний.