Полная энергия колебаний, теория и онлайн калькуляторы
Полная энергия колебаний
Энергия колебаний пружинного маятника
Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника. Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:
[E=E_k+E_p=const left(1right).]
Проверим справедливость выражения (1),) непосредственным суммированием выражений для кинетической и потенциальной энергии рассматриваемого маятника.
Уравнение колебаний маятника запишем в виде:
[x=A{cos left({omega }_0t+varphi right)(2) },]
где $x$ — смещение груза маятника по оси X. В таком случае изменение кинетической энергии груза, совершающего колебания на напружине равна:
[E_k=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)left(3right). }]
Потенциальна энергия пружинного маятника равна: потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли:
[E_p=frac{kx^2}{2}=frac{k}{2}A^2{{cos}^2 left(щ_0t+цright) }left(4right).]
Суммируем правые части выражений (3) и (4), получим:
[E=frac{m}{2}A^2{щ_0}^2{{sin}^2 left(щ_0t+цright)+ }frac{k}{2}A^2{{cos}^2 left(щ_0t+цright) }=frac{k}{2}A^2=frac{1}{2}m{omega }^2_0A^2left(5right).]
где ${{omega }_0}^2=frac{k}{m}$.
Из формулы (5) мы видим, что неизменная суммарная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:
[v_x=pm {omega }_0Aleft(6right).]
В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $frac{E}{2}$ находятся в противофазе друг с другом, частота их колебаний равна $2{omega }_0$.
[{E_k =frac{E}{2}left[1-{cos 2({omega }_0t+varphi ) }right]left(7right). }]
[E_p=frac{E}{2}left[1+{cos 2({omega }_0t+varphi ) }right]left(8right).]
И так, выражения (7) и (8) показывают, что кинетическая и потенциальная энергии колебательной системы совершают гармонические колебания вокруг их общего значения $frac{E}{2}$ с удвоенной частотой 2${omega }_0$, тогда как полная энергия системы остается постоянной. Она связана с амплитудой колебаний как:
[E=frac{k}{2}A^2.]
Энергия колебательных систем с одной степенью свободы
Все, что сказано для пружинного маятника можно применить , для любых механических колебаний систем с одной степенью свободы. Мгновенное положение такой системы можно определить, используя один параметр, который называют обобщенной координатой ($q$), например, угла поворота или смещения по оси координат. При этом величина $dot{q}=frac{dq}{dt}$ называется обобщённой скоростью.
Потенциальная энергия в таких обозначениях примет вид:
[E_p=frac{alpha q^2}{2}left(9right),]
кинетическая энергия:
[E_p=frac{beta {dot{q}}^2}{2}left(10right),]
где $alpha , beta $ — параметры системы. Полная энергия системы в нашем случае равна:
[E=frac{alpha q^2}{2}+frac{beta {dot{q}}^2}{2}=const left(11right),]
обобщенная координата совершает гармонические колебания с частотой:
[{omega }_0=sqrt{frac{alpha }{beta }}left(12right).]
Примеры задач на полную энергию колебаний
Пример 1
Задание. Какова полная энергия колебаний материальной точки массы $m=0,02$ кг, если она совершает колебания по закону: $x=0,1{cos (2pi t+frac{pi }{3})(м) }?$ Потерь энергии в колебательной системе нет.
Решение. Полную энергию гармонических колебаний, которые описаны гармоническим законом $x(t)=0,1{cos (4pi t+frac{pi }{3})(м) }$, зная, что это постоянная величина найдем как:
[E=frac{1}{2}m{omega }^2_0A^2left(1.1right).]
Из уравнения колебаний $x(t)$ мы видим, что:
[{omega }_0=4pi frac{рад}{с};;A=0,1 м.]
Вычислим энергию:
[E=frac{1}{2}0,02cdot {left(4pi right)}^2{0,1}^2=1,58cdot {10}^{-2}left(Джright).]
Ответ. $E=1,58cdot {10}^{-2}$Дж.
Пример 2
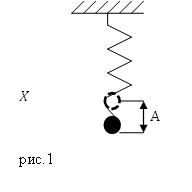
Задание. Груз на упругой пружине (рис.1) совершает колебания по оси X. Амплитуда колебаний равна $A=6cdot {10}^{-2}м$. Какова полная энергия колебаний груза, если коэффициент упругости пружины равен $k=500$ $frac{Н}{м}$? Считайте, что диссипации энергии в системе нет.
Решение. Колебания груза на упругой пружине можно считать гармоническими. По условию потерь энергии нет, следовательно, полная энергия нашего пружинного маятника сохраняется и является постоянной величиной, которую найдем как:
[E=frac{k}{2}A^2(2.1).]
Вычислим энергию системы:
[E=frac{500}{2}{(6cdot {10}^{-2})}^2=0,9 (Дж).]
Ответ. $E=0,9Дж$
Читать дальше: понятие силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Полная энергия — материальная точка
Cтраница 1
Полная энергия материальной точки, совершающей простое гармоническое колебание под влиянием упругих сил, все время остается постоянною. Не трудно доказать, что сумма кинетической и потенциальной энергии в каждое мгновение всегда равна наибольшему значению кинетической энергии, которое точка получает, когда она проходит через положение равновесия ( Р0) и когда вся ее энергия является лишь в форме кинетической.
[1]
Ее называют полной энергией материальной точки.
[2]
Мы уже знаем, что полная энергия материальной точки, движущейся в постоянном во времени поле консервативных сил, не изменяется. Но силовое поле создается какими-то телами. Для того чтобы поле было постоянным во времени, эти тела должны быть неподвижными.
[3]
Получим формальное соотношение, определяющее изменение полной энергии материальной точки из-за действия на нее неконсервативных сил.
[4]
Следовательно, Е Еа — — Т — полная энергия материальной точки в данной системе отсчета складывается из ее энергии покоя и кинетической энергии.
[5]
Следовательно, эта работа равна ( положительному или отрицательному) приращению полной энергии материальной точки. В некоторых случаях этот результат бывает удобнее выразить следующим образом: работа силы реакции, действующей на точку, равна уменьшению полной энергии точки.
[6]
Величина Е, равная сумме кинетической и потенциальной энергий, называется полной энергией материальной точки. Полученная формула (6.11) является математическим выражением закона сохранения энергии в механике.
[7]
Величина Е, равная сумме кинетической и потенциальной энергий, называется полной энергией материальной точки. Полученная формула (6.11) является математическим выражением закона сохранения эиергиив механике.
[8]
Величина Е, равная сумме кинетической и потенциальной энергий, называется полной энергией материальной точки. Полученная формула (6.11) является математическим выражением закона сохранения энергиив механике.
[9]
Одним из фундаментальных законов физики является закон сохранения энергии, в соответствии с которым полная энергия материальной точки, движущейся в гравитационном поле Земли, должна оставаться постоянной.
[10]
О таком движении говорят иногда, как о движении в постоянном силовом поле, понимая под словом поле пространство, каждой точке которого соответствует вектор действующей в пространстве силы. Если условие постоянства силового поля не выполняется, полная энергия материальной точки, вообще говоря, не сохраняется. С одним из таких примеров мы имели дело в предыдущей главе, когда рассматривали явление резонанса, возникающего при колебаниях тела, на которое помимо упругой силы действует еще внешняя вынуждающая сила. Полная энергия в этом случае растет с ростом амплитуды вынужденных колебаний.
[11]
Всякое состояние движения точки ( характеризуемое ее скоростью и положением) можно рассматривать как одаренное двумя формами энергии — кинетической и потенциальной. Самое движение в этом свете представляется как явление преобразования кинетической энергии в потенциальную, и обратно; но общее количество Е энергии постоянно остается неизменным, поскольку энергия данной точки не поглощается извне и не выделяется вс-вне. Таким образом название полной энергии материальной точки, которое обыкновенно присваивается постоянной Е, представляется вполне оправданным. Ее называют также постоянной живой силы, как говорили механики старого времени, когда вся физика еще не была проникнута общей идеей об энергии.
[12]
Материальная точка, помещенная в действующем на нее поле, например в электрическом, магнитном или гравитационном, обладает потенциальной энергией, вызванной полем и зависящей от положения точки в поле. Потенциальная энергия материальной точки равна работе, которая должна быть проделана некоторой внешней силой ( предполагается, что эта сила способна захватывать и удерживать точку), чтобы перенести ее из места, находящегося вне поля ( обычно на бесконечно удаленном расстоянии), в данную точку поля, не сообщая ей при этом кинетической энергии. Если поле отталкивает материальную точку, то потенциальная энергия положительна. Полная энергия материальной точки, движущейся в поле без каких-либо ограничений или воздействий сил, равна алгебраической сумме кинетической и потенциальной энергий.
[13]
Страницы:
1
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергии.
Полную механическую энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остаётся постоянной.
Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движению, тогда полная механическая энергия тела остаётся неизменной во времени.
Eпот+Eкин=const
Разумеется, что в повседневной жизни не существует идеальной ситуации, в которой тело полностью сохраняло бы свою энергию, так как любое тело вокруг нас взаимодействует хотя бы с молекулами воздуха и сталкивается с сопротивлением воздуха. Но, если сила сопротивления очень мала и движение рассматривается в относительно коротком промежутке времени, тогда такую ситуацию можно приближённо считать теоретически идеальной.
Закон сохранения полной механической энергии обычно применяют при рассмотрении свободного падения тела, при его вертикальном подбрасывании или в случае колебаний тела.
Пример:
При вертикальном подбрасывании тела его полная механическая энергия не меняется, а кинетическая энергия тела переходит в потенциальную и наоборот.
Преобразование энергии отображено на рисунке и в таблице.
|
Точка нахождения тела |
Потенциальная энергия |
Кинетическая энергия |
Полная механическая энергия |
|
3) Самая верхняя (h = max) |
Eпот
= m⋅g⋅h (max) |
Eкин
= 0 |
Eполная
= m⋅g⋅h |
|
2) Средняя (h = средняя) |
Eпот
= m⋅g⋅h |
Eкин
= m⋅v22 |
Eполная
= m⋅v22 + m⋅g⋅h |
|
1) Самая нижняя (h = 0) |
Eпот
= 0 |
Eкин
= m⋅v22 (max) |
Eполная
= m⋅v22 |
Исходя из того, что в начале движения величина кинетической энергии тела одинакова с величиной его потенциальной энергии в верхней точке траектории движения, для расчётов могут быть использованы ещё две формулы.
Если известна максимальная высота, на которую поднимается тело, тогда можно определить максимальную скорость движения по формуле:
Если известна максимальная скорость движения тела, тогда можно определить максимальную высоту, на которую поднимается тело, брошенное вверх, по такой формуле:
Чтобы отобразить преобразование энергии графически, можно использовать имитацию «Энергия в скейт-парке», в которой человек, катающийся на роликовой доске (скейтер) перемещается по рампе. Чтобы изобразить идеальный случай, предполагается, что не происходит потерь энергии в связи с трением. На рисунке показана рампа со скейтером, и далее на графике показана зависимость механической энергии от места положения скейтера на траектории.
На графике синей пунктирной линией показано изменение потенциальной энергии. В средней точке рампы потенциальная энергия равна (нулю). Зелёной пунктирной линией показано изменение кинетической энергии. В верхних точках рампы кинетическая энергия равна (нулю). Жёлто-зелёная линия изображает полную механическую энергию — сумму потенциальной и кинетической — в каждый момент движения и в каждой точке траектории. Как видно, она остаётся (неизменной) во всё время движения. Частота точек характеризует скорость движения — чем дальше точки расположены друг от друга, тем больше скорость движения.
На графике видно, что значение потенциальной энергии в начальной точке совпадает со значением кинетической энергии в середине рампы.
В реальной ситуации всегда происходят потери энергии, так как часть энергии выделяется в виде тепла под влиянием сил трения и сопротивления.
Поэтому для того, чтобы автомобиль двигался с равномерной и неизменной скоростью, необходимо постоянно подводить дополнительную энергию, которая компенсировала бы энергетические потери.
Скорость колеблющейся точки –
это первая производная от смещения
точки по времени (за основу возьмем
второе из пары уравнений (1.1)):
.
(1.4)
Здесь max
= Aω0—максимальнаяскорость,илиамплитуда скорости.
Ускорение – это втоpая пpоизводная
от смещения точки по времени:
(1.5)
где amax = Aω02
—максимальное ускорение,илиамплитуда ускорения.
Из формул (1.1), (1.4) и (1.5) видно, что смещение,
скорость и ускорение не совпадают
по фазе (pис. 1.2). В моменты вpемени,
когда смещение максимально, скоpость
pавна нулю, а ускоpение пpинимает
максимальное отpицательное значение.
Смещение и ускоpение находятся впpотивофазе— так говоpят, когда
pазность фаз pавна.
Ускоpение всегда напpавлено в стоpону,
пpотивоположную смещению.
Полная энергия колебаний равна
сумме кинетической и потенциальной
энеpгий колеблющейся точки:
W = Wк
+ Wп = m
2 / 2 + kx2 /
2.
Подставим в это выражение формулы (1.4)
и (1.1) с учетом k = mω02(как будет показано ниже), получим
W = k A2
/ 2 =m A2 ω02
/2. (1.6)
Из сопоставления графиков функций
х(t), Wк(t)
и Wп(t)
(рис.1.3) видно, что частота колебаний
энергии в два раза больше частоты
колебаний смещения.
Рис. 1.2
Рис.
1.3
Cреднее значение
потенциальной и кинетической энергии
за периодТравно половине полной
энергии (рис. 1.3):
П р и м е р 1. Материальная точка
массой 5 г совершает колебания согласно
уравнению
гдеx – смещение, см.
Определить максимальную силу и полную
энергию.
Р е ш е н и е. Максимальная сила
выражается формулойгде
(см. формулу (1.5)). ТогдаFmax=mAω02.
Из уравнения колебания следует, чтоПодставим числовые значения:Fmax=5∙10-3
0,1∙4 = 2∙10-3Н = 2мН.
Полная энергия
В итогеE= 0,5∙5∙10-3∙4∙10-2= 10-4Дж.
1.3. Диффеpенциальное
уpавнение
Свободных незатухающих колебаний. Маятники
Система, состоящая из тела массой m,
подвешенного к пружине, второй конец
которой закреплён, называютпружинным
маятником(рис. 1.4). Такая система
служит модельюлинейного осциллятора.
Если растянуть (сжать) пружину на величину
х, то возникнет упругая сила, которая
стремится вернуть тело в положение
равновесия. При небольших деформациях
справедлив закон Гука:F = — kx, гдеk— коэффициент жесткости пpужины. Запишем
второй закон Ньютона:

Знак «минус» означает, что сила
упругости направлена в сторону,
противоположную смещению x.Подставим в это уpавнение ускоpениеaколеблющейся точки из уpавнения (1.5),
получим
— m ω02 x = —
k x,
откудаk = m ω02, Пеpиод колебаний
(1.8)
Таким образом, период колебаний не
зависит от амплитуды.
П р и м е р 2. Под действием силы
тяжести груза пружина растянулась на
5 см. После вывода ее из состояния покоя
груз совершает гармонические колебания.
Определить период этих колебаний.
Р е ш е н и е. Период колебаний
пружинного маятника находим по формуле
(1.8). Коэффициент жесткости пружины
рассчитаем по закону Гука, исходя из
того, что пружина растягивается под
действием силы тяжести:mg
= — kx, откуда модульk = mg/x.
Подставимkв формулу
(1.8):
Выполним вычисления и вывод единицы
измерения:
Из формулы (1.7) следует дифференциальное
уравнение гармонических колебаний:
или
Заменив отношение k/m = ω02
, получимдифференциальное уравнениесобственных незатухающих колебаний в
виде
(1.9)
Его решениями являются выражения (1.1).
П р и м е р 3. Дифференциальное
уравнение незатухающих гармонических
колебаний имеет вид.
Найти частоту и период этих колебаний.
Р е ш е н и е. Запишем уравнение в
виде:.
О
следует, чтоа
Период колебаний определяется по
формуле:Следовательно,Т= 2∙3,14/2 = 3,14 с.
Физическим маятникомназывают
твёрдое тело, которое совершает колебания
под действием силы тяжести вокруг
неподвижной горизонтальной оси (рис.
1.5), проходящей через точкуО, не
совпадающую с центром массС тела.
Момент силы тяжести mgотносительно
оси вращенияО
,
где
—
длина физическогомаятника(pасстояние от точки подвеса до центpа
масс маятника
= OC).
По основному закону динамики вpащательного
движения I
= M,
ЗдесьI– момент
инерции маятника относительно оси,
проходящей через точку подвесаО,
— угловое ускорение.
Для малых отклонений sin = ,
тогда
(1.10)
Из сравнения уравнений (1.9) и (1.10) следует,
что
и пеpиод колебаний
(1.11)
М
маятникпредставляет
собой материальную точку массойm,
подвешенную на абсолютно упругой
нерастяжимой нити и совершающую
колебания под действием силы тяжести
(рис. 1.6).
В формулу (1.11) подставим момент инерции
материальной точки относительно оси,
проходящей через точку подвеса,
,
получим
Рис. 1.6
. (1.12)
Из выражений (1.11) и (1.12) следует, что
физический маятник имеет такой же период
колебаний, как и математический с длиной
.
Эту величину называют приведённой длинойфизического маятника.
Отметим, чтоI— момент
инеpцииотносительнооси, пpоходящей
чеpез точку подвесаO. По теоpеме
Штейнеpа
где IC
— момент инеpцииотносительно
оси,пpоходящей чеpез центp массмаятника. Пpедставим пpиведенную длину
маятника в виде
откуда видно, что пpиведенная длина
физического маятника больше его длины
Если от точки подвеса О отложить(см. рис. 1.5), то найдём точкуО1,
которая называетсяцентром качания.
Точка подвеса и центр качания являются
сопряженными. Это значит, что маятник,
подвешенный за центр качанияО1,
не изменит периода колебаний, а точкаOсделается новым центром качания.
П р и м е р 4. Однородный стержень
длинойb совершает
колебания в вертикальной плоскости
вокруг оси, проходящей через один из
его концов (рис.1.7). Определить период
колебаний.
Р
для определения периода колебаний
физического маятника (1.11), гдеℓ=ОС– расстояние от оси вращения до
центра масс. Это расстояниеℓ=b/2
(рис. 1.7). Момент инерции стержня
относительно его концаI=1/3mb2. Следовательно,
Сила, возвpащающая маятник в положение
pавновесия (рис. 1.6),
т. е. пpопоpциональна смещениюx, но
эта сила не упpугая по своей пpиpоде,
поэтому она называетсяквазиупругой.
Таким образом, механические гармонические
колебания возникают в системах под
действием сил, пропорциональных смещению.
Сергей Феликсович Савельев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Понятие энергии для физики является базовым. Нам известно, что закон сохранения энергии – это фундаментальный закон природы. Он служит основанием для пояснения множества явлений механики, термодинамики, электричества и других физических разделов.
Понятие энергии используется при исследовании задач техники, поскольку самая важная техническая проблема – это проблема генерации, передачи и использования энергии.
Механической энергией считают сумму потенциальной и кинетической энергии. Это энергия, которую связывают с перемещением тел, их расположением, возможностью выполнять работу, взаимодействовать.
Полная энергия тела
Самое общее понятие энергии получают из представлений теории относительности Эйнштейна.
Определение 1
Полной энергией тела ($E$) называют физическую величину, равную произведению релятивистской массы тела ($m$) на скорость света ($c$) в квадрате:
$E=mc^2 (1),$
где $m=frac{m_0}{sqrt{1-frac{v^2}{c^2}}}(2)$; $ c=3cdot 10^8$ м/c.
Определение (1) указывает на то, что полная энергия тела зависит от выбора системы отсчета. Она связана со скоростью перемещения тела относительно избранной системы отсчета, так как со скоростью связана масса $m$ тела (см. выражение (2)).
Минимальную энергию имеет тело в той системе отсчета, по отношению к которой оно покоится.
Определение 2
Энергию тела называют энергией покоя ($E_0$), если относительно рассматриваемо системы отсчета тело находится в покое.
$E_0=m_0c^2 (3).$
Кинетическая энергия
Кинетическую энергию тела можно определить как разность полной энергии и энергии покоя тела:
$E_k=E-E_0 (4).$
Кинетическая энергия зависит от скорости перемещения тела по отношению к избранной системе отсчета.
Принимая во внимание выражение (2), формулу (4) преобразуем к виду:
$E_k=mc^2(1-sqrt{1-frac{v^2}{c^2}})(5).$
Умножим и разделим выражение (5) на $1+sqrt{1-frac{v^2}{c^2}}$, получаем:
«Механическая энергия, полная механическая энергия» 👇
$E_k=frac{mv^2}{1+sqrt{1-frac{v^2}{c^2}}}=frac{p^2}{m(1+sqrt{1-frac{v^2}{c^2}})}(6).$
Кинетическая энергия в классической механике
В классической механике тела перемещаются со скоростями много меньшими, чем скорость света в вакууме, что означает величиной $frac{v^2}{c^2}$ можно пренебречь в сравнении с единицей, то есть имеем:
$sqrt{1-frac{v^2}{c^2}}approx 1$,
в этом случае для вычисления кинетической энергии мы имеем простую формулу:
$E_k=frac{mv^2}{2}=frac{p^2}{2m}(7),$
где $p$ — импульс тела.
Выражение (7) является приближенным, однако, при скоростях с которыми мы имеем дело в обыденной жизни, она дает достаточную точность. Даже, если скорость тела будет несколько сотен метров в секунду, результаты вычисления кинетической энергии при помощи формулы (7) отличны от точных (формула (6)) меньше, чем на десятитысячную часть процента.
Если скорость тела значительно меньше скорости света, кинетическая энергия будет существенно меньше энергии покоя:
$frac{E_k}{E_0}=frac{v^2}{2c^2}ll 1.$
Если тело будет обладать скоростью близкой к скорости света, то почти вся энергия будет равна кинетической энергии тела, то есть энергия покоя станет существенно меньше энергии движения. Например, в синхрофазотронах протоны разгоняют до скоростей примерно равных $v=0,9995c$, в этом случае имеем:
$frac{E_k}{E_0}=frac {(m-m_0)c^2}{m_0c^2}approx 30$.
Кинетическая энергия протонов в синхрофазотроне в 30 раз больше энергии их покоя.
Для ультра релятивистских скоростей можно считать, что:
$E_kapprox E=mc^2 (8).$
Кинетическая энергия – это часть полной энергии тела, которая связана с его движением.
Изменение кинетической энергии будет равно работе ($A$), которую выполняют силы, которые действуют на тело:
$Delta E_k=A (9).$
Потенциальная энергия
При описании взаимодействия тел при помощи сил в истории использовались две концепции:
- В первой, все взаимодействия считали контактными, реализующимися при непосредственном соприкосновении тел.
- Второй, была концепция дальнодействия (действия на расстоянии). Сторонником этой концепции был Ньютон.
Обе концепции присутствовали в науке достаточно долгое время. Для описания гравитационного взаимодействия с позиций близкодействия было введено понятие поля силы. При помощи понятия силового поля, взаимодействие тел на расстоянии определяется так:
- Одно из тел изменяет свойства пространства вокруг себя, оно создает поле.
- Второе тело «ощущает» данное изменение пространственных свойств, то есть получает со стороны силового поля некоторое воздействие, в месте своего нахождения.
- Силовое поле играет роль переносчика взаимодействия.
- Второе поле воздействует на первое по аналогии.
Все фундаментальные взаимодействия обладают полевой природой. Силовые поля — это векторные поля. Их делят на потенциальные и непотенциальные.
Определение 3
Потенциальным полем называют силовое поле, которое выражается при помощи скалярной потенциальной функции ($U(x,y,z,t)$), зависящей от пространственных координат и времени. Данную функцию называют потенциальной. При этом сила, оказывающая воздействие на частицу и потенциальная функция связаны соотношением:
$vec F(x,y,z,t)=-(frac{partial U(x,y,z,t)}{partial x}vec i+frac{partial U(x,y,z,t)}{partial y}vec j+frac{partial U(x,y,z,t)}{partial y}vec k)=-grad U (9)$.
Градиент скалярной функции – это вектор, который направлен в сторону наиболее быстрого увеличения данной функции, равный по величине скорости ее увеличения в этом направлении. Знак минус в формуле (9) показывает то, что сила имеет направление в сторону наиболее быстрого уменьшения функции $U$.
Частным случаем потенциальных полей являются поля, которые не зависят в явном виде от времени. Такие поля именуют консервативными. Для консервативных полей $U=U(x,y,z)$.
Иначе говорят, что тело (частица) находится состоянии стационарных внешних условий, например, в постоянном поле гравитации. В этом случае потенциальную функцию $U$ называют потенциальной энергией частицы во внешнем консервативном поле.
Обозначим потенциальную энергию как $E_p$, в таком случае выполняется равенство:
$vec F=- grad E_p (x,y,z)(10).$
Работа консервативной силы равна изменению потенциальной энергии материальной точки с противоположным знаком, и она не зависит от траектории по которой совершает перемещение частица.
Полная механическая энергия
В общем случае тело обладает и кинетической и потенциальной энергиями одновременно. Сумма данных энергий составляет полную механическую энергию.
Полной механической энергией называют физическую величину, равную:
$E_p+E_k=E (11).$
Изменение полной механической энергии материальной точки, которая находится в поле консервативных сил, равно работе, которую выполняют эти силы, оказывающие воздействие на частицу:
$E_2-E_1=A_{12} (12).$
Потенциальная и кинетическая энергия способны переходить друг в друга.
Полная механическая энергия системы тел, внутри которой действуют исключительно консервативные силы, складывается из потенциальной энергии системы, как единого целого и суммы кинетических энергий, входящих в нее тел.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме