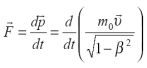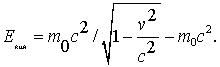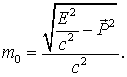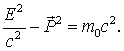Как найти полную энергию релятивистской частицы - Исправление недочетов и поиск решений вместе с Examum.ru

Релятивистская динамика

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: полная энергия, связь массы и энергии, энергия покоя.

В классической динамике мы начали с законов Ньютона, потом перешли к импульсу, а после него — к энергии. Здесь мы ради простоты изложения поступим ровно наоборот: начнём с энергии, затем перейдём к импульсу и закончим релятивистским уравнением движения — модификацией второго закона Ньютона для теории относительности.

Релятивистская энергия

Предположим, что изолированное тело массы покоится в данной системе отсчёта. Одно из самых впечатляющих достижений теории относительности — это знаменитая формула Эйнштейна:

$E=mc^{2}$ (1)

Здесь — энергия тела, — скорость света в вакууме. Поскольку тело покоится, энергия , вычиляемая по формуле (1), называется энергией покоя.

Формула (1) утверждает, что каждое тело само по себе обладает энергией — просто потому, что оно существует в природе. Образно говоря, природа затратила определённые усилия на то, чтобы «собрать» данное тело из мельчайших частиц вещества, и мерой этих усилий служит энергия покоя тела. Энергия эта весьма велика; так, в одном килограмме вещества заключена энергия

$E=1cdot (3cdot 10^{8})^{2}=9cdot 10^{16}$ Дж.

Интересно, какое количество топлива нужно сжечь, чтобы выделилось столько энергии? Возьмём, например, дерево. Его удельная теплота сгорания равна $q=10^{7}$ Дж/кг, поэтому находим: $m= E/q= 9cdot 10^{9}$ кг. Это девять миллионов тонн!

Ещё для сравнения: такую энергию единая энергосистема России вырабатывает примерно за десять дней.

Почему столь грандиозная энергия, содержащаяся в теле, до сих пор оставалась нами незамеченной? Почему в нерелятивистских задачах, связанных с сохранением и превращением энергии, мы не учитывали энергию покоя? Скоро мы ответим на этот вопрос.

Поскольку энергия покоя тела прямо пропорциональна его массе, изменение энергии покоя на величину Delta E приводит к изменению массы тела на

$Delta m= frac{Delta displaystyle E}{displaystyle c^{displaystyle 2}}$ .

Так, при нагревании тела возрастает его внутренняя энергия, и, стало быть, масса тела увеличивается! В повседневной жизни мы не замечаем этого эффекта ввиду его чрезвычайной малости. Например, для нагревания воды массой m= 1 кг на $Delta t= 100^{circ}C$ (удельная теплоёмкость воды равна $c_{b}= 4200 J/(kgcdot^{circ}C)$ ) ей нужно передать количество теплоты:

$Q= c_{b}mDelta t= 4,2cdot 10^{5}$ Дж.

Увеличение массы воды будет равно:

$Delta m= frac{Q}{c^{2}}= frac{4,2cdot 10^{5}}{9cdot 10^{16}}approx 4,7cdot 10^{-12}$ кг.

Столь ничтожное изменение массы невозможно заметить на фоне погрешностей измерительных приборов.

Формула ( 1) даёт энергию покоящегося тела. Что изменится, если тело движется?

Снова рассмотрим неподвижную систему отсчёта и систему {K} , движущуюся относительно со скоростью upsilon . Пусть тело массы покоится в системе {K} ; тогда энергия тела в системе {K} есть энергия покоя, вычисляемая по формуле ( 1). Оказывается, при переходе в систему энергия преобразуется так же, как и время — а именно, энергия тела в системе , в которой тело движется со скоростью upsilon , равна:

$E= frac{mc^{2}}{sqrt{displaystyle 1-frac{upsilon ^{displaystyle 2}}{c^{displaystyle 2}}}}$ ( 2)

Формула ( 2) была также установлена Эйнштейном. Величина — это полная энергия движущегося тела. Поскольку в данной формуле $mc^{2}$ делится на «релятивистский корень», меньший единицы, полная энергия движущегося тела превышает энергию покоя. Полная энергия будет равна энергии покоя только при .

Выражение для полной энергии ( 2) позволяет сделать важные выводы о возможных скоростях движения объектов в природе.

1. Каждое массивное тело обладает определённой энергией, поэтому необходимо выполнение неравенства

$1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}> 0$ .

Оно означает, что : скорость массивного тела всегда меньше скорости света.

2. В природе существуют безмассовые частицы (например, фотоны), несущие энергию. При подстановке m= 0 в формулу ( 2) её числитель обращается в нуль. Но энергия-то фотона ненулевая!

Единственный способ избежать здесь противоречия — это принять, что безмассовая частица обязана двигаться со скоростью света. Тогда и знаменатель нашей формулы обратится в нуль, так что формула ( 2) попросту откажет. Нахождение формул для энергии безмассовых частиц не входит в компетенцию теории относительности. Так, выражение для энергии фотона устанавливается в квантовой физике.

Интуитивно чувствуется, что полная энергия ( 2) состоит из энергии покоя и собственно «энергии движения», т. е. кинетической энергии тела. При малых скоростях движения это показывается явным образом. Используем приближённые формулы, справедливые при :

$sqrt{1-alpha }approx 1-frac{alpha }{2}$ ( 3)
$frac{1}{1-alpha }approx 1+alpha$ ( 4)

С помощью этих формул последовательно получаем из ( 2):

$E= frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}approx frac{displaystyle mc^{displaystyle 2}}{1-frac{displaystyle 1}{displaystyle 2}frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}approx mc^{2}(1+frac{displaystyle 1}{displaystyle 2}frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}})= mc^{2}+frac{displaystyle mupsilon ^{displaystyle 2}}{displaystyle 2}$ ( 5)

Таким образом, при малых скоростях движения полная энергия сводится просто к сумме энергия покоя и кинетической энергии. Это служит мотивировкой для определения понятия кинетической энергии в теории относительности:

$E_{K}=frac{mc^{2}}{sqrt{1-frac{upsilon ^{2}}{c^{2}}}}-mc^{2}$ . ( 6)

При формула ( 6) переходит в нерелятивистское выражение $E_{K}= mupsilon ^{2}/2$ .

Теперь мы можем ответить на заданный выше вопрос о том, почему до сих пор не учитывалась энергия покоя в нерелятивистских энергетических соотношениях. Как видно из ( 5), при малых скоростях движения энергия покоя входит в полную энергию в качестве слагаемого. В задачах, например, механики и термодинамики изменения энергии тел составляют максимум несколько миллионов джоулей; эти изменения столь незначительны по сравнению с энергиями покоя рассматриваемых тел, что приводят к микроскопическим изменениям их масс. Поэтому с высокой точностью можно считать, что суммарная масса тел не меняется в ходе механических или тепловых процессов. В результате суммы энергий покоя тел в начале и в конце процесса попросту сокращаются в обеих частях закона сохранения энергии!

Но такое бывает не всегда. В других физических ситуациях изменения энергии тел могут приводить к более заметным изменениям суммарной массы. Мы увидим, например, что в ядерных реакциях отличия масс исходных и конечных продуктов обычно составляют доли процента.Скажем, при распаде ядра урана $_{92}^{235}{cup }$ суммарная масса продуктов распада примерно на 0,1% меньше массы исходного ядра. Эта одна тысячная доля массы ядра высвобождается в виде энергии, которая при взрыве атомной бомбы способна уничтожить город.

При неупругом столкновении часть кинетической энергии тел переходит в их внутренюю энергию. Релятивистский закон сохранения полной энергии учитывает этот факт: суммарная масса тел после столкновения увеличивается!

Рассмотрим в качестве примера два тела массы , летящих навстречу друг другу с одинаковой скоростью 3c/5 . В результате неупругого столкновения образуется тело массы , скорость которого равна нулю по закону сохранения импульса (об этом законе речь впереди). Согласно закону сохранения энергии получаем:

$frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-frac{(displaystyle 3c/5)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}+frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-frac{(displaystyle 3c/5)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= Mc^{2}$ ,

$2cdot frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-(frac{displaystyle 3}{displaystyle 5})^{displaystyle 2}}}= Mc^{2}$ ,

$frac{displaystyle 2m}{displaystyle 4/5}= M$ ,

$M= frac{displaystyle 5}{displaystyle 2}m$ .

Мы видим, что, M> 2m — масса образовавшегося тела превышает сумму масс тел до столкновения. Избыток массы, равный m/2 , возник за счёт перехода кинетической энергии сталкивающихся тел во внутреннюю энергию.

Релятивистский импульс.

Классическое выражение для импульса не годится в теории относительности — оно, в частности, не согласуется с релятивистским законом сложения скоростей. Давайте убедимся в этом на следующем простом примере.

Пусть система {K} движется относительно системы со скоростью v = c/2 (рис. 1). Два тела массы в системе {K} летят навстречу друг другу с одинаковой скоростью {u} . Происходит неупругое столкновение.

Рис. 1. К закону сохранения импульса

В системе {K} тела после столкновения останавливаются. Давайте, как и выше, найдём массу образовавшегося тела:

$Mc^{2}= 2frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-frac{(displaystyle c/2)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= frac{displaystyle 2mc^{displaystyle 2}}{sqrt{displaystyle 1-(frac{displaystyle 1}{displaystyle 4})^{displaystyle 2}}}= frac{displaystyle 4mc^{displaystyle 2}}{sqrt{displaystyle 3}}$ ,

откуда

$M= frac{displaystyle 4m}{sqrt{displaystyle 3}}$ .

Теперь посмотрим на процесс столкновения с точки зрения системы . До столкновения левое тело имеет скорость:

$u_{1}= frac{displaystyle upsilon +{displaystyle u}$ .

Правое тело имеет скорость:

$u_{2}= frac{displaystyle upsilon -{displaystyle u}$ .

Нерелятивистский импульс нашей системы до столкновения равен:

$mu_{1}-mu_{2}= frac{displaystyle 4mc}{displaystyle 5}$ .

После столкновения получившееся тело массы двигается со скоростью .
Его нерелятивистский импульс равен:

$Mupsilon = frac{displaystyle 4m}{sqrt{displaystyle 3}}frac{displaystyle c}{displaystyle 2}= frac{displaystyle 2m}{sqrt{displaystyle 3}}$ .

Как видим, $mu_{1}-mu_{2}neq Mupsilon$ , то есть нерелятивистский импульс не сохраняется.

Оказывается, правильное выражение для импульса в теории относительности получается делением классического выражения на «релятивистский корень»: импульс тела массы , двигающегося со скоростью , равен:

$vec{p}= frac{displaystyle mvec{displaystyle upsilon }}{sqrt{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}$ . 7

Давайте вернёмся к только что рассмотренному примеру и убедимся, что теперь с законом сохранения импульса всё будет в порядке.

Импульс системы до столкновения:

$p_{before}= frac{displaystyle mu_{displaystyle 1}}{sqrt{displaystyle 1-frac{displaystyle u_{displaystyle 1}^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}- frac{displaystyle mu_{displaystyle 2}}{sqrt{displaystyle 1-frac{displaystyle u_{displaystyle 2}^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= frac{displaystyle m(displaystyle 4c/5)}{displaystyle sqrt{displaystyle 1-frac{(displaystyle 4c/5)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}-0= frac{displaystyle 4mc/5}{displaystyle 3/5}= frac{displaystyle 4mc}{displaystyle 3}$ .

Импульс после столкновения:

$p_{after}= frac{displaystyle displaystyle Mupsilon }{sqrt{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= frac{displaystyle Mc/2}{sqrt{displaystyle 1-frac{(displaystyle c/2)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}=( frac{displaystyle 4m/sqrt{displaystyle 3})(displaystyle c/2)}{sqrt{displaystyle 3/2}}= frac{displaystyle 4mc}{displaystyle 3}$

Вот теперь всё правильно: $p_{before}= p_{after}$ !

Связь энергии и импульса.

Из формул ( 2) и ( 7) можно получить замечательное соотношение между энергией и импульсом в теории относительности. Возводим обе части этих формул в квадрат:

$E^{2}= frac{displaystyle m^{displaystyle 2}c^{displaystyle 4}}{1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}$ , $p^{2}= frac{displaystyle m^{displaystyle 2}upsilon ^{displaystyle 2}}{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}$

Преобразуем разность:

$E^{2}-p^{2}c^{2}= frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 4}}{1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}-frac{displaystyle m^{displaystyle 2}upsilon ^{displaystyle 2}c^{displaystyle 2}}{1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}= frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}(displaystyle c^{displaystyle 2}-displaystyle upsilon ^{displaystyle 2})}{frac{displaystyle c^{displaystyle 2}-displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}= m^{2}c^{4}$

Это и есть искомое соотношение:

$E^{2}-p^{2}c^{2}= m^{2}c^{4}$ . ( 8)

Данная формула позволяет выявить простую связь между энергией и импульсом фотона. Фотон имеет нулевую массу и движется со скоростью света. Как уже было замечено выше, сами по себе энергия и импульс фотона в СТО найдены быть не могут: при подстановке в формулы ( 2) и ( 7) значений m=0 и мы получим нули в числителе и знаменателе. Но зато с помощью ( 8) легко находим: $E^{2}-p^{2}c^{2}= 0$ , или

E= pc ( 9)

В квантовой физике устанавливается выражение для энергии фотона, после чего с помощью формулы ( 9) находится его импульс.

Релятивистское уравнение движения.

Рассмотрим тело массы , движущееся вдоль оси под действием силы . Уравнение движения тела в классической механике — это второй закон Ньютона: ma= F . Если за бесконечно малое время приращение скорости тела равно , то , и уравнение движения запишется в виде:

$mfrac{displaystyle dupsilon }{displaystyle dt}= F$ . ( 10)

Теперь заметим, что — изменение нерелятивистского импульса тела. В результате получим «импульсную» форму записи второго закона Ньютона — производная импульса тела по времени равна силе, приложенной к телу:

$frac{dp}{dt}= F$ . ( 11)

Все эти вещи вам знакомы, но повторить никогда не помешает

Классическое уравнение движения — второй закон Ньютона — является инвариантным относительно преобразований Галилея, которые в классической механике описывают переход из одной инерциальной системы отсчёта в другую (это означает, напомним, что при указанном переходе второй закон Ньютона сохраняет свой вид). Однако в СТО переход между инерциальными системами отсчёта описывается преобразованиями Лоренца, а относительно них второй закон Ньютона уже не является инвариантным. Следовательно, классическое уравнение движения должно быть заменено релятивистским, которое сохраняет свой вид под действием преобразований Лоренца.

То, что второй закон Ньютона ( 10) не может быть верным в СТО, хорошо видно на следующем простом примере. Допустим, что к телу приложена постоянная сила. Тогда согласно классической механике тело будет двигаться с постоянным ускорением; скорость тела будет линейно возрастать и с течением времени превысит скорость света. Но мы знаем, что на самом
деле это невозможно.

Правильное уравнение движения в теории относительности оказывается совсем не сложным.
Релятивистское уравнение движения имеет вид ( 11), где p — релятивистский импульс:

$frac{displaystyle d(frac{displaystyle mupsilon }{sqrt{displaystyle 1-upsilon ^{displaystyle 2}/displaystyle c^{displaystyle 2}}})}{displaystyle dt}= F$ . ( 12)

Производная релятивистского импульса по времени равна силе, приложенной к телу.

В теории относительности уравнение ( 12) приходит на смену второму закону Ньютона.

Давайте выясним, как же в действительности будет двигаться тело массы m под действием постоянной силы . При условии из формулы ( 12) получаем:

$frac{displaystyle mupsilon }{displaystyle sqrt{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= Ft$ .

Остаётся выразить отсюда скорость:

$upsilon = frac{displaystyle cFt}{sqrt{displaystyle F^{displaystyle 2}t^{displaystyle 2}+m^{displaystyle 2}c^{displaystyle 2}}}$ . ( 13)

Посмотрим, что даёт эта формула при малых и при больших временах движения.
Пользуемся приближёнными соотношениями при :

$sqrt{displaystyle 1+alpha }approx 1+frac{displaystyle alpha }{displaystyle 2}$ , ( 14)

$frac{displaystyle 1}{displaystyle 1+alpha }approx 1-alpha$ . ( 15)

Формулы ( 14) и ( 15) отличаются от формул ( 3) и ( 4) только лишь знаком в левых частях. Очень рекомендую вам запомнить все эти четыре приближённых равенства — они часто используются в физике.

Итак, начинаем с малых времён движения. Преобразуем выражение ( 13) следующим образом:

$upsilon = frac{displaystyle cFt}{displaystyle mcsqrt{displaystyle 1+frac{displaystyle F^{displaystyle 2}t^{displaystyle 2}}{displaystyle m^{displaystyle 2}c^{displaystyle 2}}}}$ .

При малых имеем:

$frac{displaystyle F^{displaystyle 2}displaystyle t^{displaystyle 2}}{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}}ll 1$ .

Последовательно пользуясь нашими приближёнными формулами, получим:

$upsilon approx frac{displaystyle cFt}{displaystyle mc(1+frac{displaystyle 1}{displaystyle 2}frac{displaystyle F^{displaystyle 2}displaystyle t^{displaystyle 2}}{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}})}approx frac{displaystyle Ft}{displaystyle m}(1-frac{F^{displaystyle 2}t^{displaystyle 2}}{displaystyle 2m^{displaystyle 2}displaystyle c^{displaystyle 2}})$ .

Выражение в скобках почти не отличается от единицы, поэтому при малых имеем:

$upsilon approx frac{Ft}{m}= at$ .

Здесь a= F/m — ускорение тела. Мы получили результат, хорошо известный нам из классической механики: скорость тела линейно растёт со временем. Это и не удивительно — при малых временах движения скорость тела также невелика, поэтому мы можем пренебречь релятивистскими эффектами и пользоваться обычной механикой Ньютона.

Теперь переходим к большим временам. Преобразуем формулу ( 13) по-другому:

$upsilon approx frac{displaystyle cFt}{displaystyle Ftsqrt{displaystyle 1+frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}}{displaystyle F^{displaystyle 2}displaystyle t^{displaystyle 2}}}}= frac{displaystyle c}{sqrt{1+frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}}{displaystyle F^{displaystyle 2}t^{displaystyle 2}}}}$ .

При больших значениях имеем:

$frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}}{displaystyle F^{displaystyle 2}displaystyle t^{displaystyle 2}}ll 1$ ,

и тогда:

$upsilon approx frac{c}{1+frac{1}{2}frac{m^{2}c^{2}}{F^{2}t^{2}}}approx c(1-frac{m^{2}c^{2}}{2F^{2}t^{2}})$ .

Хорошо видно, что при скорость тела upsilon неуклонно приближается к скорости света , но всегда остаётся меньше — как того и требует теория относительности.

Зависимость скорости тела от времени, даваемая формулой ( 13), графически представлена на рис. 2.

Рис. 2. Разгон тела под действием постоянной силы

Начальный участок графика — почти линейный; здесь пока работает классическая механика. Впоследствии сказываются релятивистские поправки, график искривляется, и при больших временах наша кривая асимптотически приближается к прямой .

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Релятивистская динамика» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Если скорость релятивистской частицы меньше скорости света, то она называется массовой. Её собственная энергия, то есть энергия при (v=0):
(boxed{E_0=m_0cdot c^2}), ((1))
где (m_0) — масса покоя частицы, (E_0) — энергия покоя частицы.
Масса движущейся релятивистской частицы:
(boxed{m=frac{m_0}{sqrt{1-frac{v^2}{c^2}}}}). ((2))
Полная (релятивистская) энергия, или энергия свободной (невзаимодействующей) движущейся релятивистской частицы (сформулировал А. Эйнштейн):
(boxed{E=frac{m_0 c^2}{sqrt{1-frac{v^2}{c^2}}}}). ((3))
Кинетическая энергия массовой частицы:
(boxed{E_k=E-E_0}). ((4))
Импульс частицы:
(boxed{vec{p}=frac{m_0 vec{v}}{sqrt{1-frac{v^2}{c^2}}}}). ((5))
Если скорость частицы равна скорости света, то такую частицу называют безмассовой (фотон и нейтрино). В таком случае энергия и импульс свободной частицы связаны соотношением:
(boxed{E^2-p^2c^2=0}). ((6))
Таким образом, для всех свободных частиц в любой инерциальной системе можно записать:
(boxed{E^2-p^2c^2=m_0^2c^4}). ((7))

Источник

1.17.
ОСНОВЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ

Релятивистский
импульс. Уравнение движения частицы в
специальной теории относительности.
Работа и энергия. Полная энергия
тела. Взаимосвязь энергии и массы,
энергии и импульса.

Релятивистская
динамика строится на основе постулатов
Эйнштейна и их следствий — преобразований
Лоренца, которые математически
аккумулируют в себе метрические свойства
пространства и времени.

Релятивистский
импульс частицы

В
релятивистской физике для описания
механического движения вводятся
4-вектора положения частицы
,
перемещения

и скорости
.
Вводим импульс по аналогии с ньютоновой
механикой — как произведение инвариантной
массы (массы покоя), одинаковой в
инерциальных системах отсчета I
и II,
на 4-скорость. Итак, четырехмерным
импульсом называется величина
.

(17.1)

Сокращенно
пишем
,
где пространственная и временная
компоненты 4-импульса имеют вид

(17.2)

Здесь

—
так называемый релятивистский
3-импулъс.
Очевидно, 4-импульсу отвечает его
инвариант

(17.3)

Масса
покоя —
—
инвариант преобразований Лоренца. При
небольших скоростях, когда
,
он переходит в инвариант преобразований
Галилея.

Основное
уравнение релятивистской динамики

В ньютоновой
механике обычная трехмерная 3-сила
определяется как скорость изменения
во времени количества движения,
переносимого на данное тело от окружающих
тел и полей (равенство
Ньютона
является одновременно и определением
силы, и законом движения). Аналогично в
релятивистской механике будем определять
силу как производную от релятивиского
3-импулься

(17.4)

Это
равенство обобщает ньютонову трактовку
3-силы. В то же время оно представляет
основной закон движения частицы
(материальной точки) в инерциальной
системе отсчета при любых
возможных
скоростях меньших с. Законы
классической динамики получаются из
законов релятивистской динамики в
предельном случае υ
<<
c.

Энергия
свободной частицы. Связь между массой
и энергией

В ньютоновой
механике работа силы равна приращению
кинетической энергии:
.
В СТО понятие силы обобщено, и работу
релятивистской силы нужно заново
вычислить. Найдем работу релятивистской
силы
на
элементарном перемещении
частицы

.
(17.5)

Здесь
использовано правило дифференцирования
произведения функций; учтено что
и

.
Объединяя оба слагаемые под одним
дифференциалом, окончательно получаем

(17.6)

Найденное
равенство показывает, что работа силы
равна приращению величины
.
Поэтому последнюю следует истолковать
как энергию
движущегося
тела (частицы):

(17.7)

Эта
формула, установленная Эйнштейном в
1905 г., в начале прошлого столетия вызывала
сомнение, а позже обеспечила полный
триумф теории относительности. Формула
(17.7)
устанавливает связь между массой (покоя)
и энергией тела при его скорости
.

Из формулы
Эйнштейна вытекает важное открытие 20
века: любое тело в состоянии покоя
обладает колоссальной энергией, которая
называется
энергией покоя
и равна

(17.8)

Например,
тело массой m₀=
l
кг обладает энергией
Дж,
т.е. оно обладает энергией, которую,
например, Днепровская ГЭС вырабатывает
за 8 лет, давая в год 3 млрд. квт.-ч. энергии.
Соотношение
носит универсальный характер, оно
применимо ко всем формам энергии,
т.е.можно утверждать, что с энергией,
какой бы формы она не была, связана масса
и, наоборот, со всякой массой связана
энергия.

Дадим
определение: кинетической
энергией
тела
называется разность

откуда

или

(17.9)

Формула
(17.7)
для энергии определяет сумму двух
энергий: энергии покоя (она относится
в внутренней энергии)
и
кинетической
.

Связь
между энергией и импульсом частицы

Учитывая
значения временной компоненты 4-импульса
P₀
(формула (17.2))
и полной энергии Е (формула (17.7)),
4-импульс
(формула
(17.1))
можно представить в виде

(17.10)

Как
видим, в 4-импульсе объединились энергия
Е и релятивистский 3-импульс
,
что означает глубокую внутреннюю связь
между релятивистской энергией
и
релятивистским импульсом
.
При переходе из одной инерциальной
системы отсчета в другую значение каждой
из четырех компонент 4-импульса

определяется
по формулам Лоренца через все четыре
компоненты в исходной системе I.
Например, значение энергии в системе
II
определяется не только через энергию
в системе I,
но и через все компоненты импульса
.

Полезными
являются также очевидные формулы для
релятивистского импульса
и
его модуля в виде:

(17.11)

Релятивистские
инварианты. Закон сохранения
энергии-импульса

Определим
величины, сохраняющиеся при переходе
из одной системы отсчета в другую. Их
обычно называются инвариантами. Как
отмечалось, 4-импульсу
соответствует
инвариант

Подставляя
значение
получаем

(17.12)

Это
соотношение между релятивистской
энергией и релятивистским импульсом
выполняется как для частицы» так и
для тела, и даже для сложной системы,
так как при его выводе нигде не
использовалась неделимость объекта. И
общем случае в (17.12)
под Е следует понимать полную энергию
системы, а под
—
геометрическую
сумму импульсов всех
частей системы. Равенство (17.12)
можно рассматривать так же как определение
инвариантной массы (массы покоя) любой
физической системы

(17.13)

В частном
случае системы отсчета, в которой импульс
равен нулю (),
имеем

(17.14)

Следовательно, масса
покоя тела определяет его энергию покоя
(во всех ее видах). В релятивистской
механике, в отличие от классической,
энергия тела всегда положительна.

В другом
частном случае, когда масса покоя равна
нулю,
соотношение
(17.12)
дает связь между релятивистским импульсом
и энергией следующего вида

В частности, для для
фотона с нулевой массой покоя эта формула
преобразуется к виду

Вернемся
к рассмотрению 4-импульса
.
Он объединяет релятивистскую энергию

с
релятивистским импульсом
а
значит представляет собой некоторую
новую (одну единую!) величину, которую
можно определить термином энергия-импульс.
4-вектору энергия-импульс соответствует
инвариант (17.12),
играющий важную роль в атомной и ядерной
физике

В случае
изолированной физической системы эта
величина сохраняется не только при
переходе от системы отсчета I
к системе II,
но также сохраняется ее значение как
до, так и после реакции, происходящей в
физической системе.

Соседние файлы в папке физика лекцыи_1

Источник

Мы уже ввели релятивистскую частицу и эффекты, связанные с релятивистским движением. Напомним, что прилагательное «релятивистское» обозначает движение тел с близкими к световой скоростями. Большинство соотношений в данной теме вывести достаточно сложно, поэтому просто верим.

Итак, введённый нами импульс ( displaystyle p=mupsilon ) при условии релятивистской массы ( $displaystyle m=frac{{{m}_{0}}}{sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}$ ) может быть записан как:

$displaystyle p=frac{{{m}_{0}}}{sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}upsilon$ (1)

где

Немного о $displaystyle {{m}_{0}}$ — массе неподвижного в данной системе тела, называемой массой покоя.

Великим Эйнштейном было получено уникальное соотношение, характеризующее полную энергию движущейся частицы:

$displaystyle E=m{{c}^{2}}$ (2)

где

Логично предположить, что наименьшей энергией обладает тело, которое покоится в данной системе, назовём эту энергию энергией покоя:

$displaystyle {{E}_{0}}={{m}_{0}}{{c}^{2}}$ (3)

где

Тогда кинетическая энергия движущегося тела может быть найдена как разность между полной энергией и энергией покоя:

$displaystyle {{E}_{k}}=E-{{E}_{0}}$ (4)

где

Или:

$displaystyle m{{c}^{2}}(1-sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}})=frac{{{m}_{0}}{{c}^{2}}}{sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}(1-sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}})=$ $displaystyle frac{{{m}_{0}}{{upsilon }^{2}}}{1+sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}$ $displaystyle frac{{{m}_{0}}{{upsilon }^{2}}}{1+sqrt{1-frac{{{upsilon }^{2}}}{{{c}^{2}}}}}$ (5)

При условии $displaystyle frac{{{upsilon }^{2}}}{{{c}^{2}}}to 0$ (скорость тела очень мала по сравнению со скоростью света) получим $displaystyle {{E}_{k}}=frac{m{{upsilon }^{2}}}{2}$ (отношение скорости тела к скорости света стремиться к нулю), и соотношение (5) принимает вид $displaystyle {{E}_{k}}=frac{m{{upsilon }^{2}}}{2}$ — т.е. вид кинетической энергии в классической механике.

Вывод: в случае релятивистской механики (скорость частицы велика) достаточно помнить, что энергетические характеристики тела выражаются через более сложные соотношения (1) — (5). С точки зрения энергии, главное понять по задаче, какую энергию нам необходимо найти — покоя, полную или кинетическую.

Источник

Физика, 11 класс

Урок №21. Релятивистские эффекты

На уроке рассматриваются понятия: энергия покоя, полная энергия частиц; связь массы и энергии в специальной теории относительности; релятивистский импульс частицы, релятивистская кинетическая энергия; принцип соответствия.

Глоссарий урока:

Релятивистская механика — раздел физики, где описывается движение частиц со скоростями близкими к скорости света.

Закон взаимосвязи энергии и массы — тело обладает энергией и при нулевой скорости, такую энергию называют энергией покоя.

Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии.

Безмассовыми называют частицы массы, которых в состоянии покоя равны нулю, они существуют только в движении, при этом во всех инерциальных системах отсчёта их импульс и энергия не равны нулю.

Массовыми называют частицы, для которых масса является важной характеристикой, мерой инертности тела.

Принцип соответствия – это подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматриваются как частный случай релятивистских законов при скоростях намного меньших скорость света.

Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай.

Обязательная литература:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 239 – 241.
Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 147 – 149

Дополнительная литература:

Анциферов Л.И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 253-260.
Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 311-315.
Айзексон У., Эйнштейн. Жизнь гения; пер. с анг. А.Ю. Каннуниковой. – М: АСТ, 2016 – С.144-157

Основное содержание темы

«Основы физики претерпели неожиданные и радикальные изменения благодаря смелости молодого и революционно мыслящего гения.»

Вернер Гейзенберг

Эти слова и множество других восхищённых эпитетов будут высказаны в адрес гениального учёного Альберта Эйнштейна. Эйнштейн не боялся опровергать общепринятые утверждения. Он разрушил представление об абсолютном времени и незыблемости пространства. Его теория утверждала, что есть движущиеся системы координат со своим относительным временем. А пространство существует, пока в нём существует всё материальное. Время идёт тем медленнее, если быстрее движется тело. Такие удобные и понятные принципы классической физики: о постоянстве массы, длины, времени, скорости — опровергаются следствиями из постулатов специальной теории относительности Эйнштейна.

Альберт (Einstein) Эйнштейн

14 марта 1879 г. – 18 апреля 1955 г.

Физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 года, общественный деятель-гуманист.

По законам классической физики: масса – это мера инертности тела. Но Эйнштейн утверждает другое: масса – это мера энергии, содержащейся в теле.

Любое тело обладает энергией уже в силу своего существования. Альбертом Эйнштейном была установлена пропорциональность между энергией и массой:

На первый взгляд, простая формула, является фундаментальным законом природы, законом взаимосвязи энергии и массы.

Согласно этой формуле тело обладает энергией даже при нулевой скорости, в таком случае энергию называют E энергией покоя. А массу, которая входит в формулу Эйнштейна назовём m₀массой покоя.

Как же будет выглядеть закон взаимосвязи массы и энергии для движущегося тела? К нему добавляем радикал (релятивистский множитель) из преобразований Лоренца:

Такую формулу называют релятивистской энергией или полной энергией движущегося тела.

Релятивистская механика — раздел физики, где описываются движения тел и частиц со скоростями близкими к скорости света, где используются преобразования Лоренца, перехода из одной инерциальной системы в другую, когда одна система движется относительно другой со скоростью вдоль оси ОХ.

Любые изменения физических величин, связанные с сокращением размеров:

эффект замедления времени:

изменение массы тела при изменении энергии:

закон сложения скоростей:

в специальной теории относительности называют релятивистскими изменениями.

По законам классической физики полная энергия равна сумме кинетической и потенциальной энергий тела или частицы

Отсюда выразим кинетическую энергию тела

Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии

В классической физике кинетическая энергия вычисляется по формуле

Получим ещё одно выражение

Выразим кинетическую энергию из формулы релятивистской энергии:

Поставим релятивистский радикал, который можно преобразовать при малых скоростях и получим релятивистскую кинетическую энергию частицы:

Или другой способ выражения кинетической энергии, если использовать классическую кинетическую энергию, то получим

— выражение для определения релятивистской кинетической энергии.

Путём не сложных математических вычислений можно доказать, что формула определения кинетической энергии в классической физикеи формула кинетической энергии в релятивистской физике равны между собой.

Давайте проверим работают ли главные законы механики — законы Ньютона в релятивистской физике.

Первый закон Ньютона: существуют системы отсчёта, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него не действуют другие тела.

Первый постулат СТО Эйнштейна: все физические явления протекают одинаково во всех инерциальных системах отсчёта, или никакими опытами, проводимыми в инерциальной системе отсчёта, невозможно установить её движение относительно других инерциальных систем.

Внимание! Они не противоречат друг другу!

Третий закон Ньютона: силы с которыми тела действуют друг на друга равны по модулю и направлены вдоль одной прямой в противоположные стороны. Этот закон тоже работает в релятивистской физике (смотрите первый постулат СТО).

А что же со вторым законом классической механики? Второй закон Ньютона: ускорение тела прямо пропорционально силе и обратно пропорционально его массе.

Рассмотрим предельный случай: если на тело долгое время t (время стремится к бесконечности) действовать с постоянной силой F = const, то ускорение будет постоянным a = const. Ускорение в свою очередь, зависит от скорости, с которой движется тело:

Отсюда скорость тоже будет стремиться к бесконечности, а это невозможно (смотрите второй постулат СТО), так как скорость тела или частицы не может быть больше предельного значения скорости света ()!

Но давайте рассмотрим другую формулировку второго закона Ньютона, когда сила прямо пропорциональна изменению импульсов тела ко времени этого изменения:

В классической механике импульс равен произведению массы тела или частицы на его скорость: , где m – постоянная величина, мера инертности тела.

В релятивистской механике выражение импульса можно записать, используя преобразования Лоренца:

При скоростях намного меньших, чем скорость света 𝟅с, формула принимает вид классической механики Ньютона

Эти проявления — подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматривают как частный случай релятивистских законов при скоростях намного меньших скорости света и называют принципом соответствия. Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай. То есть законы классической механики подтверждаются релятивистской, но только для частиц или тел, движущихся с малыми скоростями.

В природе существуют такие частицы (фотоны, мюоны, нейтрино), скорость которых равна или близка к скорости света. Массы таких частиц в состоянии покоя равны нулю, эти частицы называют безмассовыми. Они существуют только в движении, но во всех инерциальных системах отсчёта их импульс и энергия не равны нулю. Тогда подтверждается утверждение Эйнштейна, что масса – это мера энергии тела. Частицы, для которых масса является важной характеристикой — мерой инертности, называют массовыми.

Найдём соотношение между энергией и импульсом:

Взаимно уничтожаются подкоренные выражения, сокращается произведение массы на скорость света, и мы получим простое соотношение энергии и импульса, где нет зависимости от массы.

Энергия и импульс связаны соотношением

Поэтому во всех инерциальных системах отсчёта импульс и энергия не равны нулю. При превращениях элементарных частиц, обладающих массой покоя , в частицы у которых , их энергия покоя целиком превращается в кинетическую энергию вновь образовавшихся частиц. Этот факт является наиболее очевидным экспериментальным доказательством существования энергии покоя.

Во всех инерциальных системах отсчёта импульс частицы и её энергия связаны соотношением:

или

— эта формула является фундаментальным соотношением энергии и импульса для массовых частиц релятивистской механики. Эти соотношения экспериментально подтверждены.

Следовательно, для безмассовых частиц, где или , выражение примет вид

Основное выражение энергии через её импульс записывают так:

Отсюда, масса, движущейся частицы, будет равна

Если частица покоится, то её значение можно определить из основной формулы Эйнштейна взаимосвязи массы и энергии:

В обычных условиях, при нагревании тела или его охлаждении, при химической реакции, эти приращения массы происходят, их можно вычислить, но изменения массы не так заметны. Энергию, полученную из расщепления ядер на атомных электростанциях, используют на благо человека, где незначительные массы радиоактивного топлива вырабатывают энергию, питающую электроэнергией огромные города. Но, к сожалению, такую энергию, высвобождающуюся при цепной реакции, люди использовали и военных целях, для уничтожения городов, людей. Поэтому, только в последствии, понимая ответственность за свои открытия, учёные искренне становятся общественными деятелями: правозащитниками и борцами за мир.

Рассмотрим задачи тренировочного блока урока:

1. Чтобы выработать количество энергии, которой обладает тело массой 1 кг, Красноярской ГЭС потребуется времени _________ суток (1,5·10⁷; 173,6; 182,3). Мощность Красноярской ГЭС 6000МВт.

Дано:

m = 1 кг

P = 6000 МВт = 6·10⁹Вт

t — ? (сутки)

Воспользуемся выражением, описывающим зависимость энергии тела от массы:

И зависимостью мощности от работы и времени:

Выразим секунды в часах, а затем в сутках:

Ответ: 173,6 суток.

2. Чему равен импульс протона, летящего со скоростью 8,3·10⁷ м/с? На сколько будет допущена ошибка, если пользоваться формулами классической физики? Данные поученных вычислений занесите в таблицу:

Физические величины	Показатели
Масса покоя протона, m	1,67·10^-27кг
Скорость света, с	3·10⁸ м/с
Скорость движения протона, 𝟅	8,3·10⁷ м/с
Импульс протона по классическим законам, р_к	?
Импульс протона по релятивистским законам, р_р	?
Разница в вычислениях импульса протона,	?

Воспользуемся формулами для определения импульса релятивистским и классическим способами:

Вычислим разницу показаний:

Физические величины	Показатели
Масса покоя протона, m	1,67·10^-27кг
Скорость света, с	3·10⁸ м/с
Скорость движения протона, 𝟅	8,3·10⁷ м/с
Импульс протона по классическим законам, р_к	1,38·10^-19кг·м/с
Импульс протона по релятивистским законам, р_р	5,2·10^-19 кг·м/с
Разница в вычислениях импульса протона,	в 3,8 раза

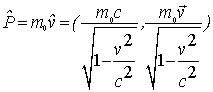
Источник

Релятивистская динамика

Релятивистская энергия

Релятивистский импульс.

Связь энергии и импульса.

Релятивистское уравнение движения.

Релятивистский импульс частицы

Основное уравнение релятивистской динамики

Энергия свободной частицы. Связь между массой и энергией

Связь между энергией и импульсом частицы

Релятивистские инварианты. Закон сохранения энергии-импульса

Релятивистский
импульс частицы

Основное
уравнение релятивистской динамики

Энергия
свободной частицы. Связь между массой
и энергией

Связь
между энергией и импульсом частицы

Релятивистские
инварианты. Закон сохранения
энергии-импульса