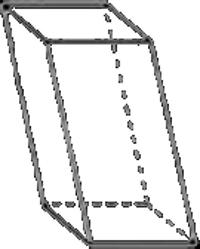
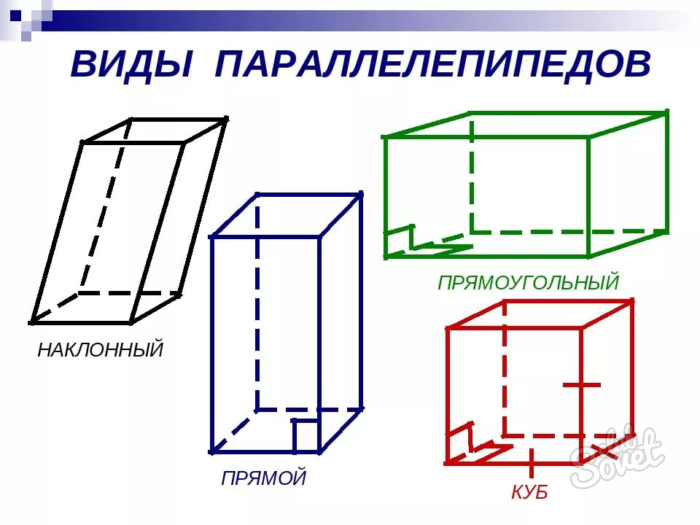
Как найти полную поверхность наклонного параллелепипеда - Исправление недочетов и поиск решений вместе с Examum.ru

Параллелепипедом называется четырехугольная призма, в основаниях которой лежат параллелограммы. Высотой параллелепипеда называют расстояние между плоскостями его основаниями. На рисунке высота показана отрезком C_1H . Различают два вида параллелепипедов: прямой и наклонный. Как правило, репетитор по математике сначала дает соответствующие определения для призмы, а затем переносит их на параллелепипед. Мы сделаем также.

Напомню, что призма называется прямой, если ее боковые ребра перпендикулярны основаниям, если перпендикулярности нет – призму называют наклонной. Эту терминологию наследует и параллелепипед. Прямой параллелепипед – ни что иное, как разновидность прямой призмы, боковое ребро которой совпадает с высотой. Сохраняются определения таких понятий, как грань, ребро и вершина, являющиеся общими для всего семейства многогранников. Появляются понятие противоположные грани. У параллелепипеда 3 пары противоположных граней, 8 вершин ти 12 ребер.

Диагональ параллелепипеда (диагональ призмы) — отрезок, соединяющий две вершины многогранника и не лежащий ни в одной из его граней.

Диагональное сечение – сечение параллелепипеда, проходящее через его диагональ и диагональ его основания.

Свойства наклонного параллелепипеда:
1) Все его грани – параллелограммы, а противоположные грани — равные параллелограммы.
2) Диагонали параллелепипеда пересекаются в одной точке и делятся в этой точки пополам.
3) Каждый параллелепипед состоит из шести равных по объему треугольных пирамид. Чтобы показать их ученику репетитор по математике должен отрезать от параллелепепеда половинку его диагональным сечением и разбить ее отдельно на 3 пирамиды. Их основания должны лежать в разных гранях исходного паралеллепипеда. Репетитор математики найдет применение этого свойства в аналитической геометрии. Оно используется для вывода объема пирамиды через смешанное произведение векторов.

Формулы объема параллелепипеда:
1) $V=S_{OCH} cdot h$ , где $S_{OCH}$ — площадь основания, h – высота.
2) Объем параллелепипеда равен произведению площади поперечного сечения на боковое ребро $V=S_{o} cdot b$ .
Репетитору по математике: Как известно, формула является общей для всех призм и если репетитор уже доказал ее, нет смысла повторять тоже самое для параллелепипеда. Однако в работе со учеником среднего уровня (слабому формула не пригодиться) преподавателю желательно действовать с точностью до наоборот. Призму оставить в покое, а для параллелепипеда провести аккуратное доказательство.
3) $V=6 cdot V_{ABDD_{1}}$ , где $V_{ABDD_{1}}$ –объем одной из шести треугольных пирамиды из которых состоит параллелепипед.
4) Если $overrightarrow{AA_1}(x_1;y_1;z_1), overrightarrow{AB}(x_2;y_2;z_2), overrightarrow{AD}(x_3;y_3;z_3)$ , то

$V_{ABCDA_1B_1C_1D_1}= pm begin{vmatrix} x_1 & y_1 & z_1 \ x_2 & y_2 & z_2 \ x_3 & y_3 & z_3 end{vmatrix}$

Площадью боковой поверхности параллелепипеда называется сумма площадей всех его граней:
Полная поверхность параллелепипеда – это сумма площадей всех его граней, то есть площадь + две площади основания: $S=S_b+2 cdot S_{OCH}$ .

О работе репетитора с наклонным параллелепипедом:
Задачами на наклонный параллелепипед репетитор по математике занимается не часто. Вероятность их появления на ЕГЭ достаточно мала, а дидактика неприлично бедная. Более-менее приличная задача на объем наклонного параллелепипеда вызывает серьезные проблемы, связанные с пределением расположения точки Н — основания его высоты. В этом случае репетитору по математике можно посоветовать обрезать параллелепипед до одной из шести его пирамид (о которых идет речь в свойстве №3), попробовать найти ее объем и умножить его на 6.

Если боковое ребро AA_1 параллелепипеда имеет равные углы со сторонами основания, то Н лежит на биссектрисе угла A основания ABCD. И если, например, ABCD — ромб, то H in AC

Задачи репетитора по математике:
1) Грани параллелепипеда равные роибы со стороной 2см и острым углом 60^circ . Найти объем параллелепипеда.
2) В наклонном параллелепипеде боковое ребро равно 5см. Сечение, перпендикулярное ему, является четырехугольником со взаимно перпендикулярными диагоналями, имеющими длины 6см и 8 см. Вычислить объем паралеллепипеда.
3) В наклонном параллелепипеде известно, что , а в онованием ABCD является ромб со стороной 2см и уголом . Определите объем параллелепипеда.

Репетитор по математике, Александр Колпаков

Источник

ВИДЕОУРОК

Параллелепипедом
называется призма, основания которой – параллелограммы.

Прямой параллелепипед.

Параллелепипед, боковые ребра которого перпендикулярны к
плоскостям оснований, называется прямым.

Свойства прямого параллелепипеда.

– в параллелепипеде противоположные грани равны и параллельны;

– диагонали параллелепипеда пересекаются в одной точке и
делятся в ней пополам;

– сумма квадратов всех диагоналей параллелепипеда равна
сумме квадратов всех его ребер;

– точка пересечения диагоналей параллелепипеда и точка
пересечения диагоналей оснований лежат на одной прямой

Поверхность прямого параллелепипеда.

Боковой поверхностью прямого параллелепипеда называется сумма
площадей всех её боковых граней.

Полною поверхностью прямого параллелепипеда называется
сумма её боковой поверхности и площадей оснований.

Боковая поверхность прямого параллелепипеда равна произведению
периметра перпендикулярного сечения на боковое ребро.

Боковая поверхность прямого параллелепипеда равна произведению
периметра оснований на высоту прямого параллелепипеда.

ЗАДАЧА:

Основание прямой призмы – параллелограмм
со сторонами

9
см и
14 см

и углом между
ними 30°. Высота призмы – 15
см. Найдите площадь полной поверхности призмы.

РЕШЕНИЕ:

S_п = S_б
+ 2S_осн.

S_осн = 9 ×
14 × sin 30° =
9 × 14 × ¹/₂ = 63 (см²).

Р_осн = 2 ×
(AB + AD) =
2 × (9 + 14) = 46 (см).

S_б = 46 ×
15 = 690 (см²).

S_п = 2 ×
63 + 690 =
126 + 690 = 816 (см²).

ОТВЕТ: 816 см².

Наклонный параллелепипед.

Параллелепипед, боковые
рёбра которого не перпендикулярные к плоскости основания, называется наклонным.

Свойства наклонного
параллелепипеда.

– в наклонном
параллелепипеде противоположные грани равны и параллельны;

– диагонали наклонного
параллелепипеда пересекаются в одной точке и делятся в ней пополам;

– сумма квадратов
всех диагоналей наклонного параллелепипеда равна сумме квадратов всех его рёбер;

Поверхность наклонного параллелепипеда.

Боковою поверхностью наклонного параллелепипеда называется
сумма площадей всех его боковых граней.

Полною поверхностью наклонного параллелепипеда будет сумма
площадей его боковой поверхности и площадей оснований.

Боковая поверхность наклонного параллелепипеда равна произведению
периметра перпендикулярного сечения на боковое ребро.

ЗАДАЧА:

Основание наклонного параллелепипеда
– квадрат со стороною а.
Одна из вершин второго основания проектируется в центр этого квадрата. Высота
параллелепипеда равна Н.
Найти боковую поверхность параллелепипеда.

РЕШЕНИЕ:

Пусть основанием наклонного
параллелепипеда

ABCDA₁B₁C₁D₁

–
квадрат ABCD со стороною

АВ = а,

О – центр этого квадрата,

А₁О = Н –
высота параллелепипеда.

Проведём ОК ⊥
АD, ОМ ⊥ АВ.
Тогда по теореме про три перпендикуляра

А₁К ⊥ АВ, А₁M ⊥ АВ,

то есть А₁К иА₁M – высоты боковых
граней

ADD₁A₁ и ABB₁A₁

соответственно. Прямоугольные треугольники

A₁OK и A₁OM

равны  (A₁O –
общий катет и ОК
= ОМ = ^a/₂), откуда

A₁K = A₁M.

Поскольку, кроме этого, AD
= AB, то

Поэтому

Поэтому,

ОТВЕТ:

ЗАДАЧА:

В основании наклонного параллелепипеда
лежит прямоугольник. Боковое ребро образует со смежными сторонами основания углы,
каждый из которых равен 60°. Найти угол, который образует это боковое ребро с плоскостью
основания параллелепипеда.

РЕШЕНИЕ:

Пусть ABCDA₁B₁C₁D₁ – заданный наклонный параллелепипед. ABCD – прямоугольник,

∠ A₁AD = ∠ A₁AB = 60°,

A₁K – высота параллелепипеда.

Проведём КN ⊥
АD и KM ⊥
АВ.

∆
A₁NA
(∠ N = 90°).

∠ AA₁N = 90° – 60° = 30°.

Поэтому, AN = ¹/₂AA_1. Аналогично в

∆ A₁MA ∠ AA₁M = 30°,

поэтому AM = ¹/₂AA₁. Поскольку

AN = AM =
¹/₂AA₁,

то AMNK – квадрат и прямоугольный треугольник ANK –
равнобедренный. Откуда

Поэтому, ∠ A₁АM = 45°.

ОТВЕТ: 45°.

Задания к уроку 5

Задание 1
Задание 2
Задание 3

Другие уроки:

Урок 1. Прямые и плоскости в пространстве
Урок 2. Прямая призма
Урок 3. Наклонная призма
Урок 4. Правильная призма
Урок 6. Прямругольный параллелепипед
Урок 7. Куб
Урок 8. Пирамида
Урок 9. Правильная пирамида
Урок 10. Усечённая пирамида
Урок 11. Цилиндр
Урок 12. Вписанная и описанная призмы
Урок 13. Конус
Урок 14. Усечённый конус
Урок 15. Вписанная и описанная пирамиды
Урок 16. Сфера и шар
Урок 17. Комбинация тел

Источник

Параллелепипед — самая распространенная фигура из тех, что окружают людей. Большинство помещений представляют собой именно его. Особенно важно знать площадь параллелепипеда, хотя бы его боковых граней, во время ремонта. Ведь нужно точно знать, сколько материала приобрести.

Что он собой представляет?

Это призма с четырехугольным основанием. Поэтому у нее четыре боковых грани, которые являются параллелограммами. То есть такое тело имеет всего 6 граней.

Для определения параллелепипеда в пространстве у него определяют площадь и объем. Первая может быть как отдельно для каждой грани, так и для всей поверхности. К тому же выделяют еще и площадь только боковых граней.

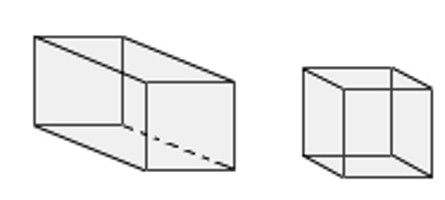
Какие существуют виды параллелепипедов?

Наклонный. Такой, у которого боковые грани образуют с основанием угол, отличный от 90 градусов. У него верхний и нижний четырехугольники не лежат друг напротив друга, а сдвинуты.

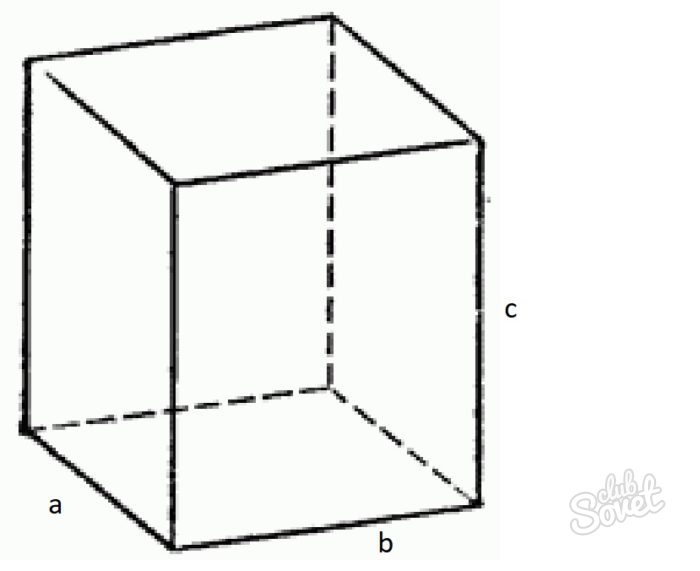
Прямой. Параллелепипед, боковые грани которого являются прямоугольниками, а в основании лежит фигура с произвольными величинами углов.

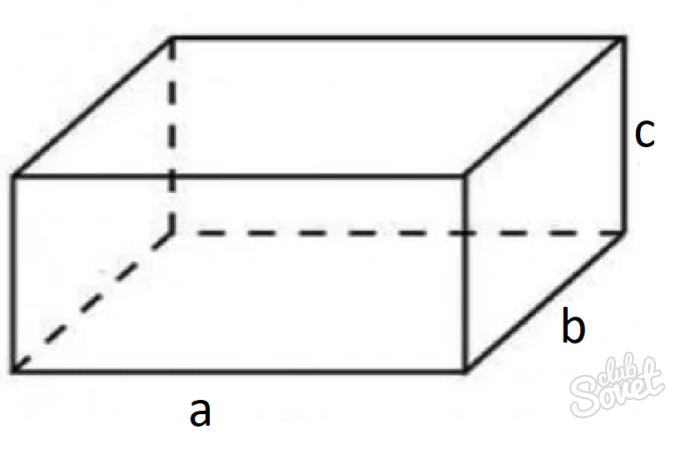
Прямоугольный. Частный случай предыдущего вида: в его основании находится прямоугольник.

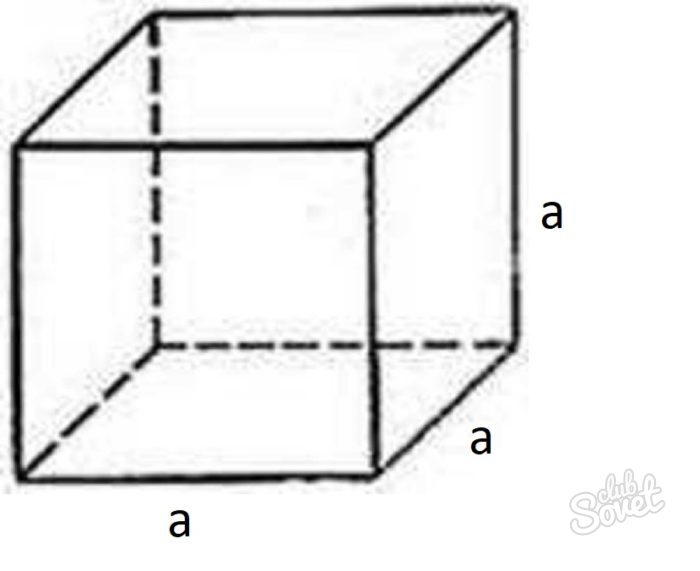
Куб. Особый тип прямого параллелепипеда, в котором все грани представлены квадратами.

Некоторые математические особенности параллелепипеда

Может возникнуть ситуация, когда они окажутся полезными в том, чтобы найти площадь параллелепипеда.

Грани, которые лежат напротив друг друга, не только параллельны, но и равны.
Диагонали параллелепипеда точкой пересечения делятся на равные части.
Более общий случай, если отрезок соединяет две точки на поверхности тела и проходит через точку пересечения диагоналей, то он делится этой точкой пополам.
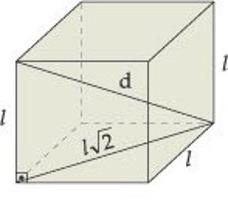
Для прямоугольного параллелепипеда справедливо равенство, в котором в одной его части стоит квадрат диагонали, а в другой — сумма квадратов его высоты, ширины и длины.

Площади прямого параллелепипеда

Если обозначить высоту тела как «н», а периметр основания буквой Р_ос, то вся боковая поверхность может быть вычислена по формуле:

S_бок = Р_ос * н

Используя эту формулу и определив площадь основания, можно сосчитать полную площадь:

S = S_бок + 2 * S_ос

В последней записи S_ос., то есть площадь основания параллелепипеда, может быть вычислена по формуле для параллелограмма. Другими словами, потребуется выражение, в котором нужно перемножить сторону и высоту, опущенную на нее.

Площади прямоугольного параллелепипеда

Принято стандартное обозначение длины, ширины и высоты такого тела буквами «а», «в» и «с» соответственно. Площадь боковой поверхности будет выражаться формулой:

S_бок= 2 * с * (а + в)

Чтобы вычислить полную площадь прямоугольного параллелепипеда, потребуется такое выражение:

S = 2 * (ав + вс + ас)

Если окажется необходимым узнать площадь его основания, то достаточно вспомнить, что это прямоугольник, а значит, достаточно перемножить «а» и «в».

Площади куба

Его боковая поверхность образована четырьмя квадратами. Значит, чтобы ее найти, потребуется воспользоваться известной для квадрата формулой и умножить ее на четыре.

S_бок = 4 * а²

А из-за того, что его основания — такие же квадраты, полная площадь определится по формуле:

S = 6 * а²

Площади наклонного параллелепипеда

Поскольку его грани — это параллелограммы, то нужно узнать площадь каждого из них и потом сложить. К счастью, противолежащие равны. Поэтому вычислять площади нужно только три раза, а потом умножить их на два. Если записать это в виде формулы, то получится следующее:

S_бок = (S₁ + S₂) * 2,

S = (S₁ + S₂ + S₃) * 2

Здесь S₁ и S₂ являются площадями двух боковых граней, а S₃ — основания.

Задачи по теме

Задание первое. Условие. Необходимо узнать длину диагонали куба, если площадь всей его поверхности равна 200 мм².

Решение. Начать нужно с получения выражения для искомой величины. Ее квадрат равен трем квадратам стороны куба. Это значит, что диагональ равна «а», умноженной на корень из 3.

Но сторона куба неизвестна. Здесь потребуется воспользоваться тем, что известна площадь всей поверхности. Из формулы получается, что «а» равно квадратному корню из частного S и 6.

Осталось только сосчитать. Ребро куба оказывается равным √ (200/6), что равно 10/ √3 (мм). Тогда диагональ получится равной (10/ √3) * √3 = 10 (мм).

Ответ. Диагональ куба равна 10 мм.

Задание второе. Условие. Необходимо вычислить площадь поверхности куба, если известно, что его объем равен 343 см².

Решение. Потребуется воспользоваться той же формулой для площади куба. В ней опять неизвестно ребро тела. Но зато дан объем. Из формулы для куба очень просто узнать «а». Оно будет равно кубическому корню из 343. Простой подсчет дает такое значение для ребра: а = 7 см.

Теперь осталось только сосчитать его квадрат и умножить на 6. а² = 7² = 49, отсюда площадь окажется равной 49 * 6 = 294 (см²).

Ответ. S = 294 см².

Задание третье. Условие. Дана правильная четырехугольная призма со стороной основания 20 дм. Необходимо найти ее боковое ребро. Известно, что площадь параллелепипеда равна 1760 дм².

Решение. Начинать рассуждения нужно с формулы для площади всей поверхности тела. Только в ней нужно учесть, что ребра «а» и «в» равны. Это следует из утверждения о том, что призма правильная. Значит, в его основании лежит четырехугольник с равными сторонами. Отсюда а = в = 20 дм.

Учитывая это обстоятельство, формула площади упростится до такой:

S = 2 * (а² + 2ас).

В ней известно все, кроме искомой величины «с», которая как раз и является боковым ребром параллелепипеда. Чтобы его найти, нужно выполнить преобразования:

разделить все неравенство на 2;
потом перенести слагаемые так, чтобы слева оказалось слагаемое 2ас, а справа — деленная на 2 площадь и квадрат «а», причем последнее будет со знаком «-»;
затем поделить равенство на 2а.

В итоге получится выражение:

с = (S/2 — а²) / (2а)

После подстановки всех известных величин и выполнения действий получается, что боковое ребро равно 12 дм.

Ответ. Боковое ребро «с» равняется 12 дм.

Задание четвертое. Условие. Дан прямоугольный параллелепипед. Одна из его граней имеет площадь, равную 12 см². Необходимо вычислить длину ребра, которое перпендикулярно этой грани. Дополнительное условие: объем тела равен 60 см³.

Решение. Пусть известна площадь той грани, которая расположена лицом к наблюдателю. Если принять за обозначение стандартные буквы для измерений параллелепипеда, то в основании ребра будут «а» и «в», вертикальное — «с». Исходя из этого, площадь известной грани определится как произведение «а» на «с».

Теперь нужно воспользоваться известным объемом. Его формула для прямоугольного параллелепипеда дает произведение всех трех величин: «а», «в» и «с». То есть известная площадь, умноженная на «в», дает объем. Отсюда получается, что искомое ребро можно вычислить из уравнения:

12 * в = 60.

Элементарный расчет дает результат 5.

Ответ. Искомое ребро равно 5 см.

Задание пятое. Условие. Дан прямой параллелепипед. В его основании лежит параллелограмм со сторонами 6 и 8 см, острый угол между которыми равен 30º. Боковое ребро имеет длину 5 см. Требуется вычислить полную площадь параллелепипеда.

Решение. Это тот случай, когда нужно узнать площади всех граней по отдельности. Или, точнее, трех пар: основание и две боковые.

Поскольку в основании расположен параллелограмм, то его площадь вычисляется как произведение стороны на высоту к ней. Сторона известна, а высота — нет. Ее нужно сосчитать. Для этого потребуется значение острого угла. Высота образует в параллелограмме прямоугольный треугольник. В нем катет равен произведению синуса острого угла, который ему противолежит, на гипотенузу.

Пусть известная сторона параллелограмма — это «а». Тогда высота будет записана как в * sin 30º. Таким образом, площадь основания равна а * в * sin 30º.

С боковыми гранями все проще. Они — прямоугольники. Поэтому их площади — это произведение одной стороны на другую. Первая — а * с, вторая — в * с.

Осталось объединить все в одну формулу и сосчитать:

S = 2 * (а * в * sin 30º + а * с + в * с )

После подстановки всех величин получается, что искомая площадь равна 188 см².

Ответ. S = 188 см².

Источник

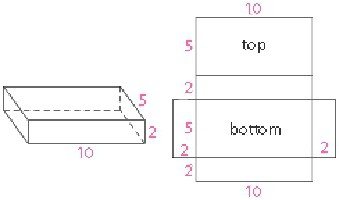
Как найти полную поверхность параллелепипеда

Чтобы найти полную поверхность параллелепипеда, необходимо просуммировать площади его боковой поверхности и двух оснований. В зависимости от вида фигуры, грани могут быть параллелограммами, прямоугольниками или квадратами.

Инструкция

Параллелепипед — многогранная пространственная фигура, состоящая из шести четырехугольников, имеющих форму параллелограмма. Различают прямой и наклонный параллелепипед. В первом боковые грани представляют собой вертикальные прямоугольники, во втором они составляют углы с основаниями, отличные от 90°.

У этой фигуры есть два распространенных частных случая – прямоугольный и кубический. В прямоугольном параллелепипеде все грани – прямоугольники, в кубе – квадраты. Эти формы часто встречаются при решении задач на построение трехмерных проекций, определение длины вектора, составление графических химических формул структуры молекулы и т.д.

Исходя из вышесказанного, можно найти полную поверхность параллелепипеда для любой его разновидности. Для этого достаточно просуммировать площади всех граней фигуры:S = 4•Sбг + 2•Sо.

Первое слагаемое называется боковой поверхностью. Рассмотрите боковые грани, которые, по свойству параллелепипеда, попарно параллельны и равны. Это параллелограммы со сторонами с, b или а, b. Известно, что площадь этой двухмерной фигуры равна произведению основания на высоту:4•Sбг = (2•а + 2•с)•h.

Нетрудно заметить, что выражение 2•а + 2•с – это периметр основания параллелепипеда, следовательно:4•Sбг = Po•h.

Площадь основания So представляет собой произведение стороны горизонтального параллелограмма на высоту ho, проведенную к ней:So = 2•с•ho.

Подставьте обе величины в общую формулу:S = P•h + 2•с•ho.

У прямого параллелепипеда высота равна длине бокового ребра:S = P•b + 2•с•ho.

То же утверждение справедливо для прямоугольного параллелепипеда, а площадь основания представляет собой удвоенное произведение длин сторон:S = 2•(а + с)•b + 2•а•с = 2•(а•b + b•с + а•с).

У куба все измерения равны:S = 6•а².

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Как найти площадь поверхности параллелепипеда

Призма, у которой все стороны являются параллелограммами, и есть параллелепипед. Коробка, холодильник, здания, аквариум, кусочек сахара-рафинада – вот немногие примеры параллелепипеда в нашей повседневной жизни.

1

Разновидность, свойства параллелепипеда

Различают прямой и наклонный параллелепипед.

Прямой – это тот, ребра которого перпендикулярны основанию плоскости. Если основанием является прямоугольник, тогда фигура называется прямоугольным параллелепипедом. Если основанием и боковыми гранями является квадрат – куб.

Наклонный параллелепипед имеет наклон боковых граней к основанию под углом, отличным от 90 градусов.

Свойства параллелепипеда:

Противоположные грани равны и параллельны.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов 3-х его измерений, т.е. D^2=a^2+b^2+c^2.
Все диагонали пересекаются в одной точке, делящей их пополам.
Параллелепипед симметричен по отношению к середине его диагонали.

2

Площадь поверхности параллелепипеда

Как известно, существует несколько разновидностей параллелепипеда, поэтому и формулы для нахождения площади полной поверхности будут различаться.

Прямоугольный параллелепипед

У прямоугольного параллелепипеда основания и боковые грани – прямоугольники.

В данном случае используется формула S(п)=2(a*b+b*c+a*c).

Куб

Куб является частным случаем параллелепипеда. У него все стороны равны. Воспользовавшись формулой выше, получаем S(п)=2(a*a+a*a+a*a). В результате преобразования можно получить сокращенную версию формулы для нахождения площади полной поверхности куба S(п)=6*a^2.

Прямой параллелепипед

В то время, когда у прямоугольного параллелепипеда основанием является прямоугольник, прямой может иметь там любой параллелограмм, будь то квадрат или ромб. Именно поэтому формула для нахождения площади полной поверхности такой фигуры будет иной: S(п)=S(б)+2S(о), где S(о) – площадь основания, S(б) – площадь боковой поверхности.

Площадь основания S(о) будет зависеть от того, какая фигура лежит в основании.

В свою очередь, площадь боковой поверхности рассчитывается, как S(б)=P(о)*h, где P(о) – периметр основания, h – высота.

3

Как найти площадь поверхности параллелепипеда – пример

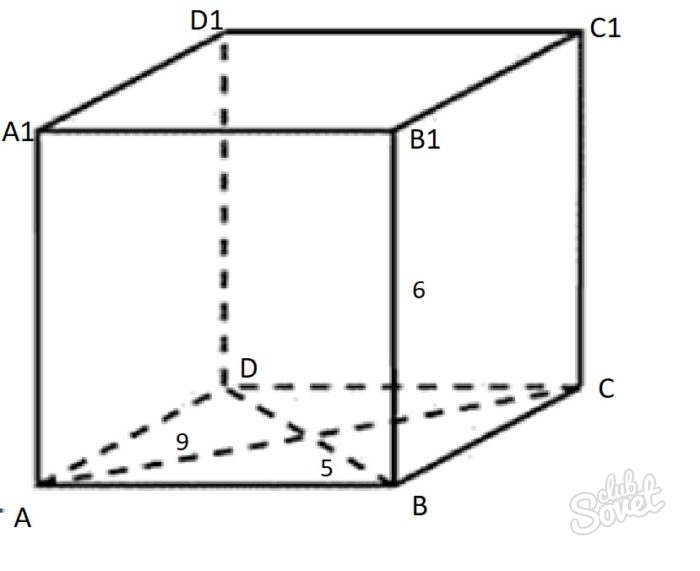
Основанием прямого параллелепипеда служит ромб. Меньшая его диагональ равна 5 см, большая диагональ – 9 см, периметр равен 20 см. Найти площадь полной поверхности параллелепипеда, если его высота равна 6 см.

Для решения задачи понадобится формула S(п)=S(б)+2S(о).

В основании параллелепипеда лежит ромб, следовательно, его площадь необходимо найти.

S(б)=P(о)*h=20*6=120 см^2

S(о)=(d1+d2)/2=(5+9)/2=7см^2

Подставив данные в формулу, получаем S(п)=120+2*7=134 см^2.

Человека окружает множество вещей-параллелепипедов. Системный блок компьютера, кирпич, шкаф, различные архитектурные сооружения. Даже не замечая, параллелепипед занял значимое место в современном мире.

Источник

ВИДЕОУРОК

Что он собой представляет?

Какие существуют виды параллелепипедов?

Некоторые математические особенности параллелепипеда

Площади прямого параллелепипеда

Площади прямоугольного параллелепипеда

Площади куба

Площади наклонного параллелепипеда

Задачи по теме

Как найти полную поверхность параллелепипеда

Как найти площадь поверхности параллелепипеда

1 Разновидность, свойства параллелепипеда

2 Площадь поверхности параллелепипеда

Прямоугольный параллелепипед

Куб

Прямой параллелепипед

3 Как найти площадь поверхности параллелепипеда – пример

1

Разновидность, свойства параллелепипеда

2

Площадь поверхности параллелепипеда

3

Как найти площадь поверхности параллелепипеда – пример