Полная условная энтропия
Для
определения полной условной энтропии,
каждая частная условная энтропия
умножается на вероятность соответствующего
состояния и все произведения складываются.
pi
= p(xi)
– вероятность
наступления события xi
;
pi
* p(yj
/ xi)
= pij
Тогда
; H(Y
/ x) = M[ — log P(y / x)]
В
целом полная условная энтропия
характеризует степень неопределённости
состояния системы Y,
оставшуюся после того, как состояние
системы X
полностью определилось.
Пример:
Имеются две
системы, объединённые в одну, вероятности
состояния которых заданы таблицей
совместных вероятностей. Определить
полную условную энтропию.
Определим
вероятности каждого события. Для этого
складываем pij
по столбцам.
-
xi
& yix1
x2
x3
rj
y1
0.1
0.2
0
0.3
y2
0
0.3
0
0.3
y3
0
0.2
0.2
0.4
pi
0.1
0.7
0.2
Построить
таблицу условных вероятностей p(y
/ x).
в каждой строке
-
yi&
xjx1
x2
x3
y1
1
0.2/0.7
0
y2
0
0.3/0.7
0
y3
0
0.2/0.7
1
бит/символ
Составим
таблицу условных вероятностей P(x
/ y).
-
xi&
yix1
x2
x3
y1
0.1/0.3
0.2/0.3
0
y2
0
1
0
y3
0
0.2/0.4
0.2/0.4
H(x
/ y) = 0.3[(0.1/0.3)
+ (0.2/0.3)]+
0.4[(0.2/0.4
+ (0.2/0.4)]
= 0.68 бит/символ
Н
— характеризует потери сигналов при
прохождении через канал связи.
Теорема сложения энтропий
Если
две системы X
и Y
объединятся в
одну, то энтропия объединений системы
равна энтропии одной из систем плюс
условная энтропия второй системы
относительно первой.
H(x,
y) = H(x) + H(y / x)
Доказательство
этой теоремы:
Запишем
H(x, y)
через.
математическое ожидание
H(x,
y) = M[ — log p(x, y)]
По
теореме умножения вероятностей
p(x,
y) = p(x) * p(y / x)
log
p(x, y) = log p(x) + log p(y / x)
M[x,
y] = M[ — log p(x)] + M[ — log p(y / x)]
H(x,
y) = H(x) + H(y / x)
Интерес
представляют частные случаи:
-
Когда
системы независимы, условная энтропия
H(y / x) =
H(y) и получаем
теорему сложения энтропий H(x,
y) = H(x) + H(y).
H(x,
y)
H(x) + H(y)
-
Когда
состояние одной системы X
полностью
определяет состояние другой системы
Y.
В этом случае условная энтропия равна
нулю.
H(y
/ x) = 0 H(y, x) = H(x)
Пример:
Передаются два элемента a,
b. Определить
количество переданной информации в
случае, когда:
1)
Элементы взаимозависимы и не равновероятны
p(a)
=
; p(b)
=; p(a
/ a) =p(b
/ a) =
p(b
/ b) = 0 p(a / b) = 1
I
= H – вероятность
события а
I
= H = — p(a)[ p(a / a) log p(a / a) + p(b / a) log p(b / a) ] –
p(b)[ p(a / b) log p(a / b) + p(b / b) log p(b / b)] = 0.685
бит/символ .
2)
не равновероятны и независимы:
p(a)
=
;p(b)
=
I
= — p(a) log p(a) – p(b) log p(b) = —
log
—
log
= 0.815бит/символ
3)
элементы независимы и равновероятны:
p(a)
= p(b) =
; I
= log2
= 1
Соседние файлы в папке Lec
- #
- #
Пусть имеются две случайные величины X и Y. Если они зависимые, то значения, принимаемые одной из них, могут оказывать влияние на значения, принимаемые другой. Приведем простейший пример: пусть у нас есть урна с двумя шарами — белым и черным. Случайная величина X — цвет шара, вытащенного первым, случайная величина Y — цвет шара, вытащенного вторым. Понятно, что если мы ЗНАЕМ значение какой-либо одной из этих случайных величин, мы также точно знаем значение и второй. Для описания подобной зависимости и используется условная энтропия.
Для расчета условной энтропии нам нужны вероятности появления всех пар значений случайных величин X и Y. В поле ввода ниже нужно ввести матрицу, элемент которой на пересечении i-ой строки и j-ого столбца равен — вероятности того, что X и Y примут значения
, соответственно. Строки соответствуют значениям случайной величины X —
а столбцы — случайной величины Y —
.
Нажав кнопку «Детали расчета» вы сможете увидеть расчет средних условных энтропий. Формулы расчета в общем виде приведены под калькулятором.
Условная энтропия
Таблица вероятности состояний (X, Y) ~ p
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Формула условной энтропии
Частная условная энтропия — это количество информации, или энтропия, которая характеризует степень неопределенности значений случайной величины Y, остающуюся после того, как стало известно, что случайная величина X приняла значение
.
Средняя или полная условная энтропия H(Y|X) — это количество информации, или энтропия, которая характеризует степень неопределенности значений случайной величины Y, остающуюся после того, как стало известно значение, принятое случайной величиной X.
Средняя условная энтропия Y по X определяется как
Предполагается что выражения вида и
трактуются как ноль.
Значения для каждой строки вычисляются суммированием ячеек в этой строке, а
— даны.
Эта формула, по факту, является взвешенным средним значением частных условных энтропий для каждого из возможных значений X.
Веса пропорциональны значению p(x), то есть
Мы ежедневно работаем с информацией из разных источников. При этом каждый из нас имеет некоторые интуитивные представления о том, что означает, что один источник является для нас более информативным, чем другой. Однако далеко не всегда понятно, как это правильно определить формально. Не всегда большое количество текста означает большое количество информации. Например, среди СМИ распространена практика, когда короткое сообщение из ленты информационного агентства переписывают в большую новость, но при этом не добавляют никакой «новой информации». Или другой пример: рассмотрим текстовый файл с романом Л.Н. Толстого «Война и мир» в кодировке UTF-8. Его размер — 3.2 Мб. Сколько информации содержится в этом файле? Изменится ли это количество, если файл перекодировать в другую кодировку? А если заархивировать? Сколько информации вы получите, если прочитаете этот файл? А если прочитаете его второй раз?
По мотивам открытой лекции для Computer Science центра рассказываю о том, как можно математически подойти к определению понятия «количество информации».
В классической статье А.Н. Колмогорова «Три подхода к определению понятия количества информации» (1965) рассматривают три способа это сделать:
-
комбинаторный (информация по Хартли),
-
вероятностный (энтропия Шеннона),
-
алгоритмический (колмогоровская сложность).
Мы будем следовать этому плану.
Комбинаторный подход: информация по Хартли
Мы начнём самого простого и естественного подхода, предложенного Хартли в 1928 году.
Пусть задано некоторое конечное множество . Количеством информации в
будем называть
.
Можно интерпретировать это определение следующим образом: нам нужно битов для описания элемента из
.
Почему мы используем биты? Можно использовать и другие единицы измерения, например, триты или байты, но тогда нужно изменить основание логарифма на 3 или 256, соответственно. В дальшейшем все логарифмы будут по основанию 2.
Этого определения уже достаточно для того, чтобы измерить количество информации в некотором сообщении. Пусть про стало известно, что
. Теперь нам достаточно
битов для описания
, таким образом нам сообщили
битов информации.
Пример
Загадано целое число
от
до
. Нам сообщили, что
делится на
. Сколько информации нам сообщили?
Воспользуемся рассуждением выше.
(Тот факт, что некоторое сообщение может содержать нецелое количество битов, может показаться немного неожиданным.)
Можно ещё сказать, что сообщение, уменшающее пространство поиска в раз приносит
битов информации. В данном примере пространство поиска уменьшилось в 1000/166 раз.
Интересно, что одного этого определения уже достаточно для того, чтобы решать довольно нетривиальные задачи.
Применение: цена информации
Загадано целое число
от
до
. Разрешается задавать любые вопросы на ДА/НЕТ. Если ответ на вопрос «ДА», то мы должны заплатить рубль, если ответ «НЕТ» — два рубля. Сколько нужно заплатить для отгадывания числа
?
Любой вопрос можно сформулировать как вопрос о принадлежности некоторому множеству, поэтому мы будем считать, что все вопросы имеют вид «?» для некоторого множества
.
Каким образом нужно задавать вопросы? Нам бы хотелось, чтобы вне зависимости от ответа цена за бит информации была постоянной. Другими словами, в случае ответа «НЕТ» и заплатив два рубля мы должны узнать в два больше информации, чем при ответе «ДА». Давайте запишем это формально.
Потребуем, чтобы
Пусть , тогда
. Подставляем и получаем, что
Это эквивалентно квадратному уравнению Положительный корень этого уравнения
. Таким образом, при любом ответе мы заплатим
рублей за бит информации, а в сумме мы заплатим примерно
рублей (с точностью до округления).
Осталось понять, как выбирать такие множества . Будем выбирать в качестве
непрерывные отрезки прямой. Пусть нам известно, что
принадлежит отрезку
(изначально это отрезок
). В следующего множества
возмём отрезок
, где
. Тогда за каждый заплаченный рубль текущий отрезок будет уменьшаться в
раз. Когда длина отрезка станет меньше единицы, мы однозначно определим
. Поэтому цена отгадывания не будет превосходить
Приведённое рассуждение доказывает только верхнюю оценку. Можно доказать и нижнюю оценку: для любого способа задавать вопросы будет такое число , для отгадывания которого придётся заплатить не менее
рублей.
Вероятностный подход: энтропия Шеннона
Вероятностный подход, предложенный Клодом Шенноном в 1948 году, обобщает определение Хартли на случай, когда не все элементы множества являются равнозначными. Вместо множества в этом подходе мы будем рассматривать вероятностное распределение на множестве и оценивать среднее по распределению количество информации, которое содержит случайная величина.
Пусть задана случайная величина , принимающая
различных значений с вероятностями
. Энтропия Шеннона случайной величины
определяется как
(По непрерывности тут нужно доопределить .)
Энтропия Шеннона оценивает среднее количество информации (математическое ожидание), которое содержится в значениях случайной величины.
При первом взгляде на это определение, может показаться совершенно непонятно откуда оно берётся. Шеннон подошёл к этой задаче чисто математически: сформулировал требования к функции и доказал, что это единственная функция, удовлетворяющая сформулированным требованиям.
Я попробую объяснить происхождение этой формулы как обобщение информации по Хартли. Нам бы хотелось, чтобы это определение согласовывалось с определением Хартли, т.е. должны выполняться следующие «граничные условия»:
Будем искать в виде математического ожидания количества информации, которую мы получаем от каждого возможного значения
.
Как оценить, сколько информации содержится в событии ? Пусть
— всё пространство элементарных исходов. Тогда событие
соответствует множеству элементарных исходов меры
. Если произошло событие
, то размер множества согласованных с этим событием элементарных исходов уменьшается с
до
, т.е. событие
сообщает нам
битов информации. Тут мы пользуемся тем, что количество информации в сообщении, которое уменьшает размер пространство поиска в
раз приносит
битов информации.
Примеры
Свойства энтропии Шеннона
Для случайной величины , принимающей
значений с вероятностями
, выполняются следующие соотношения.
-
.
-
распределение
вырождено.
-
.
-
распределение
равномерно.
Чем распределение ближе к равномерному, тем больше энтропия Шеннона.
Энтропия пары
Понятие энтропии Шеннона можно обобщить для пары случайных величин. Аналогично это обощается для тройки, четвёрки и т.д.
Пусть совместно распределённые случайные величины и
принимают значения
и
, соответственно. Энтропия пары случайных величин
и
определяется следующим соотношением:
Примеры
Рассмотрим эксперимент с выбрасыванием двух игральных кубиков — синего и красного.
Свойства энтропии Шеннона пары случайных величин
Для энтропии пары выполняются следующие свойства.
Условная энтропия Шеннона
Теперь давайте научимся вычислять условную энтропию одной случайной величины относительно другой.
Условная энтропия относительно
определяется следующим соотношением:
Примеры
Рассмотрим снова примеры про два игральных кубика.
Свойства условной энтропии
Условная энтропия обладает следующими свойствами
Взаимная информация
Ещё одна информационная величина, которую мы введём в этом разделе — это взаимная информация двух случайных величин.
Информация в о величине
(взаимная информация случайных величин
и
) определяется следующим соотношением
Примеры
И снова обратимся к примерам с двумя игральными кубиками.
Свойства взаимной информации
Выполняются следующие соотношения.
-
. Т.е. определение взаимной информации симметрично и его можно переписать так:
-
Или так:
.
-
и
.
-
.
-
.
Все информационные величины, которые мы определили к этому моменту можно проиллюстрировать при помощи кругов Эйлера.
Мы пойдём дальше и рассмотрим информационную величину, зависящую от трёх случайных величин.
Пусть ,
и
совместно распределены. Информация в
о
при условии
определяется следующим соотношением:
Свойства такие же как и обычной взаимной информации, нужно только добавить соответствующее условие ко всем членам.
Всё, что мы успели определить можно удобно проиллюстрировать при помощи трёх кругов Эйлера.
Из этой иллюстрации можно вывести все определения и соотношения на информационные величины.
Мы не будем продолжать дальше и рассматривать четыре случайные величины по трём причинам. Во-первых, рисовать четыре круга Эйлера со всеми возможными областями — это непросто. Во-вторых, для двух и трёх случайных величин почти все возможные соотношения можно вывести из кругов Эйлера, а для четырёх случайных величин это уже не так. И в третьих, уже для трёх случайных величин возникают неприятные эффекты, демонстрирующие, что дальше будет хуже.
Рассмотрим треугольник в пересечении всех трёх кругов ,
и
. Этот треугольник соответствуют взаимной информации трёх случайных величин
. Проблема с этой информационной величиной заключается в том, что ей не удаётся придать какой-то «физический» смысл. Более того, в отличие от всех остальных величин на картинке
может быть отрицательной!
Рассмотрим пример трёх случайных величин равномерно распределённых на . Пусть
и
будут независимы, а
. Легко проверить, что
. При этом
. В то же время
. Получается следующая картинка.
Мы знаем, что . При этом
. Получается, что
, а
, т.е. для таких случайных величин
.
Применение энтропии Шеннона: кодирование
В этом разделе мы обсудим, как энтропия Шеннона возникает в теории кодирования. Будем рассматривать коды, которые кодируют каждый символ по отдельности.
Пусть задан алфавит . Код — это отображение из
в
. Код
называется однозначно декодируемым, если любое сообщение, полученное применением
к символам некоторого текста, декодируется однозначно.
Код называется префиксным (prefix-free), если нет двух символов и
таких, что
является префиксом
.
Префиксные коды являются однозначно декодируемыми. Действительно, при декодировании префиксного кода легко понять, где находятся границы кодов отдельных символов.
Теорема [Шеннон]. Для любого однозначно декодируемого кода существует префиксный код с теми же длинами кодов символов.
Таким образом для изучения однозначно декодируемых кодов достаточно рассматривать только префиксные коды.
Задача об оптимальном кодировании.
Дан текст . Нужно найти такой код
, что
Пусть . Обозначим через
частоту, с которой символ
встречается в
. Тогда выражение выше можно переписать как
Следующая теорема могла встречаться вам в курсе алгоритмов.
Теорема [Хаффман]. Код Хаффмана, построенный по , является оптимальным префиксным кодом.
Алгоритм Хаффмана по набору частот эффективно строит оптимальный код для задачи оптимального кодирования.
Связь с энтропией
Имеют место две следующие оценки.
Теорема [Шеннон]. Для любого однозначно декодируемого кода выполняется
Теорема [Шеннон]. Для любых значений существует префиксный код
, такой что
Рассмотрим случайную величину , равномерно распределённую на символах текста
. Получим, что
. Таким образом, эти две теоремы задают оценку на среднюю длину кода символа при оптимальном кодировании, т.е. и для кодирования Хаффмана.
Следовательно, длину кода Хаффмана текста можно оценить, как
Применение энтропии Шеннона: шифрования с закрытым ключом
Рассмотрим простейшую схему шифрования с закрытым ключом. Шифрование сообщения с ключом шифрования
выполняется при помощи алгоритма шифрования
. В результате получается шифрограмма
. Зная
получатель шифрограммы восстанавливает исходное сообщение
:
.
Мы будем анализировать эту схему с помощью аппарата энтропии Шеннона. Пусть и
являются случайными величинами. Противник не знает
и
, но знает
, которая так же является случайной величиной.
Для совершенной схемы шифрования (perfect secrecy) выполняются следующие соотношения:
-
, т.е. шифрограмма однозначно определяется по ключу и сообщению.
-
, т.е. исходное сообщение однозначно восстанавливается по шифрограмме и ключу.
-
, т.е. в отсутствие ключа из шифрограммы нельзя получить никакой информации о пересылаемом сообщении.
Теорема [Шеннон]. , даже если условие
нарушается (т.е. алгоритм
использует случайные биты).
Эта теорема утверждает, что для совершенной схемы шифрования длина ключа должна быть не менее длины сообщения. Другими словами, если вы хотите зашифровать и передать своему знакомому файл размера 1Гб, то для этого вы заранее должны встретиться и обменяться закрытым ключом размера не менее 1Гб. И конечно, этот ключ можно использовать только однажды. Таким образом, самая оптимальная совершенная схема шифрования — это «одноразовый блокнот», в котором длина ключа совпадает с длиной сообщения.
Если же вы используете ключ, который короче пересылаемого сообщения, то шифрограмма раскрывает некоторую информацию о зашифрованном сообщении. Причём количество этой информации можно оценить, как разницу между энтропией сообщения и энтропией ключа. Если вы используете пароль из 10 символов при пересылке файла размера 1Гб, то вы разглашаете примерно 1Гб – 10 байт.
Это всё звучит очень печально, но не всё так плохо. Мы ведь никак не учитываем вычислительную мощь противника, т.е. мы не ограничиваем количество времени, которое противнику потребуется на выделение этой информации.
Современная криптография строится на предположении об ограниченности вычислительных возможностей противника. Тут есть свои проблемы, а именно отсутствие математического доказательства криптографической стойкости (все доказательства строятся на различных предположениях), так что может оказаться, что вся эта криптография бесполезна (подробнее можно почитать в статье о мирах Рассела Импальяццо, которая переведена на хабре), но это уже совсем другая история.
Доказательство. Нарисуем картинку для трёх случайных величин и отметим то, что нам известно.
-
.
-
, следовательно
, а значит
.
-
(по свойству взаимной информации), следовательно
, а значит
.
-
. Таким образом,
В доказательстве мы действительно не воспользовались тем, что .
Алгоритмический подход: колмогоровская сложность
Подход Шеннона хорош для случайных величин, но если мы попробуем применить его к текстам, то выходит, что количество информации в тексте зависит только от частот символов, но не зависит от их порядка. При таком подходе получается, что в «Войне и мире» и в тексте, который получается сортировкой всех знаков в «Войне и мире», содержится одинаковое количество информации. Колмогоров предложил подход, позволяющий измерять количество информации в конкретных объектах (строках), а не в случайных величинах.
Внимание. До этого момента я старался следить за математической строгостью формулировок. Для того, чтобы двигаться дальше в том же ключе, мне потребовалось бы предположить, что читатель неплохо знаком с математической логикой и теорией вычислимости. Я пойду более простым путём и просто буду махать руками, заметая под ковёр некоторые подробности. Однако, все утверждения и рассуждения дальше можно математически строго сформулировать и доказать.
Нам потребуется зафиксировать способ описания битовой строки. Чтобы не углубляться в рассуждения про машины Тьюринга, мы будем описывать строки на языках программирования. Нужно только сделать оговорку, что программы на этих языках будут запускаться на компьютере с неограниченным объёмом оперативной памяти (иначе мы получили бы более слабую вычислительную модель, чем машина Тьюринга).
Сложностью строки
относительно языка программирования
называется длина кратчайшей программы, которая выводит
.
Таким образом сложность «Войны и мира» относительноя языка Python — это длина кратчайшей программы на Python, которая печатает текст «Войны и мира». Естественным образом сложность отсортированной версии «Войны и мира» относительно языка Python получится значительно меньше, т.к. её можно предварительно закодировать при помощи RLE.
Сравнение языков программирования
Дальше нам потребуется научиться любимой забаве всех программистов — сравнению языков программирования.
Будем говорить, что язык не хуже языка программирования
и обозначать
, если существует константа
такая, что для для всех
выполняется
Исходя из этого определения получается, что язык Python не хуже (!) этого вашего Haskell! И я это докажу. В качестве константы мы возьмём длину реализации интепретатора Haskell на Python. Таким образом, любая программа на Haskell переделывается в программу на Python просто дописыванием к ней интерпретатора Haskell на Python.
Соломонов и Колмогоров пошли дальше и доказали существования оптимального языка программирования.
Теорема [Соломонова-Колмогорова]. Существует способ описания (язык программирования) такой, что для любого другого способа описания
выполняется
.
И да, некоторые уже наверное догадались, что — это JavaScript. Или любой другой Тьюринг полный язык программирования.
Это приводит нас к следующему определению, предложенному Колмогоровым в 1965 году.
Колмогоровской сложностью строки будем называть её сложность относительно оптимального способа описания
и будем обозначать
.
Важно понимать, что при разных выборах оптимального языка программирования колмогоровская сложность будет отличаться, но только на константу. Для любых двух оптимальных языков программирования
и
выполняется
и
, т.е. существует такая константа
, что
Это объясняет, почему в этой науке аддитивные константы принято игнорировать.
При этом для конкретной строки и конкретного выбора колмогоровская сложность определена однозначно.
Свойства колмогоровской сложности
Начнём с простых свойств. Колмогоровская сложность обладает следующими свойствами.
Первое свойство выполняется потому, что мы всегда можем зашить строку в саму программу. Второе свойство верно, т.к. из программы, выводящей строку , легко сделать программу, которая выводит эту строку дважды.
Примеры
Несжимаемые строки
Важнейшее свойство колмогоровской сложности заключается в существовании сложных (несжимаемых строк). Проверьте себя и попробуйте объяснить, почему не бывает идеальных архиваторов, которые умели бы сжимать любые файлы хотя бы на 1 байт, и при этом позволяли бы однозначно разархивировать результат.
В терминах колмогоровской сложности это можно сформулировать так.
Вопрос. Существует ли такая длина строки
, что для любой строки
колмогоровская сложность
меньше
?
Следующая теорема даёт отрицательный ответ на этот вопрос.
Теорема. Для любого существует
такой, что
.
Доказательство. Битовых строк длины всего
. Число строк сложности меньше
не превосходит число программ длины меньше
, т.е. таких программ не больше чем
Таким образом, для какой-то строки гарантированно не хватит программы.
Верна и более сильная теорема.
Теорема. Существует такое, что для
слов длины
верно
Другими словами, почти все строки длины имеют почти максимальную сложность.
Колмогоровская сложность: вычислимость
В этом разделе мы поговорим про вычислимость колмогоровской сложности. Я не буду давать формально определение вычислимости, а буду опираться на интуитивные предствления читателей.
Теорема. Не существует программы, которая по двоичной записи числа выводит строку
, такую что
.
Эта теорема говорит о том, что не существует программы-генератора, которая умела бы генерировать сложные строки по запросу.
Доказательство. Проведём доказетельство от противного. Пусть такая программа существует и
. Тогда с одной стороны сложность
не меньше
, а с другой стороны мы можем описать
при помощи
битов и кода программы
.
Это приводит нас к противоречию, т.к. при достаточно больших значениях неизбежно станет больше, чем
.
Как следствие мы получаем невычислимость колмогоровской сложности.
Следствие. Отображение не является вычислимым.
Опять же, предположим, что это нет так и существует программа , которая по строку вычисляет её колмогоровскую сложность. Тогда на основе программы
можно реализовать программу
из теоремы выше: она будет перебирать все строки длины не более
и находить лексикографически первую, для которой сложность будет не меньше
. А мы уже доказали, что такой программы не существует.
Связь с энтропией Шеннона
Теорема. Пусть длины
содержит
единиц и
нулей, тогда
Я надеюсь, что вы уже узнали энтропию Шеннона для случайной величины с двумя значениями с вероятностями и
.
Для колмогоровской сложности можно проделать весь путь, который мы проделали для энтропии Шеннона: определить условную колмогоровскую сложность, сложность пары строк, взаимную информацию и условную взаимную информацию и т.д. При этом формулы будут повторять формулы для энтропии Шеннона с точностью до . Однако это тема для отдельной статьи.
Применение колмогоровской сложности: бесконечность множества простых чисел
Начнём с довольно игрушечного применения. С помощью колмогоровской сложности мы докажем следующую теорему, знакомую нам со школы.
Теорема. Простых чисел бесконечно много.
Очевидно, что для доказательства этой теоремы никакая колмогоровская сложность не нужна. Однако на этом примере я смогу продемонстрировать основные идеи применения колмогоровской сложности в более сложных ситуациях.
Доказательство. Проведём доказательство от обратного. Пусть существует всего простых чисел:
. Тогда любое натуральное
раскладывается на степени простых:
т.е. определяется набором степеней . Каждое
, т.е. задаётся
битами. Поэтому любое
можно задать при помощи
битов (помним, что
— это константа).
Теперь воспользуемся теоремой о существовании несжимаемых строк. Как следствие, мы можем заключить, что существуют -битовые числа
сложности не менее
(можно взять сложную строку и приписать в начало единицу). Получается, что сложное число можно задать при помощи небольшого числа битов.
Противоречие.
Применение колмогоровской сложности: алгоритмическая случайность
Колмогоровская сложность позволяет решить следующую проблему из классической теории вероятностей.
Пусть в лаборатории живёт обезьянка, которую научили печатать на печатной машинке так, что каждую кнопку она нажимает с одинаковой вероятность. Вам предлагается посмотреть на лист печатного текста и сказать, верите ли вы, что его напечатала эта обезьянка. Вы смотрите на лист и видите, что это первая страница «Гамлета» Шекспира. Поверите ли вы? Очевидно, что нет. Хорошо, а если это не Шекспир, а, скажем, текст детектива Дарьи Донцовой? Скорей всего тоже не поверите. А если просто какой-то набор русских слов? Опять же, очень сомневаюсь, что вы поверите.
Внимание, вопрос. А как объяснить, почему вы не верите? Давайте для простоты считать, что на странице помещается 2000 знаков и всего на машинке есть 80 знаков. Вы можете резонно заметить, что вероятность того, что обезьянка случайным образом породила текст «Гамлета» порядка , что астрономически мало. Это верно.
Теперь предположим, что вам показали текст, который вас устроил (он с вашей точки зрения будет похож на «случайный»). Но ведь вероятность его появления тоже будет порядка . Как же вы определяете, что один текст выглядит «случайным», а другой — не выглядит?
Колмогоровская сложность позволяет дать формальный ответ на этот вопрос. Если у текста отстутствует короткое описание (т.е. в нём нет каких-то закономерностей, которые можно было бы использовать для сжатия), то такую строку можно назвать случайной. И как мы увидели выше почти все строки имеют большую колмогоровскую сложность. Поэтому, когда вы видите строку с закономерностями, т.е. маленькой колмогоровской сложности, то это соответствует очень редкому событию. В противоположность наблюдению строки без закономерностей. Вероятность увидеть строку без закономерностей близка к 1.
Это обобщается на случай бесконечных последовательностей. Пусть . Как определить понятие случайной последовательности?
(неформальное определение)
Последовательность случайна по Мартину–Лёфу, если каждый её префикс является несжимаемым.
Оказывается, что это очень хорошее определение случайных последовательностей, т.к. оно обладает ожидаемыми свойствами.
Свойства случайных последовательностей
-
Почти все последовательности являются случайными по Мартину–Лёфу, а мера неслучайных равна
.
-
Всякая случайная по Мартину-Лёфу последовательность невычислима.
-
Если
случайная по Мартин-Лёфу, то
Заключение
Если вам интересно изучить эту тему подробнее, то я рекомендую обратиться к следующим источникам.
-
Верещагин Н.К., Щепин Е.В. Информация, кодирование и предсказание. МЦНМО. (нет в свободном доступе, но pdf продаётся за копейки)
-
В.А. Успенский, А.Х. Шень, Н.К. Верещагин. Колмогоровская сложность и алгоритмическая случайность.
-
Курс «Введение в теорию информации» А.Е. Ромащенко в Computer Science клубе.
Если вам интересны подобные материалы, подписывайтесь в соцсетях на CS клуб и CS центр, а так же на наши каналы на youtube: CS клуб, CS центр.
Содержание
Для понимания материалов настоящего раздела рекомендуется ознакомиться с разделом ТЕОРИЯ ВЕРОЯТНОСТЕЙ.
.
Статус документа: черновик.
Теория информации по Шеннону
Энтропия
Пусть случайное событие заключается в осуществлении одного из несовместимых состояний $ S_{1},dots,S_n $, вероятности появления которых даются таблицей
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1.
$$
Эти вероятности известны, но это — все, что нам известно относительно того какое состояние осуществится. Можно ли найти «меру» насколько велик выбор из такого набора состояний и сколь неопределено для нас событие?
Если наше событие (опыт) состоит в определении цвета первой встретившейся нам вороны, то мы можем почти с полной уверенностью рассчитывать, что
этот цвет будет черным. Несколько менее определено событие (опыт), состоящее в выяснении того, окажется ли первый встреченный нами человек левшой или нет — здесь тоже предсказать результаты опыта можно, почти не колеблясь, но опасения в относительно правильности этого предсказания будут более обоснованны, чем в предыдущем случае. Значительно труднее предсказать заранее пол первого встретившегося нам на улице человека. Но и этот опыт имеет относительно небольшую степень неопределенности по сравнению, например с попыткой определить победителя в чемпионате страны по футболу с участием двадцати совершенно незнакомых нам команд.
Для практики важно уметь численно оценивать степень неопределенности самых разнообразных случайных событий (опытов), чтобы иметь возможность сравнивать их с этой стороны. Искомая численная характеристика должна быть функцией числа $ n_{} $ возможных состояний. Некоторые свойства этой функции $ f(n) $ определяются соображениями здравого смысла. При $ n_{}=1 $ событие вообще не является случайным, т.е. следует положить $ f(1)=0 $. При возрастании числа $ n_{} $ возможных состояний эта функция должна возрастать поскольку увеличение количества возможных исходов опыта увеличивает неопределенность в предсказании его результатов.
Идем далее: рассмотрим два независимых события $ A_{} $ и $ B_{} $. Пусть событие $ A_{} $ имеет $ k_{} $ равновероятных исходов, а событие $ B_{} $ имеет $ ell_{} $ равновероятных исходов. Рассмотрим событие, состоящее в произведении (совместном осуществлении) событий $ A_{} $ и $ B_{} $, обозначим это событие $ AB_{} $. Например, если событие $ A_{} $ заключается в появлении масти карты — бубновой
♦
, червовой
♥
, трефовой
♣
или пиковой
♠
—
при выборе ее из колоды в $ 36_{} $ карт, а событие $ B_{} $
заключается в появлении достоинства карты — шестерки,семерки, восьмерки, девятки, десятки, валета, дамы, короля или туза — при выборе ее из той же колоды, то событие $ AB_{} $ заключается в появлении конкретной карты колоды. Очевидно, что неопределенность события $ AB_{} $ больше неопределенности события $ A_{} $, так как к неопределенности $ A_{} $ добавляется неопределенность события $ B_{} $. Естественно потребовать, чтобы мера неопределенности события $ AB_{} $ была равна сумме неопределенностей, характеризующих события $ A_{} $ и $ B_{} $. Это требование обеспечивается следующим следующим свойством функции $ f_{} $:
$$
f(kell)=f(k)+f(ell) ,
$$
имеющего тот смысл, что число $ kell $ как раз и дает число возможных исходов события $ AB_{} $.
Последнее равенство наталкивает на мысль принять за меру неопределенности опыта, имеющего $ n_{} $ равновероятных исходов, число $ log n $. Можно доказать, что логарифмическая функция является единственной непрерывной функцией аргумента $ nin mathbb R $, удовлетворяющей такому функциональному уравнению. При этом выбор основания системы логарифмов несуществен, так как, в силу известной формулы $ log_b n = log_b a cdot log_a n $, переход от одной системы логарифмов к другой сводится лишь к умножению функции $ f(n)=log n $ на постоянный множитель $ log_b a $, т.е. равносилен простому изменению единицы измерения степени неопределенности. Единственным ограничением является естественное требование, чтобы основание было большим $ 1 $: число $ log_b n $ должно быть положительным
Как правило, в дальнейшем будем пользоваться логарифмом по основанию $ 2_{} $; такой выбор в одном из последующих пунктов будет подкреплен некоторыми дополнительными «бонусами». В ближайших же пунктах будем просто писать $ log $ без указания основания.
Таблица вероятностей события, имеющего $ n_{} $ равновероятных состояний, имеет вид
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
1/n & 1/n & dots & 1/n
end{array}
$$
Так как общая неопределенность события по нашему условию равна $ log n $, то можно считать, что каждое в отдельности состояние вносит неопределенность равную $ frac{1}{n} log n = — frac{1}{n} log frac{1}{n} $. Но тогда естественно считать, что в событие, таблица вероятностей состояний которого имеет вид
$$
begin{array}{l|l|l}
S_1 & S_2 & S_3 \
hline
1/2 & 1/3 & 1/6
end{array}
$$
состояние $ S_1 $ вносит неопределенность, равную $ left( — frac{1}{2} log frac{1}{2} right) $, состояние $ S_2 $ — неопределенность, равную $ left( — frac{1}{3} log frac{1}{3} right) $, а состояние $ S_3 $ — неопределенность, равную
$ left( — frac{1}{6} log frac{1}{6} right) $, так что суммарная неопределенность события равна
$$
— frac{1}{2} log frac{1}{2} — frac{1}{3} log frac{1}{3} — frac{1}{6} log frac{1}{6} .
$$
Аналогично этому можно положить, что для события $ A_{} $ с таблицей вероятностей
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1
$$
мера его неопределенности равна
$$
-sum_{j=1}^n P_j log P_j = — P_1 log P_1 — P_2 log P_2 — dots — P_n log P_n = log frac{1}{P_1^{P_1} P_2^{P_2}times
dots times P_n^{P_n}} .
$$
Это число будем называть энтропией события $ A_{} $ и обозначать либо $ H(A) $ либо $ H(P_1,P_2,dots,P_n) $. Величина энтропии зависит от выбранного основания логарифмической функции; в случае основания $ 2_{} $ единицу измерения энтропии называют «бит», в случае основания $ 10_{} $ — «дит», в случае основания $ e=2.718281828459045dots $ — «нат».
В случае, когда $ P_j=0 $ при каком-то значении $ j_{} $, полагают $ P_j log P_j=0 $ (на основании известного из мат.анализа факта $ displaystyle lim_{xto +0} x log x = 0 $).
Можно проверить, что функция $ H(P_1,P_2,dots,P_n) $ симметрична относительно своих переменных; этот факт имеет тот
смысл, что мера неопределенности события не зависит от способа нумерации его возможных состояний. Кроме того эта функция
обладает следующими свойствами.
1.
$ H_{} $ непрерывна по каждой своей переменной;
2.
Если все вероятности одинаковы: $ P_1=1/n,P_2=1/n,dots,P_n=1/n $, то $ H_{} $ монотонно возрастающая функцией по $ n_{} $:
$$H bigg(underbrace{frac{1}{n},dots,frac{1}{n}}_n bigg)<Hbigg(underbrace{frac{1}{n+1},frac{1}{n+1},dots,frac{1}{n+1}}_{n+1}bigg) $$
(при равновероятности состояний, неопределенность события тем больше, чем больше количество этих состояний).
3.
При распадении какого-то события на два последовательных, величина $ H_{} $ должна вычисляться как взвешенная сумма составляющих значений $ H_{} $. Иллюстрирую на примере, который беру у Шеннона, но при этом излагаю в русском фольклорном стиле.
П
Пример. Предположим, что найденная Иваном-царевичем лягушка в течение минуты либо
-
превращается в бабу-Ягу с вероятностью $ 1/3 $;
-
превращается в красавицу Василису Премудрую с вероятностью $ 1/6 $;
-
остается лягушкой, и вероятность этого события равна $ 1/2 $.
Мера неопределенности этого события $ H(1/3,1/6,1/2) $. Теперь посчитаем меру неопределенности по-другому, объединив сначала первые два состояния в одно. Лягушка в течение минуты
-
превращается в женщину с вероятностью $ 1/2 $;
-
остается лягушкой с вероятностью $ 1/2 $.
Кроме того известно, что если лягушка точно превратилась в женщину, то ( условная ) вероятность того, что она стала бабой-Ягой равна $ 2/3 $, и, следовательно, вероятность появления Василисы Премудрой оказывается равной $ 1/3 $. В результате получаем два значения для функции $ H_{} $, именно $ H(1/2,1/2 ) $ и $ H(2/3 , 1/3 ) $.
Как должны быть связаны эти новые величины со старой — с $ H(1/3,1/6,1/2) $? Конечный результат у обоих событий одинаков, во втором случае мы просто искусственно «вставили» одно промежуточное событие. Так вот, имеет место равенство:
$$H(1/3,1/6,1/2)=H(1/2,1/2 )+frac{1}{2} H(2/3 , 1/3 ) , $$
здесь весовой множитель $ 1/2 $ в составе второго слагаемого возникает из-за того, что ситуация второго события происходит только в половине случаев.
♦
Формализуем: утверждается, что функция $ H_{} $ удовлетворяет условию
$$
H(P_1,P_2,P_3,dots,P_n)=H(P_1+P_2,P_3,dots,P_n)+(P_1+P_2)Hleft(frac{P_1}{P_1+P_2}, frac{P_2}{P_1+P_2} right) ;
$$
а уж из последнего можно вывести и еще более общее:
$$
H(P_1,dots,P_n)=H(P_1+dots+P_m,P_{m+1},dots,P_n)+
$$
$$
+(P_1+dots+P_m)Hleft(frac{P_1}{P_1+dots+P_m}, frac{P_2}{P_1+dots+P_m},dots,
frac{P_m}{P_1+dots+P_m} right)
$$
при $ forall min {2,dots,n-1} $.
Перечисленные свойства
1
—
3
оказываются настолько «жесткими», что будучи формально наложенными на произвольную функцию $ H_{} $, задают ее, фактически,
однозначно:
Т
Теорема [Шеннон]. Единственной функцией, удовлетворяющей условиям
1
—
3
,
является функция
$$ H=- K sum_{j=1}^n P_j log P_j . $$
Здесь $ K_{} $ — положительная константа, а логарифм берется по произвольному основанию большему $ 1_{} $.
Можно сказать, что свойства
1
—
3
являются определяющими свойствами энтропии — по аналогии с определяющими свойствами определителя как функции столбцов (или строк) матрицы.
После приведения этой формулировки, Шеннон пишет:
Эта теорема, равно как и необходимые для ее доказательства условия, не являются необходимыми для собственно излагаемой теории. Она приведена, главным образом, для придания правдоподобия1) некоторым последующим определениям. Действительное же обоснование этих определений, однако, остается за их применениями.
Образно говоря, следующее определение энтропии как меры неопределенности само в себе имеет некоторую меру неопределенности
И
Происхождение слова «энтропия»
☞
ЗДЕСЬ.
В дальнейшем, если не оговаривается особо, будем считать энтропию при логарифмической функции, взятой по основанию $ 2_{} $, и этот индекс при написании будем часто опускать.
П
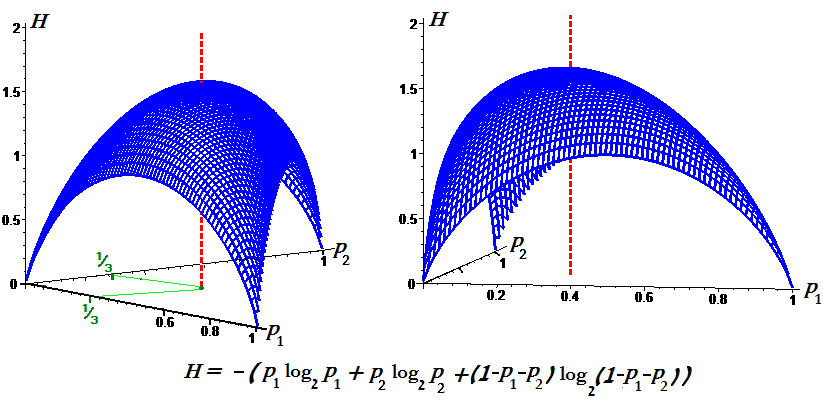
Пример. Графики энтропии для $ n_{}=2 $
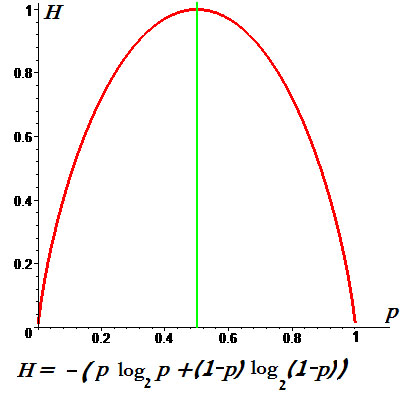
и для $ n_{}=3 $:
Формула для энтропии была получена в XIX веке Больцманом в его работах по статистической физике. Больцман показал, что если в газе, состоящем из большого числа молекул, вероятности состояний отдельных молекул равны $ P_1,dots,P_n $, то энтропия системы определяется соотношением
$$ H=- c sum_{j=1}^n P_j ln P_j , $$
где $ c_{} $ — некоторая константа. Можно считать, что энтропия системы является мерой неопределенности состояния молекул, составляющих эту систему. Эта интерпретация позволяет понять, почему Шеннон использовал ту же формулу в теории информации. Информация — это убыль неопределенности. До осуществления случайного события мы пребываем в полной неопределенности относительно того, какое из своих состояний оно может принять. После осуществления события, неопределенность устраняется. В одном из следующих пунктов мы покажем, что величина энтропии $ H_{} $ может быть интерпретирована как количество информации, содержащейся в событии.
Свойства энтропии
Проанализируем теперь формулу для энтропии.
Т
Теорема 1. $ H=0 $ тогда и только тогда, когда одна из вероятностей равна $ 1_{} $ при всех остальных, равных нулю (мера недостоверности наверняка осуществимого события равна $ 0_{} $).
Т
Теорема 2. При фиксированном $ n_{} $ максимум функции $ H_{} $ достигается при всех вероятностях одинаковых:
$$ max_{P_1+dots+P_n=1} H(P_1,dots,P_n)=Hleft(frac{1}{n},dots,frac{1}{n} right) = log n $$
(при равновероятности состояний предсказание об осуществимости какого-то конкретного из них максимально недостоверно).
Т
Теорема 3. Пусть случайные события $ A_{} $ и $ B_{} $ независимы. Тогда энтропия произведения (совместного осуществления) событий $ A cdot B $ равна сумме энтропий перемножаемых событий:
$$ H ( A cdot B) = H(A) + H(B) . $$
Доказательство. Пусть случайное событие $ A_{} $ может находиться в состояниях $ S_1,dots,S_n $ с вероятностями, заданными таблицей
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1,
$$
а случайная величина $ B_{} $ может находиться в состояниях $ U_1,dots,U_m $ с вероятностями, заданными таблицей
$$
begin{array}{l|l|l|l}
U_1 & U_2 & dots & U_m \
hline
Q_1 & Q_2 & dots & Q_m
end{array} quad mbox{ при } quad Q_1+Q_2+dots+Q_m=1.
$$
Тогда случайная величина $ Acdot B $ может находиться в состояниях
$$ { S_jU_k mid quad jin {1,dots,n}, kin {1,dots,m } } ; $$
здесь $ S_jU_k $ означает такое состояние «сложного» события, которое заключается в одновременном выполнении двух условий: событие $ A_{} $ находится в состоянии $ S_j $, a событие $ B_{} $ — в состоянии $ U_k $. Поскольку, по предположению, события $ A_{} $ и $ B_{} $ независимы, то вероятность такого состояния равна $ P_jQ_k $.
Тогда
$$ H(Acdot B)= sum_{j=1}^n sum_{k=1}^{m} P_jQ_k log frac{1}{P_jQ_k}=
sum_{j=1}^n sum_{k=1}^{m} P_jQ_k left( log frac{1}{P_j} + log frac{1}{Q_k}right)=
$$
$$
= underbrace{left( sum_{k=1}^{m} Q_k right)}_{=1} sum_{j=1}^n P_j log frac{1}{P_j} +
underbrace{left( sum_{j=1}^{n} P_j right)}_{=1}
sum_{k=1}^{m} Q_klog frac{1}{Q_k}= H(A) + H(B) .
$$
♦
=>
Для любых случайных событий $ A_{} $ и $ B_{} $ энтропия их произведения (совместного появления) $ A cdot B $ не превосходит суммы энтропий перемножаемых событий:
$$ H ( A cdot B) le H(A) + H(B) . $$
Условная энтропия
Предположим теперь, что события $ A_{} $ и $ B_{} $ не являются независимыми. Выясним, чему равна энтропия произведения этих событий.
Общая формула для энтропии дает
$$
H(AB)=-sum_{j=1}^n sum_{k=1}^{m} P(S_jU_k) log P(S_jU_k) .
$$
В общем случае уже нельзя заменить вероятность $ P(S_jU_k) $ на произведение соответствующих вероятностей; в соответствии с теоремой из пункта
☞
УСЛОВНЫЕ ВЕРОЯТНОСТИ имеет место равенство
$$ P(S_jU_k)=P(S_j)P_{S_j}(U_k)=P_j P_{S_j}(U_k) , $$
где $ P_{S_j}(U_k) $ означает условную вероятность состояния $ U_k $ при условии нахождения события $ A_{} $ в состоянии $ S_j $. Каждое слагаемое под знаком суммы в выражении для энтропии представляется тогда в виде
$$
P(S_jU_k) log P(S_jU_k)=P_j P_{S_j}(U_k) left( log P_j + log P_{S_j}(U_k) right) .
$$
Тогда
$$
H(AB)=-sum_{j=1}^n P_j log P_j left( sum_{k=1}^{m} P_{S_j}(U_k) right)- sum_{j=1}^n P_j left( sum_{k=1}^m P_{S_j}(U_k) log P_{S_j}(U_k) right) .
$$
Сумма
$$
sum_{k=1}^{m} P_{S_j}(U_k)=P_{S_j}(U_1+U_2+dots+U_k)=1 ,
$$
поскольку событие $ U_1+U_2+dots+U_k $ — достоверное (какое-то из состояний $ U_1,U_2,dots,U_k $ событие $ B_{} $ принимает). Поэтому первое слагаемое в правой части формулы для $ H(AB) $ равно просто $ H(A_{}) $. Во втором слагаемом сумма
$$
— sum_{k=1}^m P_{S_j}(U_k) log P_{S_j}(U_k)
$$
представляет собой энтропию события $ B_{} $ при условии, что событие $ A_{} $ оказалось в состоянии $ S_{j} $. Эта энтропия называется условной энтропией события $ B_{} $ при условии нахождения события $ A_{} $ в состоянии $ S_{j} $ (или частной условной энтропией) и обозначается $ H_{S_j}(B) $ или $ H(B mid S_j) $. Тогда сумму
$$
sum_{j=1}^n P_j H_{S_j}(B)
$$
естественно считать средней условной энтропией события $ B_{} $ при условии выполнения события $ A_{} $; эту величину называют условной энтропией $ B_{} $ при условии выполнения $ A_{} $ и обозначается $ H_A(B) $ или $ H(B mid A) $.
Перепишем теперь все эти определения с использованием матричного формализма. Если обозначить
$$ P_{jk}=P_{S_j}(U_k) , $$
т.е. условную вероятность состояния $ U_k $ при условии $ S_{j} $, то из этих вероятностей можно составить матрицу
$$ mathfrak P=left[ P_{jk} right]_{j=1,dots,n atop k=1,dots,m} $$
по следующей схеме
$$
begin{array}{c}
\
S_1 \
dots \
S_n
end{array}
begin{array}{c}
begin{array}{llll}
U_1 & U_2 & dots & U_m
end{array} \
left( begin{array}{llll}
P_{11} & P_{12} & dots & P_{1m} \
dots &&& dots \
P_{n1} & P_{n2} & dots & P_{nm}
end{array} right) .
end{array}
$$
В одном из следующих ПУНКТОВ эта матрица получит специальное название и обозначение, а пока подчеркну только, что элементы этой матрицы неотрицательны и сумма их в каждой строке равна $ 1_{} $.
Введем в рассмотрение новую матрицу:
$$
tilde{mathfrak P}
=
left( begin{array}{llll}
P_{11} log P_{11} & P_{12} log P_{12} & dots & P_{1m} log P_{1m} \
dots &&& dots \
P_{n1} log P_{n1} & P_{n2} log P_{n2} & dots & P_{nm} log P_{nm}
end{array} right) .
$$
Тогда условная энтропия $ H_{S_j}(B) $ равна сумме элементов $ j_{} $-й строки этой матрицы. С использованием операции умножения матриц условные энтропии можно собрать в один столбец:
$$
left( begin{array}{c}
H_{S_1}(B) \
vdots \
H_{S_n}(B)
end{array}
right)= -tilde{mathfrak P}
left( begin{array}{c}
1 \
vdots \
1
end{array}
right) .
$$
Тогда условная энтропия $ B_{} $ при условии выполнения $ A_{} $ вычисляется по формуле
$$ H_A(B) = sum_{j=1}^n P_j H_{S_j}(B) = — (P_1,dots,P_n) tilde{mathfrak P}
left( begin{array}{c}
1 \
vdots \
1
end{array}
right) .
$$
Т
Теорема 4. Для энтропии произведения случайных событий $ A_{} $ и $ B_{} $ имеет место правило сложения энтропий:
$$ H(AB)=H(A)+ H_A(B) . $$
Проиллюстрируем результат теоремы на примере, который подробно будем разбирать во всех последующих пунктах. Источник приведенных в нем данных
☞
ЗДЕСЬ.
П
Пример. Пусть случайный процесс заключается в ежесекундном появлении на экране монитора одной буквы русского алфавита
в соответствии с приведенными ниже вероятностями
| и | м | о | т | пробел | |
|---|---|---|---|---|---|
| $ P_{} $ | 0.219 | 0.104 | 0.295 | 0.148 | 0.234 |
Таким образом, случайным событием $ A_{} $ является появление какой-то из указанных букв и
$$ H(A) = — sum_{j=1}^5 P_j log_2 P_j approx 2.237 quad mbox{ бит .} $$
Теперь предположим, что каждое следующее событие $ B_{} $ — появление на экране буквы — зависит от результата предыдущего по времени (но только от одного предыдущего). Условные вероятности, полученные в результате натурных экспериментов, соберем в матрицу
$$
mathfrak P= left[ P_{jk} right]_{j,k=1}^5=
left(
begin{array}{ccccc}
0.170 & 0.130 & 0.144 & 0.065 & 0.491 \
0.259 & 0.029 & 0.231 & 0.111 & 0.370 \
0.204 & 0.116 & 0.268 & 0.206 & 0.206 \
0.161 & 0.077 & 0.523 & 0.052 & 0.187 \
0.304 & 0.113 & 0.356 & 0.227 & 0
end{array} right)
.
$$
Так, значение $ P_{3,2}=0.116 $ означает, что если в данный момент времени на экране появилась буква о, то в следующий момент времени буква м появится примерно в $ 116 $ случаях из $ 1000 $. Выражение для матрицы $ tilde{mathfrak P} $ приведено в одном из последующих
☞
ПУНКТОВ. С ее помощью вычисляем условную энтропию события $ B_{} $ при условии события $ A_{} $:
$$ H_A(B)=
— (P_1,P_2,P_3,P_4,P_5) tilde{mathfrak P}
left( begin{array}{c}
1 \
1 \
1 \
1 \
1
end{array}
right) approx 2.036 quad mbox{ бит .}
$$
Теперь вычислим энтропию произведения событий $ A_{} $ и $ B_{} $, то есть события, заключающемся в последовательном появлении двух букв. Для этого нам потребуются вероятности появления каждой пары букв, приведенные ☞ ВСЁ ТАМ ЖЕ.
| ии | им | ио | ит | и_ | ми | мм | мо | мт | м_ | ои | ом | оо | от | о_ | ти | тм | то | тт | т_ | _и | _м | _o | _т | _ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $ hat P $ | 0.037 | 0.028 | 0.031 | 0.014 | 0.108 | 0.027 | 0.003 | 0.024 | 0.011 | 0.038 | 0.060 | 0.034 | 0.079 | 0.061 | 0.061 | 0.024 | 0.011 | 0.077 | 0.008 | 0.028 | 0.071 | 0.027 | 0.084 | 0.053 | 0.000 |
Имеем:
$$H(AB)=- sum_{j=1}^{25} hat P_j log_2 hat P_j approx 4.268 quad mbox{ бит .} $$
Проверка: $ H(A)+H_A(B)approx 4.273 $ бит.
♦
§
Пока мы только лишь формально осваиваем введенный математический аппарат, оставляя обсуждение лежащего под ним здравого смысла до следующих пунктов.
Т
Теорема 5. Для условной энтропии выполняются неравенства
$$ 0 le H_A(B) le H(B) . $$
Это утверждение хорошо согласуется со смыслом энтропии как меры неопределенности: предварительное осуществление события $ A_{} $ может лишь уменьшить степень неопределенности события $ B_{} $, но никак не может ее увеличить. Здесь необходимо отметить, что частная условная энтропия $ H_{S_j}(B) $ может быть и больше $ H(B) $, но усреднение всего набора частных энтропий по вероятностям всё-таки
приводит к ограничению типа $ le $.
Поскольку события $ AB_{} $ и $ BA_{} $ одинаковы, то
$$ H(AB)=H(A)+ H_A(B) =H(B)+H_B(A) . $$
Из последнего равенства можно определить и условную энтропию события $ A_{} $ при условии осуществления события $ B_{} $:
$$ H_B(A)=H(A)-H(B)+H_A(B) . $$
П
Пример. Пусть события $ A_{} $ и $ B_{} $ заключаются в извлечении одного шара из ящика, содержащего $ m_{} $ черных и
$ n-m $ белых шаров. Чему равны энтропии $ H(A), H(B), H_A(B), H_B(A) $?
Понятие об информации
Рассмотрим величину $ H(B) $, характеризующую степень неопределенности события $ B_{} $. Равенство этой величины нулю означает, что
состояние события $ B_{} $ заранее известно; большее или меньшее значение числа $ H(B) $ отвечает большей или меньшей неопределенности события. Какое-либо состояние события $ A_{} $, предшествующее событию $ B_{} $, может ограничить количество возможных состояний для события $ B_{} $ и тем самым уменьшить степень его неопределенности. Для того чтобы состояние события $ A_{} $ могло сказаться на последующем событии $ B_{} $, необходимо, чтобы это состояние не было известно заранее; поэтому $ A_{} $ можно рассматривать как вспомогательное событие, также имеющее несколько допустимых состояний. Тот факт, что осуществление $ A_{} $ уменьшает степень неопределенности $ B_{} $, находит свое отражение в том, что условная энтропия $ H_A(B) $ события $ B_{} $ при условии выполнения события
$ A_{} $ оказывается не больше первоначальной энтропии $ H(B) $ того же события. При этом, если событие $ B_{} $ не зависит от $ A_{} $,
то $ H_A(B)=H(B) $; если же состояние события $ A_{} $ полностью предопределяет событие $ B_{} $, то $ H_A(B)=0 $. Таким образом, разность
$$ I(A,B)=H(B)-H_A(B) $$
указывает, насколько осуществление события $ A_{} $ уменьшает неопределенность $ B_{} $, т.е. сколько нового мы узнаем о событии $ B_{} $, осуществив событие $ A_{} $. Эту разность называют количеством информации относительно события $ B_{} $, содержащимся в событии $ A_{} $.
Введенное таким образом определение можно «развернуть», определив энтропию $ H(B) $ события как информацию о событии $ B_{} $, содержащуюся в самом этом событии (поскольку осуществление события $ B_{} $ полностью определяет его исход и, следовательно, $ H_B(B)=0 $), или как наибольшую информацию относительно $ B_{} $, какую только можно иметь. Иными словами, энтропия $ H(B) $ события $ B_{} $ равна той информации, которую мы получаем при осуществлении этого события, т.е. средней информации, содержащейся в состояниях $ U_1,dots, U_m $ события $ B_{} $. Чем больше неопределенность какого-то события, тем бóльшую информацию дает определение его состояния.
Следует также иметь в виду, что информация относительно события $ B_{} $, содержащаяся в событии $ A_{} $, по определению представляет собой среднее значение (математическое ожидание) случайной величины $ { H(B)-H_{S_j}(B) }_{j=1}^n $, связанной с отдельными состояниями $ { S_{j} }_{j=1}^n $ события $ A_{} $; поэтому ее можно назвать средней информацией относительно $ B_{} $, содержащейся в $ A_{} $. Часто может случиться, что при определении состояния какого-либо события $ B_{} $ мы можем по-разному выбирать вспомогательные состояния (опыты, измерения, наблюдения) события $ A_{} $; так, например, при нахождении самого тяжелого груза из заданного набора грузов мы можем в разном порядке сравнивать отдельные грузы.
Информационная избыточность
Задача. Имея сообщение, записанное символами некоторого алфавита $ {S_1,dots,S_n} $, закодировать его наиболее выгодным способом.
Здесь кодирование понимается как процесс перехода от исходного алфавита к некоторому новому $ {U_1,dots,U_m} $, в котором каждому символу $ S_{j} $ однозначно сопоставляется последовательность символов $ (U_{j_1},dots, U_{j_k}) $.
Будем считать кодирование тем более выгодным, чем меньше элементарных сигналов приходится затратить на передачу данного сообщения.
Если считать, что коммуникация каждого из символов нового алфавита «стоит» одинакового количества ресурсов (энергии, времени), то наиболее выгодный код позволит сэкономить эти ресурсы.
П
Пример. Пусть $ n=10, m=2 $, т.е., к примеру, исходный алфавит, состоящий из цифр $ 0,1,dots, 9 $, мы кодируем двоичным кодом. Кодовая таблица
$$
begin{array}{c|c|c|c|c|c|c|c|c|c}
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \
hline
0000 & 0001 & 0010 & 0011 & 0100 & 0101 & 0110 & 0111 & 1000 & 1001
end{array}
$$
фактически соответствует переводу десятичных чисел в двоичную систему счисления. С одним только различием: каждый блок кода состоит из $ 4 $-х цифр, разрядов2) , т.е. код является равномерным. Требование равномерности понятно: оно позволяет получателю закодированного сообщения однозначно выделить блоки, соответствующие закодированным символам. Заметим, что вопрос о количестве этих разрядов равносилен задаче о том сколько вопросов, имеющих ответы «да» или «нет» надо задать, чтобы отгадать задуманное целое число среди $ 0,1,dots, 9 $.
Рассмотрим теперь вопрос о выгодности (т.е. экономности) построенного кода. Каждая цифра числового сообщения, записанного в привычной десятичной системе счисления, может принимать одно из десяти значений, т.е. может содержать информацию, равную, самое большее, $ log_2 10 approx 3.32 $ бит. Следовательно, сообщение, состоящее из $ N_{} $ десятичных цифр, может содержать, самое большее, $ N log_2 10 approx 3.32 N $ бит. Каждый разряд закодированного сообщения может принимать одно из двух значений, т.е. может содержать информацию, равную, самое большее $ log_2 2=1 $ биту. Но при использовании рассмотренного нами двоичного кода мы затрачиваем на передачу одного символа алфавита $ 4_{} $ разряда, а на передачу сообщения из $ N_{} $ символов алфавита — $ 4, N $ разрядов. Однако с помощью $ 4, N $ двоичных разрядов можно было бы передать информацию, равную $ 4, N $ бит. Разность $ 4,N-3.32, N=0.68, N $ отражает величину неэкономичности нашего кода. Нетрудно также объяснить, почему предложенный код не будет наиболее экономичным: в нем значения $ 0_{} $ и $ 1_{} $ не являются равновероятными: если в кодируемом сообщении все цифры $ 0,1,dots, 9 $ равновероятны, то в закодированном сообщении $ 0_{} $ будет встречаться в $ 25/15=5/3 $ раз чаще, чем $ 1_{} $. Между тем для того, чтобы последовательность из определенного количества символов $ 0_{} $ и $ 1_{} $ содержала наибольшую информацию, требуется, чтобы все цифры этой последовательности принимали оба значения с одинаковой вероятностью (и были взаимно независимы).
Легко понять, как можно построить более выгодный двоичный код. Разобьем наше сообщение на последовательные пары цифр и будем переводить в двоичную систему счисления не отдельно каждую цифру, к каждое двузначное десятичное число разбиения. Число двоичных разрядов кодовых блоков, требуемое для записи всех двузначных чисел $ 00,01,dots,99 $ равно $ 7_{} $:
$$
begin{array}{c|c|c|c}
0 & 1 & dots & 99 \
hline
0000000 & 0000001 & dots & 1100011
end{array}
$$
При такой схеме кодирования на два символа исходного алфавита тратится $ 7_{} $ бит, а не $ 8_{} $ — как в первой схеме, т.е. для передачи числа из $ N_{} $ десятичных цифр надо передать $ 7, (N+1)/2 approx 3.5 N $ двоичных цифр.
Еще выгоднее было бы разбить передаваемое число на триплеты — блоки из трех цифр. В этом случае «стоимость» кодирования понижается до $ approx 3.33 N $ бит. Выгода от перехода к разбиению сообщения на еще более крупные блоки практически оказывается уже совсем небольшой.
При переходе от триплетов к квадруплетам (блокам из четырех цифр) экономность кодирования даже уменьшается: на передачу последних требуются $ 14 $-тиразрядные двоичные блоки. Тем не менее, применяя разбиение кодируемого $ N_{} $-значного числа на еще более крупные блоки, мы можем еще более «сжать» получаемый двоичный, подойдя максимально близко к значению $ N log_2 10 $.
♦
Эта последняя граница может быть получена и из других соображений — без использования понятия информации. Количество всевозможных
$ N_{} $-буквенных слов, составленных из букв алфавита $ { S_1,dots,S_n } $, равно $ n^N $, количество всевозможных $ k_{} $-разрядных двоичных блоков равно $ 2^k $. Для однозначности кодирования необходимо, чтобы $ 2^k ge n^N $.
Способ кодирования $ k_{} $-разрядными двоичными блоками фактически заключается в том, что мы разбиваем множество всевозможных $ k_{} $-значных чисел на две равные части и числам из одной части сопоставляем первую разрядную цифру равную $ 0_{} $, а числам из второй части — равную $ 1_{} $. Далее, каждая из половинок множества снова разбивается на две равные части, каждой из которых приписывается $ 0_{} $ или $ 1_{} $.
Т
Теорема [Хартли]. Если в заданном множестве $ mathbb S $, состоящем из $ mathfrak N $ элементов:
$$ operatorname{Card}(mathbb S) = mathfrak N $$
выделен какой-то элемент $ U_{} $, о котором заранее известно, лишь что $ U in mathbb S $, то, для того, чтобы найти $ U_{} $ необходимо получить информацию, равную $ log_2 mathfrak N $ бит.
На первый взгляд кажется, что если число букв в исходном алфавите равно $ n_{} $, а в кодирующем алфавите равно $ m_{} $, то число $ log_m n $ характеризует наиболее экономичный код. Однако это утверждение ошибочно. Разумеется, верно, что текст из $ N_{} $ букв $ n_{} $-буквенного алфавита может содержать информацию, самое большее равную $ N log_2 n $ бит, но в действительности такой текст, если только он является осмысленным, никогда такой информации не содержит. Это ясно из свойств энтропии: каждая буква текста может содержать наибольшую информацию $ log_2 n $ бит лишь в том случае, когда все буквы алфавита будут встречаться одинаково часто. Известно, однако, что частоты встречаемости букв o или е во много раз больше частот встречаемости букв ф или щ.
Частота встречаемости букв в обычном (неспециальном) тексте (без учета пробелов) [2]:
| a | б | в | г | д | е,ё | ж | з | и | й | к | л | м | н | о | п | р |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.075 | 0.017 | 0.046 | 0.016 | 0.030 | 0.087 | 0.009 | 0.018 | 0.075 | 0.012 | 0.034 | 0.042 | 0.031 | 0.065 | 0.110 | 0.028 | 0.048 |
| с | т | у | ф | х | ц | ч | ш | щ | ъ,ь | ы | э | ю | я | |||
| 0.055 | 0.065 | 0.025 | 0.002 | 0.011 | 0.005 | 0.015 | 0.007 | 0.004 | 0.017 | 0.019 | 0.003 | 0.007 | 0.022 |
Энтропия достигает своего максимума, если все символы алфавита $ {S_1,dots,S_n} $ независимы и генерируются источником с одинаковой вероятностью. Можно сказать, что в равновероятном алфавите все символы несут максимальную информационную нагрузку. Если же алфавит неравновероятен, то некоторые его символы будут иметь меньшую информационную нагрузку, чем другие. Так, если считать, что в русском алфавите $ 31_{} $ буква (отождествляем е и ё, а также ь и ъ) и все они равновероятны, то
$$ H_0= — sum_{j=1}^{31} 1/31 log_2 (1/31) = log_2 31 approx 4.954 mbox{ бит } . $$
Если учитывать частоты букв в соответствии с приведенной таблицей, то получим:
$$ H_1= — sum_{j=1}^{31} P_j log_2 (P_j) approx 4.460 mbox{ бит } , $$
т.е. средняя информация, приходящаяся на одну букву русского текста, заметно понижается.
Аналогичные результаты справедливы и для других языков.
Если латинский алфавит содержит $ 26_{} $ букв и, следовательно, $ H_0 = log_2 26 approx 4.700 $ бит,
то значения $ H_{1} $ для основных европейских языков приведены в таблице
| английский | французский | немецкий | |
|---|---|---|---|
| $ H_{1} $ | 4.126 | 3.986 | 4.096 |
Однако, даже с учетом частот появления букв в тексте языков, мы все равно получим значение средней удельной информации на единицу текста,
превосходящую фактическое значение этой величины. В самом деле, для русского алфавита, например, информация в $ 4.460 $ бит на одну букву получилась бы, если бы каждая буква текста определялась с помощью извлечения карточки из ящика с перемешанными $ 1000 $ карточками, среди которых на $ 110 $ карточках написана буква о, на $ 87 $ карточках — буква е, и т.д., на $ 2_{} $ карточках — буква ф. Энтропия каждого такого события (извлечения карточки) $ A_1 $ примерно равна $ 4.460 $ бит; если $ [A_1,A_2,dots,A_N] $ обозначают $ N_{} $ последовательных событий3), то
$$ H([A_1, A_2, dots , A_N])= sum_{ell=1}^N H(A_{ell}) approx N cdot 4.460 mbox{ бит } . $$
Однако, появление каждой буквы текста на «естественном» языке не является независимым событием: вероятности появления каждой буквы зависят от предыдущих букв. Так, например, в русском языке после появления гласной буквы, существенно увеличивается вероятность появления согласной; если последняя появившаяся буква ч, то следующей уже никак не может быть ы, ю, или я, а весьма вероятно появление одной из букв
и, е или т. Аналогичные закономерности имеются и во всех других языках. Поэтому, если $ [A_1,A_2] $ — сложное событие, состоящее в последовательном появлении двух, то информация, содержащаяся в этом событии, равна
$$ H([A_1,A_2])=H(A_1)+H_{A_1}(A_2) le H(A_1)+H(A_2) . $$
Среднюю информацию на одну букву следует вычислять как условную энтропию:
$$
H_2=H_{A_1}(A_2)=-sum_{j,ell=1}^n P([S_j,S_{ell}]) log_2 P_{jell} ,
$$
где $ n_{} $ — число букв алфавита, $ P_{jell}= P_{S_j}(S_{ell}) $
— условная вероятность появления буквы $ S_{ell} $, если известно, что непосредственно перед ней стоит буква $ S_{j} $,
а $ P([S_j,S_{ell}]) $ — вероятность появления двухбуквенного сочетания (диграммы) $ [S_j,S_{ell}] $.
Как правило, $ P([S_j,S_{ell}]) ne P([S_{ell},S_j]) $; сочетание ый встречается значительно чаще йы4).
Можно переписать последнюю формулу в матричном виде с использованием условных вероятностей.
По правилу умножения вероятностей:
$$
P([S_j,S_{ell}])=P(S_j)P_{S_j}(S_{ell})=P_j P_{jell} .
$$
Составим из условных вероятностей матрицу:
$$
mathfrak P =left[ P_{jk} right]_{j,k=1}^n
$$
— она называется матрицей условных (или переходных) **вероятностей. На ее основе построим матрицу
$$
tilde{mathfrak P}= left[P_{jk} log P_{jk} right]_{j,k=1}^n
left( begin{array}{llll}
P_{11} log P_{11} & P_{12} log P_{12} & dots & P_{1n} log P_{1n} \
dots &&& dots \
P_{n1} log P_{n1} & P_{n2} log P_{n2} & dots & P_{nn} log P_{nn}
end{array} right) ;
$$
В нашем случае — в отличие от общего случая пункта
☞
УСЛОВНАЯ ЭНТРОПИЯ — матрицы $ mathfrak P $ и $ tilde{mathfrak P} $ будут квадратными. В полном соответствии с пунктом
☞
УСЛОВНАЯ ЭНТРОПИЯ можем записать:
$$
H_2=
— (P_1,dots,P_n) tilde{mathfrak P}
left( begin{array}{c}
1 \
vdots \
1
end{array}
right) .
$$
П
Пример. Обратимся к примеру сокращенного русского языка из букв $ S_1= $и, $ S_2= $м, $ S_3= $о, $ S_4= $т и $ S_5= $пробел, рассмотренному
☞
ЗДЕСЬ. Сделаем сначала «привязку» к только что введенным обозначениям:
$$ P_1=0.219, P_2=0.104, P_3= 0.295, P_4=0.148, P_5=0.234 . $$
Матрица условных вероятностей:
$$
mathfrak P=left[P_{jk}right]_{j,k=1}^5 =
left(
begin{array}{ccccc}
0.170 & 0.130 & 0.144 & 0.065 & 0.491 \
0.259 & 0.029 & 0.231 & 0.111 & 0.370 \
0.204 & 0.116 & 0.268 & 0.206 & 0.206 \
0.161 & 0.077 & 0.523 & 0.052 & 0.187 \
0.304 & 0.113 & 0.356 & 0.227 & 0
end{array} right)
$$
Вычисляем матрицу
$$
tilde{mathfrak P}=left[P_{jk} log_2 P_{jk} right]_{j,k=1}^5 =
left(
begin{array}{ccccc}
-0.435 & -0.383 & -0.403 & -0.256 & -0.504 \
-0.505 & -0.148 & -0.488 & -0.352 & -0.530 \
-0.467 & -0.360 & -0.509 & -0.470 & -0.470 \
-0.424 & -0.285 & -0.489 & -0.222 & -0.452 \
-0.522 & -0.355 & -0.530 & -0.486 & 0
end{array} right) .
$$
Величины энтропий (в битах):
$$ H_0=log_2 5 approx 2.322, H_1=-sum_{j=1}^5 P_j log_2 P_j approx 2.237,
$$
$$
H_2 =
— (P_1,P_2,P_3,P_4,P_5) tilde{mathfrak P}
left( begin{array}{c}
1 \
1 \
1 \
1 \
1
end{array}
right) approx 2.036 . $$
♦
Продолжаем дальнейшее продвижение в намеченном направлении. Если учесть информацию о двух предыдущих буквах текста, то для средней информации на одну букву получается формула:
$$
H_3=H_{A_1A_2}(A_3)=- sum_{j,ell,r=1}^n P([S_j,S_{ell},S_r]) log_2 P_{[S_j,S_{ell}]}(S_r) ,
$$
где $ P([S_j,S_{ell},S_r]) $ — вероятность трехбуквенного сочетания (триграммы) $ [S_j,S_{ell},S_r] $, а
$ P_{[S_j,S_{ell}]}(S_r) $ — условная вероятность появления буквы $ S_r $ после появления биграммы $ [S_j,S_{ell}] $.
Нетрудно понять как строятся величины $ H_M $ при $ M> 3 $. Также понятно, что с возрастанием $ M_{} $ величины $ H_M $ будут убывать, приближаясь к некоторому предельному значению $ H_{infty} $, которое и можно считать теоретическим значением средней удельной информации при передаче длинного текста.
Значения $ H_{M} $ (в битах) для русского5) и английского языков6):
| $ M $ | $ 0_{} $ | $ 1_{} $ | $ 2_{} $ | $ 3_{} $ |
|---|---|---|---|---|
| русский | 5.000 | 4.348 | 3.521 | 3.006 |
| английский | 4.754 | 4.029 | 3.319 | 3.099 |
Учтя также и статистические данные о частотах появления различных слов в английском языке, Шеннон сумел приблизительно оценить и значения величин $ H_5 $ и $ H_8 $:
$$ H_{5} approx 2.1, H_{8} approx 1.9 . $$
П
Пример [обезьяна за клавиатурой]. Известна теорема о бесконечных обезьянах: абстрактная обезьяна, ударяя случайным образом по клавишам печатной машинки7) в течение неограниченно долгого времени, рано или поздно напечатает любой наперёд заданный текст (например «Войны и мира»). В указанной ссылке приводятся оценки времени наступления этого события. Следующие примеры 
Картинка в тему
☞
ЗДЕСЬ
Приближения нулевого порядка (символы независимы и равновероятны):
ФЮНАЩРЪФЬНШЦЖЫКАПМЪНИФПЩМНЖЮЧГПМ ЮЮВСТШЖЕЩЭЮКЯПЛЧНЦШФОМЕЦЕЭДФБКТТР МЮЕТ
Приближение первого порядка (символы независимы, но с частотами, свойственными русскому языку):
ИВЯЫДТАОАДПИ САНЫАЦУЯСДУДЯЪЛЛЯ Л ПРЕЬЕ БАЕОВД ХНЕ АОЛЕТЛС И
Приближение второго порядка (частотность диграмм такая же как в русском языке):
ОТЕ ДОСТОРО ННЕДИЯРИТРКИЯ ПРНОПРОСЕБЫ НРЕТ ОСКАЛАСИВИ ОМ Р ВШЕРГУ П
Приближение третьего порядка (частотности триграмм такие же как в русском языке):
С ВОЗДРУНИТЕЛЫБКОТОРОЧЕНЯЛ МЕСЛОСТОЧЕМ МИ ДО
Вместо того, чтобы продолжить процесс приближения с помощью тетраграмм, пентаграмм и т.д., легче и лучше сразу перейти к словарным единицам. Приближение первого порядка на уровне слов9): cлова выбираются независимо, но с соответствующими им частотами.
СВОБОДНОЙ ДУШЕ ПРОТЯНУЛ КАК ГОВОРИТ ВСПОМНИТЬ МИЛОСТЬ КОМНАТАМ РАССКАЗА ЖЕНЩИНЫ МНЕ ТУДА ПОНЮХАВШЕГО КОНЦУ ИСКУСНО КАЖДОМУ РЯСАХ К ДРУГ ПЕРЕРЕЗАЛО ВИДНО ВСЕМ НАЧИНАЕТЕ НАД ДВУХ ЭТО СВЕТА ХОДУНОМ ЗЕЛЕНАЯ МУХА ЗВУК ОН БЫ ШЕЮ УТЕР БЕЗДАРНЫХ
Приближение второго порядка на уровне слов. Переходные вероятности от слова к слову соответствуют русскому языку,
но «более дальние» зависимости не учитываются:
ОБЩЕСТВО ИМЕЛО ВЫРАЖЕНИЕ МГНОВЕННОГО ОРУДИЯ К ДОСТИЖЕНИЮ ДОЛЖНОСТЕЙ ОДИН В РАСЧЕТЫ НА БЕЗНРАВСТВЕННОСТИ В ПОЭЗИИ РЕЗВИТЬСЯ ВСЕ ГРЫЗЕТ СВОИ БРАЗДЫ ПРАВЛЕНИЯ НАЧАЛА ЕГО ПОШЛОЙ
С каждым проделанным шагом сходство с обычным текстом заметно возрастает. До текста «Войны и мира» осталось совсем немного…
♦
Уменьшение информационной нагрузки на один символ алфавита вследствие неравновероятности, а также взаимозависимости появления, символов называют избыточностью языка10). Информационная избыточность рассчитывается по формуле
$$ R_{}= frac{H_0-H_{infty}}{H_0}=1-frac{H_{infty}}{log n} . $$
Величина $ H_0-H_{infty} $ называется недогруженностью алфавита, а отношение $ H_{infty}/H_0 = H_{infty}/log n $ — коэффициентом его оптимальности. Равенство избыточности величине $ 1/L_{} $ огрубленно эквивалентно утверждению о том, что каждая $ L_{} $-я буква алфавита является «лишней», однозначно восстанавливаемой по $ (L-1) $-й предыдущей. Избыточность наиболее распространенных европейских языков близка к $ 1/2 $, т.е., огрубляя, можно утверждать, что в тексте на одном из этих языков можно исключить до 50 % букв с тем, чтобы затем восстановить содержание текста по его оставшейся части.
Как определить величину $ H_M $ и оценить $ H_{infty} $ ? Для малых значений $ M_{} $ еще можно произвести частотный анализ, но вот уже для определения $ H_9 $ требуется знание вероятностей $ 32^9 approx 3.5 cdot 10^{13} $
всех девятибуквенных комбинаций. Шеннон предложил для оценки $ H_M $ использовать экспертное оценивание
☞
ЗДЕСЬ.
Явление избыточности влечет за собой как отрицательные, так и положительные последствия. Отрицательные последствия вызваны тем, что наличие «лишних» символов увеличивает затраты ресурсов при коммуникации. Положительный аспект избыточности заключается в повышении помехоустойчивости процесса коммуникации. Наличие высокой избыточности естественных языков позволяет понимать речь при значительных дефектах произношения, смене диалектов, а тексты — при лингвистических ошибках, сокращении слов и плохом почерке. См. также по этому поводу феномены Глокой куздры и Пушистых браздов.
Код Шеннона — Фано
Для понимания материалов настоящего пункта крайне желательно ознакомиться с материалами пункта
☞
ПРЕФИКСНЫЕ КОДЫ.
Для решения задачи наиболее экономичного кодирования приходится расширять алфавит. Поясню эту фразу. Если считать, что «исходный» алфавит состоит из символов $ S_1,dots,S_{n} $, то рассуждения из начала предыдущего пункта показывают, что уже переход к алфавиту, состоящему из набора биграмм $ {[S_j,S_{ell}]}_{j,ell=1}^n $ с последующим кодированием двоичным кодом может существенно снизить «стоимость» кодирования текста. А соображения предыдущего пункта позволят еще больше сэкономить — но, правда, при наличии дополнительной информации о новом алфавите — информации о частоте встречаемости каждой из биграмм в кодируемом тексте. Требование равномерности кода (одинакового количества разрядов в кодовых словах) снимается и в кодовую таблицу допускаются кодовые наборы с варьируемым количеством разрядов. Основным принципом кодирования становится:
чаще встречаемость — короче кодовая последовательность.
Реализация последнего принципа возможна различными способами. Исторически первым является кодирование по методу Шеннона-Фано. Чтобы не вводить новых обозначений, будем считать что алфавит состоит из «букв» $ S_1,dots,S_{n} $, при этом каждая «буква» может быть произвольным символом или набором символов, например: $ S_1 = $
в
, $ S_2 $=
о
с
, $ S_3 = 210 $ Д, $ S_4 = $
शब्द
, $ S_5=sqrt[3]{int_{3}^{-5} sin x^{2y} d, x} $,… лишь бы только алфавит был «полон» («покрывал» весь текст) и не «переполнен» (включенные в него символы реально в тексте присутствовали). И главное требование: частоты встречаемости «букв» в тексте должны быть нам известны. Для кодирования этих «букв» бинарным кодом ранжируем «буквы» по частоте встречаемости и разбиваем алфавит
$ {S_1,S_2,dots,S_n } $ на два подмножества, по возможности, равной вероятности. «Буквам» из одного подмножества ставим в соответствие $ 0_{} $, из второго — $ 1_{} $. Это — первые разряды соответствующих кодовых последовательностей. Далее процесс повторяется для каждого из подмножеств — производится деление их на подмножества по возможности равной вероятности с последующим присвоением им номера $ 0_{} $ или $ 1_{} $. Процесс заканчивается когда в каждом из образовавшихся подмножеств не останется ровно по одной «букве». В результате каждая из них получает свой индивидуальный бинарный «номер» — то есть, кодировку.
П
Пример. Рассмотрим пример с кодированием $ 10_{} $ букв русского алфавита с частотами, полученными на основании искусственного текста, созданного ☞ ЗДЕСЬ.
| е | и | а | в | д | к | з | б | г | ж | всего | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| количество | 236 | 231 | 195 | 111 | 94 | 94 | 46 | 42 | 40 | 30 | 1119 |
| вероятность | 0.211 | 0.206 | 0.174 | 0.099 | 0.084 | 0.084 | 0.041 | 0.038 | 0.036 | 0.027 |
Множество этих букв разобьем на два подмножества, (примерно) одинаковые по вероятности. Например, суммарная вероятность букв е,
и, д равна $ 0.51 $. Так что два образуемых подмножества: $ { mbox{ е, } mbox{ и, } mbox{ д } } $ и
$ { mbox{ а, } mbox{ б, } mbox{ г, } mbox{ в, } mbox{ ж, } mbox{ к, } mbox{ з } } $. Каждое из этих подмножеств снова разобьем на два подмножества (примерно) одинаковые по вероятности. Первое подмножество делится плохо, но что поделать — делим как получится! Продолжаем процесс деления пока не дойдем в таких разбиениях до отдельных букв. Последовательность построения схемы разбиения приведена на рисунке.
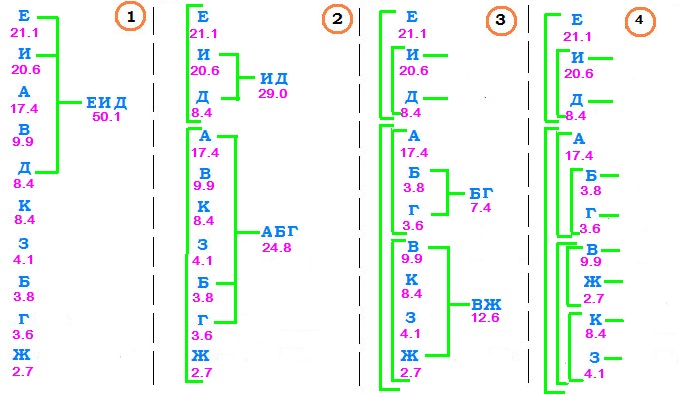
Оформляем эту схему в виде дерева и, идя от корня к листьям, нумеруем ветви после каждого узла (точки ветвления): верхней даем номер $ 0_{} $, а нижней — номер $ 1_{} $.
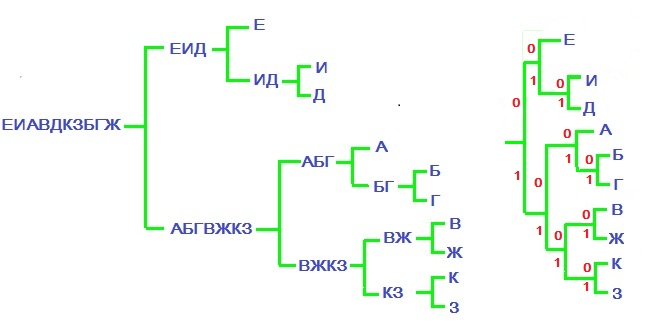
Результатом оказывается кодовая таблица
| е | и | д | а | б | г | в | ж | к | з |
|---|---|---|---|---|---|---|---|---|---|
| 00 | 010 | 011 | 100 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Стоимость кодирования текста по такой таблице равна
$$ 236cdot 2+231cdot 3+94 cdot 3+195 cdot 3+42 cdot 4+40 cdot 4+111 cdot 4+30 cdot 4+94 cdot 4+46 cdot 4=3423 mbox{ бит, } $$
то есть, в среднем, $ 3.11_{} $ бит на букву. Это неплохое достижение, но оно всё-таки хуже полученного использованием кода Хаффмана, также основанного на частотном анализе букв алфавита.
♦
Сходство кода Шеннона-Фано с кодом Хаффмана проявляется и в алгоритмах построения обоих кодов, только направление построения кодового дерева меняется на противоположное: от корня к листьям. Так же как и код Хаффмана, код Шеннона-Фано относится к префиксным кодам: ни одно его кодовое слово не совпадает с начальным отрезком какого-то другого кодового слова. И при всех при этих сходствах, код Шеннона-Фано менее экономичен, чем код Хаффмана и поэтому практически не используется.
Алгоритм построения кода Шеннона-Фано основан на решении задачи из раздела computer science, известной как partition problem: для заданного конечного набора $ mathbb S $ чисел11) требуется найти такое разбиение его на два набора $ mathbb S_1 $ и $ mathbb S_2 $, чтобы разность между суммами чисел составляющих наборов была минимальной. Проблема известна как $ NP $-сложная.
А теперь перейдем к фундаментальному результату теории кодирования, связав код Шеннона-Фано с понятием энтропии.
Т
Теорема [Шеннон]. Сообщение из большого количества $ N_{} $ букв алфавита $ {S_1,dots,S_n} $, частоты встречаемости которых в сообщении заданы таблицей:
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1,
$$
всегда можно закодировать бинарным кодом таким образом, чтобы количество двоичных разрядов в кодовой последовательности было сколь угодно близким к величине
$$Hcdot N quad mbox{ где } quad H=-sum_{j=1}^n P_j log_2 P_j ; $$
но никогда не меньшим ее.
Доказательство (совершенно нестрогое: очень сильная «выжимка» из рассуждений, приведенных в [2]; которые, в свою очередь, тоже не абсолютно строги). Пусть источник сообщений случайным образом генерирует символы из алфавита $ {S_1,dots,S_n} $. Пусть передаваемое сообщение состоит из достаточно большого числа $ N_{} $ символов. Рассмотрим подмножество $ mathbb S $ всевозможных сообщений длины $ N_{} $, в которых количества вхождений символов $ { S_j }_{j=1}^n $ примерно соответствуют указанным вероятностям. Именно, если $ N_j $ — количество вхождений символа $ S_j $, то $ N_j/N approx P_j $. Тогда вероятность вхождения в сообщение всех символов $ S_{j} $ в количестве $ N_{j} $ при $ jin {1,dots,n} $, в соответствии с теоремой об умножении вероятностей, равна
$$ P_1^{N_1} P_2^{N_2}times dots times P_n^{N_n} approx P_1^{N, P_1} P_2^{N,P_2}times dots times P_n^{N,P_n}=underbrace{left(P_1^{P_1}P_2^{P_2} times dots times P_n^{P_n} right)^N}_{=Q} . $$
Строго говоря, здесь надо сослаться на закон больших чисел, но пока не буду с этим заморачиваться.
Будем для простоты считать, что это — вероятность любого сообщения из подмножества $ mathbb S_{} $, т.е. количество элементов во множестве $ mathbb S_{} $ примерно совпадает с $ 1/Q $:
$$ mathfrak N = operatorname{Card} (mathbb S) approx 1/Q . $$
Сколько стоит найти один-единственный элемент этого множества: как найти во множестве $ mathbb S $ какое-то конкретное сообщение — не просто состоящее из нужных букв в требуемом количестве — но, например, определяющее осмысленный текст? В соответствии с теоремой Хартли, это число
$$ approx log_2 mathfrak N approx — N cdot left(P_1 log_2 P_1+P_2 log_2 P_2+dots+ P_n log_2 P_n right) mbox{ бит.} $$
♦
Теперь обсудим полученный результат. Итак, «на входе» имеем документ — самый произвольный, содержащий возможно осмысленный, но не обязательно нам понятный текст (он записан на неизвестном языке, содержит специфические символы из неизвестной нам научной отрасли и т.п.). Наша цель — закодировать его бинарным кодом, с тем, чтобы иметь возможность передать по каналу связи. Первое, что мы делаем — строим алфавит. Слово «алфавит» понимается в том смысле, что упомянут в начале пункта. Пытаемся, по-возможности, определять часто повторяющиеся блоки — их будем включать в состав алфавита целиком, как отдельные «буквы». Стоп.
Стоп!
— Что же получается: для каждого документа — делать свой отдельный алфавит?! — Вообще говоря, да12). Другое дело, что если этот документ не единствен, а предполагается коммуникация целой серии документов, и эти документы написаны на одном языке, и в них содержится разве лишь строго ограниченное количество специальных символов,… — и вот при всех при этих обстоятельствах имеет смысл предварительным анализом составить алфавит общий для всех документов. После того как алфавит создан, вычисляем частоты вхождений составляющих его букв в исходный документ. Кодируем по методу Шеннона-Фано. Кодовую таблицу храним в надежном файле и передаем адресату (на бумажном (электронном) носителе при личной встрече, курьером, по электронной почте и т.п.). И что у нас имеется для оценки стоимости кодирования нашего документа? — Оценка снизу для количества бит на букву: $ H_{} $. Что такое $ H_{} $? — Энтропия случайного события, состоящего в появлении в тексте букв алфавита при известных их вероятностях (т.е. как если бы случайный источник генерировал буквы алфавита независимо друг от друга, но с частотами, примерно соответствующими их вероятностям). Хорошо подобрали алфавит, каждый документ — достаточно длинный, этих документов много — тогда, в среднем, результаты нашего кодирования не должны слишком уж сильно превосходить этой величины. Сколько это: «слишком сильно»? — Решает заказчик. Если ему хочется улучшить результат — придется увеличивать алфавит. Но тогда решение одной проблемы приведет к появлению другой…
П
Пример. Обратимся к рассмотренному
☞
ЗДЕСЬ примеру сокращенного русского языка
| и | м | о | т | пробел | |
|---|---|---|---|---|---|
| $ P_{} $ | 0.219 | 0.104 | 0.295 | 0.148 | 0.234 |
Для алфавита, состоящего из этих букв, с указанными в таблице вероятностями
величина энтропии $ H approx 2.237 $. Следовательно, кодирование приведенного ЗДЕСЬ текста из $ 1050 $ букв по теореме Шеннона оценивается в $ 2349 $ двоичных разряда. Код Шеннона-Фано для этого алфавита имеет вид
| и | м | о | т | пробел |
|---|---|---|---|---|
| 11 | 010 | 10 | 011 | 00 |
и точная стоимость кодирования — $ 2364 $ разряда.
Если же перейти к алфавиту, составленному из биграмм
| ии | им | ио | ит | и_ | ми | мм | мо | мт | м_ | ои | ом | оо | от | о_ | ти | тм | то | тт | т_ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $ hat P $ | 0.037 | 0.028 | 0.031 | 0.014 | 0.108 | 0.027 | 0.003 | 0.024 | 0.011 | 0.038 | 0.060 | 0.034 | 0.079 | 0.061 | 0.061 | 0.024 | 0.011 | 0.077 | 0.008 | 0.028 |
| _и | _м | _o | _т | __ | ||||||||||||||||
| $ hat P $ | 0.071 | 0.027 | 0.084 | 0.053 | 0.000 |
то код Хаффмана этого алфавита (уже из $ 25_{} $ «букв») имеет вид
| ии | им | ио | ит | и_ | ми | мм | мо | мт | м_ | ои | ом | оо | от | о_ | ти | тм | то | тт | т_ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11000 | 10001 | 10100 | 010001 | 000 | 01101 | 0010100 | 00100 | 010000 | 11001 | 0101 | 10101 | 1110 | 0111 | 1001 | 01001 | 001011 | 1101 | 0010101 | 10000 |
| _и | _м | _o | _т | ||||||||||||||||
| 1011 | 01100 | 1111 | 0011 |
и стоимость кодирования текста, разбитого на $ 525 $ биграмм по схеме
Ои
|
то
|
ми
|
и_
|
о_
|
им
|
и_
|
оо
|
ои
|
тм
|
и_
|
о_
|
о_
|
о_
|
оо
|
ии
|
им
|
то
|
ми
|
им
|
от
|
ои
|
м_
|
…
будет равна $ 2193 $ бит. Величина энтропии $ H approx 2.036 $ бит и теорема Шеннона дает оценку в $ 2138 $ двоичных разрядов.
♦
Пропускная способность канала связи
Рассуждения предыдущего пункта относились к случаю, когда процесс коммуникации происходит без искажений. Обратимся теперь от теории к реальности: помехи всегда будут.
Предполагаем, что по каналу связи передается последовательность бит (т.е. $ 0_{} $ или $ 1_{} $), задающая символы (или буквы некоторого алфавита) $ S_{1},dots, S_n $. Предполагается, что символ $ S_j $ представлен набором из $ t_{j} $ двоичных сигналов. На передачу по каналу связи каждого информационного двоичного сигнала тратится некоторая единица времени. Исходя из этого будем говорить о сигнале $ S_j $
как имеющем длительность $ t_{j} $.
П
Пример. Шеннон рассматривает пример из телеграфии, где имеется всего $ 4_{} $ «символа алфавита»:
-
точка, создаваемая замыканием линии на $ 1_{} $ единицу времени и последующим размыканием на $ 1_{} $ единицу времени;
-
тире, создаваемая замыканием на $ 3_{} $ единицы времени и последующим размыканием на $ 1_{} $ единицу;
-
пробел между буквами13), создаваемый размыканием линии на $ 3_{} $ единицы времени;
-
пробел между словами, создаваемый размыканием линии на $ 6_{} $ единиц времени.
Если заменить слова «замыкание линии» на $ 1_{} $, а «размыкание линии» — на $ 0_{} $, то получим двоичную кодировку алфавита
$ mathfrak C ( $
точка
$ )=10 $,
$ mathfrak C ( $
тире
$ )=1110 $,
$ mathfrak C ( $
пробел между буквами
$ )=000 $,
$ mathfrak C ( $
пробел между словами
$ )=000000 $.
Таким образом, используя в качестве вспомогательного алфавита для передачи латинских букв азбуку Морзе, получаем кодировку сообщения:
SOS
=
••• − − − •••
$ = 101010000111011101110000101010000000 $
Дополнительно вводятся ограничения на допустимые к передаче последовательности — например, запрет двух пробелов подряд между словами.
♦
Пропускная способность канала связи без помех задается формулой
$$ C=lim_{Tto infty} frac{log_2 N(T)}{T} . $$
Здесь $ N(T) $ — число сигналов длительности $ T_{} $. Очевидно, что $ N(T)le 2^T $.
Пусть все символы алфавита $ S_1,dots,S_n $ допустимы и имеют длительности $ t_1,dots,t_n $.
Если $ N(t) $ число сигналов длительности $ t_{} $, то справедлива следующая формула:
$$ N(t)=N(t-t_1)+N(t-t_2)+dots+N(t-t_n) . $$
Последняя формула представляет тот очевидный факт, что концом любого сигнала длительности $ t_{} $ должен быть один из символов множества $ {S_{j}}_{j=1}^n $ (или набор этих символов).
Эта формула определяет линейное разностное уравнение порядка
$$ tau= max_{jin {1,dots,n}} t_j . $$
Его общее решение может быть явно выражено через корни уравнения
$$ 1= lambda^{-t_1}+lambda^{-t_2}+dots+lambda^{-t_n} . $$
Это уравнение — домножением на $ lambda^{tau} $ — может быть преобразовано в характеристический полином разностного уравнения.
Предположив, для простоты рассуждений, что все корни этого полинома $ lambda_1,dots,lambda_{tau} $ различны, получим общее решение разностного уравнения в виде
$$ N(t)=C_1lambda_1^t+C_2lambda_2^t+dots+C_{tau}lambda_{tau}^t $$
при величинах $ C_1,C_2,dots,C_{tau} $, не зависящих от $ t_{} $.
Тогда если через $ lambda_{ast} $ обозначить максимальный по модулю корень полинома:
$$ | lambda_{ast} | =max_{jin{1,dots,tau}} | lambda_j | , $$
то
$$ lim_{Tto infty} frac{log_2 N(T)}{T} = lim_{Tto infty} frac{log_2 C_{ast} lambda_{ast}^T }{T} = log_2 lambda_{ast} . $$
Тут надо бы проверить несколько предположений, например, что максимальный по
модулю корень характеристического полинома единствен — тогда, хотя бы, он обязательно будет веществен. Пока могу с определенностью утверждать, что при $ nge 2 $ у этого полинома все корни по модулю не превосходят $ 2_{} $ (см. ☞ теорему Маклорена ),что существует единственный положительный вещественный корень (см. ☞ правило знаков Декарта ), и что этот корень лежит в интервале $ ]1,2[ $. Еще одно преположение, нуждающееся в обосновании: коэффициент $ C_{ast} $ не должен равняться нулю,… Но поскольку сам Шеннон не заморачивался такими мелочами, то и я пока не буду.
П
Пример. Для рассмотренного выше «телеграфного» примера имеем разностное уравнение в виде
$$ N(t)=N(t-2)+N(t-4)+N(t-5)+N(t-7)+N(t-8)+N(t-10) . $$
Это уравнение имеет порядок $ 10_{} $, его характеристический полином
$$ lambda^{10}=lambda^{8}+lambda^{6}+lambda^{5}+lambda^{3}+lambda^{2}+1 $$
имеет максимальный по модулю корень $ lambda_{ast} approx 1.453 $. Таким образом,
пропускная способность канала равна $ approx 0.539 $.
♦
Пусть символы алфавита имеют вероятности появления в любом месте сообщения, заданные таблицей
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1.
$$
Тогда при отсутствии помех сообщение по линии связи может быть передано со скоростью сколь угодно близкой к
$$ v=C/H quad mbox{ букв } / mbox{ единица времени } , $$
где $ C_{} $ — пропускная способность линии связи, а $ H=-sum_{j=1}^n P_j log_2 P_i $ — энтропия одной буквы передаваемого сообщения; однако скорость передачи, превосходящая $ v_{} $ никогда не может быть достигнута.
При наличии помех в линии связи дело будет обстоять иначе. В этом случае только наличие избыточности в передаваемой последовательности сигналов может помочь нам точно восстановить переданное сообщение по принятым данным. Ясно, что использование кода, приводящего к наименьшей избыточности закодированного сообщения здесь уже нецелесообразно и скорость передачи сообщения должна быть уменьшена. Насколько уменьшена?
Для ответа на этот вопрос придется предварительно описать линию связи с помехами. Пусть линия связи использует $ m_{} $ различных элементраных сигналов $ A_1,A_2,dots,A_m $, но из-за наличия помех переданный сигнал $ A_j $ может оказаться по выходе из канала каким-то другим сигналом $ A_k $; пусть известна вероятность этого события $ hat P_{jk}^{} $. Из этих вероятностей можно составить квадратную матрицу
$$
hat{mathfrak P} =
left( begin{array}{llll}
hat P_{11} & hat P_{12} & dots & hat P_{1m} \
hat P_{21} & hat P_{22} & dots & hat P_{2m} \
dots & & & dots \
hat P_{m1} & hat P_{m2} & dots & hat P_{mm}
end{array}
right)
$$
Предположим, для простоты, что по линии связи передается два элементарных сигнала — $ A_1=0 $ и $ A_{2}=1 $ (и на выходе канала связи других сигналов быть не может). Предположим, что вероятность безошибочного приема любого из передаваемых сигналов равна $ 1-p_{} $, а вероятность ошибки равна $ p_{} $. Можно составить матрицу переходных вероятностей:
$$
begin{array}{l}
\
A_1 \
A_2
end{array}
begin{array}{l}
begin{array}{llll}
& & A_{1} & A_{2}
end{array} \
left(begin{array}{cc}
1-p & p \
p & 1-p
end{array}
right)
end{array}
$$
Пусть $ P(A_{j}) $ — вероятность того, что передаваемым сигналом является $ A_{j} $, имеем: $ P(A_1)+P(A_2)=1 $.
Опыт $ B_{} $, заключающийся в выяснении того, какой сигнал передается, будет иметь энтропию
$$ H(B)=-P(A_{1}) log P(A_1) — P(A_2) log P(A_{2}) . $$
Опыт $ A_{} $, заключающийся в выяснении того, какой именно сигнал при этом будет принят на выходе, является опытом
с двумя исходами, зависящими от опыта $ B_{} $. Условные энтропии
$$ H_{A_1}(B)=-(1-p) log (1-p)-p log p,quad H_{A_2}(B)=-p log p — (1-p) log (1-p) $$
оказываются одинаковыми и
$$ H_{A}(B)=P(A_1) H_{A_1}(B) + P(A_2) H_{A_2}(B)=-(1-p) log (1-p)-p log p_{} $$
независимо от величин вероятностей $ P(A_{1}), P(A_{2}) $.

Статья не закончена!
Источники
[1]. Шеннон К. Математическая теория связи. (Shannon C.E. A Mathematical Theory of Communication. Bell System Technical Journal. — 1948. — Т. 27. — С. 379-423, 623–656.)
[2]. Яглом А.М., Яглом И.М. Вероятность и информация. М. Наука. 1973.
.
From Wikipedia, the free encyclopedia
In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable 




Definition[edit]
The conditional entropy of 

|
|
(Eq.1) |
where 



Note: Here, the convention is that the expression 

Intuitively, notice that by definition of expected value and of conditional probability, 
![{displaystyle H(Y|X)=mathbb {E} [f(X,Y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e7cfdc7f8953ec5eed3ea5897b0b24223941d6b)













Motivation[edit]
Let 










![{displaystyle mathrm {H} (Y):=mathbb {E} [operatorname {I} (Y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f114631caeb95e508a74994486e35e972220b378)
where 





Note that 




![{displaystyle E_{X}[mathrm {H} (y_{1},dots ,y_{n}mid X=x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c42f84b74f174cb4c172b6f91074f65dbd915e40)
Given discrete random variables 








Properties[edit]
Conditional entropy equals zero[edit]



Conditional entropy of independent random variables[edit]
Conversely, 


Chain rule[edit]
Assume that the combined system determined by two random variables 








[3]: 17
The chain rule follows from the above definition of conditional entropy:
In general, a chain rule for multiple random variables holds:
[3]: 22
It has a similar form to chain rule in probability theory, except that addition instead of multiplication is used.
Bayes’ rule[edit]
Bayes’ rule for conditional entropy states
Proof. 


If 


Other properties[edit]
For any 

where 


For independent 

and
Although the specific-conditional entropy 





Conditional differential entropy[edit]
Definition[edit]
The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called conditional differential (or continuous) entropy. Let 



|
|
(Eq.2) |
Properties[edit]
In contrast to the conditional entropy for discrete random variables, the conditional differential entropy may be negative.
As in the discrete case there is a chain rule for differential entropy:
[3]: 253
Notice however that this rule may not be true if the involved differential entropies do not exist or are infinite.
Joint differential entropy is also used in the definition of the mutual information between continuous random variables:



Relation to estimator error[edit]
The conditional differential entropy yields a lower bound on the expected squared error of an estimator. For any random variable 


This is related to the uncertainty principle from quantum mechanics.
Generalization to quantum theory[edit]
In quantum information theory, the conditional entropy is generalized to the conditional quantum entropy. The latter can take negative values, unlike its classical counterpart.
See also[edit]
- Entropy (information theory)
- Mutual information
- Conditional quantum entropy
- Variation of information
- Entropy power inequality
- Likelihood function
References[edit]
- ^ «David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book». www.inference.org.uk. Retrieved 2019-10-25.
- ^ Hellman, M.; Raviv, J. (1970). «Probability of error, equivocation, and the Chernoff bound». IEEE Transactions on Information Theory. 16 (4): 368–372. doi:10.1109/TIT.1970.1054466.
- ^ a b c d e f g T. Cover; J. Thomas (1991). Elements of Information Theory. ISBN 0-471-06259-6.


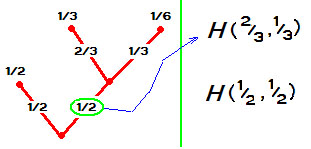






![{displaystyle {begin{aligned}mathrm {H} (Y|X)&=sum _{xin {mathcal {X}},yin {mathcal {Y}}}p(x,y)log left({frac {p(x)}{p(x,y)}}right)\[4pt]&=sum _{xin {mathcal {X}},yin {mathcal {Y}}}p(x,y)(log(p(x))-log(p(x,y)))\[4pt]&=-sum _{xin {mathcal {X}},yin {mathcal {Y}}}p(x,y)log(p(x,y))+sum _{xin {mathcal {X}},yin {mathcal {Y}}}{p(x,y)log(p(x))}\[4pt]&=mathrm {H} (X,Y)+sum _{xin {mathcal {X}}}p(x)log(p(x))\[4pt]&=mathrm {H} (X,Y)-mathrm {H} (X).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/501bd3a915d2218c4464e1ea8cfefc3fba872320)








![{displaystyle mathbb {E} left[{bigl (}X-{widehat {X}}{(Y)}{bigr )}^{2}right]geq {frac {1}{2pi e}}e^{2h(X|Y)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab916a1ac9b14193bf90b79742772b686bb771c3)