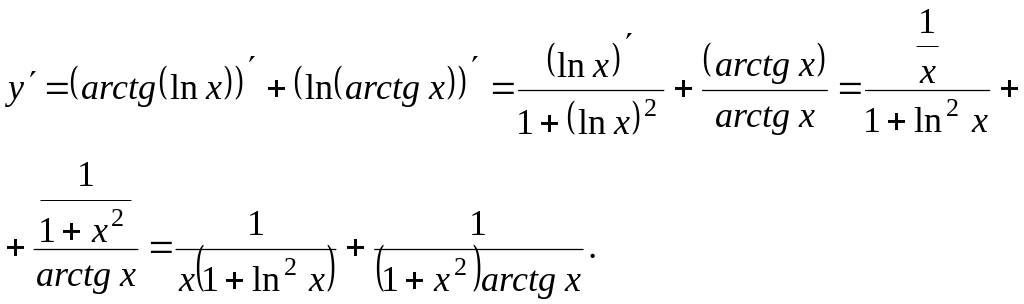Как найти полный дифференциал неявно заданной функции

Дифференцирование функции, заданной неявно

Определение
1. Равенство
F(x,
y)
= 0 определяет
у как функцию у
= у(х), задает
эту функцию неявно.

Для нахождения
производной функции у,
заданной неявно, нужно продифференцировать
равенство F(x,
y)
= 0 по аргументу
х
и решить уравнение относительно у’.

Примеры 1 – 4.
Продифференцировать функцию у
= у(х), заданную
неявно.

1. х³
   + у²
   — 5х = 0.

Решение.
Продифференцируем это равенство:

(х³
+ у²
— 5х)’ = 0;

3х²
+ 2уу’ = 0;

Решим полученное
равенство относительно у’:

1. ху²
   + sin y – 2x = 3.

Решение.
Продифференцируем равенство по х,
считая у функцией по х:

(ху²)’
+ (sin y)’
– 2(x)’
= (3)’;

(х)’
у²
+ х
(у²)’
+ cos
у 
y’
– 2 = 0;

у²
+ х

2у

у‘
+ cos
y

y’
= 2;

Решим уравнение
относительно у’:

2х

у

у‘
+ cos
y

y’
= 2 — у²
;

у‘(2х

у
+ cos
y)
= 2 — у²;

Пользуясь формулами
и правилами дифференцирования, найдем
производные следующих функций.

Пример 1. Найти
производные следующих функций

Решение. Имеем:

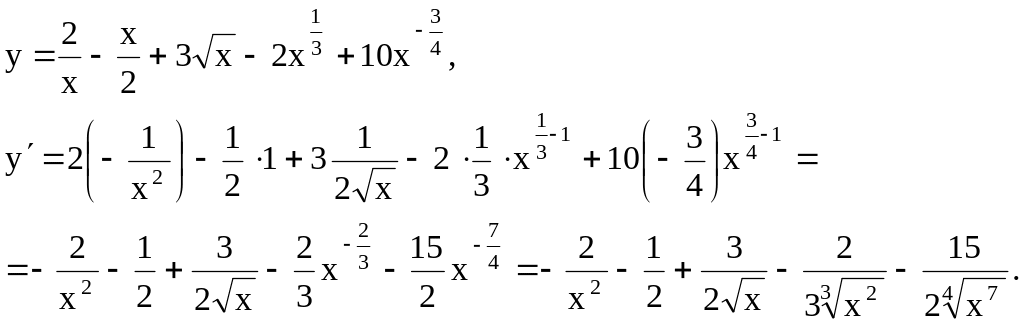
Пример 2. у
= х² (cos
x
– 4 sin
x).

Решение. Воспользуемся
формулой 9 и таблицей производных.

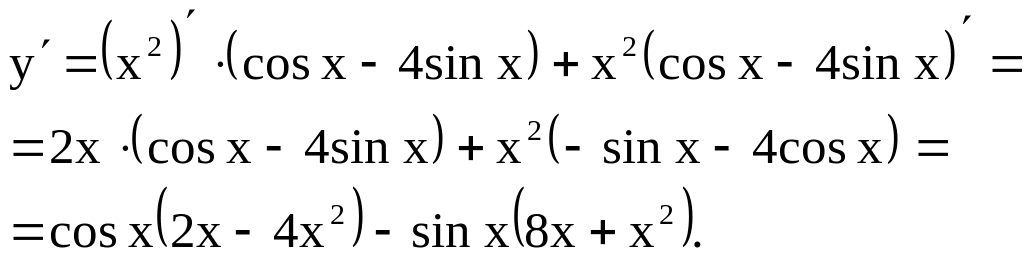
Пример 3. у
= (3х²
+ 5х
– 1)³.

Решение. Имеем
сложную функцию, последнее действие
производится над выражением u
= 3х²
+ 5х
– 1.

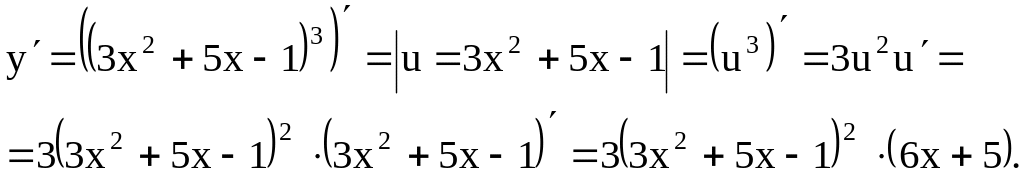
Пример 4. y
= arctg⁸
x

Решение. Имеем
сложную функцию, последнее действие –
возведение в 8ую степень производится
над u
= arctg
x.

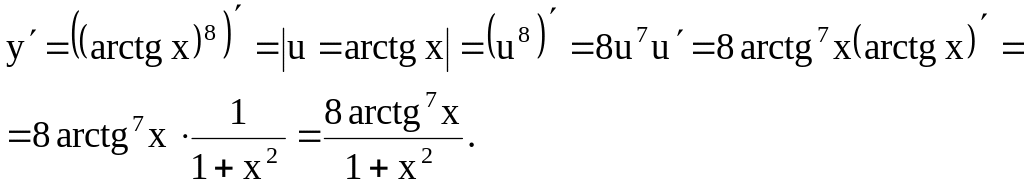
Пример 5. у =

Решение. Имеем
дважды сложную функцию

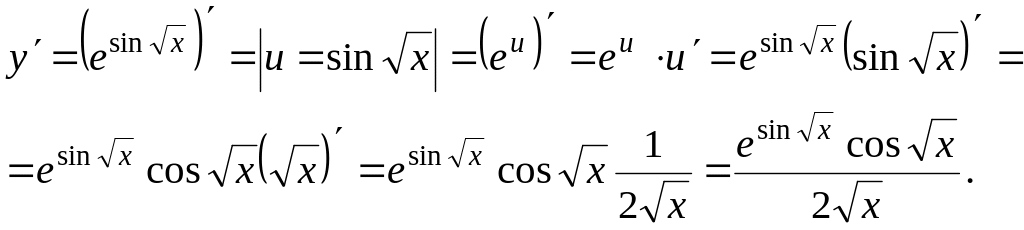
Пример 6.

Решение. Воспользуемся
формулой 11

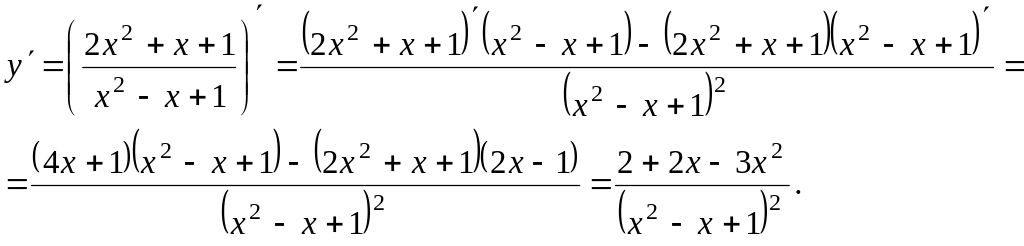
Пример
7. y
= arctg (ln x) + ln (arctg x).

Решение. Имеем
сумму двух сложных функций, воспользуемся
правилами дифференцирования суммы
функций, при вычислении значения функции
в первом слагаемом последнее действие
– (вычисление арктангенса) производится
над логарифмом, значит, промежуточный
аргумент – ln
x,
а во втором слагаемом (вычисление
логарифма) – над arctg
x,
значит промежуточный аргумент – arctg
x.

Пример 8.

Решение.
Имеем функцию у
= у(х), заданную
неявно. Продифференцируем это равенство,
считая, что sin
y,
e
^{– y}
– сложные функции:

В
левой части группируем слагаемые с у’,
в правую часть переносим слагаемые, не
содержащие у’.

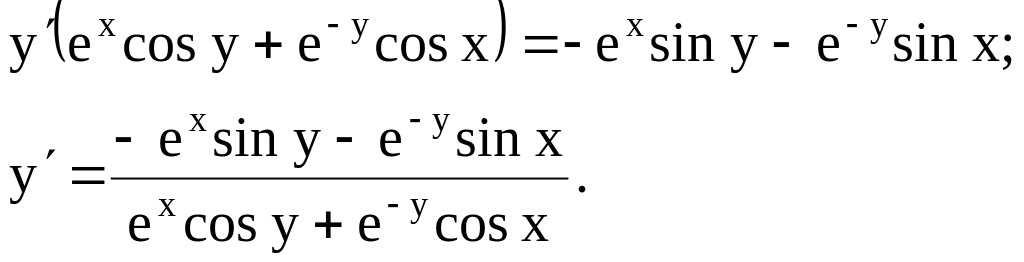
Пример 9.

.

Решение. Имеем
показательно-степенную функцию

.

Прологарифмируем
данное равенство:

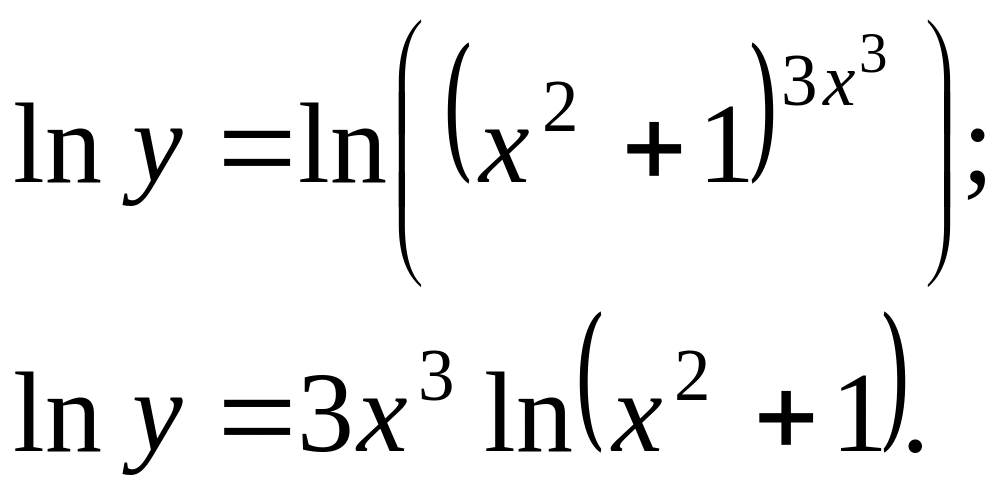
Продифференцируем
данное равенство:

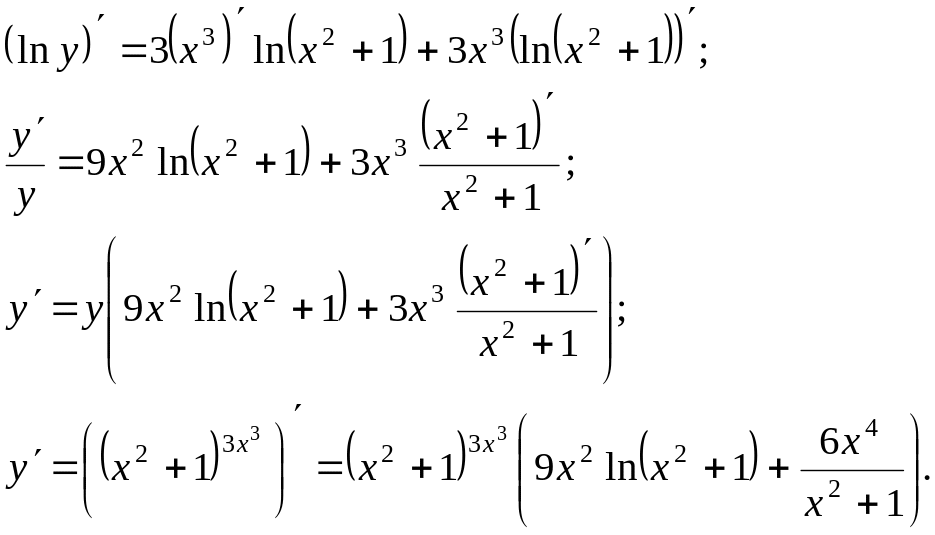
Дифференциал функции и его приложение

Пусть функция y
= f(x)
дифференцируема в точке х,
тогда f
’(x)
=

,
а по теореме о связи функции, имеющей
предел и бесконечно-малой

,
т.е. приращение функции можно представить
в виде двух слагаемых, одно зависит от
х
линейно, а второе содержит степени х
не ниже второй.

Опр. 1. Дифференциалом
функции называется главная часть ее
приращения, линейная относительно
приращения аргумента.

Обозначается:

(34)

Для f
(x)
= x;
dx
= х,
тогда dy
= f
’(x)dx

Поэтому производную
функции y
= f(x)
можно обозначить:

(35.)

Из определения
(4.29) следует, что свойства дифференциалов
аналогичны свойствам производной:

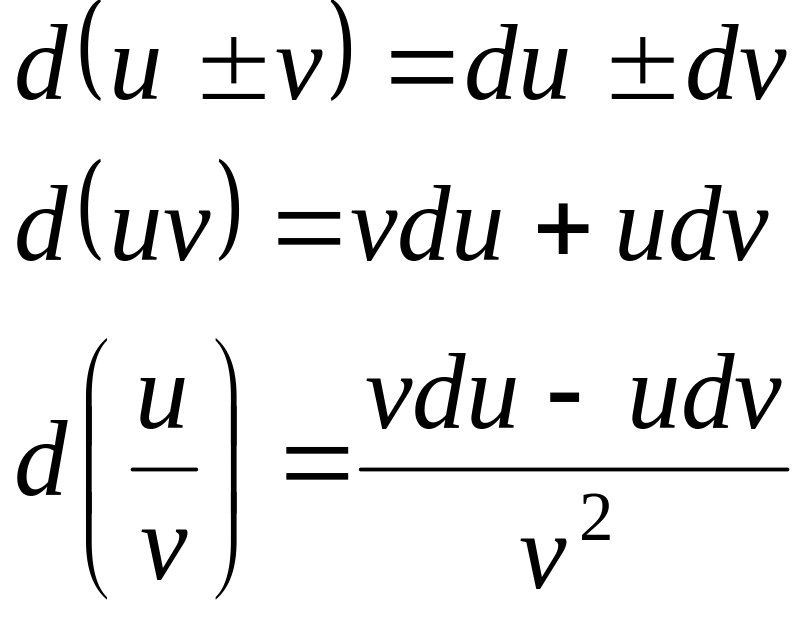
Приложения
дифференциала основываются на приближенной
формуле:

(36)

1. Приближенные
   вычисления.

Пусть известно
значение функции y
= f
(x)
в точке х₀,
т.е. f
(х₀).
Тогда

.
Обозначим х
= х₀
+ х,
получим

(37)

Пример. Вычислить
приближенно значение

1)

.

Решение. Имеем

х
= 4,01; х
= х — х₀=0,01.

Поэтому

1. 

Имеем
f
(x)
= sin
x;
x=33⁰=
,
берем

sin
33⁰
= sin

1. Оценка погрешности.

Пусть имеем
зависимость y
= f
(x),
а х
измеряется с ошибкой х,
тогда у
получит ошибку у:

.

Например, найдем
ошибку при вычислении ln
2,1. Т.к. х
= 2,1, то ошибка х
= 0,05, f
(x)
= ln
x;

поэтому

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как найти дифференциал неявной функции

Правило 1. Уравнение

при известных условиях задает переменную как неявную функцию аргументов х, у. Чтобы найти полный дифференциал этой функции, надо продифференцировать уравнение (1), т. е. приравнять к нулю полный дифференциал его левой части. Полученное равенство надо разрешить относительно и мы найдем полный дифференциал функции Коэффициенты при дадут соответствующие частные производные.

Таким же образом поступаем при любом числе аргументов.

Пример 1. Найти полный дифференциал и частные производные неявной функции аргументов х, у, заданной уравнением

Решение. Дифференцируя, находим:

Разрешив это равенство относительно получаем полный дифференциал функции (в произвольной точке)

В данной точке (1; -2; -2) имеем:

Коэффициенты при дают значения частных производных в данной точке:

Проверка. Решив уравнение относительно получим:

(перед радикалом берем знак минус, так как при должны иметь ). Из (6) находим:

Подставляя сюда значения снова получаем формулы (5).

Замечание 1. В правиле 1 предполагается, что функция дифференцируема в некоторой точке удовлетворяющей уравнению (1), и в достаточной близости от нее (т. е. во всех точках некоторого шара с центром в точке ). Кроме того, предполагается, что уравнение, полученное дифференцированием, однозначно разрешимо относительно что коэффициент при отличен от нуля). При этих условиях можно утверждать:

1) что уравнение (1) действительно задает как неявную функцию аргументов она определена в некотором круге с центром и принимает значение при

2) что функция дифференцируема в упомянутом круге и, в частности, в точке

В примере 1 вышеперечисленные условия выполнялись. В следующем примере рассмотрен один из разнообразных случаев их нарушения.

Пример 2. Уравнение

задает как неявную функцию аргументов Явное ее выражение таково:

Пытаясь применить правило 1 к нахождению полного дифференциала функции в точке мы получили бы из (7) равенство

В точке это равенство не допускает однозначного решения относительно так как оно обращается в тождество Таким образом, правило 1 не даст возможности найти ни полного дифференциала, ни частных производных функции в рассматриваемой точке.

Дополнительное исследование показывает, что в этой точке функция недифференцируема (§ 434), но имеет частные производные

Правило 2. Система двух уравнений

при известных условиях задает две переменные как неявные функции аргументов Чтобы найти полные дифференциалы этих функций, надо продифференцировать уравнения (10). Полученную систему равенств надо разрешить относительно и мы найдем полные дифференциалы функций Коэффициенты при дадут соответствующие частные производные.

Таким же образом поступаем, когда число уравнений в системе больше двух (при любом числе аргументов).

Пример 3. Найти полные дифференциалы и частные производные неявных функций заданных системой уравнений

Решение. Дифференцируя, находим:

Разрешив систему (12) относительно получаем полные дифференциалы функций

Коэффициенты при дают частные производные

Замечание 2. В правиле 2 предполагается, что функции дифференцируемы в некоторой точке и в достаточной близости от нее. Кроме того, предполагается, что система уравнений, полученная дифференцированием, однозначно разрешима относительно (т. е. что определитель, составленный из коэффициентов при отличен от нуля). При этих условиях можно утверждать:

1) что система (10) действительно задает как неявные функции аргументов эти функции определены в некотором шаре с центром и принимают значения при

Дифференциал неявной функции

Если независимая переменная и функция связаны уравнением которое нельзя разрешить относительно то говорят, что функция задана неявно.

По определению дифференциал функции равен

То есть вначале надо найти производную заданной неявно функции а затем подставить ее в последнее соотношение.

Чтобы найти указанную производную, необходимо продифференцировать обе части уравнения и из полученного равенства выразить производную

Отметим, что при дифференцировании надо не забывать, что не является независимой переменной, а есть функция от поэтому производную от нее надо находить как от сложной функции.

Примеры вычисления дифференциалов неявных функций

Согласно свойствам производной, производная суммы равна сумме производных. Тогда имеем:

Из последнего равенства находим производную :

Итак, искомый дифференциал

Дифференцируем левую и правую части последнего равенства:

Производная суммы равна сумме производных, а также производная константы равна нулю. Тогда получаем:

Находим записанные производные и производную от находим как производную сложной функции:

Дифференцирование неявных функций

Частные производные функций, заданных неявно. Если выполнены все условия приведенной выше теоремы и, кроме того, функция дифференцируема в окрестности точки , то функция дифференцируема в окрестности точки и ее производные и могут быть найдены из уравнений

Если функция дифференцируема достаточное число раз, то последовательным дифференцированием этих уравнений вычисляются производные высших порядков от функции .

Дифференцирование неявных функций, заданных системой уравнений. Пусть функции удовлетворяют следующим условиям:

1) обращаются в нуль в точке ;

2) дифференцируемы в окрестности точки ;

3) функциональный определитель (якобиан) в точке .

Тогда система уравнений

однозначно определяет в некоторой окрестности точки систему дифференцируемых функций

удовлетворяющих системе уравнений и начальным условиям

Дифференциалы этих неявных функций могут быть найдены из системы

Пример 6.1. Найти в точке (1;1) частные производные функции , заданной неявно уравнением

Решение. Из уравнения найдем значение функции в данной точке:

. Функция равна нулю в точке (1;1;2) и непрерывна в ее окрестности, а ее частные производные

Поэтому функция является непрерывно дифференцируемой в окрестности точки (1;1;2) и ее частные производные можно найти по формулам:

а значение в точке (1;1;2):

Пример 6.2. Найти производные первого и второго порядков неявных функций в точке , если эти функции заданы системой уравнений

и удовлетворяют условиям .

Решение. Функции

дифференцируемы в окрестности точки . Частные производные

непрерывны в точке . Так как и , а якобиан в точке отличен от нуля, т. е.

то система уравнений (1) определяет единственную пару функций , дважды дифференцируемых в окрестности точки .

Продифференцируем систему (1) по переменной :

Подставив координаты точки в эту систему, получим

Тогда . Еще раз продифференцируем по систему (2):

6.1. Уравнение определяет как многозначную функцию от . В каких областях эта функция: 1) однозначна, 2) двузначна, 3) трехзначна, 4) четырехзначна? Определить точки ветвления этой функции и ее однозначные ветви.

Найти и для функций, определяемых следующими уравнениями:

6.4. Доказать, что для кривой второго порядка

Для функции найти частные производные первого и второго порядков, если:

6.7. Найти при , если

6.10. Найти , если .

6.11. Найти , если .

6.12. Найти и , если .

6.13. Найти и , если , .

6.14. Система уравнений

определяет дифференцируемые функции и такие, что и . Найти и .

6.15. Функция задана уравнением

Ответы: 6.1.1) нигде; 2) ; 3) ; 4) ; однозначные ветви: ,

Явные и неявные

В этой статье мы познакомимся с неявными функциями и техникой их дифференцирования. Вспомним для начала, как выглядят функции, заданные явно. Это “обычные” функции вида y=f(x)y=f(x), с которыми вы уже имели дело и умеете вычислять их производные. Запись y=f(x)y=f(x) обозначает, что мы функцию yy смогли выразить (явно представить) через её аргумент xx. З неявными функциями дело обстоит иначе. Здесь мы не можем “перетащить” yy в левую сторону выражения, а все что содержит xx — в правую. Такие функциональные зависимости в общем виде можно записать так:

F(x,y)=0F(x, y)=0

Эта запись означает, что величины xx и yy как-то связанны между собой, но ничего не говорится о том, как yy выражается через xx (и можно ли это вообще сделать). Одну и ту же функцию (но не каждую) можно записать как в явном так и в неявном виде. Например, неявно заданную функцию F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x} можно записать явно: y(x)=−53x2y(x)=-frac{5}{3x^2}. В этом случае нам удалось выразить yy через xx. Или, если:

F(x,y)=x2+y2−1=0F(x, y)=x^2+y^2-1=0

то

y=±1−x2y=pm sqrt{1-x^2}

Здесь функция получилась многозадачной (именно двузначной, отвечающей двум знакам), но это не страшно. Мы все-равно представили yy как выражение зависящее от xx. В правой стороне у нас присутствует только xx.
Но существуют случаи, когда этого сделать нельзя. Можно навести множество примеров таких функций. Например:

F(x,y)=yln⁡x+eyy2F(x, y)=yln x+e^yy^2

Ну попробуйте выразить отсюда yy через xx. То есть запишите эту функцию в виде y=f(x)y=f(x). Вот вам и пример неявной заданной функции. Ещё пример:

F(x,y)=xsin⁡x+ysin⁡y−12F(x, y)=xsin x+ysin y-12

Здесь, мы хотя и не можем выразить yy через xx, но мы все-равно можем считать yy функцией от аргумента xx. Так как каждому значению xx будут соответствовать какие-то значения yy.
Естественно, возникает вопрос о дифференцировании подобных функций. Вы уже понимаете, что эта операция очень важна, и было бы тяжело поверить, что математики ничего не придумали на этот счет.

Дифференцирование неявно заданных функций

Оказывается, что для того чтобы посчитать производную от yy по xx нам не обязательно решать уравнение:

F(x,y)=0F(x, y)=0

Теоретически можно доказать (пользуюсь определением производной, производя предельный переход и т. д.), что:

Формула дифференцирования неявной функции

dydx=−∂F(x,y)∂x∂F(x,y)∂yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}

Обозначение ∂partial обозначает частную производную. Мы здесь имеем дело с двумя переменными xx и yy и берем производные от функции F(x,y)F(x, y) по этим величинам. Так, выражение:

∂F(x,y)∂xfrac{partial F(x, y)}{partial x}

говорит, что берется производная от F(x,y)F(x, y) по xx, при этом величина yy считается постоянной. Следует обратить внимание на знак “минус” перед дробью, а также на то, что мы не можем сократить числитель и знаменатель на ∂F(x,y)partial F(x, y), так как производные берутся по разным величинам. Вооружившись этой главной формулой вычисления производных от неявных функций, перейдем к разбору нескольких примеров.

Примеры

Пример 1

F(x,y)=x2+y2−1F(x, y)=x^2+y^2-1

∂F(x,y)∂x=2x,     ∂F(x,y)∂y=2yfrac{partial F(x, y)}{partial x}=2x, frac{partial F(x, y)}{partial y}=2y

dydx=−∂F(x,y)∂x∂F(x,y)∂y=−2x2y=−xyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{2x}{2y}=-frac{x}{y}

Пример 2

F(x,y)=xsin⁡x+ysin⁡y−12F(x, y)=xsin x+ysin y-12

∂F(x,y)∂x=sin⁡x+xcos⁡x,     ∂F(x,y)∂y=sin⁡y+ycos⁡yfrac{partial F(x, y)}{partial x}=sin x+x cos x, frac{partial F(x, y)}{partial y}=sin y+y cos y

dydx=−∂F(x,y)∂x∂F(x,y)∂y=−sin⁡x+xcos⁡xsin⁡y+ycos⁡yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{sin x+xcos x}{sin y+ycos y}

Пример 3

1. F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x}

∂F(x,y)∂x=3y−5×2,     ∂F(x,y)∂y=3xfrac{partial F(x, y)}{partial x}=3y-frac{5}{x^2}, frac{partial F(x, y)}{partial y}=3x

dydx=−∂F(x,y)∂x∂F(x,y)∂y=−3y−5x23x=−3yx2−53x3frac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{3y-frac{5}{x^2}}{3x}=-frac{3yx^2-5}{3x^3}

Но здесь мы можем выразить yy через xx явно:

y=−53x2y=-frac{5}{3x^2}

Подставим это выражение в формулу для производной выше:

dydx=103x3frac{dy}{dx}=frac{10}{3x^3}

А теперь поступим так, как будто нам с самого начала была известна явная зависимость y=f(x)y=f(x). То есть продифференцируем функцию y(x)=−53x2y(x)=-frac{5}{3x^2} по xx:

dydx=ddx(−53×2)=−53(−2)1×3=103x3frac{dy}{dx}=frac{d}{dx}Big(-frac{5}{3x^2}Big)=-frac{5}{3}(-2)frac{1}{x^3}=frac{10}{3x^3}

Получили то же самое. Значит мы все сделали правильно.

Дифференцирование сложных и неявно заданных функций.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича. 

Сложные функции одной и нескольких независимых переменных.

Если $u=f(x_1, x_2, .., x_n)-$ дифференцируемая функция переменных $x_1, x_2, …, x_n,$ которые сами являются дифференцируемыми функциями независимой переменной $t:$ $$x_1=varphi_1(t),quad x_2=varphi_2(t),quad, x_n=varphi_n(t),$$ то производная сложной функции $u=f(varphi_1(t)),,varphi_2(t),, varphi_n(t))$ вычисляется по формуле $$frac{du}{dt}=frac{partial u}{partial x_1}.frac{dx_1}{dt}+frac{partial u}{partial x_2}.frac{dx_2}{dt}+…+frac{partial u}{partial x_n}.frac{dx_n}{dt}.$$ В частности, если $t$ совпадает, например, с переменной $x_1,$ то «полная» производная функции $u$ по $x_1$ равна $$frac{du}{dx_1}=frac{partial u}{partial x_1}+frac{partial u}{partial x_2}cdotfrac{dx_2}{dx_1}+…+frac{partial u}{partial x_n}cdotfrac{dx_n}{dx_1}.$$ Пусть $u=f(x_1, x_2, .., x_n),$ где $$x_1=varphi_1(t_1, t_2, …, t_m),quad x_2=varphi_2(t_1, t_2, …, t_m),quad, x_n=varphi_n(t_1, t_2, …, t_m),$$ $(t_1, t_2,…, t_m) -$ независимые переменные. Частные производные функции $u$ по $t_1, t_2, …, t_m$ выражаются следующим образом: $$frac{partial u}{partial t_1}=frac{partial u}{partial x_1}cdotfrac{partial x_1}{partial t_1}+frac{partial u}{partial x_2}cdotfrac{partial x_2}{partial t_1}+…+frac{partial u}{partial x_n}cdotfrac{partial x_n}{partial t_1},$$  $$frac{partial u}{partial t_2}=frac{partial u}{partial x_1}cdotfrac{partial x_1}{partial t_2}+frac{partial u}{partial x_2}cdotfrac{partial x_2}{partial t_2}+…+frac{partial u}{partial x_n}cdotfrac{partial x_n}{partial t_2},$$ $$cdots$$  $$frac{partial u}{partial t_m}=frac{partial u}{partial x_1}cdotfrac{partial x_1}{partial t_m}+frac{partial u}{partial x_2}cdotfrac{partial x_2}{partial t_m}+…+frac{partial u}{partial x_n}cdotfrac{partial x_n}{partial t_m}.$$При этом выражение для дифференциала 1-го порядка  сохраняет свой вид $$du=frac{partial u}{partial x_1}dx_1+frac{partial u}{partial x_2}dx_2+…+frac{partial u}{partial x_n}dx_n.$$ Выражения для дифференциалов высших порядков сложной функции, вообще говоря, отличаются от выражения вида $$d^mu=left(frac{partial}{partial x_1}dx_1+frac{partial}{partial x_2}dx_2+…+frac{partial}{partial x_n}dx_nright)^mu.$$ Например, дифференциал 2-го порядка выражается формулой

$$d^2u=left(frac{partial}{partial x_1}dx_1+frac{partial}{partial x_2}dx_2+…+frac{partial}{partial x_n}dx_nright)^2u+$$ $$+frac{partial u}{partial x_1}d^2x_1+frac{partial u}{partial x_1}d^2x_2+…+frac{partial u}{partial x_n} d^2x_n.$$

Неявные функции одной и нескольких независимых переменных.

Пусть уравнение $f(x, y)=0,$ где $f-$ дифференцируемая функция переменных $x$ и $y$ определяет $y$ как функцию $x.$ Первая производная этой неявной функции $y=y(x)$ в точке $x_0$ выражается по формуле $$left.frac{dy}{dx}right|_{x_0}=-frac{f’_x(x_0, y_0)}{f’_y(x_0, y_0)}qquadqquadqquad(1)$$ при условии, что $f’_y(x_0, y_0)neq 0,$ где $y_0=y(x_0), f(x_0, y_0)=0.$

Производные высших порядков вычисляются последовательным дифференцированием формулы (1).

Примеры:

7.114. Найти $frac{dz}{dt},$ если $z=e^{2x-3y},$ где $x=tg t, ,, y=t^2-t.$

Решение.

Мы будем пользоваться формулой $$frac{du}{dt}=frac{partial u}{partial x_1}.frac{dx_1}{dt}+frac{partial u}{partial x_2}.frac{dx_2}{dt}+…+frac{partial u}{partial x_n}.frac{dx_n}{dt}.$$

Найдем частные производные:

$frac{partial z}{partial x}=e^{2x-3y}(2x-3y)’_x=2e^{2x-3y};$

$frac{partial z}{partial y}=e^{2x-3y}(2x-3y)’_y=-3e^{2x-3y};$

$frac{dx}{dt}=frac{1}{cos^2t};$

$frac{dy}{dt}=2t-1.$

Отсюда $$frac{dz}{dt}=2e^{2x-3y}frac{1}{cos^2t}-3e^{2x-3y}(2t-1)=frac{2e^{2tg t-3(t^2-2)}}{cos^2 t}-3e^{(2tg t-3t^2-2)}(2t-1).$$

Ответ: $frac{2e^{2tg t-3(t^2-2)}}{cos^2t}-3e^{3(t^2-2)}(2t-1).$ 

7.115. Найти $frac{dz}{dt},$ если $z=x^y,$ где $x=ln t, ,, y=sin t.$

Решение. 

Мы будем пользоваться формулой $$frac{du}{dt}=frac{partial u}{partial x_1}.frac{dx_1}{dt}+frac{partial u}{partial x_2}.frac{dx_2}{dt}+…+frac{partial u}{partial x_n}.frac{dx_n}{dt}.$$

Найдем частные производные: 

$frac{partial z}{partial x}=(x^y)’_x=yx^{y-1};$

$frac{partial z}{partial y}=(x^y)’_y=x^yln x;$

$frac{dx}{dt}=(ln t)’=frac{1}{t};$ 

$frac{dy}{dt}=(sin t)’=cos t.$

Отсюда  

$$frac{dz}{dt}=yx^{y-1}frac{1}{t} +x^y ln xcos t=frac{sin tcdot ln t^{sin t -1}}{t}-(ln t)^{sin t}cos tlnln t.$$

Ответ: $frac{dz}{dt}=frac{sin tcdot ln t^{sin t -1}}{t}-(ln t)^{sin t}cos tlnln t.$

7.118.  Найти $frac{partial z}{partial x}$ и $frac{dz}{dx},$ если $z=ln(e^x+e^y),$ где $ y=frac{1}{3}x^3+x.$

Решение. 

$$frac{partial z}{partial x}=(ln(e^x+e^y))’_x=frac{1}{e^x+e^y}(e^x+e^y)’_x=frac{e^x}{e^x+e^y}.$$

Для нахождения $frac{dz}{dx},$ будем пользоваться формулой $$frac{du}{dx_1}=frac{partial u}{partial x_1}+frac{partial u}{partial x_2}cdotfrac{dx_2}{dx_1}+…+frac{partial u}{partial x_n}cdotfrac{dx_n}{dx_1}.$$

$$frac{partial z}{partial y}=(ln(e^x+e^y))’_y=frac{1}{e^x+e^y}(e^x+e^y)’_y=frac{e^y}{e^x+e^y};$$

$$frac{dy}{dx}=(frac{1}{3}x^3+x)’=frac{3x^2}{3}+1=x^2+1.$$

Отсюда  

$$frac{dz}{dz}=frac{partial z}{partial x}+frac{partial z}{partial y}cdotfrac{dy}{dx}=frac{e^x}{e^x+e^y}+frac{e^y}{e^x+e^y}(x^2+1).$$

Ответ: $frac{e^x}{e^x+e^y};$ $frac{e^x+e^y(x^2+1)}{e^x+e^y}.$

7.123. Найти $frac{partial z}{partial x}$ и $frac{partial z}{partial y},$ если $z=f(u, v),$ где $ u=ln(x^2-y^2),, v=xy^2.$

Решение. 

Мы будем пользоваться формулами $$frac{partial z}{partial x}=frac{partial z}{partial u}cdotfrac{partial u}{partial x}+frac{partial z}{partial v}cdotfrac{partial v}{partial x},$$  $$frac{partial z}{partial y}=frac{partial z}{partial u}cdotfrac{partial u}{partial y}+frac{partial z}{partial v}cdotfrac{partial v}{partial y},$$ 

Найдем частные производные:  

$$frac{partial u}{partial x}=(ln(x^2-y^2))’_x=frac{1}{x^2-y^2}(x^2-y^2)’_x=frac{2x}{x^2-y^2};$$

$$frac{partial u}{partial y}=(ln(x^2-y^2))’_y=frac{1}{x^2-y^2}(x^2-y^2)’_y=frac{-2y}{x^2-y^2};$$

$$frac{partial v}{partial x}=(xy^2)’_x=y^2;$$

$$frac{partial v}{partial y}=(xy^2)’_y=2xy;$$

Отсюда   

$$frac{partial z}{partial x}=z’_ufrac{2x}{x^2-y^2}+z’_vy^2,$$  

$$frac{partial z}{partial y}=z’_ufrac{-2y}{x^2-y^2}+2z’_vxy.$$

Ответ: $frac{partial z}{partial x}=z’_ufrac{2x}{x^2-y^2}+z’_vy^2,$  $frac{partial z}{partial y}=z’_ufrac{-2y}{x^2-y^2}+2z’_vxy.$

7.125. Найти $dz,$ если $z=f(u, v),$ где  $ u=sinfrac{x}{y},, v=sqrt{x/y}.$

Решение. 

Мы будем пользоваться формулой $$dz=frac{partial z}{partial u}du+frac{partial z}{partial y}dy.$$ 

Найдем частные производные:  

$$frac{partial u}{partial x}=left(sinfrac{x}{y}right)’_x=frac{1}{y}cosfrac{x}{y};$$

$$frac{partial u}{partial y}=left(sinfrac{x}{y}right)’_y=frac{-x}{y^2}cosfrac{x}{y};$$

$$frac{partial v}{partial x}=left(sqrt{x/y}right)’_x=frac{1}{2sqrt{x/y}}left(frac{x}{y}right)’_x=frac{1}{2ysqrt{x/y}};$$ 

$$frac{partial v}{partial y}=left(sqrt{x/y}right)’_y=frac{1}{2sqrt{x/y}}left(frac{x}{y}right)’_y=frac{-x}{2y^2sqrt{x/y}}.$$ 

Отсюда  

$$du=frac{1}{y}cosfrac{x}{y}dx-frac{x}{y^2}cosfrac{x}{y}dy.$$

$$dv=frac{1}{2ysqrt{x/y}}dx-frac{x}{2y^2sqrt{x/y}}dy.$$ 

Таким образом, 

$$dz=f’_uleft(frac{1}{y}cosfrac{x}{y}dx-frac{x}{y^2}cosfrac{x}{y}dyright)+f’_vleft(frac{1}{2ysqrt{x/y}}dx-frac{x}{2y^2sqrt{x/y}}dyright)=$$ $$=frac{1}{y^2}left(yf’_ucosfrac{x}{y}+yf’_vfrac{1}{2sqrt{x/y}}right)dx-left(xcosfrac{x}{y}+frac{x}{2sqrt{x/y}}right)dy.$$

Ответ: $frac{1}{y^2}left(yf’_ucosfrac{x}{y}+yf’_vfrac{1}{2sqrt{x/y}}right)dx-left(xcosfrac{x}{y}+frac{x}{2sqrt{x/y}}right)dy.$

7.138.  Найти $d^2u,$ если $u=f(ax,by,cz).$

Решение.

Обозначим $$x_1=ax,$$ $$x_2=by,$$ $$x_3=cz.$$ Будем пользоваться формулой 

$$d^2u=left(frac{partial}{partial x_1}dx_1+ frac{partial}{partial x_2}dx_2+frac{partial}{partial x_3}dx_3right)^2u+frac{partial u}{partial x_1}d^2x_1+ frac{partial u}{partial x_1}d^2x_2+frac{partial u}{partial x_3} d^2x_3.$$ 

Далее находим,

$$dx_1=d(ax)=adx;$$

$$dx_2=d(by)=bdy;$$

$$dx_3=d(cz)=cdz;$$

$$d^2x_1=(ax)»_xdx^2=0;$$

$$d^2x_2=(by)»_ydy^2=0;$$

$$d^2x_3=(cz)»_zdz^2=0.$$

Таким образом,

$$d^2u=left(frac{partial}{partial x_1}dx_1+ frac{partial}{partial x_2}dx_2+frac{partial}{partial x_3}dx_3right)^2u+frac{partial u}{partial x_1}d^2x_1+ frac{partial u}{partial x_1}d^2x_2+frac{partial u}{partial x_3} d^2x_3=$$  

$$=frac{partial^2u}{partial x_1^2}dx_1^2+ frac{partial^2u}{partial x_2^2}dx_2^2+frac{partial^2u}{partial x_3^2}dx_3^2+2frac{partial^2u}{partial x_1partial x_2}dx_1dx_2+ 2frac{partial^2u}{partial x_1x_3}dx_1dx_3+2frac{partial^2u}{partial x_2partial x_3}dx_2dx_3=$$ $$=frac{partial^2u}{partial x_1^2}a^2dx^2+ frac{partial^2u}{partial x_2^2}b^2dy^2+frac{partial^2u}{partial x_3^2}c^2dz^2+2frac{partial^2u}{partial x_1partial x_2}abdxdy+ 2frac{partial^2u}{partial x_1x_3}acdxdz+2frac{partial^2u}{partial x_2partial x_3}bcdydz.$$ 

Ответ: $frac{partial^2u}{partial x_1^2}a^2dx^2+ frac{partial^2u}{partial x_2^2}b^2dy^2+frac{partial^2u}{partial x_3^2}c^2dz^2+2frac{partial^2u}{partial x_1partial x_2}abdxdy+ 2frac{partial^2u}{partial x_1x_3}acdxdz+2frac{partial^2u}{partial x_2partial x_3}bcdydz.$

7.140. Найти $frac{dy}{dx},$ если $x^2e^{2y}-y^2e^{2x}=0.$

Решение.

Производную$frac{dy}{dx}$ ищем по формуле $$frac{dy}{dx}=-frac{f’_x(x, y)}{f’_y(x, y)}.$$ Здесь  $f(x,y)=x^2e^{2y}-y^2e^{2x}.$

Найдем частные производные

$$f’_x(x,y)=(x^2e^{2y}-y^2e^{2x})’_x=2xe^{2y}-2y^2e^{2x};$$

$$f’_y(x,y)=(x^2e^{2y}-y^2e^{2x})’_y=2x^2e^{2y}-2ye^{2x}.$$

Отсюда находим

$$frac{dy}{dx}=-frac{f’_x(x, y)}{f’_y(x, y)}=-frac{2xe^{2y}-2y^2e^{2x}}{2x^2e^{2y}-2ye^{2x}}=frac{y^2e^{2x}-xe^{2y}}{x^2e^{2y}-ye^{2x}}.$$

Ответ: $frac{y^2e^{2x}-xe^{2y}}{x^2e^{2y}-ye^{2x}}.$

7.143. Найти $frac{dy}{dx},$ $frac{d^2y}{dx^2},$ если $x-y+arctg y=0.$

Решение.

Производную$frac{dy}{dx}$ ищем по формуле $$frac{dy}{dx}=-frac{f’_x(x, y)}{f’_y(x, y)}.$$ Здесь  $f(x,y)=x-y+arctg y.$

Найдем частные производные

$$f’_x(x,y)=(x-y+arctgy)’_x=1;$$

$$f’_y(x,y)=(x-y+arctgy)’_y=-1+frac{1}{1+y^2}.$$

Отсюда находим

$$frac{dy}{dx}=-frac{f’_x(x, y)}{f’_y(x, y)}=-frac{1}{-1+frac{1}{1+y^2}}=frac{1+y^2}{y^2}.$$

Производную второго порядка $frac{d^2y}{dx^2}$ находим, дифференцируя выражение $frac{dy}{dx}=frac{1+y^2}{y^2}$ по переменной $x.$

$$frac{d^2y}{dx^2}=frac{(1+y^2)’_xy^2-(y^2)’_x(1+y^2)}{y^4}=frac{2yy’_xy^2-2yy’_x(1+y^2)}{y^4}=-2frac{y’_x}{y^3}=$$ $$=-2frac{frac{1+y^2}{y^2}}{y^3}=-2frac{1+y^2}{y^5}$$

Ответ: $frac{dy}{dx}=frac{1+y^2}{y^2};$ $frac{d^2y}{dx^2}=-2frac{1+y^2}{y^5}.$

7.152. Найти $frac{partial^2z}{partial x^2},$ $frac{partial^2z}{partial xpartial y},$ $frac{partial^2z}{partial y^2},$ если $x+y+z=e^z.$

Решение. 

Производные $frac{dz}{dx}$ и $frac{dz}{dy}$ ищем по формулам $$frac{dz}{dx}=-frac{f’_x(x, y, z)}{f’_z(x, y, z)};$$ $$frac{dz}{dy}=-frac{f’_y(x, y, z)}{f’_z(x, y, z)};$$ Здесь  $f(x, y, z)=x+y+z-e^z.$ 

Найдем частные производные

$$f’_x(x,y,z)=(x+y+z-e^z)’_x=1;$$

$$f’_y(x,y,z)=(x+y+z-e^z)’_y=1;$$

$$f’_z(x,y,z)=(x+y+z-e^z)’_z=1-e^z.$$

Отсюда находим 

$$frac{dz}{dx}=-frac{f’_x(x, y, z)}{f’_z(x, y, z)}=-frac{1}{1-e^z}.$$

$$frac{dz}{dy}=-frac{f’_x(x, y, z)}{f’_z(x, y, z)}=-frac{1}{1-e^z}.$$ 

Производные второго порядка находим, дифференцируя найденные производные первого порядка по соответствующим переменным.

$$frac{d^2z}{dx^2}=frac{(1-e^z)’_x}{(1-e^z)^2}=-frac{e^zz’_x}{(1-e^z)^2}=-frac{-e^zcdotfrac{1}{1-e^z}}{(1-e^z)^2}=frac{e^z}{(1-e^z)^3}.$$ $$frac{d^2z}{dxdy}=frac{(1-e^z)’_y}{(1-e^z)^2}=-frac{e^zz’_y}{(1-e^z)^2}=-frac{-e^zcdotfrac{1}{1-e^z}}{(1-e^z)^2}=frac{e^z}{(1-e^z)^3}.$$ $$frac{d^2z}{dy^2}=frac{(1-e^z)’_y}{(1-e^z)^2}=-frac{e^zz’_y}{(1-e^z)^2}=-frac{-e^zcdotfrac{1}{1-e^z}}{(1-e^z)^2}=frac{e^z}{(1-e^z)^3}.$$

Ответ: $frac{d^2z}{dx^2}=frac{d^2z}{dxdy}=frac{d^2z}{dy^2}=frac{e^z}{(1-e^z)^3}.$