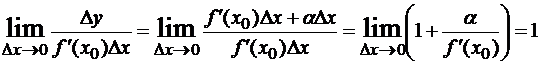Полный дифференциал функции
Как найти?
Постановка задачи
Найти полный дифференциал функции двух переменных $ z = f(x,y) $
План решения
Формула полного дифференциала функции записывается следующим образом:
$$ dz = f’_x (x,y) dx + f’_y (x,y) dy $$
- Находим первые частные производные функции $ z = f(x,y) $
- Подставляя полученные производные $ f’_x $ и $ f’_y $ в формулу, записываем ответ
Примеры решений
| Пример 1 |
| Найти полный дифференциал функции двух переменных $ z = 2x + 3y $ |
| Решение |
|
Находим частные производные первого порядка: $$ f’_x = 2 $$ $$ f’_y = 3 $$ Подставляем полученные выражения в формулу полного дифференциала и записываем ответ: $$ dz = 2dx + 3dy $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ dz = 2dx + 3dy $$ |
| Пример 2 |
| Найти полный дифференциал функции нескольких переменных $ u = xyz $ |
| Решение |
|
Так как функция состоит из трёх переменных, то в формуле полного дифференциала функции необходимо это учесть и добавить третье слагаемое $ f’_z dz $: $$ du = f’_x dx + f’_y dy + f’_z dz $$ Аналогично как и в случае функции двух переменных находим частные производные первого порядка: $$ u’_x = yz $$ $$ u’_y = xz $$ $$ u’_z = xy $$ Используя формулу записываем ответ: $$ du = yzdx + xzdy + xydz $$ |
| Ответ |
| $$ du = yzdx + xzdy + xydz $$ |
| Пример 3 |
| Вычислить значение полного дифференциала функции $ z = x^3+y^4 $, при $ x = 1 $, $ y = 2 $, $ dx = 0.03 $ и $ dy = -0.01 $ |
| Решение |
|
Берем частные производные первого порядка: $$ z’_x = 3x^2 $$ $$ z’_y = 4y^3 $$ Воспользовавшись формулой составляем полный дифференциал: $$ dz = 3x^2 dx + 4y^3 dy $$ Из условия задачи известны все переменные для вычисления значения дифференциала. Подставив их и вычислим значение: $$ dz = 3cdot 1^2 cdot 0.03 + 4 cdot 2^3 cdot (-0.01) = 0.09 — 0.32 = -0.23 $$ |
| Ответ |
| $$ dz = -0.23 $$ |
moz писал(а):
Помогите, пжл, найти полный дифференциал следующей функции:
[math]z=sin^2{x}cos^2{y}[/math]
Спасибо!
Надеюсь, Вы хоть пытались самостоятельно сделать это простейшее задание.
Находите частную производную по x
[math]frac{partial{z}}{partial{x}}=2sin{x}cos{x}cos^2y=sin2xcos^2y.[/math]
Находите частную производную по y
[math]frac{partial{z}}{partial{y}}=-2sin^2xcos{y}sin{y}=-sin^2xsin2y.[/math]
Зная частные производные, записываете свой полный дифференциал:
[math]dz=frac{partial{z}}{partial{x}},dx+frac{partial{z}}{partial{y}},dy=left(sin2xcos^2yright)dx-left(sin^2xsin2yright)dy.[/math]
1. Основные определения
Определение
1.
Соответствие, которое каждой паре (x; y)
значений переменных x и y, принадлежащей
некоторому множеству пар D, сопоставляет
одно и только одно число zR,
называется функцией двух переменных,
определенной на множестве D со значениями
в R. При этом пишут z = f(x;y). D = D(f) – область
определения функции f.
2. Частные и полное приращения функции двух переменных
Если
в функции z = f(x; y) двух переменных x и y
зафиксировать значение
одной из них, например y = y0,
то получим функцию z = f(x;
y0),
зависящую от одной переменной х.
Аналогично,
если зафиксировать переменную x = x0,
получим функцию z = f(x0;
y) одной переменной у.
Определение
2. Величина
xz
= f(x0+x;
y0)
f(x0;
y0)
называется частным
приращением
функции
z = f(x; y) в точке (x0;
y0)
по аргументу х.
Определение
3. Величина
yz
= f(x0;
y0+y)
f(x0;
y0)
называется частным
приращением
функции
z = f(x; y) в точке (x0;
y0)
по аргументу y.
Определение
4. Величина
z
= f(x0+x;
y0+y)
f(x0;
y0)
называется полным
приращением
функции z =
f(x; y) в точке (x0;
y0).
3. Частные производные функции двух переменных
Пусть
дана функция z = f(x; y) двух независимых
переменных x и
y. Фиксируя одну из них, например, полагая
у = const, приходим к функции одной переменной
x. Тогда можно ввести понятие производной
полученной функции по x, которую обозначим
.
Согласно определению производной
функции одной переменной имеем:
Определение
5. Предел
отношения частного приращения xz
функции z=f(x; y) по переменной x к приращению
x
переменной x при x,
стремящимся к нулю, называется частной
производной
функции по
x и обозначается
;
;
Аналогично
определяется и обозначается частная
производная
функции z = f(x; y) по переменной y.
Пример
1. Найти
частные производные функций:
-
f(x;
y) = x3 +
x2 y2
+ y3
+ 3; -
z
= xy +
yx.
Решение
1.
Полагая y = const, и считая при этом x
независимой переменной, найдем
Аналогично
при x = const, получим
.
2.
При
y = const
;
при
x = const
Все сказанное можно
распространить на функции любого числа
переменных.
Пример
2. Найти
частные производные функции
u
= f(x; y; z) = cos(x2
+ y2
+ z2).
Решение
sin(x2
+ y2
+
z2)
2x, y = const, z = const;
sin(x2
+
y2
+
z2)
2y, x = const, z = const;
sin(x2
+ y2
+ z2)
2z, x = const, y = const.
Поскольку
частные производные от функции нескольких
переменных также являются, вообще
говоря, функциями нескольких переменных,
то для них можно также вычислять частные
производные. Эти производные называют
частными
производными высших порядков.
Например,
для функции f(x; y) двух переменных имеются
следующие типы производных второго
порядка:
вторая
частная производная по x;
и
=
смешанные частные производные
вторая
частная производная по у.
4. Полный дифференциал функции двух переменных
Определение
6. Полным
дифференциалом функции z=f(x;y) двух
переменных x и y называется главная часть
полного приращения z,
линейная относительно приращений
аргументов x
и y.
C
учетом того, что x
= dx и y
= dy полный дифференциал функции z = f(x; y)
вычисляется по формуле
dz
=
.
(3.5)
Пример
3. Вычислить
полный дифференциал функции
z
= ln (x2 +
y2).
Решение.
Найдем частные производные
и
данной функции
;
После
их подстановки в формулу (3.5) получим
dz
=
Найти
частные производные функций
284.
z =
x2
+ 2xy + y2
+ 5 285. z = (x + y)3
286.
z =
287. z =
288.
z = x3y
y3x
289. z = 2y
290.
z = x y ln(x + y) 291. z = ln
292.
z = ln
+ ln x·y 293. z =
294.
z = ey/x
– ex/y
295. z = xy
+ sin
296.
z = sin(x2y
+ xy2)
297. z
= yx
+ arctg
Найти
частные производные второго порядка
298.
z = x4
+ 4x2y3
+ 7xy + 1 299. z = x2y
300.
z = 4x3
+ 3x2y
+ 3xy2
– y3
301. z
= xy + sin(x + y)
302.
z = sin
x
cos
y
303. z =
304.
z = xey
305. z = x + y +
306.
z = x2y
307. z
= ln(x + exy)
Проверить,
что
308.
z =
309. z = ln(x
2y)
310.
z =
311. z = x2
sin
312.
z =
313. z = arctg
Найти полный
дифференциал функций
314.
z = xy3
3x2y2
+ 2y4
+1 315. z
= 3x2y5
316.
z = sin(x2
+ y2)
317. z = xy
318. z = exy
319.
z = ex
cos
y
320. z = ey
cos
x
321. z
= cos+sin
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дифференциалом функции
называется главная (линейная по
) часть приращения функции. Чтобы понять данное определение, рассмотрим следующий рисунок.
На рисунке изображён график функции
и
касательной
к ней в точке
.
Дадим аргументу функции
некоторое приращение
,
тогда функция
также получит некоторое приращение
.
Величина
называется
дифференциалом функции
.
При этом, из графика следует, что
равно приращению ординаты касательной, проведённой в точке
к функции
.
Именно поэтому дифференциалом называют линейную часть приращения функции, т.е. приращение ординаты касательной.
Из рисунка следует, что угол наклона касательной
,
который она образует с положительным направлением оси
и
— равны. Кроме того, тангенс угла наклона касательной равен значению производной функции в точке касания:
Из треугольника
следует, что:
Таким образом, дифференциал функции выражается следующей формулой:
Рассмотрим ещё такой момент: из рисунка следует, что
, причем
. Причем, чем меньше
, тем меньший вклад в величину
вносит значение
. Т.е. при достаточно малых значениях
, можно считать, что
. Данное соотношение позволяет вычислять приближенное значение функции в точке
, если известно её значение в точке
.
Дифференциал высшего порядка (например порядка
) определяется как дифференциал от дифференциала
-ого порядка:
Например, дифференциал второго порядка вычисляется следующим образом:
Аналогичным образом получаем формулу для вычисления дифференциала
-ого порядка:
где
—
-ая производная функции
по переменной
.
Пару слов стоит сказать о вычислении дифференциала функции многих переменных, который в этом случае называется
полным дифференциалом. Полный дифференциал функции, зависящей от
-переменных
определяется по формуле:
Выражения для дифференциалов высших порядков функции многих переменных можно получить исходя из общей формулы:
В общем случае, для возведения суммы в
-ую степень необходимо воспользоваться формулой бинома Ньютона. Рассмотрим процесс получения формулы полного дифференциала второго порядка функции двух переменных:
Наш онлайн калькулятор способен вычислить дифференциалы разных порядков для любых функций одной или нескольких переменных с описанием подробного решения на русском языке.
Дифференциал функции
dy=f′(x)dx
Как видим, для нахождения дифференциала нужно умножить производную на dx. Это позволяет из таблицы формул для производных сразу записать соответствующую таблицу для дифференциалов.
Полный дифференциал для функции двух переменных: 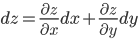
Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz
- Решение онлайн
- Видеоинструкция
- Также решают
Примеры
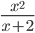
cos2(2x+π) ≡ (cos(2*x+pi))^2
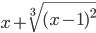
см. также Вычисление приближенно с помощью дифференциала
Определение. Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение в этой точке можно представить в виде ∆y=A∆x + α(∆x)∆x, где A – константа, а α(∆x) – бесконечно малая при ∆x → 0.
Требование дифференцируемости функции в точке эквивалентно существованию производной в этой точке, причем A=f’(x0).
Пусть f(x) дифференцируема в точке x0 и f ‘(x0)≠0, тогда ∆y=f’(x0)∆x + α∆x, где α= α(∆x) →0 при ∆x→0. Величина ∆y и каждое слагаемое правой части являются бесконечно малыми величинами при ∆x→0. Сравним их: 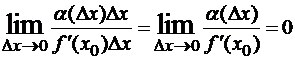
то есть ∆y~f’(x0)∆x. Следовательно, f’(x0)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x0 и обозначают dy(x0) или df(x0). Итак, для произвольных значений x
dy=f′(x)∆x. (1)
Полагают dx=∆x, тогда
dy=f′(x)dx. (2)
Пример. Найти производные и дифференциалы данных функций.
а) y=4tg2x
Решение:
дифференциал:
б)
Решение:
дифференциал:
в) y=arcsin2(lnx)
Решение:
дифференциал:
г)
Решение:

дифференциал: 
Пример. Для функции y=x3 найти выражение для ∆y и dy при некоторых значениях x и ∆x.
Решение. ∆y = (x+∆x)3 – x3 = x3 + 3x2∆x +3x∆x2 + ∆x3 – x3 = 3x2∆x+3x∆x2+∆x3; dy=3x2∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x2 + ∆x3.