Полный образ и полный прообраз
Рассмотрим
в соответствии R
= <X,Y,GR>,
где GR
XY
все пары вида (a;
у),
где
и
,
для которых верно аRу.
Множество
всех таких у
из
множества Y,
для
которых верно аRy,
назовём полным
образом элемента
а
Х
в соответствии R
между элементами множеств Х
иY.



Y3
Пусть
у=bY.
Расмотрим все пары вида (х,b)
для которых верно хRb.
Тогда
множество таких х
из множества Х,
для
которых верно
хRb,
назовём полным
прообразом
элемента b
соответствии R
между элементами множеств Х
и Y.
X Y


X3
X4
В
примере 1 полный прообраз элемента 4
состоит из одного элемента: 2; полный
образ элемента 3 состоит из одного
элемента: 9.
Способы задания соответствий
1)
по определению бинарное соответствие
будет задано, если будут заданы множества
Х,Y,
и GR
—
это самый общий способ задания
cоответствия;
2)
соответствие может быть задано своим
графиком: GR
=
{(x,у)|
хХ,
уR
,хRy}.
График
соответствия может быть задан перечислением
элементов или указанием характеристических
свойств;.
3)
если множества Х
иY
конечные, то соответствие между
элементами этих множеств может быть
задано с помощью графа:

R
Y
4)
с помощью таблицы, если множества Х и
Y-конечные;
|
Х |
4 |
9 |
|
2 |
||
|
3 |
||
|
5 |
5)
соответствие может быть задано графически
на плоскости , если множества Х
и Y-числовые.
В
примере 1

М2
М1
(2;4).
М2(3;9).

2 3 5
6)
с помощью двухместного предиката, то
есть предложения с двумя переменными,
выражающего факт вступления элементов
в соответствие.
R(х;
у): хRy,
хХ,
у
Y
R(x;
у): «x
– делитель y»,
х
Х , у
Y
.
Рассмотрим
между элементами множеств
Х = {2; 3; 4} и Y
= {5; 6; 8} соответствие
R:
х —
делитель
у.
Тогда Х
— область отправления соответствия, Y—
область прибытия. Область определения
соответствия: ДR
=
{2,3,4}, множество
значений соответствия: ЕR
=
{6;8}.
Пусть
соответствие между элементами множеств
X
и Y
задано
при
помощи графа.

R
Y
.
Тогда
полный
образ
элемента
2состоит
из двух элементов: 6 и 8:
R(2)
= {6;8}; R(3)
= {6}; R(4)
= {8}. R(7)
– пуст.
Полный
прообраз элемента 5
пуст;
;
.
Типы соответствий
Пусть
R
= <X,Y,GR>,
где
GR
XY
и
GR
=
{(x,у)|
хХ,
yY,
хRy}.
Определение:
Если
множество GR
(график соответствия R
между элементами множеств X
иY)
совпадает с множеством
,
то это соответствие называется полным.
Пример:
X
= {1,2,3}
Y
= {5,7,8}.
R(x;
y):
х < y.
ХY
= {(1,5),(1,7),(1,8),(2,5),(2,7),(2,8),(3,5),(3,7),(3,8)}
GR
=
{(1,5),(1,7),(1,8),(2,5),(2,7),(2,8),(3,5),(3,7),(3,8)}.
Тогда
GR
=.
Следовательно, R—
полное соответствие.
Определение:
Если график соответствия
R
между элементами множеств Х
и Y-есть
пустое множество (GR
=
Ǿ }, то такое соответствие называется
пустым.
Пример:
X
= {1,2,3}
Y
=
{5,7,8}.
R(x;
y):
х > y.
Очевидно,
GR
=
Ǿ
= > R—
пустое соответствие.
Определение:
Соответствия F
и R
между элементами множеств X
и Y
называется
противоположными,
если их графики являются дополнениями
друг друга до множества ХY,
то есть GFGR
=
Ǿ и GFGR
=
ХY
=> F
и
R
— противоположные.
Если
соответствие F
задано предикатом F(x,у),
то противоположное ему соответствие
задаётся предикатом, который есть
отрицание предиката F(x,у).
Пример
: X
=
{1,2,3},
Y
=
{5,7,8}.
Пусть
F(x,у):
х < y.
Тогда
:
х
y
– противоположное
ему соответствие
.
Очевидно,
G
=
Ǿ, а
G
=
{(1,5),(1,7),(1,8),(2,5),(2,7),(2,8),(3,5),(3,7),(3,8)}.
Они являются противоположными
соответствиями.
Определение:
Соответствия F
и
R
между элементами множеств Х
и Y
называются несовместимыми,
если GF∩GR
=
Ǿ.
Это
значит, что нет ни одной пары (х,у),
для которой одновременно выполняются
условия хFy
и хRy.
Ясно,
что противоположные соответствия, можно
называть несовместимыми, а наоборот —
нельзя.
Определение:
Если график соответствия F
между элементами множеств Х
иY
является
подмножеством
графика соответствия R
между элементами множеств Х
иY
(
то есть
GFGR),
то соответствие R
называется следствием
соответствия
F.
Пример
1:
Х
—
множество треугольников плоскости.
F:
∆ х = ∆у.
R:
∆ х ~ ∆y.
GF
GR
=>
R
—
следствие соответствия F.
Пример
2:
X
= {1,
2, 3}
Y
=
{2, 3, 5}
F:
х
y.
Тогда GF
=
{(1,2),(1,3),(1,5),(2,2),(2,3),(2,5),(3,5)}.
R:
х < y.
GR
=
{(1,2),(1,3),(1,5),(2,3),(2,5),(3,5)}.
GR
GF
=>
F—
следствие соответствя R.
Определение:
Обратным
к соответствию R
= <X,Y,GR>
между
элементами множеств X
и Y
называется
такое соответствие
между элементами множеств Y
и X
, при котором
тогда
и только тогда, когда
.
Граф
обратного соответствия получается из
графа данного соответствия путём замены
стрелок на противоположные.
Пусть
GR
– график данного соответствия между
элементoв
множества Х
и Y,
тогда, чтобы построить график обратного
соответствия R-1
между элементoв
множества Y
и
Х,
надо поменять местами компоненты пар.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Полный прообраз
- Полный прообраз
-
В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.
Содержание
- 1 Определения
- 2 Обозначения
- 3 Связанные определения
- 4 Свойства
- 4.1 Свойства прообразов и образов
- 5 Классы функций
- 6 Вариации и обобщения
- 6.1 Функции нескольких аргументов
- 7 Примечания
- 8 См. также
- 9 Литература
Определения
- Нестрогое определение: функция — это «закон», по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
- Строгое определение: функция или отображе́ние — это бинарное отношение, обладающее свойством:
- Функция называется инъективной, если
Обозначения
Связанные определения
- Множество F(X) называется образом отображения F и обозначается
.
Свойства
Свойства прообразов и образов
Классы функций
При необходимости можно различать отображения в зависимости от природы множеств X и Y. Если X и Y — числовые множества, такие, как
или
, то отображение называют функцией. Если X или Y многомерны, например,
или
, то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
Вариации и обобщения
- многозначная функция
Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Пусть даны множества
и множество Y, тогда упорядоченное множество всех кортежей
называется функцией n аргументов тогда и только тогда, когда для любых
и
из
следует, что
.[1]
Примечания
- ↑ Кудрявцев Л. Д. Курс математического анализа. — том 1. — М.: Высшая школа, 1981. — с. 8.
См. также
- Композиция функций
- График функции
- Сюръективность
- Инъективность
- Биективность
- Функция с множеством значений {0, 1}
- Функциональное уравнение
Литература
- Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Полный прообраз» в других словарях:
-
Прообраз — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
-
ОТОБРАЖЕНИИ КЛАССЫ — важнейшие классы непрерывных отображений, рассматриваемые в общей топологии и ее приложениях. К ним относятся: открытые отображения такие, что образ любого открытого множества является открытым множеством; замкнутые отображения такие, при к рых… … Математическая энциклопедия
-
Непрерывное отображение — или непрерывная функция в математике это отображение из одного пространства в другое, при котором близкие точки области определения переходят в близкие точки области значений. Наиболее общее определение формулируется для отображений… … Википедия
-
ИДЕАЛ — специального рода подобъект в иек рой алгебраич. структуре. Понятие И. возникло первоначально в теории колец. Название И. ведет свое происхождение от идеальных чисел. Для алгебры, кольца или полугруппы Аидеал I есть подалгебра, подкольцо или… … Математическая энциклопедия
-
ОБРАТНАЯ ФУНКЦИЯ — функция, определенная на множестве значений заданной функции и ставящая в соответствие каждому его элементу множество всех тех элементов из области определения рассматриваемой функции, к рые в него отображаются, т. е. его полный прообраз. Если… … Математическая энциклопедия
-
РАЗМЕРНОСТНЫЙ ИНВАРИАНТ — целое число d(X), определяемое для каждого топологич. пространства Xданного класса и обладающее достаточным количеством свойств, сближающих его с обычным числом измерений евклидовых многомерных пространств. При этом от класса требуется, чтобы он… … Математическая энциклопедия
-
Измеримая функция — Измеримые функции представляют естественный класс функций, связывающих пространства с выделенными алгебрами, в частности измеримыми пространствами. Содержание 1 Определение 2 Замечания … Википедия
-
Отображение — (матем.) множества А в множество В, соответствие, в силу которого каждому элементу х множества А соответствует определённый элемент у = f (x) множества В, называют образом элемента х (элемент х называют прообразом элемента у). Иногда под… … Большая советская энциклопедия
-
ФАКТОРНОЕ ОТОБРАЖЕНИЕ — отображение f то пологич. пространства Xна топологич. пространство Y, при к ром множество открыто в пространстве Yв том и только том случае, если его прообраз f 1v открыт в пространстве X. Если дацрэ отображение f топологич. пространства Xна… … Математическая энциклопедия
-
Идеал (алгебра) — У этого термина существуют и другие значения, см. Идеал (значения). Идеал одно из основных понятий абстрактной алгебры. Наибольшее значение идеалы имеют в теории колец, но также определяются и для полугрупп, алгебр и некоторых других… … Википедия
-
У этого термина существуют и другие значения, см. функция.
Отображе́ние или фу́нкция ( лат. functio — «исполнение, осуществление») — одно из основных понятий математики, выражающее зависимость одной величины от другой.
Отображение функции.
Наиболее распространенная трактовка понятия функции состоит в его отождествлении с понятием отображения:
Определение. Пусть 

Закон 






Отображения обозначают так:
При этом:
Функции считаются равными, если у них одинаковые области определения и значений и если они определяются одним правилом. Например, все три следующие функции различны:
При необходимости можно различать отображения в зависимости от природы множеств 











Способы задания функции
Словесный
игрек равно целая часть от х. (![{displaystyle ~f(x)=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/435e7fcd500b6e0fd346a5bf1f52f7ca4ed93659)
Аналитический

Графический
С помощью графика.
Таблицы
Функция задается таблицей значений. Например:
| X | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Y | 0 | 1 | 8 | 27 |
Интуитивно можно догадаться, что y = x3.
Смежные понятия
Сужение функции.
Пусть дано отображение 




.
Это определение подчеркивает, что фиксация области определения является частью определения функции.
Образ множества
Пусть 


.
Множество 

Прообраз
Пусть задано отображение 








Пример. Пусть дана функция 

Полный прообраз элемента
Пусть задано отображение 




Пример. Пусть 

.
Полный прообраз множества
Пусть 


.
Пример. Пусть 

Свойства прообразов и образов
;
График
Файл:Cubicpoly.svg Фрагмент графика функции
Пусть дано отображение 

,
где 


Исторический очерк
Как и остальные понятия математики, понятие функции сложилось не сразу, а прошло долгий путь развития. В работе П. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. 1679) говорится: «Всякий раз, когда в заключительном уравнении имеются две неизвестные величины, налицо имеется место». По существу здесь идёт речь о функциональной зависимости и её графическом изображении («место» у Ферма означает линию). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У И. Барроу («Лекции по геометрии», 1670) в геометрической форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует уже о совершенно отчётливом владении понятием функции. В геометрическом и механическом виде это понятие мы находим и у И. Ньютона. Однако термин «функция» впервые появляется лишь в 1692 у Г. Лейбница и притом не совсем в современном его понимании. Г. Лейбниц называет функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.
Первое определение функции в смысле, близком к современному, встречается у И. Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Л. Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств». Впрочем, уже Л. Эйлеру не чуждо и современное понимание функции, которое не связывает понятие функции с каким-либо аналитическим её выражением. В его «Дифференциальном исчислении» (755) говорится: «Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функциями вторых».
Всё же в XVIII веке отсутствовало достаточно ясное понимание различия между функцией и её аналитическим выражением. Это нашло отражение в той критике, которой Л. Эйлер подверг решение задачи о колебании струны, предложенное Д. Бернулли (1753). В основе решения Д. Бернулли лежало утверждение о возможности разложить любую функцию в тригонометрический ряд. Возражая против этого, Л.Эйлер указал на то, что подобная разложимость доставляла бы для любой функции аналитическое выражение, в то время как функция может и не иметь его (она может быть задана графиком, «начертанным свободным движением руки»). Эта критика убедительна и с современной точки зрения, ибо не все функции допускают аналитическое изображение (правда, у Д. Бернулли речь идёт о непрерывной функции, которая, как установил в 1885 К. Вейерштрасс, всегда аналитически изобразима, но она может и не разлагаться в тригонометрический ряд). Однако другие аргументы Л.Эйлера уже ошибочны. Например, он считал, что разложение функции в тригонометрический ряд доставляет для неё единое аналитическое выражение, в то время как она может быть «смешанной» функцией, представимой на разных отрезках разными формулами. На самом деле одно другому не противоречит, но в ту эпоху казалось невозможным, чтобы два аналитических выражения, совпадая на части отрезка, не совпадали на всём его протяжении..
С начала XIX века уже всё чаще и чаще определяют понятие функции без упоминания об её аналитическом изображении. В «Трактате по дифференциальному и интегральному исчислению» (1797—1802) С. Лакруа говорится: «Всякая величина, значение которой зависит от одной или многих других величин, называется функцией этих последних». В «Аналитической теории тепла» Ж. Фурье (1822) имеется фраза: «Функция 






Примечания
См. также
- Композиция функций
- Сюръекция
- Инъекция
- Биекция
- Непрерывность
- Дифференцируемость
- Гладкость
- Выпуклость
- Рациональность
- Среднее значение функции
Различные классы функций:
- Интегрируемые функции
- Интегрируемые по Лебегу функции
- Равномерно непрерывные функции
- Целые функции
Литература
- Ильин В. А., Позняк Э. Г. Основы математического анализа, ч.1, 3 изд., М., 1971;. ч.2, 2 изд., М., 1980;
- Кудрявцев Л. Д., Математический анализ, 2 изд., т.1-2, 1973,
- Никольский С. М., Курс математического анализа, 2 изд., т.1-2, М., 1975;
- История математики, т.2-3, М., 1970-72.
- Функция. Математический энциклопедический словарь. Гл. ред. Ю. В. Прохоров. М.: «Большая российская энциклопедия». 1995.
Эта статья содержит материал из статьи Функция русской Википедии.
Что такое прообраз окружности
Введение в теорию множеств и комбинаторику
Практическая работа № 8. Отображения. Виды отображений
Вопросы к работе
- Что такое «отображение множества в множество»?
- Что такое «образ», что такое «прообраз» при данном отображении?
- Что такое полный f — образ, что такое полный f — прообраз, при отображении f ?
- Назовите типы отображений, дайте их определения и приведите примеры.
- Какие два множества называются эквивалентными? Приведите примеры.
- Какое множество называется счетным? Приведите примеры.
Образцы решения заданий
Пример 1. Пусть А = <1; 2; 3; 4; 5; 6; 7; 8; 9> N и В = <0; 1> Z Поставим в соответствие каждому числу x A его остаток при делении на 2.
Является ли это соответствие отображением? Какой тип у этого отображения? Какой элемент является образом элемента 6, 7? Найдем полный прообраз элемента 1.
Решение. Изобразим заданное соответствие с помощью графа:
1) каждый элемент множества А , является точкой исхода;
2) у каждой точки исхода, имеется только по одной точке прибытия. (Значит, указанное соответствие является отображением множества А в множество В);
3) Каждый элемент множества В является точкой прибытия. (Значит, это отображение «на»).
Так как в множестве В есть элемент (например, 0), для которого прообразом является ни один элемент из А , то это отображение не является взаимооднозначным.
Образом числа 6 является число 0 В , образом числа 7 – число 1 В . Полный прообраз числа 1 В есть множество чисел <1; 3; 5; 7; 9> А .
Пример 2. Пусть Х – множество треугольников плоскости, Y = R. Выберем единицу измерения длин и сопоставим каждому треугольнику число – периметр этого треугольника. Будет ли это соответствие отображением? Какой тип у заданного отображения? Каков полный прообраз числа у R ?
Решение. Каждый треугольник на плоскости имеет однозначно определенный периметр. Поэтому каждому треугольнику из множества Х сопоставляется единственное число из R , т. е. это соответствие является отображение Х в R . При этом у двух разных треугольников может быть одинаковый периметр. Другими словами, отображение не является взаимооднозначным. Кроме того, не существует треугольника, периметр которого равен отрицательному числу, т.е. отображение не является отображением «на». Пусть у R . Тогда:
- у > 0, полный образ – множество всех треугольников плоскости, периметр которых равняется числу у , это множество бесконечное.
- у ≤ 0, полный образ – пустое множество.
Пример 3. Х = <0; 1; 2; 3; 4> N , Y = Z. Отображение f множества Х в множество Y задано следующим образом:
Определим тип этого отображения и построим его график.
Решение. Для каждого x X найдем образ y Y. Соответствующие результаты запишем в таблицу:
Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Отображение — определение (что это в математике). Образ, прообраз элемента и отбражения
Primary tabs
Forums:
Отображение — закон (или правило), по которому каждому $Large x in X$ ставится в соответствие некоторый (единственный) $Large y in Y$.
ПРИМЕЧЕНИЕ: множества $X$ и $Y$ могут совпадать, тогда можно говорить о преобразовании.
Образ и прообраз отображения
Если отображение $P$ ставит в соответствие всем элементам из множества $X$ некоторые (или все) элементы из множества $Y$, то:
- $X$ называется прообразом отображения отображения
- $Y_0$ (подмножество $Y$) — образом отображения (при этом $Y$ и $Y_0$ могут и совпадать, это уже зависит от конкретного отображения).
Образ и прообраз [конкретного] элемента
Если элементу $x$ из $Х$ соответствует $y$ из $У$, то y называется образом элемента $x$, а $x$ — прообразом элемента $y$. Пишут:
.
Множество $A$ всех элементов , имеющих один и тот же образ , называется полным прообразом элемента $y$.
http://www.stranamam.ru/post/8974384/
http://fkn.ktu10.com/?q=node/6466
Соответствия и бинарные отношения на множествах
Отображение из множества
в множество
считается заданным, если каждому элементу
сопоставлен единственный элемент
. Отображение
из множества
в множество
обозначают записью
или
. Элемент
, который отображением
сопоставляется элементу
, называют образом элемента
при отображении
и обозначают
.
Каждое отображение однозначно определяет множество упорядоченных пар , являющееся подмножеством декартова произведения
множества
на множество
и называемое графиком отображения
.
Наоборот, пусть в декартовом произведении задано такое подмножество
, что:
1) для любого существует
, для которого
;
2) для любых двух пар и
множества
из равенства
следует равенство
.
Тогда множество единственным образом определяет некоторое отображение из
в
. Это отображение, обозначаемое также
, элементу
сопоставляет элемент
, удовлетворяющий условию
. Таким образом, мы можем отождествить отображения с их графиками и считать, что отображение есть подмножество декартова произведения.
Отображение множества
в себя называют тождественным, если
при всех
из
.
В общем случае для отображения может существовать несколько различных элементов множества
, образы которых совпадают. Множество всех элементов
, для которых
, называют прообразом элемента
при отображении
.
Так, прообраз числа при отображении
есть множество всех решений уравнения
, т.е. множество
Прообраз элемента может быть пустым множеством. Это имеет место, например, для числа
при отображении
.
Множество всех , таких, что найдется
, для которого
, называют областью значений отображения
. Область значений отображения
будем обозначать
.
Отображение называют инъективным (инъекцией), если каждый элемент из области его значений имеет единственный прообраз, т.е. из
следует
.
Отображение называют сюръективным (сюръекцией), если его область значений совпадает со всем множеством
. Сюръективное отображение из
в
называют также отображением множества
на множество
.
Отображение называют биективным (биекцией), если оно одновременно инъективно и сюръективно.
Таким образом, если отображение биективно, то каждому элементу множества
отвечает единственный элемент множества
и наоборот. Тогда говорят, что множества
и
находятся между собой во взаимно однозначном соответствии.
Биекцию множества на себя называют автоморфизмом множества
. Используют также термин «подстановка множества».
Пример 1.2. а. Отображение, заданное равенством , есть, как нетрудно показать, биекция множества натуральных чисел
на его подмножество
.
б. Отображение есть биекция множества всех натуральных чисел на множество всех четных натуральных чисел.
в. Любая показательная функция , есть биекция множества
всех действительных чисел на множество
всех положительных действительных чисел.
г. Функция есть биекция множества
на интервал
.
д. Поворот окружности на заданный угол , т.е. отображение, сопоставляющее каждой точке окружности точку, в которую она перейдет при повороте всей окружности вокруг ее центра на угол
, есть автоморфизм множества точек окружности.
Образ и прообраз множества
Пусть задано отображение и
— некоторое множество. Множество
элементов
, таких, что
, называют образом множества
при отображении
. Например, при отображении
отрезок
является образом множества (отрезка)
, равно как и любого объединения отрезков вида
(для произвольного целого
). При
это можно записать следующим образом:
.
Заметим, что для любого отображения образ
всего множества
есть область значений данного отображения.
Для произвольного множества множество всех элементов
, таких, что
, называют прообразом множества
при отображении
.
Например, для любого действительного числа множество, которое является объединением всех отрезков вида
есть прообраз отрезка при отображении
.
Прообраз области значений произвольного отображения совпадает со всем множеством
.
Множество всех отображений из в
будем обозначать как
.
Частичное отображение и его область определения
Понятие отображения можно обобщить. Обобщение может проходить по двум позициям. Во-первых, можно отказаться от полной определенности отображения, полагая, что образ определен не для каждого элемента множества , а для некоторых элементов этого множества. Тогда придем к понятию частичного отображения. При этом подмножество всех элементов
, для которых определен образ, называют областью определения данного частичного отображения.
Многие элементарные функции являются частичными отображениями множества всех действительных чисел в себя. Например, функция
есть частичное отображение с областью определения
Во-вторых, можно отказаться от однозначности отображения, полагая, что данному сопоставлен не один, а несколько образов (множество образов) в множестве
. В этом случае говорят, что задано соответствие из множества
в множество
.
Примером могут служить обратные тригонометрические функции: скажем, «большой» арксинус, сопоставляющий каждому множество всех таких чисел
, что
, т.е. множество, являющееся прообразом элемента
при отображении, определяемом графиком функции
.
Если задано соответствие из
в
, будем использовать обозначение
по аналогии с обозначением
для отображений, понимая при этом, что
есть уже не элемент множества
, а его подмножество.
Аналогично графику отображения можно определить график соответствия из множества
в множество
как множество
упорядоченных пар
, таких, что
и элементы
связаны соответствием
, то есть
. Указанное множество
упорядоченных пар есть подмножество декартова произведения
.
Обратно, фиксируя на декартовом произведении какое-либо подмножество
, мы тем самым однозначно определяем некоторое соответствие
из
в
, а именно
Нетрудно заметить, что графиком соответствия будет как раз множество
, а соответствием, отвечающим графику
, будет
. Поэтому можно отождествить соответствие с его графиком и считать, что соответствие из множества
в множество
есть некоторое подмножество
декартова произведения
, то есть
. В частности, при
получаем пустое соответствие, а при
, совпадающем со всем указанным декартовым произведением, — универсальное соответствие.
При этом будем писать для упорядоченных пар, связанных соответствием
.
Используют также термины «частичное мультиотображение» и «частичная многозначная функция».
Пример 1.3. Рассмотрим множество программистов и множество программ
. Зададим соответствие
из
в
, связывающее программистов и разрабатываемые ими программы:
Область определения соответствия из множества
в множество
— это множество всех первых компонент упорядоченных пар из
Область значения соответствия — это множество всех вторых компонент упорядоченных пар из
Из определения вытекает, что . Соответствие из
в
называют всюду определенным, если его область определения совпадает с множеством
.
Сечением соответствия для фиксированного элемента
будем называть множество
. Можно сказать, что сечение соответствия
есть множество всех «образов» элемента
при данном соответствии.
Сечением соответствия по множеству
будем называть множество
Пример 1.4. Область определения соответствия т из примера 1.3 есть все множество , а область значения — все множество
. Сечением соответствия
по элементу
будет множество
.
Бинарные отношения на множествах
Соответствие из множества
в себя, т.е. подмножество множества
, называют бинарным отношением на множестве
.
Пример 1.5. Простейшим примером бинарного отношения является отношение нестрогого неравенства на множестве действительных чисел . Здесь каждому
поставлены в соответствие такие
, для которых справедливо
.
Для произвольного бинарного отношения на некотором множестве часто используют запись вместо
, говоря при этом об элементах, связанных бинарным отношением
. Это согласуется с традиционной формой записи некоторых часто используемых бинарных отношений. Так, пишут
, а не
. Для таких бинарных отношений употребляют устоявшиеся словосочетания. Например, запись
читается так: «
не больше
«.
Бинарное отношение на множестве , состоящее из всех пар
, т.е. пар с совпадающими компонентами, называют диагональю множества
и обозначают
. Нетрудно понять, что диагональ
есть тождественное отображение
на себя.
Иногда говорят о диагонали в множестве , хотя правильнее было бы называть это отношение диагональю декартова квадрата множества
.
Для наглядного изображения соответствий из в
(бинарных отношений, в частности) будем использовать два способа. Первый из этих способов состоит в интерпретации соответствия как подмножества декартова произведения, которое можно изображать примерно так же, как на плоскости можно изображать подмножества декартова квадрата числовых множеств. Второй способ, применяемый для конечных множеств
в
, — построение так называемого графа соответствия. В этом случае элементы множеств
в
изображаются на плоскости кружочками. Если и только если пара
принадлежит соответствию
, то в графе соответствия из кружочка, обозначающего элемент
, проводим стрелку к кружочку, обозначающему элемент
. Для бинарного отношения на конечном множестве
часто удобнее использовать граф другого вида. Элементы множества
изображаются кружочками только один раз, а стрелки проводятся по тем же правилам, что и в графе соответствия. Заметим, что при таком построении возможно соединение кружочка стрелкой с самим собой (петля).
Пример 1.6. а. На рис. 1.1, а изображены график и граф бинарного соответствия из примера 1.3.
б. Пусть . Бинарное отношение
на
определим как множество всех упорядоченных пар
, таких, что
. Тогда
Область определения отношения , область значений
. График и два варианта графа отношения
изображены на рис. 1.1, б.
в. Множество точек окружности есть график бинарного отношения на множестве действительных чисел, состоящего из всех таких упорядоченных пар
, что
, или, что равносильно, компоненты пары удовлетворяют уравнению
. Область определения бинарного отношения есть отрезок
, область значения — также отрезок
.
Функциональное соответствие
Соответствие называют функциональным по второй (первой) компоненте, если для любых двух упорядоченных пар
и
из равенства
следует
(и из
следует
). Функциональность соответствия по второй компоненте означает, что, фиксируя в любой упорядоченной паре, принадлежащей данному соответствию, первую компоненту, мы однозначно определяем и вторую компоненту. Таким образом, мы можем сказать, что соответствие, функциональное по второй компоненте, есть отображение (возможно, частичное).
Поэтому соответствие является отображением из
в
, если и только если оно всюду определено (т.е.
) и функционально по второй компоненте. Отметим также, что отображение из
в
является инъекцией тогда и только тогда, когда оно функционально по первой компоненте.
Отношения произвольной арности
В заключение обобщим понятие соответствия, определив отношения произвольной арности.
Определение 1.4. Произвольное подмножество декартова произведения
называют (п-арным или п-местным) отношением на множествах
.
В случае если все множества совпадают, т.е.
, говорят об n-арном отношении на множестве
.
Если — n-арное отношение на множествах
и
, то говорят об элементах
, связанных отношением
.
Замечание 1.3. При получаем бинарное отношение на множествах
. Это не что иное, как соответствие из
в
, где множества
и
, вообще говоря, различны.
При получаем введенное ранее бинарное отношение на множестве, т.е. подмножество декартова квадрата
.
Таким образом, в общем случае (при произвольном ) следует, строго говоря, различать термины «n-арное отношение» и «n-арное отношение на множестве».
Связь между введенными понятиями отношения, соответствия и отображения проиллюстрирована на рис. 1.2.
Пусть n-арное отношение удовлетворяет условию: для любых двух кортежей
и
из выполнения равенств для любого
следует, что и
. Тогда отношение
называют функциональным по i-й компоненте
.
Другими словами, функциональность n-местного отношения по i-й компоненте равносильна условию, что, фиксируя все компоненты, кроме i-й, мы однозначно определяем и i-ю компоненту.
Пример 1.7. а. Представим строку учебного расписания как кортеж вида
(преподаватель, группа, дисциплина, аудитория, день, час).
Тогда расписание можно рассматривать как секстарное (шестиместное) отношение на соответствующих множествах. Оно будет функционально по первой компоненте, если, конечно, предположить, что два преподавателя или более не проводят одно и то же занятие одновременно в одном и том же месте (хотя, например, на лабораторных работах это возможно). Оно также функционально по третьей компоненте (один преподаватель не может вести одновременно занятия по разным дисциплинам), по четвертой (преподаватель со своей группой не могут находиться в разных аудиториях) и не будет, вообще говоря, функционально по второй, пятой и шестой компонентам.
б. Рассмотрим на множестве геометрических векторов в пространстве тернарное (трехместное) отношение
, состоящее из всех упорядоченных троек
компланарных векторов. Это отношение не является функциональным ни по одной компоненте, так как любым двум векторам соответствует бесконечно много векторов, образующих с ними компланарную тройку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
















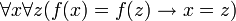
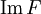 .
.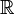 или
или 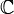 , то отображение называют функцией. Если
, то отображение называют функцией. Если  или
или 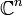 , то отображение называют ве́ктор-фу́нкцией. Если
, то отображение называют ве́ктор-фу́нкцией. Если 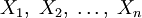 и множество
и множество 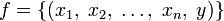 называется функцией
называется функцией 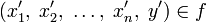 и
и 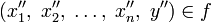 из
из 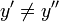 следует, что
следует, что ![x_{n}' neq x_{n}'',forall xin [1,;n]capZ](https://dic.academic.ru/pictures/wiki/files/51/34b01413828b3a6b8b4f43b4c45d1446.png) .[1]
.[1]





