Загрузить PDF
Загрузить PDF
Поделить отрезок пополам совсем легко, когда известна его длина или ее можно измерить. Но даже если длина отрезка неизвестна, его также можно разделить пополам с помощью циркуля и линейки.
-
1
Начертите отрезок, который необходимо поделить пополам. Если этот отрезок не задан сразу, вам потребуется нарисовать его с помощью линейки.
-
2
Возьмите циркуль подходящего размера. Если циркуль в максимально раскрытом положении охватывает лишь половину длины отрезка или меньше того, то вам необходим циркуль большего размера.
-
3
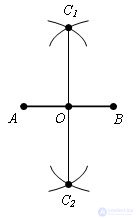
Установите ножку циркуля на один из концов отрезка. Просто установите острие циркуля на любую конечную точку отрезка. Раскройте циркуль таким образом, чтобы его радиус заходил несколько дальше середины отрезка.[1]
Реклама
-
1
Нарисуйте циркулем дуги по одну и по другую стороны от отрезка. Убедитесь в том, что ножка циркуля остается на одном месте, а настройка самого циркуля не смещается.
- Конкретная длина дуг не имеет особого значения.
-
2
Переставьте циркуль на другой конец отрезка. Убедитесь в том, что настройки циркуля не сбились.
-
3
Нарисуйте очередную пару дуг по одну и по другую стороны от отрезка. Убедитесь в том, что ножка циркуля остается на одном месте, а настройка самого циркуля не смещается.
- Две пары дуг должны пересечься между собой.
-
4
Соедините точки пересечения. Чтобы это сделать, необходимо приложить линейку к точке пересечения по одну сторону от отрезка и выровнять ее с точкой пересечения, расположенной по другую сторону от отрезка.
-
5
Начертите перпендикуляр к отрезку. Линия, которая соединяет две точки пересечения дуг, проходит строго под углом в девяносто градусов к отрезку и делит его ровно пополам.
-
6
Поймите принцип деления отрезка таким способом. Вы использовали циркуль, чтобы нарисовать две пересекающиеся окружности с центрами на концах отрезка. Точки пересечения нарисованных дуг представляют собой точки, равноудаленные от обоих концов отрезка на длину радиуса.
- Радиус обеих окружностей одинаков, так как вы использовали одну и ту же настройку циркуля.[2]
Реклама
- Радиус обеих окружностей одинаков, так как вы использовали одну и ту же настройку циркуля.[2]
Советы
- Следите за тем, чтобы карандаш циркуля был острым. Если он затупится, то рисуемая им широкая черта может привести к некоторой погрешности, когда вы будете выставлять циркуль или линейку.
- Если нарисованные дуги не пересеклись, то вы либо нарисовали их недостаточно длинными, либо раскрыли циркуль недостаточно широко. В последнем случае требуется стереть предыдущие дуги, а затем сильнее раскрыть циркуль и нарисовать новые дуги, которые будут пересекаться.
Реклама
Предупреждения
- Убедитесь в том, что при перестановке циркуля на второй конец отрезка настройки циркуля не сбились.
Реклама
Об этой статье
Эту страницу просматривали 76 996 раз.
Была ли эта статья полезной?
Download Article
Download Article
Bisecting a line (dividing a line in half) is easy enough if you know the length of the line, or can measure the line. But if you don’t know the length of the line, you can still bisect it using a straightedge and compass.
-
1
Draw the line segment you need to bisect. If the line segment is not already given, you will need to make it using a straightedge.
-
2
Choose an appropriately sized compass. If you open the compass completely, and it spans one-half the length of the line or less, you need to choose a bigger compass.[1]
Advertisement
-
3
Position the compass on an endpoint. To do this, place the needle of the compass on either endpoint. Open the compass so that it spans a little more than half the length of the line.[2]
Advertisement
-
1
Draw an arc above and below the line segment. Make sure the needle stays on the endpoint, and that you do not adjust the compass setting.[3]
- The length of the arcs does not matter.
-
2
Reposition the compass on the other endpoint. Make sure you do not change the compass setting.[4]
-
3
Draw another set of arcs, above and below the line segment. Make sure the needle stays on the endpoint, and that you do not adjust the compass setting.[5]
- The two sets of arcs you’ve drawn should intersect.
-
4
Connect the arc intersections. To do this, place your straightedge on the point where the arcs above the line intersect, and align it with the point where the arcs below the line intersect.[6]
-
5
Draw your perpendicular bisector. The line you draw between the two arc intersections bisects the line at a ninety degree angle.[7]
-
6
Understand why this works. You have used the compass to outline two congruent circles centered over either endpoint. The intersecting arcs represent the endpoint of a radii from the center of either circle.[8]
- The length of the radii will be the same, since the circles are the same size.
Advertisement
Add New Question
-
Question
How can I construct a line which bisects a given arc of a circle without center?
Place the compass point at one end of the arc. Strike arcs of a given radius on each side of the circle’s arc. Place the compass point at the other end of the circle’s arc, and strike arcs of the same given radius on each side of the circle’s arc so that they intersect the first two arcs you drew. Use the straightedge to draw a line connecting the two points where your arcs intersect each other. That line will bisect the circle’s arc.
-
Question
How do I construct a line that bisects a given arc of a circle?
Treat the arc as if it were a straight line segment, and perform the operation shown in the article above. You can also strike arcs only on the outside of the circle and draw a line from their intersection to the center of the circle. That line will bisect the circle’s arc.
-
Question
How do I bisect a line segment into 1/2, 1/4 and so on?
Perform the operation shown in the article above to bisect the line segment. Then do it again using only one-half of the line segment. Then do it again using only one-quarter of the line segment, etc.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If the two arcs do not intersect, then either you didn’t draw the arcs long enough, or you didn’t open the compass wide enough. Erase the arcs, open the compass wider, and try again.[9]
-
Keep the pencil tip sharp. If it gets dull, the wide lines it makes can lead to errors when placing the compass point or the ruler.
Thanks for submitting a tip for review!
Advertisement
-
Make sure you do not change the compass width when you switch from one endpoint to the other.[10]
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 104,338 times.
Did this article help you?
wikiHow Tech Help Pro:
Level up your tech skills and stay ahead of the curve
Let’s go!
Привет, мой друг, тебе интересно узнать все про деление отрезка пополам, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
деление отрезка пополам , настоятельно рекомендую прочитать все из категории Планометрия.
деление отрезка пополам » />
Разделить отрезок пополам.
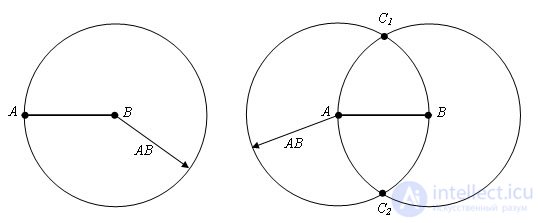
Пусть AB данный отрезок . Об этом говорит сайт https://intellect.icu . Описываем окружность радиусом AB с центром в точках A и B. Пусть эти окружности пересекаются в точках С1 и С2.
Точки С1 и С2 лежат в разных полуплоскостях от прямой AB. Проведем через точки С1 и С2 прямую. Пусть она пересекает прямую AB в некоторой точке О. Точка О – средина отрезка AB.
Доказательство. Δ C1AC2 = Δ C1BC2 по третьему признаку равенства треугольников (AC1 = BC1, AC2 = BC2, по построению и С1С2 — общая). Поэтому ∠ AC1C2 = ∠ BC1C2. Отсюда следует Δ AC1O = Δ BC1O по второму признаку равенства треугольников (∠ AC1C2 = ∠ BC1C2, AC1 = BC1 по построению, OC1 – общая). Следовательно AO = OB и O – середина отрезка AB.
Понравилась статья про деление отрезка пополам? Откомментируйте её Надеюсь, что теперь ты понял что такое деление отрезка пополам
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Планометрия
Из статьи мы узнали кратко, но емко про деление отрезка пополам
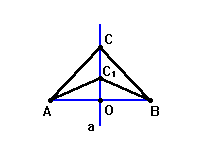
Анализ. Пусть [AB] – данный отрезок, точка O – его середина, прямая a – серединный перпендикуляр к отрезку AB. Выберем произвольную точку C на прямой a, отличную от точки O. В треугольнике ACB CO – одновременно медиана и высота. Следовательно, треугольник ACB равнобедренный, и AC = BC. Отсюда возникает следующий способ построения точки O – середины отрезка AB.
Рис. 7.8.1. Деление отрезка пополам
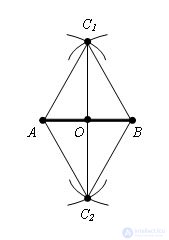
Построение. Из точек A и B циркулем описывается окружность радиусом AB. Пусть C и C1 – точки пересечения этих окружностей. Они лежат в разных полуплоскостях относительно прямой AB. С помощью линейки соединить точки C и C1. Отрезок CC1 пересекает отрезок AB в точке O. Эта точка – середина отрезка AB.
Нужно поделить отрезок AB пополам и середину отрезка обозначить точкой O.
Соединим точки C и C1 с концами отрезка AB. По построению AC1 = AC = C1B = CB. Поэтому равнобедренные треугольники CAC1 и CBC1 равны по трем сторонам. Отсюда следует равенство углов ACO и BCO. В равнобедренном треугольнике ABC CO – биссектриса, проведенная к основанию, следовательно, она медиана и высота. Отсюда AO = OB, и точка O – середина отрезка AB.
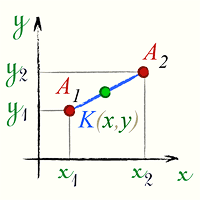
Деление отрезка пополам, формула
Деление отрезка пополам
Координаты середины отрезка A1A2 равны полу суммам соответствующих координат его концов.
[
x = frac{x_1 + x_2}{2} \ medspace \
y = frac{y_1 + y_2}{2}
]
Эти формулы получаются из формул деления отрезка в данном отношении если положить:
[ m = n = 1 \ medspace \ λ = 1 ]
Построить деление отрезка пополам на координатной плоскости
Найти координаты середины отрезка по формуле (1)
| x1 | y1 |
| x2 | y2 |
Построить
нажмите кнопку для расчета
Деление отрезка пополам |
стр. 140 |
|---|