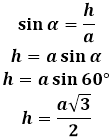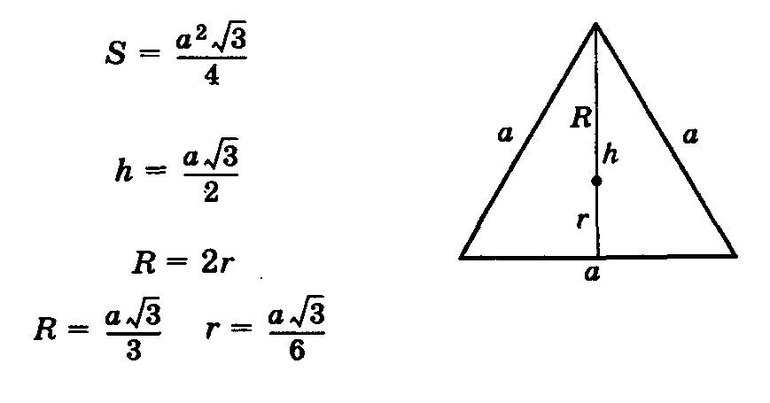Как найти половину высоты в равностороннем треугольнике - Исправление недочетов и поиск решений вместе с Examum.ru

В данной публикации мы рассмотрим основные свойства высоты в равностороннем (правильном) треугольнике. Также разберем пример решения задачи по этой теме.

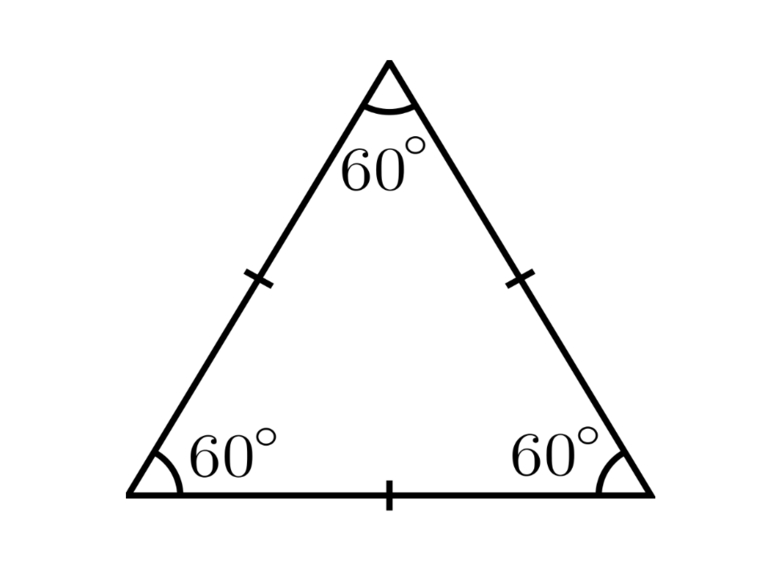
Примечание: треугольник называется равносторонним, если все его стороны равны.

Свойства высоты в равностороннем треугольнике
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
Пример задачи

Свойства высоты в равностороннем треугольнике

Свойство 1

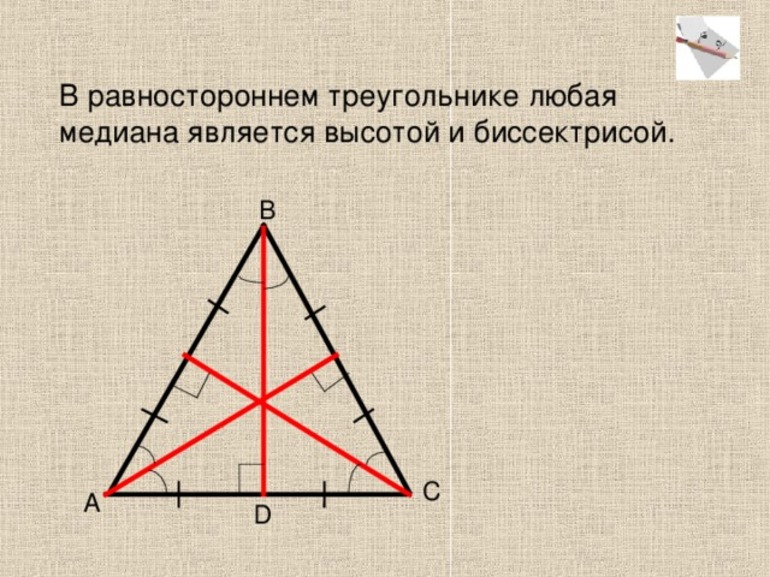
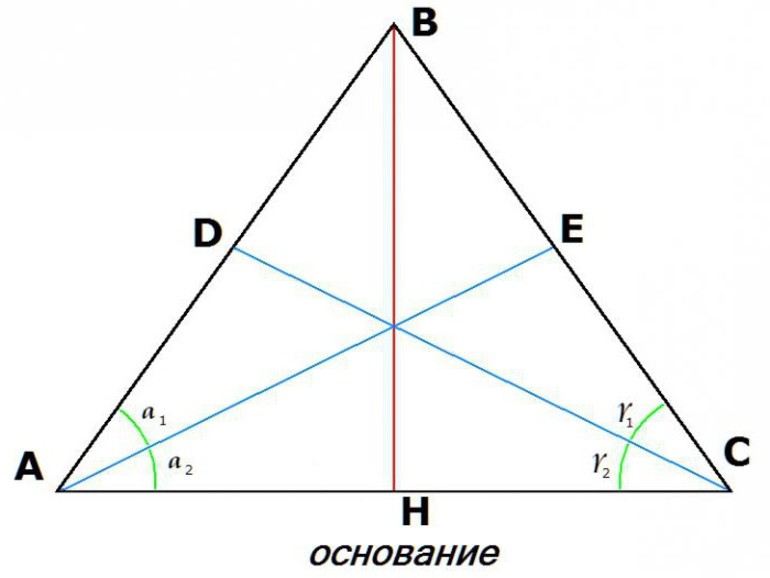
Любая высота в равностороннем треугольнике одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.

BD – высота, опущенная на сторону AC;
BD – медиана, которая делит сторону AC пополам, т.е. AD = DC;
BD – биссектриса угла ABC, т.е. ∠ABD = ∠CBD;
BD – серединный перпендикуляр, проведенный к AC.

Свойство 2

Все три высоты в равностороннем треугольнике имеют одинаковую длину.

AE = BD = CF

Свойство 3

Высоты в равностороннем треугольнике в ортоцентре (точке пересечения) делятся в отношении 2:1, считая от вершины, из которой они проведены.

AO = 2OE
BO = 2OD
CO = 2OF

Свойство 4

Ортоцентр равностороннего треугольника является центром вписанной и описанной окружностей.

R – радиус описанной окружности;
r – радиус вписанной окружности;
R = 2r (следует из Свойства 3).

Свойство 5

Высота в равностороннем треугольнике делит его на два равных по площади (равновеликих) прямоугольных треугольника.

S₁ = S₂

Три высоты в равностороннем треугольнике делят его на 6 равных по площади прямоугольных треугольников.

Свойство 6

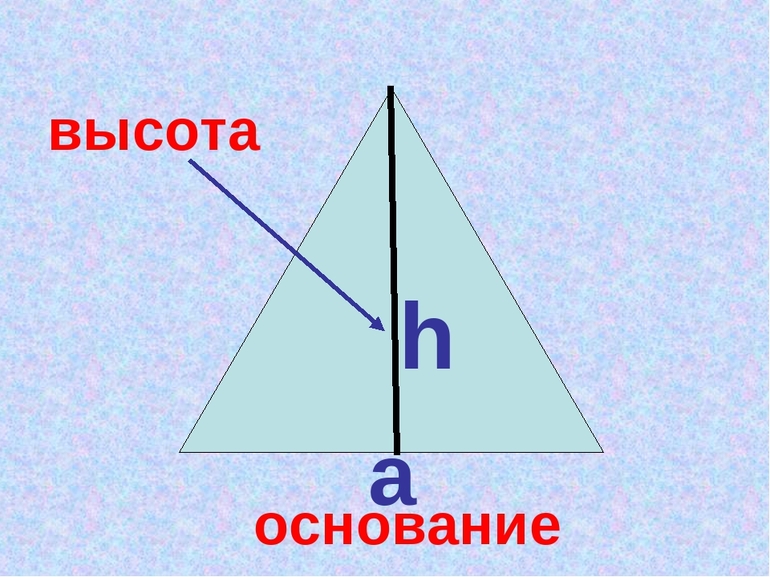
Зная длину стороны равностороннего треугольника его высоту можно вычислить по формуле:

a – сторона треугольника.

Пример задачи

Радиус окружности, описанной вокруг равностороннего треугольника, равняется 7 см. Найдите сторону этого треугольника.

Решение
Как мы знаем из Свойств 3 и 4, радиус описанной окружности составляет 2/3 от высоты равностороннего треугольника (h). Следовательно, h = 7 ∶ 2 ⋅ 3 = 10,5 см.

Теперь остается вычислить длину стороны треугольника (выражение выведено из формулы в Свойстве 6):

Источник

Равносторонний треугольник

Тип	Правильный многоугольник
Ребра и вершины	3
Schläfli символ	{3}
диаграмма Кокстера
Группа симметрии	D3
Площадь	3 4 a 2 { displaystyle { tfrac { sqrt {3}} {4}} a ^ {2} } $tfrac { sqrt {3}} {4} a ^ 2$
Внутренний угол (градусов )	60 °

В геометрии, равносторонний треугольник представляет собой треугольник в у которых все три стороны имеют одинаковую длину. В известной евклидовой геометрии равносторонний треугольник также равноугольный ; то есть все три внутренних угла также конгруэнтны друг другу и имеют угол 60 °. Это также правильный многоугольник, поэтому его также называют правильным треугольником .

Содержание

1 Принцип свойства
2 Характеристики
- 2.1 Стороны
- 2.2 Полупериметр
- 2.3 Углы
- 2.4 Площадь
- 2.5 Окружной радиус, внутренний и внешний радиус
- 2.6 Равные чевианы
- 2.7 Совпадающие центры треугольников
- 2.8 Шесть треугольников, образованных разделением по медианам
- 2.9 Точки на плоскости
3 Известные теоремы
4 Другие свойства
5 Геометрическое построение
6 Вывод формулы площади
- 6.1 Использование Теорема Пифагора
- 6.2 Использование тригонометрии
7 В культуре и обществе
8 См. Также
9 Ссылки
10 Внешние ссылки

Основные свойства

Равносторонний треугольник. Он имеет равные стороны (

a = b = c { displaystyle a = b = c}

), равные углы (

α = β = γ { displaystyle alpha = beta = gamma}

) и равные высоты (

ha = hb = hc { displaystyle h_ {a} = h_ {b} = h_ {c}}

${ displaystyle h_ {a} = h_ {b} = h_ {c}}$ ).

Обозначение общей длины стороны равностороннего треугольника как a { displaystyle a}, с помощью теоремы Пифагора мы можем определить, что:

Обозначив радиус описанной окружности R, мы можем определить с помощью тригонометрии, что:

Площадь треугольника равно A = 3 3 4 R 2 { displaystyle mathrm {A} = { frac {3 { sqrt {3}}} {4}} R ^ {2}} ${ displaystyle mathrm {A} = { frac {3 { sqrt {3}}} {4}} R ^ {2}}$

Многие из этих величин имеют простые отношения к высоте («h») каждой вершины с противоположной стороны:

В равностороннем треугольнике высота, биссектриса угла, серединный перпендикуляр и медиана каждой стороны совпадают.

Характеристики

Треугольник ABC со сторонами a, b, c, полупериметр s, площадь T, exradii ra, r b, r c (касательная к a, b, c соответственно), и где R и r — радиусы описанной окружности и вписанный в круг соответственно, является равносторонним тогда и только тогда, когда истинно любое из утверждений в следующих девяти категориях. Таким образом, эти свойства уникальны для равносторонних треугольников, и знание того, что любое из них истинно, прямо подразумевает, что у нас есть равносторонний треугольник.

Стороны

Полупериметр

Углы

Площадь

Окружной радиус, внутренний и внешний радиус

Равные чевианы

Три вида чевианов совпадают и равны для (и только для) равносторонних треугольников:

Три вида высоты имеют равную длину.
Три медианы имеют равную длину.
Три биссектрисы угла имеют равную длину.

Совпадающие центры треугольников

Каждый центр равностороннего треугольника совпадает с wi th его центроид, что подразумевает, что равносторонний треугольник является единственным треугольником без линии Эйлера, соединяющей некоторые из центров. Для некоторых пар центров треугольников их совпадения достаточно, чтобы треугольник был равносторонним. В частности:

Треугольник является равносторонним, если любые два из центра описанной окружности, центра, центроида или ортоцентра совпадают.
Это также является равносторонним, если его центр описанной окружности совпадает с точкой Нагеля или если его центр совпадает с его центром из девяти точек.

Шесть треугольников, образованных разделением медианами

Для В любом треугольнике три медианы делят треугольник на шесть меньших треугольников.

Треугольник является равносторонним тогда и только тогда, когда любые три из меньших треугольников имеют одинаковый периметр или одинаковый радиус.
Треугольник является равносторонним тогда и только тогда, когда центры окружности любых трех меньших треугольников имеют одинаковое расстояние от центроида.

Точки на плоскости

Треугольник является равносторонним тогда и только тогда, когда для каждой точки P на плоскости имеются расстояния p, q и r до сторон треугольника и расстояния x, y и z в его вершины,

4 (p 2 + q 2 + r 2) ≥ x 2 + y 2 + z 2. { displaystyle 4 (p ^ {2} + q ^ {2} + r ^ {2}) geq x ^ {2} + y ^ {2} + z ^ {2}.}

Известные теоремы

Наглядное доказательство теоремы Вивиани

1.	Показаны ближайшие расстояния от точки P до сторон равностороннего треугольника ABC.
2.	Линии DE, FG и HI, параллельные AB, BC и CA, соответственно, определяют меньшие треугольники PHE, PFI и PDG.
3.	Поскольку эти треугольники равносторонние, их высоту можно повернуть вертикально.
4.	Поскольку PGCH представляет собой параллелограмм, треугольник PHE можно сдвинуть вверх, чтобы показать, что сумма высот равна высоте треугольника ABC.

Теорема Морли о трисекторах утверждает, что в любом треугольнике три точки пересечения смежных трисекторов угла образуют равносторонний треугольник.

Теорема Наполеона гласит, что если равносторонние треугольники построены на сторонах любого треугольника, либо все наружу, либо все внутрь, центры этих равносторонних треугольников сами образуют равносторонний треугольник.

Версия изопериметрического неравенства для треугольников гласит, что треугольник с наибольшей площадью среди всех треугольников с заданным периметром является равносторонним.

Теорема Вивиани утверждает, что для любой внутренней точки P в равностороннем треугольнике с расстояниями d, e и f от сторон и высотой h,

d + e + f = h, { displaystyle d + e + f = h,}

независимо от расположения P.

Теорема Помпейу утверждает, что если P — произвольная точка в плоскости равностороннего треугольника ABC, но не на его описанной окружности, то существует треугольник со сторонами длиной PA, PB и PC. То есть PA, PB и PC удовлетворяют неравенству треугольника , согласно которому сумма любых двух из них больше третьего. Если P находится на описанной окружности, то сумма двух меньших из них равна самому длинному, и треугольник выродился в линию, этот случай известен как теорема Ван Скутена.

Другие свойства

By неравенство Эйлера, равносторонний треугольник имеет наименьшее отношение R / r радиуса описанной окружности к внутреннему радиусу любого треугольника: в частности, R / r = 2.

Треугольник с наибольшей площадью из всех этих вписанная в данный круг — равносторонняя; и треугольник наименьшей площади из всех описанных вокруг данного круга является равносторонним.

Отношение площади вписанной окружности к площади равностороннего треугольника, π 3 3 { displaystyle { frac { pi} {3 { sqrt {3}}}}} ${ frac { pi} {3 { sqrt {3}}}}$ , больше, чем у любого неравностороннего треугольника.

Отношение площади к квадрату периметр равностороннего треугольника, 1 12 3, { displaystyle { frac {1} {12 { sqrt {3}}}},} $frac {1} {12 sqrt {3}},$ больше, чем у любого другого треугольника.

Если сегмент разделяет равносторонний треугольник на две области с равным периметром и с областями A 1 и A 2, то

7 9 ≤ A 1 А 2 ≤ 9 7. { displaystyle { frac {7} {9}} leq { frac {A_ {1}} {A_ {2}}} leq { frac {9} {7}}.} $frac {7} {9} leq frac {A_1} {A_2} leq frac {9} {7}.$

Если треугольник помещается в комплексную плоскость с комплексными вершинами z 1, z 2 и z 3, затем для любого нереального кубический корень ω { displaystyle omega} omega из 1 треугольник является равносторонним тогда и только тогда, когда

z 1 + ω z 2 + ω 2 z 3 = 0. { displaystyle z_ { 1} + omega z_ {2} + omega ^ {2} z_ {3} = 0.} $z_ {1} + omega z_ {2} + omega ^ {2} z_ {3} = 0.$

Для точки P внутри равностороннего треугольника отношение суммы ее расстояний от вершин сумма расстояний от сторон больше или равна 2, равенство сохраняется, когда P является центроидом. Ни в каком другом треугольнике нет точки, для которой это отношение было бы равно 2. Это неравенство Эрдеша – Морделла ; более сильным вариантом этого является неравенство Барроу, которое заменяет перпендикулярные расстояния до сторон на расстояния от P до точек, где биссектрисы угла APB, ∠BPC и ∠ CPA пересекает стороны (A, B и C — вершины).

Для любой точки P на плоскости с расстояниями p, q и t от вершин A, B и C соответственно

3 (p 4 + q 4 + t 4 + a 4) = (р 2 + д 2 + т 2 + а 2) 2. { displaystyle displaystyle 3 (p ^ {4} + q ^ {4} + t ^ {4} + a ^ {4}) = (p ^ {2} + q ^ {2} + t ^ {2} + a ^ {2}) ^ {2}.} $displaystyle 3 (p ^ {4} + q ^ {4} + t ^ {4} + a ^ {4}) = (p ^ {2} + q ^ {2} + t ^ {2} + a ^ {2 }) ^ {2}.$

Для любой точки P на плоскости с расстояниями p, q и t от вершин

p 2 + q 2 + t 2 = 3 ( R 2 + L 2) { displaystyle displaystyle p ^ {2} + q ^ {2} + t ^ {2} = 3 (R ^ {2} + L ^ {2})} ${ displaystyle displaystyle p ^ {2} + q ^ {2} + t ^ {2} = 3 (R ^ {2} + L ^ {2})}$

п 4 + q 4 + t 4 = 3 [(R 2 + L 2) 2 + 2 R 2 L 2], { displaystyle displaystyle p ^ {4} + q ^ {4} + t ^ {4} = 3 [(R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2} L ^ {2}],} ${ displaystyle displaystyle p ^ {4} + q ^ {4} + t ^ {4} = 3 [(R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2} L ^ {2}],}$

где R — описанный радиус, а L — расстояние между точками P и центр тяжести равностороннего треугольника.

Для любой точки P вписанной окружности равностороннего треугольника с расстояниями p, q и t от вершин

4 (p 2 + q 2 + t 2) = 5 a 2 { displaystyle displaystyle 4 (p ^ {2} + q ^ {2} + t ^ {2}) = 5a ^ {2}} $displaystyle 4 (p ^ {2} + q ^ {2} + t ^ {2 }) = 5a ^ {2}$

16 (p 4 + q 4 + t 4) = 11 а 4. { displaystyle displaystyle 16 (p ^ {4} + q ^ {4} + t ^ {4}) = 11a ^ {4}.} $displaystyle 16 (p ^ {4} + q ^ {4} + t ^ {4}) = 11a ^ {4}.$

Для любой точки P на малой дуге BC описанной окружности с расстояния p, q и t от A, B и C соответственно,

p = q + t { displaystyle displaystyle p = q + t}

q 2 + qt + t 2 = а 2; { displaystyle displaystyle q ^ {2} + qt + t ^ {2} = a ^ {2};} $displaystyle q ^ {2} + qt + t ^ {2} = a ^ {2};$

кроме того, если точка D на стороне BC делит PA на сегменты PD и DA, причем DA имеет длину z и PD имеет длину y, тогда

z = t 2 + tq + q 2 t + q, { displaystyle z = { frac {t ^ {2} + tq + q ^ {2}} {t + q} },} $z = frac {t ^ {2} + tq + q ^ 2} {t + q},$

, что также равно t 3 — q 3 t 2 — q 2 { displaystyle { tfrac {t ^ {3} -q ^ {3}} {t ^ {2} -q ^ {2}}}} $tfrac {t ^ {3} -q ^ {3}} {t ^ {2} -q ^ {2 }}$ если t ≠ q; и

1 q + 1 t = 1 y, { displaystyle { frac {1} {q}} + { frac {1} {t}} = { frac {1} {y}},} ${ frac {1} {q}} + { frac {1} {t}} = { frac {1} {y}},$

, которое является оптическим уравнением .

Существует множество неравенств треугольника , которые выполняются с равенством тогда и только тогда, когда треугольник является равносторонним.

Равносторонний треугольник — это наиболее симметричный треугольник, имеющий 3 линии отражения и симметрию вращения порядка 3 относительно его центра. Его группа симметрии — это двугранная группа порядка 6 D3.

Равносторонние треугольники — единственные треугольники, у которых эллипс Штейнера является окружностью (в частности, это вписанная окружность).

Целочисленный равносторонний треугольник — единственный треугольник с целыми сторонами и тремя рациональными углами, измеренными в градусах.

Равносторонний треугольник — единственный остроугольный треугольник, который подобен своему ортогональному треугольнику (с вершинами в основании на высотах ) (семиугольный треугольник является единственным тупым треугольником).

Правильный тетраэдр состоит из четырех равносторонних треугольников.

Равносторонние треугольники встречаются во многих других геометрических конструкциях. Пересечение окружностей, центры которых находятся на расстоянии радиуса друг от друга, представляет собой пару равносторонних арок, в каждую из которых можно вписать равносторонний треугольник. Они образуют грани правильных и однородных многогранников. Три из пяти Платоновых тел состоят из равносторонних треугольников. В частности, правильный тетраэдр имеет четыре равносторонних треугольника для граней и может считаться трехмерным аналогом формы. Плоскость может быть выложена плиткой с использованием равносторонних треугольников, что дает треугольную мозаику.

Геометрическая конструкция

Построение равностороннего треугольника с циркулем и линейкой

Равносторонний треугольник легко построить с помощью линейка и циркуль, потому что 3 — это простое число Ферма. Нарисуйте прямую линию, поместите точку циркуля на один конец линии и проведите дугу от этой точки до другой точки отрезка. Повторите то же самое с другой стороной линии. Наконец, соедините точку, где две дуги пересекаются с каждым концом отрезка линии

Альтернативный метод — нарисовать круг с радиусом r, поместить точку циркуля на круг и нарисовать еще один круг с такой же радиус. Два круга пересекутся в двух точках. Равносторонний треугольник можно построить, взяв два центра окружностей и любую из точек пересечения.

В обоих методах побочным продуктом является образование vesica piscis.

Доказательство того, что полученная фигура представляет собой равносторонний треугольник, является первым предложением Книги I Элементов Евклида.

Вывод формулы площади

Формула площади A = 3 4 a 2 { displaystyle A = { frac { sqrt {3}} {4}} a ^ {2}} $A = frac { sqrt {3}} {4} a ^ 2$ с точки зрения длины стороны a может быть получено непосредственно с помощью теоремы Пифагора или с помощью тригонометрии.

Использование теоремы Пифагора

Площадь треугольника равна половине одной стороны, умноженной на высоту h с этой стороны:

A = 1 2 a h. { displaystyle A = { frac {1} {2}} ах.} $A = frac {1} {2} ах.$

Равносторонний треугольник со стороной 2 имеет высоту √3, так как синус 60 ° равно √3 / 2.

Катеты любого прямоугольного треугольника, образованного высотой равностороннего треугольника, составляют половину основания a, а гипотенуза — это сторона a равностороннего треугольника. Высоту равностороннего треугольника можно найти с помощью теоремы Пифагора

(a 2) 2 + h 2 = a 2 { displaystyle left ({ frac {a} {2}} right) ^ {2} + h ^ {2} = a ^ {2}} $left ( frac {a} {2} right) ^ 2 + h ^ 2 = a ^ 2$

, так что

h = 3 2 a. { displaystyle h = { frac { sqrt {3}} {2}} a.} $h = frac { sqrt { 3}} {2} a.$

Подстановка h в формулу площади (1/2) ah дает формулу площади равностороннего треугольника:

A = 3 4 а 2. { displaystyle A = { frac { sqrt {3}} {4}} a ^ {2}.} $A = frac { sqrt {3}} {4} a ^ 2.$

Используя тригонометрию

Используя тригонометрию, площадь треугольник с любыми двумя сторонами a и b, а угол C между ними равен

A = 1 2 ab sin ⁡ C. { displaystyle A = { frac {1} {2}} ab sin C.} $A = frac {1} {2} ab sin C.$

Каждый угол равностороннего треугольника равен 60 °, поэтому

A = 1 2 a b sin ⁡ 60 ∘. { displaystyle A = { frac {1} {2}} ab sin 60 ^ { circ}.} $A = frac {1} {2} ab sin 60 ^ circ.$

Синус 60 ° равен 3 2 { displaystyle { tfrac { sqrt { 3}} {2}}} ${ tfrac { sqrt {3}} {2}}$ . Таким образом,

A = 1 2 ab × 3 2 = 3 4 ab = 3 4 a 2 { displaystyle A = { frac {1} {2}} ab times { frac { sqrt {3}} { 2}} = { frac { sqrt {3}} {4}} ab = { frac { sqrt {3}} {4}} a ^ {2}} $A = frac {1} {2} ab times frac { sqrt {3}} {2} = frac { sqrt {3}} { 4} ab = frac { sqrt {3}} {4} a ^ 2$

, поскольку все стороны равностороннего треугольника равны.

В культуре и обществе

Равносторонние треугольники часто появлялись в искусственных сооружениях:

Форма встречается в современной архитектуре, например, в поперечном сечении Арки ворот.
Его применение во флагах и геральдике включает флаг Никарагуа и флаг Филиппин.
Это форма различных дорожных знаков, включая знак уступки.

См. Также

Ссылки

Внешние ссылки

v t Фундаментальный выпуклый правильный и равномерный многогранник в измерениях 2–10
An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Треугольник	Квадрат	p- гон	Шестиугольник	Пентагон
Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
5-элементный	16 ячеек • Tesseract	Demitesseract	24-элементный	120-элементный • 600-элементный
5-симплексный	5-ортоплексный • 5-куб	5-полукуб
6-симплекс	6-ортоплекс • 6-куб	6-полукуб	122 • 221
7-симплекс	7-ортоплекс • 7-куб	7-полукуб	132 • 231 • 321
8-симплекс	8-ортоплекс • 8-куб	8-полукуб	142 • 241 • 421
9-симплекс	9-ортоплекс • 9-куб	9-демикуб
10-симплекс	10-ортоплекс • 10-куб	10-полукуб
n-симплекс	n-ортоплекс • n- куб	n-полукуб	1k2 • 2k1 • k21	n-пятиугольный многогранник
Темы: Семейства многогранников • Обычные многогранник • Список правильных многогранников и соединений

Источник

Равносторонний треугольник является правильным многоугольником (геометрическая фигура, у которой все углы и все стороны равны). Фактически, это значительно упрощает процесс вычисления любых параметров, характеризующих такой треугольник, в том числе, длину высоты.

В равностороннем треугольнике все три высоты — одинаковой длины, поэтому найдя любую из них, можно применять полученное значение в отношении всех трех линий. Более того, все высоты полностью совпадают со всеми тремя медианами, биссектрисами и серединными перпендикулярами, называемыми иначе медиатриссами. Точка пересечения всех трех линий обладает свойствами точки пересечения высот, точки пересечения медиан и точки пересечения биссектрис одновременно, являя собой любой из возможных центров треугольника, в том числе центр вписанной и описанной окружностей.

Исходя из этого, чтобы найти высоту равностороннего треугольника, можно использовать абсолютно любые известные параметры, например, сторону треугольника.

Высота равностороннего треугольника, проведенная к любой стороне, создает внутри него прямоугольный треугольник, в котором можно ее вычислить, используя тригонометрические отношения, так как известно, что все углы в равностороннем треугольнике имеют по 60 градусов. Для полученного прямоугольного треугольника высота будет катетом, противолежащем углу в 60 градусов, а сторона равностороннего треугольника — гипотенузой, соответственно, чтобы найти высоту, нужно применить синус. Если подставить вместо угла альфа 60 градусов, получится, что высота равностороннего треугольника равна половине стороны, умноженной на корень из трех.

Источник

Формулы, используемые для этого, несложны. Вывод выражений основан на свойствах треугольника, при этом точка пересечения высот считается замечательной и даже имеет своё название — ортоцентр.

Общие сведения

Три отрезка, не принадлежащие одной прямой, каждый из которых соединяется с другими в двух точках, образуют геометрическую фигуру — треугольник. Прямые линии — это стороны, а точки их соприкосновения вершины. Один из отрезков, обычно который проходит параллельно горизонтальной плоскости, называют основанием.

В зависимости от размера внутренних углов замкнутой фигуры, треугольники разделяют на следующие виды:

остроугольные — все углы тела не превышают 90 градусов;
тупоугольные — один из разворотов имеет тупую форму;
прямоугольные — размер одного из трёх углов составляет 90 градусов.

По числу равных сторон треугольные фигуры разделяют на разносторонние, равнобедренные, равносторонние. Последние часто называют правильными, так как все стороны у такого объекта равны друг другу. Кроме этого, из особенностей равносторонней фигуры можно отметить, что центры вписанной и описанной окружности совпадают, а каждый из углов равен 60 градусам. Сумма всех углов треугольника равняется 180 градусам.

В любой трёхугольной фигуре можно построить так называемые 3 замечательные линии: медиана, биссектриса и высота.

В правильном треугольнике эти 3 отрезка совпадают, то есть линия, опущенная из вершины к противолежащей стороне, одновременно являясь медианой, биссектрисой и высотой, образует прямой угол с основанием. При этом она делит его пополам. Фактически высота играет роль катета.

Получается, что в середине фигуры можно построить 3 отрезка, которые и будут высотами. Две из них будут опущены на боковые грани, а одна на основание. Точка пересечения перпендикулярных линий называется ортоцентром. Она располагается внутри геометрического тела и совпадает с центром вписанной окружности.

Для трёхугольного тела существует 2 теоремы. Одна из них утверждает, что противолежащие боковые стороны имеют одинаковую длину, а вторая, что если 2 угла невырожденного треугольника равны, то грани, противоположные им, также равны.

Интересно то, что эти правила справедливы как для абсолютной, так и сферической геометрии.

Свойства равносторонней фигуры

При решении задач, связанных с нахождением высоты в равностороннем треугольнике, часто приходится использовать его свойства. Зная их, найти нужные параметры будет несложно. Тем более что все они связаны с главной особенностью фигуры — равенством его всех сторон.

Равностороннее тело с тремя углами обладает следующими особенностями:

в нём все углы одинаковые и равны 60 градусов;
середина пересечения отрезков, совпадающих с высотой, биссектрисой и медианой, является центром геометрического тела;
радиус описанной окружности превышает радиус вписанной в 2 раза;
в равностороннем треугольнике длины всех элементов выражаются через длину стороны.

Эти свойства очевидны. Если начертить треугольник с равными сторонами и вписать его в окружность, за центр можно принять точку O, при этом радиус описанного круга будет OK. Тогда линия, проведённая из неё к вершине, будет радиусом. Пусть конечная точка будет B. Но так как место пересечения является общим и для высот и медиан, из свойства последних можно сделать вывод, что в точке линия делится в отношении 2 к 1. Отсчёт следует вести с вершины треугольника. Значит: OB = 2 * OK.

Из основных формул, которые используются при вычислениях, в первую очередь нужно запомнить:

радиус описанной окружности: R = (a * √3) / 3;‎
диаметр вписанного круга: r = (a * √3) / 6;
медиана: h = (a * √3) / 2;
площадь: s = (a2 * √3) / 4;
периметр: p = 3 * a.

Если рассмотреть треугольник ABC с проведённой высотой BN, можно утверждать, что грань АВ = ВС = АС = AN /2 = NC /2. Так как фигура ABN является копией BNC в зеркальном отражении, разделённые углы у вершины будут одинаковыми, а и их разворот составлять 30 градусов. Из этого следует, что угол A равен 60 градусам, значит, отрезок BN = AB * sin 60⁰ = (AB * √3) / 2.

Зная длину медианы (высоты), вычислить другие параметры треугольника не составит труда. Например, периметр, P = 2 √3 * h; площадь — S = (h * 2) / √3.

При этом замечательным свойством является ещё и то, что ортоцентр одновременно будет в фигуре и центром тяжести (центроидом), поэтому точка пересечения высот и делит отрезок в отношении 2 к 1.

Формула высоты

В равностороннем треугольнике длина стороны равна произведению удвоенной высоты и квадратного корня из трёх. Эту формулу легко доказать, используя теорему Пифагора. Так как высота одновременно является и биссектрисой, она, проведённая на противоположное основание, разделяет треугольник на 2 симметричные фигуры. Исходя из того, что отрезок — это перпендикуляр, полученные геометрические тела будут прямоугольными.

Гипотенуза будет являться гранью основного тела, одним из катетов — проведённая линия, а вторым — половина основания. Последнее утверждение правдиво, так как в равносторонней фигуре все стороны равны. Соответственно, используя теорему Пифагора: c² = b² + a², для рассматриваемого случая можно записать следующую формулу: a² = h² + a²/ 2², где: a — грань. После математических преобразований выражение примет вид: a = (2 * h) / √‎3. Отсюда уже можно вывести формулу для нахождения длины: h = (a * √‎3) / 2.

Аналогичное определение можно получить, используя для доказательства формулу Герона. Отрезок, являющийся высотой, можно найти из выражения: h = (2 * √‎p * (p — a) * (p — b) * (p — a)) / b. В равенстве p является периметром и находится как сумма всех сторон: p = (a + b + a). Так как одна из граней делится пополам, формулу можно привести к виду: p = (a + b + a) / 2 = a + b / 2.

После подстановки полученного выражения в формулу Герона, оно примет вид: h = 2 * √((a + b/2) * (b/2) * (a -b/2) * (b/2)) / b. Используя формулу сокращённого умножения: разность квадратов, равенство можно привести к виду: (a + b / 2) * (a — b / 2) = a² — (b / 2)².

Для упрощения выражения под корень можно внести двойку и знаменатель b. Таким образом, формула примет вид: h = √(2² * (a² — (b/2)² * (b/2)²) * b²). Выполнив ряд сокращений, равенство можно будет представить: h = √(a² — (b²/4)). Из-за того, что стороны в трёхугольной фигуре совпадают, окончательный вариант можно записать: h = (a√3) / 2. Что и следовало доказать.

Высоту можно определить, и зная радиус вписанной окружности. Её можно найти по формуле: r = (a √ 3) / 6. Если выражение переписать как r = (1 / 3) * ((a √3) / 2), возможно увидеть, что второй множитель как раз и есть высота. Соответственно, r = (1/3) * h. Отсюда: h = 3 * r. Это довольно простая формула, которая часто используется при геометрических вычислениях, поэтому её тоже нужно запомнить.

Решение примеров

Самостоятельное решение задач позволяет закрепить теоретические знания и запомнить формулы. Существуют определённые типы примеров, с помощью которых можно довольно быстро проработать весь изученный материал. Вот некоторые из них, рассчитанные на учеников восьмых классов средней школы:

Определить высоту равносторонней фигуры, если её грань равняется 6 см. Решение задачи нужно строить следующим образом. У такого треугольника все стороны равны. Так как высота является медианой, она делит противоположную сторону вершины, из которой опущена, на 2 равные части. Треугольник можно обозначить ABC, а искомый перпендикуляр BH. Образованное геометрическое тело является прямоугольным. Причём, согласно условию, у него известна гипотенуза и катет. Оставшийся катет, который и является высотой, легко найти по теореме Пифагора: BH² + 3² = 6². Отсюда: BH² = 25. Высота рассматриваемой фигуры будет равна 5 см.
Сторона правильного треугольного тела равна √3. Узнать, чему будет равен радиус описанной окружности. Эту задачу можно решить, воспользовавшись свойством высоты в равностороннем треугольнике: точка пересечения медиан делит их в отношении 2 :1. Для наглядности можно нарисовать треугольник c вершинами ABC и высоту AK, а точку пересечения обозначить буквой O. Линия AO будет искомым радиусом окружности и составлять 2/3 от всей высоты AK. Длина отрезка равна: AK = √ (AB2 — AK2). Отсюда: R = (2 * √ (AB2 — AK2)) / 3 = (2 * √ (√ 32 — (3/2)2)) / 3 = 1. Задача решена.

Проверить правильность решения можно, используя онлайн-калькуляторы. Это интернет-сервисы, которые позволяют своим пользователям в автоматическом режиме вычислять различные математические примеры. Свои услуги они предоставляют бесплатно, от пользователя требуется только установленный веб-обозреватель и подключение к сети.

Важно ещё, что калькуляторы не только выдают быстро правильный ответ, но и показывают пошаговое решение. Это очень удобно, когда необходимо определить, на каком этапе была допущена ошибка.

Кроме этого, на своих страницах такого рода сервисы содержат краткий теоретический материал и даже примеры заданий. Так что калькуляторы будут полезны и на стадии обучения.

Источник

Зная высоту в равностороннем треугольнике, вычислить сторону не составляет труда. Для этого нужно умножить высоту на два и разделить на корень из трех.
a=2h/√3

Теперь имея равноценное стороне выражение, можно найти все остальные параметры равностороннего треугольника. Периметр равен утроенной стороне, в данном случае коэффициент сократится с корнем из трех, и периметр получится равен двум корням из трех, умноженным на высоту.
P=3a=(3*2h)/√3=2√3 h

Чтобы найти площадь равностороннего треугольника через высоту, нужно корень из трех, деленный на четыре, умножить на выражение, соответствующее стороне, возведенное в квадрат. Получится высота в квадрате, деленная на корень из трех.
S=√3/4 (2h/√3)^2=(√3 h^2)/3=h^2/√3

Медианы и биссектрисы через высоту в равностороннем треугольнике можно не считать, так как они равны между собой и совпадают при наложении. (рис.99)
h=m=l

Средняя линия в равностороннем треугольнике расположена параллельно стороне таким образом, чтобы делить боковые стороны ровно пополам точками пересечения. При таком расположении средняя линия равна ровно половине стороны. Найти среднюю линию через высоту можно, разделив ее на корень из трех. (рис. 97.3)
M=h/√3

Чтобы вычислить радиусы вписанной и описанной окружности около равностороннего треугольника, необходимо разделить сторону на два или один корень из трех соответственно. Таким образом, используя выражение стороны через высоту, корень из трех уходит и остаются следующие формулы. (рис. 97.4,97.5)
r=a/(2√3)=h/3
R=a/√3=2h/3

Источник