Нейтральная ось
– линия, во всех точках которой нормальные
напряжения равны нулю. При этом в точках
сечения, наиболее удаленных от нейтральной
оси нормальные напряжения принимают
свои экстремальные значения – минимум
и максимум.
Рис.7.7.
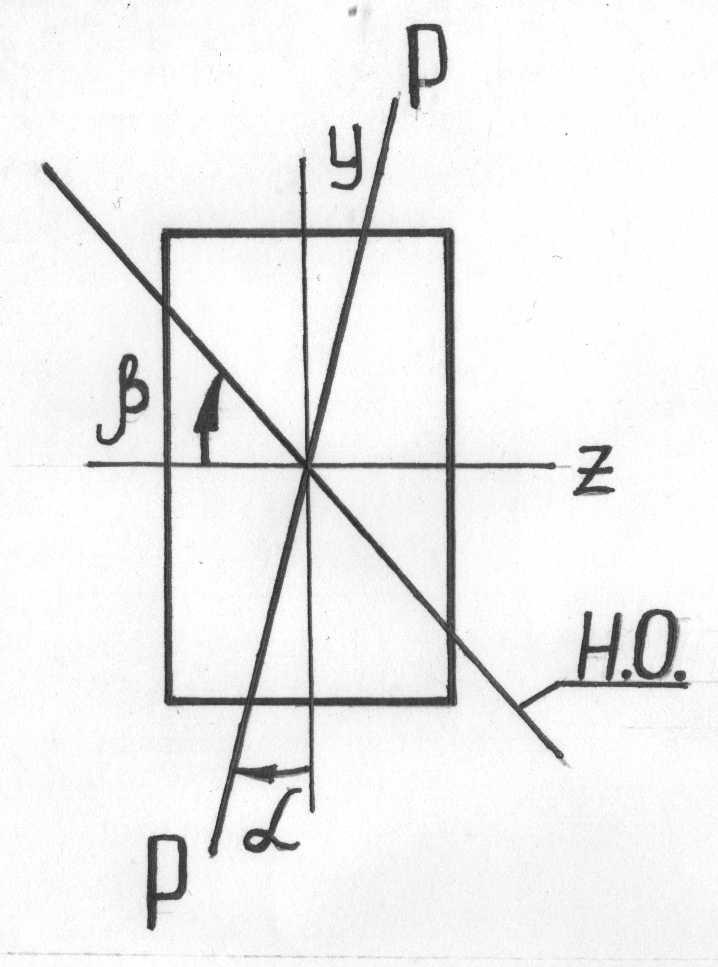
Положение нейтральной оси
Заметим, что при плоском
изгибе нейтральная ось совпадала с
одной из главных осей сечения (Oy
или Oz),
при косом же изгибе это не так. Выведем
формулу для определения положения
нейтральной оси при косом изгибе.
Так
как
=0,
то можем записать:
Отсюда найдем
уравнение нейтральной оси:
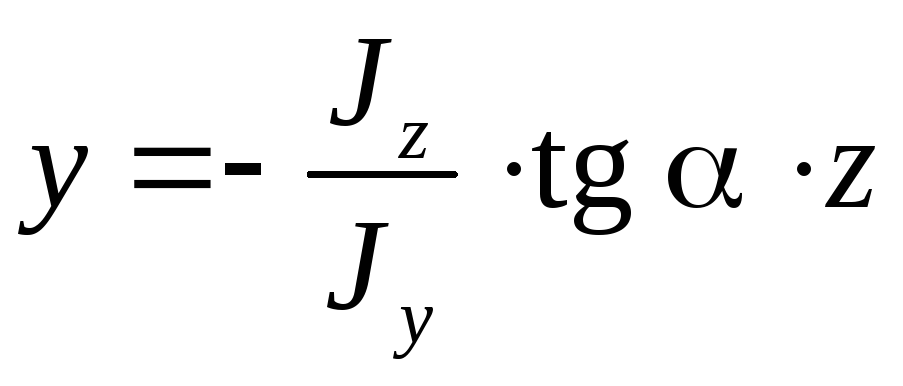
Более
удобно записать это уравнение через
угол
наклона нейтральной линии к осиOz:
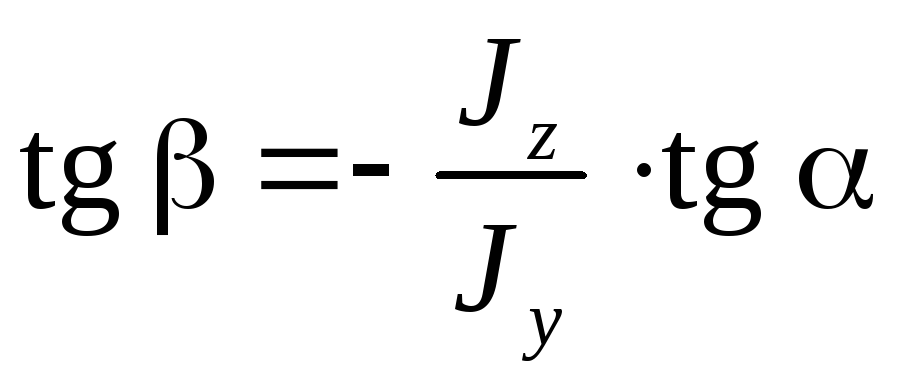
Знак
«минус» в этой формуле показывает, что
углы
и
откладываются от разноименных осей, но
в одном направлении.
Как видим, в случае,
когда Jz
≠ Jy,
углы
и
не равны друг другу, а, значит, и плоскость
кривизны (плоскость максимальных
прогибов) бруса не будет совпадать с
плоскостью действия сил. Поэтому такой
изгиб и назван «косым».
Определим
максимальные нормальные напряжения
при косом изгибе и запишем условие
прочности.
Как известно,
нормальные напряжения достигают своих
экстремальных значений в точках, наиболее
удаленных от нейтральной оси (координаты
таких точек обозначим ymax
и zmax):
,
или
(7.12)
Для прямоугольного
сечения – это точки A
и B.
При M>0
(см. рис.7.8).
Для материалов,
одинаково сопротивляющихся растяжению
(сжатию), максимальные напряжения
определяются так:
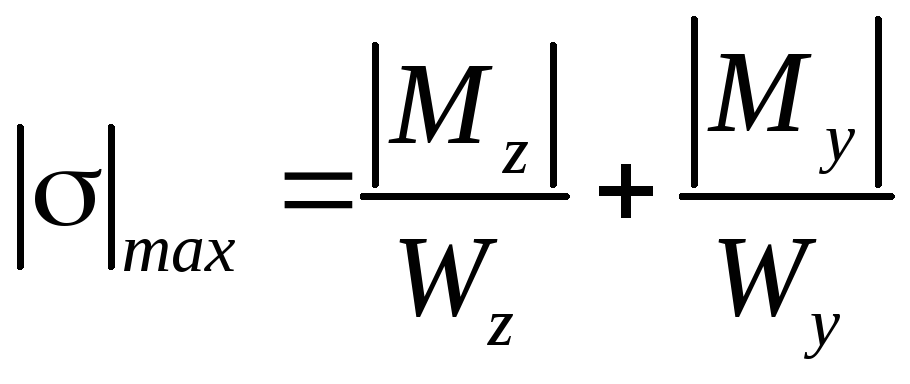
или
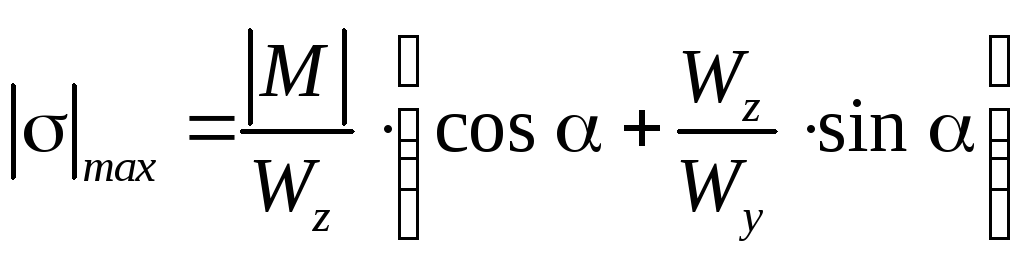
(7.13)
г
и
– моменты сопротивления сечения
относительно осейz
и y.
В случае косого
изгиба, как правило, проверка прочности
осуществляется только по нор-мальным
напряжениям (действие касательных
невелико). Поэтому условие прочности
записывается в виде:
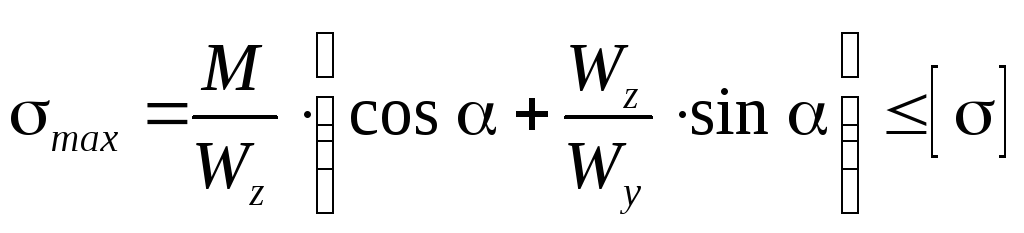
При косом изгибе
(впрочем, как и при остальных видах
нагружения) имеем три задачи расчета
на прочность:
—
проверка прочности;
—
подбор сечения (определить Wz
(размеры сечения) при заданном отношении
Wz/Wy);
—
проверка по несущей способности
(определить M).
7.4. Изгиб с кручением. Определение внутренних усилий и напряжений
Ранее нами был
рассмотрен расчет на прочность валов
при чистом кручении. Однако круглые
валы редко работают на чистое кручение.
Как правило, при работе вал изгибается
собственным весом, весом шкивов, давлением
на зубья шестерен, натяжением ремней и
т. д. В таком случае вал будет находиться
в условиях сложного сопротивления и
испытывать совместное действие кручения
и изгиба.
Изгиб с кручением
– частный случай сложного сопротивления,
который может рассматриваться как
сочетание чистого кручения и поперечного
изгиба.
P1
P2
P3
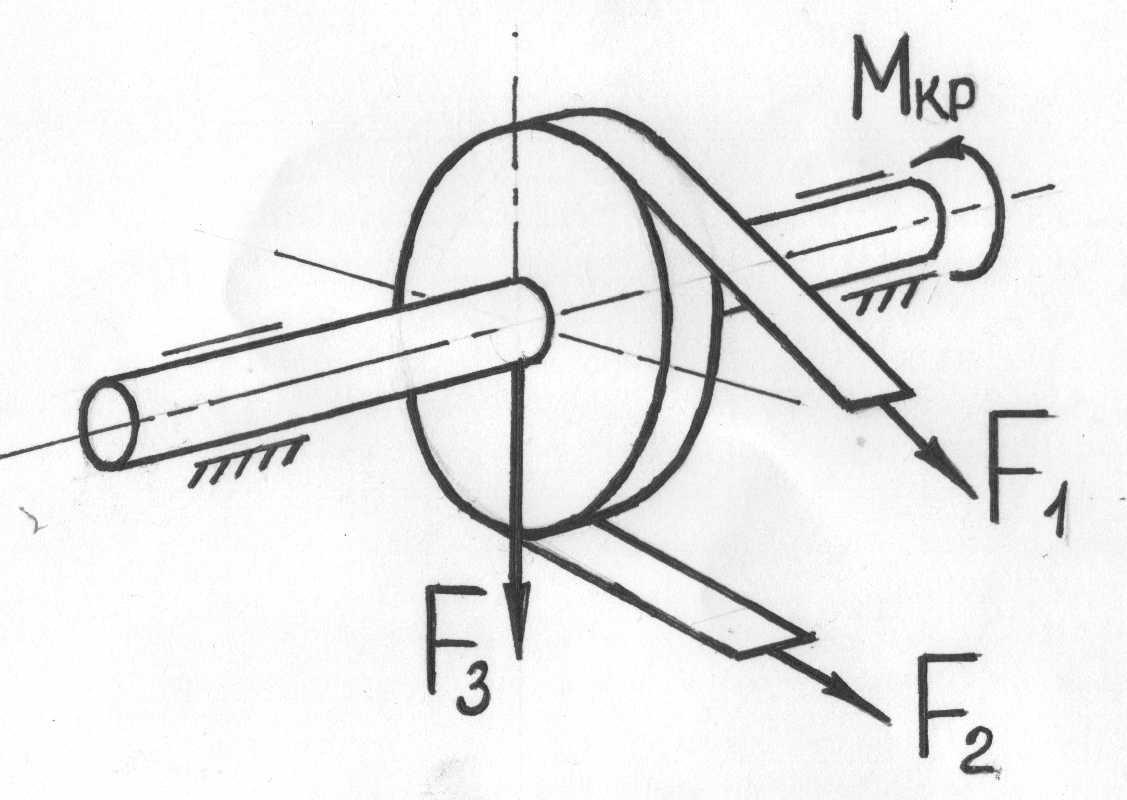
Рис.7.9.
Изгиб с кручением
P
Определение внутренних
усилий и напряжений при кручении с
изгибом. Для определения
внутренних усилий воспользуемся методом
сечений:
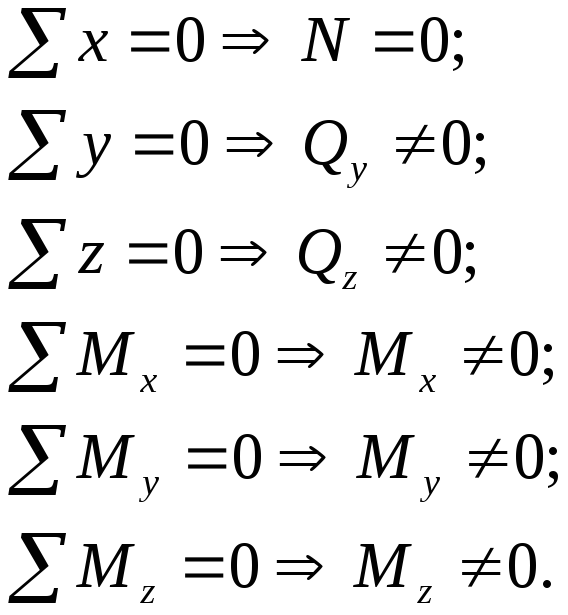
Обычно две
составляющие попе-речной силы (Qy,
Qz)
и изгибающего момента (My,
Mz)
приводят к их полным результирующим
(7.16)
Заметим, что часто
поперечной силой пренебрегают (для
достаточно длинных валов) и рассматривают
кручение с изгибом как совместное
действие крутящего (Mx,
Mкр,
T)
и изгибающего (Mи)
моментов.
Опасное сечение
вала будем искать, как и прежде, по эпюрам
внутренних усилий. При построении эпюр
внутренних усилий при кручении с изгибом
необходимо иметь ввиду следующие
правила:
—
эпюры крутящего момента Mx,
а также эпюры составляющих поперечной
силы Qy,
Qz
и изгибающего момента My,
Mz
строятся с использованием метода
сечений;
—
результирующая поперечная сила Q
может не лежать в плоскости действия
результирующего изгибающего момента
Mи,
а потому между ними уже не будет
соблюдаться зависимость Журавского
(dM/dx=Q),
а, следовательно, и правила проверки
эпюр, введенные для плоского изгиба;
—
эпюра полного изгибающего момента будет
прямой только на тех участках, где My
и Mz
ограничены прямыми с общей нулевой
точкой, на участках, где такая общая
точка отсутствует эпюра Mи
будет описываться вогнутой кривой и
строится по точкам (связано с тем, что
вектор Mи
в разных сечениях имеет различное
направление).
Опасное сечение
при кручении с изгибом устанавливается
из совместного анализа эпюр крутящего
Mx
и полного изгибающего Mи
моментов. Опасным будет считаться то
сечение, где оба момента достигают своей
максимальной величины. Если моменты
достигают максимума в разных сечениях,
необходимо проверить все сечения, в
которых эти внутренние усилия достаточно
велики.
Для определения максимальных
напря-жений используем принцип
независимости дей-ствия сил и найдем
напряжения отдельно от кручения и
отдельно от изгиба:
напряжения при
кручении
,
(7.17)
;
(7.18)
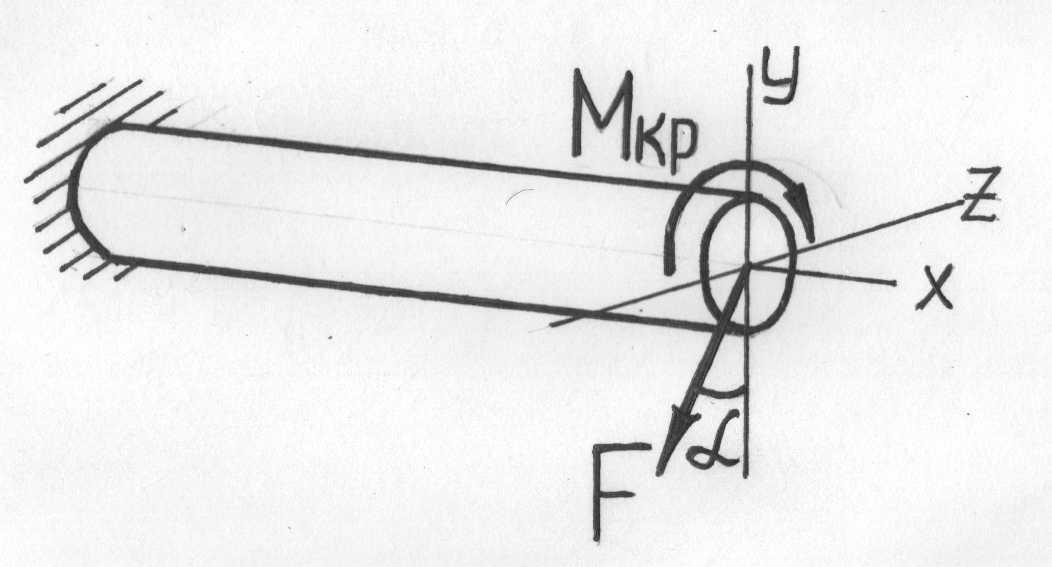
Рис.7.10.
Напряжения
напряжения при изгибе
,
или
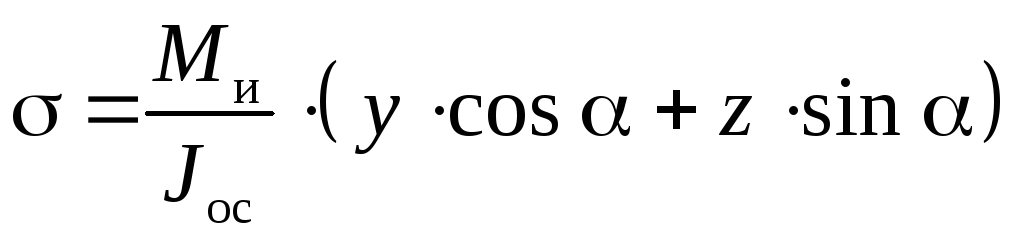
(7.19)
где
Jос
– осевой момент инерции для круглого
сечения (Jос
= Jz
= Jy).
Вводя обозначение
,
можем записать
(7.20)
при
этом
, (7.21)
где
Wос
– осевой момент сопро-тивления для
круглого сечения (Wос=Jос/max,
max=d/2).
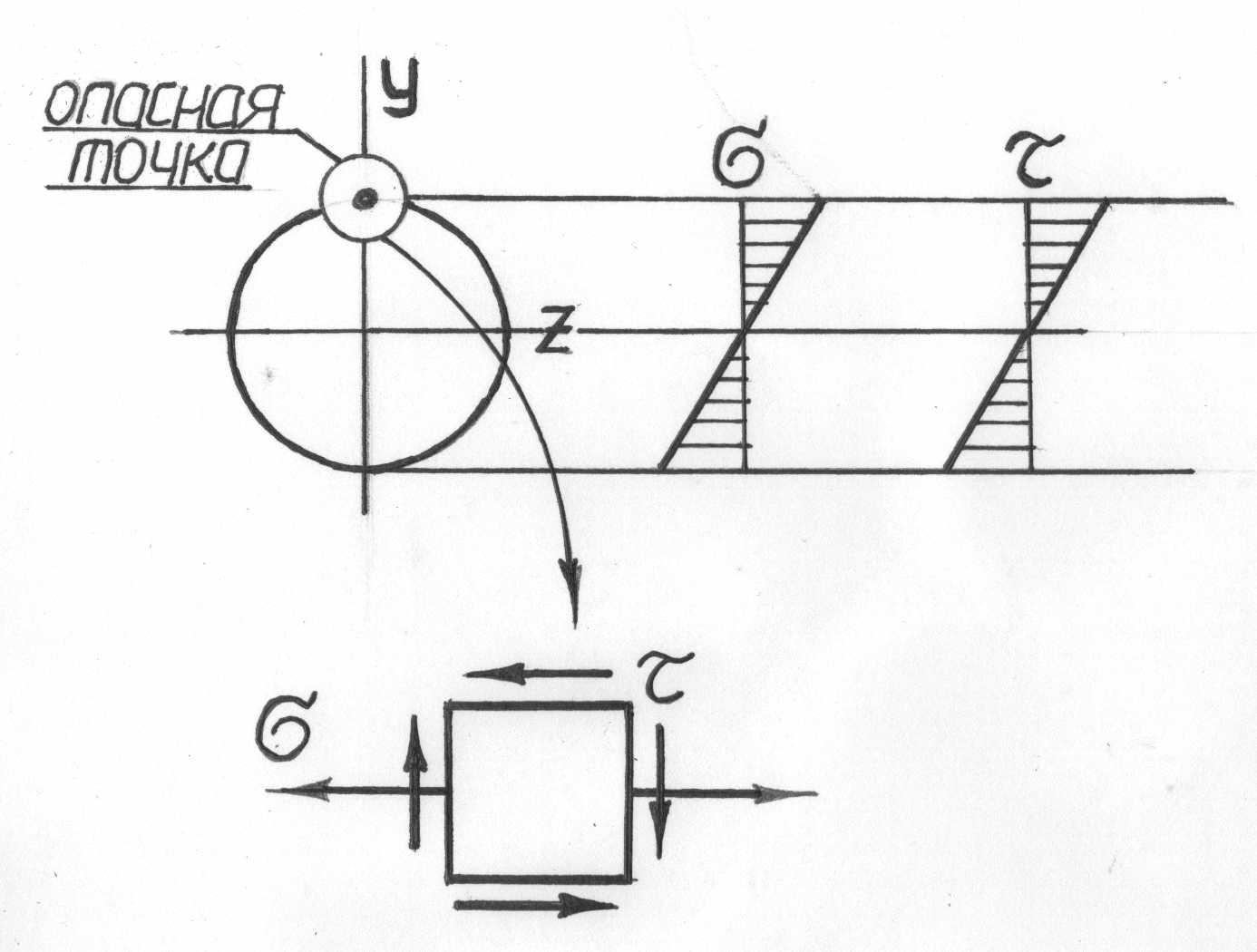
О
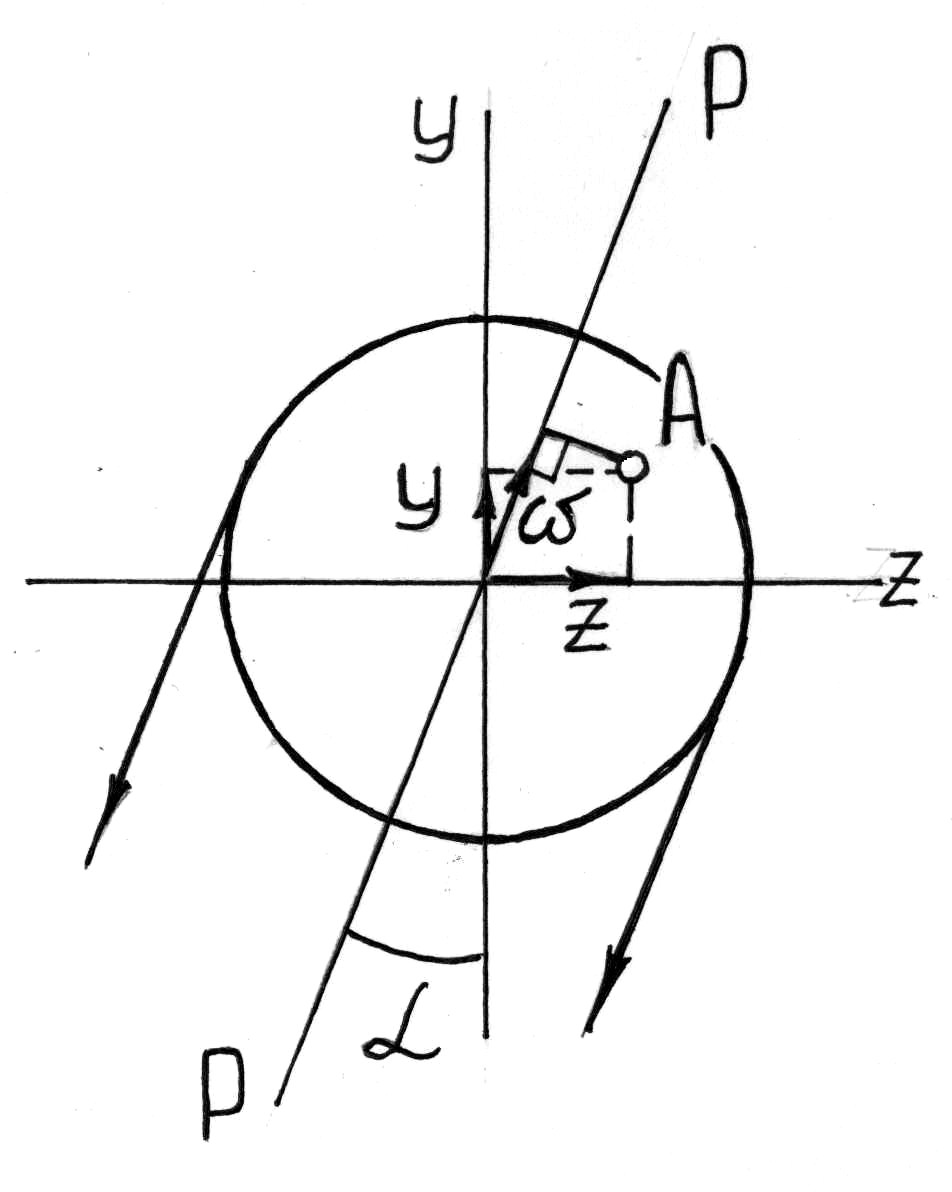
Рис.7.11.
Напряженное состояние
в опасной точке
пасными точками в сечении будут
являться точки наиболее удаленные от
нейтральной оси (для круглого сечения
– линии, перпендикулярной плоскости
действия результирующего изгибающего
момента). При этом в токах сечения будет
возникать плоское напряженное состояние,
а потому расчет на прочность необходимо
проводить с привлечением известных
теорий прочности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
7.3 Определение положения нейтральной оси и максимальных нормальных напряжений при косом изгибе. Условие прочности
Нейтральная ось – линия, во всех точках которой нормальные напряжения равны нулю. При этом в точках сечения, наиболее удаленных от нейтральной оси нормальные напряжения принимают свои экстремальные значения – минимум и максимум.
Заметим, что при плоском изгибе нейтральная ось совпадала с одной из главных осей сечения (Oy или Oz), при косом же изгибе это не так. Выведем формулу для определения положения нейтральной оси при косом изгибе.
Так как 
Отсюда найдем уравнение нейтральной оси:

Более удобно записать это уравнение через угол 
Рекомендуемые материалы

Знак «минус» в этой формуле показывает, что углы 

Как видим, в случае, когда Jz ≠ Jy, углы 

Определим максимальные нормальные напряжения при косом изгибе и запишем условие прочности.
Как известно, нормальные напряжения достигают своих экстремальных значений в точках, наиболее удаленных от нейтральной оси (координаты таких точек обозначим yуд. и zуд.). Стало быть, можем записать:

или

Для прямоугольного сечения – это точки A и B. При M>0 
Для материалов, одинаково сопротивляющихся растяжению (сжатию), максимальные напряжения определяются так:

или

где 

Лекция «Джон Голсуорси» также может быть Вам полезна.
В случае косого изгиба, как правило, проверка прочности осуществляется лишь по нор-мальным напряжениям (действие касательных невелико). Поэтому условие прочности запишем в виде:
При косом изгибе (впрочем, как и при остальных видах нагружения) имеем три задачи расчета на прочность:
1) проверка прочности;
2) подбор сечения [определить Wz (размеры сечения), при заданном отношении Wz/Wy];
3) проверка по несущей способности (определить M).
From Wikipedia, the free encyclopedia
Beam with neutral axis (x).
The neutral axis is an axis in the cross section of a beam (a member resisting bending) or shaft along which there are no longitudinal stresses or strains. Building trades workers should have a basic understanding of the concept and follow industry rules and guidelines, to avoid dangerously compromising the structural safety of a building.
Theory[edit]
If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid of a beam or shaft. All fibers on one side of the neutral axis are in a state of tension, while those on the opposite side are in compression.
Since the beam is undergoing uniform bending, a plane on the beam remains plane. That is:

Where 

There is a compressive (negative) strain at the top of the beam, and a tensile (positive) strain at the bottom of the beam. Therefore by the Intermediate Value Theorem, there must be some point in between the top and the bottom that has no strain, since the strain in a beam is a continuous function.
Let L be the original length of the beam (span)
ε(y) is the strain as a function of coordinate on the face of the beam.
σ(y) is the stress as a function of coordinate on the face of the beam.
ρ is the radius of curvature of the beam at its neutral axis.
θ is the bend angle
Since the bending is uniform and pure, there is therefore at a distance y from the neutral axis with the inherent property of having no strain:

Therefore the longitudinal normal strain 


Therefore, we can solve for ρ, and find that:

Substituting this back into the original expression, we find that:

Due to Hooke’s Law, the stress in the beam is proportional to the strain by E, the modulus of elasticity:

Therefore:


From statics, a moment (i.e. pure bending) consists of equal and opposite forces. Therefore, the total amount of force across the cross section must be 0.

Therefore:

Since y denotes the distance from the neutral axis to any point on the face, it is the only variable that changes with respect to dA. Therefore:

Therefore the first moment of the cross section about its neutral axis must be zero. Therefore the neutral axis lies on the centroid of the cross section.
Note that the neutral axis does not change in length when under bending. It may seem counterintuitive at first, but this is because there are no bending stresses in the neutral axis. However, there are shear stresses (τ) in the neutral axis, zero in the middle of the span but increasing towards the supports, as can be seen in this function (Jourawski’s formula);
where
T = shear force
Q = first moment of area of the section above/below the neutral axis
w = width of the beam
I = second moment of area of the beam
This definition is suitable for the so-called long beams, i.e. its length is much larger than the other two dimensions.
Arches[edit]
Arches also have a neutral axis if they are made of stone; stone is an inelastic medium, and has little strength in tension. Therefore as the loading on the arch changes the neutral axis moves- if the neutral axis leaves the stonework, then the arch will fail.
This theory (also known as the thrust line method) was proposed by Thomas Young and developed by Isambard Kingdom Brunel.
Practical applications[edit]
Building trades workers should have at least a basic understanding of the concept of neutral axis, to avoid cutting openings to route wires, pipes, or ducts in locations which may dangerously compromise the strength of structural elements of a building. Building codes usually specify rules and guidelines which may be followed for routine work, but special situations and designs may need the services of a structural engineer to assure safety.[1][2]
See also[edit]
- Neutral plane
- Second moment of inertia
References[edit]
- ^ «Digital Codes». ICC Codes. International Code Council, Inc. Retrieved 2023-02-10.
- ^ Yeh, Borjen; Herzog, Benjamin. «Effect of holes on the structural capacities of laminated veneer lumber» (PDF). APA Wood. APA – The Engineered Wood Association. Retrieved 2023-02-10.
Определение положения нейтральной оси при косом изгибе
Рассмотрим сечение прямоугольной формы (рис. 113). Так как это сечение имеет оси симметрии, поэтому известно положение его главных центральный осей инерции — это сами оси симметрии.
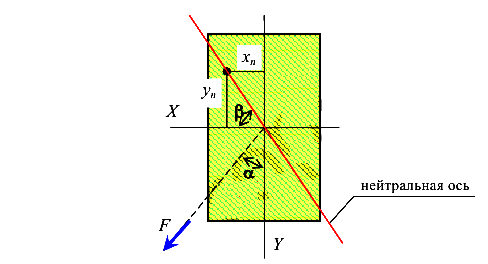
при косом изгибе
Линия, в каждой точке которой напряжения равны нулю, называется нейтральной линией (осью).
Пусть 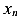
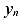
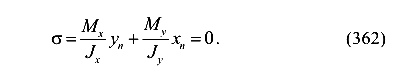
Так как 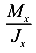
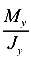
Разделим обе части уравнения (381) на 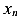
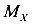
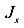

Перенесем второе слагаемое на правую сторону уравнения (363) и получим
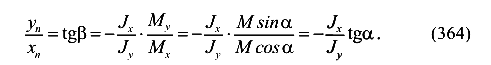
Без учета знака получим

Из формулы (362), очевидно, что напряжение в центре тяжести сечения, то есть при 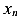
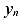
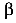
Угол 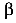
Если 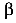
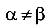
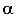
Для сечений, у которых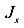
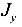
Рассмотрим частный случай косого изгиба.
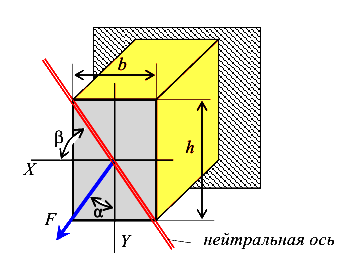
Дана балка прямоугольного сечения (рис.114). Пусть силовая плоскость проходит через диагональ сечения.
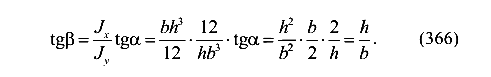
Таким образом, нейтральная ось совпадает с другой диагональю сечения.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
Определение положения нейтральной оси при косом изгибе
Определение положения нейтральной оси при косом изгибе
Рассмотрим сечение прямоугольной формы (рис. 113). Так как это сечение имеет оси симметрии, поэтому известно положение его главных центральный осей инерции — это сами оси симметрии.
Линия, в каждой точке которой напряжения равны нулю, называется нейтральной линией (осью).
Пусть 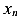
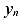
Так как 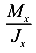
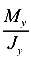
Разделим обе части уравнения (381) на 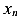
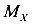
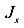
Перенесем второе слагаемое на правую сторону уравнения (363) и получим
Без учета знака получим
Из формулы (362), очевидно, что напряжение в центре тяжести сечения, то есть при 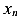
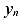
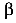
Угол 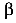
Если 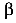
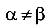
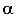
Для сечений, у которых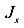
Рассмотрим частный случай косого изгиба.
Дана балка прямоугольного сечения (рис.114). Пусть силовая плоскость проходит через диагональ сечения.
Таким образом, нейтральная ось совпадает с другой диагональю сечения.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Дополнительные страницы которые вам будут полезны:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Сложное сопротивление
По этой ссылке вы найдёте полный курс лекций по математике:
Сложное сопротивление 1.1. Общие понятия 1.2. Косой изгиб 1.3. Нормальные напряжения при косом изгибе 1.4. Перемещение при косом изгибе 1.5. Примеры расчетов на косой изгиб 1.6. Изгиб с растяжением или сжатием 1.7. Внецентренное растяжение или сжатие стержней большой жесткости 1.8. Ядро сечения 1.9. Пример построения ядра сечения 1.10. Изгиб с кручением стержней круглого сечения Библиографический список 4 1. Сложное сопротивление 1.1
Общие понятия Под сложным сопротивлением понимают совокупность простых видов деформаций бруса, при которых в его поперечных сечениях одновременно возникает более одного внутреннего силового фактора. Исключением является прямой поперечный изгиб, который не принято рассматривать, как случай сложного сопротивления, хотя при этом в сечениях и возникают два внутренних силовых фактора: изгибающий момент и поперечная сила.
Этот вид деформации рассматривается как простой потому, что в подавляющем большинстве случаев расчеты на прочность и жесткость ведутся без учета влияния поперечных сил, т. е. по одному силовому фактору – изгибающему моменту. Напряжения и деформации при сложном сопротивлении могут быть в большинстве случаев вычислены на основании принципа независимости действия сил. Для этого сложная деформация раскладывается на простые.
Для каждой простой деформации находят напряжения и перемещения. Суммарное напряжение или перемещение определяют алгебраическим или геометрическим их сложением. Среди случаев сложного сопротивления стержней наиболее часто встречаются следующие сочетания простых видов нагружения: косой изгиб (рис. 1.1, а), внецентренное растяжение или сжатие (рис. 1.1, б) и одновременное действие кручения с изгибом (рис. 1.1, в), изгиб с растяжением или сжатием и т. д. Рис. 1.1 1.2.
Косой изгиб Косым изгибом называется такой вид изгиба, при котором плоскость действия изгибающего момента в поперечном сечении бруса не проходит ни через 5 одну из главных центральных осей этого сечения, или не совпадает ни с одной из главных плоскостей (рис. 1.2). Под главной плоскостью понимают плоскость, проходящую через продольную ось балки и одну из главных центральных осей поперечного сечения. Например, для прямоугольного сечения (рис. 1.2, г) – это плоскости, проходящие через оси ZX, YX.
Косой изгиб можно подразделить на плоский и пространственный. Плоский косой изгиб – это вид сложного сопротивления, когда все внешние силы расположены в одной плоскости (рис. 1.1, а,1.2, а), называемой силовой, и эта плоскость не совпадает ни с одной из главных плоскостей. Пространственный косой изгиб отличается от плоского лишь тем, что внешние силы не находятся в одной плоскости и изогнутая ось балки будет уже не плоской, а пространственной кривой.
Плоский косой изгиб представляет собой частный случай пространственного изгиба. Рис. 1.2 1.3. Нормальные напряжения при косом изгибе 6 Рассмотрим определение напряжений при косом изгибе (рис. 1.2, а). Прежде всего, все нагрузки, действующие в произвольной плоскости, разложим на составляющие, расположенные в главных плоскостях (рис. 1.2, б), и построим эпюры изгибающих моментов Мz и Му (рис. 1.2, в), т. е. приведем сложный изгиб к двум плоским изгибам М Мz2 М у2 .
В произвольном сечении с координатой х установим величину и направление изгибающих моментов Мz и Му (1.2, в). Напряжение в какой-либо точке сечения найдём в соответствии с принципом независимости действия сил (рис. 1.3.): Знак нормальных напряжений зависит от направления изгибающих моментов. Например, для точки В (рис. 1.3, а) оба слагаемых положительны, так как оба момента Мz и Му вызывают в точке В растяжение, растягивающее напряжение. В точке D напряжение определяется как где уD и zD – координаты точки.
Для произвольной точки сечения напряжения определяются по формуле (1.2) Все параметры, входящие в эту формулу, подставляются по модулю, а знаки перед составляющими слагаемыми определяем из физических соображений: если изгибающий момент Мz или Му вызывает в точке растягивающее напряжение, то перед составляющей должен быть знак плюс, сжимающее напряжение – знак минус. Опасные точки в сечении при косом изгибе определяются по положению нейтральной линии.
Возможно вам будут полезны данные страницы:
Нейтральная линия – это геометрическое место точек, в которых нормальные напряжения равны нулю. Уравнение нейтральной линии при косом изгибе имеет вид (1.4) где β – угол наклона нейтральной линии. По положению нейтральной линии определяется положение точки в сечении, как наиболее удалённой от нейтральной оси, например точка В и точка D (рис. 1.3). В опасных точках напряжения достигают наибольшей величины.
Для пластичных материалов условие прочности запишется для одной, наиболее удалённой точки от нейтральной оси (рис.1.3): где ув и zв – координаты опасной точки. Для сечений типа прямоугольного, двутавра, швеллера и т.д. имеющих ярко выраженные угловые точки, условие прочности можно записать в виде: – осевые моменты сопротивления. Для хрупких материалов условие прочности записывают для двух опасных точек, наиболее удалённых от нейтральной линии (точки В и т. D): координаты опасных точек. 8 1.4.
Перемещение при косом изгибе Определим прогиб консольно-защемленной балки, нагруженной на конце силой Р, действующей под углом α к вертикали. Разложим силу Р на составляющие РуР soc. (рис. 1.4). Прогиб на свободном конце балки по оси у от силы Ру составит аналогично Суммарный прогиб балки Рис. 1.4 1.5. Примеры расчетов на косой изгиб Пример 1.1 Рассмотрим балку длиной l = 3 м, составленную из двух швеллеров № 16 и нагруженную силами Р1 = 6 кН и Р2 = 4 кН, как показано на рис. 1.5.
Угол наклона сечения к горизонту α = 15є (рис. 1.5, б). 9 Найти величину наибольшего напряжения в опасном сечении и величину и направление полного перемещения сечения С. Рис. 1.5 Решение 1. Геометрические характеристики сечения. Находим по сортаменту геометрические характеристики для швеллера №16 и с учетом этого вычисляем их для рассматриваемого сечения (рис. 1.5): где 18,1 – координата центра тяжести швеллера (рис. 1.5, в).
10 Тогда осевые моменты сопротивления Wz и Wу определяется по зависимости – ширина полки швеллера. 2. Найдем проекции внешних сил на главные оси сечения. 3.Определяем реакции опор в главных плоскостях и строим эпюры изгибающих моментов (рис. 1.6) в этих плоскостях. Плоскость Плоскость Выполняем проверку правильности определение реакции Аналогично Реакции определены, верно. Вычисляем изгибающие моменты в характерных сечениях: Строим эпюры Мz и Му (рис. 1.6, а,б) Рис. 1.6 4.
Находим максимальные напряжения в сечении С: Максимальное напряжение в сечении D Видим, что опасным является сечение D 5. Устанавливаем положение нейтральной линии в сечении С. Используем формулу (1.4): Отсюда находим угол наклона β нейтральной линии: β=25є30’ (отсчитывается от оси Z). 6. Направление полного перемещения перпендикулярно к нейтральной линии (отсчитывается таким же углом β=25є30’ от оси У (рис. 1.5)). 7. Найдём вертикальную составляющую ∆у полного перемещения (рис. 1.5).
Для этого используем интеграл Мора и формулу Верещагина. 12 Приложим к сечению С единичную силу и построим эпюру единичных моментов (рис 1.6, в). Тогда прогиб в вертикальной плоскости: Аналогично определяются перемещения в горизонтальной плоскости где М 2 – эпюра изгибающих моментов от единичной силы, приложенной в точке С параллельно оси Z (в горизонтальной плоскости): Полный прогиб определяем как геометрическую сумму прогибов в вертикальной и горизонтальной плоскостях: 1.6.
Изгиб с растяжением или сжатием Изгибом с растяжением (сжатием) называется такой вид сложного сопротивления, при котором в поперечном сечении стержня возникают продольная сила и изгибающий момент (моменты). Если на балку действуют силы, пересекающие ее ось, но не лежащие ни в одной из главных плоскостей, то имеет место сложный изгиб с растяжением или сжатием (рис. 1.8, а). При расчете прежде всего показываем расчётную схему (рис. 1.8, б) стержня.
Для этого разложим все нагрузки на составляющие по главным осям сечения (Z, У), продольной оси Х балки и построим эпюры внутренних усилий (рис. 1.8, в). Для других точек (например, точки D) нормальные напряжения будут определятся по формуле (1.6) т. е. знаки минус связаны с тем, что силовые факторы Мz и Му вызывают в точке D деформацию сжатие. Таким образом, если силовые факторы – продольная сила N, моменты Мz, Му вызывают в рассматриваемой точке сжатие, то вводится знак минус перед соответствующим членом уравнения, если растяжение, то плюс. С учетом этого формула (1.6) для нормальных напряжений имеет вид (1.7)
Для проверки прочности балки необходимо найти опасную точку в сечении, в которой нормальные напряжения достигнут максимальной величины.
Опасные точки в сечении определяются по положению нейтральной линии. Это точки наиболее удалённые от нее. Рис. 1.8 При выводе уравнения нейтральной линии введём условность: главные центральные оси (У, Z) направлять таким образом, чтобы в первом квадранте складывались напряжения одного и того же знака (рис. 1.8, г). Эта условность позволяет при записи уравнения нейтральной линии опустить знаки перед составляющими в формуле (1.7).
С учётом этого уравнение нейтральной линии имеет вид (1.8) где у0 и z0 – координаты точек, лежащих на нейтральной линии. Из формулы (1.8) видим, что нейтральная линия не проходит через центр тяжести сечения и представляет собой прямую, отсекающую отрезки на осях координат. Отрезки, отсекаемые ею на осях координат: при 0 , (1.9) Знак минус в формуле (1.9) означает, что отрезки должны быть отложены в сторону, противоположную направлению главных центральных осей Z, Y.
Для сечения (рис. 1.9) наиболее опасными точками являются точка В и точка D. Рис. 1.9 Для хрупких материалов опасных точек в сечении две – это точки В и D как наиболее удалённые от нейтральной оси. В этом случае условие прочности для двух опасных точек где индекс » р ” – означает растяжение, «c” – сжатие. 1.7. Внецентренное растяжение или сжатие стержней большой жесткости. 16 Внецентренным растяжением или сжатием называется такой вид деформации, при котором равнодействующая внешних сил параллельна оси стержня, но смещена относительно этой оси. Точка приложения силы называется полюсом п (рис. 1.10,а).
Расстояние l от полюса до центра тяжести сечения называется эксцентриситетом силы. Эксцентриситеты силы (zр и ур) относительно главных осей У и Z являются координатами полюса. Рис. 1.10 Таким образом, при внецентренном растяжении (сжатии) силой Р в поперечных сечениях возникают три внутренних силовых фактора, постоянных по длине стержня (рис. 1.10, б): Следовательно, внецентренное растяжение (сжатие) представляет собой совокупность изгиба и осевого растяжения (сжатия).
Нормальные напряжения в произвольной точке какого-либо сечения с координатами z, у определяются по формуле, аналогично формуле (1.7) где знаки слагаемых можно определить, исходя из характера деформации, также как при изгибе с растяжением (сжатием). Подставив сюда выражение (1.10), получим Из раздела «Геометрические характеристики плоских сечений” известно, что где iz и iу – радиусы инерции сечения. Подставив (1.12) в (1.10), получим формулу для определения нормальных напряжений в этом виде: Уравнение нейтральной линии находим из условия, что σ = 0, тогда где у и z – координаты текущей точки нейтральной линии.
Из выражения (1.14) видно, что нейтральная линия не проходит через начало координат, и ее положение удобнее находить по отрезкам, отсекаемым ею на координатных осях (рис. 1.11), либо по формуле (1.9). (1.15) Формулы (1.15) показывают, что отрезки ay иaz имеют знаки, противоположные координатам точки приложения ур и zр. Так, если внешняя сила Р приложена в точке первого квадранта, то нейтральная линия отсекает отрезки ay и z a в третьем квадранте (рис. 1.12).
Чем ближе полюс к центру тяжести сечения, тем дальше от него нейтральная линия и наоборот. Рис. 1.12 Зная положение нейтральной линии и определив координаты опасных точек уоп и zоп, как наиболее удаленных от неё, можно записать формулы для нормальных напряжений в этих точках и условие прочности (1.16) В случае, представленном на рис. 1.11, опасными являются точки В и D. 1.8. Ядро сечения 19 Существуют некоторые материалы, которые плохо сопротивляются растяжению (кирпич, камень, бетон и т.п.).
Для рационального проектирования конструкций из таких материалов необходимо, чтобы в сечениях элементов не появлялись растягивающие напряжения. Этого можно добиться, если точка приложения силы будет размещена в некоторой области вокруг центра тяжести сечения, называемой ядром сечения. Ядро сечения характеризуется тем, что всякая продольная сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения нормальные напряжения одного знака.
Для построения ядра сечения рекомендуется задавать возможные положения нейтральной линии так, чтобы она касалась контура сечения, не пересекая его, и находить соответствующую точку приложения силы, соответствующую одной из вершин ядра сечения. При повороте нейтральной линии вокруг угла контура сечения точки полюса будут находиться на линии, соединяющей вершины ядра. 1.9. Пример построения ядра сечения Рассмотрим методику построения ядра сечения на примере прямоугольной фигуры (рис. 1.13). Рис. 1.13
Сечение имеет размеры В Ч Н; его геометрические характеристики Пусть нейтральная линия занимает положение 1-1, тогда отрезки, отсекаемые ею на координатных осях, По формуле (1.15) найдём координаты первой точки (приложения силы (вершины ядра сечения)): Если повторить подобные рассуждения для положенной нейтральной линии 2- 2, 3-3 и 4-4, то получим координаты точек 2, 3 и 4. Соединив эти точки прямыми линиями, получим ядро сечения для прямоугольника.
Таким образом, ядро сечения имеет форму прямоугольника, содержащего столько строк, сколько касательных можно провести к данному сечению. Пример 1.2 Колонна, поперечное сечение которой показано на рис.1.14, нагружена сжимающей силой Р=240кН, приложенной в точке К. Размеры сечения В1=16 см, Н1=4 см, В2=2 см, Н2=20 см. Требуется: 1. Определить положение нейтральной линии. 2. Определить наибольше растягивающее и сжимающее напряжения. 3. Построить плоскую эпюру напряжений. 21 Рис. 1.14 Решение 1.
Вычисляем геометрические характеристики сечения: — Площади элементов сечения А1=16 ּ4=64 см2; А2=20 ּ2=40 см2; А=А1+ А2=64+40=104 см2; — Положение центра тяжести — Проводим центральную ось Z. — Расстояние между осями Z1, Z2 простых фигур и центральной осью Z: — Моменты инерции относительно центральных осей: — Квадраты радиусов инерции сечения: 2. Координаты полюса: 2. Отрезки, отсекаемые нейтральной линией на осях координат: 3. Проводим нейтральную линию в сечении (рис.1.15).
Опасные точки сечения: точка D – наибольшие сжимающие напряжения; координаты точки zD=-8,0 см; уD=-6,6 см; точка В – наибольшие растягивающие напряжения; 23 координаты точки zВ=8,0 см; уВ=-2,6 см. Рис. 1.15 5. Находим напряжения в опасных точках по формуле (1.16) Напряжения сжатия: Напряжения растяжения: 6. Строим эпюру напряжений (рис. 1.15). 24 1.10.
Изгиб с кручением стержней круглого сечения Это такой вид сложного сопротивления, когда в поперечных сечениях стержня (вала) возникают изгибающий и крутящий моменты. Сочетания изгиба с кручением стержней круглого поперечного сечения чаще всего встречается при расчёте валов. Силы, действующие на вал (давление зубчатых колёс или натяжение ремней, собственный вес шкивов и вала), вызывают в поперечных сечениях в общем случае крутящий момент (Мк), изгибающие моменты (Мz , Му) и поперечные силы (Qу , Qz) в двух плоскостях (рис. 1.16).
В поперечном сечении круглого стержня возникают нормальные напряжения от изгиба, а также касательные напряжения от кручения и изгиба. Вследствие малой величины касательными напряжениями от поперечных сил можно пренебречь. Для расчёта стержней круглого поперечного сечения прежде всего необходимо построить эпюры изгибающих и крутящих моментов от заданных внешних сил. Нагрузки раскладывают на составляющих вдоль координатных осей и строят эпюры изгибающих моментов Мz и Му (рис. 1.16).
Поскольку вал имеет круглое поперечное сечение, то любая ось, проходящая через центр тяжести его, является главной осью. Следовательно, при действии изгибающих моментов в разных плоскостях не будет косого изгиба, а будет происходить лишь плоский изгиб в плоскости действующего результирующего изгибающего момента ММM и zу 22 . (1.17) По эпюрам результирующего изгибающего и крутящего моментов (рис. 1.16, г, д) находят опасное сечение, где эти моменты достигают наибольшего значения. 25 Рис. 1.16
На участках вала, где линии, очерчивающие эпюры моментов, пересекают базовую ось в одной точке, эпюра результирующих моментов очерчивается прямой линией (крайний правый участок ВС). На участках CD и DE эпюра результирующих моментов очерчивается параболой, так как вышесказанное условие не соблюдается. Здесь силовые линии в каждом смежном сечении меняют своё положение. Рассмотрим произвольное сечение вала на расстоянии х от правого конца. В этом сечении (рис. 1.17), как следует из построенных эпюр, действуют изгибающие моменты Mz, M y, крутящий момент Mк и поперечные силы. Рис. 1.17
Наибольшие касательные напряжения при кручении в данном поперечном сечении действуют на поверхность вала и определяются по зависимости xam, где Mк крутящий момент в рассматриваемом сечении; полярный момент сопротивления; радиус сечения. Для сплошного круглого сечения . Наибольшее нормальное напряжение от результирующего изгибающего момента Ми определяется по зависимости Wи WzWy момент сопротивления при изгибе. Для круглого сечения Сопоставляя Wи с W , можно заметить, что WWи.
Точки, в которых действуют максимальные нормальные напряжения, находятся на пересечении границы контура (окружности) плоскостью результирующего изгибающего момента (рис. 1.18) Рис.1.18 27 Таким образом, наибольшие нормальные напряжения будут в точках В и D, а так же наибольшие касательные напряжения от кручения, а следовательно, и главные напряжения. Причем касательные напряжения действуют в плоскости поперечного сечения, а нормальные перпендикулярно сечению (рис. 1.19). Рис. 1.19
Ввиду того что нормальное и касательное напряжения взаимно перпендикулярны, материал испытывает плоское напряженное состояние, и расчет на прочность ведется с использованием теорий прочности. Третья теория прочности (теория наибольших касательных напряжений) и четвертая (энергетическая теория) используются для пластичных материалов, а теория Мора — для хрупких.
В соответствии с третьей теорией прочности условие прочности записывается через эквивалентные напряжения экв и имеет вид (1.20) а по четвертой теории прочности (1.21) Подставляя в эту формулу выражения для напряжений (1.19) и (1.18), получим где называют приведенным моментом по четвертой теории прочности. При расчете по третьей теории 28 Если вал выполнен из хрупкого материала, то следует пользоваться теорией прочности Мора:
Обратим внимание, что если материал пластичный, то тогда из (1.24) вытекает третья теория прочности. Пример 1.3 Стальной вал круглого поперечного сечения (рис. 1.20) вращается с постоянной скоростью и передает мощность N=81,2 кВт посредством зубчатого колеса с окружным усилием Р и шкива, усилия в ведущей и ведомой ветвях которого соответственно равны 2t и t. Ветви ремня параллельны друг другу и наклонены к горизонту под углом , а окружное усилие действует под углом β 0.
Частота вращения вала n 970 об/мин. Диаметр шкива D1=650 мм, диаметр зубчатого колеса D2=400 мм. Длины участков: l150 мм. Допускаемое напряжение []=100 МПа. Требуется: 29 1. Изобразить расчетную схему вала и перенести на нее все внешние силы и моменты (включая реакции опор). 2. Разложить окружное усилие и усилия ветвей ремня на составляющие в вертикальной и горизонтальной плоскостях.
Построить эпюры изгибающих и крутящих
Построить эпюры изгибающих и крутящих моментов. 3. Установить опасное сечение вала и определить его диаметр, используя четвертую теорию прочности. 30 Рис. 1.20 Решение 1. Угловая скорость вращения вала 2. Крутящий момент, подаваемый на вал 3. Усилия, действующие на вал: 4 Нк. 4. Проекция внешних сил на координатные оси и реакции опор: плоскость XOУ: плоскость XOZ: 5.
Расчетная схема вала с нагрузками показана на рис. 1.20, б. 6. Находим значения изгибающих моментов в характерных сечениях и строим эпюры моментов: Эпюры изгибающих моментов МZ и M у показаны на рис. 1.20, в, г. 7. Строим суммарную эпюру изгибающих моментов Эпюра суммарных изгибающих моментов показана на рис. 1.20, д. Эпюра крутящих моментов – на рис. 1.3, е. 8. Опасным является левое опорное сечение, где Ми 1,618 м и 9.
Приведенный момент по четвертой теории прочности 10. Из условия прочности требуемая геометрическая характеристика Учитывая, что 0,1 3, найдем требуемый диаметр вала 11. Окончательно принимаем значение диаметра d в соответствии со стандартными значениями, которые в интервале от 50 до 100 мм кратные пяти, а в интервале от 100 и выше кратные десяти. Для нашего случая принимаем d5 5 мм.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Определение положения нейтральной оси и максимальных нормальных напряжений при косом изгибе
7.3 Определение положения нейтральной оси и максимальных нормальных напряжений при косом изгибе. Условие прочности
Нейтральная ось – линия, во всех точках которой нормальные напряжения равны нулю. При этом в точках сечения, наиболее удаленных от нейтральной оси нормальные напряжения принимают свои экстремальные значения – минимум и максимум.
Заметим, что при плоском изгибе нейтральная ось совпадала с одной из главных осей сечения (Oy или Oz), при косом же изгибе это не так. Выведем формулу для определения положения нейтральной оси при косом изгибе.
Так как 
Отсюда найдем уравнение нейтральной оси:

Более удобно записать это уравнение через угол 
Рекомендуемые файлы

Знак «минус» в этой формуле показывает, что углы 

Как видим, в случае, когда Jz ≠ Jy, углы 

Определим максимальные нормальные напряжения при косом изгибе и запишем условие прочности.
Как известно, нормальные напряжения достигают своих экстремальных значений в точках, наиболее удаленных от нейтральной оси (координаты таких точек обозначим yуд. и zуд.). Стало быть, можем записать:


Для прямоугольного сечения – это точки A и B. При M>0 
Для материалов, одинаково сопротивляющихся растяжению (сжатию), максимальные напряжения определяются так:


где 

Лекция «Джон Голсуорси» также может быть Вам полезна.
В случае косого изгиба, как правило, проверка прочности осуществляется лишь по нор-мальным напряжениям (действие касательных невелико). Поэтому условие прочности запишем в виде: 
При косом изгибе (впрочем, как и при остальных видах нагружения) имеем три задачи расчета на прочность:
1) проверка прочности;
2) подбор сечения [определить Wz (размеры сечения), при заданном отношении Wz/Wy];
3) проверка по несущей способности (определить M).
http://natalibrilenova.ru/slozhnoe-soprotivlenie/
http://studizba.com/lectures/73-fizika/1057-lekcii-po-soprotivleniyu-materialov/19263-73-opredelenie-polozheniya-neytralnoy-osi-i-maksimalnyh-normalnyh-napryazheniy-pri-kosom-izgibe.html