Физика. Кинематика
Равноускоренное движение по прямой и под углом к горизонту
Как определить положение тела в пространстве? И для чего нужны координаты?
Школьный курс физики начинается с раздела кинематика. Именно она закладывает фундамент для дальнейшего изучения, все остальные разделы так или иначе будут соприкасаться с этим разделом.
Что же такое кинематика? Это раздел физики, который изучает движение некоторого тела в пространстве. При это мы НЕ рассматриваем, что вызывает это движение, что является его причиной. У нас просто есть какое-то двигающееся тело и мы пытаемся его изучить. А на вопрос почему происходит движение, кинематика нам ответа не дает, это мы будем изучать в следующих разделах физики.
Начнем с простого вопроса – что такое «тело»? Это может быть все, что угодно – машина, самолет, мячик, капля воды, планета и т.д., то есть любой движущийся объект. Любое тело в школьной физике мы будем представлять в виде материальной точки.
Определение. Материальная точка – это тело, размерами которого мы можем пренебречь в данной задаче.
Мы просто договариваемся, что любой объект, будь то ракета или песчинка с пляжа, мы представляем в виде точки. Это необходимо для того, чтобы размеры тела не оказывали влияния на наши задачи. Так, например, автобус, двигающийся из Москвы в Санкт-Петербург, можно считать материальной точкой. Его размеры очень малы по сравнению с расстоянием между этими городами. Но движение пассажиров при выходе из автобуса уже нельзя считать материальной точкой, потому что пассажиры относительно автобуса не такие уж и маленькие. Такое школьное допущение (а в физике допущений будет много) упростит нам жизнь. При более глубоком изучении физики вы будете учитывать все эти допущения, в том числе и размеры тела, но в школе вам это, как правило, не нужно.
Задача кинематики – предсказать или описать при помощи законов физики, как этот объект будет двигаться в будущем, например, через час, если ничего не изменится.
Зачем нам это? Очень просто: если мы знаем, по каким законам двигается машина, мы легко сможем предсказать будущее и узнать, где она будет через какое-то время и с какой скоростью будет двигаться. Естественно, мы можем точно так же предсказывать движение брошенного камня и любых других объектов. Например, зная начальную скорость камня и как вы его кинули, можно предсказать, как далеко или высоко он улетит, или через сколько времени и с какой скоростью он упадет на землю.
Траектория, путь и перемещение. Что это такое и чем они отличаются?
Перед тем, как писать формулы, познакомимся еще с несколькими определениями, которые нам понадобятся в дальнейшем. Представим, что человек идет из пункта (А) в пункт (В) (см Рис.1.).
Рис.1. Траектория (зеленая линия). Путь(длина зеленой линии). Перемещение(фиолетовая стрелка)
- Траектория – линия, вдоль которой движется тело. На рис.1 показана зеленой линией.
- Путь – длина траектории. Обычно обозначается буквой (S).
- Перемещение – вектор, соединяющий начальную и конечную точки (фиолетовая линия). О том, что такое вектор, мы поговорим чуть позже. А на нашем рисунке перемещение — это длина отрезка (АВ), кроме длины перемещение еще показывает куда движется тело из начальной точки (А) в конечную (В).
Разберемся подробнее на примере. Если вы ходите по комнате с шагомером туда-сюда и вернетесь в итоге в исходную точку, то ваше перемещение будет равно 0, а путь будет расстоянием, которое вы находили, его покажет шагомер.
Что такое координаты и зачем они нужны?
Все это звучит здорово, но как нам определить положение тела в пространстве? Для этого люди придумали очень удобную штуку, которая называется координатная плоскость. С этим понятием вы должны были сталкиваться в курсе алгебры – построение графиков в осях (х) и (y). Помните, у вас были функции типа (y=x^2-3) и нужно было построить график этой функции по точкам? Вы брали какие-то значения (x) подставляли в (y=x^2-3) и получали значение (y). Потом отмечали получившуюся точку на координатной плоскости. Именно эта плоскость нас и будет интересовать.
Координаты используются людьми повсюду. Например, вся поверхность Земли расчерчена линиями, которые называются долгота и широта. Этих линий очень много, но указав пересечение некоторой долготы (37) с какой-то широтой (55), я укажу вполне конкретную точку на земной поверхности – это примерное расположение города Москва (37;55). Именно такой способ используется для определения положения любого объекта на Земле в географических картах и навигаторах – город, озеро, здание, машина, человек и т.д.
Для начала давайте рассмотрим одномерное движение – это такое движение, при котором машина может двигаться только вперед по дороге или назад, никуда свернуть она не может. (Рис.2.). Наложим на нашу дорогу ось Х, направленную вправо, как на рисунке. Теперь вся наша дорога размечена координатами. И мы можем определить положение машины, просто сказав ее координату. Начало координат мы можем выбрать как угодно, пусть оно будет в точке О. Тогда на рисунке наша машина находится в начальной координате (x_0=3). Из этой точки она может поехать влево (координата будет уменьшаться) или вправо (координата будет увеличиваться).
Расстояние можно измерять в различных единицах измерения: километры, метры, сантиметры, миллиметры и т.д. Пусть все координаты у нас измеряются в метрах, тогда можно сказать, что на рисунке машина находится на расстоянии 3 метра от точки О.
Итак, мы научились определять положение тела в пространстве при помощи координат.
Что такое скорость?
На интуитивном уровне это понятно. Но давайте попробуем вникнуть поглубже. В чем всегда измеряется скорость? В автомобиле это обычно километры в час (км/ч), измеряется при помощи спидометра. То есть спидометр машины показывает, сколько километров проедет машина за один час, если не будет менять скорость. Точно так же скорость можно измерять в метрах в секунду (м/с), километрах в секунду (км/с) и т.д. Значит, если я умножу скорость на количество часов, которые едет машина с этой скоростью, то получу расстояние, пройденное машиной за это время. Можно записать в виде известной формулы движения с постоянной скоростью:
$$S=V*t;$$
Итак, при движении с постоянной скоростью (V), можно посчитать расстояние (S), которое проходит тело за время (t).
Теперь давайте предположим, что машина двигается с постоянной скоростью 1 (м/с) влево из начальной точки с координатой (x_0=3(м)). Это означает, что машина за 1 секунду сдвинется на (S=V*t=1*1=1(м)) метр влево, то есть окажется в точке с координатой (2) (м). Через 2 секунды она пройдет расстояние (S=V*t=1*2=2(м)) и попадет в координату (1)(м), а через 6 секунд на (S=V*t=1*6=6(м)) и окажется в координате (-3)(м).
Скорость кроме величины еще имеет направление – в нашем случае это означает, что если машина едет вправо (туда же, куда направлена ось (х)), то скорость будет положительна, а если влево (в противоположную сторону направлению оси (х)), то скорость будет отрицательна.
Все, что имеет величину и направление, называется вектором. То есть скорость ни что иное, как вектор. Вектор – это ключевое понятие физики. Мы часто будем сталкиваться с величинами, у которых кроме числа есть еще и направление – ускорение, сила.
Немного отвлечемся, и обсудим, что такое вектор.
Вектор – это математический объект, у которого есть величина и направление.
В геометрии вектор – это направленный отрезок. Он имеет величину, равную длине отрезка, и направление.
Например, в случае двигающегося автомобиля принято показывать его направление движения стрелкой, а длина этой стрелки обычно указывает на величину скорости по модулю. Модуль, напомню, все отрицательные величины превращает в положительные. Чем больше длина стрелки, тем больше скорость машины. (См.Рис.3.)
В случае 1 стрелка у красной машины указывает нам на то, что автомобиль двигается вправо. Стрелка подписана сверху (vec{|V_1|}=90(км/ч)). Эта запись означает, что величина скорости красной машины по модулю равна (90(км/ч)).
Если я напишу вектор скорости красной машины без модуля, то он будет выглядеть вот так:
$$ vec{V_1}=+90(км/ч);$$
Знак плюс указывает на то, что скорость машины сонаправлена с выбранной нами осью (х).
В случае 2 синяя машина двигается влево. Ее вектор скорости запишется так:
$$vec{V_2}=-45(км/ч);$$
Знак минус указывает на то, что машина едет в противоположную сторону оси (х).
Как видите, по одной только записи вектора можно сразу сказать, куда едет машина и с какой скоростью – это очень удобно. Знак указывает на направление, а число – на величину.
Обратите внимание, что у красной машины вектор скорости длиннее, чем у синей, это означает, что красная едет быстрее. Не глядя на числа, мы можем с уверенностью сказать это, посмотрев на рисунок. Так принято обозначать. Это тоже удобно.
Равномерное движение
Любое движение с постоянной скоростью называется равномерным движением. Все, что мы рассматривали выше – это примеры равномерного движения.
Теперь мы готовы составить первые уравнения, описывающие равномерное движение. В кинематике нас будет интересовать уравнение, которое описывает положение тела в пространстве в зависимости от времени (изменение координаты тела со временем). Оно выглядит так:
$$ x(t)=x_0+V*t;$$
(x_0) – это начальная координата тела, где оно находилось в момент времени (t=0). Например, на рис.2. начальная координата автомобиля (x_0=3(м)).
(V) – это скорость, с которой двигается тело.
(t) – это время, которое прошло с момента начала движения.
(x(t)=x_{конечная}) – это конечная координата, то есть координата, где окажется тело через время (t). Я написал (x(t)), чтобы показать, что координата тела зависит от времени, ведь в разные моменты времени двигающееся тело находится в разных точках.
Разберем на примере, как работает это уравнение.
Пример 1
Автомобиль начал движение из координаты (x_0=-3(м)) со скоростью (V=5(м/с)) вправо. Где будет автомобиль через 3 секунды? Через какое время автомобиль окажется в точке с координатой (x=12(м))?
Решение: Первым делом всегда рисуем рисунок, он поможет правильно расставить знаки в уравнениях и лучше представить задачу. Чтобы ответить на поставленные вопросы, воспользуемся уравнением для координаты при равномерном движении (x(t)=x_0+V*t.)
Подставим известные величины:
$$x(t)=-3+5*t;$$
Обратите внимание, что скорость входит в уравнение со знаком (+), так как автомобиль едет по условию вправо, а это сонаправленно с осью (х). Если бы он ехал влево, то уравнение выглядело бы так: $$x(t)=-3-5t.$$
Получили уравнение, которое полностью задает движение автомобиля.
Действительно, если в это уравнение подставить некоторое время вместо (t), то можно узнать координату, где находится автомобиль в различные моменты времени.
Например, если (t=0), момент начала движения:
$$x(t=0)=-3+5*0=-3(м);$$
Логично, что в начале автомобиль находился в координате (x_0=-3). Чтобы узнать, где он будет через секунду, подставим (t=1(c)):
$$ x(t=1)=-3+5*1=-3+5=2(м);$$
Отрицательное время подставлять нет смысла, так как время не может быть отрицательным. А координата и скорость могут.
Теперь вспоминаем про задачу. Нам нужно узнать, где будет машина через 3 секунды. Просто подставляем в уравнение (t=3(с)):
$$ x(t=3)=-3+5*3=-3+15=12(м);$$
А как понять, через сколько по времени машина окажется в координате (x(t)=12(м))? Подставим:
$$12=-3+5*t;$$
Осталось решить простое линейное уравнение:
$$t=3(c).$$
Ответ: ( x(t=3)=12(м);) и (t=3(c)).
Равноускоренное движение
Если скорость не меняется, то все понятно. А что делать если скорость непостоянна?
В школе рассматривается случай, когда скорость у тела изменяется (увеличивается или уменьшается) равномерно, то есть за каждую следующую секунду скорость увеличивается/уменьшается на одну и ту же величину. Такое движение называют равноускоренным или равнозамедленным соответственно.
Пример такого движения. Представьте, что лыжник скатывается с горки из состояния покоя, при этом его скорость постоянно увеличивается, например, на 2 м/с ежесекундно. То есть:
$$V(t=0)=0(м/с);$$
$$V(t=1)=V(t=0)+2=0+2=2(м/с);$$
$$V(t=2)=V(t=1)+2=2+2=4(м/с);$$
$$V(t=3)=V(t=2)+2=4+2=6(м/с);$$
$$V(t=4)=V(t=3)+2=6+2=8(м/с);$$
Величина, на которую ежесекундно увеличивается/уменьшается скорость, называется ускорением и обозначается буквой (a).
Ускорение измеряется в (frac{м}{с^2}).
Разумеется, в жизни бывают случаи, когда скорость изменяется неравномерно. Но в школьном курсе такие задачи крайне редкие, и мы их рассматривать не будем.
Как выглядит уравнение, описывающие равноускоренное движение?
$$x(t)=x_0+V_0*t+frac{a*t^2}{2};$$
По сравнению с равномерным движением, у нас добавилось еще одно слагаемое (frac{a*t^2}{2}), которое отвечает за ускоренность/замедленность движения.
Так как скорость теперь переменная величина, для нее тоже можно записать уравнение:
$$V(t)=V_0+at;$$
- (x_0) – начальная координата тела;
- (V_0) – начальная скорость тела; скорость, с которой тело начало движение;
- (x(t)) – конечная координата;
- (V(t)) – конечная скорость;
- (a) – ускорение;
- (t) – время.
Уравнения для координаты и для скорости при равноускоренном движении являются основными уравнениями всей школьной кинематики. Если в них хорошо разобраться, то больше никаких формул учить не нужно. Все выводится из них. Я рекомендую пользоваться только этими двумя уравнениями и не забивать себе голову ничем посторонним.
Внимание! Вообще говоря, ускорение — это векторная величина, так же, как и скорость. Мы это обсуждали в начале темы. И помним, что если вектор сонаправлен с выбранным нами направлением оси координат, то ускорение положительно, а если нет, то отрицательно.
Если же вектора скорости и ускорения направлены в одну сторону, то тело ускоряется. А если в разные, то тормозит.
Посмотрите на рисунки:
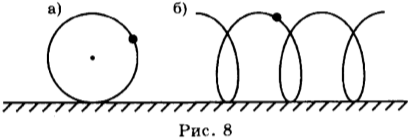
В случае а) скорость сонаправлена с осью х, значит она будет положительна. Ускорение тоже сонаправлено с осью х, значит оно положительно. А раз вектора скорости и ускорения направлены в одну сторону, то это значит, что тело ускоряется.
Случай б): скорость положительна, ускорение отрицательно. Раз вектор скорости и вектор ускорения направлены в разные стороны, значит тело замедляется.
Случай в): скорость и ускорение отрицательны, но сонаправлены – тело ускоряется.
Случай г): скорость отрицательна, ускорение положительно – тело замедляется.
Со знаками разобрались, теперь давайте разберем пример.
Пример 2
Лыжник скатывается с горки с нулевой начальной скоростью ((V_0=0(м/с))). Через 5 секунд после начала движения его скорость была (V(t=5(c))=15(м/с)). Определите с каким ускорением движется лыжник и какое расстояние он проедет за 10 секунд?
Решение:
Рисуем рисунок, чтобы представить, что происходит, и правильно расставить знаки. Ось х выбираем, как угодно. Я направил вниз.
Как мы уже обсуждали выше, у нас есть всего два уравнения – для координаты и для скорости, которые полностью описывают любое движение:
$$x(t)=x_0+V_0*t+frac{a*t^2}{2};$$
$$V(t)=V_0+at;$$
Так как нам даны начальная и конечная скорости, то разумно воспользоваться уравнением для скорости. Не забываем про знаки скорости и ускорения – оба вектора сонаправлены с выбранной мною осью х, а значит, и скорость, и ускорение будут в уравнениях положительны.
$$V(t)=V_0+at;$$
$$15=0+a*5;$$
$$a=frac{15}{5}=3frac{м}{с^2};$$
Зная ускорение, с которым движется лыжник, мы можем найти, где будет лыжник через 10 секунд, используя уравнение для координаты:
$$x(t=10)=x_0+V_0*t+frac{a*t^2}{2}=0+0*10+frac{3*10^2}{2}=150(м);$$
Таким образом, мы получили, что лыжник за 10 секунд успеет проехать (150) метров, если будет двигаться с постоянным ускорением (a=3(frac{м}{с^2})).
Работа с графиками в кинематике
В ЕГЭ по физике кинематика часто встречается в самом первом задании и, как правило, там задача с графиками. Графики помогают нам визуально описывать поведение одной некоторой величины в зависимости от другой. В школе вы должны были часто строить графики зависимостей (y) от (x). В кинематике же обычно строят графики зависимости координаты или скорости от времени. Давайте построим пару таких графиков и обсудим, как их читать.
Главное, нужно понять, что перед вами не траектория и не картинка, на которой изображено, как движется тело. Это зависимость одной физической величины от другой. На наших рисунках изображены графики зависимостей координаты и скорости от времени некоторого объекта (пусть это будет велосипедист) при различных видах движения. Например, на графике ((в)) НЕ показано движение некоторого объекта в гору, а просто координата по мере движения увеличивается.
- На графике ((а)) показана зависимость координаты велосипедиста от времени. В моменты времени (t_1) и (t_2) велосипедист находится в одной и той же координате, а значит, он стоит на месте. То есть здесь велосипедист находится в покое.
- На графике ((б)) зависимость скорости от времени. Визуально он очень похож на график ((а)), но смысл совершенно другой. Так как тут показана скорость, мы видим, что в моменты времени (t_1) и (t_2) у велосипедиста была одна и та же скорость (V_0). А раз в различные моменты времени скорость одинаковая, то это равномерное движение или движение с постоянной скоростью. Более того, еще можно сделать вывод, что велосипедист движется вправо (туда, куда направлена ось (х)), потому что скорость положительна.
- В ((в)) линейная зависимость координаты тела от времени (то есть по прямой). Замечаем, что координата с течением времени увеличивается, а это значит, что объект движется вправо. Если бы координата уменьшалась, то движение было бы влево (в противоположную сторону оси (х)). Отметим на графике несколько точек через одинаковый интервал времени. В момент времени (t_1) велосипедист был в координате (x_1), а в момент (t_2) в (x_2). За время (Delta t=t_2-t_1) он прошел расстояние (Delta x=x_2-x_1). И за каждый следующий промежуток времени (Delta t) он будет проходит одинаковое расстояние (Delta x). Это означает, что он двигается с одной и той же скоростью – равномерное движение.
- График под пунктом ((г)) показывает нам линейный рост скорости от времени. Если посмотреть, какая скорость будет у велосипедиста через одинаковые промежутки времени, то мы увидим, что она все время растет на одинаковую величину (Delta V). Если скорость растет, то значит движение ускоренное, а если растет еще и линейно, то равноускоренное. Скорость здесь положительна, значит велосипедист едет вправо (туда, куда направлена ось (х)).
- График ((д)) – это зависимость координаты от времени. Видно, что каждый следующий промежуток времени координата успевает измениться на бОльшую величину – за время (t_4-t_3) он проходит бОльшее расстояние, чем за (t_2-t_1). Значит велосипедист ускоряется. Так как координата по ходу движения уменьшается, значит он двигается влево (противоположную сторону оси (х)).
- И на последнем графике ((е)) показана зависимость скорости от времени. Видим, что скорость с течением времени уменьшается, и каждый следующий промежуток времени скорость меняется быстрее, чем на предыдущем. Так как скорость положительна, велосипедист едет вправо (туда же, куда направлена ось х). Так как скорость уменьшается неравномерно, значит на рисунке показано замедленное движение с переменным ускорением.
Движение в поле тяжести Земли
Теперь рассмотрим движение объектов в поле тяжести нашей планеты Земли. Любое тело, свободно падающее (отпущенное с некоторой высоты без начальной скорости) на Земле, будет двигаться с ускорением свободного падения (g=9.8(м/с^2)). Важно помнить, что (g) всегда направлено к центру Земли.
Внимательно посмотрите на рисунок 8: на нем изображено движение камня, брошенного вертикально вверх с некоторой начальной скоростью (V_0). Сначала он будет двигаться равнозамедленно, пока не достигнет наивысшей точки подъема (H), там остановится (скорость (V=0)), и начнет падать обратно, постепенно набирая скорость, пока не упадет обратно к вам в руку со скоростью (V_к). Для того, чтобы лучше разобраться, представьте, что вы подбросили вверх камень – он будет двигаться именно так, как мы обсудили. Таким образом, задачи на движение в поле тяжести Земли ничем не отличаются от задач равноускоренного / равнозамедленного движения по дороге, только на этот раз нам всегда известно ускорение — (g=9.8 (м/с^2)).
Давайте составим уравнения, описывающие это движение. Как всегда, их будет два – для скорости и для координаты:
$$y(t)=y_0+V_0*t-frac{g*t^2}{2};$$
$$V(t)=V_0-gt;$$
Что изменилось?
- Во-первых, координата теперь не (x), а (y) – тело двигается вдоль вертикальной оси, а ее принято обозначать за (Y).
- Вместо ускорения (a) мы теперь пишем (g) – ускорение свободного падения, оно нам известно.
Разбираемся со знаками: начальная скорость (V_0) направлена вверх (сонаправленно с осью (Y)). Ускорение во время всего движения направленно вниз к центру Земли (в противоположную сторону (Y)). Получаем, что в системе координат, выбранной на рисунке, начальная скорость будет с плюсом, а ускорение с минусом. Систему координат вы можете выбрать и другую, но тогда знаки будут меняться в соответствии с правилами расстановки знаков.
Обратите внимание!Не нужно писать отдельно уравнения для движения вверх и вниз. Уравнения сами учитывают, что тело после подъема полетит вниз.
Решим несколько задач и обсудим еще пару важных нюансов.
Пример 3
Пусть камень брошен вертикально вверх с начальной скоростью (V_0=10(м/с)). Найдите максимальную высоту подъема и время полета.
Решение
Для решения воспользуемся старым рисунком (рис.8).
Любая задача начинается с написания уравнений в общем виде:
$$y(t)=y_0+V_0*t-frac{g*t^2}{2};$$
$$V(t)=V_0-gt;$$
Выберем за начальное положение тела внизу, на Земле. А за конечное – наивысшую точку. Координата камня в наивысшей точке подъема будет — (y(t)=H), а скорость будет равна (V(t)=0 ) (смотрите на рисунок 8).
Важно! Скорость в наивысшей точке подъема будет равна 0 (камень останавливается), мы часто будем это использовать при решении подобных задач.
Начальная координата (y_0=0).
Начальная скорость (V_0=10(м/c)) из условия.
Получим уравнения:
$$H=10*t-frac{9.8*t^2}{2};$$
$$0=10-9.8*t;$$
Из уравнения для скорости можно найти время полета от Земли до наивысшей точки:
$$t=10/9.8=1.02 /,(с)$$
Подставим в первое уравнение:
$$H=10*1.02-frac{9.8*1.02^2}{2}=5.1 (м);$$
Обращаю ваше внимание, что (t) – время полета от Земли до наивысшей точки. А по условию задачи нам нужно найти время всего полета. Для этого нужно время подъема умножить на два.
Важно! Время подъема всегда равно времени падения.
$$T=2*t=1.02*2=2.04 c.$$
Ответ: (T=2.04 /,(с).)
Пример 4
Рассмотрим падение камня с некоторой высоты (H) вертикально вниз с начальной скоростью (V_0). Как тогда будут выглядеть уравнения, описывающие движение камня? (см. Рис.9.)
За конечное положение выберем Землю (y(t)=0), за начальное — высоту (y_0=H).
$$0=H-V_0*t-frac{g*t^2}{2};$$
$$-V_к=-V_0-gt;$$
Знаки расставлены с учетом направления осей координат.
Многие часто полагают, что при броске камня вниз, его конечная скорость у земли будет равна 0, ведь камень останавливается. Но это не так. К сожалению, уравнения кинематики не учитывают воздействие земли на камень, поэтому, говоря «конечная скорость», мы подразумеваем скорость за мгновение до удара о землю, и она, очевидно, не будет равна нулю.
Основные моменты
- В поле тяжести Земли вертикально брошенное тело всегда движется с ускорением свободного падения (g=9.8(м/с^2)).
- Если тело бросили с земли и оно упало обратно на землю, то время падения равно времени подъема.
- Скорость в верхней точке подъема всегда равно нулю.
Рассмотрим, как выглядят графики зависимостей координаты и скорости от времени при бросании камня.
Бросок тела вертикально вверх
Чтобы хорошо разобраться, рекомендую представить полет камня.
Скорость.При движении вверх скорость камня линейно уменьшается, он тормозит с ускорением (g), пока не остановится в верхней точке. После этого камень сразу начинает падать вниз, скорость увеличивается также с ускорением (g). Если же его бросили с земли, и он упал обратно на землю, то начальная скорость броска будет равна конечной скорости за мгновение до удара о землю. (Рис. 10 (б))
Координата. На рисунке 10 (а) изображено, как меняется координата (y(t)) в зависимости от времени полета. Обратите внимание на форму графика – это парабола. Не попадайтесь в визуальную ловушку, перед вами НЕ линия вдоль которой движется камень, в просто зависимость координаты от времени. Видно, что в начале полета тело успевает пройти за единицу времени большее расстояние, чем ближе к середине полета – координата растет сначала быстро, а потом все медленнее и медленнее, и останавливается в наивысшей точке подъема. Это связано с тем, что скорость в начале полета больше. Затем тело начинает падать, постепенно набирая скорость, и координата начинает изменяться все быстрее и быстрее, пока тело не упадет обратно на землю. (Рис. 10 (а))
Аналогичные рассуждения для броска камня вниз с нулевой начальной скоростью. (См. Рис.11)
Рис.10. Бросок камня вертикально вверх
Рис.11. Бросок тела вертикально вниз с нулевой начальной скоростью
Движение тела под углом к горизонту
До этого мы рассматривали одномерные задачи, где движение происходило вдоль одной прямой. В школьном курсе физики подавляющее большинство задач двумерны.
Рассмотрим классическую двумерную задачу кинематики – бросок камня под углом к горизонту в поле тяжести Земли. Представьте, что вы играете в игру, кто дальше кинет камень. Траектория камня будет похожа на параболу, зеленая линия. (См. Рис. 12) Именно такое движение мы и постараемся описать при помощи математики. Для этого нам понадобится двумерная система координат (XoY). Ось (X) будет отвечать за дальность полета, ось (Y) – за высоту. Точка (O) – точка начала движения. (V_0) – начальная скорость, скорость, которую мы придали камню в момент броска. Точка (А) – точка наивысшего подъема.
Рис.12. Движение под углом к горизонту
Для того, чтобы описать такое сложное двумерное движение, разобьем его на два – отдельно горизонтальное, и отдельно вертикальное движения. Мы можем представить, что наш камень в некоторый момент времени летит с вертикальной скоростью (V_y) и ускорением (a_y) вдоль оси (Y), и с горизонтальными скоростью (V_x) и ускорением (a_x) вдоль оси (X). Вместе эти два движения, если их наложить друг на друга, дают сложное двумерное движение по зеленой параболе с скоростью (V) и ускорением (a).
Скорость тела при двумерном движении в любой момент времени направлена по касательной к траектории. На рис.12. она показана красными стрелками в точках (О, А) и (В).
Рассуждая таким образом, мы можем записать уравнения для координаты и скорости по вертикали и потом по горизонтали – всего 4 уравнения, каждое из которых отвечает за свою ось.
$$y(t)=y_0+V_{0y}*t+frac{a_{y}*t^2}{2};$$
$$V_{y}(t)=V_{0y}+a_{y}*t;$$
$$x(t)=x_0+V_{0x}*t+frac{a_{x}*t^2}{2};$$
$$V_{x}(t)=V_{0x}+a_{x}*t;$$
Возникает справедливый вопрос, откуда нам взять все горизонтальные и вертикальные скорости. Есть начальная скорость (V_0), одновременно направленная по обеим осям. Нам нужно как-то рассмотреть эту скорость, как совокупность двух отдельных скоростей – горизонтальной и вертикальной. Вот для этого нам понадобится некоторый математический прием – проекции.
Проекция вектора
Пусть у нас есть некоторый вектор (vec{a}). Напоминаю, что вектор – это направленный отрезок. У него есть начало – т.А, и конец – т.В. (см.Рис.13). Опустим перпендикуляры из точек А и В на ось (Х). Получим соответственно точки (A_x) и (B_x), который называются проекциями точек (A) и (В) на ось (Х). Получившийся отрезок ({A}_{x} {B}_{x}) будет называться проекцией вектора (vec{a}) на ось (Х). Для краткости записи обозначим ({A}_{x} {B}_{x}=a_x) Аналогичным образом получим проекцию (vec{a}) на ось (Y): ({A}_{y} {B}_{y}=a_y).
Посчитаем чему равны (a_x) и (a_y), если нам известен угол и длина вектора (vec{a}). Достроим наш вектор до прямоугольного треугольника с гипотенузой (vec{a}) и катетами (a_x) и (a_y) (На рис.13. показаны зеленым).
Напоминаю, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, а косинус – прилежащего катета к гипотенузе:
$$ sin{alpha}=frac{a_y}{a};$$
$$cos{alpha}=frac{a_x}{a};$$
Из этих формул можно выразить (a_x) и (a_y):
$$a_x=a*sin{alpha};$$
$$a_y=a*cos{alpha}.$$
Таким образом, зная длину вектора и угол, мы можем легко найти его проекции. Запомните это.
Вернемся к нашей задаче. Мы остановились на том, что нужно найти горизонтальную и вертикальную составляющие начальной скорости и ускорения. Оказывается, проекции начальной скорости (V_0) на оси (X) и (Y) и будут искомыми начальными скоростями по горизонтали и вертикали. (См. Рис. 12). Оранжевым показаны проекции (V_{0x})- начальная горизонтальная скорость, и (V_{0y})-вертикальная. Заметим, что (BB_x=V_{0y}) и (AB_x=V_{0x}). (См. Рис.14.). Из треугольника (ABB_x) получаем:
Рис.14. Проекция скорости на оси х и y
$$sin{alpha}=frac{BB_x}{AB}=frac{V_{0y}}{V_0};$$
$$cos{alpha}=frac{AB_x}{AB}=frac{V_{0x}}{V_0}.$$
Отсюда
$$V_{0y}=V_0*cos{alpha};$$
$$V_{0x}=V_0*sin{alpha}.$$
Зная угол к горизонту (alpha), под которым бросили тело, и его начальную скорость, мы можем по формулам выше найти начальные скорости для горизонтального и вертикального движений.
Разберемся теперь с каким ускорением движется тело по вертикали и горизонтали. Если вы бросаете камень на Земле, то у него будет вертикальное постоянное ускорение, направленное к центру Земли – ускорение свободного падения (g=9,8(м/с^2)). (См.Рис.12).
По горизонтали ускорение, оказывается, будет равно нулю. Другими словами, по горизонтали камень будет лететь равномерно, с постоянной скоростью. Это связано с тем, что в горизонтальном направлении на тело во время полета не действует никаких сил, то есть ничто не может изменить его скорость. А по вертикали действует сила притяжения Земли, которая вызывает ускорение свободного падения.
Можно просто запомнить, что по вертикали ускорение всегда (g), а по горизонтали ускорение 0.
Используем все наши рассуждения для записи системы уравнений, описывающих движение под углом к горизонту:
$$y(t)=y_0+V_{0y}*t+frac{a_{y}*t^2}{2};$$
$$V_{y}(t)=V_{0y}+a_{y}*t;$$
$$x(t)=x_0+V_{0x}*t+frac{a_{x}*t^2}{2};$$
$$V_{x}(t)=V_{0x}+a_{x}*t;$$
Подставим (V_{0x}=V_0*sin{alpha},, V_{0y}=V_0*cos{alpha},, a_x=0,,a_y=g):
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Знания и понимания этих четырех уравнений достаточно, чтобы решить любую школьную задачу по кинематике. Часто в школах дают большое количество формул, связывающих расстояние, скорость и ускорение и т.п. Если вы разобрались, как были получены уравнения выше, то в этих формулах нет необходимости. Они легко выводятся.
Основные моменты движения тела, брошенного под углом к горизонту:
- Сложное двумерное движение разбиваем на два: горизонтальное и вертикальное.
- Ускорение по вертикали равно ускорению свободного падения и всегда направлено вниз, к центру Земли. Ускорение по горизонтали в отсутствии сопротивления воздуха равно 0. По горизонтали движение равномерное.
- Скорость полета тела всегда направлена по касательной к траектории полета. Скорость по горизонтали и вертикали можно найти соответственно из формул:
$$V_x=V*cos{alpha};$$
$$V_y=V*sin{alpha};$$ - Дальностью полета называют расстояние по горизонтали между точкой броска и точкой падения камня на землю. На рис.12. дальность показана буквой (S).
- Время подъема равно времени падения. При условии, что тело бросили с Земли и оно упало обратно на Землю.
- Скорость по вертикали в наивысшей точке подъема равна 0. Этот факт часто используют для нахождения времени подъема до наивысшей точки из уравнения для скорости по оси (y):
$$0=V_{0y}-gt.$$
Разберем несколько задач на движение под углом к горизонту.
Пример 5
Камень бросили под углом (alpha=30^о) к горизонту с начальной скоростью (V_0=20(м/с)). Найти дальность его полета. И максимальную высоту подъема.
Бросок камня под углом к горизонту
Решение
Первым делом выпишем все уравнения в общем виде:
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Начальная скорость направлена вверх и вправо, поэтому в уравнениях она будет со знаком плюс. Ускорение свободного падения направлено вниз – ставим минус.
Выбираем начальное и конечное положение тела, для которого будем записывать уравнение. Логично, что начальная точка – это момент броска с координатами (0;0), а за конечную выберем т.А ((S/2;H)) – наивысшую точку подъема, так как мы знаем, что скорость там по оси (y): (V_y=0).
Подставим координаты и известные величины в систему уравнений:
$$H=20*sin{30}*t-frac{9.8*t^2}{2};$$
$$0= 20*sin{30}-9.8*t;$$
$$S= 20*cos{30}*t;$$
$$V_{x}= 20*cos{30}.$$
Из уравнения для скорости по (y) (2-е уравнение) можно найти (t) – время подъема тела до наивысшей точки.
$$t=frac{20*sin{30}}{9.8}=1.02 (c);$$
Чтобы найти максимальную высоту подъема, подставим найденное время в первое уравнение для координаты (y). Камень будет в наивысшей точке через половину времени полета, потому что время подъема равно времени падения:
$$H=20*sin{30}*1.02-frac{9.8*1.02^2}{2}=5.1(м);$$
Полное время полета:
$$T=2*t=2.04 (c);$$
Найдем дальность, используя уравнения для координаты (x):
$$S= 20*cos{30}*2.04=35.3(м);$$
Мы решили задачу. Рассчитали высоту (H) и дальность полета камня (S), если бросить его под углом в (30^0) и с начальной скоростью (V_0=20(м/с)). Весь полет займет чуть больше 2-х секунд.
Ответ:(S=35.3(м)) и (H=5.1(м)) и (T=2.04(c)).
Пример 6
Камень бросили с балкона с высоты (y_0=20(м)), придав ему начальную скорость (V_0=10(м/с)) и под углом к горизонту (60^0).Найти дальность и максимальную высоту полета.
Бросок камня под углом к горизонту с некоторой высоты
Решение:
Запишем уравнения в общем виде:
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Подставим все данные в уравнения для координат, согласно условию задачи. За начальную точку выберем точку броска (x_0=0, . y_0=H_0), а за конечную точку падения (x(t)=S, . y(t)=0):
$$0=H_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$S= V_0*cos{alpha}*t;$$
С учетом данных в условии задачи
$$0=20+10*sin{60^0}*t-frac{g*t^2}{2};$$
$$S= 10*cos{60^o}*t;$$
Выразим время всего полета
$$20+5sqrt{3}*t-4.9*t^2=0;$$
Решаем через дискриминант квадратное уравнение и находим время всего полета
$$t=3.04(с);$$
Чтобы найти дальность полета, подставим найденное время в уравнение для координаты (х)
$$S= V_0*cos{alpha}*t;$$
$$S= 10*cos{60^0}*3.04=15.2(м);$$
Обращаю внимание, что в данной задаче время подъема не равно времени падения, так как задача несимметричная – камень бросают с балкона, а падает он на землю.
Для нахождения максимальной высоты подъема воспользуемся тем, что скорость по (Y) в верхней точке траектории равна (0), и найдем время полета до этой точки:
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$0= 10*sin{60^0}-g*t;$$
$$t=0.88(c);$$
Подставим найденное время в уравнение для координаты (у):
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$H=20+10*sin{60^0}*0.88-frac{9.8*0.88^2}{2}=28.65-3.79=24.86(м).$$
Ответ: (S=15.2(м)) и (H=24.86(м)).
Пример 7
Тело бросили ГОРИЗОНТАЛЬНО с балкона высотой 20 метров ((H_0=20м)) с начальной скоростью (V_0=10м/с). Найти под каким углом к горизонту будет направлена скорость тела через (t=0.5 с), время всего полета и дальность.
Рис.15. Бросок тела с некоторой высоты горизонтально
Как обычно, начинаем решение задачи с написания всех уравнений в общем виде:
$$y(t)=y_0+V_{0Y}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_{0Y}-g*t;$$
$$x(t)=x_0+ V_{0X}*t;$$
$$V_{x}(t)= V_{0X}.$$
Найдем время всего полета и дальность. Начальная точка – это точка броска с координатами ((0;H_0)), конечная точка – падение на Землю ((L;0)).
Обратите внимание, что начальная скорость тела горизонтальна, а значит у нас нет вертикальной составляющей начальной скорости – мы не сообщаем телу начальную скорость по (Y). Поэтому (V_{0y}=0), а (V_{0x}=V_0).
Уравнение по (Y) принимает вид:
$$0=H_0-frac{g*t^2}{2};$$
$$0=20-frac{9.8*t^2}{2};$$
Находим время всего полета
$$t=sqrt{frac{2*20}{9.8}}=2,02(c);$$
Чтобы найти дальность, подставим найденное время в уравнение для координаты (х)
$$L=V_0*t=10*2.02=20.2(м);$$
И осталось ответить на последний вопрос – под каким углом к горизонту будет направлена скорость через (t=0,5(c)). Предположим, что тело в этот момент будет находиться в точке (А) (См.Рис.15). Скорость тела в любой момент времени направлена по касательной к траектории — (V_A).
Для решения этой задачи нам понадобится найти проекции (V_A) на оси (X) и (Y), на рисунке они показаны оранжевым цветом — (V_{AX};. V_{AY}).
Так как движение по горизонтали равномерное, то скорость по (X) в любой момент времени будет постоянна и равна начальной скорости (V_0).
Для нахождения (V_{AY}) запишем уравнение для скорости по (Y)
$$V_{y}(t)= V_{0Y}-g*t;$$
$$V_{0Y}=0;$$
$$V_{y}(t=0.5c)=-g*t;$$
$$V_{y}(t=0.5c)=-9.8*0.5=-4.9м/с;$$
Скорость получилась отрицательная, потому что она направлена вниз – в противоположную сторону оси (Y).
Рис.16. Проекции скорости в произвольной точки траектории
Зная проекции скорости (V_{AX}) и (V_{AY}) мы можем найти угол, под которым направлена скорость. Посмотрите на рис.16. Так как (ABCD) прямоугольник, то (AB=CD=V_{AX}). Тогда из треугольника (ADC) можно найти тангенс (alpha)
$$tg{alpha}=frac{V_{AY}}{V_{AX}}=frac{4.9}{10}=0.5;$$
$$alpha=27^0.$$
Ответ: (t=2.02(c);, L=20.2(м);, alpha=27^0.)
I. Механика
Тестирование онлайн
Положение предметов в пространстве. Тело отсчета.
Предлагаю игру: выбрать предмет в комнате и описать его местонахождение. Выполнить это так, чтобы угадывающий не смог ошибиться. Вышло? А что выйдет из описания, если другие тела не использовать? Останутся выражения: «слева от…», «над …» и подобное. Положение тела можно задать только относительно какого-нибудь другого тела.
Местонахождение клада: «Стань у восточного угла крайнего дома села лицом на север и, пройдя 120 шагов, повернись лицом на восток и пройди 200 шагов. В этом месте вырой яму в 10 локтей и найдешь 100 слитков золота». Клад найти невозможно, иначе его давно откопали бы. Почему? Тело, относительно которого совершается описание не определено, неизвестно в каком селе находится тот самый дом. Необходимо точно определиться с телом, которое возьмется за основу нашего будущего описания. Такое тело в физике называется телом отсчета. Его можно выбрать произвольно. Например, попробуйте выбрать два различных тела отсчета и относительно их описать местонахождение компьютера в комнате. Выйдет два непохожих друг на друга описания.
Система координат
Рассмотрим картинку. Где находится дерево, относительно велосипедиста I, велосипедиста II и нас, смотрящих на монитор?
Относительно тела отсчета — велосипедист I — дерево находится справа, относительно тела отсчета — велосипедист II — дерево находится слева, относительно нас оно впереди. Одно и то же тело — дерево, находящееся постоянно в одном и том же месте, одновременно и «слева», и «справа» и «впереди». Проблема не только в том, что выбраны различные тела отсчета. Рассмотрим его расположение относительно велосипедиста I.
На этом рисунке дерево справа от велосипедиста I
На этом рисунке дерево слева от велосипедиста I
Дерево и велосипедист не меняли своего месторасположения в пространстве, однако дерево одновременно может быть «слева» и «справа». Для того, чтобы избавиться от неоднозначности описания самого направления, выберем определенное направление за положительное, противоположное выбранному будет отрицательным. Выбранное направление обозначают осью со стрелкой, стрелка указывает положительное направление. В нашем примере выберем и обозначим два направления. Слева направо (ось, по которой движется велосипедист), и от нас внутрь монитора к дереву — это второе положительное направление. Если первое, выбранное нами направление, обозначить за X, второе — за Y, получим двухмерную систему координат.
Относительно нас велосипедист движется в отрицательном направлении по оси X, дерево находится в положительном направлении по оси Y
Относительно нас велосипедист движется в положительном направлении по оси X, дерево находится в положительном направлении по оси Y
А теперь определите, какой предмет в комнате находится в 2 метрах в положительном направлении по оси X (справа от вас), и в 3 метрах в отрицательном направлении по оси Y (позади вас). (2;-3) — координаты этого тела. Первой цифрой «2» принято обозначать расположение по оси X, вторая цифра «-3» указывает расположение по оси Y. Она отрицательная, потому что по оси Y находится не в стороне дерева, а в противоположной стороне. После того, как выбрано тело отсчета и направления, месторасположение любого предмета будет описано однозначно. Если вы повернетесь спиной к монитору, справа и позади вас будет уже другой предмет, но и координаты у него будут другие (-2;3). Таким образом, координаты точно и однозначно определяют расположение предмета.
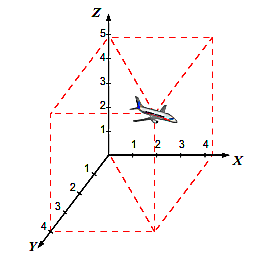
Пространство, в котором мы живем, — пространство трех измерений, как говорят, трехмерное пространство. Кроме того, что тело может находится «справа» («слева»), «впереди» («позади»), оно может быть еще «выше» или «ниже» вас. Это третье направление — принято обозначать его осью Z
Можно ли выбирать не такие направления осей? Можно. Но нельзя менять их направления в течение решения, например, одной задачи. Можно ли выбрать другие названия осей? Можно, но вы рискуете тем, что вас не поймут другие, лучше так не поступать. Можно ли поменять местами ось X с осью Y? Можно, но не путайтесь в координатах: (x;y).
При прямолинейном движении тела для определения его положения достаточно одной координатной оси.
Для описания движения на плоскости используется прямоугольная система координат, состоящая из двух взаимно перпендикулярных осей (декартовая система координат).
С помощью трехмерной системы координат можно определить положение тела в пространстве.
Подробнее о системе координат и проекциях
Система отсчета
Каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Определять его положение уже умеем. Если с течением времени положение тела не изменяется, то оно покоится. Если же с течением времени положение тела изменяется, то это означает, что тело движется. Все в мире происходит где-то и когда-то: в пространстве (где?) и во времени (когда?). Если к телу отсчета, системе координат, которые определяют положение тела, добавить способ измерения времени — часы, получим систему отсчета. При помощи которой можно оценить движется или покоится тело.
Относительность движения
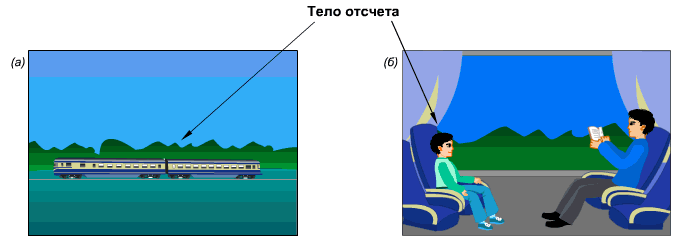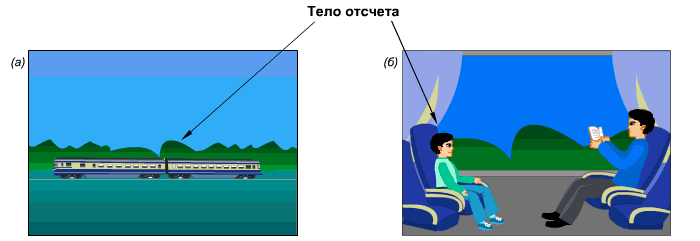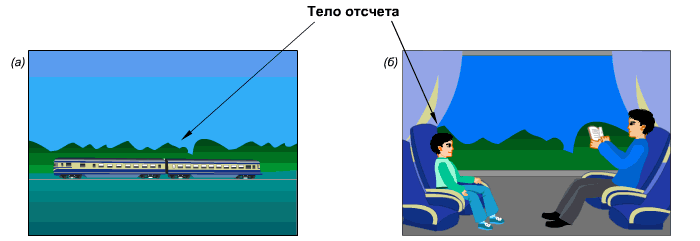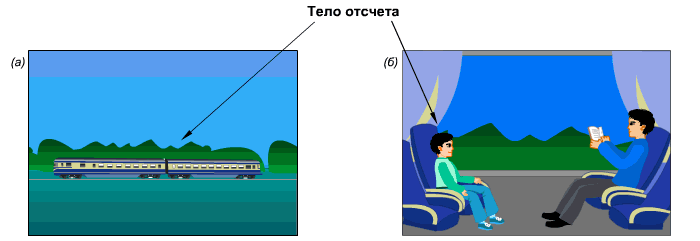
Космонавт вышел в открытый космос. В состоянии покоя или движения он находится? Если рассматривать его относительно друга космонавта, находящегося рядом, он будет покоиться. А если относительно наблюдателя на Земле, космонавт движется с огромной скоростью. Аналогично с поездкой в поезде. Относительно людей в поезде вы неподвижно сидите и читаете книгу. Но относительно людей, которые остались дома, вы двигаетесь со скоростью поезда.
Примеры выбора тела отсчета, относительно которого на рисунке а) поезд движется (относительно деревьев), на рисунке б) поезд покоится относительно мальчика.
Сидя в вагоне, ожидаем отправления. В окне наблюдаем за электричкой на параллельном пути. Когда она начинает двигаться, трудно определить кто движется — наш вагон или электричка за окном. Для того, чтобы определиться, необходимо оценить движемся ли мы относительно других неподвижных предметов за окном. Мы оцениваем состояние нашего вагона относительно различных систем отсчета.
Изменение перемещения и скорости в разных системах отсчета
Перемещение и скорость изменяются при переходе из одной системы отсчета в другую.
Скорость человека относительно земли (неподвижной системы отсчета) различная в первом и втором случаях.
Правило сложения скоростей: Скорость тела относительно неподвижной системы отсчета — это векторная сумма скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной.
Аналогично вектора перемещения. Правило сложения перемещений: Перемещение тела относительно неподвижной системы отсчета — это векторная сумма перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной.
Пусть человек идет по вагону по направлению (или против) движения поезда. Человек — тело. Земля — неподвижная система отсчета. Вагон — подвижная система отсчета.
|
Вектора подвижной со и тела относительно подвижной со совпадают по направлению |
Вектора подвижной со и тела относительно подвижной со противоположные по направлению |
Изменение траектории в разных системах отсчета
Траектория движения тела относительна. Например, рассмотрим пропеллер вертолета, спускающегося на Землю. Точка на пропеллере описывает окружность в системе отсчета, связанного с вертолетом. Траектория движения этой точки в системе отсчета, связанной с Землей, представляет собой винтовую линию.
Поступательное движение
Движение тела — это изменение его положения в пространстве относительно других тел с течением времени. Каждое тело имеет определенные размеры, иногда разные точки тела находятся в разных местах пространства. Как же определить положение всех точек тела?
НО! Иногда нет необходимости указывать положение каждой точки тела. Рассмотрим подобные случаи. Например, это не нужно делать, когда все точки тела движутся одинаково.
Одинаково движутся все токи чемодана, машины.
Движение тела, при котором все его точки движутся одинаково, называется поступательным
Материальная точка
Не нужно описывать движение каждой точки тела и тогда, когда его размеры очень малы по сравнению с расстоянием, которое оно проходит. Например, корабль, преодолевающий океан. Астрономы при описании движения планет и небесных тел друг относительно друга не учитывают их размеров и их собственное движение. Несмотря на то, что, например, Земля громадная, относительно расстояния до Солнца она ничтожно мала.
Нет необходимости рассматривать движение каждой точки тела, когда они не влияют на движение тела всего целиком. Такое тело можно представлять точкой. Все вещество тела как бы сосредотачиваем в точку. Получаем модель тела, без размеров, но она имеет массу. Это и есть материальная точка.
Одно и то же тело при одних его движениях можно считать материальной точкой, при других — нельзя. Например, когда мальчик идет из дома в школу и при этом проходит расстояние 1 км, то в этом движении его можно считать материальной точкой. Но когда тот же мальчик выполняет зарядку, то точкой его считать уже нельзя.
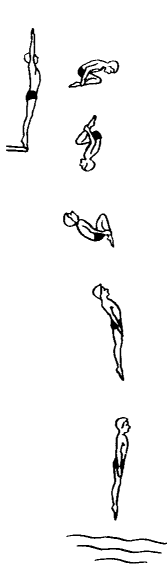
Рассмотрим движущихся спортсменов
В этом случае можно спортсмена моделировать материальной точкой
В случае прыжка спортсмена в воду (рисунок справа) нельзя моделировать его в точку, так как от любого положения рук и ног зависит движение всего тела
Главное запомнить
1) Положение тела в пространстве определяется относительно тела отсчета;
2) Необходимо задать оси (их направления), т.е. систему координат, которая определяет координаты тела;
3) Движение тела определяется относительно системы отсчета;
4) В разных системах отсчета скорость тела может быть разной;
5) Что такое материальная точка
Видеодемонстрация относительности движения
Сложение скоростей
Упражнения
Мимо стоящего велосипедиста проезжает колонна движущихся с одинаковой скоростью машин. Движется ли каждая из машин относительно велосипедиста? Движется ли машина относительно другой машин? Движется ли велосипедист относительно машины?
Из центра горизонтально расположенного вращающегося диска по его поверхности пущен шарик. Каковы траектории шарика относительно Земли и диска?
Чему равно перемещение какой-либо точки, находящейся на краю диска радиусом R при его повороте относительно подставки на 600? на 1800? Решить в системах отсчета, связанных с подставкой и диском.
Почему дождевые капли в безветренную погоду оставляют наклонные прямые полосы на стеклах равномерно движущегося поезда?
Каким образом можно определить скорость бега, если тренироваться на беговой дорожке со сломанным автоматическим определением скорости? Ведь относительно стен зала не пробегаешь ни одного метра.
Эскалатор метро движется вверх со скоростью 0,75 м/с. а) С какой скоростью и в каком направлении надо идти по эскалатору, чтобы быть все время на уровне одного из фонарей освещения туннеля? б) С какой скоростью относительно поднимающейся лестницы надо было бы передвигаться, чтобы опускаться вниз со скоростью пассажиров, неподвижно стоящих на другой опускающейся лестнице?
Какую систему координат следует выбрать (одномерную, двухмерную, трехмерную) для определения положения таких тел:
1. трактор в поле;
2. поезд;
3. люстра в комнате;
4. лифт;
5. подводная лодка;
6. шахматная фигура
Наверняка каждый из вас неоднократно договаривался с другом, родителями или учителем о встрече. При этом всегда возникал вопрос: где встретиться? Хорошо, если намеченное место встречи было известно, и вы могли его назвать или показать. Но как быть, если вы договариваетесь о месте встречи по телефону или сообщаете о нем в письме?
Обратимся за примером к одному из древних авторов, который сообщал в послании другу, как найти зарытый в землю клад. «Найдя одинокий дуб перед воротами моего замка, прижмись к его стволу спиной. Обратив лицо к восходящему Солнцу, отсчитай десять шагов вперед, и ты окажешься над искомым». При использовании подобного наставления трудно не найти спрятанный сундук с сокровищами. Ясно, что найти клад было бы значительно труднее, если бы в послании говорилось, что надо отсчитать десять шагов от замка, а не от достаточно малого по размерам конкретного места — дуба.
Вдумаемся, что использовал автор послания. Во-первых, он указал точку на поверхности Земли перед своим замком (дуб), от которого надо начинать поиск. Физики говорят, что было указано тело отсчета и начало отсчета (земля вокруг замка и дуб соответственно). Во-вторых, он указал направление (восходящее Солнце, т. е. восток) и расстояние от начала отсчета до искомого места вдоль этого направления, выраженное в единицах длины — шагах. Говоря иначе, он ввел ось координат, связанную с телом отсчета.
Телом отсчета называют тело, относительно которого определяют положение остальных тел. Некоторую точку этого тела называют началом отсчета и присваивают этой точке координату нуль. Из начала отсчета в нужном направлении проводят координатную ось. Отметим, что расстояние между любыми точками тела отсчета должно быть неизменным.
Обратим внимание, что ось координат имеет:
- начало отсчета (в данном случае — дуб);
- положительное направление (восходящее Солнце — восток);
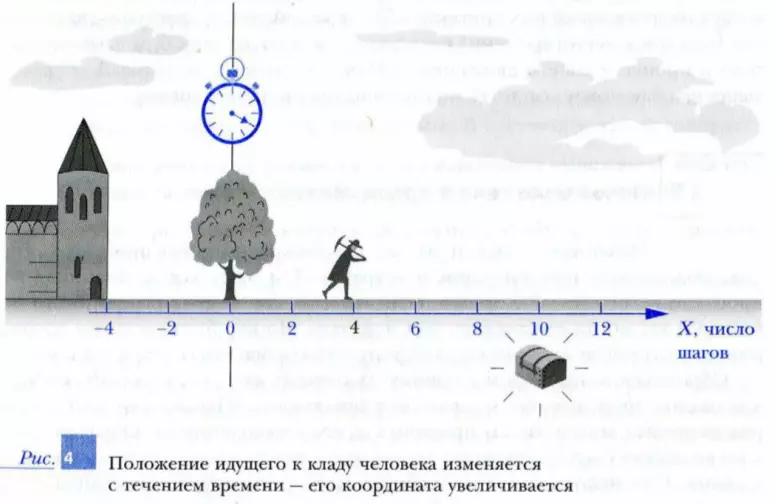
- нанесенные на нее метки, соответствующие выбранной единице длины (шаг).
Теперь любой точке на этой оси можно приписать конкретное число, равное расстоянию в заданных единицах длины (шагах) от начала отсчета до этой точки. Это число называют координатой точки по этой оси. Например, точка, где находится клад (рис. 4), имеет координату по этой оси xкл = 10 шагов. А точка, в которой находится изображенный на рисунке человек, имеет координату xч = 4 шага. Координата дуба xд = 0. Отметим еще раз, что точку с нулевой координатой называют началом отсчета.
Координаты точек, которые находятся на оси от начала отсчета в направлении, противоположном положительному, считают отрицательными. Поэтому координата стены у ворот замка на рис. 4 имеет отрицательное значение xс = -4 шага.
Подведем итог нашим рассуждениям. Чтобы описать положение конкретной точки (или тела, замененного этой точкой), следует:
- выбрать тело отсчета, относительно которого будем проводить дальнейшее описание;
- ввести ось координат, связанную с этим телом отсчета, начало отсчета (ось имеет направление, начало отсчета и единицу длины);
- указать координату интересующей нас точки.
Отметим, что для нахождения искомого места необходимо использовать все три понятия: тело отсчета, координатная ось и координата. Скажем, если кто-то из вас предложит другу встретиться завтра в точке с координатой x = 18, не указав ни тела отсчета, ни оси, ни единицы длины вдоль этой оси, то встречи, скорее всего, не будет. Однако если вы договоритесь с одноклассниками встретиться в 10 метрах на север от памятника А. С. Пушкину на Тверском бульваре, например, 18 марта этого года в 10 часов утра, то, будете уверены, никто не заблудится.
Обратим внимание на то, что в последнем условии помимо места указано время встречи. Любое устройство, предназначенное для отсчета времени, называют часами.
Часы — это любое устройство для отсчета времени.
Пользуясь часами, можно ответить и на другой интересующий нас вопрос — когда? То есть в какой момент времени должна, например, произойти встреча в заданной точке пространства.
Можно сказать, что, взяв часы, мы тем самым вводим еще одну ось — ось времени, на которой, как на секундомере, нанесены метки, соответствующие выбранной единице времени, например секунде.
Точно так же, как на оси координат, на оси времени должно быть отмечено начало отсчета — нулевая точка. Это может быть, например, момент включения секундомера.
Совокупность тела отсчета, с которым связана ось координат, и часов называют системой отсчета.
Имея систему отсчета, мы можем ответить на вопросы: «Где и когда находится интересующее нас тело?».
Итоги
Для того чтобы описать положение данного тела в пространстве, необходимо:
- выбрать тело отсчета и начало отсчета на нем;
- связать с ним координатную ось, проходящую через начало отсчета в нужном направлении, и указать единицу длины.
При этом расстояние от начала отсчета до данного тела, выраженное в выбранных единицах длины и взятое с соответствующим знаком, называют координатой этого тела.
Поступив так, мы будем говорить, что описали положение данного тела относительно выбранного тела отсчета.
Если мы выберем в качестве тела отсчета другое тело или другую ось координат, то и координат данного тела может стать другой.
Совокупность тела отсчета, с которым связана ось координат, и часов называют системой отсчета.
Вопросы
- Что такое ось координат, координата точки, тело отсчета, часы?
- Что такое система отсчета?
- Что и в какой последовательности нужно сделать для того, чтобы описать положение тела в пространстве?
- Расскажите, как выбирают тело отсчета и начало отсчета. Объясните, почему в качестве тела отсчета нельзя выбрать точечное тело. Перед ответом на последний вопрос скажите, какое минимальное число точек определяет положение прямой линии.
Упражнения
- Опишите положение (найдите координаты): а) дуба; б) человека; в) клада, изображенных на рис. 4, если в качестве начала отсчета выбрать: стену у ворот замка; клад.
- Опишите систему отсчета, позволяющую задать на местности координаты (место) и время встречи одноклассников. Для выполнения упражнения используйте компас, часы, рулетку. Какие физические модели вы будете применять при выполнении упражнения?
Положение тела
или точки можно задать только относительно
какого-нибудь другого тела, которое
называют телом
отсчета.
Тело отсчета можно выбрать произвольно.
Им может быть дом, в котором мы живем,
вагон поезда, в котором мы едем, и т.д.
Телами отсчета могут служить тела,
звезды, Земля, Солнце.
Когда тело отсчета
выбрано, через какую-нибудь его точку
проводят оси координат, и положение
любой точки в пространстве описывают
ее координатами.
Для определения
положения тела в пространстве используется
система координат.
При прямолинейном
движении тела для определения его
положения достаточно одной координатной
оси. Например, если автомобиль движется
по прямой дороге, то его движение
описывается одной координатой.
Для описания
движения на плоскости используется
прямоугольная система из двух взаимно
перпендикулярных осей, такая система
еще называется декартовой
системой координат. Например,
когда автомобиль едет из одного города
в другой, то его движение, как правило,
является криволинейным и описывается
двумя координатами.
Движение тела в
поле тяжести Земли нельзя описать двумя
координатами. В этом случае используют
трехмерную систему координат, с помощью
которой можно определить положение
тела в пространстве.
Итак, положение
точки на линии, плоскости и в пространстве
определяют соответственно одним, двумя
или тремя числами – координатами.
Пространство, в котором мы живем, —
пространство трех измерений, трехмерное
пространство.
Но если необходимо
определить путь, который прошло тело
за определенный промежуток времени, то
нам потребуется еще приборы для измерения
времени – часы. Система
координат,
связанная с телом
отсчета, и
часы
для отсчета времени образуют систему
отсчета,
позволяющую определять положение
движущегося тела в любой момент времени.
1.4 Перемещение
В процессе
механического движения положение тела
в пространстве изменяется. Раньше мы
использовали понятие пути
– длины траектории, пройденной телом
за время наблюдения.
Путь обозначают буквой
l,
единицей пути в СИ является метр (1м).
Путь является величиной скалярной,
т.е. не имеющей направления.
Однако для решения
практических задач недостаточно задать
только путь. Например, из лыжной базы в
15 км к северу от города вышел лыжник и
за 2 ч прошел 15 км. Как определить куда
он пришел? Он мог дойти до города – путь
Б, а мог и вернуться обратно – путь А. В
любом случае путь будет равен 15 км, но
положение в пространстве будет разным.
Чтобы избежать
такой неопределенности, вводиться
понятие перемещения.
Перемещение – направленный отрезок,
соединяющий начальное и конечное
положение тела.
Таким образом, перемещение – величина
векторная, то есть имеющая направление.
Перемещение обозначается символом
, единицей перемещения, как пути, является
метр.
В том случае, когда
вектор перемещения лыжника был направлен
на юг, то модуль перемещения равен 15 км,
и мы можем сказать, что лыжник дошел до
города. А в случае, когда лыжник пришел
обратно на базу, его перемещение равно
нулю.
Изменение положения
тела в пространстве можно изобразить
графически, используя понятие перемещения.
Однако в большинстве случаев необходимо
вычислить
положение этого тела, то есть определить
его координаты. При этом вычисления
проводят не с координатами векторов
как таковыми, а с их проекциями
на оси координат и модулями
векторов,
то есть с величинами, представляющими
собой положительные или отрицательные
числа.
Особенно важен
частный случай проектирования вектора
на два взаимноперпендикулярных
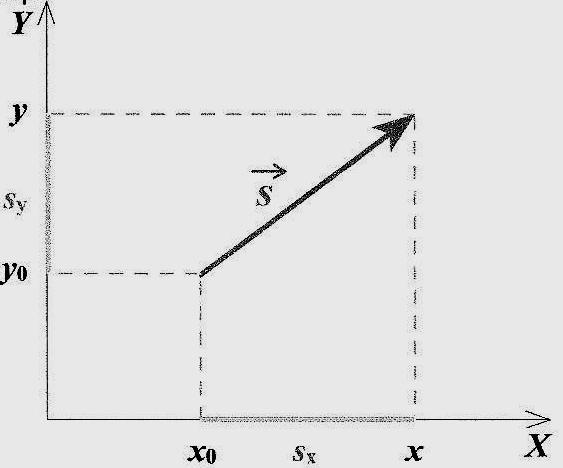
направления. Здесь (x0,y0)
и (x,
y)
— координаты начала и конца вектора.
Проекция вектора
равна разности координат конца и начала
вектора:
Sx
= x
– x0
Sy
= y
– y0
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Механическое движение. Траектория. Путь. Перемещение
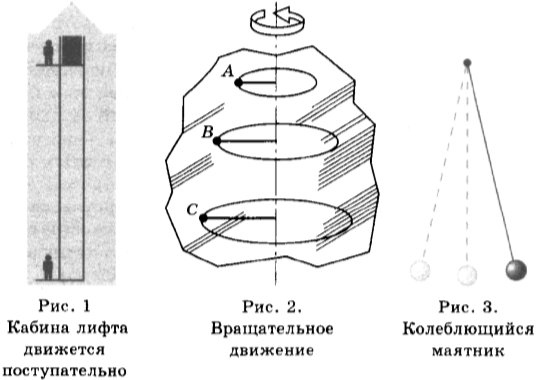
1. Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. Существуют различные виды механического движения. Если все точки тела движутся одинаково и любая прямая, проведённая в теле, при его движении остаётся параллельной самой себе, то такое движение называется поступательным (рис. 1).
Точки вращающегося колеса описывают окружности относительно оси этого колеса. Колесо как целое и все его точки совершают вращательное движение (рис. 2).
Если тело, например шарик, подвешенный на нити, отклоняется от вертикального положения то в одну, то в другую сторону, то его движение является колебательным (рис. 3).
2. В определение понятия механического движения входят слова «относительно других тел». Они означают, что данное тело может покоиться относительно одних тел и двигаться относительно других тел. Так, пассажир, сидящий в автобусе, движущемся относительно зданий, тоже движется относительно них, но покоится относительно автобуса. Плот, плывущий по течению реки, неподвижен относительно воды, но движется относительно берега (рис. 4). Таким образом, говоря о механическом движении тела, необходимо указывать тело, относительно которого данное тело движется или покоится. Такое тело называют телом отсчёта. В приведённом примере с движущимся автобусом в качестве тела отсчёта может быть выбран какой-либо дом, или дерево, или столб около автобусной остановки.
Для определения положения тела в пространстве вводят систему координат, которую связывают с телом отсчёта. При рассмотрении движения тела вдоль прямой линии используют одномерную систему координат, т.е. с телом отсчёта связывают одну координатную ось, например ось ОХ (рис. 5).
Если тело движется по криволинейной траектории, то система координат будет уже двухмерной, поскольку положение тела характеризуют две координаты X и Y (рис. 6). Таким движением является, например, движение мяча от удара футболиста или стрелы, выпущенной из лука.
Если рассматривается движение тела в пространстве, например движение летящего самолёта, то система координат, связанная с телом отсчёта, будет состоять из трёх взаимно перпендикулярных координатных осей (OX, OY и OZ) (рис. 7).
Поскольку при движении тела его положение в пространстве, т.е. его координаты, изменяются с течением времени, то необходим прибор (часы), который позволяет измерять время и определить, какому моменту времени соответствует та или иная координата.
Таким образом, для определения положения тела в пространстве и изменения этого положения с течением времени необходимы тело отсчёта, связанная с ним система координат и способ измерения времени, т.е. часы, которые все вместе представляют собой систему отсчёта (рис. 7).
3. Изучить движение тела — это значит определить, как изменяется его положение, т.е. координата, с течением времени.
Если известно, как изменяется координата со временем, можно определить положение (координату) тела в любой момент времени.
Основная задача механики состоит в определении положения (координаты) тела в любой момент времени.
Чтобы указать, как изменяется положение тела с течением времени, нужно установить связь между величинами, характеризующими это движение, т.е. найти математическое описание движения или, иными словами, записать уравнение движения тела.
Раздел механики, изучающий способы описания движения тел, называют кинематикой.
4. Любое движущееся тело имеет определённые размеры, и его различные части занимают разные положения в пространстве. Возникает вопрос, как в таком случае определить положение тела в пространстве. В делом ряде случаев нет необходимости указывать положение каждой точки тела и для каждой точки записывать уравнение движения.
Так, поскольку при поступательном движении все точки тела движутся одинаково, то нет необходимости описывать движение каждой точки тела.
Движение каждой точки тела не нужно описывать и при решении таких задач, когда размерами тела можно пренебречь. Например, если нас интересует, с какой скоростью пловец проплывает свою дистанцию, то рассматривать движение каждой точки пловца нет необходимости. Если же необходимо определить действующую на мяч выталкивающую силу, то пренебречь размерами пловца уже нельзя. Если мы хотим вычислить время движения космического корабля от Земли до космической станции, то корабль можно считать единым целым и представить в виде некоторой точки. Если же рассчитывается режим стыковки корабля со станцией, то, представив корабль в виде точки, решить эту задачу невозможно.
Таким образом, для решения ряда задач, связанных с движением тел, вводят понятие материальной точки.
Материальной точкой называют тело, размерами которого можно пренебречь в условиях данной задачи.
В приведённых выше примерах материальной точкой можно считать пловца при расчёте скорости его движения, космический корабль при определении времени его движения.
Материальная точка — это модель реальных объектов, реальных тел. Считая тело материальной точкой, мы отвлекаемся от несущественных для решения конкретной задачи признаков, в частности, от размеров тела.
5. При перемещении тело последовательно проходит точки пространства, соединив которые, можно получить линию. Эта линия, вдоль которой движется тело, называется траекторией. Траектория может быть видимой или невидимой. Видимую траекторию описывают трамвай при движении по рельсам, лыжник, скользя по лыжне, мел, которым пишут на доске. Траектория летящего самолёта в большинстве случаев невидима, невидимой является траектория ползущего насекомого.
Траектория движения тела относительна: её форма зависит от выбора системы отсчёта. Так, траекторией точек обода колеса велосипеда, движущегося по прямой дороге, относительно оси колеса является окружность, а относительно Земли — винтовая линия (рис. 8 а, б).
6. Одной из характеристик механического движения является путь, пройденный телом. Путём называют физическую величину, равную расстоянию, пройденному телом вдоль траектории.
Если известны траектория тела, его начальное положение и пройденный им путь за время ( t ), то можно найти положение тела в момент времени ( t ). (рис. 9)
Путь обозначают буквой ( l ) (иногда ( s )), основная единица пути 1 м: ( [,mathrm{l},] )= 1 м. Кратная единица пути — километр (1 км = 1000 м); дольные единицы — дециметр (1 дм = 0,1 м), сантиметр (1 см = 0,01 м) и миллиметр (1 мм = 0,001 м).
Путь — величина относительная, значение пути зависит от выбора системы отсчёта. Так, путь пассажира, переходящего из конца движущегося автобуса к его передней двери, равен длине автобуса в системе отсчёта, связанной с автобусом. В системе отсчёта, связанной с Землёй, он равен сумме длины автобуса и пути, который проехал автобус относительно Земли.
7. Если траектория движения тела неизвестна, то значение пути не позволит установить его положение в любой момент времени, поскольку направление движения тела не определено. В этом случае используют другую характеристику механического движения — перемещение.
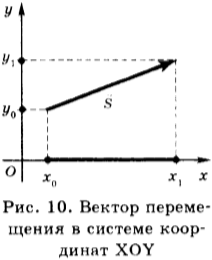
Перемещение — вектор, соединяющий начальное положение тела с его конечным положением (рис. 10)
Перемещение — векторная физическая величина, имеет направление и числовое значение, обозначается ( overrightarrow{s} ). Единица перемещения ( [,mathrm{s},] ) = 1 м.
Зная начальное положение тела, его перемещение (направление и модуль) за некоторый промежуток времени, можно определить положение тела в конце этого промежутка времени.
Следует иметь в виду, что перемещение в общем случае не совпадает с траекторией, а модуль перемещения — с пройденным путём. Это совпадение имеет место лишь при движении тела по прямолинейной траектории в одну сторону. Например, если пловец проплыл 100-метровую дистанцию в бассейне, длина дорожки которого 50 м, то его путь равен 100 м, а модуль перемещения равен нулю.
Перемещение, так же как и путь, величина относительная, зависит от выбора системы отсчёта.
При решении задач пользуются проекциями вектора перемещения. На рисунке 10 изображены система координат и вектор перемещения в этой системе координат.
Координаты начала перемещения — ( x_0, y_0 ); координаты конца перемещения — ( x_1, y_1 ). Проекция вектора перемещения на ось ОХ равна: ( s_x=x_1-x_0 ). Проекция вектора перемещения на ось OY равна: ( s_y=y_1-y_0 ).
Модуль вектора перемещения равен: ( s=sqrt{s^2_x-s^2_y} ).
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
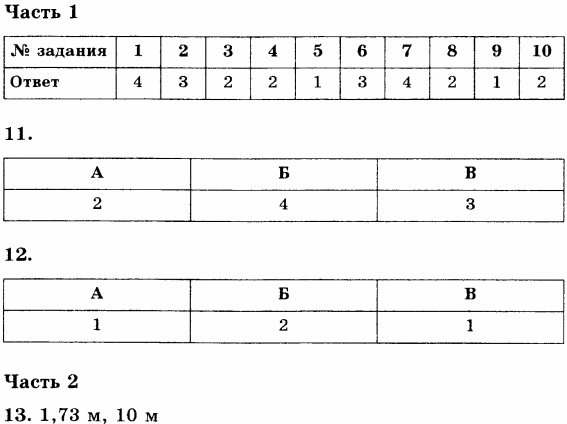
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. В состав системы отсчёта входят
1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы
2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно
1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора
4. Относительно какого тела покоится автомобиль, движущийся по автостраде?
1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода
5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 20 м/с
3) 40 м/с
4) -20 м/с
6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 15 м/с
3) 30 м/с
4) -15 м/с
7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?
1) прямая
2) окружность
3) дуга
4) винтовая линия
8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь ( l ) и модуль перемещения ( s ) мяча за всё время движения?
1) ( l )= 3,3 м, ( s ) = 3,3 м
2) ( l ) = 3,3 м, ( s ) = 0,7 м
3) ( l )= 0,7 м, ( s ) = 0,7 м
4) ( l )= 0,7 м, ( s ) = 3,3 м
9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?
1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй
10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса ( R ). Чему равны при этом путь ( l ) и модуль перемещения ( s ) точки обода?
1)( l=2R ), ( s=2R )
2)( l=pi R ),( s=2R )
3)( l=2R ),( s=pi R )
4) ( l=pi R ), ( s=pi R ).
11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор
ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта
12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения
ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная
Часть 2
13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.
Ответы
Механическое движение. Траектория. Путь. Перемещение
2.8 (56.85%) 216 votes