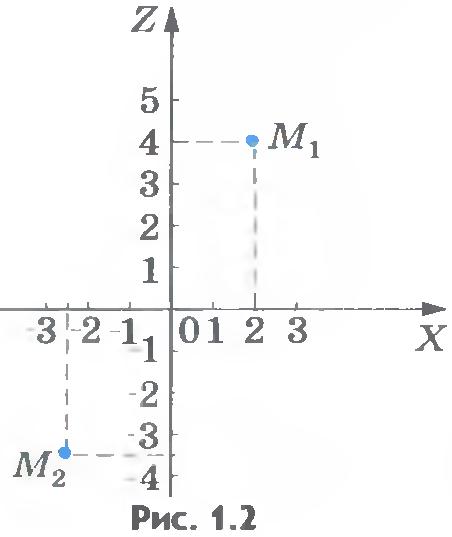Положение точки в пространстве
Положение точки в пространстве представим с помощью пространственного макета. Пусть даны в пространстве точка A и три взаимно перпендикулярные плоскости проекции.
Построим проекции точки А, расположенной в первом октанте пространства. Для этого через точку проведем проецирующие лучи, идущие перпендикулярно плоскостям проекций . На пересечении этих лучей с плоскостями проекций H, V, W находятся проекции самой точки А (A`, A», A»`).
Положение точки в пространстве
Положение точки в пространстве определяется тремя координатами (x, y, z), показывающими величины расстояний, на
которые она удалена от плоскостей проекций.
Чтобы определить эти расстояния, достаточно через точку A провести прямые,
перпендикулярные к плоскостям проекций, определить точки A`, A», A»` встречи этих
прямых с плоскостями проекций и измерить величины отрезков [AA`], [AA»], [AA»`],
которые укажут соответственно значение аппликаты z, ординаты y, абсциссы x
точки A.
Точки A`, A», A»` называют ортогональными проекциями точки A, при этом согласно принятым обозначениям:
A` — горизонтальная проекция точки A;
A» — фронтальная проекция точки A;
A»` — профильная проекция точки A.
Отрезки:
[AA`] — [OAx] — абсцисса точки A;
[AA»] — [OAy] — ордината точки A;
[AA»`] — [OAz] — аппликата точки A.
Прямые (AA` ⊥ H), (AA» ⊥ V), (AA»` ⊥ W) называют проецирующими прямыми или проецирующими лучами.
Прямую (AA`), проецирующую точку A на горизонтальную плоскость проекций, называют горизонтально проецирующей прямой (лучом).
Прямую (AA») проецирующую точку A на фронтальную плоскость проекций называют фронтально проецирующей прямой (лучом).
Прямую (AA»`) проецирующую точку A на профильную плоскость проекций называют профильно-проецирующей прямой (лучом).
Две проецирующие прямые, проходящие через точку A, определяют плоскость, которую принято называть проецирующей.
Чтобы получить эпюр точки A, выполним преобразование пространственного макета в эпюр Монжа:
— фронтальная проекция точки A остается на месте, как принадлежащая плоскости V, которая не меняет своего положения при рассматриваемом преобразовании.
— горизонтальная проекция A` вместе с горизонтальной плоскостью проекции опустится вниз и расположится на одном перпендикуляре к оси x с фронтальной проекцией A».
— профильная проекция AA»` будет вращаться вместе с профильной плоскостью проекции и к концу преобразования займет положение, указанное на рисунке. При этом AA»` будет принадлежать перпендикуляру к оси z, проведенному через
A» и удалена от оси z на такое же расстояние, на какое горизонтальная проекция A` удалена от оси x.
Положение точки в пространстве
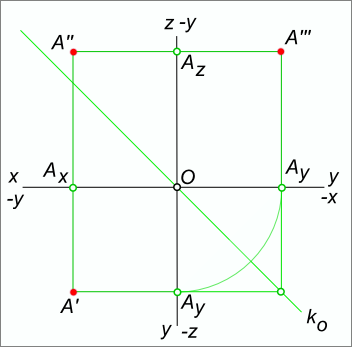
Связь между горизонтальной и профильной проекциями точки может быть установлена с помощью двух ортогональных отрезков [A`Ay] и [AyA»`] и сопрягающей их дуги окружности, с центром в точке пересечения координатных осей.
Отмеченной связью пользуются для нахождения недостающей профильной или горизонтальной проекции.
Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям
может быть найдено и без проведения дуги окружности. В этом случае связь между горизонтальной и профильной
проекциями может быть установлена с помощью ломаной линии A`,Ao,A»` с вершиной
Ao на биссектрисе угла, образованного осями y.
Биссектрису O,Ao,A»` называют постоянной прямой ko эпюра Монжа.
Представленная на рисунке плоская модель (эпюр) несет такую же информацию, какая содержится в пространственном макете.
Действительно: чтобы определить положение точки в пространстве, необходимо знать три координаты точки A — (x, y, z) — это длины отрезков [AA»`], [AA»], [AA`].
Величины этих отрезков могут быть легко определены на эпюре:
[AA»`] ≅ [A`Ay] ≅ [A»Az];
[AA»] ≅ [A`Ax] ≅ [A»`Az];
[AA`] ≅ [A»Ax] ≅ [A»`Ay].
Горизонтальная проекция точки A определяется абсциссой x и ординатой y
Фронтальная проекция — абсциссой x и аппликатой z
Профильная проекция — ординатой y и аппликатой z
A[A`(x, y); A»(x, z); A»`(y, z)]
Из записи следует:
1. Точка в пространстве удалена:
а) от плоскости проекции W на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси y (или же фронтальная проекция A» от оси z);
б) от плоскости проекции V на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси x (или ее профильная проекция A»` от оси z);
в) от плоскости проекции H на такую же величину, на какую ее фронтальная проекция A» удалена от оси x (или ее профильная проекция A»` от оси y).
2. Положение точки в пространстве вполне определяется положением ее двух ортогональных проекций.
Как следствие из этого — по двум любым заданным ортогональным проекциям точки всегда можно построить недостающую ее третью ортогональную проекцию.
Действительно: какое бы сочетание из двух ортогональных проекций мы не взяли, они всегда дают нам значение всех трех координат точки.
3. a) горизонтальная и фронтальная проекции любой точки принадлежат одному перпендикуляру к оси x.
Если принять во внимание, что на эпюре прямые, перпендикулярные к осям проекций и соединяющие разноименные проекции точек, называют линиями связи (проекционной связи), то пункт 3. а) может быть сформулирован иначе:
горизонтальная и фронтальная проекции любой точки принадлежат одной линии связи.
б) горизонтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси y;
в) фронтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси z.
+
Метод координат в пространстве
Положение
любой точки в пространстве можно
однозначно определить с помощью
прямоугольной системы координат. Эта
система включает три взаимно
перпендикулярные оси, пересекающиеся
в одной точке О
– начале координат.
Одну из осей называют
осью абсцисс
(ось Ох),
другую –
осью ординат
(Оу),
третью –
осью аппликат
(Oz).
Плоскости XOY,
XOZ
и YOZ
называются координатными плоскостями.
Какой-либо отрезок принимается за
единицу
масштаба
для всех трех осей.
Положительные направления на осях
выбираются так, чтобы поворот на 900,
совмещающий положительный луч OX
с положительным лучом OY,
казался проходящим против часовой
стрелки, если смотреть со стороны луча
OZ.
Такая система координат называется
правой.
Положение
любой точки М
в пространстве можно определить тремя
координатами следующим образом.
Через М
проводим плоскости, параллельные
плоскостям XOY,
XOZ
и YOZ.
В пересечении с осями получаем точки,
например, P,
Q
и R
соответственно. Числа
х
(абсцисса),
у (ордината),
z
(аппликата),
измеряющие отрезки OP,
OQ
и OR
в избранном масштабе, называются
прямоугольными
координатами
точки
М.
Они берутся положительными или
отрицательными в зависимости от того,
лежат ли соответствующие отрезки на
положительной или отрицательной полуоси.
Каждой тройке чисел (х;
у;
z)
соответствует одна и только одна точка
пространства, и наоборот.
Расстояние
между двумя точками
и


Координаты
(x;
y;
z)
точки М,
делящей в заданном отношении

(
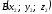
определяются по формулам:



В
частности, при

делит отрезок АВ
пополам), получаются формулы для
определения координат середины отрезка:



Пример
4:
На оси
Оу
найти точку, равноудаленную от двух
точек
и

Решение:
Точка М,
лежащая на оси
Оу,
имеет координаты

По условию задачи
|АМ| = |ВМ|.
Найдем расстояния
|АМ|
и |ВМ|,
используя формулу (1.6):
Получим
уравнение:
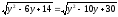
Отсюда
находим, что 4у
= 16, т. е.
у =
4. Искомая точка есть М(0;
4; 0).
Пример
5:
Отрезок АВ
разделен на 3 равные части. Найти
координаты точек деления, если известны
точки
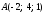
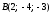
Решение:
Обозначим
точки деления отрезка АВ
в следующем порядке:
С
и
D.
По условию задачи
|АС| = |CD| = |DB|.
Поэтому точка
С
делит отрезок
АВ
в отношении

Пользуясь формулами (1.7), находим
координаты точки С:



Имеем,

По
формулам (1.8) находим координаты точки
D
– середины отрезка СВ:



То
есть точка D имеет координаты:

Пример
6:
В точках
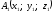



m2,
m3,
m4.
Найти координаты центра тяжести системы
этих масс.
Решение:
Как
известно из курса физики центр тяжести
масс m1
и m2,
помещенных в точках
А
и
В,
делит отрезок
АВ
на части, обратно пропорциональные
массам, сосредоточенным на концах
отрезка (
Исходя из этого, найдем сначала центр
тяжести
и m2,
помещенных в точках
А1и
А2:



Центр
тяжести системы трех масс m1
и m2
и m3
(
находим аналогично:
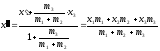


Находим,
наконец, центр тяжести системы трёх
масс m1,
m2,
m3
и m4:
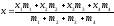


Вопросы
для контроля:
-
Опишите
прямоугольную систему координат на
плоскости и все ее компоненты. -
Как
определяются координаты произвольной
точки плоскости? -
Напишите
формулу для нахождения расстояния
между двумя точками на
плоскости. -
Как
найти координаты
точки, делящей в заданном отношении
отрезок? -
Напишите
формулы координат середины отрезка. -
Напишите
формулу, по которой вычисляется площадь
треугольника, если известны координаты
его вершин. -
Опишите
полярную систему координат. -
Что
называют полярным радиусом? В каких
пределах он измеряется? -
Что
называют полярным углом? Пределы его
измерения? -
Как
найти
прямоугольные координаты точки, для
которой известны полярные координаты? -
Как
найти
полярные координаты точки, для которой
известны прямоугольные координаты? -
Как
найти расстояние
между точками в полярной системе
координат? -
Опишите
прямоугольную систему координат в
пространстве и все ее компоненты. -
Как
определить координаты точки в
пространстве? -
Запишите
формулу для нахождения расстояния
между двумя точками в пространстве. -
Запишите
формулы для нахождения координат точки,
делящей отрезок в данном отношении для
трехмерной системы координат.
Мы продолжаем тему
классической механики Ньютона. Механика делится на два основных раздела: кинематика
и динамика. Мы начнём с изучения кинематики.
Кинематика изучает
движение тел, способы описания этого движения, а также, его характеристики.
Описать движение человека
или полет бабочки математически — это крайне сложная задача. Но есть задачи и
проще: например, описать движение материальной точки. Добавим теперь, что эта
точка двигается равномерно и прямолинейно. Тогда, описать её движение не так уж
сложно. Именно с таких идеализированных моделей и следует начать изучение
кинематики. Ведь если мы сможем описать движение каждой точки тела, то мы также
сможем описать движение самого тела.
В первую очередь, нужно
создать систему отсчёта. Система отсчёта состоит из тела отсчёта, системы
координат и счётчика времени.
Тело отсчёта — это
физическое тело, относительно которого задаётся положение данного тела или
точки.
Понять это довольно
просто. На рисунке изображено дерево.
На каком расстоянии
находится это дерево? На каком расстоянии от чего? — спросите вы. Конечно,
нам нужно выбрать точку отсчета. Это может быть белый треугольник на камне, а
может быть флажок на за́мке. В зависимости от этого выбора, ответ на
вопрос будет различным. Необходимо выбрать какую-то точку за точку отсчёта, то
есть за ноль. Скажем, мы можем обозначить за ноль центр картинки.
Далее, мы используем
декартовы координаты, чтобы описать положения тел. Выбираем единичный отрезок
и, исходя из этого определяем положения тел. Это положение задаётся с помощью
координат. Например, точка А имеет координаты четыре и минус три, а точка Б —
три и два. Также, можно задать положение тела с помощью радиус-вектора — это
вектор, который соединяет точку и начало координат.
Радиус-вектор обозначается
латинской буквой r и, как и любой
другой вектор, имеет длину и направление. Длиной радиус-вектора будет
является геометрическая сумма координат точки. Иными словами, мы вычисляем
длину радиус-вектора, используя теорему Пифагора. То есть, длина радиус-вектора,
описывающего положение точки B
будет равна .
Модуль и направление
любого вектора находят с помощью проекций этого вектора на оси координат.
Что же такое проекция?
Давайте рассмотрим вектор с
начальной точкой А и конечной точкой B,
находящийся в системе координат на плоскости.
Из точек А и B
опустим перпендикуляры на ось икс. Длина отрезка А1 B1
— это и есть проекция вектора цэ на ось x.
Точно таким же способом находится проекция вектора на
ось y. Как видно из
построения: .
Аналогично можно найти проекцию на ось y:
..
Проекция вектора на ось —
это алгебраическая величина. Её знак можно определить
так: если, двигаясь от начальной точки проекции до конечной точки проекции,
надо идти в положительном направлении, то проекция положительная, а в противном
случае — она отрицательная.
Иначе это можно объяснить
так: если вектор составляет острый угол с направлением оси, на которую мы
собираемся сделать проекцию, то проекция будет положительной, а если угол между
вектором и направлением оси — тупой, то проекция будет отрицательной.
Нетрудно догадаться, что если
вектор перпендикулярен оси, то его проекция на эту ось будет равна нулю.
Аналогично, если
вектор параллелен оси, то его проекция на эту ось будет равна модулю вектора.
Рассмотрим теперь, как
задать положение точки в пространстве, а не на плоскости. Как вы знаете, у есть
три пространственных измерения, поэтому, чтобы задать положение точки в
пространстве нам нужно три координаты. Сначала мы точно также, как и ранее,
находим точку на плоскости, а потом от этой точки откладываем числовое значение
координаты z параллельно оси Z.
Положение такой точки точно
также можно задать с помощью радиус-вектора. Его модуль также будет находиться
с помощью геометрической суммы координат точки.
Примеры решения задач.
Задача 1. В
системе координат отметьте точку N
(1;3;7), постройте соответствующий радиус-вектор и найдите его длину.
Задача 2. В
системе координат отметьте точку N
(1;3;7), постройте соответствующий радиус-вектор и найдите его длину.
Задача 3. Постройте
проекции вектора на
оси x и y
и найдите их числовые значения, если ,
а угол между и
осью x составляет 30.
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Положение точки в пространстве
Чтобы решить задачу о движении тела, прежде всего надо уметь определять, или, что одно и то же, задавать, положение его в пространстве. Как же определяют положение точки?
Наблюдая за любым телом, мы замечаем, что его положение в один и тот же момент времени относительно различных тел различно. Например, космический корабль, запущенный с космодрома Байконур, занимает совершенно различные положения относительно Земли, Луны и Солнца. Поэтому в данном случае обязательно надо указать физическое тело, относительно которого задается положение данного тела или же данной точки. Такое тело называют телом отсчета.
Тело отсчета можно выбрать произвольно. Им может быть космодром, самолет, в котором мы летим, космический корабль, Земля, Солнце, звезды и т. д. Но относительно различных точек тела отсчета положение любого другого тела или точки тоже различно. Если, например, за тело отсчета принять Землю, то положение спутника Земли относительно Москвы будет иным, нежели относительно космодрома Байконур. Строго говоря, мы должны указать, относительно какой точки выбранного тела отсчета задается положение данной точки или тела.
Если тело отсчета выбрано, то относительно него положение точки можно задать с помощью координат или радиус-вектора. Выбор системы отсчета и системы координат должен быть разумным, чтобы описание движения тела выглядело достаточно просто, но в то же время мы могли бы ответить на все вопросы задачи.
Рассмотрим эти два способа задания положения точки.
Задание положения точки с помощью координат. Из курса математики вы знаете, что положение точки на плоскости можно задать с помощью двух чисел, которые называются координатами этой точки. Для этого, как известно, можно на плоскости провести две пересекающиеся взаимно перпендикулярные оси, например оси ОХ и ОY. Точку пересечения осей называют началом координат, а сами оси — координатными осями.
Координаты точки М1 (рис.1.2) равны x1 = 2,у1 = 4; координаты точки М2 равны х2 = -2,5, у2 = -3,5.
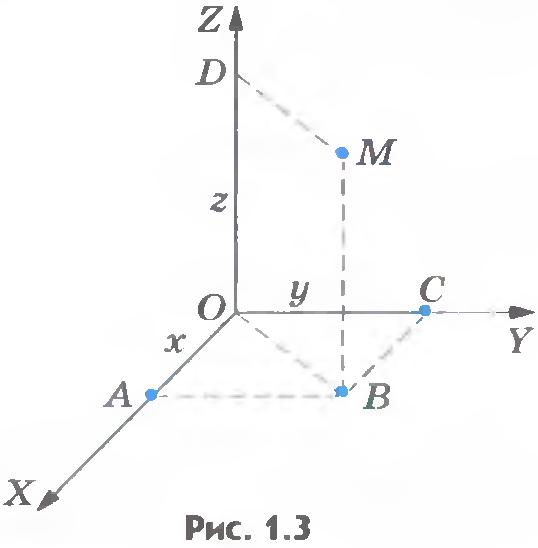
Положение точки М в пространстве относительно тела отсчета можно задать с помощью трех координат. Чтобы это сделать, необходимо через выбранную точку тела отсчета провести три взаимно перпендикулярные оси ОХ, ОY, 0Z. В полученной системе координат положение точки будет определяться тремя координатами х, у, z.
Если число х положительно, то отрезок откладывается в положительном направлении оси ОХ (рис.1.3) (x = ОА). Если же число х отрицательно, то отрезок откладывается в отрицательном направлении оси ОХ. Из конца этого отрезка проводят прямую, параллельную оси ОY, и на этой прямой откладывают отрезок от оси ОХ, соответствующий числу у (у = АВ) — в положительном направлении оси ОY, если число у положительно, и в отрицательном направлении оси ОY, если число у отрицательно.
Далее из точки В другого отрезка проводят прямую, параллельную оси ОZ. На этой прямой от координатной плоскости ХОY откладывают отрезок, соответствующий числу z. Направление, в котором откладывают этот отрезок, определяют так же, как и в предыдущих случаях.
Конец третьего отрезка и есть та точка, положение которой задается координатами х, у, z.
Чтобы определить координаты данной точки, необходимо провести в обратной последовательности те операции, которые мы осуществляли, находя положение этой точки по ее координатам.
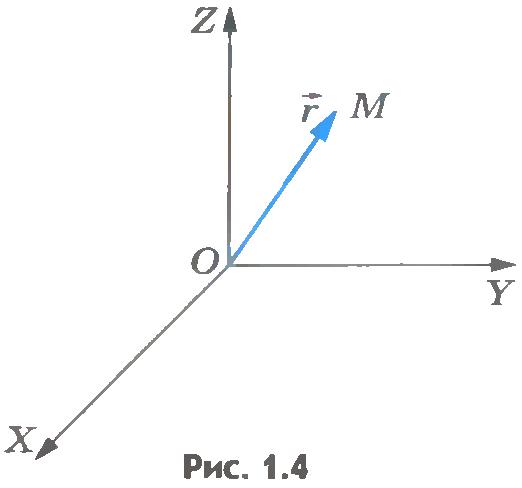
Задание положения точки с помощью радиус-вектора. Положение точки можно задать не только с помощью координат, но и с помощью радиус-вектора. Радиус-вектор — это направленный отрезок, проведенный из начала координат в данную точку.
Радиус-вектор принято обозначать буквой . Длина радиус-вектора, или, что одно и то же, его модуль (рис.1.4), есть расстояние от начала координат до точки М.
Положение точки будет определено с помощью радиус-вектора только в том случае, если известны его модуль (длина) и направление в пространстве. Лишь при этом условии мы будем знать, в каком направлении от начала координат следует отложить отрезок длиной r, чтобы определить положение точки.
Итак, положение точки в пространстве определяется ее координатами или ее радиус-вектором.
Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось?
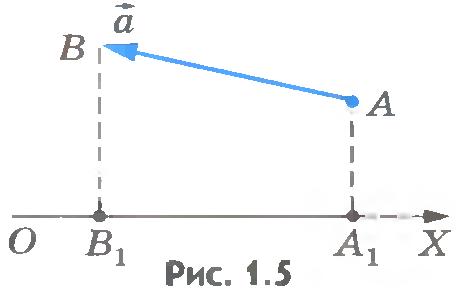
Изобразим какую-либо ось (рис.1.5), например ось ОХ.
Опустим из начала А и концаВ вектора перпендикуляры на ось ОХ.
Точки А1 и В1 есть проекции, соответственно, начала и конца вектора на эту ось.
Проекцией вектора на какую-либо ось называется длина отрезка А1В1 между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, аx и аy — проекции вектора на оси координат ОХ и ОY.
Согласно определению проекции вектора на ось можно записать:
Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора.
Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций. В противном случае (см. рис.1.5) она считается отрицательной.
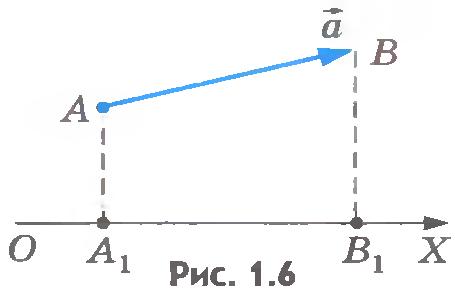
Из рисунков 1.5 и 1.6 нетрудно увидеть, что проекция вектора на ось будет положительной, когда вектор составляет острый угол с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекций тупой угол.
Положение точки в пространстве можно задавать с помощью координат или радиус-вектора, соединяющего начало координат и точку.
???
1. Что называется телом отсчета?
2. Какими способами можно задать положение точки?
3. Как задают положение точки в пространстве с помощью координат?
4. Что называется радиус-вектором?
5. Что называется проекцией вектора на ось?
6. Чему равна проекция вектора на ось, если вектор направлен так же, как и ось проекции?
7. Чему равна проекция вектора на ось, если вектор направлен противоположно оси проекции?
8. Чему равна проекция вектора на перпендикулярную к нему ось?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Материалы по физике, задание и ответы по классам, планы конспектов уроков по физике для 10 класса
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Построение ортогональных проекций точек
Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.
По заданному комплексному чертежу точек A и B необходимо:
- Записать их координаты.
- Достроить проекции т. A и B на плоскость П3.
- Определить положение точек в пространстве (октант или плоскость проекций).
- Построить наглядное изображение точек в системе плоскостей П1, П2, П3.
Определение координат точек по их проекциям
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно Aх, Aу. Координата х для т. A равна длине отрезка AхO со знаком плюс, так как Aх лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка AуO со знаком минус, так как т. Aу лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A» имеет координаты х и z. Опустим перпендикуляр из A» на ось z и найдем Az. Координата z точки A равна длине отрезка AzO со знаком минус, так как Az лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).
Координаты т. B можно записать в виде B (x, y, z). Рассмотрим горизонтальную проекцию точки B – т. В’. Так как она лежит на оси х, то Bx = B’ и координата Bу = 0. Абсцисса x точки B равна длине отрезка BхO со знаком плюс. С учетом масштаба чертежа x = 30. Фронтальная проекция точки B – т. B˝ имеет координаты х, z. Проведем перпендикуляр из B» к оси z, таким образом найдем Bz. Аппликата z точки B равна длине отрезка BzO со знаком минус, так как Bz лежит в области отрицательных значений оси z. С учетом масштаба чертежа определим значение z = –20. Таким образом, координаты B (30, 0, -20). Все необходимые построения представлены на рисунке ниже.
Построение проекций точек
Точки A и B в плоскости П3 имеют следующие координаты: A»’ (y, z); B»’ (y, z). При этом A» и A»’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B» и B»’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса AуO. После этого проведем перпендикуляр из Aу до пересечения с перпендикуляром, восстановленным из точки A» к оси z. Точка пересечения этих двух перпендикуляров определяет положение A»’.
Точка B»’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B» к оси z. Точка пересечении этого перпендикуляра с осью z есть B»’.
Определение положения точек в пространстве
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П1, П2 и П3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П2.
Другим вариантом решения данной задачи является метод исключений. Например, координаты точки A (10, -30, -10). Положительная абсцисса x позволяет судить о том, что точка расположена в первых четырех октантах. Отрицательная ордината y говорит о том, что точка находится во втором или третьем октантах. Наконец, отрицательная аппликата z указывает на то, что т. A расположена в третьем октанте. Приведенные рассуждения наглядно иллюстрирует следующая таблица.
| Октанты | Знаки координат | ||
| x | y | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Координаты точки B (30, 0, -20). Поскольку ордината т. B равна нулю, эта точка расположена в плоскости проекций П2. Положительная абсцисса и отрицательная аппликата т. B указывают на то, что она расположена на границе третьего и четвертого октантов.
Построение наглядного изображения точек в системе плоскостей П1, П2, П3
Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П1, П2, П3, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.
Построение наглядного изображения т. A (10, -30, -10) начнем с её горизонтальной проекции A’. Отложив по оси абсцисс и ординат соответствующие координаты, найдем точки Aх и Aу. Пересечение перпендикуляров, восстановленных из Aх и Aу соответственно к осям x и y определяет положение т. A’. Отложив от A’ параллельно оси z в сторону её отрицательных значений отрезок AA’, длина которого равна 10, находим положение точки A.
Наглядное изображение т. B (30, 0, -20) строится аналогично – в плоскости П2 по осям x и z нужно отложить соответствующие координаты. Пересечение перпендикуляров, восстановленных из Bх и Bz, определит положение точки B.