На этой странице вы узнаете
- Игра в прятки: как значение одной переменной может помочь найти другую?
- Парадокс: как стоять на месте и бежать с любой скоростью одновременно?
- Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром?
Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье.
Что такое параметр
Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов?
Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно (frac{20}{5} = 4). А если было 10 градусов, то искомое число было бы равно (frac{20}{10} = 2).
Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными.
Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a” называется параметр.
Параметр — это условная буква, вместо которой можно подставить число.
То есть параметр — это еще одна переменная, которая может принять несколько значений.
Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.
Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется.
Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.
Поскольку параметр — переменная в уравнении, которая является коэффициентом, его значение задает и корни уравнения. То есть переменные а и х зависят друг от друга так же, как и зависят корни обычного уравнения от его коэффициентов.
Линейные уравнения с параметром
Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a.
(x = frac{20}{a})
Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5
Что, если a=0? Мы получаем уравнение (x = frac{20}{0}), у которого нет решения, поскольку на 0 делить нельзя.
Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0.
Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a (neq) 0 — x = 20a.
Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев.
1) b (neq) 0.
Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b.
Получаем уравнение ax = 15. Как найти начальную скорость Пети? (x = frac{15}{a}).
Такое уравнение мы уже решали выше. Получаем два случая:
- Если a = 0 — решений нет.
- Если a (neq) 0, то изначальная скорость Пети была равна (x = frac{15}{a}).
Когда Пете нужно увеличить скорость в 0 раз, получается парадокс.
С какой бы скоростью ни бежал Петя, он все равно будет стоять на месте, поскольку 0 * x = 0. Даже если он изначально бегал со скоростью света, его скорость останется равна 0, а не 15 км/ч.
2) b = 0.
Мы получаем уравнение ax = 0. Также разберем два случая значений параметра:
- a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось?
Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений.
- a (neq) 0. Здесь получается, что равен 0 уже х: (x = frac{0}{a} = 0).
Подведем итог. Как можно решить уравнение вида ax = b?
- Если a = 0, b = 0 — бесконечное множество решений.
- Если a = 0, b (neq) 0 — решений нет.
- Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}).
Квадратные уравнения с параметром
Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции».
Квадратное уравнение имеет вид ax2 + bx + c = 0, а графиком функции y = ax2 + bx + c будет парабола.
Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.
Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней:
- При D > 0 уравнение имеет два корня.
- При D = 0 уравнение имеет один корень.
- При D < 0 уравнение не имеет корней.
Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х.
Рассмотрим три уравнения.
1) x2 — x — 2 = 0
Решим уравнение с помощью дискриминанта.
D = 12 — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня.
(x_1 = frac{1 + 3}{2} = 2)
(x_2 = frac{1 — 3}{2} = -1)
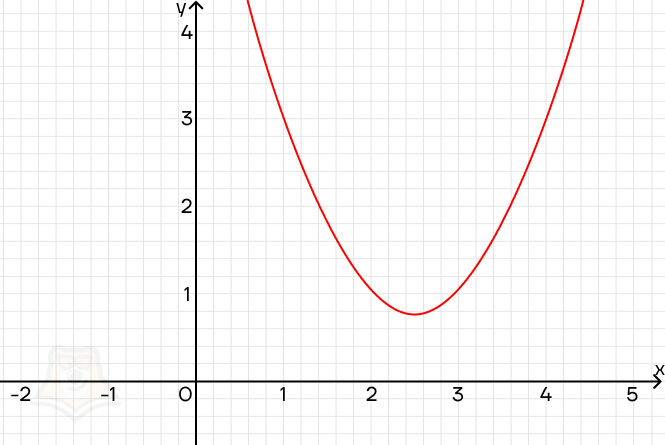
Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) .

2) x2 -4x + 4 = 0
Решим уравнение с помощью дискриминанта.
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень.
(x = frac{4}{2} = 2)
Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0).

3) x2 — 5x + 7 = 0
Решим уравнение с помощью дискриминанта.
D = 25 — 4 * 1 * 7 = 25 — 28 = -3
Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет.
Где можно применить эти знания, решая параметры?
Пример 1. Найдите все значения параметра a, при которых уравнение x2 + (3a + 11)x + 18,25 + a = 0 имеет два различных решения.
Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?
Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным.
1. Для начала найдем сам дискриминант.
D = (3a + 11)2 — 4 * 1 * (a + 18,25) = 9a2 + 66a + 121 — 4a — 73 = 9a2 + 62a + 48
2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a2 + 62a + 48 > 0
3. Решим его «Методом интервалов».
9a2 + 62a + 48 = 0
D = 3844 — 1728 = 2116
(a_1 = frac{-62 + 46}{18} = -frac{16}{18} = -89)
(a_2 = frac{-62 — 46}{18} = -frac{108}{18} = -6)

4. Дискриминант будет положительным при (a in (-infty; -6) cup (-frac{8}{9}; +infty)). Это и будет ответ.
Ответ: (a in (-infty; -6) cup (-frac{8}{9}; +infty)).
Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения.
Пример 2. При каких значениях параметра a уравнение (2a + 1)x2 — ax + 3a + 1 = 0 имеет два различных решения?
Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0?
Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи.
Если перед x2 стоит коэффициент, обязательно проверить, чтобы он не был равен 0. В противном случае уравнение из квадратного превращается в линейное, а это уже совершенно другой алгоритм решений уравнений.
1. Поскольку по условию должно быть 2 решения, мы получаем, что a (neq) -0,5.
2. Найдем дискриминант уравнения. Он должен быть строго больше 0, чтобы у уравнения было два решения.
D = a2 — 4 * (2a + 1) * (3a + 1) = a2 — 24a2 — 20a -4 = -23a2 — 20a — 4
3. Составим неравенство и решим его:
-23a2 — 20a — 4 > 0
23a2 + 20a + 4 < 0
23a2 + 20a + 4 = 0
D = 400 — 4 * 23 * 4 = 400 — 368 = 32
(a_1 = frac{-20 + 4 sqrt{2}}{46} = frac{2sqrt{2} — 10}{23})
(a_2 = frac{-20 — 4sqrt{2}}{46} = frac{-2sqrt{2} — 10}{23})
4. Разложим уравнение на множители:
(23a^2 + 20a + 4 = 23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23}))
5. Получаем неравенство:
(23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23} < 0)
6.Тогда (a in (frac{-2sqrt{2} — 10}{23}; frac{2sqrt{2} — 10}{23})). Вспомним, что a (neq) -0,5, следовательно, мы получаем ответ (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23})).

Ответ: (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23}))
Теорема Виета
Дискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax2 + bx + c = 0, то его корни можно найти с помощью следующей системы:

Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения.
Пример 3. При каких значениях параметра a корни уравнения x2 — 3ax — a(a — 1) = 0 удовлетворяют условию x1 = 5x2.
Решение. 1. Корни уравнения — это два различных числа. Значит, дискриминант должен быть строго больше 0:
D = 9a2 — 4 * 1 * (-a2 + a) = 9a2 + 4a2 — 4a = 13a2 — 4a = a(13a — 4)
Получаем неравенство a(13a — 4) > 0, следовательно, (a in (-infty; 0) cup (frac{4}{13}; +infty)).
2. По теореме Виета найдем корни уравнения:

3. По условию x1 = 5x2, тогда 5x2 + x2 = 6x2 = 3a, откуда получаем:
(x_2 = frac{3a}{6} = frac{a}{2})
(x_1 = 5 * a_2 = frac{5a}{2})
4. Подставим во второе уравнение системы:
(frac{a}{2} * frac{5a}{2} = a — a^2)
(frac{5a^2}{4} = a — a^2 | * 4)
5a2 = 4a — 4a2
(9a^2 — 4a = 0 rightarrow a(9a — 4) = 0 rightarrow a = 0, a = frac{4}{9})
5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня.
a = 0 не подходит, поскольку ограничение (a in (-infty; 0) cup (frac{4}{13}; +infty)) не включает точку 0.
(a = frac{4}{9}) подходит, поскольку (frac{4}{9} > frac{4}{13}).
Ответ: (a = frac{4}{9})
Условия на корни квадратного трехчлена
Однако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев.
1. Корни квадратного трехчлена меньше, чем число N.
Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз.
Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N.

Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту.
Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка.

Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа.
Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы.
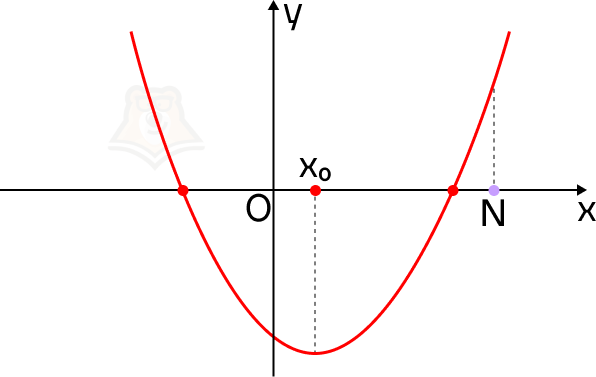
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N.
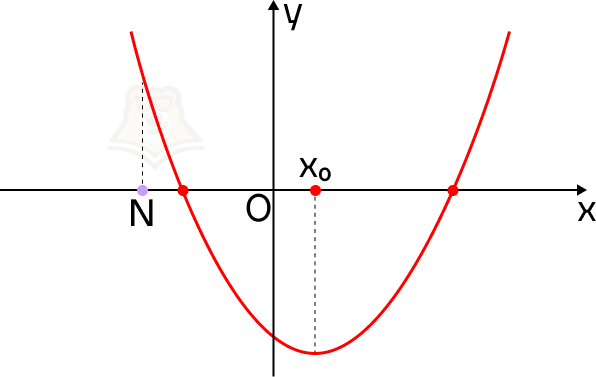
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов.

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними.

В этом случае смотровая площадка окажется между привалами.
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:

Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг.
Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы.

Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения.
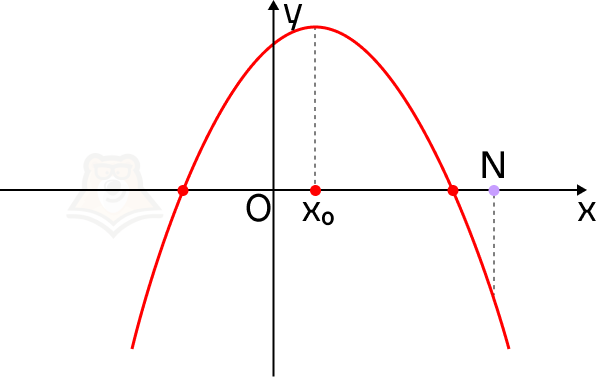
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:

2. Корни квадратного трехчлена больше, чем число N.
Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы.
Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы.
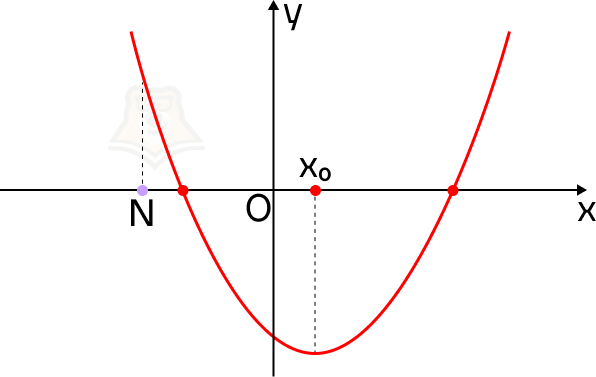
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:

Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения.

Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:

С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько.
Достаточно начертить примерный график функции и расставить на оси х нужные точки. Чтобы составить систему, необходимо:
1. Определить, куда направлены ветви параболы и задать условие для коэффициента перед x2.
2. Определить, сколько корней имеет уравнение и задать условие для дискриминанта.
3. Определить расположение вершины параболы относительно точек на графике и задать условие для их абсцисс.
4. Определить, какое значение принимает функция в данных точках относительно корней уравнения.
В итоге должна получиться система, с помощью которой можно решить задачу.
Фактчек
- Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется.
- При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b (neq) 0 — решений нет. Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}).
- При решении квадратного уравнения обязательно проверять коэффициент перед x2. Если коэффициент будет равен 0, то уравнение станет линейным.
- При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней.
- Решить квадратное уравнение можно и с помощью теоремы Виета.
- Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций.
Проверь себя
Задание 1.
Что такое параметр?
- Это буква a, вместо которой можно подставить число.
- Это коэффициент перед x2 в квадратном уравнении.
- Это переменная х.
- Это значение функции в определенной точке.
Задание 2.
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?
- Решений нет.
- Одно решение.
- Бесконечное множество решений.
- Невозможно определить количество решений.
Задание 3.
При каких значениях дискриминанта уравнение будет иметь корни?
- D > 0
- D = 0
- D < 0
- D (neq) 0
Задание 4.
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?
- Справа.
- Слева.
- Совпадать с точкой А.
- Невозможно определить расположение вершины.
Задание 5.
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?
- Значение функции в точке В будет меньше 0.
- Значение функции в точке В будет равно 0.
- Значение функции в точке В будет больше 0.
- Невозможно определить значение функции.
Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.
Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.
Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.
Вот список тем, которые стоит повторить:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
2. Преобразование графиков функций.
3. Построение графиков функций.
4. Базовые элементы для решения задач с параметрами.
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.
Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).
1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.
Получим систему:
В первом уравнении выделим полный квадрат:
Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.
Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.
Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.
Кроме того, точка не должна лежать на прямой , которая пересекает окружность в точках
и
Координаты этих точек легко найти, подставим
в уравнение окружности.
Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.
Это значит, что
2. Найдите все значения a, при которых уравнение имеет единственное решение.
Уравнение равносильно системе:
Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).
Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.
Приводим подобные слагаемые в уравнении.
Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:
Решим систему графически:
Уравнение задает окружность с центром в точке
, где радиус
Неравенство задает полуплоскость, которая расположена выше прямой
, вместе с самой этой прямой.
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением
Пусть С — точка касания.
На координатной плоскости отметим точки и
, в которых прямая
пересекает оси Y и Х.
Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.
Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.
Тогда
Решая это уравнение, получаем, что
Ответ:
3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.
График уравнения — окружность
с центром
и радиусом равным 2.
График уравнения — две симметричные окружности
и
радиуса 2 c центрами в точках
и
Второе уравнение при задает окружность
с центром в точке
и радиусом a.
Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.
Система имеет единственное решение в случаях, когда окружность , задаваемая вторым уравнением, касается только левой окружности
или только правой
Если a — радиус окружности , то это значит, что
(только правая) или
(только левая).
Пусть А — точка касания окружности и окружности
Для точки А:
,
(как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),
В — точка касания окружности и окружности
Для точки В:
длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4;
Тогда для точки В получим:
Есть еще точки С и D, в которых окружность касается окружности
или окружности
соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:
, но
и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность
и система будет иметь не одно, а три решения.
Аналогично, для точки D:
и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность
и система будет иметь три решения.
Ответ: или
4. При каких значениях a система уравнений имеет 4 решения?
Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)
И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!
Просто выделили полный квадрат во втором уравнении.
Сделаем замену Система примет вид:
Вот теперь все видно! Рисовать будем в координатах
Графиком первого уравнения является ромб, проходящий через точки с координатами и
Графиком второго уравнения является окружность с радиусом и центром в начале координат.
Когда же система имеет ровно 4 решения?
1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.
Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.
Диагонали нашего ромба равны 8 и 6. Значит,
Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то
При этом
Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда
Мы получили ответ:
2) Есть второй случай, и мы его найдем.
Давайте посмотрим — если уменьшить радиус окружности, сделав , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.
Пусть радиус окружности больше, чем , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.
Пусть радиус окружности равен 3. Тогда система имеет 6 решений.
А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!
Значит, Объединим случаи и запишем ответ:
Ответ:
Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Графический метод решения задач с параметрами» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Цель данной работы – изучение различных способов решения задач с параметрами.
Возможность и умение решать задачи с параметрами демонстрируют владение методами
решения уравнений и неравенств, осмысленное понимание теоретических сведений,
уровень логического мышления, стимулируют познавательную деятельность. Для
развития этих навыков необходимы длительнее усилия, именно поэтому в профильных
10-11 классах с углубленным изучением точных наук введен курс: “Математический
практикум”, частью которого является решение уравнений и неравенств с
параметрами. Курс входит в число дисциплин, включенных в компонент учебного
плана школы.
Успешному изучению методов решения задач с параметрами могут помочь
элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с
параметрами”.
Рассмотрим четыре больших класса задач с параметрами:
- Уравнения, неравенства и их системы, которые необходимо решить для
любого значения параметра, либо для значений параметра, принадлежащих
определенному множеству. - Уравнения, неравенства и их системы, для которых требуется определить
количество решений в зависимости от значения параметра. - Уравнения, неравенства и их системы, для которых требуется найти все те
значения параметра, при которых указанные уравнения (системы, неравенства)
имеют заданное число решений. - Уравнения, неравенства и их системы, для которых при искомых значениях
параметра множество решений удовлетворяет заданным условиям в области
определения.
Методы решений задач с параметрами.
1. Аналитический метод.
Это способ прямого решения, повторяющий стандартные процедуры нахождения
ответа в задачах без параметра.
Пример 1. Найдите все значения параметра
a, при которых уравнение:
(2a – 1)x2 + ax + (2a – 3) =0 имеет не более
одного корня.
Решение:
При 2a
– 1 = 0 данное уравнение квадратным не является, поэтому случай
a =1/2 разбираем отдельно.
Если a = 1/2, то уравнение принимает вид
1/2x – 2 = 0, оно имеет один корень.
Если a ≠ 1/2,
то уравнение является квадратным; чтобы оно имело не более одного корня
необходимо и достаточно, чтобы дискриминант был неположителен:
D = a2 – 4(2a – 1)(2a – 3) = -15a2
+ 32a – 12;
Чтобы записать окончательный ответ, необходимо понять,
2. Графический метод.
В зависимости от задачи (с переменной x
и параметром a)
рассматриваются графики в координатной плоскости (x;y)
или в плоскости (x;a).
Пример 2. Для каждого значения параметра a
определите количество решений уравнения
.
Решение:
Заметим, что количество решений уравнения
равно количеству точек пересечения графиков функций
и y = a.
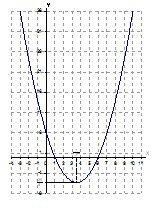
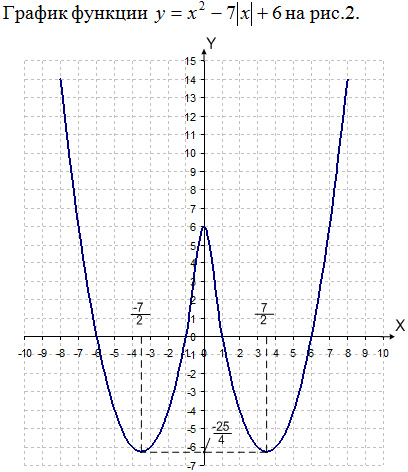
График функции
показан на рис.1.
Рис.1
Рис. 2
Рис. 3
y = a – это горизонтальная прямая. По графику несложно
установить количество точек пересечения в зависимости от a
(например, при a =
11 – две точки пересечения; при a
= 2 – восемь точек пересечения).
Ответ: при a < 0 – решений нет; при a
= 0 и a = 25/4 – четыре решения; при
0 < a < 6 – восемь решений; при a
= 6 – семь решений; при
6 < a < 25/4 – шесть решений; при a >
25/4 – два решения.
3. Метод решения относительно параметра.
При решении этим способом переменные х и а принимаются
равноправными, и выбирается та переменная, относительно которой аналитическое
решение становится более простым. После упрощений нужно вернуться к исходному
смыслу переменных х и а и закончить решение.
Пример 3. Найти все значения параметра а , при каждом из которых
уравнение
= —ax +3a +2 имеет единственное решение.
Решение:
Будем решать это уравнение заменой переменных. Пусть
= t , t ≥ 0
, тогда x = t2 + 8 и
уравнение примет вид at2 + t + 5a – 2 = 0
. Теперь задача состоит в том, чтобы найти все а,
при которых уравнение at2 + t + 5a – 2 =
0 имеет единственное неотрицательное решение. Это имеет
место в следующих случаях.
1) Если а = 0, то уравнение имеет единственное решение t
= 2.
Решение некоторых типов уравнений и неравенств с параметрами.
Задачи с параметрами помогают в формировании логического мышления, в
приобретении навыков исследовательской деятельности.
Решение каждой задачи своеобразно и требует к себе индивидуального,
нестандартного подхода, поскольку не существует единого способа решения таких
задач.
Ⅰ. Линейные уравнения.
Задача № 1.
При каких значениях параметра b
уравнение
не имеет корней?
Ⅱ. Степенные уравнения, неравенства и их системы.
Задача №2. Найти все значения параметра a,
при которых множество решений неравенства:
содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.
Решение:
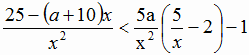
Преобразуем обе части неравенства.
Для того, чтобы множество решений неравенства содержало число 6, необходимо и
достаточно выполнение условия:
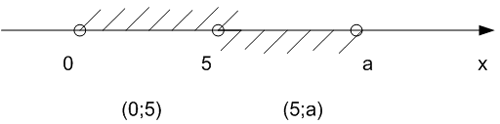
При a > 6 множество
решений неравенства:
.
Интервал (0;5) не может содержать ни одного отрезка
длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в
интервале (5; a).
Это
Ⅲ. Показательные уравнения, неравенства и системы.
Задача № 3. В области определения функции
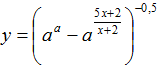
все целые положительные числа и сложили их. Найти все значения, при которых
такая сумма будет больше 5, но меньше 10.
Решение:
1) Графиком дробно-линейной функции
является гипербола. По условию x > 0. При
неограниченном возрастании х дробь
монотонно убывает и приближается к нулю, а значения функции z возрастают
и приближаются к 5. Кроме того, z(0) = 1.
Рис. 5
2) По определению степени область определения D(y)
состоит из решений неравенства
.
При a = 1 получаем неравенство, у которого решений
нет. Поэтому функция у нигде не определена.
3) При 0 < a < 1 показательная функция с
основанием а убывает и неравенство
равносильно неравенству
. Так как x > 0 , то z(x) >
z(0) = 1 . Значит, каждое положительное значение х
является решением неравенства
. Поэтому для таких а указанную в условии сумму нельзя найти.
4) При a > 1 показательная функция с основанием
а возрастает и неравенство
равносильно неравенству
. Если a ≥ 5,
то любое положительное число является его решением, и указанную в условии сумму
нельзя найти. Если 1 < a < 5, то множество
положительных решений – это интервал (0;x0)
, где a = z(x0) .
5) Целые числа расположены в этом интервале подряд, начиная с 1. Вычислим
суммы последовательно идущих натуральных чисел, начиная с 1 : 1; 1+2 = 3; 1+2+3
= 6; 1+2+3+4 = 10;… Поэтому указанная сумма будет больше 5 и меньше 10, только
если число 3 лежит в интервале (0;x0),
а число 4 не лежит в этом интервале. Значит, 3 < x0
≤ 4 . Так как
возрастает на
,
то z(3) < z(x0)
≤ z(4) .
Решение иррациональных уравнений и неравенств, а также уравнений, неравенств
и систем, содержащих модули рассмотрены в Приложении 1.
Задачи с параметрами являются сложными потому, что не существует единого
алгоритма их решения. Спецификой подобных задач является то, что наряду с
неизвестными величинами в них фигурируют параметры, численные значения которых
не указаны конкретно, но считаются известными и заданными на некотором числовом
множестве. При этом значения параметров существенно влияют на логический и
технический ход решения задачи и форму ответа.
По статистике многие из выпускников не приступают к решению задач с
параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению
таких задач, и процент их верного решения невысок: 2–3%,
поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе
задач с параметрами, учащимися школ по-прежнему остается актуальным.
Блок 1. Введение
| 1.1 | Решите уравнения с параметром а: а) ax = − 5; б) (a−1)x = −3; в) (a−2)x = 2−a г) (a−2)x = (a−2)(a+3) |
Смотреть видеоразбор |
| 1.2 | Определите при каких значениях параметра а: а) уравнение |x| = a−3 имеет один корень; б) уравнение |x| = a2−5 не имеет корней. |
Смотреть видеоразбор |
| 1.3 | Функция задана формулой y=x^2+ax+b. Найдите a и b, если: а) график функции проходит через точки (0;3) и (-1;8); б) наименьшее значение, равное −4, функция принимает при x = 1 |
Смотреть видеоразбор |
Блок 2. Координатно-параметрический метод
| 2.1 | Найдите все значения параметра а, при каждом из которых уравнение frac{|3x|-2x-2-a}{x^2-2x-a}=0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.2 | Найдите все значения а, при каждом из которых система уравнений begin{cases} frac{xy^2-3xy-3y+9}{sqrt{x+3}}=0 \ y=ax end{cases} имеет ровно два различных решения | Смотреть видеоразбор |
| 2.3 | Найдите все значения параметра а, при каждом из которых уравнение frac{x^2-4x+a}{5x^2-6ax+a^2} = 0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.4 | Найти все значения а, при каждом из которых уравнение sqrt{3x-2} cdot ln(x-a) = sqrt{3x-2} cdot ln(2x+a) имеет ровно один корень на отрезке [0; 1] | Смотреть видеоразбор |
| 2.5 | Найти все значения а, при каждом из которых уравнение (4^x-3 cdot 2^x + 3a — a^2)cdotsqrt{2-x} = 0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.6 | Найти все действительные значения величины h , при которых уравнение x(x+1)(x+h)(x+1+h) = h^2 имеет 4 действительных корня | Смотреть видеоразбор |
Блок 3. Преобразование графиков
| 3.1 | Найдите все значения a, при каждом из которых наименьшее значение функции f(x) = 2ax+|x^2-8x+7| больше 1 | Смотреть видеоразбор |
| 3.2 | Найти все значения параметра a, при каждом из которых уравнение (|x-2|+|x+a|)^2-7(|x-2|+|x+a|)-4a(4a-7) = 0 имеет ровно два корня | Смотреть видеоразбор |
| 3.3 | Максимальное значение выражения x + 2y при условии log_{frac{x^2+y^2}{2}}ay ge 1 равно 4. Чему равно положительное значение параметра a? | Смотреть видеоразбор |
| 3.4 | Найти все значения параметра a, при каждом из которых уравнение f(x) = |a+2|sqrt[3]{x} имеет 4 решения, где f — чётная периодическая функция с периодом T=frac{16}{3}, определённая на всей числовой прямой, причём f(x)=ax^2, если 0 le x le frac{8}{3} | Смотреть видеоразбор |
Блок 4. Системы с параметром
| 4.1 | Найдите все положительные значения a, при каждом из которых система begin{cases} (|x|-5)^2+(y-4)^2=9 \ (x+2)^2+y^2=a^2 end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.2 | Найдите все значения параметра a, при каждом из которых система уравнений begin{cases} frac{(y^2-xy-4y+2x+4)sqrt{x+4}}{sqrt{5-y}} \ a=x+y end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.3 | Найдите все значения параметра a, при каждом из которых система уравнений begin{cases} (x-2a+3)^2+(y-4)^2=2,25 \ (x+3)^2+(y-a)^2=a^2+2a+1 end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.4 | Найти все значения параметра a, при каждом из которых система begin{cases} ((x-5)^2+(y-3)^2-9)((x-2)^2+(y-1)^2) le 0 \ y=ax+a+3 end{cases} не имеет решений | Смотреть видеоразбор |
Блок 5. Квадратичная функция
| 5.1 | Найти все значения параметра a, при каждом из которых неравенство |frac{x^2+ax+1}{x^2+x+1}| lt 3 выполняется при всех значениях x | Смотреть видеоразбор |
| 5.2 | При каких значениях p вершины парабол y=-x^2+2px+3 и y=x^2-6px+p расположены по разные стороны от оси x? | Смотреть видеоразбор |
| 5.3 | Найти все значения a, при каждом из которых f(x)=x^2-|x-a^2|-5x имеет хотя бы одну точку максимума | Смотреть видеоразбор |
| 5.4 | Найдите все значения параметра a при каждом из которых множество значений функции y=frac{3x+3-2ax}{x^2+2(2a+1)x+4a^2+4a+2} содержит отрезок [0;1] | Смотреть видеоразбор |
| 5.5 | Найти все значения параметра a, при каждом из которых множество значений функции y=frac{5a-15x+ax}{x^2-2ax+a^2+25} содержит отрезок [0;1] | Смотреть видеоразбор |
| 5.6 | Найдите все значения параметра a, при каждом из которых неравенство |frac{x^2+x-2a}{x+a}-1| le 2 не имеет решений на интервале (1;2) | Смотреть видеоразбор |
| 5.7 | Найдите все значения параметра a, при каждом из которых уравнение frac{a^3-(x+2)a^2+xa+x^2}{a+x} = 0 имеет ровно один корень | Смотреть видеоразбор |
| 5.8 | Найдите все значения a, при каждом из которых множество значений функции y=frac{cos{x}-a}{cos{2x}-4}содержит число −2 | Смотреть видеоразбор |
| 5.9 | Найти все значения параметра a, при каждом из которых уравнение (4cos{x}-3-a)cos{x}-2,5cos{2x}+1,5=0 имеет хотя бы один корень | Смотреть видеоразбор |
| 5.10 | Найти все значения параметра a, при каждом из которых уравнение 4^{|x|}=frac{7a}{a-5}cdot 2^{|x|}-frac{12a+17}{a-5} имеет ровно два различных корня | Смотреть видеоразбор |
| 5.11 | Найдите все значения а, при каждом из которых множество решений неравенства frac{a-(a^2-2a-3)cos{x}+4}{sin^2{x}+a^2+1} lt 1 содержит отрезок [-frac{pi}{3}; frac{pi}{2}] | Смотреть видеоразбор |
Блок 6. Расположение корней квадратного уравнения
| 6.1 | Найти все значения параметра a, при которых разность между корнями уравнения x^2+3ax+a^4=0 максимальна | Смотреть видеоразбор |
| 6.2 | Найти все значения параметра а, при каждом из которых уравнение log_{1-x}(a-x+2) = 2 имеет хотя бы один корень, принадлежащий промежутку (-1;1] | Смотреть видеоразбор |
Блок 7. Аналитический метод
| 7.1 | При каких значениях а корни уравнения |x-a^2|=-a^2+2a+3 имеют одинаковые знаки? | Смотреть видеоразбор |
| 7.2 | Найти все значения параметра а, при которых неравенство x^2+2|x-a| ge a^2 справедливо для всех действительных x | Смотреть видеоразбор |
| 7.3 | Найти все значения параметра а, при каждом из которых уравнение |sin^2{x}+2cos{x}+a|=sin^2{x}+cos{x}-a имеет на промежутке (frac{pi}{2};pi] единственный корень | Смотреть видеоразбор |
| 7.4 | Найти все значения параметра а, при каждом из которых уравнение (x^2-4ax+a(4a-1))^2-3(x^2-4ax+a(4a-1))-|a|(|a|-3)=0 имеет более двух корней | Смотреть видеоразбор |
Блок 8. Функциональные методы
| 8.1 | Найти все значения параметра a, при каждом из которых уравнение x^2+(a+7)^2=|x-7-a|+|x+a+7| имеет единственный корень | Смотреть видеоразбор |
| 8.2 | Найти все значения параметра a, при каждом из которых система begin{cases} ax^2+4ax-8y+6a+28 le 0 \ ax^2-6ay-8x+11a-12 le 0 end{cases} имеет ровно одно решение | Смотреть видеоразбор |
| 8.3 | Найдите все значения параметра alpha из интервала (0; pi), при каждом из которых система begin{cases} x^2+y^2-4(x+y)sin{alpha}+8sin^2{alpha} = 2sin{alpha}-1 \ frac{x}{y}+frac{y}{x} = 2sin{alpha}+4sin^2{alpha} end{cases} имеет единственное решение | Смотреть видеоразбор |
| 8.4 | Найдите все неотрицательные значения параметра a, при каждом из которых множество решений неравенства 1 le frac{2a+x^2-4log_{frac{1}{3}}(4a^2-4a+9)}{5sqrt{18x^4+7x^2}+2a+4+(log_{frac{1}{3}}(4a^2-4a+9))} состоит из одной точки и найти это решение. | Смотреть видеоразбор |
| 8.5 | Найдите все значения a, для каждого из которых уравнение 8x^6+(a-|x|)^3+2x^2-|x|+a=0 имеет более трёх различных решений. | Смотреть видеоразбор |
| 8.6 | Найти все значения параметра a, при каждом из которых уравнение x^10+(a-2|x|)^5+x^2-2|x|+a=0 имеет более трёх различных решений. | Смотреть видеоразбор |
| 8.7 | Найти все значения параметра a, при каждом из которых уравнение 64x^6-(a-3x)^3+4x^2+3x=a имеет более одного корня. | Смотреть видеоразбор |
| 8.8 | Найти все значения параметра a, для каждого из которых существует хотя бы одна пара чисел x и y , удовлетворяющих неравенству 5|x-2|+3|x+a| le sqrt{4-y^2}+7 | Смотреть видеоразбор |
| 8.9 | Найти все значения параметра a, при каждом из которых уравнение (log_7(2x+2a)-log_7(2x-2a))^2-8a(log_7(2x+2a)-log_7(2x-2a))+12a^2+8a-4 имеет ровно два корня. | Смотреть видеоразбор |
| 8.10 | Найти все значения параметра a, при каждом из которых уравнение a^2-10a+5sqrt{x^2+25}=4|x-5a|-8|x| имеет хотя бы один корень | Смотреть видеоразбор |
| 8.11 | Найти все значения параметра a, при которых уравнение (a+2)^2 cdot log_3(2x-x^2)+(3x-1)^2 cdot log_{11}(1-frac{x^2}{2})=0 имеет решение | Смотреть видеоразбор |
| 8.12 | При каких значениях параметра a уравнение ax^6=e^x имеет одно положительное решение? | Смотреть видеоразбор |
Блок 9. Разные задачи с параметром
| 9.1 | Найти все значения параметра a, при которых уравнение sqrt{1-(x^2-4x-a^2+2a+3)^6}+sqrt{1+(x^2-4x-a^2+2a+3)^6} = 2 имеет только один положительный корень | Смотреть видеоразбор |
| 9.2 | Найти все положительные значения параметра a, при каждом из которых наименьшее значение f(x)=2x^3-3ax^2+5 на отрезке, заданном неравенством |x-2| le 1, не меньше, чем −3 | Смотреть видеоразбор |
| 9.3 | Найдите все значения параметра b , при каждом из которых для любого a неравенство (x-a-2b)^2+(y-3a-b)^2 lt frac{1}{2} имеет хотя бы одно целочисленное решение (x, y). | Смотреть видеоразбор |
| 9.4 | Найти все a, при каждом из которых уравнение sqrt{a-9cos^4{x}}=sin^2{x} имеет решение | Смотреть видеоразбор |
| 9.5 | Найдите наибольшее целое значение a, при котором уравнение 3x^2-12x+3a+9=4sin{frac{4x-x^2-a-3}{2}} cdot cos{frac{x^2-2x-a-1}{2}} имеет ровно два различных решения | Смотреть видеоразбор |
| 9.6 | Найдите все целые отрицательные значения параметра a, при каждом из которых существует такое действительное число b>a, что неравенство 21b ge 6|a+b|-3|b-2|-|a-b|-9|a^2-b+2|+16 не выполнено | Смотреть видеоразбор |
Квадратные уравнения с параметром
Уравнение называется квадратным, если имеет вид (ax^2+bx+c=0,) где (a,b,c) — любые числа ((a≠0)). При этом надо быть внимательным, если (a=0), то уравнение будет линейным, а не квадратным. Поэтому, первым делом при решении квадратного уравнения с параметром, рекомендую смотреть на коэффициент при (x^2) и рассматривать 2 случая: (a=0) (линейное уравнение); (a≠0) (квадратное уравнение). Квадратное уравнение часто решается при помощи дискриминанта или теоремы Виета.
Исследование квадратного многочлена
Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1) Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:
- Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа (γ): (x_1≤x_2 0)); ветки параболы направлены вниз ((a 0). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)>0).
- (a 0). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа (γ).
В итоге получаем:
если (a*f(γ) 0), то (γ∉(x_1,x_2)).
Нам осталось наложить условие, чтобы наши корни были слева от числа (γ). Здесь нужно просто сравнить положение вершины нашей параболы (x_0) относительно (γ). Заметим, что вершина лежит между точками (x_1) и (x_2). Если (x_0 0, \x_0
При каких значениях параметра a уравнение $$a(a+3) x^2+(2a+6)x-3a-9=0$$ имеет более одного корня?
1 случай: Если (a(a+3)=0), то уравнение будет линейным. При (a=0) исходное уравнение превращается в (6x-9=0), корень которого (x=1,5). Таким образом, при (a=0) уравнение имеет один корень.
При (a=-3) получаем (0*x^2+0*x-0=0), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.
2 случай: Если (a≠0; a≠-3), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня: $$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-frac<1><3>.$$ С учетом (a≠0;) (a≠-3), получим, что уравнение имеет два корня при (a∈(-frac<1><3>;0)∪(0;+∞)). Объединив оба случая получим (внимательно прочитайте, что от нас требуется):
Найти все значения параметра a, при которых корни уравнения $$(a+1) x^2-(a^2+2a)x-a-1=0$$ принадлежат отрезку ([-2;2]).
1 случай: Если (a=-1), то (0*x^2-x+1-1=0) отсюда (x=0). Это решение принадлежит ([-2;2]).
2 случай: При (a≠-1), получаем квадратное уравнение, с условием, что все корни принадлежат ([-2;2]). Для решения введем функцию (f(x)=(a+1) x^2-(a^2+2a)x-a-1) и запишем систему, которая задает требуемые условия:
Подставляем полученные выражения в систему:
Уравнения с параметром
Разделы: Математика
Справочный материал
Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.
Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.
Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет
Если 1 – а 0, т.е. а 1, то х =
Пример 4.
Если а = 1, то 0х = 0
х – любое действительное число
Если а = -1, то 0х = -2
Корней нет
Если а 1, а -1, то х = 
Это значит, что каждому допустимому значению а соответствует единственное значение х.
если а = 5, то х =
=
;
Дидактический материал
3. а = 
4. + 3(х+1)
5. = –
6. =
Ответы:
- При а1 х =;
- При а3 х = ;
- При а1, а-1, а0 х = ;
при а = 1 х – любое действительное число, кроме х = 1
- При а2, а0 х = ;
- При а-3, а-2, а0, 5 х =
- При а + с0, с0 х = ;
Квадратные уравнения с параметром
Пример 1. Решить уравнение
х = –
В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.
Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16
a =
a =
Если а -4/5 и а 1, то Д > 0,
х =
х = – = –
Пример 2. При каких значениях параметра а уравнение
х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?
| В итоге | 4(а – 1)(а – 6) > 0 — 2(а + 1) 0 |
а 6 а > — 1 а > 5/9 |
6 |
Пример 3. Найдите значения а, при которых данное уравнение имеет решение.
Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а
4а 2 – 16 0
4а(а – 4) 0
а(а – 4)) 0
Ответ: а 0 и а 4
Дидактический материал
1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а 2 – 6а + 
4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?
5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?
Показательные уравнения с параметром
Пример 1.Найти все значения а, при которых уравнение
9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.
Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение
3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)
Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или
Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log32 , или х 2 – хlog32 + 1 = 0.
Это уравнение не имеет действительных корней, так как его Д = log 2 32 – 4 х+1/х = а то х + 1/х = log3а, или х 2 – хlog3а + 1 = 0. (3)
Уравнение (3) имеет ровно два корня тогда и только тогда, когда
Д = log 2 32 – 4 > 0, или |log3а| > 2.
Если log3а > 2, то а > 9, а если log3а 9.
Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?
Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х1 = -3, х2 = а = >
а – положительное число.
Дидактический материал
1. Найти все значения а, при которых уравнение
25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.
2. При каких значениях а уравнение
2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?
3. При каких значениях параметра а уравнение
4 х — (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?
Ответ:
- 0 25/2
- при а = 1, а = -2,2
- 0 0, х1/4 (3)
х = у
| Если а = 0, то – | 2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4 |
Не выполняется (2) условие из (3).
Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.
Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).
Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х
Выражая х из (1) и подставляя в (2), получаем неравенство
2 – а > 1 – а (3)
Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.
Решения неравенства (3) образуют промежуток (а0; 2), где а0 2
а0 =
Ответ: x + 9a 3 ) = x имеет ровно два корня.
Ответы:
-
при а 16.06.2009
Квадратные уравнения и квадратичные неравенства с параметрами
Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.
Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.
1. Найдите все значения a, при которых уравнение не имеет действительных корней.
Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.
Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.
Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.
Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.
Если и – корни квадратного уравнения
, то по теореме Виета:
Решим первое неравенство системы
Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .
Возведем второе уравнение системы в квадрат:
Из этих двух уравнений выразим сумму квадратов и .
Значит, сумму квадратов корней уравнения можно выразить через параметр
График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:
3) Найдите все значения , при каждом из которых все решения уравнения
Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно
1) . Получим линейное уравнение
У него единственный корень, причем положительный. Это удовлетворяет условию задачи.
2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .
Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:
— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.
Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.
— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.
Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.
Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим
Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.
С учетом пункта 1 получим ответ
4. При каких значениях параметра a уравнение
имеет единственное решение?
Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .
Сделаем замену
Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.
1) В случае уравнение будет линейным
Значит, подходит. В этом случае уравнение имеет единственный положительный корень.
2) Если , уравнение будет квадратным.
Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.
Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.
Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.
Объединив все случаи, получим ответ.
И наконец – реальная задача ЕГЭ.
5. При каких значениях a система имеет единственное решение?
Решением квадратного неравенства может быть:
В каких случаях система двух квадратных неравенств имеет единственное решение:
1) единственная общая точка двух лучей-решений ( или интервалов-решений)
2) одно из неравенств имеет решение – точку, которая является решением второго неравенства
Рассмотрим первый случай.
Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или
Если , при этом система примет вид:
Второй корень первого уравнения:
Второй корень второго первого:
Если , при этом система примет вид:
– бесконечно много решений, не подходит.
Рассмотрим второй случай.
– решением является точка, если – является решением второго неравенства.
– решением является точка, если – не является решением первого неравенства.
http://urok.1sept.ru/articles/534897
Квадратные уравнения и квадратичные неравенства с параметрами





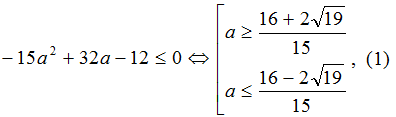
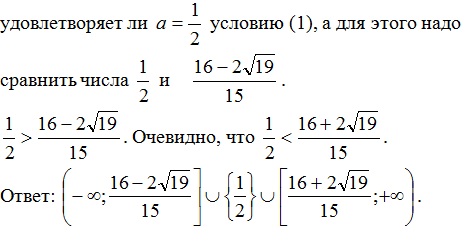
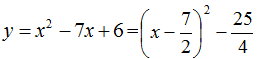

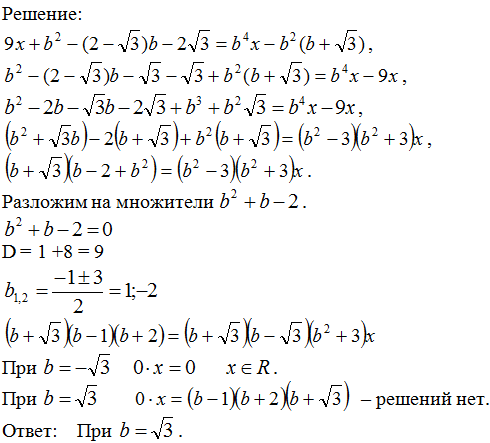
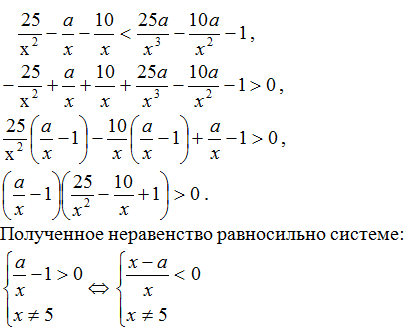
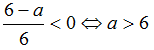
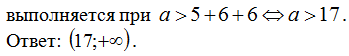
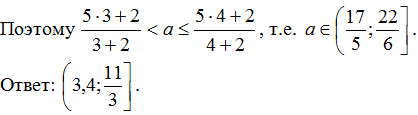


 =
=  ;
;