Перейти к содержанию
Положительные элементы главной диагонали
Просмотров 3.5к. Обновлено 26 октября 2021
Диагонали выделяют только в том случае, если матрицы квадратные, то есть количество строк равно количеству столбцов. Элементы главной диагонали имеют индексы [1,1], [2,2], … [N,N] (при условии индексации с единицы).
Поскольку первый индекс равен второму, то, перебирая матрицу в цикле, при обращении к элементам главной диагонали достаточно использовать одну переменную счетчик (например, i): имя_массива[i,i].
Если очередной элемент диагонали больше нуля, то выводим его на экран.
Pascal
const
N = 10;
var
arr: array[1..N,1..N] of integer;
i,j: byte;
begin
randomize;
for i:=1 to N do begin // просто заполнение матрицы
for j:=1 to N do begin
arr[i,j] := random(100) - 50;
write(arr[i,j]:4);
end;
writeln;
end;
writeln;
for i:=1 to N do // решение задачи
if arr[i,i] > 0 then
write(arr[i,i]:4);
writeln;
end.
-27 -12 37 -33 4 -44 44 5 21 -11
-46 -18 2 2 31 -36 47 -33 -11 41
-12 47 41 14 25 26 6 22 49 -48
-22 -7 -25 49 -13 -26 13 31 -15 -11
-5 30 31 -26 -48 26 44 1 -49 -4
22 -49 18 -20 -5 -25 0 -8 16 -19
-21 -5 30 -14 27 -35 -34 42 39 21
-2 -24 19 -48 -13 2 -35 44 -1 14
-47 45 -21 29 17 -9 27 -38 25 7
47 -20 -45 -22 -36 -43 12 5 40 -2241 49 44 25
Язык Си
#include < stdio.h>
#define N 10
main() {
int a[N][N], i, j;
srand(time(NULL));
for (i=0; i< N; i++) {
for (j=0; j< N; j++) {
a[i][j] = rand()%100 - 50;
printf("%4d", a[i][j]);
}
printf("n");
}
printf("n");
for (i=0; i< N; i++)
if (a[i][i] > 0) {
printf("%4d", a[i][i]);
}
printf("n");
}
Python
from random import random
N = 10
a = []
for i in range(N):
z = []
for j in range(N):
n = int(random() * 100) - 50
z.append(n)
print("%4d" % n, end='')
print()
a.append(z)
print()for i in range(N):
if a[i][i] > 0:
print("%4d" % a[i][i], end='')
print()
КуМир
алг полож элем диаг
нач
цел N=10
цел таб a[1:N,1:N]
цел i, j
нц для i от 1 до N
нц для j от 1 до N
a[i,j] := int(rand(0,100)) - 50
вывод a[i,j]:4
кц
вывод нс
кц
вывод нснц для i от 1 до N
если a[i,i] > 0 то
вывод a[i,i], " "
все
кц
вывод нс
кон
Basic-256
N = 10
dim a(N,N)
for i=0 to N-1
for j=0 to N-1
a[i,j] = int(rand*100)-50
print a[i,j]+" ";
next j
next ifor i=0 to N-1
if a[i,i] > 0 then print a[i,i] + " ";
next i
Python
Python задачи
Задачка. Положительные элементы главной диагонали
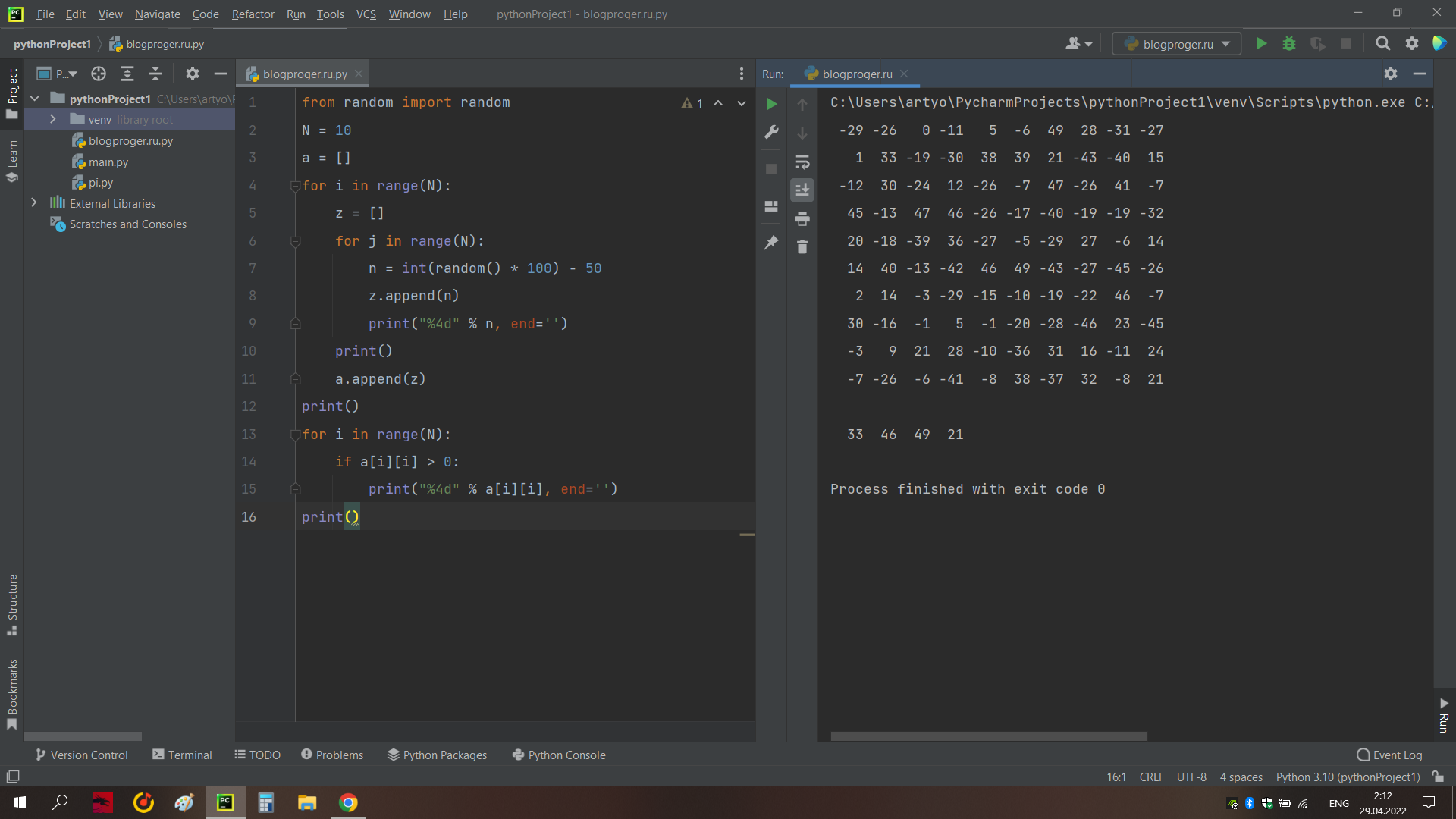
Найти положительные элементы главной диагонали квадратной матрицы.Разбор задачи на Python
задача на python
Диагонали выбираются только в том случае, если матрицы квадратные, то есть количество строк равно количеству столбцов. Элементы главной диагонали имеют индексы , , … (при условии нумерации от единицы).
Поскольку первый индекс равен второму, при обходе матрицы в цикле достаточно использовать одну переменную-числитель (например, i): имя_массива при обращении к элементам главной диагонали.
Если следующий диагональный элемент больше нуля, отобразите его на экране.
решение задачи с python
from random import random
N = 10
a = []
for i in range(N):
z = []
for j in range(N):
n = int(random() * 100) — 50
z.append(n)
print(«%4d» % n, end=»)
print()
a.append(z)
print()
for i in range(N):
if a[i][i] > 0:
print(«%4d» % a[i][i], end=»)
print()
Python
Python задачи
Все задачи на python
Репост статьи
29 апреля 2022 г.
Комментарии могут оставлять только зарегестрированные пользователи!
Комментарии
Ваш комментарий будет первым !
Опишите алгоритм определения количества положит…
Задание:
Опишите на русском языке или на одном из языков программирования алгоритм определения количества положительных элементов квадратной матрицы, превышающих по величине среднее арифметическое всех элементов главной диагонали.
Решение:
В этой задаче нужно сначала найти среднее арифметическое всех элементов главной диагонали. Для этого требуется один простой (не вложенный!) цикл, потому что для элементов главной диагонали номер строки равен номеру столбца.
Пусть N (константа) – количество строк (и столбцов!) матрицы A. Введем вещественную переменную sred, в которой сначала подсчитаем сумму всех элементов главной диагонали. Введем целую переменную i, обозначающую номер строки. Запишем в sred начальное значение 0. В цикле изменяем i от 1 до N с шагом 1, добавляем к значению переменной sred значение элемента матрицы A[i,i]. После окончания цикла разделим sred на N (на главной диагонали всего N элементов), таким образом, в sred находится среднее значение элементов главной диагонали.
Теперь можно считать (только!) положительные элементы всей матрицы, которые больше sred. Вводим целочисленные переменные j (номер столбца) и count (счетчик «нужных» элементов) . В счетчик записываем начальное значение 0.
Организуем двойной цикл, перебирающий все комбинации (i,j) для i=1..N и j=1..N. В теле цикла проверяем элемент матрицы A[i,j]: если он больше нуля и больше sred, увеличиваем счетчик count на 1.
После окончания двойного цикла выводим значение count.
Программа может выглядеть так:
const N=5;
var A:array[1..N,1..N] of integer;
i, j, count: integer;
sred: real;
begin
for i:=1 to N do { ввод матрицы }
for j:=1 to N do readln(A[i,j]);
sred := 0; { находим сумму главной диагонали }
for i:=1 to N do
sred := sred + A[i,i];
sred := sred / N; { находим среднее }
count := 0; { считаем нужные элементы }
for i:=1 to N do
for j:=1 to N do
if (A[i,j] > 0) and (A[i,j] > sred) then
count := count + 1;
writeln(count)
end.
Заметим, что можно немного улучшить программу. В условном операторе в последнем двойном цикле можно заменить сложное условие простым, если вместо 0 и sred использовать максимальное из этих значений. Перед двойным циклом нужно добавить оператор
if sred < 0 then sred := 0;
а условный оператор изменить так:
if A[i,j] > sred then
count := count + 1;
Во-вторых, можно немного более грамотно обработать условие A[i,j] > sred. Дело в том, что при делении в операторе
sred := sred / N; { находим среднее }
может получиться вещественное число (с дробной частью). Вещественные числа (за редким исключением ) хранятся в памяти компьютера неточно, потому что в двоичном коде содержат (теоретически) бесконечное число разрядов. Поэтому лучше НЕ делить полученную сумму sred на N, а для проверки вместо условия A[i,j] > sred/N использовать равносильное ему A[i,j]*N > sred. Плюс в том, что в последнем случае все операции выполняются с целыми числами и ошибок из-за неточного представления дробных чисел в памяти гарантированно не будет. Однако, есть и минус: вместо одного деления (на всю программу) придется выполнять N2 умножений (для каждого элемента матрицы). Вот еще одна версия программы:
const N=5;
var A:array[1..N,1..N] of integer;
i, j, count: integer;
sred: real;
begin
for i:=1 to N do { ввод матрицы }
for j:=1 to N do readln(A[i,j]);
sred := 0; { находим сумму главной диагонали }
for i:=1 to N do
sred := sred + A[i,i];
count := 0; { считаем нужные элементы }
if sred < 0 then sred := 0;
for i:=1 to N do
for j:=1 to N do
if A[i,j]*N > sred then
count := count + 1;
writeln(count)
end.
Матрица— это двумерный массив,
каждый элемент которого имеет два
индекса: номер строки — i; номер
столбца — j. Поэтому для работы
с элементами матрицы необходимо
использовать два цикла. Если значениями
параметра первого цикла будут номера
строк матрицы, то значениями параметра
второго — столбцы (или наоборот). Обработка
матрицы заключается в том, что вначале
поочередно рассматриваются элементы
первой строки (столбца), затем второй и
т.д. до последней. Рассмотрим основные
операции, выполняемые над матрицами
при решении задач.
4.2. Алгоритм ввода-вывода матриц
Матрицы, как и массивы, нужно вводить
(выводить) поэлементно. Блок-схема ввода
элементов матрицы изображена на рис.
4.1. Вывод матрицы организуется аналогично
вводу.
|
|
|
|
Рис. 4.1. Ввод |
Рис. 4.2. |
Рассмотрим несколько задач обработки
матриц. Для их решения напомним читателю
некоторые свойства матриц (рис. 4.2):
-
если номер строки элемента совпадает
с номером столбца (i = j), это
означает что элемент лежит на главной
диагонали матрицы; -
если номер строки превышает номер
столбца (i > j), то элемент
находится ниже главной диагонали; -
если номер столбца больше номера строки
(i<j), то элемент находится
выше главной диагонали. -
элемент лежит на побочной диагонали,
если его индексы удовлетворяют равенству
i+j-1
= n; -
неравенство i+j-1
< n характерно для элемента
находящегося выше побочной диагонали; -
соответственно, элементу лежащему ниже
побочной диагонали соответствует
выражение i+j-1
> n.
4.3. Примеры алгоритмов обработки матрицами
ПРИМЕР 4.1. Найти сумму элементов
матрицы, лежащих выше главной диагонали
(рис 4.3).
|
|
|
Рис. 4.3. |
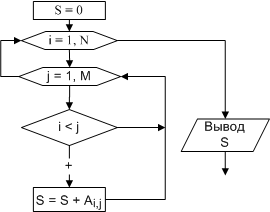
Алгоритм решения данной задачи (рис.
4.4) построен следующим образом: обнуляется
ячейка для накапливания суммы (переменная
S). Затем с помощью двух циклов
(первый по строкам, второй по столбцам)
просматривается каждый элемент матрицы,
но суммирование происходит только в
том случае если, этот элемент находится
выше главной диагонали, то есть выполняется
свойство i < j.
На рисунке 4.5 изображен еще один вариант
решения данной задачи. В нем проверка
условия i<j не выполняется,
но, тем не менее, в нем так же суммируются
элементы матрицы, находящиеся выше
главной диагонали. Для того чтобы понять,
как работает этот алгоритм, вернемся к
рисунку 4.3. В первой строке заданной
матрицы необходимо сложить все элементы,
начиная со второго. Во второй — все,
начиная с третьего, в i-й строке
процесс начнется с (i+1)-го
элемента и так далее. Таким образом,
первый цикл работает от 1 до N,
а второй от i+1
до M. Предлагаем читателю
самостоятельно составить программу,
соответствующую описанному алгоритму.
|
|
|
|
Рис. 4.4. |
Рис. 4.5. |
ПРИМЕР 4.2. Вычислить количество
положительных элементов квадратной
матрицы, расположенных по ее периметру
и на диагоналях. Напомним, что в квадратной
матрице число строк равно числу столбцов.
Прежде чем преступить к решению задачи
рассмотрим рисунок 4.6, на котором
изображена схема квадратных матриц
различной размерности. Из условия задачи
понятно, что не нужно рассматривать все
элементы заданной матрицы. Достаточно
просмотреть первую и последнюю строки,
первый и последний столбцы, а так же
диагонали. Все эти элементы отмечены
на схеме, причем черным цветом выделены
элементы, обращение к которым может
произойти дважды. Например, элемент с
номером (1,1) принадлежит как к первой
строке, так и к первому столбцу, а элемент
с номером (N,N) находится в
последней строке и последнем столбце
одновременно. Кроме того, если N
— число нечетное (на рисунке 4.6 эта матрица
расположена слева), то существует элемент
с номером (N/2+1, N/2+1), который
находится на пересечении главной и
побочной диагоналей. При нечетном
значении N (матрица справа на
рис. 4.6) диагонали не пересекаются.
|
|
|
Рис. 4.6. |
Итак, разобрав подробно постановку
задачи, рассмотрим алгоритм ее решения.
Для обращения к элементам главной
диагонали вспомним, что номера строк
этих элементов всегда равны номерам
столбцов. Поэтому, если параметр i
изменяется циклически от 1 до N,
то Ai,i — элемент главной диагонали.
Воспользовавшись свойством, характерным
для элементов побочной диагонали
получим: i+j-1
= n > j = n-i+1,
следовательно, для i=1,2,…,n
элемент Аi,n-i+1
— элемент побочной диагонали. Элементы,
находящиеся по периметру матрицы
записываются следующим образом: А1,i
— первая строка, АN,i — последняя
строка и соответственно Аi,1 —
первый столбец, Аi,N — последний
столбец.
Блок-схема описанного алгоритма
изображена на рис. 4.7. В блоке 1 организуется
цикл для обращения к диагональным
элементам матрицы. Причем в блоках 2-3
подсчитывается количество положительных
элементов на главной диагонали, а в
блоках 5-6 на побочной. Цикл в блоке 6
задает изменение параметра i
от 2 до N-1. Это необходимо для
того, чтобы не обращать к элементам,
которые уже были рассмотрены: A11,
A1N, AN,1
и AN,N. Блоки 7-8
подсчитывают положительные элементы
в первой строке, 9 и 10 — в последней строке,
11 и 12 — в первом столбце, а 13 и 14 в последнем.
Блок 15 проверяет, не был ли элемент,
находящийся на пересечении диагоналей,
подсчитан дважды. Напомним, что это
могло произойти только в том случае,
если N — нечетное число и этот
элемент был положительным. Эти условия
и проверяются в блоке 16, который уменьшает
вычисленное количество положительных
элементов на единицу.
|
|
|
Рис. 4.7. |
ПРИМЕР 4.3. Проверить, является
ли заданная квадратная матрица единичной.
Единичной называют матрицу, у которой
элементы главной диагонали — единицы,
а все остальные — нули.
|
|
Решать задачу будем так. Предположим,
что матрица единичная (FL=ИСТИНА)
и попытаемся доказать обратное. Если
окажется, что хотя бы один диагональный
элемент не равен единице или любой из
элементов вне диагонали не равен нулю,
то матрица единичной не является
(FL=ЛОЖЬ). Воспользовавшись
логическими операциями все эти условия
можно соединить в одно и составить
блок-схему (рис. 4.8).
|
|
|
Рис. 4.8. |
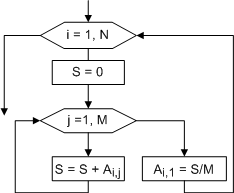
ПРИМЕР 4.4. Преобразовать
исходную матрицу так, чтобы первый
элемент каждой строки был заменен
средним арифметическим элементов этой
строки.
Для решения данной задачи необходимо
найти в каждой строке сумму элементов,
которую разделить на их количество.
Полученный результат записать в первый
элемент соответствующей строки.
Блок-схема алгоритма решения приведена
на рис. 4.9.
ПРИМЕР 4.5. Задана матрица An,
m. Сформировать вектор Pm,
в который записать номера строк
максимальных элементов каждого столбца.
Алгоритм решения этой задачи следующий:
для каждого столбца матрицы находим
максимальный элемент и его номер, номер
максимального элемента j-го
столбца матрицы записываем в j-й
элемент массива P. Блок-схема
алгоритма приведена на рис. 4.10.
|
|
|
|
Рис. 4.9. |
Рис. 4.10. |
ПРИМЕР 4.6. Написать программу
умножения двух матриц An,m и
Bm,l.
Например, необходимо перемножить две
матрицы
|
|
Воспользовавшись правилом «строка
на столбец», получим матрицу:
|
|
В общем виде формула для нахождения
элемента Ci,j матрицы имеет вид:
|
|
где i = 1,N и |
Обратите внимание, что проводить операцию
умножения можно только в том случае,
если количество строк левой матрицы
совпадает с количеством столбцов правой.
Кроме того, A ><
B ≠ B >< A.
Блок-схема, изображенная на рис. 4.11,
реализует расчет каждого элемента
матрицы C в виде суммы по
вышеприведенной формуле.
ПРИМЕР 4.7. Поменять местами
n-й и l-й столбцы матрицы A(k,m).
Блок-схема приведена на рис. 4.12.
|
|
|
|
Рис. 4.11. |
Рис. 4.12. |
ПРИМЕР 4.8. Преобразовать матрицу
A(m,n) таким образом, чтобы каждый
столбец был упорядочен по убыванию.
Алгоритм решения этой задачи сводится
к тому, что уже известный нам по предыдущей
главе алгоритм упорядочивания элементов
в массиве выполняется для каждого
столбца матрицы. Блок-схема приведена
на рис. 4.13.
ПРИМЕР 4.9. Преобразовать матрицу
A(m,n) так, чтобы строки с нечетными
индексами были упорядочены по убыванию,
c четными — по возрастанию. Блок-схема
приведена на рис. 4.14.
|
|
|
|
Рис 4.13. |
Рис. 4.14. |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 01.11.2016 Сообщений: 35 |
|
|
1 |
|
Найти первый и последний положительный элемент в строках матрицы26.01.2017, 16:28. Показов 3048. Ответов 2
Организовать двухмерный массив с вещественными числами и найти первый и последний положительный элемент в строках массива.
0 |
|
FreeYourMind 147 / 147 / 104 Регистрация: 13.11.2016 Сообщений: 557 |
||||
|
26.01.2017, 16:43 |
2 |
|||
|
Решение
0 |
|
MrGluck Форумчанин 8194 / 5044 / 1437 Регистрация: 29.11.2010 Сообщений: 13,453 |
||||
|
26.01.2017, 16:52 |
3 |
|||
0 |










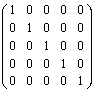









 Сообщение было отмечено SlavaCherep как решение
Сообщение было отмечено SlavaCherep как решение