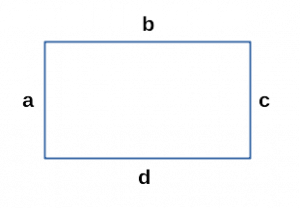
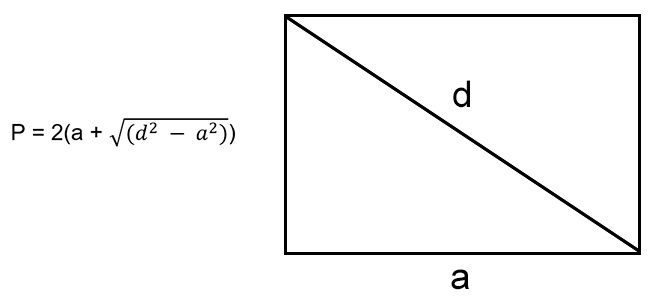Периметр прямоугольника
Периметр прямоугольника — это сумма
всех сторон прямоугольника.
Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.
Самый простой способ найти периметр
прямоугольника, это сложить все стороны.
Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.
Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.
В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.
Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.
Формулы периметра прямоугольника
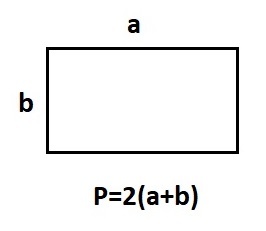
- Периметр прямоугольника через четыре стороны
Полупериметр
Полупериметр — это половина периметра.
Обозначается латинской буквой p.
Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.
[ p = frac
= P cdot 0.5 ]
Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.
Основные определения и величины
Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.
Обозначается латинской буквой a.
Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.
Обозначается латинской буквой b.
Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.
Обозначается латинской буквой a или b.
Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.
Обозначается латинской буквой c или d.
Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.
Обозначается латинской буквой l.
Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.
Обозначается латинской буквой R.
Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.
Как вычислить площадь и периметр прямоугольника
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество просмотров этой статьи: 15 252.
Прямоугольник — это четырехугольник (двумерная фигура) с четырьмя прямыми углами. Параллельные стороны прямоугольника равны. [1] X Источник информации Прямоугольник, у которого все стороны равны, называется квадратом. Все квадраты являются прямоугольниками, но не все прямоугольники — квадраты. Периметр фигуры равен сумме значений ее сторон. [2] X Источник информации Площадь фигуры равна произведению ее длины на ширину. [3] X Источник информации
Как найти периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Варианты нахождения периметра прямоугольника
По сторонам
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
где (a) и (b) — это две соседние стороны фигуры.
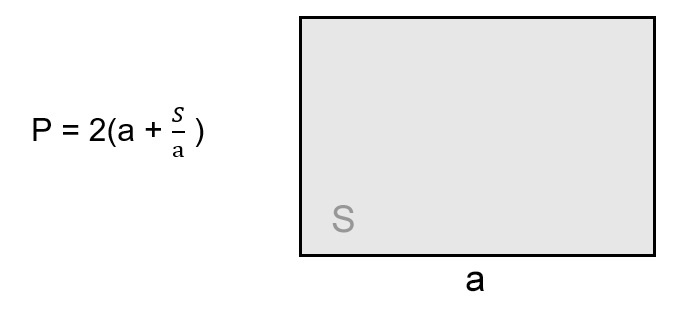
По любой стороне и площади
Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
Так как площадь прямоугольника — это произведение двух его смежных сторон ((S=atimes b)) , чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: (b=frac Sa) .
Получается, что формула для расчета (P) рассматриваемой фигуры будет выглядеть следующим образом:
По любой стороне и диагонали
В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.
где (d) — диагональ прямоугольника, а (b) — неизвестная сторона.
Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:
По любой стороне и радиусу описанной окружности
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:
где (R) — радиус описанной окружности.
Тогда формула для расчета P будет выглядеть так:
Примеры решения задач
Задача 1
Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.
Решение:
Применяем самую первую формулу для расчета:
Задача 2
Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 (см^2) , одна из его сторон равна 6 см. Вычислить Р фигуры.
Решение:
Берем формулу (P=2(frac Sa+a)) и подставляем известные значения:
Задача 3
Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.
Решение:
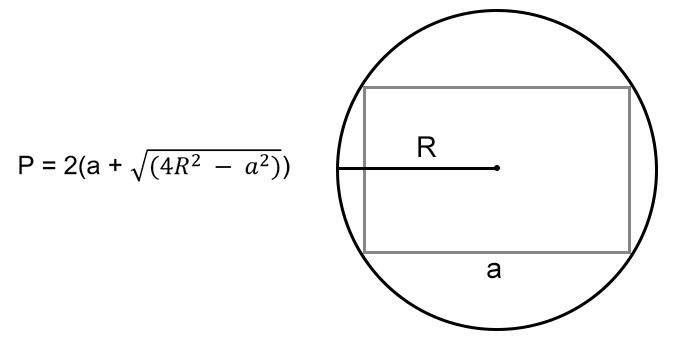
Вспоминаем формулу для расчета (P=2(a+sqrt)) и вставляем известные величины:
Задача 4
Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.
Решение:
В этом случае для расчета суммы длин всех сторон применяем формулу (P=2(a+sqrt)) . Используем известные значения и получаем:
Как найти периметр, если известна площадь и ширина
1 апреля 2012
Автор КакПросто!
Периметр — это сумма всех сторон многоугольника. Если несколько сторон многоугольника имеют одинаковый размер, суммирование при вычислении периметра можно сочетать с умножением для ускорения расчета. Для правильных многоугольников применяются готовые формулы нахождения периметра.
Статьи по теме:
Инструкция
Чтобы вычислить периметр при заданных площади и ширине многоугольника, нужно знать знать тип многоугольника. Параметры «длина» и «ширина» обычно применяются для характеристики прямоугольника. Прямоугольником называется четырехугольник с прямыми углами и попарно равными сторонами.
Определите длину прямоугольника. Для этого разделите заданную в условии площадь на ширину.
Периметр прямоугольника вычислите по формуле Р=2L+2S,где Р — искомый периметр; S — заданная в условии ширина; L — длина, вычисленная в п.2.
Частный случай прямоугольника — квадрат. Все четыре стороны квадрата равны. Поэтому для вычисления периметра достаточно знать размер одной стороны. Вычислите периметр квадрата по формуле Р=4S,где Р — искомый периметр; S — заданная в условии ширина.
Параллелограмм — тоже правильный многоугольник. Стороны в нем попарно равны и параллельны. Вычислить размер стороны параллелограмма по известной площади и другой стороне нельзя. Необходимо знать угол между сторонами параллелограмма. Заданных условий недостаточно для вычисления периметра параллелограмма.
Начертите произвольный параллелограмм. На сторону с известным по условию размером опустите высоту из вершины параллелограмма. При заданных ширине и площади высота параллелограмма — величина неизменная и равна частному от деления площади на ширину. Угол между сторонами параллелограмма по условию не задан. При изменении угла будет меняться размер неизвестной стороны параллелограмма. Таким образом задача имеет множество решений.
www.kakprosto.ru
Если известна площадь как вычислить периметр
Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет. Задание 6. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет. Решение. Пусть катет BC=x, тогда катет AC = x+2. Площадь.
Как найти периметр если известна площадь
Площадь и периметр — основные числовые характеристики любых геометрических фигур. Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных.
Спонсор размещения P&G Статьи по теме «Как найти периметр если известна площадь» Как найти площадь треугольника Как найти площади треугольника и прямоугольника Как определить площадь трапеции
Задача: найдите периметр прямоугольника, если известно, что площадь равна 18, а длина прямоугольника в 2 раза больше ширины.
Решение: запишите формулу площади для прямоугольника – S = a*b. По условию задачи b = 2*a, отсюда 18 = a*2*a, a = v9 = 3. Очевидно, что b = 6. По формуле периметр равен сумме всех сторон прямоугольника – P = 2*a + 2*b = 2*3 + 2*6 = 6 + 12 = 18. В данной задаче периметр совпал по значению с площадью фигуры.
Задача: найдите периметр квадрата, если его площадь равна 9.
Решение: по формуле площади квадрата S = a^2, отсюда найдите длину стороны a = 3. Периметр равен сумме длин всех сторон, следовательно, P = 4*a = 4*3 = 12.
Задача: дан произвольный треугольник ABC, площадь которого равна 14. Найдите периметр треугольника, если проведенная из вершины B высота делит основание треугольника на отрезки длиной 3 и 4 см.
Решение: по формуле площадь треугольника – это половина произведения основания на высоту, т. е. S = ?*AC*BE. Периметр равен сумме длин всех сторон. Длину стороны AC найдите, сложив длины AE и EC, AC = 3 + 4 = 7. Найдите высоту треугольника BE = S*2/AC = 14*2/7 = 4.
Рассмотрите прямоугольный треугольник ABE. Зная катеты AE и BE, можно найти гипотенузу по формуле Пифагора AB^2 = AE^2 + BE^2, AB = v(3^2 + 4^2) = v25 = 5.
Рассмотрите прямоугольный треугольник BEC. По формуле Пифагора BC^2 = BE^2 + EC^2, BC = v(4^2 + 4^2) = 4*v2.
Теперь известны длины всех сторон треугольника. Найдите периметр из их суммы P = AB + BC + AC = 5 + 4*v2 + 7 = 12 + 4*v2 = 4*(3+v2).
Задача: известно, что площадь окружности равна 16*?, найдите ее периметр.
Решение: запишите формулу площади окружности S = ?*r^2. Найдите радиус окружности r = v(S/?) = v16 = 4. По формуле периметр P = 2*?*r = 2*?*4 = 8*?. Если принять, что? = 3.14, то P = 8*3.14 = 25.12.
Другие новости по теме:
Задачи на нахождение длины сторон являются одними из самых распространенных в курсе геометрии. Алгоритм их решения зависит от исходных данных, особенностей рассматриваемой фигуры. Вам понадобится — тетрадь; — линейка; — карандаш; — ручка; — калькулятор. Спонсор размещения P&G Статьи по теме
Периметр любой геометрической фигуры, в том числе треугольника, равен совокупной длине границ этой фигуры. Он обозначается заглавной латинской буквой P и легко находится методом сложения длин всех сторон данной фигуры. Спонсор размещения P&G Статьи по теме «Как вычислить периметр треугольника»
Площадь прямоугольника находится по формуле S = ab, где a и b – смежные стороны данной фигуры. Поэтому если известна длина только одной из этих сторон, то первое, что вам нужно сделать, – вычислить длину второй. Спонсор размещения P&G Статьи по теме «Как найти площадь прямоугольника, если известна
Треугольник — это многоугольник, имеющий три стороны и три угла. Как же вычислить его периметр? Спонсор размещения P&G Статьи по теме «Как находить периметр треугольника» Как найти периметр треугольника, заданного координатами своих вершин Как найти площадь треугольника Как найти длину и ширину
Геометрия изучает свойства и характеристики двумерных и пространственных фигур. Числовыми величинами, характеризующими такие конструкции, являются площадь и периметр, вычисление которых производится по известным формулам или выражается одно через другое. Спонсор размещения P&G Статьи по теме «Как
Казалось бы, что может быть проще, чем вычисление площади и периметра треугольника – измерил стороны, поставил цифры в формулу – и все. Если вы так считаете, значит, забыли, что для этих целей существует не две простенькие формулы, а гораздо больше – для каждого вида треугольника – своя. Вам
Квадрат — правильный четырехугольник, у которого все стороны равны, и все углы прямые. Периметром квадрата называется сумма длин всех его сторон, а площадью – произведение двух сторон или квадрат одной стороны. Исходя из известных соотношений, через один параметр можно вычислить другой. Спонсор
Формулы для нахождения площади и периметра прямоугольника кажутся так же крепко засевшими в памяти, как и таблица умножения. Впрочем, иногда заветные символы оказываются совсем уж глубоко в дебрях памяти, так что не лишним будет повторить их. Вам понадобится Линейка, карандаш Спонсор размещения P&G
С задачей найти периметр или площадь многоугольника сталкиваются не только ученики на уроках геометрии. Порой ее случается решать и взрослому человеку. Приходилось ли вам рассчитывать необходимое количество обоев для комнаты? Или, может быть, вы измеряли протяженность дачного участка, чтобы
Периметром плоской фигуры называют сумму длин всех ее сторон. Но найти стороны фигуры, зная только периметр — не всегда выполнимая задача. Часто требуются дополнительные данные. Спонсор размещения P&G Статьи по теме «Как найти стороны, если известен периметр» Как найти периметр
Если известна площадь как вычислить периметр
Как найти периметр если известна площадь
Площадь и периметр — основные числовые характеристики любых геометрических фигур. Нахождение этих величин у
poiskvstavropole.ru
Как рассчитать площадь, зная периметр
Судя по формулировке вопроса, длины сторон непосредственно измерены Вами, т. е имеется либо чертеж четырехугольника, либо сам четырехугольник в натуральном виде. Тогда ничего не стоит измерить длины диагоналей, достаточно даже одной. Диагональ разбивает Ваш четырехугольник на два треугольника, длины сторон каждого из которых известны (измерены) . Тогда площадь каждого треугольника вычисляется по формуле Герона S=√(p*(p-a)*(p-b)*(p-c)), где p — полупериметр треугольника: p=(a+b+c)/2, a, b, c — длины сторон треугольника. Ну, и сложить площади двух треугольников.
никак
он неправильный
можно в AutoСade
Вычертить полилинией. В Свойствах покажет площадь.
Представьте себе, что фигура сделана из стержней, шарнирно
соединенных в вершинах. Форму такой фигуры можно изменять
в довольно широких пределах — при этом периметр не изменяется.
Вывод: по периметру площадь однозначно найти нельзя.
Ещё должна быть известна длина одной из диагоналей.
мне кажется что периметр нужно поделить на 4 и потом помножить на 2 получится площадь
touch.otvet.mail.ru
Как найти периметр зная площадь
Затеяв ремонт, необходимо в первую очередь иметь план действий и рассчитать свой бюджет. Только при грамотной планировке можно добиться качественной работы в короткие сроки. Если вы собираетесь сделать ремонт своего потолка, то необходимо сделать необходимые замеры. Зная площадь потолка можно примерно рассчитать, сколько материалов нужно будет купить и сколько будет стоимость услуги мастеров, если собираетесь обратиться к ним. Но площадь прямоугольника – это еще не все. Иногда бывает так, что нужно знать периметр прямоугольника . встает вопрос можно ли узнать периметр, зная при этом площадь? Рассмотрим этот вопрос повнимательнее, и постараемся найти периметр прямоугольника.
Данные необходимые для того чтобы найти периметр
Сумма всех сторон прямоугольника называется периметром – это еще мы уяснили из курса арифметики начальных классов. Как видно из условия необходимо знать длину сторон. Площадь же – результат умножения двух сторон, в этом случае так же необходимо знать длину сторон. И в первом и во втором случае обязательным условием является знание длин сторон А и В.
Как же через показатель площади найти у прямоугольника периметр? Тут может быть два варианта: первый, если наш прямоугольник с равными сторонами, то есть квадрат, а второй, если длина сторон разная.
При условии, что потолок квадратный то найти периметр очень просто. Зная формулу нахождения площади квадрата, можно выяснить найти длину всех сторон, ведь они у квадрата одинаковые.
- Площадь = длина стороны во второй степени. Чтобы найти длину стороны нам нужно переделать данную формулу следующим образом:
- Длина стороны = корень квадратный от площади
- Так длина стороны при площади 4 квадратных метров, будет 2 метра, а при 16 квадратных метров 4 метра.
- Периметр = длина квадрата умноженная на 4. При длине стороны 2 метра, то периметр будет 8 метров. Тут все просто.
Довольно простой способ, который позволит посчитать периметр квадратного потолка. Квадратный потолок будет отличаться тем что, при большом показателе периметра будет относительно не большие площади. Однако квадратные потолки – это довольно редкий случай. Как правило, такие помещения не очень смотрятся, поэтому наиболее распространенные являются прямоугольные потолки.
Можно ли также найти периметр не квадратного прямоугольника?
Данный способ для прямоугольника с разными сторонами не подходит. Ведь вариантов разности сторон может быть до бесконечности много. И тут для определения периметра обязательным условием является знание хотя бы одной из сторон и площади.
Площадь = длина первой стороны умножается на длину второй стороны
Исходя из этой формулы, зная площадь найти две неизвестные стороны прямоугольника невозможно, но возможно выяснить длину одной стороны, если есть длина первой. Так если площадь прямоугольника 10 квадратных метров, а длина одной из сторон 2 метра, то можно посчитать
10 = 2 умножить на длину неизвестной стороны, следовательно, неизвестная сторона = 10 разделить на 2. Получаем ответ 5 метров.
Периметр = ( 5 + 2 ) * 2. Периметр такого прямоугольника будет 14 метров.
Таким образом, с подсчетом не возникнет проблем, если вы хорошо учили арифметику. Однако для того чтобы упростить себе жизнь, можно обратиться в фирмы по ремонту квартир. Мастера подобных организаций берут на себя весь процесс расчетов и монтажных работ, вам только необходимо будет подписать с ними соответствующие документы и все. Использование подобных услуг – это очень простой способ решения нудной проблемы ремонта потолков. Вы получаете компетентную помощь от высококвалифицированной бригады мастеров, которые имеют большой опыт работы. А подписывая с ними контракт, вы страхуете себя от ненужных проблем, которые порою бывают из-за недопонимания. Договоры о сотрудничестве содержат все нюансы работы, и выполняются в соответствии с законом.
При планировании бюджета на ремонт потолка, после проведенных расчетов необходимо закупить расходные материалы. Рекомендуется покупать немного больше требуемого объема материалов, так как бывают случаи с неожиданным результатом. Так хорошо будет брать запас в 15 процентов – это оптимальный объем. Но еще более приемлемым будет заказать ремонт потолков под ключ, ведь в этом случае нет надобности беспокоиться о закупках. Мастера сами предложат выбрать материалы для ремонта, после того как выбор был сделан они привезут и сделают ремонт. Как правило, у них налажена система логистики, поэтому с доставкой не возникает проблем. Если вы цените свое время и нервы, рекомендуется обратиться к подобным компаниям по ремонту потолков под ключ. Вы получите качественный сервис в короткие сроки, и ваш потолок будет радовать вас как никогда прежде. В любом случае решение остается за вами!
opotolkax.com
Как вычислить площадь по периметру
Содержание
Геометрия изучает свойства и характеристики двумерных и пространственных фигур. Числовыми величинами, характеризующими такие конструкции, являются площадь и периметр, вычисление которых производится по известным формулам или выражается одно через другое. Инструкция
|
completerepair.ru
Площадь по периметру калькулятор. Рассчитываем площадь и периметр помещения
Как рассчитать площадь и периметр помещения и в каких случаях следует ее знать?
Главная / Монтаж, ремонт, уход / Рассчитываем площадь и периметр помещения
Любое важное начинание надо просчитывать заранее, ремонт не исключение. Поскольку затраты предстоят большие, надо их оптимизировать и уменьшить по максимуму, особенно, если хочется сделать что-то дорогостоящее, например натяжные потолки с несколькими уровнями. Если покупать материалы «на глазок», легко можно ошибиться – купить или слишком много или придется идти в магазин и докупать недостающие стройматериалы. Для того, чтобы не купить лишнего дорогого стройматериала и сэкономить семейный бюджет, надо знать, как рассчитать площадь помещения. Вот с этого то и начнем.
В каких случаях нужны расчеты?
Расчет квадратных метров обязателен, если в проекте установить подвесные потолки. Для наглядности посмотрим, что нужно для гипсокартонных конструкций. Площадь комнаты рассчитывается, чтобы закупить гипсокартон в нужном количестве, а периметр надо знать для покупки пристенного профиля для установки обрешетки. Гипсокартон и профиля берем с запасом примерно 15-20% на обрезку, ведь не всегда можно изобразить на бумаге точный эскиз расположения на потолке гипсокартона или декоративных панелей.
Для заказа натяжного потолка делать расчет квадратуры комнаты требуется, что запланировать будущие траты и проконтролировать фирму-установщика в правильности их расчетов. Фирма, изготавливающая натяжные потолки обычно указывает цену за квадратный метр и плюсует работу по установке. Зная площадь и стоимость квадрата, можно легко определить конечную цену.
Вычислить площадь требуется даже для банальной покраски пола или потолка, чтобы знать, сколько закупать краски. Важно купить нужное количество краски, иначе если не хватит, а краску в магазине колорировали, то можно не угадать с цветом. Примерный расход краски на метр квадратный поверхности указывается на банке.
Пример расчета потребности в краске:
Квадратура пола составляет 30 м2
расход краски согласно данным на упаковке – 0,20 кг/м2
30 х 0,2 = 6 кг
Полагается брать краску свыше расчетного количества на 10%.
Поэтому получаем 6 + 10% = 6,6 кг. Это подойдет ведро 7 кг или приближенная расфасовка в зависимости от вида краски.
Как посчитать площадь комнаты
Если вы владелец небольшой прямоугольной комнаты, то большого труда вычислить квадратуру комнаты это не составит. Достаточно вспомнить школьный курс геометрии. А что делать, если на месте потолка сложный многоугольник или имеются всевозможные ниши или выступы?
Прямоугольная комната
Приступаем к расчетам. Повторение – мать учения, поэтому для тех, кто забыл, как считать площадь комнаты и ее периметр, напомним курс пятого класса. К примеру, имеем типовую прямоугольную комнату с шириной равной 2,5м и длиной, равной 4 м. Тогда, площадь равна длине, умноженной на ширину, или 2,5 х 4 =10 м2 . Периметр в нашем примере равен сумме длин всех сторон или 2,5 + 4 + 2,5 + 4 = 13м. Значит для натяжного потолка вам надо заказать пленку размером 10 м2 и приобрести профилей суммарной длины 18 + 20% (на обрезку) = 15,6 м. Естественно, при покупке багетов надо округлить суммарную длину до значения, кратного длине одной планки. Если в магазине имеется двухметровый профиль, то потребуется купить 16 м или 8 планок.
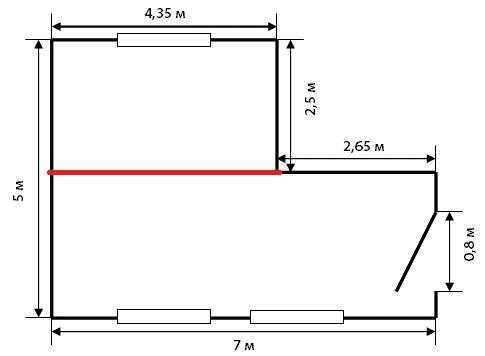
Комната сложной формы
Очень часто в домах старой постройки встречаются комнаты с нишами, выступами, встроенными кладовками. Нам предстоит решить задачку посложнее, но оказывается все просто. Потребуется лист в клетку или простой, на котором мы нарисуем эскиз комнаты с приблизительным сохранением пропорций. Далее измеряем метраж прямых стен и записываем на эскизе рядом с соответствующими линиями, обозначающими стены.
А вот теперь порисуем. Эскиз надо разбить на прямоугольники при помощи угольника и линейки, соблюдая прямые углы. Причем, одной из сторон прямоугольника должна быть измеренная полная стена. Теперь надо вычислить квадратные метры каждого из нарисованных прямоугольников и суммировать их. Периметр вычислить в любом случае проще – просто складываем длины всех стен и закоулочков.
Расчет площади многогранной комнаты
Что д
ep2nnov.ru
Площадь через периметр — Как вычислить площадь фигуры зная ее периметр? — 22 ответа
Площадь по периметру
В разделе Естественные науки на вопрос Как вычислить площадь фигуры зная ее периметр? заданный автором Невролог лучший ответ это В Компас 3D нанести план и автоматически посчитать площадь. По периметру площадь произвольного многоугольника не посчитать. Все равно придется разбивать на отдельные фигуры.
Будут вопросы — пиши в агент.
Ответ от 22 ответа[гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Как вычислить площадь фигуры зная ее периметр?
Ответ от Ѐамис Ш[новичек]
..
Ответ от силосовать[гуру]
1.выбрать центр
2.измерить расстояние от центра до углов
3.измерить стороны вашего многоугольника
4.вычислить периметры получившихся N треугольников
5.вычислить площади всех треугольников, используя формулу Герона-через полупериметр.
6.суммировать все площади
7.выбрать мой ответ лучшим.
8.все
Ответ от Взрослить[гуру]
попробуй разделить периметр на 4 и потом перемножить полученное друг на друга
Ответ от ScrAll[гуру]
Вырезаешь из бумаги и взвешиваешь.
Или разбиваешь на треугольники.
Половина основания на высоту…
Ответ от Алексей Зайцев[гуру]
Проще и безошибочнее начертить эскизик — вид сверху с размерами. Затем по этому эскизику площадь разделить на прямоугольники, посчитать и просуммировать их площади
Ответ от Мария Кемпель[активный]
нереально
Ответ от Nemo[гуру]
Нереально. По периметру вычисляется площадь только ПРАВИЛЬНЫХ фигур. Советую кусочным способом
Ответ от Djon[гуру]
лучше всего разбить сложную фигуру на несколько простых, и посчитать площадь отдельно, затем сложить
Ответ от Lavavoth[гуру]
Нереально.. . Лучше выложи план зала, есть другие способы подсчета, но нужно видеть план.
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Периметр на Википедии
Посмотрите статью на википедии про Периметр
Полупериметр на Википедии
Посмотрите статью на википедии про Полупериметр
Формула площади Гаусса на Википедии
Посмотрите статью на википедии про Формула площади Гаусса
Ответить на вопрос:
22oa.ru
Площадь треугольника через стороны
Площадь треугольника через стороны — это
площадь треугольника, которая выражена через
три стороны треугольника и полупериметр.
Полупериметр — это половина суммы
длин всех сторон треугольника.
Площадь любого треугольника можно рассчитать по
разным формулам. Одна из популярных формул:
С помощью этой формулы можно найти площадь
треугольника зная длину основания и высоту.
Но, иногда требуется найти площадь треугольника,
зная только стороны треугольника. Так, как у
каждого треугольника три стороны, то соответственно
три длины. Но, как же найти площадь?
Площадь треугольника через стороны легко рассчитать
зная Формулу Герона.Герон — греческий математик, в
честь которого и была названа эта формула. В чем суть
формулы Герона? Как найти площадь треугольника через длины сторон?
Площадь произвольного треугольника равна квадратному
корню из произведения полупериметра на разницу
между полупериметром и стороной a, полупериметром
и стороной b, полупериметром и стороной c.
Можно сделать вывод, что, чтобы рассчитать площадь треугольника
по Формуле Герона, нужно знать все стороны данного треугольника.
Формула Герона:
a, b, c — длины сторон треугольника;
p — полупериметр;
S — площадь;
Формула полупериметра:
Обобщение площади треугольника через стороны:
Подставив в вышеперечисленные формулы длины всех сторон,
можно найти площадь любого треугольника. С помощью формулы
площади треугольника через три стороны, можно также
найти не только площадь, но и периметр.
Формула Герона для треугольника
В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.
Формула площади
Площадь треугольника ( S ) равняется квадратному корню из произведения его полупериметра ( p ) на разности полупериметра и каждой из его сторон ( a, b, c ).
Полупериметр ( p ) вычисляется таким образом:
Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.
Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.
Примеры задач
Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.
Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.
Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
= .
Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.
Решение
Пусть гипотенуза – это c , известный катет – a , а неизвестный – b .
Применим Теорему Пифагора, чтобы найти длину катета b :
b 2 = = = , следовательно,
Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.
Остается только использовать формулу для нахождения площади:
= = .
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
http://mozgan.ru/Geometry/AreaTriangle
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника
— сумма длин всех его сторон. Формула для подсчета периметра прямоугольника
: , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром
. Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.
Периметр
— это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
Отличительные особенности прямоугольника
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Как вычислить периметр прямоугольника
Существует 2 способа его нахождения:
- 1 способ.
Складываем все стороны. P = a + а + b + b
- 2 способ.
Сложить ширину и длину, и умножить на 2. P = (a + b) · 2.
ИЛИ Р = 2 · а + 2 · b.
Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a»
— длина прямоугольника, более длинная пара его сторон.
«b»
— ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр
— это сумма одной длины и одной ширины.
- Полупериметр прямоугольника —
когда выполняешь первое действие в скобках – (a+b)
. - Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2
, где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник
— это четырехугольник со всеми прямыми углами. - Квадрат
— прямоугольник, у которого все стороны равны.
- Прямоугольник
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Умение находить периметр прямоугольника очень важно для решения многих геометрических задач. Ниже приведена подробная инструкция по нахождению периметра разных прямоугольников.
Как найти периметр обычного прямоугольника
Обычный прямоугольник – четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:
Складываем все стороны.
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина – 6.
Решение (последовательность действий и рассуждения):
- Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
- Складываем все стороны (3 + 3 + 6 + 6) = 18 см.
Ответ: P = 18 см.
Второй способ заключается в следующем:
Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a – ширина, b – длина.
В рамках данной задачи получим такое решение:
2×(3 + 6) = 2×9 = 18.
Ответ: P = 18.
Как найти периметр прямоугольника – квадрат
Квадрат является правильным четырехугольником. Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:
- Сложить все его стороны.
- Умножить его сторону на 4.
Пример: Найти периметр квадрата, если его сторона = 5 см.
Так как нам известна сторона квадрата, мы сможем найти его периметр.
Складываем все стороны: 5 + 5 + 5 + 5 = 20.
Ответ: P = 20 см.
Умножаем сторону квадрата на 4 (потому что все равны): 4×5 = 20.
Ответ: P = 20 см.
Как найти периметр прямоугольника – онлайн-ресурсы
Несмотря на то, что вышеупомянутые действия легки для понимания и освоения, вам может пригодиться несколько онлайн-калькуляторов, которые помогут вам вычислить периметры (площадь, объем) разных фигур. Просто вбейте необходимые значения и мини-программа рассчитает периметр нужной вам фигуры. Ниже приведен небольшой список.
Сегодня у нас речь пойдет о том, как вычислить периметр многоугольника
. Но сначала поговорим о многообразии фигур. Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.
И как же найти периметр этих фигур?
Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон
.
Периметр обозначается заглавной латинской буквой Р
.
Давайте рассмотрим несколько примеров.
Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:
Р = 15 + 17 + 10 + 10 + 20 + 15 = 87
Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:
Р = 15 × 2 + 10 × 2 + 17 + 20 = 87
Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.
Прямоугольник
– это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а
и б
, надо сложить эти стороны и умножить полученный результат на 2
:
Р(прямоугольника) = (а + б) × 2
То есть, если сторона прямоугольника а = 5 см
, а сторона прямоугольника б = 3 см
, то периметр прямоугольника будет:
Р = (5 + 3) × 2 = 16 см
А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?
Р(прямоугольника) = 2 × а + 2 × б
а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2
Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?
Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны. Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.
сторона б = (16 – 2 × 5) ÷ 2 = 3 см
Ответ: у прямоугольника две стороны по 5 см и две по 3 см.
Квадрат
– это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:
Р(квадрата) = а × 4
Например, у квадрата В сторона а = 5 см.
Чтобы найти его периметр:
Р(В) = 5 × 4 = 20 см
А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:
а = Р ÷ 4
Пример: Периметр квадрата 24 см. Чему равны его стороны?
а = 24 ÷ 4 = 6
Ответ: Стороны квадрата равны 6 см.
По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников
. То есть равен длине одной его стороны умноженной на количество сторон.
Если длина одной стороны многоугольника равна а
, а число его сторон равно n
, то его периметр будет равен:
Р(равностороннего многоугольника) = а × n
Например, у пятиугольника Д сторона а = 6 см
. Найдем его периметр:
Р(Д) = 6 × 5 = 30 см
Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.
Ниже в статье вы узнаете что такое и как найти периметр прямоугольника если известны его стороны. А также как найти стороны прямоугольника, если известен его периметр. И ещё одна интересная строительная прикладная задача.
Немного теории:
Периметр — это длина геометрической фигуры по её внешней границе.
Периметр прямоугольника — это сумма длин его сторон.
Формулы для вычисления периметра прямоугольника: P = 2*(a+b) или P = a + a + b + b.
Резюмируем! Для того чтобы вычислить периметр прямоугольника необходимо сложить все его стороны.
Типовые математические и практические задачи:
Задача №1:
Исходные данные: Определить периметр прямоугольника с длинами сторон 5 см и 10 см.
Решение:
Согласно формуле периметр прямоугольника равен = 2 * (5 + 10) = 30 см.
Ответ: 30 см.
Задача №2:
Исходные данные: Определить стороны прямоугольника выраженные целыми числами, если периметр прямоугольника равен 10.
Решение:
По формуле определяем сумму длин сторон (a + b) = P / 2 = 10 / 2 = 5
Целыми значениями сторон могут быть только значения 1 + 4 = 5 и 2 + 3 = 5
Ответ: Длины сторон могут быть только 2 и 3 или 1 и 4.
Задача №3 (практическая):
Исходные данные: Определить число плинтусов в достаточном количестве для ремонта пола в комнате длиной 5 метров и шириной 3 метра, если длина одного плинтуса равна 3 метра.
Решение:
Периметр комнаты = 2 * (5 + 3) = 16 метров
Количество плинтусов = 16 / 3 = 5,33 штук
Обычно в строительных магазинах плинтусы продаются не погонными метрами, а поштучно. Поэтому принимаем следующее целое число. Это шесть.
Ответ: Количество плинтусов 6 штук.
В заключение:
Решение задачи вычисления периметра является достаточно простой математической задачей, но имеющей очень важное практическое значение например в строительстве или генеральном планировании территории.
На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника. С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина.
Школьная математика » Блог » Как найти стороны прямоугольника при известных периметре и площади
В этой статье я хочу рассмотреть две математические задачи повышенной сложности для 4 класса.
Видеоурок по теме этой статьи можно посмотреть по ссылке.
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
С этими задачами, я уверен, без труда справится более старший школьник, знакомый с решением системы уравнений и квадратных уравнений. Кстати, подобная задача есть в учебнике по геометрии Атанасяна, глава VI № 454 пункт б за 8 класс.
Но почему же эти задачи указаны в математических сборниках как задачи для 4 класса, в котором еще не изучают алгебраические понятия и методы решения? Нет ли здесь ошибки?
Нет, никакой ошибки здесь нет. Эти, и аналогичные им задачи можно решить и без использования алгебраических знаний.
Первое, что приходит на ум – это по значению периметра прямоугольника (а периметр – это удвоенная сумма двух его сторон) найти сумму двух сторон, а после простым подбором определить два числа, произведение которых равно данной по условию площади прямоугольника, а сумма – половине периметра.
Я хочу показать вам математически точное решение, которое безо всяких подборов приводит к правильному результату.
Нахождение сторон прямоугольника при известных периметре и площади
Рассмотрим первую задачу:
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Как известно, периметр прямоугольника находится по формуле ({color{red} P=2cdot (a+b)}) , площадь – по формуле ({color{red} S=acdot b}) .
Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:
({color{red} a + b = 24 : 2 = 12}) см.
А дальше мы рассуждаем так.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной ({color{red} 12 : 2 = 6}) см.
Тогда площадь этого квадрата равна
({color{red}S_{k}=6cdot 6=36}) см2.
По условию нашей задачи площадь прямоугольника составляет 32 см2. Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.
({color{red} S–S _{k}=36-32=4}) см2.
Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.
Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной. То есть, ширину уменьшить, а длину увеличить на одно и то же число.
Но на какое?
Площадь 4 см2 – это квадрат со стороной 2 см. Это и есть нужное нам число.
Тогда, ширина искомого прямоугольника будет равна:
({color{red} a=6-2=4}) см
а длина:
({color{red} b=6+2=8}) см.
Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:
({color{red} P=2cdot (4+8)=2cdot 12=24}) см
({color{red} S=4cdot 8=32}) см2.
Задача решена верно.
Теперь рассмотрим вторую задачу.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
Находим полупериметр, то есть, сумму двух сторон прямоугольника.
({color{red} a+b=46:2=23}) см.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица. Это прямоугольник со сторонами 11 и 12, т.к. ({color{red} 23=11+12}).
Площадь такого прямоугольника равна:
({color{red}S_{2}=11cdot 12=132}) см2.
Разница между полученной площадью и заданной по условию задачи составляет:
({color{red}S_{2}-S=132-126=6}) см2.
6 см2 – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.
Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см2, а именно, на 2.
Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).
Находим ширину искомого прямоугольника:
({color{red} a=11-2=9}) см.
Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:
({color{red} b=12+2=14}) см.
Проведем проверку:
({color{red} P=2cdot (9+14)=2cdot 23=46}) см.
({color{red}S=9cdot 14=126}) см2.
И эта задача решена тоже верно.
На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.