Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.
Системы небесных координат отличаются друг от друга выбором основной плоскости и началом отсчёта. В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.
Содержание
- 1 Горизонтальная система координат
- 2 Первая экваториальная система координат
- 3 Вторая экваториальная система координат
- 4 Эклиптическая система координат
- 5 Галактическая система координат
- 6 Изменения координат при вращении небесной сферы
- 7 История и применение
- 8 Использование различных систем координат
- 9 Примечания
- 10 См. также
Горизонтальная система координат
В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.
Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.
Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.
Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)
Первая экваториальная система координат
В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.
Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.
Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.
Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0h до +12h) к западу и от 0° до −180° (от 0h до −12h) к востоку.
Вторая экваториальная система координат
Использование экваториальной системы координат.
В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α.
Прямым восхождением (RA,α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере).
RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор в весеннее равноденствие.
Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.
- Объект на небесном экваторе имеет склонение 0°
- Склонение северного полюса небесной сферы равно +90°
- Склонение южного −90°
У склонения всегда указывается знак, даже если склонение положительно.
Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ < −90° + φ , то объект называется невосходящим, а значит он ненаблюдаем на широте φ.[1]
Эклиптическая система координат
В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.
Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.
Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.
Галактическая система координат
В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.
Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.
Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.
Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.
Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).
Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:
Изменения координат при вращении небесной сферы
Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.
История и применение
Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.
Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.
Использование различных систем координат
Горизонтальная система координат используется для определения направления на светило с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.
Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.
Вторая экваториальная система координат является общепринятой в астрометрии. В этой системе составляются звёздные карты и описываются положения светил в каталогах.
Эклиптическая система координат используется в теоретической астрономии при определении орбит небесных тел.
Примечания
- ↑ Зигель Ф. Ю. Сокровищница звёздного неба — путеводитель по созвездиям и Луне / Под ред. Г. С. Куликова. — 5-е изд. — М.: Наука, 1986. — С. 57—58. — 296 с. — 200 000 экз.
См. также
- Небесная сфера
Wikimedia Foundation.
2010.
Системы небесных координат используются в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, системы небесных координат являются сферическими системами координат, в которых третья координата — расстояние — часто неизвестна и не играет роли. Эти системы отличаются друг от друга выбором основной плоскости и началом отсчёта.
В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.
Горизонтальная система координат
В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.
Высота
Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило.
Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.
Зенитное расстояние
Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило.
Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.
Азимут
Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила.
Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)
Первая экваториальная система координат
В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.
Склонение
Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило.
Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.
Полярное расстояние
Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило.
Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.
Часовой угол
Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила.
Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0h до +12h) к западу и от 0° до −180° (от 0h до −12h) к востоку.
Вторая экваториальная система координат
Файл:Экваториальная система координат.png Использование экваториальной системы координат.
В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α.
Прямое восхождение
Прямым восхождением α светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила.
Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере).
Эклиптическая система координат
В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.
Эклиптическая широта
Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило.
Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до -90° к южному полюсу эклиптики.
Эклиптическая долгота
Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила.
Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.
Галактическая система координат
В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.
Галактическая широта
Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.
Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до -90° к южному галактическому полюсу.
Галактическая долгота
Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила.
Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.
Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).
Изменения координат при вращении небесной сферы
Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.
История и применение
Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.
Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.
Использование различных систем координат
Горизонтальная система координат используется для определения направления на светило с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.
Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.
Вторая экваториальная система координат является общепринятой в астрометрии. В этой системе составляются звёздные карты и описываются положения светил в каталогах.
Эклиптическая система координат используется в теоретической астрономии при определении орбит небесных тел.
См. также
- Небесная сфера
bs:Nebeski koordinatni sistem
de:Astronomische Koordinatensysteme
en:Celestial coordinate system
es:Coordenadas celestes
fr:Système de coordonnées célestes
he:מערכת קואורדינטות שמימית
hr:Nebeski koordinatni sustavi
hu:Csillagászati koordinátarendszer
it:Coordinate celesti
nl:Hemelcoördinaat
nn:Himmelkoordinat
pl:Układ współrzędnych astronomicznych
ro:Coordonate astronomice
uk:Системи небесних координат
vi:Hệ tọa độ thiên văn
zh:天球坐标系统
Материал из Викитеки — свободной библиотеки
< ЭСБЕ
Перейти к навигации
Перейти к поиску
| ← Полярное море | Полярное расстояние светила Энциклопедический словарь Брокгауза и Ефрона |
Полярной звезды орден → |
Словник: Повелительное наклонение — Полярные координаты. Источник: т. XXIV (1898): Повелительное наклонение — Полярные координаты, с. 474 ( скан ) • Даты российских событий указаны по юлианскому календарю.
- Википроекты
Википедия (поиск)
Данные
Полярное расстояние светила — дуга между светилом и ближайшим к нему полюсом мира, считаемая по кругу склонений от 0° до 90°. Иногда, особенно в английских картах и каталогах, считается для всех звезд от северного полюса от 0° до 180° (обозначается тогда NPD). Сумма П. расстояния и склонения светила равна 90°.
Источник — https://ru.wikisource.org/w/index.php?title=ЭСБЕ/Полярное_расстояние_светила&oldid=3630291
Категории:
- ЭСБЕ
- ЭСБЕ:П
- ЭСБЕ:47 полутом
- ЭСБЕ:Астрономия
Скрытые категории:
- 50%
- Ссылка из Викиданных:Викитека
- Ручная ссылка:Википедия
- Ссылка из Викиданных:Викиданные
- Викиданные:Страницы с элементами
- Викиданные:Страницы с элементами без указания элемента темы
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Кафедра кадастра недвижимости, землеустройства и геодезии
АСТРОНОМИЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторных работ для студентов направления
21.03.03 «Геодезия и дистанционное зондирование» всех форм обучения
Воронеж 2022
УДК 52(07) ББК 22.6я7
Составители: В. В. Шумейко, Н. В. Невинская
Астрономия: методические указания к выполнению лабораторных работ
|
для студентов |
направления |
21.03.03 |
«Геодезия |
и |
дистанционное |
|
зондирование» |
всех форм обучения |
/ |
ФГБОУ |
ВО |
«Воронежский |
|
государственный |
технический |
университет»; |
сост.: |
В. |
В. Шумейко, |
Н. В. Невинская.- Воронеж: Изд-во ВГТУ, 2022. — 26 с.
Содержат основные понятия астрономии и даны краткие сведения различных разделов астрономии. Даны основные задачи, которые решает современная астрометрия, теоретическая астрономия, астрофизика и рассмотрены методы их решения.
Предназначены для студентов направления 21.03.03 «Геодезия и дистанционное зондирование», всех форм обучения.
Методические указания подготовлены в электронном виде и содержатся в файле МУ Астрономия 21.03.03.pdf.
Ил. 8. Библиогр.: 10 назв.
УДК 52(07)
ББК 22.6я7
Рецензент – В. А. Костылев, ст. преп. каф. кадастр недвижимости, землеустройство и геодезия ВГТУ
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ВВЕДЕНИЕ
По направлению 21.03.03 «Геодезия и дистанционное зондирование» учебным планом предусматривается изучение дисциплины «Астрономия».
Цель дисциплины «Астрономия» — формирование современного мировоззрения о Вселенной на основе законов движения и эволюции небесных объектов, приобретение необходимых навыков применения астрономических методов при решении практических задач (служба времени, составление карт и планов, навигация и др.).
В ходе учебного процесса студент должен прослушать курс лекций по данной дисциплине, выполнить лабораторные работы и сдать экзамен.
Настоящие методические указания предусмотрены для выполнения лабораторных работ по астрономии с использованием звездных атласов, подвижных карт звездного неба, астрономических календарей и справочников.
Выполнение лабораторных работ направлено на решение следующих
задач:
изучение звездной карты мира в целях вычисления местонахождения светил, а также моментов времени восхода и захода их;
получение основ построения небесных координат, систем счета времени;
изучение методов и средств практической астрономии и астрометрии; Знания, полученные при изучении дисциплины «Астрономия»,
необходимы в дальнейшем, для изучения других дисциплин.
3
Лабораторная работа № 1
Звездные атласы. Подвижная карта звездного неба. Астрономические календари и справочники
Цель работы: ознакомиться с содержанием звездных атласов, астрономических календарей и справочников. Использование подвижной карты при изучении звездного неба.
Оборудование: атлас звездного неба, астрономический календарь, подвижная карта звездного неба, школьный астрономический календарь. Электронные справочники и базы данных.
Задание: взять из общего каталога звезд атласа координаты (α и δ) звезды и определить ее координаты на данныйгод,используя таблицупрецессий за100 лет.
Общие теоретические сведения
Небесный свод, как одно целое, со всеми находящимися на нем светилами плавно вращается около некоторой воображаемой оси, проходящей через место наблюдения. Это вращение небесного свода и светил называется суточным движением, так как одно полное обращение совершается за сутки. Вследствие суточного вращения звезды и другие небесные тела непрерывно меняют свое положение относительно сторон горизонта.
Если наблюдать суточное движение звезд в северном полушарии Земли (но не близко к ее полюсу) и при этом стоять лицом к южной стороне горизонта, то их вращение происходит слева направо, т.е. «по часовой стрелке». На восточной стороне горизонта (если наблюдать не на полюсе Земли) звезды восходят, поднимаются выше всего над южной стороной горизонта и заходят на западной стороне. При этом каждая звезда всегда восходит в одной и той же точке восточной стороны горизонта и заходит всегда в одной и той же точке западной стороны. Максимальная высота над горизонтом для каждой данной звезды и для данного места наблюдения также всегда постоянна.
Если же стать лицом к северной стороне горизонта, то наблюдения покажут, что одни звезды будут также восходить и заходить, а другие — описывать полные круги над горизонтом, вращаясь вокруг общей неподвижной точки. Эта точка называется северным полюсом мира.
Приблизительное положение северного полюса мира на небе можно найти по положению Полярной звезды (α Малой Медведицы). Расстояние Полярной звезды от северного полюса мира в настоящее время меньше 1°.
4
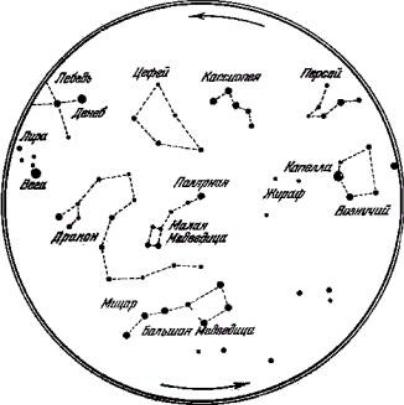
Рис. 1. Околополярные созвездия
Сцелью ориентировки по небу яркие звезды давно уже были объединены
вгруппы, названные созвездиями. Созвездия обозначались названиями животных (Большая Медведица, Лев, Дракон и т.п.), именами героев греческой мифологии (Кассиопея, Андромеда, Персей и т.д.) или просто названиями тех предметов, которые напоминали фигуры, образованные яркими звездами Северная Корона, Треугольник, Стрела и т.п.).
СXVII в. отдельные з везды в каждом созвездии стали обозначаться буквами греческого алфавита. Первой из них α (альфа) обозначают самую яркую звезду, а затем следуют звезды, обозначенные буквами β (бета), γ (гамма), δ (дельта), ε (эпсилон) и т. д.
Наиболее яркие звезды в созвездиях служат хорошими ориентирами для нахождения на небе более слабых звезд, или других небесных объектов. Поэтому необходимо научиться быстро находить то или иное созвездие непосредственно на небе.
Прежде всего надо научиться находить Полярную звезду, находящуюся на конце ручки «ковша» Малой Медведицы. Она находится на продолжении линии, проходящей через α и β Большой Медведицы (5 расстояний). Под Полярной звездой на горизонте находится точка севера. По соседству, вокруг Полярной звезды расположены созвездия: Кассиопея, Цефей, Дракон и Большая Медведица, которые называются околополярными и в средних широтах видны
над горизонтом на протяжении всего года.
5
Большинство других созвездий лучше всего наблюдать в определенное время года. Рассмотрим сезонные треугольники, являющиеся хорошим ориентиром в звездном небе. Чтобы найти сезонные треугольники нужно стать лицом к югу.
Летом одними из первых на вечернем летнем небе появляются Вега (α Лиры), Денеб (α Лебедя), Альтаир ( α Орла), образующие летний треугольник. Вега самая яркая звезда в северного неба.
Осень – удобное время для наблюдения созвездий Пегаса и Андромеды, яркие звезды которых, расположены в виде огромного ковша с ручкой, значительно превосходящего созвездие Большой Медведицы. «Ковш представлен тремя звездами Пегаса (α, β, γ) и звездой α Андромеды.
Зимнее вечернее небо украшает группа созвездий, из которых выделяется очень красивое созвездие Орион. Над «поясом» Ориона блестит Бетельгейзе (α Ориона), а ниже пояса – Ригель (β Ориона). Представим себе спиральную линию, начинающуюся от звезды γ Ориона и проходящую через звезды α, β. Мысленно продолжая эту линию, мы будем последовательно встречать яркие звезды: Альдебаран (α Тельца), Капеллу (α Возничего), Поллукс (β Близнецов), Процион (α Малого Пса) и, након ец, самую яркую звезду неба — Сириус (α Большого Пса). Бетельгейзе, Процион и Сириус составляют зимний треугольник.
Весной легко найти на небе созвездие Льва, запомнив, что его яркие звезды образуют большую трапецию. Правая нижняя звезда трапеции – Регул (α Льва), а левая нижняя – Денебола. На продолжении ручки ковша Большой Медведицы мы найдем Арктур (α Волопаса) и Спику (α Девы). Три звезды Арктур, Спика и Денебола образуют весенний треугольник.
К отдельной группе можно отнести зодиакальные созвездия. Через которые проходит эклиптика (годовой путь Солнца по небесной сфере). Их число соответствует числу месяцев в году. Первые три созвездия (Рыбы, Овен, Телец) Солнце проходит в весенние месяцы, следующие три (Близнецы, Рак, Лев) — в летние, еще три следующих (Дева, Весы, Скорпион) — в осенние и, наконец, последние три (Стрелец, Козерог, Водолей) — в зимние месяцы.
Пример выполнения работы
Задание: взять из общего каталога звезд атласа координаты (α и δ) звезды Дубхе и определить ее координаты на 2004 год, используя таблицу прецессий за 100 лет.
Определим к какому созвездию принадлежит звезда Дубхе с помощью таблиц : «Собственные имена звезд» и «Названия созвездий». Латинское название звезды Дубхе- λ Има. Название созвездия ИмаБольшая Медведица.
На карте атласа находим λ Има и определяем экваториальные координаты: α = 11h ; δ= 62 °
В звездном каталоге уточним координаты: α1950 = 11h 07m и δ1950= 62°1′ – координаты на 1950 год.
Находим разницу в годах: t = 2004 – 1950 = 54 года.
6
|
Из таблицы прецессий находим: |
α100 =6,2m и δ100 = -32′ |
|
|
Приращение координат за 54 года: |
||
|
α54 = 100α 0х54 = 3,35m , |
(1.1) |
|
|
δ54 = 100δ 0х54 = -17,3′ , |
(1.2) |
|
|
Координаты звезды Дубхе на 2004 год: |
||
|
α 2004 = α1950 + |
α54 = 11h 3,42m , |
(1.3) |
|
δ 2004 = δ1950 + |
δ54 = 61°43,7′ , |
(1.4) |
Лабораторная работа № 2
Основные элементы небесной сферы. Системы небесных координат. Условие видимости светил на различных широтах
Цель работы: изучение основных элементов и суточного вращения небесной сферы. Знакомство с системами небесных координат. Изучение условий видимости светил на различных широтах.
Оборудование: модель небесной сферы.
Задание: изобразить на чертеже небесную сферу и положение ее основных элементов для определенной широты и показать на ней точки с заданными координатами:
Общие теоретические сведения.
В астрономии используют различные системы координат, которые различаются между собой выбором основной (координатной) плоскости и началом отсчета.
Положение светила (точки) на небе определяется двумя величинами (центральными углами или дугами больших кругов), которые называются небесными координатами.
ГОРИЗОНТАЛЬНАЯ СИСТЕМА КООРДИНАТ Основной плоскостью является плоскость небесного горизонта. Началом отсчета является точка юга S и Z.
Одной координатой является высота h. Высотой h светила М называется центральный угол mОМ между плоскостью небесного горизонта и направлением на светило. Отсчитывается от небесного горизонта к зениту от 0° до +90° и от 0° до —90° к надиру.
7

Иногда, вместо высоты используется зенитное расстояние z. Зенитным расстоянием z светила М центральный угол ZOM между отвесной линией и направлением на светило. Отсчитывается от 0° до 180° в направлении от зенита к надиру. Между зенитным расстоянием и высотой одного и того же светила имеется соотношение:
Азимутом А светила М называется центральный угол SOm измеряющий двухгранный угол между плоскостями небесного меридиана и вертикального круга светила.
Отсчитывается от точки юга S по часовой стрелке, от 0° до 360°.
В геодезии азимуты отсчитываются от точки севера N по часовой стрелке,
от 0° до 360°.
Рис. 2. Горизонтальная система координат
Горизонтальные координаты h, А непрерывно изменяются вследствие суточного вращения небесной сферы, так как они отсчитываются от неподвижных точек, не участвующих в этом вращении, а плоскости небесного экватора и небесного горизонта не параллельны друг другу.
Горизонтальная система координат используется для непосредственных определений видимых положений светил с помощью угломерных инструментов.
ПЕРВАЯ ЭКВАТОРИАЛЬНАЯ СИСТЕМА КООРДИНАТ Основной плоскостью является плоскость небесного экватора QQ’. Началом отсчета является верхняя точка небесного экватора Q.
Одной координатой является склонение светила δ. или центральный угол mОМ между плоскостью небесного экватора и направлением на светило.
Склонения отсчитываются в пределах от 0° до + 90° к северному полюсу мира и от 0° до — 90° к южному полюсу мира. Иногда склонение δ заменяется полярным расстоянием ρ, т.е. дугой РМ круга склонения от северного полюса
8

мира до светила или центральным углом РОМ между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному. Очевидно:
Часовым углом t светила М называется центральный угол QOm измеряющий двухгранный угол между плоскостями небесного меридиана и круга склонения светила.
Часовые углы отсчитываются в сторону суточного вращения небесной сферы (по часовой стрелке) от верхней точки Q небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере).
Рис. 3. Экваториальная система координат
При вращении небесной сферы склонение δ не меняется, так как суточные параллели параллельны небесному экватору. Часовой угол t непрерывно изменяется.
Первая экваториальная система используется преимущественно при определении точного времени.
ВТОРАЯ ЭКВАТОРИАЛЬНАЯ СИСТЕМА КООРДИНАТ Основной плоскостью является плоскость небесного экватора QQ’. Началом отсчета является точка весеннего равноденствия γ.
Одной координатой является склонение δ (реже полярное расстояние ρ). Другой координатой, определяющей положение круга склонения светила, является прямое восхождение α. Прямым восхождение α светила М называется центральный угол γОm между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Точкой весеннего равноденствия γ называется точка пересечения небесного экватора с эклиптикой. Точка весеннего равноденствия γ находится в созвездии Рыб. В этой точке Солнце, двигаясь по эклиптике, пересекает экватор в день весеннего равноденствия
(21 марта).
9

Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы (против хода часовой стрелки), в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Экваториальные координаты светила δ, α из-за суточного вращения небесной сферы не меняются, так как они отсчитываются от точек небесного экватора, которые сами участвуют в суточном вращении, и следовательно, положение светила относительно этих точек не изменяется.
Вторая экваториальная система является основной при решении задач фундаментальной астрометрии. В этой системе составляются списки звездных положений (звездные каталоги) и звездные карты.
Пример выполнения работы
Задание: изобразить на чертеже небесную сферу и положение ее основных элементов для широты φ=-15˚ и показать на ней точки со следующими координатами:
горизонтальные: А = 135˚, h = 45˚
экваториальные: t = 2h, δ =- 45˚ и a = 9h, δ = +75˚
|
т. М1 (А=135˚, h=45˚) |
|
|
Основные элементы небесной сферы |
т. М2 (t=2h, δ=-45˚) |
|
для широты φ=-15˚ |
т. М3 (a=9h, δ=75˚) |
Рис. 4. Схема небесной сферы с указанием координат точек
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #