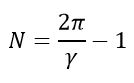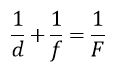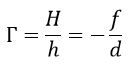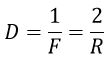Сферические зеркала
Сферическое зеркало представляет собой сферический сегмент, зеркально отражающий свет.
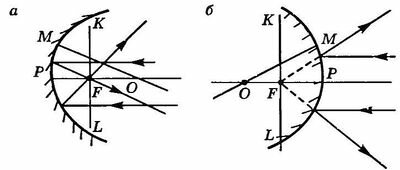
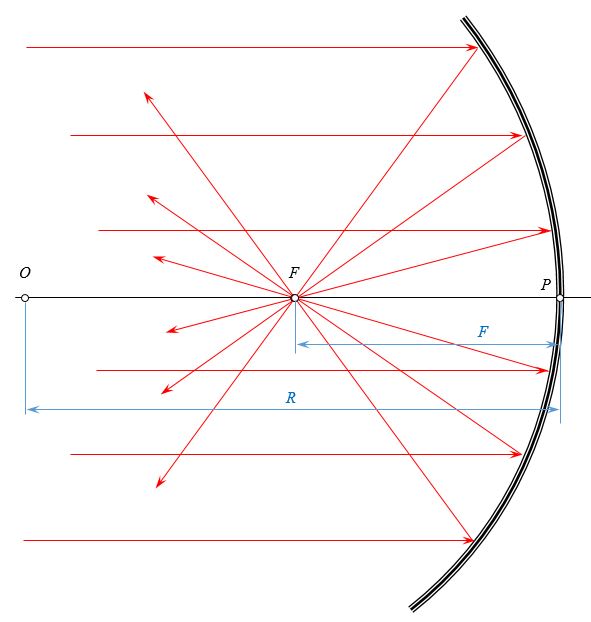
Сферические зеркала бывают вогнутые (рис. 16.13, а) — у них отражающее покрытие нанесено на внутреннюю поверхность, и выпуклые (рис. 16.13, б) — у них отражающее покрытие нанесено на внешнюю поверхность.
Геометрический центр О сферической поверхности зеркала радиусом R называется центром зеркала, а точка Р, являющаяся вершиной сферического сегмента — полюсом зеркала. Любая прямая (например, ОМ и ОР), проходящая через центр О зеркала, называется оптической осью. Оптическая ось ОР, проходящая через полюс зеркала, называется главной оптической осью, все остальные оси — побочными оптическими осями. Ясно, что любая оптическая ось в точке пересечения с поверхностью зеркала является нормалью к последней (любой радиус перпендикулярен к касательной к поверхности сферы). Точка F на главной оптической оси, через которую проходят после отражения от зеркала лучи (или их продолжения), падающие на зеркало параллельно главной оптической оси, называется фокусом зеркала. У вогнутого зеркала фокус действительный, у выпуклого зеркала фокус мнимый. Расстояние от фокуса сферического зеркала до его полюса PF называется фокусным расстоянием. Его принято обозначать также буквой F. Плоскость KL, проходящая через фокус перпендикулярно к главной оптической оси, называется фокальной плоскостью. В фокальной плоскости пересекаются после отражения от зеркала лучи (или их продолжения), падающие на зеркало параллельно какой-либо побочной оптической оси.
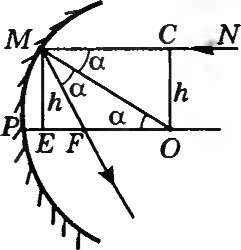
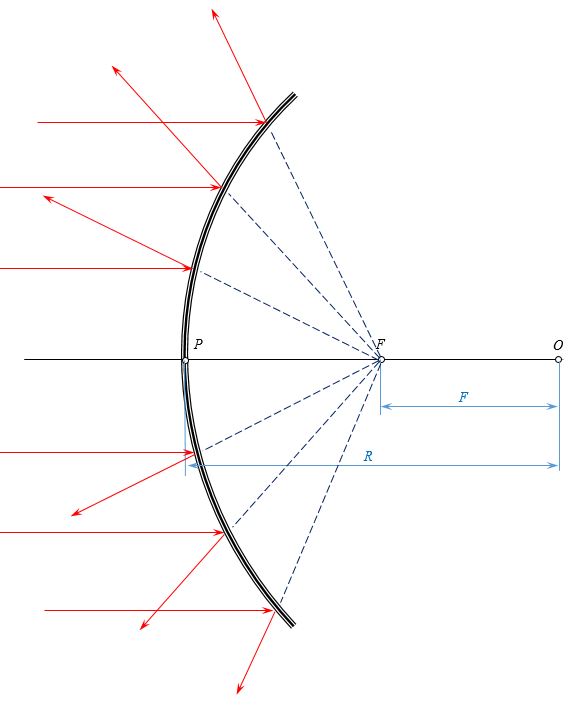
Определим положение фокуса сферического зеркала. Пусть на зеркало (рис. 16.14) падает луч NM, параллельный главной оптической оси. Отраженный от зеркала луч MF пройдет через фокус F. Луч NM составляет с радиусом ОМ угол (~alpha). Угол отражения (~ang OMF=alpha) и (~ang MOF=alpha) как накрест лежащие при параллельных прямых MN и РО и секущей МО. Следовательно, (~Delta MOF) — равнобедренный (FO = MF). Угол MFE = 2(~alpha) (угол внешний по отношению к (~Delta MOF)).
Будем рассматривать только так называемые параксиальные пучки, т.е. узкие пучки, составляющие с оптической осью зеркала очень малые углы (в широком пучке три луча, образующие значительные углы друг с другом, не пересекаются в одной точке). Тогда ( PE ll R, EF approx PF) и (tg alpha approx sin alpha = alpha ).
Из (~Delta MOC) ( sin alpha = frac{h}{R} Rightarrow alpha approx frac{h}{R} ) Из (~Delta MEF) ( tg 2 alpha = frac{h}{EF} Rightarrow 2 alpha approx frac{h}{PF}. )
Отсюда (2 frac{h}{R}=frac{h}{PF} Rightarrow PF=frac{R}{2}.) Таким образом, точка F лежит на главной оптической оси и делит радиус зеркала ОР на две одинаковые части. Значит, фокусное расстояние (F=frac{F}{2}.)
Аналогично можно доказать, что фокус выпуклого сферического зеркала лежит на главной оптической оси за зеркалом и удален от полюса зеркала на расстояние, равное половине радиуса зеркала. Фокусное расстояние выпуклого зеркала принято считать отрицательным (так как увыпуклого зеркала фокус мнимый), т.е. у выпуклого зеркала (F=-frac{F}{2}.)
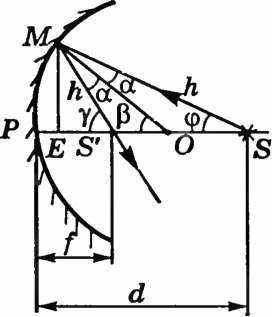
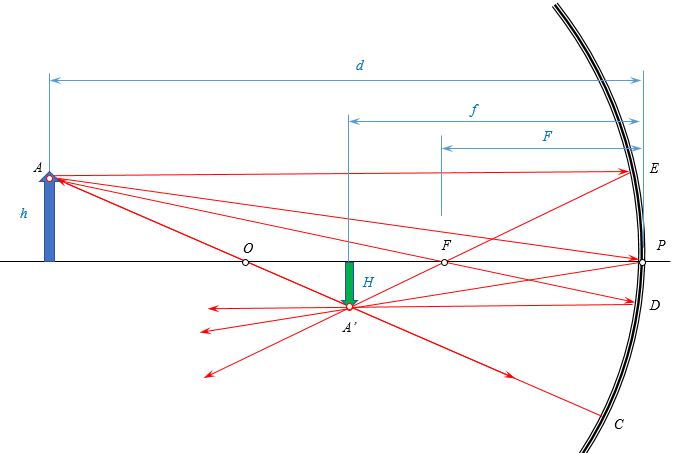
Формула сферического зеркала. Пусть точечный источник света S (рис. 16.15) расположен на главной оптической оси зеркала на расстоянии SP = d. Угол падения луча SM на поверхность зеркала (~ang SMO = alpha). Отраженный луч пересекает главную оптическую ось в точке S’. Угол отражения ( ang OMS’ = alpha) (по закону отражения). Обозначим угол наклона падающего луча к главной оптической оси (ang MSO = varphi), угол наклона отраженного луча (ang MS’P = gamma), угол наклона радиуса (ang MOP = beta,) расстояние от точки М до главной оптической оси через ME = h.
Угол (~beta) — внешний по отношению к (Delta OMS). Поэтому (beta = alpha + varphi).
Угол (~gamma) — внешний по отношению к (Delta S’OM). Поэтому (~gamma = alpha + beta).
Из этих равенств получаем
16.1
(gamma + varphi = 2 beta)
Из (Delta S’EM) находим ( tg gamma= frac{h}{ES’} approx frac{h}{f}). Из (Delta OME) имеем (tg beta=frac{h}{OE} approx frac{h}{R}.)
Из (Delta SEM) имеем (tg varphi= frac{h}{SE} approx frac{h}{d})
Так как мы рассматриваем только параксиальные лучи, то тангенсы углов можно заменить значениями самих углов в радианах.
Следовательно, (gamma = frac{h}{f};) (beta = frac{h}{R};) (varphi = frac{h}{d}.) Подставим в (16.1), получим ( frac{h}{f} + frac{h}{d} = 2 frac{h}{R} Rightarrow frac{1}{d} + frac{1}{f} = frac{2}{R}. )А так как (F=frac{R}{2},) то можно записать
(16.2)
(frac{1}{d} + frac{1}{f} = frac{1}{F})
Это выражение называют формулой сферического зеркала. Формулу (16 2) можно применять и для выпуклых сферических зеркал, если использовать правило знаков: считать знаки величин d, f, R и F положительными, если эти расстояния измерены от полюса зеркала в ту сторону, откуда на зеркало падает свет от предмета, и отрицательными, если они отсчитаны от полюса за зеркало. Для выпуклых зеркал d>0, a R<0, F<0. Если изображение мнимое, то f<0.
Так как в формулу (16.1) не входят значения h и угла (varphi), то это означает, что любой луч, выходящий из S, пройдет через точку S’. Следовательно, точка S’ является изображением точки S.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 461-464.


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 14.05.2023 15:12

Мышковская Антонина Петровна
учитель физики
38 лет
13 845
1 565
Местоположение
Республика Беларусь, Мозырь
Сферические зеркала
Сферическое зеркало ‒ это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет.
- Если лучи отражаются от внутренней поверхности сферического сегмента, то зеркало называют вогнутым
- Если лучи отражаются от внешней поверхности сферического сегмента, то зеркало называют выпуклым
Основные понятия:
- Оптический центр зеркала (точка O
) ‒ центр сферы, из которой вырезан сегмент
- Полюс зеркала (точка P
) ‒ вершина сферического сегмента
- Оптическая ось ‒ любая прямая, проходящая через оптический центр
- Главная оптическая ось ‒ прямая, проходящая через оптический центр и полюс зеркала
- Остальные оптические оси ‒ побочные.
- Главный фокус зеркала F
‒ точка, в которой пересекаются отраженные от сферического зеркала лучи или их продолжения, падающие параллельно главной оптической оси зеркала
- В вогнутом зеркале в фокусе пересекаются отраженные лучи, и фокус является действительным
- В выпуклом зеркале в фокусе пересекаются не сами отраженные лучи, а их продолжения, поэтому фокус выпуклого зеркала является мнимым
- Фокусное расстояние F
‒ расстояние от главного фокуса до полюса зеркала, ‒ равно половине радиуса сферы, частью которой является зеркало F=R2
- Предмет будет действительным, если лучи, падающие от него на зеркало, расходящиеся
- Предмет будет мнимым, если лучи, падающие от него на зеркало, сходящиеся
- Изображение называют действительным, если оно получено пересечением отраженных лучей
- Изображение называют мнимым, если оно получено пересечением продолжений отраженных лучей
Построение изображений в зеркалах
Вогнутое зеркало
Выпуклое зеркало
- Луч, проходящий через оптический центр зеркала,
- Луч, продолжение которого проходит через оптический центр зеркала,
после отражения идет в обратном направлении
- Луч, проходящий через фокус зеркала
- Луч, продолжение которого проходит через главный фокус зеркала
после отражения идет параллельно главной оптической оси
- Луч, падающий на зеркало в его полюсе, и отраженный луч симметричны относительно главной оптической оси
- Луч, идущий параллельно главной оптической оси зеркала
после отражения проходит через фокус
после отражения идет так, что его продолжение проходит через фокус
Свойства изображений:
- Если предмет перпендикулярен главной оптической оси, то и изображение также перпендикулярно главной оптической оси
- Если точка лежит на главной оптической оси, то и ее изображение также будет лежать на главной оптической оси
- Мнимое изображение получается в выпуклых зеркалах во всех случаях, и в вогнутом зеркале, если предмет находится между фокусом и зеркалом
- Мнимое изображение всегда является прямым, а действительное изображение, наоборот, всегда перевернуто
- Выпуклое зеркало всегда дает мнимое, уменьшенное изображение
- Во всех задачах по умолчанию предмет действительный d>0
13.01.2019 09:47
Рекомендуем курсы ПК и ППК для учителей
Похожие записи
Asked
4 years, 9 months ago
Viewed
51 times
$begingroup$
I know that pole is the geometric centre of a spherical mirror. But how do you really find it for an irregularly cut mirror in real life?
asked Aug 22, 2018 at 4:41
$endgroup$
$begingroup$
The pole of a mirror is the point where the axis meets the mirror.
If your irregularly cut mirror is a paraboloid, it has an identifiable axis — so wherever that axis intersects the mirror would be the pole.
If the irregularly cut mirror is spherical, then it will not have a unique axis. In that case, any point on the mirror could reasonably be called the pole.
answered Aug 22, 2018 at 5:05
S. McGrewS. McGrew
24.4k3 gold badges28 silver badges73 bronze badges
$endgroup$
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света.
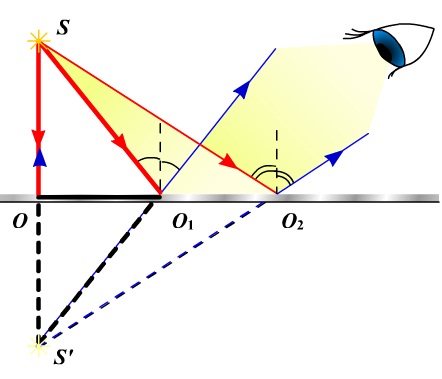
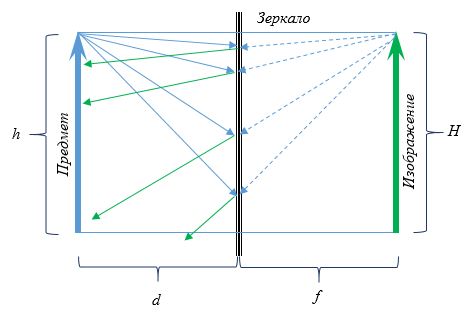
Изображение в плоском зеркале формируется за плоскостью зеркала на том же расстоянии от зеркала f, на каком находится предмет перед зеркалом d:
f = d
Изображение в плоском зеркале является:
- прямым;
- мнимым;
- равным по величине предмету: h = H.
Если плоские зеркала образуют между собой некоторый угол, то они формируют N изображений источника света, помещенного на биссектрису угла между зеркалами:
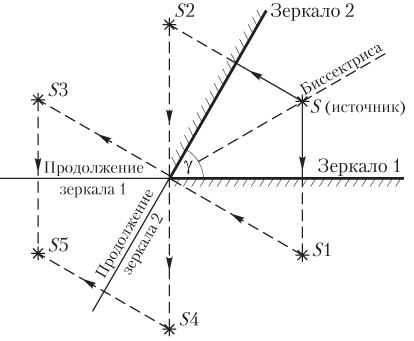
где γ — угол между зеркалами (в радианах).
Примечание: Формула справедлива для таких углов γ, для которых отношение 2π/γ является целым числом.
Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента.
Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.
Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом F зеркала. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала.
Фокусное расстояние у сферического зеркала равно половине радиуса кривизны, причем у вогнутого зеркала F > 0, у выпуклого F < 0.
Изображение какой-либо точки A предмета в сферическом зеркале можно построить с помощью любой пары стандартных лучей:
- луч AOC, проходящий через оптический центр зеркала; отраженный луч COA идет по той же прямой;
- луч AFD, идущий через фокус зеркала; отраженный луч идет параллельно главной оптической оси;
- луч AP, падающий на зеркало в его полюсе; отраженный луч симметричен с падающим относительно главной оптической оси.
- луч AE, параллельный главной оптической оси; отраженный луч EFA1 проходит через фокус зеркала.
Положение изображения и его размер можно также определить с помощью формулы сферического зеркала:
Здесь d – расстояние от предмета до зеркала, f – расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:
- d > 0 и f > 0 – для действительных предметов и изображений;
- d < 0 и f < 0 – для мнимых предметов и изображений.
Линейное увеличение сферического зеркала Γ определяется как отношение линейных размеров изображения H и предмета h.
Величине H удобно приписывать определенный знак в зависимости от того, является изображение прямым (H > 0) или перевернутым (H < 0). Величина h всегда считается положительной. При таком определении линейное увеличение сферического зеркала выражается формулой
Оптическая сила зеркала — величина, обратная фокусному расстоянию, измеряется в диоптриях (дптр)
Задачи


11
Расстояние от этого источника до одного зеркала 3 см, до другого 4 см. Расстояние между первыми изображениями 10 см. Найдите угол между зеркалами.
Решение.
Расстояние от источника до первого изображения 2а = 6 см, расстояние от источника до второго изображения 2b = 8 см. Т.к. задано расстояние с = 10 см между изображениями, то в треугольнике, вершинами которого являются источник и два изображения, известны все три стороны. По
теореме косинусов угол А равен: cosA = (4b2 + 4a2 –c2)/8ab = 0, т.о. угол А = 900 и угол между зеркалами равен:
1800 – 900 =900.
ЗАДАЧА 2.
На плоскопараллельную стеклянную пластину (n = 1,5) толщиной d = 5 см падает под углом α пучок света. Определите боковое смещение луча, прошедшего сквозь эту пластинку.
Решение.
Из рисунка искомая вели-
чина х = ЕD = CD sin(90-α)
СD = BD – BC, BD =d tgα BC = d tg r.
Из закона преломления находим: sinr = sinα/n.
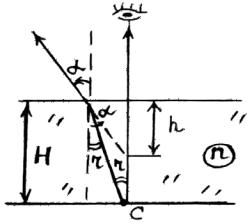
12
Следовательно, х = (d tgα — d tgr) cos α = d sinα(1 – cosα/ n2 – sin2α ).
х = 9,69 мм.
ЗАДАЧА 3.
Человек с лодки рассматривает предмет, лежащий на дне водоёма (n =1,33). Определите его глубину, если при определении на «глаз» по вертикальному направлению глубина водоёма кажется равной 1,5 м.
|
Решение. |
|
|
h = 1,5 м |
Для определения кажущегося местопол о- |
|
жения |
|
|
n = 1,33 |
точки построим два луча, исходящих из |
|
точки |
H = ? и попадающих в глаз наблюдателя. Пусть один из лучей перпендикулярен поверхности воды, второй
падает на поверхность воды под малым углом α, преломляется под углом r и попадает в глаз наблюдателя.

13
Которому кажется, что точка находится на пересечении продолжений лучей на расстоянии h от поверхности воды.
Из рисунка видно, tgα/tgr, где α и tgr, следовательно, tgα/tgr = n, тогда
H = h n. H = 2 м.
|
что h tgα = H tgr, откуда |
H = h |
|
|
r – малые углы, для которых Sinr |
= |
|
|
закон преломления даёт: sinα/sinr |
= |
ЗАДАЧА 4.
На дне сосуда с жидкостью с показателем преломления 5/3 помещён точечный источник света. Какого минимального радиуса должен быть непрозрачный диск, плавающий на поверхности жидкости, чтобы, глядя сверху, нельзя было увидеть этот источник? Высота слоя жидкости
12 см.
|
Решение. |
||
|
Лу- |
чи от и |
с- |
|
точника, |
падающие |
|
|
на границу воды с воздухом |
вне диска, не должны вых |
о- |
дить из воды, значит, они должны
падать под углом, большим предельного угла полного внутреннего отражения. При минимальном радиусе диска выполняется соотношение R = h tgrпр.
14
Угол полного внутреннего отражения определяется соотношением sinrпр =1/n = 3/5. Отсюда находим cosrпр =
4/5, tgrпр = 3/4, и радиус диска R= h tgrпр = 12 ¾ = 9 см.
Сферические зеркала
Сферические зеркала представляет собой хорошо отполированную поверхность тела, имеющую форму сферического сегмента, с нанесенным на одну из его сторон, (выпуклую или вогнутую), специального отражающего покрытия, чаще всего, металлизированного.
Такое покрытие зеркально отражает свет. Центр С сферической поверхности, из которой вырезан сегмент, называется оптическим центром зеркала; вершина О сферического сегмента – полюсом зеркала. Любая прямая, проходящая через оптический центр зеркала С, называется оптической осью зеркала. Оптическая ось СО, проходящая через оптический центр зеркала и его полюс, называется главной оптической осью.
Главной оптической осью сферической поверхности называется прямая, проходящая через точечный источник света S и центр кривизны С сферической поверхности. Приведенные выше условия справедливы лишь для узкого конуса световых лучей, имеющих ось, перпендикулярную к сферической границе раздела. Только такие пучки световых лучей, называемые параксиальными (приосевыми) пучками, после преломления или отражения остаются гомоцентрическими и дают изображение светящейся точки S в виде точки S ’. Расстояния отсчитываются от точки О пересечения сферической поверхности с оптической осью и считаются положительными в направлении распространения света и отрицательными в противоположном направлении.
Лучи параксиального пучка , параллельные главной оптической оси, после отражения от зеркала пересекаются в

15
одной точке F, называемой фокусом (главным фокусом) зеркала. Расстояние OF = f от полюса О до фокуса зеркала F называется фокусным расстоянием: f = R/2, где R – радиус кривизны зеркала. Плоскость, проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью.
4о. Формула сферического зеркала для параксиальных световых пучков лучей:
,
где R – радиус кривизны линзы, a — расстояние от зеркала до светящейся точки, расположенной на главной оптической оси, a’ – расстояние от зеркала до изображения. Правило знаков для R, a и a’ указано выше.
Изображение в сферическом зеркале действительное, когда источник и его изображение находятся по одну сторону от зеркала. Если источник и его изображение находятся по разные стороны о зеркала, то изображение в зеркале – мнимое.
Зеркало является выпуклым, если с учетом правила знаков, R > 0. В таком зеркале изображение мнимое – всегда.
Рис.1 На рисунке 1 (Рис.1) показаны вогнутое (а) и выпуклое (б) сферические зеркала.
Линейное увеличение k предмета, определяемое отношением размера изображения к размеру предмета (в направлении, перпендикулярном главной оптической оси зеркала) определено формулой
16
.
где a – расстояние от предмета до зеркала, a’ – расстояние от зеркала до изображения предмета.
В задачах настоящего раздела рассматриваются только лучи, составляющие с главной оптической осью зеркала малые углы (предполагается, что зеркало представляет собой малый сегмент сферы).
Примеры решения задач.
Задача 1. На рисунке 2 показан ход луча, отразившегося
от сферического зеркала. Построением определите положение фокуса зеркала. Рассмотрите отражение луча от вогнутого и выпуклого сферических зеркал. На рисунке показана главная оптическая ось зеркала.
Рис. 2
Решение:
Определение положения фокуса зеркала в задаче показано на рис.3.
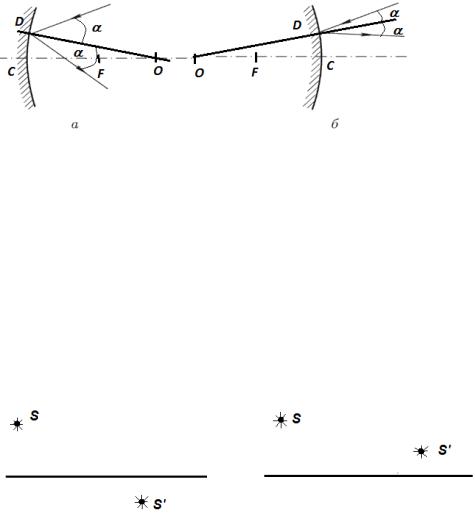
17
Рис.3 Построением (из элементарного курса планиметрии средней школы) строится биссектриса угла, образованного падающим и отраженным лучами от поверхности зеркала. Пересечение биссектрисы с главной оптической осью определяет центр сферического зеркала. Фокус зеркала определяется половиной расстояния OC: f = CF 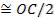
Задача 2 На рисунке 4 а, б показаны положения оптической оси
сферического зеркала ММ’, светящейся точки S и ее изображения S’. Найдите построением положения вершины зеркала и его центра для обоих случаев.
Решение:
Пусть задача решена. Тогда источник и его изображение будут располагаться, как показано на рис.5
18
а) б) Рис.5
Для вогнутого зеркала положения источника и его изображения показаны на рис.5а, а выпуклого – рис.5б (изображение источника – мнимое).
Рассмотрим вначале рис.5а. Найдем сперва точку С — полюс зеркала. Если обозначить SA =h, S’A’ = h’, CA = a, C
|
A’= a’, то, в силу подобия |
ASC и |
A’S’C можно записать |
|
|
. |
Тогда |
справедливо |
соотношение |
|
или |
. В данном случае Δh = SA-S’A’, a = CA-CA’ |
||
|
= AA’. Тогда |
. Тогда надо |
построить разность от- |
резков Δh = SA-S’A’, и соединить полученную точку с точкой A’ (рис.6а). После этого из точки S необходимо провести прямую, параллельную S”A до пересечения с главной оптической осью в точке С. Это и будет полюсом вогнутого зеркала.
а) б) Рис.6
19
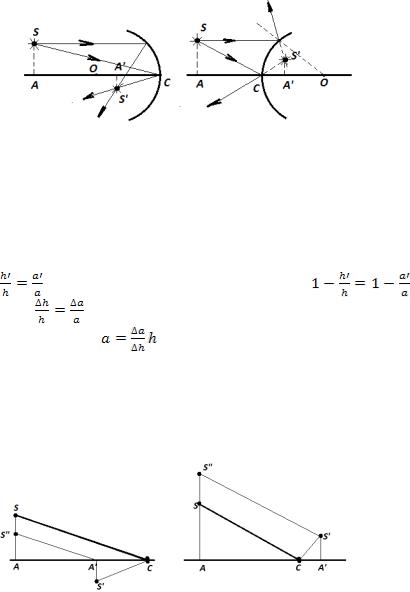
Для построения полюса выпуклого зеркала (рис.6б) необходимо вначале к отрезку SA добавить отрезок S’A’: S’A’ + SA = S”A. После этого точку S” надо соединить с точкой S’. Далее из точки S нужно провести прямую, параллельную S”S’. Данное построение следует из формул:
AC + A’C = AA’; 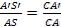
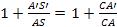
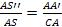
.
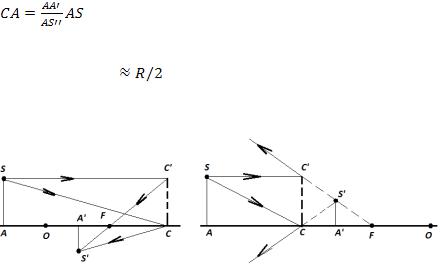
Для определения положения фокуса и центра зеркала можно воспользоваться обстоятельством, что для параксиальных лучей f и кривизной сферы для них можно пренебречь. Тогда, исходя из рис.5 а,б, положение фокуса и центра зеркала определяется по рис.7 а,б.
а)
б)
Рис.7
Луч CS’, рис.7а (или его продолжение, рис.7б) пересекает главную оптическую ось АО в точке F. Это и есть положение фокуса. Положение центра зеркала определяется из условия R = 2f и определяется построением отрезка СO = 2CF.
Задача 3 Луч света падает на вогнутое сферическое зеркало ра-
диусом R параллельно оптической оси СО на расстоянии “а” от нее (рис.8) и после отражения пересекает оптическую ось СО в точке B. Найдите отношение меж-

20
ду a и R, при котором относительная ошибка, которую мы делаем, принимая OB = 0,5R, равна 1%.
Решение:
|
Рис. 8 |
|||
|
На рис.8 |
рассмотрим |
АСВ. Точка С |
— центр сфериче- |
|
ского зеркала. Треугольник – равнобедренный, т.к. ∟ACB |
|||
|
= ∟BAC. Сторона ВС = R/2cosα. Из |
АСК видно, что |
||
|
sinα=a/R. Тогда cosα = |
. Величина отрезка ВС рав- |
||
|
няется |
BС = |
По условию задачи относительная ошибка, которую мы делаем, принимая OB = 0,5R, равна 1%, или
Т.е. ВО = R •0,495. Из рисунка следует ВС = СО – ВО = R
– 0,495•R = 0,505•R. Подставляя это значение в формулу для ВС, получим
0,505•R = или
После элементарных расчетов получается a/R =0,14.
Соседние файлы в предмете Оптика
- #
- #
- #