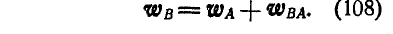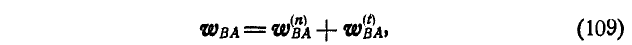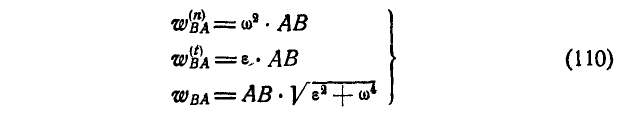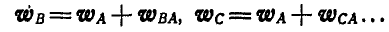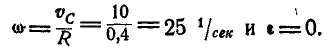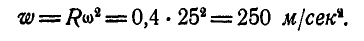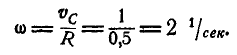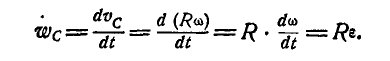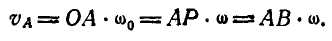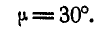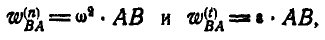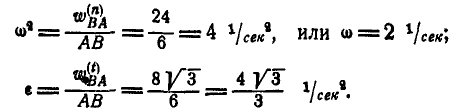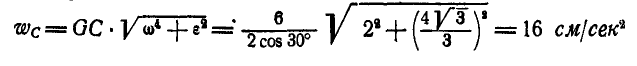Содержание:
- Плоское движение тела
- Определение скоростей точек тела
- Уравнения плоского движения
- Скорости точек фигуры. Мгновенный центр скоростей
- Определение положения мгновенного центра скоростей
- Порядок решения задач на тему: Определение скоростей точек тела
- Примеры решения задач на тему: Определение скоростей точек тела
- Решение задачи графоаналитическим способом
- Решение задачи с помощью мгновенного центра скоростей
- Определение ускорений точек тела
- Ускорения точек плоской фигуры
- Порядок решения задач на тему: Определение ускорений точек тела
- Примеры решения задач на тему: Определение ускорений точек тела
- План скоростей
- Порядок решения задач на тему: План скоростей
- Примеры решения задач на тему: План скоростей
- План ускорений
- Примеры решения задач на тему: План ускорений
Плоское движение тела — это такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Плоское движение тела
Плоскопараллельное движение (плоское движение) — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости. Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге
Определение скоростей точек тела
Скорости точек тела пропорциональны их расстояниям до мгновенного центра скоростей, и это отношение определяет угловую скорость тела в данный момент времени: Частные случаи определения положения мгновенного центра скоростей. Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого, то точка касания Р имеет в данный момент времени скорость равную нулю, и, следовательно является мгновенным центром скоростей .
Уравнения плоского движения
Плоским называется такое движение тела, при котором траектории всех его точек лежат в плоскостях, параллельных данной неподвижной плоскости.
При таком движении все точки твердого тела, лежащих на перпендикуляре к этой плоскости, имеют одинаковые траектории, скорости и ускорения.
Плоское движение фигуры можно рассматривать как сложное (то есть, абсолютное) движение, которое включает поступательное движение вместе с произвольно выбранной точкой 
На рис.4.1 с телом 





Уравнения (4.1) называются уравнениями плоского движения твердого тела.
При этом, поступательная часть плоского движения описывается двумя уравнениями:
а относительная вращательная вокруг полюса — третьим уравнением:
Координаты любой точки 



Скорости точек фигуры. Мгновенный центр скоростей
Поскольку плоское движение тела состоит из поступательного вместе с полюсом и вращательного вокруг него, то скорость любой точки тела 





Вектор относительной скорости 



Модуль и направление абсолютной скорости 


Относительная скорость 


где 
Найти скорость любой точки тела можно также на основе теоремы, которая гласит:
Проекции скоростей двух точек фигуры на прямую, что соединяет эти точки, равны между собой.
Согласно этой теореме (рис.4.3) :
или
Если известна скорость 

При плоском движении тела в каждый момент времени существует точка тела, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей и, как правило, обозначается буквой 
Если мгновенный центр скоростей известен, то легко можно найти мгновенное распределение скоростей всех точек тела (рис.4.4).
Выберем за полюс поступательного движения мгновенный центр скоростей 


где 









Поскольку скорость выбранного полюса 

По модулю скорости вращения точек 


Разделив 

Таким образом, мгновенное распределение скоростей точек тела при его плоском движении, такое же, какое было бы при его вращательном движении вокруг мгновенного центра скоростей.
Определение положения мгновенного центра скоростей
Существует несколько способов нахождения положения мгновенного центра скоростей.
Случай 1. Известна скорость 


Мгновенный центр скоростей 


Для нахождения направления перпендикуляра надо повернуть вектор 


Случай 2. Известны направления скоростей 



Мгновенный центр скоростей должен лежать как на перпендикуляре к вектору 


Случай 3. Скорости двух точек 

Говорят, что в этом случае мгновенный центр скоростей лежит на бесконечности. Угловая скорость вращения равна нулю, а скорости всех точек тела геометрически равны, то есть в данный момент времени тело выполняет поступательное движение.
Случай 4. Скорости двух точек 




Мгновенный центр скоростей находится на продолжении отрезка 
Решив это уравнение относительно 
Таким образом, для определения положения мгновенного центра скоростей надо знать не только направления скоростей, но и их величину.
Случай 5. Скорости двух точек 


Мгновенный центр скоростей лежит на отрезке 

Решив уравнение относительно 
Таким образом, для нахождения положения мгновенного центра скоростей надо знать величины и направления скоростей обеих точек.
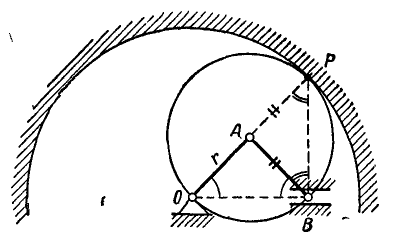
Случай 6. Тело катится без проскальзывания по неподвижной поверхности (рис.4.10).
В этом случае мгновенный центр скоростей находится в точке 

Тогда и скорость точки 
Порядок решения задач на тему: Определение скоростей точек тела
а) решение графоаналитическим методом:
- выбрать за полюс ту точку тела, скорость которой известна по величине и направлению или легко определяется из условий задачи;
- найти точку тела, направление скорости которой известно;
- пользуясь формулами плоского движения найти скорость этой точки;
- определить угловую скорость тела в данный момент времени;
- по известной угловой скорости и скорости полюса, пользуясь формулами плоского движения найти скорости других точек тела.
б) решение с помощью мгновенного центра скоростей:
- определить положение мгновенного центра скоростей одним из известных способов;
- определить значение мгновенного радиуса той точки тела, скорость которой известна, и найти угловую скорость тела;
- найти скорости других точек тела.
Примеры решения задач на тему: Определение скоростей точек тела
Задача №1
Стержень 






Определить величину скорости точки 

Решение задачи графоаналитическим способом
1. Выберем за полюс точку 
2. Используя формулу распределения скоростей при плоском движении, запишем векторное уравнение для определения скорости точки 
где 




Данное векторное уравнение можно решить построением векторного треугольника скоростей (рис.4.12). Для этого из произвольной точки плоскости 
При построении правой части уравнения (1) из точки 









Теперь из точки 



Точка 


В результате построения получили замкнутый треугольник скоростей, стороны которого в выбранном масштабе определяют искомую скорость точки 

В этом треугольнике известны все углы и одна сторона 

3. Определим угловую скорость вращения стержня 

4. Найдем скорость точки 



где 




Скорость 

Отложив от точки 







Поскольку стороны 




Решение задачи с помощью мгновенного центра скоростей
1. Определим положение мгновенного центра скоростей. Для этого с точек 




2. Определим мгновенные радиусы. Поскольку треугольник 
3. Вычислим угловую скорость вращения фигуры вокруг мгновенного центра скоростей:
4. Найдем скорости точек 

где 




Если надо было бы определить только величину скорости 
Тогда:
Ответ:
Задача №2
Колесо радиусом 


Определить: скорости точек 


Решение.
1. В качестве полюса выберем точку 
2.Используя формулу распределения скоростей точек тела при плоском движении определяем скорости других точек колеса.
Для точки 
где 


По модулю 
Скорость 



Из точки 


Тогда:
Векторное уравнение для определения скорости точки 
где 


Эта скорость параллельна скорости 
Из точки 


Поскольку векторы коллинеарны, то:
Таким образом, скорость точки 


Составляем векторное уравнение для определения скорости точки 
где 


По модулю 
Скорость 


Из точки 






Поскольку векторы 


Ответ:
Задача №3
Колесо радиусом 
Определить: скорости точек 


Решение. Решим задачу с помощью мгновенного центра скоростей.
1. Определим положение мгновенного центра скоростей. Поскольку колесо катится по неподвижной поверхности, то мгновенный центр скоростей находится в точке 
2. Мгновенный радиус для точки 


Направлена угловая скорость по ходу часовой стрелки.
3. Определим величину и направление скоростей точек 


Соединим точки 








По модулю скорости будут равны:
где
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 16.2; 16.4; 16.11; 16.12 [2]
Определение ускорений точек тела
Теорема: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.
Ускорения точек плоской фигуры
Формула распределения ускорений при плоском движении тела имеет вид:
где 






Ускорение любой точки 

Графическое определение ускорения точки 
Вычисление величины ускорения точки 


Учитывая, что 


где
Вектор 




Тогда уравнение (4.10) примет вид:
Если точка 


Порядок решения задач на тему: Определение ускорений точек тела
1. Выбрать точку, которая будет полюсом при записи уравнения плоского движения (как правило выбирают точку, ускорение которой известно).
2. Записать векторное уравнение распределения ускорений.
3. Спроектировать уравнение распределения ускорений на две взаимно перпендикулярные оси, одна из которых совпадает с нормальным ускорением, а вторая – с тангенциальным.
4. Определить мгновенное угловое ускорение плоской фигуры.
5. Найти искомые ускорения точек с помощью уравнения распределения ускорений.
Примеры решения задач на тему: Определение ускорений точек тела
Задача №1
Прямоугольная (рис.4.18, а) пластина 




Ускорение точки 



Определить мгновенную угловую скорость и мгновенное угловое ускорение пластины, и ускорение точки 
Решение.
1. Выберем за полюс точку 
2. Составим векторное уравнение для ускорения точки 
где 









Поскольку направление углового ускорения неизвестное, то направлением 
3. Спроектируем составленное уравнение (1) на оси 

В проекции на ось 
В проекции на ось 
4. Из уравнения (2) получим величину нормального ускорения:
Найдем мгновенную угловую скорость фигуры:
5. Из уравнения (3) получим величину тангенциального ускорения:
Угловое ускорение фигуры:
Поскольку величина 
6. Определим ускорение точки 
Для вычисления ускорения точки 


Направление векторов 

Спроектируем записанное уравнение на оси 

где
Полное ускорение точки 
Ответ: 
Задача №2
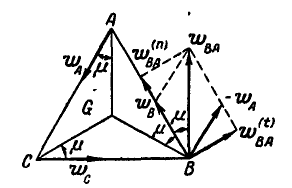
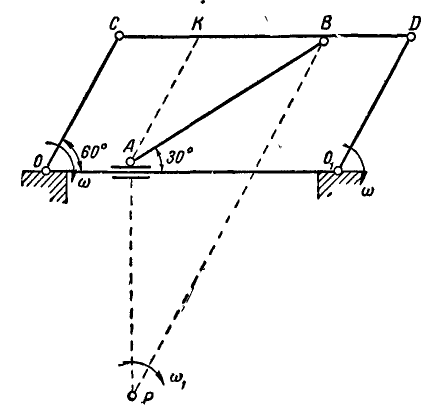
Равносторонний треугольник 



Определить ускорение вершины 
Решение. Если известны ускорения двух точек плоской фигуры, например 

1. Рассматривая первую точку 


2. Из уравнения проекций определить величину нормального ускорения 

3. Спроектировать векторное уравнение распределения ускорений при плоском движении на прямую, которая перпендикулярна 


4. Если нужно, то, используя формулу распределения ускорений при плоском движении, определить ускорение любой другой точки плоской фигуры.
Решим задачу, придерживаясь приведенной последовательности.
1. Выберем за полюс точку 

где 









Спроектируем записанное равенство (1) на прямую 
2. Откуда:
Поскольку 
3. Спроектируем векторное уравнение на прямую, которая перпендикулярна 
Откуда:
Учитывая то, что 
Поскольку величина тангенциального ускорения 
4. Определим ускорение точки 

где 










Учитывая, что 
От точки 
Выберем систему координат 


Спроектируем равенство (2) на оси выбранной системы координат:
Подставляя числовые данные, получим:
Таким образом, ускорение вершины 
Поскольку проекция ускорения 






Ответ:
Задача № 3
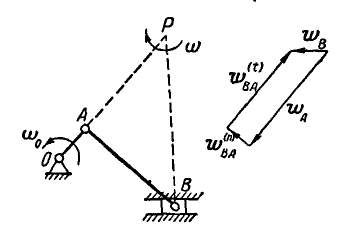
В шарнирном механизме (рис.4.21) в данный момент времени угловая скорость и угловое ускорение кривошипа 




Найти ускорение точки 


Решение. Скорость точки 

Направлена скорость 


Точка 


Поскольку скорости точек 

Ускорение точки 
где
Направления ускорений 

Выберем точку 


или
где 









Свяжем с точкой 


С другой стороны, при движении точки 


где 






По величине нормальное 

Спроектируем уравнение (4) на оси выбранной системы координат:
Подставим в (3) все рассчитанные величины:
Поскольку
то
Положительное значение величины 

Угловое ускорение тела 
Угловое ускорение 

Для определения тангенциального ускорения 

Откуда
Поскольку величина 

Полное ускорение точки 
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 18.12; 18.14; 18.22 [2].
План скоростей
План скоростей и план ускорений – физическое изображение векторных уравнений, связывающих скорости и ускорения точек механизма. Изображение механизма, выполненное с помощью условных обозначений (см. выше) называется структурной схемой механизма.
Определение скоростей различных точек движущейся плоской фигуры легко может быть выполнено графически с помощью построения плана скоростей.
План скоростей – это графическое изображение из единого центра (полюса) векторов абсолютных скоростей точек фигуры в фиксированный момент ее движения.
План скоростей может быть построен, если:
- известная скорость одной точки плоской фигуры и направление скорости другой точки;
- известная скорость одной точки плоской фигуры и мгновенная угловая скорость фигуры
Пусть известные скорости 













Установим свойства и правила построения плана скоростей.
По уравнению распределения скоростей при плоском движении фигуры, если за полюс принять точку 

где 





С другой стороны для векторов треугольника 
Учитывая, что векторы 





Таким образом, отрезок 

где 
Аналогично:
Отсюда мгновенная скорость вращения плоской фигуры:
Вектор 






Из рассматриваемого вытекает:
Порядок решения задач на тему: План скоростей
1. Изображают на чертеже в выбранном масштабе плоскую фигуру и вектор скорости той точки, скорость которой известна.
2. Определяют направление скорости второй точки плоской фигуры.
3. Записывают векторное уравнение распределения скоростей при плоском движении, принимая за полюс точку, скорость которой известна, а за искомую ту точку, направление скорости которой известно.
4. Решают записанное векторное уравнение графически путем построения в выбранном масштабе плана скоростей.
5. Определяют мгновенную угловую скорость вращения плоской фигуры.
6. Определяют скорость других точек плоской фигуры.
Примеры решения задач на тему: План скоростей
Задача №1
Найти угловую скорость 

Решение.
1. Согласно исходным данным в произвольном масштабе строим схему механизма (рис.4.25, а).
2. Учитывая, что кривошип 1 вращается вокруг неподвижной точки 


Направлена скорость 


3. Следующей точкой шатуна, скорость которого можно определить, является точка 
Для определения скорости точки 

где 





4. Решим уравнение (1) графически (рис.4.25, б). Для этого с произвольной точки 







Вектор который будет на плане скоростей изображать абсолютную скорость точки 




Определим направление отрезка 







Полученный векторный треугольник 








Перенесем из плана скоростей в точку 


Поскольку скорость 








Аналогично, 



Таким образом, и угол при вершине 



5. Определяем мгновенную угловую скорость шатуна 2. Поскольку 
где 

Направление угловой скорости 


Ответ:
Задача №2
Найти угловые скорости шатуна 2 и коромысла 3 и абсолютные скорости точек 



Угловая скорость кривошипа 1 — 
Решение.
1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.27, а).
2. Так как точка 


Вектор скорости 

2. Шатун 2 механизма движется плоскопараллельно. Скорость точки 






3. Для определения скорости точки 
где 









4. Решаем записанное уравнение графически. Для этого из произвольной точки 



Через конец вектора 




Скорость точки 




Полученный на рис. 4.27, б векторный треугольник 










Перенесем направления скоростей 


Поскольку 






Таким образом
Угол при вершине 






Тогда угол при вершине 
Для определения сторон 
Из уравнения (1) получим:
Таким образом:
5. Определим мгновенные угловые скорости шатуна 2 и коромысла 3. Поскольку 
Направление угловой скорости 


Угловая скорость коромысла 3 равна:
где
Направление 

6. Определить величины скоростей 

Поскольку вектор 

Скорости 



Тогда:
7. Для определения скорости точки 
Поскольку фигура 

В левой части пропорции (2) отношение отрезков на схеме механизма, а в правой — на плане скоростей.
Из уравнения (2) получим расстояние от точки 

Поскольку на схеме механизма отрезок 









Вектор скорости 



Ответ: 


Задача №3
В состав рычажного механизма (рис.4.29) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 вращается с угловой скоростью 

Найти угловые скорости шатунов 2 и 3 и абсолютные скорости точек 



Решение. Особенность этой задачи заключается в том, что определить сразу направление скорости точки 





1. В соответствии с исходными данными в произвольном масштабе строим схему механизма (рис.4.30, а).
2. Так как точка 


Вектор скорости 

Шатун 2 механизма движется плоскопараллельно. Скорость точки 

Для определения скорости точки 
где 








В уравнении (1) три неизвестных: величина и направление скорости точки 

для плоскости позволяет определить только две неизвестных, то решить уравнение (1) невозможно.
3. Рассмотрим определение скорости точки 

Скорость точки 
Вектор скорости 

Учитывая, что шатун 3 механизма движется плоскопараллельно, то для определения скорости точки 
где 






В записанной системе векторных уравнений (1,2) четыре неизвестных: величина и направление скорости точки 


4. Решаем записанную систему векторных уравнений (1) и (2) графически. Для этого из произвольной точки 
Согласно уравнению (1) из произвольной точки 





Тогда масштабный коэффициент плана скоростей будет равен:
Через конец вектора 




Теперь построим из того же самого полюса 




Через конец вектора 




Точка пересечения 





Полученный на рис. 4.30,б четырехугольник 






Перенесем направления скоростей 

5. Определим мгновенные угловые скорости шатунов.
Поскольку 
Направление угловой скорости 


Аналогично, угловая скорость шатуна 3 равна:
Направление 

Для определения скорости точки 



Вектор скорости 



Ответ: 
План ускорений
План ускорений – построенный в определенном масштабе векторный график, характеризующие ускорения всех точек и звеньев механизма. Произвольная точка ра, из которой производится построение плана ускорений, называется полюсом плана ускорений.
Рассмотрим графический способ определения ускорений точек плоской фигуры (тела) с помощью плана ускорений.
Планом ускорений плоской фигуры является геометрическое место концов векторов ускорений любых точек фигуры, что отложены из одной произвольной точки, которую называют полюсом плана ускорений.
Построение плана ускорений основано на представлении ускорения 

где 











Поскольку для определения величины 

Для того, чтобы уравнение (4.18) можно было решить, должно быть известно ускорение 

Кроме того, должно быть известно:
Рассмотрим определение ускорений точек 





Для ускорения точки 

Решим уравнение (4.18) графически. Для этого (рис.4.31, б) из произвольной точки 





Величину ускорения 
а направлен этот вектор вдоль 


К нормальному ускорению добавим, согласно уравнению (4.18), тангенциальное ускорение 





Направление абсолютного ускорения 









Для определения ускорения точки 


Запишем векторные уравнения для ускорения точки 


где 









Первым решаем уравнение (4.19). Поскольку ускорение 






Через конец вектора 



Следующим построим уравнение (4.20). Поскольку ускорение 






Через конец вектора 



Таким образом, конец вектора 




Векторы 







Кроме абсолютных и относительных ускорений точек фигуры 



Для определения же направления углового ускорения 



Треугольник 

Таким образом, для плана ускорений справедливо
правило подобия: фигура, которую образуют концы векторов абсолютных ускорений точек тела на плане ускорений подобная фигуре, которую одноименные точки образуют на теле.
Примеры решения задач на тему: План ускорений
Задача №1
Найти ускорение точки 


Решение. План скоростей для этого механизма был построен в задаче № 1 занятия № 7 (рис.4.25,б) и была определена угловая скорость шатуна 2 
1.Построим схему механизма (рис. 4.32, а).
2. Сначала найдем ускорение точки 

Учитывая, что угловая скорость кривошипа постоянная 





По модулю:
Направлено ускорение 



3. Для определения ускорения точки 

где 













Поскольку направление ускорения точки 

4. Решим уравнение (1) графически путем построения плана ускорений.
Из произвольной точки 

















Поскольку ускорение 








4. Из построенного плана ускорений определим абсолютные величины ускорений 







Из векторного четырехугольника 
Спроектируем векторное уравнение (2) на прямую 
Учитывая, что 


Откуда:
Теперь спроектируем уравнение (2) на прямую 
Учитывая, что 

Откуда:
Поскольку 
Из полученного результата следует, что в данный момент времени шатун механизма вращается равномерно 
Ответ:
Если построение плана ускорений выполнять с соблюдением масштаба, то ускорения характерных точек можно определить непосредственно измерением соответствующих отрезков на плане ускорений.
Задача №2
Найти абсолютное ускорение точек 




Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче № 2 занятие № 7 (рис.4.27, б) и определены мгновенные угловые скорости шатуна 2 и коромысла 3:
Решим задачу путем построения в масштабе плана ускорений.
1. Сначала в произвольном масштабе строим схему механизма (рис.4.34, а).
2.Определим ускорение точки 
Поскольку кривошип 1 вращается вокруг неподвижной точки 





По модулю 
Направлено ускорение 


3.Запишем векторные уравнения для определения ускорения точки 
Точка 







где 



















4.Решим графически систему векторных уравнений (1,2).
Сначала построим уравнение (1). Для этого из произвольной точки 







От конца вектора 






Через конец вектора 




Следующим построим уравнение (2).
Поскольку 


От точки 






Через конец вектора 


Решением системы (1,2) будет точка 




Вектор абсолютного ускорения 



Величины тангенциальных ускорений 

Поскольку 



где 
Для определения направления углового ускорения 




Аналогично, для определения направления 



5.Для определения ускорения точки 



В левой части пропорции (3) отношение отрезков на схеме механизма, а в правой — на плане ускорений.
Из уравнения (3) получим расстояние от точки 

Поскольку на схеме механизма отрезок 









Вектор абсолютного ускорения 



Ответ: 
Задача №3
В состав рычажного механизма (рис.4.35) входят два кривошипа 1 и 4, и два шатуна 2 и 3. Кривошип 1 в настоящий момент времени вращается равномерно с угловой скоростью 

Найти угловые ускорения шатунов 2 и 3 и абсолютные ускорения точек 



Решение. План скоростей механизма для положения, что рассматривается, был построен в задаче №3 занятия №7 (рис.4.30, б) и определены мгновенные угловые скорости шатуна 2 и шатуна 3:
1. В произвольном масштабе построим схему механизма (рис. 4.36, а).
2.Сначала определим абсолютные ускорения точек 

Поскольку кривошип 1 вращается вокруг неподвижной точки 


Направлено ускорение 



Кривошип 4 вращается вокруг неподвижной точки 


Абсолютное ускорение точки 
Нормальная составляющая ускорения точки 



а тангенциальная — перпендикулярно 

3. Запишем векторные уравнения для определения ускорения точки 
Точка 





В уравнении (2):






В уравнении (3):






4. Решим графически систему векторных уравнений (2,3).
Сначала построим уравнение (2). Для этого из произвольной точки 







От конца вектора 






Через конец вектора 




Следующим построим уравнение (3).
Для построения вектора 






Длины векторов 

Абсолютное ускорение 


От точки 






Через конец вектора 


Решением системы (2,3) будет точка 




Вектор абсолютного ускорения 



Величины тангенциальных ускорений 

Поскольку 



Направления угловых ускорений 






5. Для определения ускорения точки 







Ответ: 
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
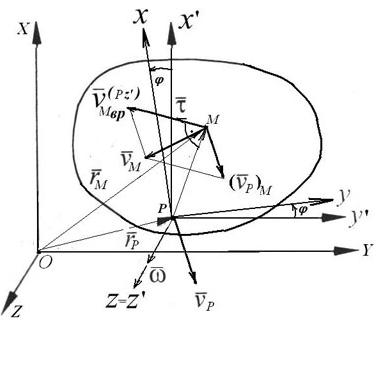
3.2.1. Метод полюса
Рис.3.4
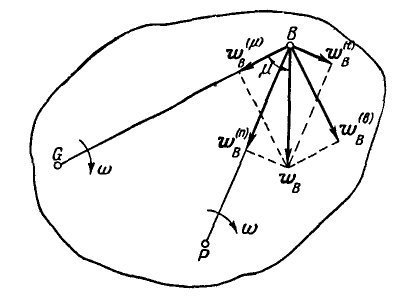
На рис.3.4 представлено положение плоской
фигуры S и ее
отрезка PM в
неподвижной системе координат OXYZ,
Для произвольного момента времени
справедливо векторное равенство:
(3.3)
При движении плоской фигуры векторы
и
изменяются и по модулю и по направлению,
вектор же
изменяется только по направлению,
так как его модуль равен для твердого
тела расстоянию между точками P
и M. Продифференцировав
по времени равенство (3.3), получим:
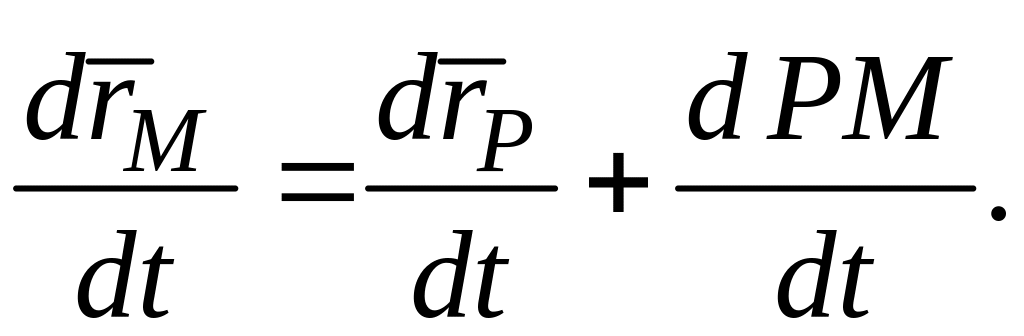
Обозначив
и назвав
скоростью точки M
тела при вращении его вокруг оси Pz’,
проходящей через полюс P
перпендикулярно плоскости плоской
фигуры, получим
(3.4)
Рассмотрим вектор
.
Поскольку вектор
вектор
постоянного модуля, то
=
,
где
вектор, лежащий в плоскости фигуры,
перпендикулярный
и направленный против хода
часовой стрелки. Тогда вектор
лежит в плоскости фигуры, перпендикулярен
отрезку PM,
соединяющему точку M
с полюсом P, и
направлен в сторону вращения плоской
фигуры вокруг оси Pz’
(рис.3.4).
Модуль вектора определяется как:
(3.5)
Применив векторную формулу Эйлера,
определяющую вектор скорости точки
тела, вращающегося вокруг оси, равный
векторному произведению вектора угловой
скорости тела на радиус-вектор точки
относительно какой-либо точки, лежащей
на оси вращения тела (см. 2.14):
можно представить выражение (3.5) в
векторной форме:
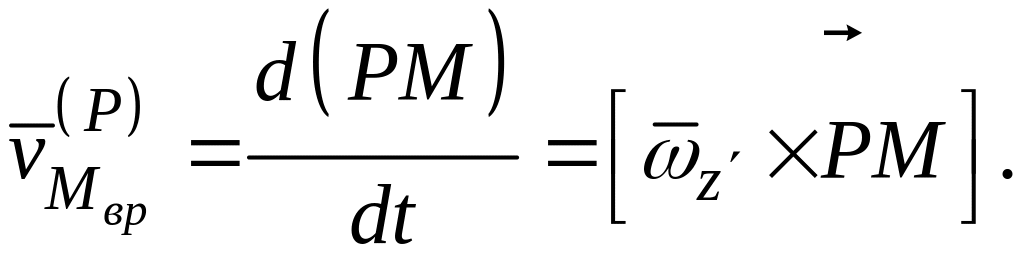
Окончательно имеем выражение для
определения скоростей точек плоской
фигуры методом полюса:
(3.6)
Таким образом, скорость любой точки
плоской фигуры при ее плоском движении
по методу полюса равна
векторной сумме скорости полюса,
построенной при рассматриваемой точке
M, и скорости данной
точки при вращении фигуры вокруг оси
Pz’,
проходящей через полюс перпендикулярно
плоскости плоской фигуры.
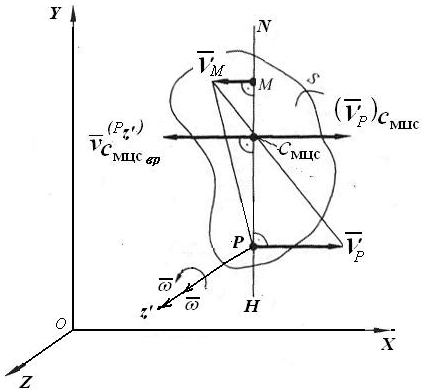
3.2.2. Метод мгновенного центра скоростей
Мгновенным центром скоростей называется
точка на плоскости, скорость которой в
данный момент времени равна нулю. Найдем
эту точку, обозначив ее
.
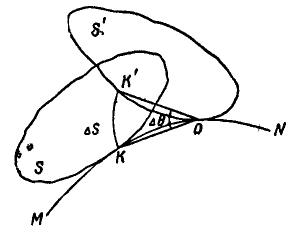
Пусть в данный момент времени скорость
точки P, принятой за
полюс, равна
и фигура S вращается
с угловой cкоростью
Проведем прямую РNH,
перпендикулярную вектору
,
в направлении вращения
(рис.3.5),
отложим на этой прямой отрезок P
=
и определим скорость полученной точки
,
выбрав за полюс точку P:
Отсюда следует, что векторы
и
должны быть равны по модулю и противоположны
по направлению. Так как вектор
перпендикулярен отрезку P
,
то прямая, на которой должна
н
аходиться
точка
,
перпендикулярна вектору
.
Чтобы
Рис.3.5
выполнялось условие
=
,
точка
должна находиться на прямой PNH.
Поскольку
=
,
а
,
мгновенный радиус (расстояние от
точки до мгновенного центра скоростей
)
будет равен: P
=
.
Таким образом, приняв за полюс плоской
фигуры S точку
,
можно определить скорость любой точки
(пусть точки M) по формуле:

(3.7)
где
расстояние от точки
M до мгновенного
центра скоростей
.
Вектор
перпендикулярен отрезку
и направлен в сторону вращения фигуры
вокруг оси
,
проходящей через
z’,
а его модуль пропорционален мгновенному
радиусу =
.
Таким образом, скорости точек плоской
фигуры в данный момент времени вычисляются
так же, как если бы фигура вращалась
вокруг оси, проходящей через
z’
перпендикулярно плоскости плоской
фигуры и плоскости движения, с той же
угловой скоростью
.
Метод МЦС значительно упрощает
определение скоростей точек твердого
тела при плоском движении. Поэтому важно
уметь определять положение МЦС, т.е.
точки
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
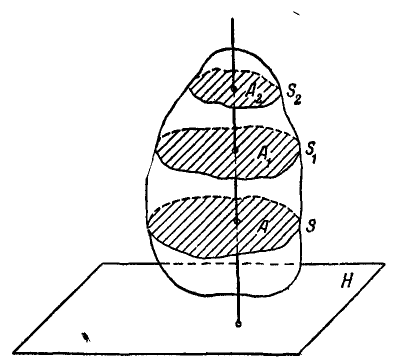
Плоско-параллельное движение твердого тела:
Плоско-параллельным или плоским называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных данной неподвижной плоскости.
Рис. 171.
Пусть неподвижная плоскость Н и тело А совершают плоское движение (рис. 171). Рассекая это тело плоскостями
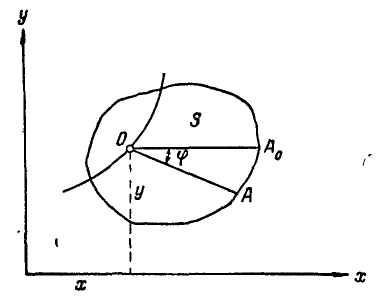
Отсюда следует, что при изучении плоского движения тела достаточно изучить движение некоторой плоской фигуры, взятой в теле параллельно неподвижной плоскости, движущейся в своей плоскости (рис. 172). Выберем на подвижной фигуре 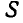
Рис.172.
Если бы все точки плоской фигуры двигались так же, как и выбранная нами точка О, то движение фигуры было бы поступательным. В общем, же случае движение плоской фигуры S можно рассматривать как поступательное движение вместе с полюсом О и в то же время делающей поворот вокруг О.
Если через полюс О провести две любые прямые, 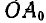
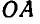
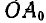
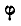
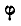
Уравнения (105) называются уравнениями плоско-параллельного движения.
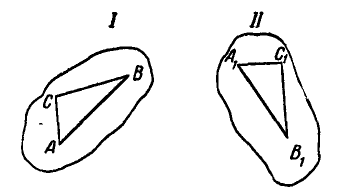
Покажем, что при изучении движения подвижной фигуры достаточно изучить движение двух каких-либо ее точек. Пусть фигура из положения I перейдет в положение II (рис. 173).
Рис. 173.
Тогда взятые на ней точки А и В, переместившись вместе с фигурой, займут в новом положении II фигуры места 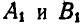
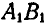
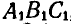
Отсюда следует, что для исследования движения подвижной плоскости по неподвижной достаточно.исследовать движение отрезка, принадлежащего к подвижной плоскости.
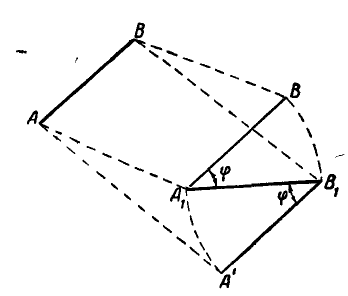
Пусть прямая АВ, принадлежащая к подвижной фигуре, переместится при своем движении в положение 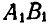
Рис. 174.
Если за полюс принять точку А, то это перемещение можно представить как поступательное движение отрезка вместе с полюсом А в положение 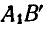
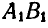
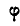
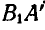
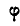
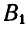
Таким образом, перемещение отрезка может быть выполнено при помощи двух операций: параллельного переноса до совпадения одной из точек с ее конечным положением и поворота около этой точки до совпадения отрезка с требуемым положением. Независимо от того, какой из концов отрезка А или В выбран нами за полюс, поворот отрезков 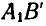
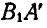
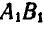
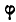
В нашем случае поворот отрезка на угол 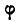
Докажем теперь следующую теорему Эйлера.
Всякое непоступательное перемещение плоской фигуры в ее плоскости можно осуществить путем вращения вокруг некоторого центра.
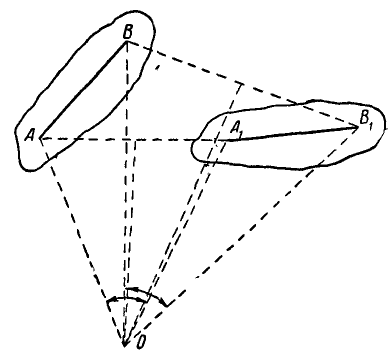
Пусть фигура вместе с прямой АВ переместится в положение 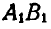
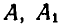
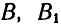
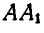
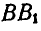
Рис. 175.
Полученные треугольники ОАВ и 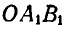
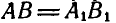
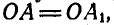
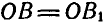
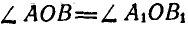
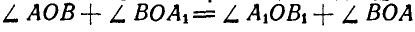
Если мы повернем отрезок АВ вокруг точки О на угол 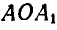
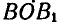
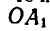
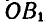
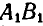
Переходя к изучению плоского движения как непрерывного процесса, рассматриваем его состоящим из бесконечно большого числа бесконечно малых элементарных перемещений.
Применяя к каждому из них теорему Эйлера, приходим к заключению, что плоское движение может быть рассматриваемо в пределе, как непрерывный ряд бесконечно малых вращений около различных центров, которые называются полюсами мгновенных вращений или мгновенными центрами вращения.
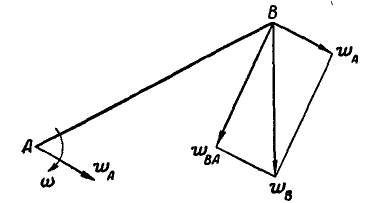
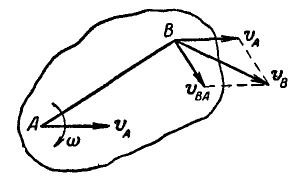
Мы уже знаем, что движение плоскости можно рассматривать как сложное, состоящее из поступательного движения вместе с полюсом и из вращательного — около полюса. Если бы полюс А (рис. 176) был неподвижным, то скорость любой точки В фигуры определилась бы как вращательная по отношению к точке А по формуле (89):
Рис. 176.
В общем же случае скорость полюса А (произвольно выбранной нами точки) не равна нулю, а поэтому к вращательной скорости точки В по отношению к А присоединится еще и скорость 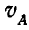
Полная скорость точки В получится как сумма двух скоростей: скорости точки А и скорости точки В по отношению к полюсу А. Складывая эти скорости как векторы по правилу параллелограмма, находим:
или
Проектируя обе’части векторного равенства (106) на направление АВ и замечая, что 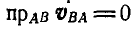
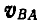
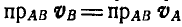
Покажем теперь, что при непоступательном движении плоской фигуры существует точка этой фигуры, скорость которой в данный момент равна нулю. Эта точка называется мгновенным центром скоростей и, как было отмечено выше, расположена на самой подвижной плоскости.
Та же точка неподвижной плоскости, с которой в данный момент совпадает мгновенный центр скоростей, называется мгновенным центром вращения, или полюсом мгновенного вращения. Очевидно, что положения мгновенных центров скоростей и мгновенных центров вращения при движении плоской фигуры по неподвижной плоскости будут непрерывно меняться.
Допустим, что некоторая подвижная плоскость движется по неподвижной плоскости.
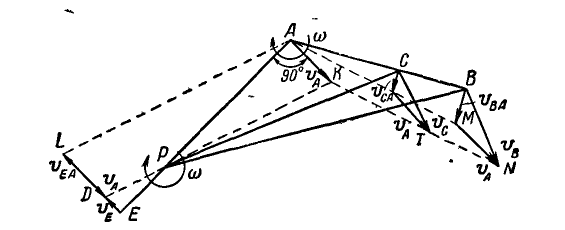
Вместо подвижной плоскости рассмотрим движение отрезка АВ, принадлежащего этой плоскости (рис. 177). Обозначим мгновенную угловую скорость отрезка 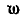
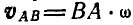
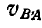
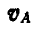
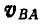
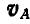
Легко видеть, что концы векторов, изображающих полные скорости точек прямой АВ (или ее продолжения), лягут на прямой KN, параллельной АМ ; например, скорость точки С изобразится вектором СТ. Однако движение плоскости мы могли бы задать каким-либо другим отрезком АЕ, составляющим, например, с вектором 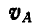
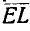
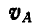
Рис. 177.
По предыдущему заключаем, что концы векторов полных скоростей точек отрезка АЕ должны лежать на прямой DK. Тогда полная скорость точки Е изобразится вектором 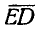
Мгновенный центр скоростей не следует смешивать с другими точками подвижной плоскости, в частности с полюсами. Эта неподвижная точка фигуры для данного момента только одна, тогда как в качестве полюсов, вообще говоря, могут быть выбраны любые точки фигуры. Выбирая в качестве полюса точку Р—мгновенный центр скоростей, найдем по формуле (106,а), например, скорость точки В:
но так как 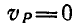
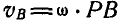
Отсюда следует, что скорости всех точек плоской фигуры пропорциональны их расстояниям до мгновенного центра вращения (так называемым мгновенным радиусам) и перпендикулярны к этим радиусам.
Для нахождения положения мгновенного центра вращения достаточно знать вид траекторий двух точек плоской фигуры. Пусть, например, отрезок АВ, принадлежащий этой фигуре, перемещается так, что точка А его движется по траектории 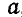
Рис. 178.
Задача №1
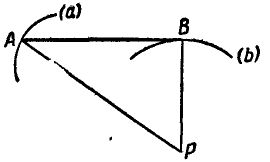
Найти построением мгновенный центр Р отрезка АВ в следующих случаях:
1) линейки АВ, могущей перемещаться своими концами А и В по сторонам угла АСВ (рис. 179, а);
Рис. 179.
2) шатуна АВ кривошипно-шатунного механизма (рис.. 179, б);
3) линейки АВ, могущей перемещаться своими концами А и В по направляющим двух кругов с центрами 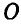
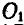
4) шатуна АВ шарнирного четырехзвенника ОABC (рис. 179, г).
Найти также направление линии, вдоль которой направлена скорость точки D конца прилива шатуна АВ.
Указание: полюс мгновенного вращения Р найдется для всех случаев на пересечении нормалей к траекториям точек А и В. Линию, вдоль которой направлена скорость точки D (рис. 179, г), найдем, если соединим точку D с полюсом-мгновенного вращения Р и проведем через точку D прямую, перпендикулярную к направлению мгновенного радиуса PD.
Задача №2
Определить построением ту точку М шатуна АВ кривошипно-шатунного механизма; скорость которой направлена вдоль шатуна АВ, а также найти величину этой скорости (рис. 180), Длина кривошипа 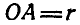
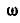
Рис. 180.
Решение. Найдем полюс Р мгновенного вращения шатуна АВ; он находится на пересечении нормалей к траекториям точек А и В. Опуская из .точки Р перпендикуляр на направление шатуна АВ, получим ту точку М, скорость которой направлена вдоль шатуна АВ.
Если мы обозначим мгновенную угловую скорость вращения шатуна АВ вокруг мгновенного центра Р через 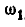
Для определения мгновенной угловой скорости 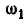
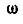
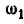
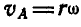
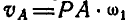
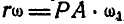
а поэтому
Задача №3
Показать, что при качении без скольжения подвижной фигуры 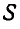
Рис. 181.
Решение. Пусть катящаяся фигура в моменты 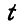
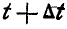
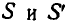
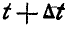
или
и
при
а отсюда скорость 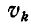
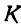
Задача №4
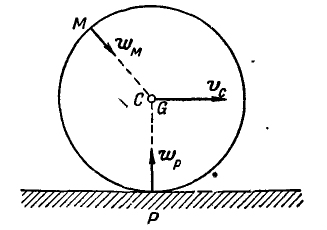
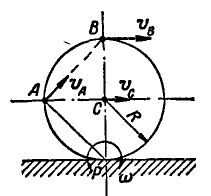
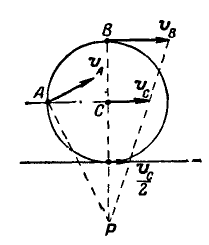
Колесо автомобиля радиусом R= 40 см катится без скольжения по неподвижной прямой так, что скорость его центра 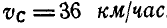
Рис. 182.
Решение. Так как полюс мгновенного вращения колеса находится в точке Р касания колеса с прямой, то скорости 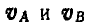
Величины же скоростей точек А и В найдутся по формуле (89):
Задача №5
Кривошипы ОС и 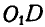
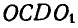
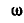
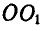
Рис. 183.
Решение. Мгновенный центр звена CD находится в бесконечности, так как кривошипы ОС и 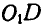
Рис. 184.
Отсюда заключаем, что звено CD движется поступательно. Для нахождения мгновенного центра звена АВ проведем нормали к траекриям точек А и В, т. е. 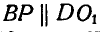
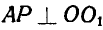
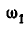
Проведя 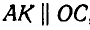
Величина мгновенной угловой скорости 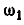
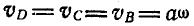
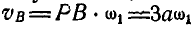
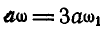
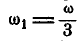
Скорость же точки А:
Задача №6
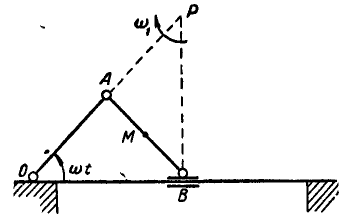
Найти скорость и ускорение ползуна В кривошипно-шатунного механизма ОАВ (рис. 185), если длины шатуна и кривошипа одинаковы: 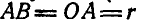
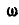
Найти также угловую скорость 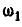
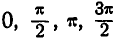
Рис. 185.
Решение. Полюс Р мгновенного вращения шатуна АВ найдется в пересечении прямых OA и 

Точка В движется прямолинейно, поэтому она обладает только касательным ускорением:
При 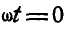

При 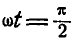
При 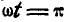
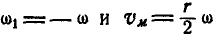
При 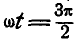
Задача №7
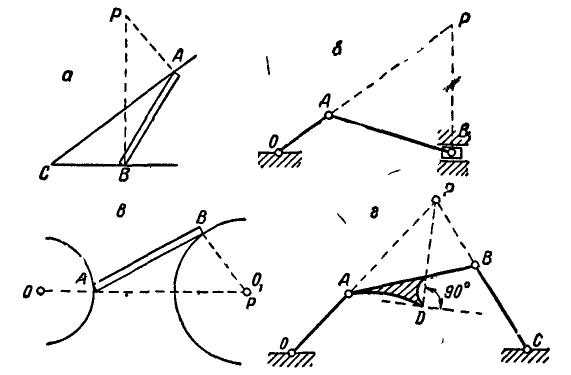
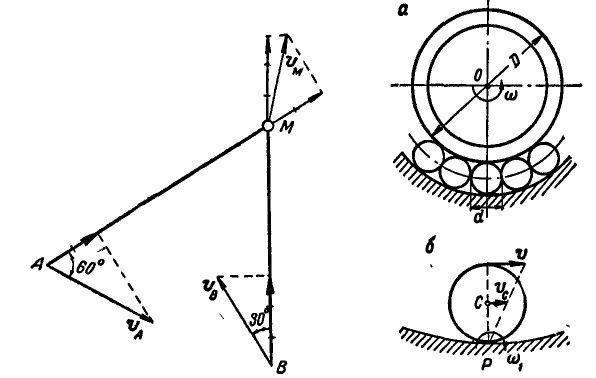
Двухповодковая группа состоит из двух стержней AM и MB, соединенных между собой шарниром М (рис. 186). Зная скорости 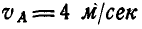
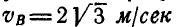
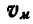
Решение. Скорость точки М найдется из условия, что проекции скорости точки М на направления AM и ВМ соответственно равны проекциям скоростей точек А и В на те же направления. Перенося проекции скоростей точек А и В на направления AM и ВМ в точку М, восстановим из концов проекций скоростей перпендикуляры до взаимного их пересечения и, соединив эту точку с точкой М, получим вектор скорости 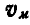
Ответ:
Рис. 186. Рис. 187.
Задача №8
Шариковый подшипник достоит из внутреннего кольца диаметра D, вращающегося с угловой скоростью 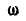
Решение. Окружная скорость кольца равна 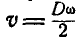
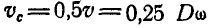
Задача №9
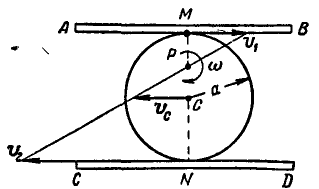
Две параллельные рейки АВ и CD (рис. 188) движутся в противоположные стороны с постоянными скоростями
Между рейками находится диск радиуса 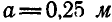
Рис. 188.
так что скорости точек М и N касания его с рейками соответственно равны 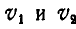
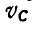
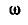
Решение. Диск совершает плоско-параллельное движение. Полюс мгновенного вращения его Р находится на пересечении прямой, соединяющей концы векторов скоростей 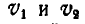
Для определения положения точки Р имеем два уравнении
Отсюда находим, что РМ=0,5а и, следовательно, 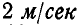
Угловая скорость вращения диска определится из равенства 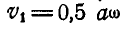
Задача №10
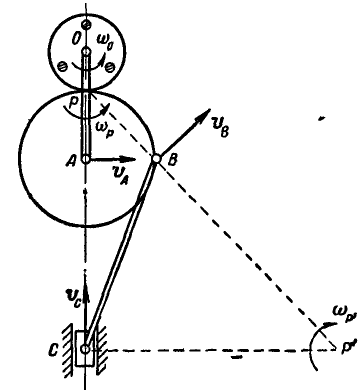
Кривошип ОА = 30 см вращается вокруг оси О с угловой скоростью 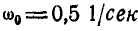
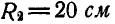
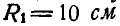
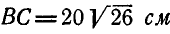
Рис. 189.
Решение. Линейная скорость точки А колеса:
Колесо радиуса 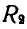
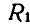
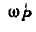
Скорость точки В колеса:
Шатун СВ совершает также плоско-параллельное движение; зная скорость точки В и то, что скорость другой точки С направлена по прямой АС, находим мгновенный центр шатуна Р на пересечении перпендикуляров к скоростям точек В и С.
Мгновенная угловая скорость 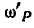
Теперь легко находим скорость точки С шатуна:
- Заказать решение задач по теоретической механике
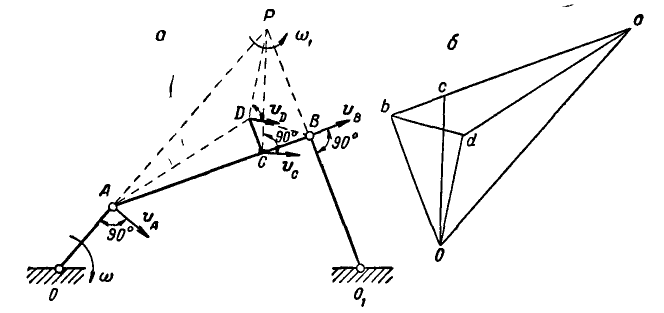
Задача №11
Для данного положения механизма шарнирного четырехзвенника 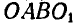
Рис. 190.
Решение. Найдем сначала полюс мгновенного вращения звена АВ; он будет находиться в точке пересечения нормалей OA и 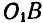
Обозначив угловую скорость вращения звена АВ вокруг Р через 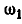
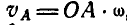
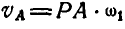
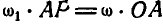
Величины отрезков OA и АР могут быть определены путем непосредственного измерения по чертежу.
Соединяя точки С и D, принадлежащие звену АВ, с полюсом мгновенного вращения Р звена АВ и проведя 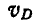
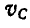
Скорости точек звена АВ можно было бы найти иначе, применив графический способ. Перейдем сейчас к изложению этого способа. Зная положение мгновенного центра Р звена АВ, находим, что 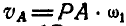
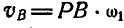
Возьмем теперь произвольно точку О (рис. 190, б) и отложим по направлениям, параллельным РА и РВ, отрезки Оа и Ob, пропорциональные величинам скоростей 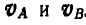
Соединив точки а и b между собой, получим треугольник Oab, подобный’ треугольнику РАВ; это следует из того, что стороны этих треугольников пропорциональны.
Согласно выражениям (107) в треугольнике Oab стороны Оа и Ob изображают в масштабе а скорости точек А и В звена АВ, но повернутые при этом относительно истинных направлений на 90°. Следовательно, стороны Оа и Ob представляют собой векторы повернутых скоростей 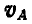
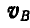
Из треугольника Oab следует: 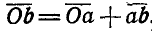
Умножая обе части на масштаб а, получим: 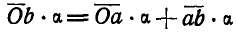
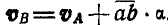
Сравнивая это равенство с формулой (106), находим, что 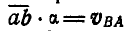
Следовательно, сторона ab треугольника Oab представляет собой в масштабе а повернутую на 90° скорость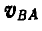
Треугольник Oab называется планом скоростей отрезка АВ, точка О — полюсом плана скоростей, а — масштабом плана скоростей.
Для построения плана скоростей механизма нет необходимости отыскивать полюсы мгновенных вращений, которые иногда уходят за пределы чертежа. Чтобы построить план скоростей какого-либо звена, например АВ, достаточно знать направления нормалей РА и РВ к траекториям точек А и В.
Для нахождения скорости точки С звена АВ можно было бы на плане скоростей разделить отрезок ab точкой с на части, пропорциональные отрезкам АС и СВ звена, т. е.:
или провести из полюса плана скоростей О отрезок 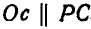
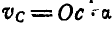
Найдем теперь скорость точки D.
Так как точка D принадлежит тому же звену, что и точки А и В, то, как мы видели, направление нормали к траектории точки D будет PD. Проводя из того же полюса плана скоростей О параллель к этой нормали, а из точки а параллель к отрезку AD, получаем в пересечении этих двух прямых точку d, которая определит скорость точки D, а именно: 
Легко видеть, что прямая bd параллельна прямой BD. Из изложенного получаем следующие правила построения плана скоростей.
- 1. Для построения плана скоростей какого-либо звена, например АВ, надо иметь вектор скорости одной точки звена и направление нормали к траектории (или раму траекторию) другой точки.
- 2. Должно быть соответствие между планом скоростей и чертежом, т. е. векторы плана скоростей
изображающие в масштабе а повернутые относительные скорости точек А — по отношению к В; D — по отношению к В; В — по отношению к С, должны быть параллельны соответствующим отрезкам АВ, DB, ВС механизма.
- 3. Для каждого звена на плане скоростей получается фигура, подобная фигуре звена и одинаково с ней расположенная.
Так, например, на рисунках 190, а и б треугольник abd подобен треугольнику ABD и, кроме того, 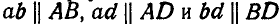
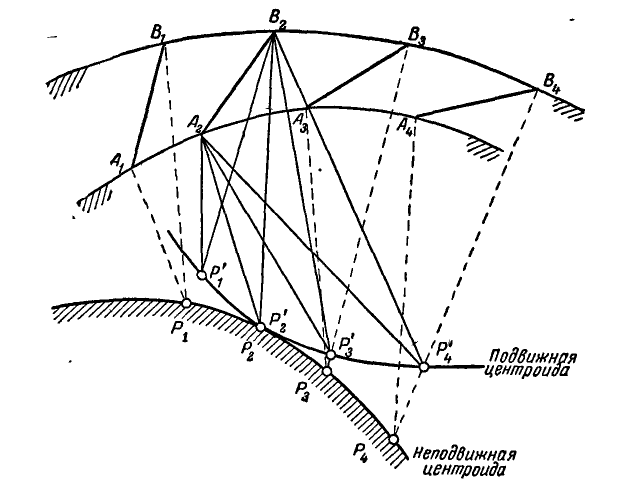
Перейдем теперь к вопросу о центроидах (или полодиях). Пусть отрезок АВ (рис. 191), принадлежащий подвижной плоскости, движется так, что за последующие промежутки времени 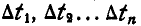
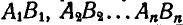
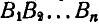
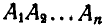
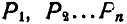
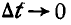
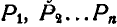
Таким образом, неподвижная центроида является геометрическим местом мгновенных центров скоростей на неподвижной плоскости при плоском движении неизменяемой фигуры.
Перенесем теперь все треугольники 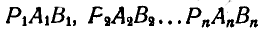
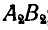
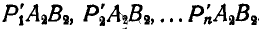
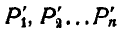
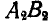
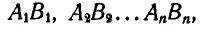
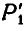
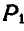
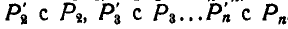
Рис. 191.
Следовательно, подвижная центроида связана с подвижной фигурой и является геометрическим местом мгновенных центров скоростей на движущейся фигуре. Ясно, что в каждый момент времени подвижная и неподвижная центроида имеют общую точку касания.
Следовательно, всякое плоское перемещение подвижной фигуры происходит так, как если бы соединенная с ней подвижная центроида 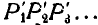
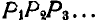
Задача №12
Найти неподвижную и подвижную центроиды шатуна АВ (рис. 192), длина которого равна длине кривошипа 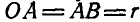
Решение. Полюс мгновенного вращения шатуна АВ находится в точке пересечения прямых ОА и BP, нормалей к траекториям точек А и В. Как видно из чертежа, при всяком положении шатуна 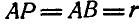
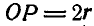
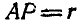
Отсюда заключаем, что неподвижной центроидой является окружность радиуса 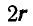
Рис. 192.
Если из прозрачной бумаги вырезать круг радиуса 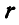
Задача №13
Шарнирный четырехзвенник EBAD (рис. 193), в котором 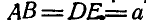
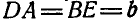
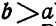
Рис. 193.
Решение. Так как точки А и В движутся по окружностям радиусов и DА и ЕВ, то полюсом мгновенного вращения звена ВА является точка Р пересечения прямых DA и ЕВ.
Из равенства треугольников DAE и ВАЕ заключаем, что 
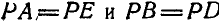
Отсюда следует, что полюс мгновенного вращения Р отстоит от неподвижных точек D и Е, а также от точек А и В звена АВ так, что 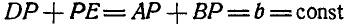
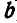

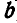
Изучив вопрос о скоростях точек подвижной фигуры, обратимся к нахождению ускорений ее точек. Для этого достаточно изучить вопрос об ускорениях точек любого ее отрезка АВ (рис. 194).
Рис. 194.
Если известно ускорение 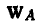
Здесь ускорения 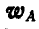
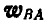
Если известна мгновенная угловая скорость 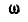
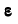
где
Покажем теперь, что в каждый момент существует точка движущейся фигуры, ускорение которой равно нулю. Пусть движение фигуры задано отрезком АВ (рис. 195) и пусть 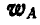
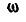
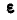
Отсюда следует простой способ построения векторов ускорений точек отрезка, если известно ускорение какой-либо одной его точки, например А, и мгновенные угловая скорость 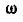
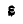
Принимая сначала точку А (полюс) за неподвижную, найдем, что ускорения 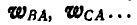
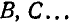
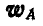
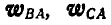
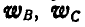
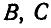
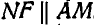
Отложив, например, от точки А отрезок АЕ, составляющий угол 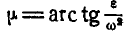
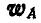
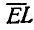
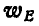
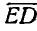
Рис. 195.
Таким образом, прямая ND аналогична прямой NF является геометрическим местом концов векторов, изображающих полные ускорения точек отрезка АЕ. Нетрудно видеть, что ускорение точки О отрезка АЕ равно нулю; эта точка называется мгновенным центром ускорений.
Если принять мгновенный центр ускорения G за полюс, то, вычисляя ускорения точек В, С отрезка АВ по формуле (108), найдем:
но так как 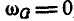
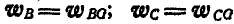
Следовательно, ускорения точек фигуры пропорциональны расстояниям их от мгновенного центра ускорений и образуют с отрезками, соединяющими эти точки с мгновенным центром ускорений, один и тот же угол 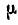
Подобно тому, как скорости, точек плоской, фигуры пропорциональны расстояниям их до мгновенного центра скоростей и образуют с мгновенными радиусами углы 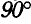
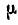
Не следует, однако, думать, что мгновенный центр скоростей Р и мгновенный центр ускорений G совпадают между собой. Это имеет место только для случая вращения тела вокруг неподвижной оси.
Рис. 196.
Если за полюс принята точка G, то полное ускорение какой-либо точки В плоской фигуры (рис. 196) может быть представлено в виде двух составляющих: 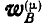
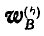
Если же за полюс принята точка Р, то полное ускорение точки В удобно разложить на нормальное 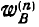
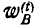
при этом радиус кривизны траектории 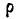
Задача №14
Найти ускорение любой точки обода колеса, катящегося без скольжения по прямолинейному рельсу с постоянной скоростью 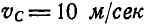
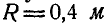
Рис. 197.
Решение. Мгновенный центр ускорений О находится в центре колеса С, так как эта точка движется прямолинейно и равномерно. Мгновенный же центр скоростей находится в точке Р касания колеса с рельсом, поэтому угловая скорость и угловое ускорение колеса соответственно равны:
Отсюда заключаем, что ускорение любой точки обода направлено к центру колеса и равно по величине:
Задача №15
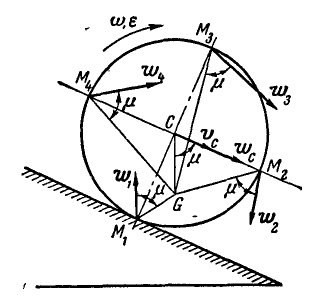
Колесо катится без скольжения в вертикальной плоскости по наклонному прямолинейному пути. Найти ускорения концов двух взаимно-перпендикулярных диаметров колеса, из которых один параллелен рельсу, если в рассматриваемый момент времени скорость центра колеса 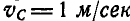
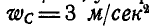
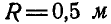
Рис. 198.
Решение. Центр мгновенного вращения колеса находится в точке касания, поэтому его угловая скорость:
Центр колеса движется прямолинейно, следовательно его ускорение:
Отсюда находим, что в данный момент времени угловое ускорение колеса:
Зная ускорение какой-либо точки плоской фигуры, в нашем случае ускорение 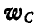
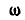
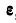
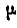
При этом угол 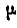
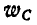
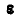
Положение мгновенного центра ускорений на полупрямой определится посредством равенства (92):
Найдя мгновенный центр ускорений, можно построить вектор ускорения любой точки колеса, например 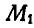
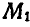
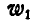
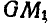
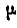
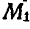
Так как
то окончательно находим:
Аналогично находим ускорения остальных точек колеса:
Векторы ускорений для рассматриваемых точек колеса построены на чертеже.
Задача №16
Найти ускорения пальца кривошипа А, ползуна В и точки С середины шатуна АВ кривошипно-шатунного механизма, если длины шатуна и кривошипа одинаковы: 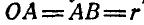
Рис. 199.
Решение. Ускорение точки А равно 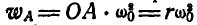
Полюс мгновенного вращения шатуна АВ найдется в пересечении прямых OA и 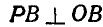
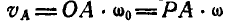
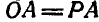

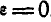
Мгновенный центр ускорений 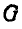
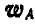
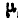
откуда 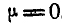
Положение точки G на полупрямой АО определится равенством (92):
т. е. мгновенный центр ускорений G совпадает с осью вращения О кривошипа. Отсюда ускорения точек В и С определятся:
и будут направлены к точке О.
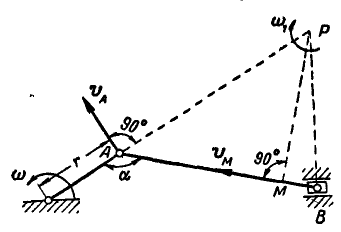
Задача №17
Кривошип ОА механизма режущего аппарата сенокосилки вращается с постоянной угловой скоростью 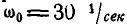
Рис. 200.
Найти угловую скорость 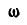
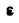
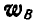
Решение. Найдем мгновенный центр Р шатуна АВ; тогда скорость точки А будет:
Отсюда угловая скорость шатуна:
Ускорение точки В может быть найдено из равенств (108) и (109):
Это уравнение можно переписать иначе:
Знак минус у вектора 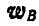
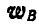
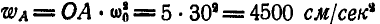
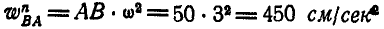
Зная, что вектор 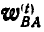
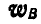
Угловое ускорение шатуна:
Задача №18
Равносторонний треугольник ABC со стороной а = 6 см движется в плоскости чертежа. Ускорения вершин А и В в данный момент времени равны 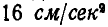
Рис. 201.
Решение. Применяя равенство (108), имеем: 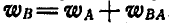
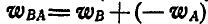
Из последнего равенства следует, что для нахождения вектора 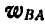
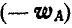
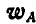
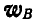
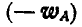
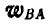
откуда
Откладывая от векторов 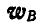
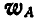
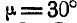
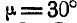
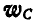
Определим угловую скорость и угловое ускорение треугольника.
Согласно равенствам (110) имеем:
откуда:
Ускорение:
и направлено по CВ от С к В.
- Движение твердого тела, имеющего неподвижную точку
- Движение твердого тела
- Сложение движений точки
- Сложение движений твердого тела в теоретической механике — формулы и определения с примерами
- Центр параллельных сил и центр тяжести
- Поступательное движение твердого тела
- Вращение твердого тела вокруг неподвижной оси
- Сферическое движение твердого тела
72,2% бесплатных материалов
967 руб. средняя цена курсовой работы
353 руб. средняя цена домашнего задания
116 руб. средняя цена решённой задачи
161 руб. средняя цена лабораторной работы
174 руб. средняя цена реферата
177 руб. средняя цена доклада
1626 руб. средняя цена ВКР
665 руб. средняя цена диссертации
596 руб. средняя цена НИР
358 руб. средняя цена отчёта по практике
277 руб. средняя цена ответов (шпаргалок)
202 руб. средняя цена лекций
232 руб. средняя цена семинаров
280 руб. средняя цена рабочей тетради
187 руб. средняя цена презентации
67 руб. средняя цена перевода
143 руб. средняя цена изложения
150 руб. средняя цена сочинения
308 руб. средняя цена статьи
Гарантия возврата средств






















































































































































































































































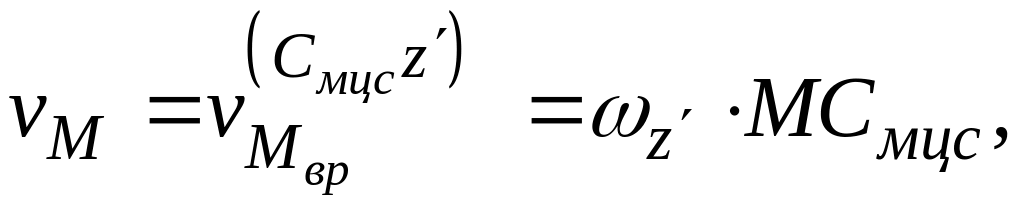
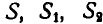
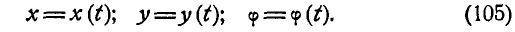
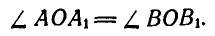
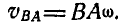
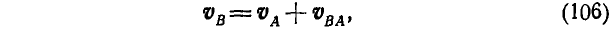
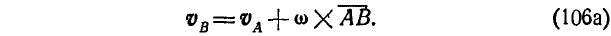
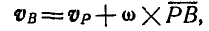
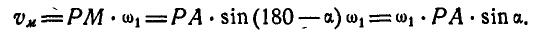
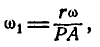
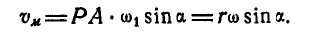
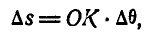
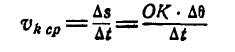
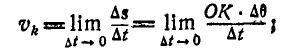
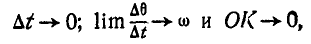
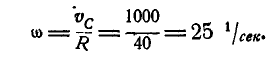
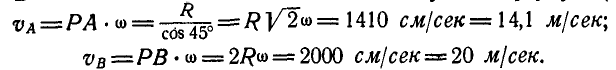
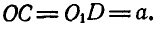
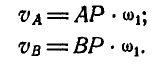
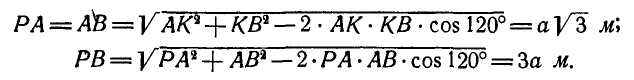
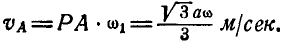
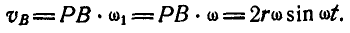
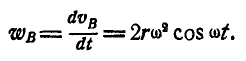
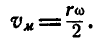
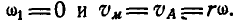
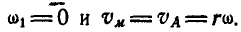
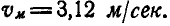
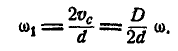
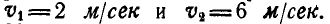
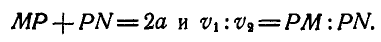
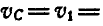
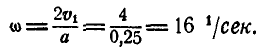
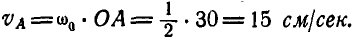
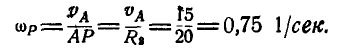
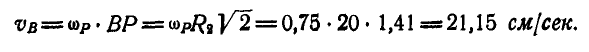
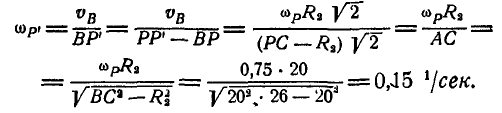
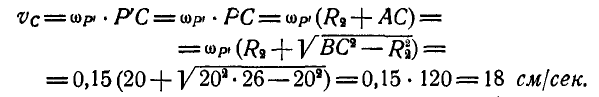
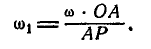
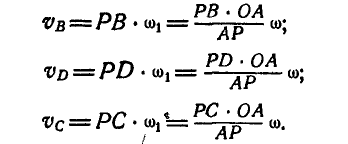
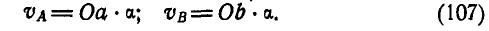
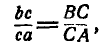
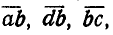 изображающие в масштабе а повернутые относительные скорости точек А — по отношению к В; D — по отношению к В; В — по отношению к С, должны быть параллельны соответствующим отрезкам АВ, DB, ВС механизма.
изображающие в масштабе а повернутые относительные скорости точек А — по отношению к В; D — по отношению к В; В — по отношению к С, должны быть параллельны соответствующим отрезкам АВ, DB, ВС механизма.