Как найти полюса формула

Изолированные особые точки функций и полюсы

Классификация особых точек

Важное место в изучении и применении теории функций комплексного переменного занимает исследование их поведения в особых точках, где нарушается аналитичность функции. В частности, это точки, где функция не определена.

Исследование функции в особой точке z_0 определяется поведением ее в окрестности этой точки, т.е. исследованием $limlimits_{zto z_0}f(z)$ . Очевидно, имеют место три возможности:

а) $limlimits_{zto z_0}f(z)$ не существует;
б) $limlimits_{zto z_0}f(z)$ существует и равен конечному числу;
в) $limlimits_{zto z_0}f(z)$ равен бесконечности.

Исследование пределов функции в комплексной области — задача более сложная, чем в действительной области, так как, согласно определению, переменная стремится к z_0~(zto z_0) по любому направлению. Вычисление пределов в точках аналитичности не представляет интереса, так как в этих случаях $limlimits_{zto z_0}f(z)=f(z_0)$ .

Будем рассматривать $limlimits_{zto z_0}f(z)$ , где z_0 — особая точка.

Пример 4.1. Исследовать существование $limlimits_{zto0}exp frac{1}{z},~ limlimits_{zto0} exp frac{1}{z^2}$ в случаях a) z=xinmathbb{R} ; б) zinmathbb{C} .

Решение

a) В действительной области $limlimits_{zto0}exp frac{1}{z}$ не существует, так как не равны односторонние пределы $limlimits_{xto0+0}exp frac{1}{x}=infty,~ limlimits_{xto0-0}exp frac{1}{x}=0$ , но существует предел второй функции: $limlimits_{xto0}exp frac{1}{x^2}=infty$ .

б) В комплексной области, очевидно, $limlimits_{zto0}exp frac{1}{z}$ не существует, так как он не существует в частном случае z=x .

Но для второй функции полученного выше результата $limlimits_{xto0}exp frac{1}{x^2}=infty$ не достаточно, так как рассмотрены только два направления на плоскости — по действительной положительной и действительной отрицательной полуосям.

Рассмотрим еще какое-нибудь направление, например по мнимой оси, т.е. z=iy,~ yto0colon

$limlimits_{zto0}exp frac{1}{z^2}= limlimits_{zto0}exp frac{1}{(iy)^2}= limlimits_{zto0}exp frac{-1}{y^2}=0.$

Сравнивая этот результат с полученным выше $limlimits_{xto0}exp frac{1}{x^2}=infty$ , заключаем, что в комплексной области $limlimits_{zto0}exp frac{1}{z^2}$ не существует.

Аналогично можно показать, что не существует $limlimits_{zto0}exp frac{1}{z^4}$ , хотя $limlimits_{zto0}exp frac{1}{z^4}=infty$ для случаев z=x и z=iy (по действительной и мнимой осям).

Эти простые примеры показывают, что исследование функции в особой точке с помощью $limlimits_{zto z_0}f(z)$ может представлять большие сложности. Но, с другой стороны, в примере 3.36 при вычислении пределов функции в особых точках было использовано разложение функции в ряд.

Представление функции в виде ряда как один из способов ее аналитического задания, может быть использовано для исследования функции, в частности, в особых точках.

Будем рассматривать изолированные особые точки функций, т.е. особые точки, для каждой из которых существует такая ее окрестность, в которой нет других особых точек функции.

В частности, конечная особая точка $z_0inmathbb{C}$ является изолированной особой точкой функции f(z) , если существует число r>0 , такое, что в круге |z-z_0|<r эта точка- единственная особая точка f(z) , а в проколотой окрестности, т.е. в 0<|z-z_0|<r функция f(z) аналитическая.

Бесконечно удаленная особая точка z_0=infty является изолированной особой точкой функции f(z) , если существует число R>0 , такое, что в области |z|>R эта точка — единственная особая точка f(z) , а в кольце R<|z|<infty функция f(z) — аналитическая.

Согласно теореме Лорана, функция, аналитическая в кольце, в частности, в проколотой окрестности особой точки, может быть представлена рядом Лорана. Это позволяет свести исследование функции в изолированной особой точке к исследованию соответствующего ряда. Особенности рядов как представления аналитических функций можно заметить, проанализировав некоторые примеры предыдущих лекций.

Пример 4.2. Исследовать поведение и вид ряда Лорана в окрестности особой точки z=0 функций:

а) $frac{sin z}{z}$ ; б) $frac{sin z}{z^n},~n>1$ ; в) $exp frac{1}{z}$ .

Решение

Эти простые примеры показывают, что поведение функции в особой точке связано с видом главной части ряда Лорана: трем отмеченным выше случаям нахождения предела функции в точке z_0 соответствуют три различных случая вида главной части ряда Лорана в окрестности точки. В примере 4.2 исследовалась конечная особая точка. Такой же результат можно получить, рассматривая точку z=infty , например, для функций $exp frac{1}{z},~ z^2+frac{1}{z}$ и e^z .

Типы особых точек функции

В зависимости от трех случаев поведения функции в особой точке (исследования $limlimits_{zto z_0}f(z)$ ) особые точки функций делят на три типа — производится классификация особых точек. В качестве определения типа особых точек можно выбрать либо поведение функции в особой точке, либо вид ряда Лорана. Выберем первый подход.

Изолированная особая точка $z_0in overline{C}$ функции f(z) называется:

– устранимой особой точкой, если $limlimits_{zto z_0}f(z)$ существует и конечен (4.1);
– полюсом, если $limlimits_{zto z_0}f(z)=infty$ (4.2);
– существенно особой точкой, если $limlimits_{zto z_0}f(z)$ не существует (4.3).

Замечание 4.1. Если в случае устранимой особой точки z_0 положить $f(z_0)= limlimits_{zto z_0}f(z)$ , то f(z) будет аналитической в $O_{delta}(z_0)$ и точку z_0 можно считать правильной, т.е. не особой. В этом случае говорят, что в точке z_0 устранена особенность.

Пример 4.3. Определить тип особой точки z=0 для функций $frac{sin z}{z};~~frac{sin z}{z^n},~n>1;~~exp frac{1}{z},~~ exp frac{1}{z^2}$ .

Решение

На основании результатов решения примеров 4.1, 4.2 заключаем, что z=0 является устранимой особой точкой функции $frac{sin z}{z}$ ; полюсом для $frac{sin z}{z^n}$ при любом n>1 ; существенно особой точкой для функций $exp frac{1}{z}$ и $exp frac{1}{z^2}$ .

Пример 4.4. Определить тип особой точки z=infty для функций $f_1(z)=z^nsin frac{1}{z}$ и f_2(z)=e^z .

Решение

Рассмотрим $limlimits_{ztoinfty}f(z)$ . Для удобства введем обозначение $frac{1}{z}=xi$ . Для функции f_1(z) получим $limlimits_{ztoinfty}f_1(z)= limlimits_{xito0} frac{sinxi}{xi^n}=infty~(n>1)$ (см. пример 4.2), поэтому z=infty является полюсом функции $f_1(z)=z^nsin frac{1}{z}$ . Для функции f_2(z)=e^z точка z=infty является существенно особой, так как $limlimits_{ztoinfty}e^z= limlimits_{xito0}exp frac{1}{xi}$ не существует (см. пример 4.1).

Пример 4.5. Найти все конечные особые точки функций: а) $f_1=frac{sin z}{z^4+1}$ б) $f_2(z)= frac{sin z}{sin z^{-1}}$ и определить их тип.

Решение

Особыми точками дробей являются особые точки числителя, особые точки знаменателя и нули знаменателя.

а) Так как числитель и знаменатель функции f_1(z) — функции аналитические, то ее особыми точками являются только нули знаменателя, т.е. корни уравнения z^4+1=0 . Это четыре точки $z_k=exp frac{(pi+2kpi)i}{4},~k=0,1,2,3$ , или в алгебраической форме: $z_{1,2}= frac{pm1+i}{sqrt{2}},~ z_{3,4}= frac{pm1-i}{sqrt{2}}$ . Заметим, что точки расположены в вершинах квадрата, вписанного в окружность радиуса R=1 с центром в начале координат, и справедливы равенства $z_2=iz,~ z_3=-z_1,~ z_4= overline{z}_1$ .

Очевидно, все точки изолированные и являются полюсами, так как $limlimits_{zto z_k}f_1(z)=infty$ для любой точки z_k,~k=1,2,3,4 .

б) Особыми точками функции f_2(z) являются нули знаменателя, т.е. точки, для которых $frac{1}{z_k}=kpi$ или $z_k=frac{1}{kpi},~ k=pm1,pm2,ldots$ , а также z=0 — особая точка знаменателя. Точки z_k являются полюсами, так как $limlimits_{zto z_k}f_2(z)=infty$ . Точка z=0 — неизолированная особая точка функции, так как в любой ее окрестности |z|<r ( — любое число, r>0 ), кроме этой точки, расположено бесконечное множество особых точек вида $z_k=frac{1}{kpi},~ k=pm1,pm2,ldots$ . Точку z=0 в таком случае называют предельной точкой полюсов $z_k=frac{1}{kpi}$ , так как $limlimits_{ktoinfty}z_k=0$ .

Теоремы Сохоцкого и Пикара

Для исследования поведения функции в существенно особой точке имеют место следующие две теоремы.

Теорема 4.1 (Сохоцкого). Если r_0 — существенно особая точка функции f(z) , то для любого Ain overline{mathbb{C}} существует последовательность ${z_n}$ , сходящаяся к точке z_0 , такая, что $limlimits_{ntoinfty}f(z_n)=A$ .

Теорема 4.2 (Пикара). В любой окрестности существенно особой точки функция f(z) принимает любое значение (причем бесконечное число раз) кроме, быть может, одного.

Пример 4.6. Исследовать поведение следующих функций в существенно особых точках, проиллюстрировать теоремы Сохоцкого и Пикара:

a) $f_1(z)=exp frac{1}{z},~ f_2(z)= exp frac{1}{z^2},~ z_0=0$ ; б) f_3(z)=e^z,~ z_0=infty .

Решение

В примерах 4.3 и 4.4 показано, что точки z_0=0 и z_0=infty являются существенно особыми точками соответствующих функций. Исследуем пределы функций.

а) Для иллюстрации теоремы Сохоцкого выбираем A=0 и A=infty . Используя результат примера 4.1, имеем $limlimits_{zto0}exp frac{1}{z}=0$ , если z=x<0 , и $limlimits_{zto0}exp frac{1}{z}=infty$ , если z=x>0 , то есть $limlimits_{ntoinfty}f_1(z_n)=0$ для последовательности z_n=x_n , такой, что $limlimits_{ntoinfty}x_n=0$ и x_n<0 , и $limlimits_{ntoinfty}f_1(z_n)=0$ для последовательности z_n=x_n , такой, что $limlimits_{ntoinfty}x_n=0$ и x_n>0 .

Аналогично исследуем функцию f_2(z) . Для числа A=0 выбираем z_n=iy_n , где $limlimits_{ntoinfty}y_n=0$ и тогда $limlimits_{ntoinfty}f_2(z_n)=0$ , а для A=infty выбираем z_n= x_n , где $limlimits_{ntoinfty}x_n=0$ и тогда $limlimits_{ntoinfty} f_2(z_n)=infty$ .

Справедливость теоремы Пикара для этих функций следует из рассмотрения уравнений $exp frac{1}{z}=A,~ exp frac{1}{z^2}=A$ , которые, как известно, имеют бесконечное множество решений для любого Ain mathbb{C},~ Ane0 .

Например, для функции $f_1(z)= expfrac{1}{z}$ имеем $expfrac{1}{z}=A$ . Отсюда получаем

$frac{1}{z}= operatorname{Ln}A,quad frac{1}{z}= ln|A|+i(arg A+2kpi),quad k=0,pm1,pm2,ldots$ или $z_k=frac{1}{ln|A|+i(arg A+2kpi)}$ .

В частности, функция $exp frac{1}{z}$ в любой окрестности точки z_0=0 принимает значение A=1 бесконечное множество раз: в точках $z_k=frac{-i}{2kpi},~ k=pm1,pm2,ldots$ (рис. 4.1).

Рис. 4.1.

б) Точка z=infty является существенно особой точкой функции e^z (пример 4.4). Обозначив $z=frac{1}{xi}$ , можно повторить рассуждения предыдущего пункта для функции $expfrac{1}{xi}$ и точки xi=0 .

Ряд Лорана в окрестности особой точки

В предыдущем разделе на примере простых функций (см. пример 4.2) было высказано предположение, что вид ряда Лорана в окрестности особой точки зависит от типа особой точки и потому задача исследования функции в особой точке может быть сведена к исследованию соответствующего ряда Лорана . Подтверждением этого предположения в общем случае является доказательство соответствующих утверждений.

Утверждение 4.1

1. Для того чтобы особая точка функции была ее устранимой особой точкой, необходимо и достаточно, чтобы в разложении функции в ряд Лорана в окрестности этой точки отсутствовала главная часть. Это означает, что если z_0 — устранимая особая точка, то ряд Лорана функции f(z) имеет вид

$f(z)= sum_{n=0}^{infty} c_n(z-z_0)^n,quad 0<|z-z_0|<r$

(4.4)

для z_0 — конечной точки $z_0inmathbb{C}$ , и (для z_0=infty )

$f(z)= c_0+sum_{n=1}^{infty} frac{c_{-n}}{z^n},quad R<|z|<infty.$

(4.5)

2. Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов. Ряд Лорана функции f(z) в случае z_0 полюса имеет вид

$f(z)=sum_{k=-n}^{infty} c_k(z-z_0)^k,quad 0<|z-z_0|<r,$

(4.6)

если $z_0inmathbb{C}$ , и (если z_0=infty )

$f(z)=sum_{k=-infty}^{n}c_kz^k,quad R<|z|<infty,$

(4.7)

3. Для того чтобы особая точка функции была ее существенно особой точкой, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала бесконечное число членов. Ряд Лорана функции f(z) в случае z_0 — существенно особой точки имеет вид

$f(z)= sum_{n=-infty}^{infty} c_n(z-z_0)^n,quad 0<|z-z_0|<r,$

(4.8)

если $z_0inmathbb{C}$ , и (если z_0=infty )

$f(z)= sum_{n=-infty}^{infty}c_nz^n,quad R<|z|<infty.$

(4.9)

Замечания 4.2

1. Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.

Так, точка $z_0inmathbb{C}$ является полюсом порядка (Pi(n)) функции f(z) , если в разложении (4.6) $c_{-n}ne0,~ c_k=0$ при k<-n . Точка z_0=infty является полюсом порядка (Pi(n)) функции f(z) , если в разложении (4.7) c_nne0,~ c_k=0 при k>n .

2. Главная часть ряда Лорана в случае полюса порядка и записывается следующим образом:

а) в случае $z_0inmathbb{C}$ в виде $sum_{k=-n}^{-1} c_k(z-z_0)^n$ , или $sum_{k=1}^{n} frac{c_{-k}}{(z-z_0)^k}$ , или, подробнее:

$frac{c_{-n}}{(z-z_0)^n}+frac{c_{-n+1}}{(z-z_0)^{n-1}}+ ldots+ frac{c_{-1}}{z-z_0},quad c_{-n}ne0,;$

(4.10)

б) в случае z_0=infty в виде $sum_{k=1}^{n}c_nz^k$ , или $sum_{k=-n}^{-1} frac{c_{-k}}{z^k}$ (см. (4.7)), или, подробнее:

$c_ncdot z^n+ c_{n-1}cdot z^{n-1}+ldots+c_1cdot z,quad c_nne0.$

(4.11)

3. Главная часть ряда Лорана в случае существенно особой точки записывается так:

а) в случае $z_0inmathbb{C}$ в виде $sum_{n=-infty}^{-1} c_n(z-z_0)^n$ , или $sum_{n=1}^{infty} frac{c_{-n}}{(z-z_0)^n}$ (см.(4.8)), или, подробнее:

$frac{c_{-1}}{z-z_0}+ frac{c_{-2}}{(z-z_0)^2}+ ldots+ frac{c_{-n}}{(z-z_0)^n}+ldots;$

(4.12)

б) в случае z_0=infty в виде $sum_{n=-infty}^{-1} frac{c_{-n}}{z^n}$ или $sum_{n=1}^{infty}c_nz^n$ (см.(4.9)), или, подробнее:

c_1cdot z+c_2cdot z^2+ldots+c_ncdot z^n+ldots

(4.13)

Пример 4.7. Определить тип особых точек функций: а) $f_1(z)=frac{z+2}{z^2-2z-3}$ ; б) $f_2(z)=frac{z+2}{(z+1)^2(z-3)}$ .

Решение

Особыми точками функций являются z_1=-1,~z_2=3,~z_3=infty . Чтобы определить тип особой точки, используем разложения функций в окрестности каждой точки, полученные в примерах 3.31 , 3.33 , 3.34.

a) $f_1(z)= frac{-1}{4}cdot frac{1}{z+1}-sum_{n=0}^{infty} frac{5(z+1)^n}{4^{n+2}},~ 0<|z+1|<4$ . В главной части разложения — один член ряда: $frac{-1}{4}cdot frac{1}{z+1}$ , здесь $c_{-1}=frac{-1}{4}ne0$ , все c_n=0 для n<-1 . Следовательно, в точке z=-1 — полюс первого порядка, т.е. простой полюс функции f_1(z) .

Аналогично из разложения $f_1(z)= frac{5}{4}cdot frac{1}{z-3}+ sum_{n=0}^{infty} frac{(-1)^{n+1}}{4^{n+2}}(z-3)^n,~ 0<|z-3|<4$ получим такой же результат: точка z=3 — простой полюс функции f_1(z) .

Разложение $f_1(z)= sum_{n=1}^{infty} frac{(-1)^n+5cdot3^{n-1}}{4}cdot frac{1}{z^n},~ |z|>3$ . Функции в окрестности z=infty не содержит главной части — разложение имеет вид (4.5). Следовательно, точка z=infty — устранимая особая точка функции f_1(z) .

б) Из разложения $f_2(z)= frac{5}{16}cdot frac{1}{z-3}+ sum_{n=0}^{infty} frac{(-1)^{n+1}(n+6)}{4^{n+3}}(z-3)^n,~ 0<|z-3|<4$ следует, что z=3 — простой полюс функции f_2(z) .

Из разложения $f_2(z)= frac{-5}{16}cdot frac{1}{z+1}+ frac{-1}{4}cdot frac{1}{(z+1)^2}+ sum_{n=0}^{infty} frac{-5(z+1)^n}{4^{n+3}},~ 0<|z+1|<4$ , где $c_{-2}=frac{-1}{4}ne0$ и все c_n=0 для n<-2 , получаем, что z=-1 — полюс второго порядка функции f_2(z) .

Разложение f_2(z) в окрестности z=infty и не содержит положительных степеней, в чем можно убедиться, проанализировав разложения элементарных дробей (см. пример 3.34). Поэтому z=infty — устранимая особая точка функции f_2(z) .

Пример 4.8. Определить тип конечных особых точек для функций:

а) $exp frac{1}{z-a},~ sin frac{1}{z-a},~ cos frac{1}{z-a}$ ; б) $frac{sin z}{z^n},~ frac{1-cos z}{z^3}$ .

Решение

а) Используем разложения функций по степеням (z-a)colon

$begin{gathered}exp frac{1}{z-a}= 1+frac{1}{z-a}+ frac{1}{2!(z-a)^2}+ldots;qquad sinfrac{1}{z-a}= frac{1}{z-a}- frac{1}{3!(z-a)^3}+ldots;\ cosfrac{1}{z-a}= 1-frac{1}{2!(z-a)^2}+ldots end{gathered}$

Убеждаемся, что для всех указанных функций точка z=a является существенно особой точкой, так как в разложениях главная часть содержит бесконечное число членов, т.е. имеется бесконечное число членов с отрицательными степенями (см. п.1 утверждения 4.1).

б) Запишем разложения функций по степеням zcolon

$begin{aligned}frac{sin z}{z^n}&= frac{1}{z^n}! left(z-frac{z^3}{3!}+ldotsright)= frac{1}{z^{n-1}}-frac{1}{z^{n-3}cdot3!}+ldots;\ frac{1-cos z}{z^3}&= frac{1}{z^3}! left(1-left(1-frac{z^2}{2!}+frac{z^4}{4!}+ldotsright)right)= frac{1}{2!z}-frac{z}{4!}+ldots end{aligned}$

Для первой функции при n=1 в разложении отсутствует главная часть — совокупность членов с отрицательными степенями. Следовательно, согласно п.1 утверждения 4.1, точка z=0 для $frac{sin z}{z}$ является устранимой особой точкой.

При n>1 главная часть разложения содержит конечное число членов, поэтому точка z=0 для $frac{sin z}{z^n}$ является полюсом (см. п.2 утверждения 4.1). Кроме того, так как при n>1 в разложении старшая отрицательная степень равна (n-1) , то, согласно п. 1 замечаний 4.2, заключаем, что z=0 для $frac{sin z}{z^n}$ при n>1 является полюсом порядка (n-1) . Рассуждая аналогично, получаем, что z=0 является полюсом первого порядка — простым полюсом для функции $frac{1-cos z}{z^3}$ .

Сравнивая разложения функций по степеням в окрестности z_0=0 (формулы (4.4),(4.6),(4.8) при z_0=0 ) и z=infty (формулы (4.5), (4.7), (4.9)), можно сделать следующее заключение.

Утверждение 4.2

1. Чтобы z=infty была устранимой особой точкой функции f(z) , необходимо и достаточно, чтобы точка xi=0 была устранимой (или не особой) для $varphi(xi)= f!left(frac{1}{xi}right)$ .

2. Чтобы z=infty была полюсом порядка функции f(z) , необходимо и достаточно, чтобы точка xi=0 была полюсом порядка функции $varphi(xi)= f!left(frac{1}{xi}right)$ .

3. Чтобы z=infty была существенно особой точкой функции f(z) , необходимо и достаточно, чтобы точка xi=0 была существенно особой точкой функции $varphi(xi)= f!left(frac{1}{xi}right)$ .

Замечание 4.3. Как и в случае конечной особой точки z_0 , в которой функция не определена, но $limlimits_{zto z_0}f(z)=0$ (см. утверждение 3.5) , так и для z=0 в случае $limlimits_{ztoinfty}f(z)=0$ , устранимую особую точку z=infty можно считать нулем функции f(z) . Порядок нуля можно определить как порядок нуля функции varphi(xi) в точке xi=0 .

Пример 4.9. Исследовать точку z=infty для функций: a) $f(z)=frac{1}{z^2(z-2)}$ ; б) $f(z)=frac{z^2+1}{3z^2-2}$ ; в) $f(z)= zsinfrac{1}{z}$ .

Решение

Правила определения порядка полюса

Используя формулу (4.6) разложения функции в ряд в окрестности полюса, можно получить практически удобные правила определения порядка полюса, не требующие записи разложений в ряд в каждом конкретном случае.

Пусть $z_0~(z_0in mathbb{C})$ — полюс порядка n~(Pi(n)) функции f(z) . Разложение (4.6), где главная часть имеет вид (4.10) , преобразуем следующим образом:

$f(z)=frac{1}{(z-z_0)^n}bigl[c_{-n}+c_{-n+1}cdot (z-z_0)+ ldots+c_0(z-z_0)+ ldotsbigr]$ или $f(z)=frac{varphi(z)}{(z-z_0)^n}$ ,

где varphi(z) — функция, аналитическая в точке z_0 , как сумма степенного ряда, записанного в скобках, и $varphi(z_0)=c_{-n}ne0$ .

Далее рассмотрим функцию $F(z)=frac{1}{f(z)}$ , то есть $F(z)=frac{(z-z_0)^n}{varphi(z)}$ или F(z)=(z-z_0)^n varphi_1(z) , где — аналитическая в точке z_0 и varphi_1(z_0)ne0 . Из этого, согласно утверждению 3.5, следует, что z_0 является нулем порядка функции F(z) . Можно доказать и обратное утверждение.

А именно, если функция представлена в виде $f(z)=frac{varphi(z)}{(z-z_0)^n}$ , где — функция, аналитическая в точке z_0 , и varphi(z_0)ne0 , то z_0 — полюс порядка функции f(z) , а также, если z_0 — нуль порядка функции F(z) , то для функции $f(z)=frac{1}{F(z)}$ эта точка является полюсом порядка .

Кроме того, рассмотрим частное $f(z)=frac{f_1(z)}{f_2(z)}$ , где точка z_0 является нулем порядка для функции f_1(z) и нулем порядка для функции f_2(z) , то есть $f(z)= frac{(z-z_0)^k varphi_1(z)}{(z-z_0)^m varphi_2(z)}$ . При m>k получаем $f(z)= frac{varphi(z)}{(z-z_0)^{m-k}}$ , из чего, с учетом приведенных выше рассуждений, находим, что z_0 — полюс порядка (m-k) . Заметим, что при m=k точка z_0 — устранимая особая точка; случай m<k рассмотрен ранее. Результаты приведенных рассуждений запишем в виде утверждения.

Утверждение 4.3

1. Для того чтобы точка z_0 была полюсом порядка функции f(z) , необходимо и достаточно, чтобы ее можно было записать в виде

$f(z)= frac{varphi(z)}{(z-z_0)^n},quad varphi(z_0)ne0.$

(4.14)

2. Для того чтобы точка z_0 была полюсом порядка функции f(z) , необходимо и достаточно, чтобы она была нулем порядка функции $frac{1}{f(z)}$ (связь нулей с полюсами).

3. Если точка z_0 является нулем порядка функции f_1(z) и нулем порядка функции f_2(z)~(m>k) , то она — полюс порядка (m-k) для $frac{f_1(z)}{f_2(z)}$ .

Пример 4.10. Определить порядок полюсов функций из примеров: а) 4.7 ; б) 4.8.

Решение

Замечания 4.4

1. Так как конечными особыми точками рациональной дроби $frac{P_n(z)}{Q_m(z)}$ являются только нули знаменателя, то это либо полюсы, либо устранимые особые точки функции.

2. Такое же заключение можно сделать и для функции вида $f(z)= frac{varphi(z)}{Q_m(z)}$ , где — аналитическая функция. При этом, используя определение устранимой особой точки (4.1) и правила определения порядка нуля и полюса (утверждения 3.5 и 4.3), можно сделать следующие выводы относительно особой точки z_0 — нуля порядка k~[0(k)] знаменателя:

а) z_0 — полюс порядка функции f(z) , если varphi(z_0)ne0 ;
б) z_0 — полюс порядка (k-n) , если z_0 — нуль порядка функции varphi(z) и k>n ;
в) z_0 — устранимая особая точка функции f(z) , если z_0 — нуль порядка функции ;

г) z_0 — нуль порядка (n-k) функции f(z) , если z_0 — нуль порядка функции varphi(z) и n>k ; при этом полагаем $f(z_0)= limlimits_{zto z_0}f(z)=0$ .

▼ Примеры нахождения особых точек и определения их типа

Пример 4.11. Найти конечные особые точки следующих функций и определить их тип:

а) $f(z)= frac{z^2-4z+3}{(z-1)^3(z+2)^2}$ ; б) $f(z)= frac{z+2i}{z^3+8i}$ .

Решение

Конечными особыми точками этих рациональных дробей являются нули знаменателя. Чтобы для каждой их этих точек определить, является ли она полюсом или устранимой особой точкой, нужно, согласно определению, найти предел функции в этой точке. В случае полюса, т.е. когда $limlimits_{zto z_0}f(z)=infty$ , далее следует определить его порядок. Для этого используется утверждение 4.3.

Можно поступить иначе — согласно замечанию 4.4. Для этого нужно найти и нули числителя.

а) Особые точки функции z_1=1,~ z_2=-2 . Для точки z_2=-2 можно применить формулу (4.14) и из $f(z)= frac{varphi(z)}{(z+2)^2}$ , где $varphi(z)= frac{z^2-4z+3}{(z-1)^3}$ и varphi(-2)ne0 , получить, что эта точка — полюс второго порядка. Для точки z_1=1 формула (4.14) не применима, так как из $varphi(z)= frac{z^2-4z+3}{(z+2)^2}$ имеем varphi(1)=0 . Поступаем далее согласно замечанию 4.4. Раскладываем на множители числитель и записываем функцию

$f(z)= frac{(z-1)(z-3)}{(z-1)^3(z+2)^2}= frac{z-3}{(z-1)^2(z+2)^2}= frac{varphi(z)}{(z-1)^2},quad varphi(1)ne0.$

Получаем, что z=1 — полюс второго порядка для f(z) .

б) Особые точки функции — корни уравнения z^3+8i=0 , то есть z=sqrt[LARGE{3}]{-8i} или $z_k= exp left[left(-frac{pi}{6}+ frac{2kpi}{3}right)!iright],~ k=0,1,2$ . Все эти точки: $z_{1,3}=2! left(pmfrac{sqrt{3}}{2}-i frac{1}{2}right)!,~ z_2=2i$ — простые нули знаменателя, и так как числитель в этих точках не обращается в нуль, то они — простые полюсы функции f(z) .

Пример 4.12. Найти конечные особые точки следующих функций и определить их тип:

а) $f(z)= frac{z^6+z^4-z^2-1}{(z^2-4z+3)^2}$ ; б) $f(z)= frac{z-2i}{z^3+8i}$ .

Решение

Пример 4.13. Найти конечные особые точки функций и определить их тип:

а) $f(z)=frac{cospi z}{(4z^2-1)(z^2+3)}$ ; б) $f(z)=frac{sinpi z}{z^4-1}$ .

Решение

Конечными особыми точками этих функций вида $f(z)= frac{varphi(z)}{Q_4(z)}$ , где — аналитическая функция, являются только нули знаменателя.

а) Особые точки функции: $z_1=frac{2}{2},~ z_2=-frac{1}{2},~ z_3=isqrt{3},~-i sqrt{3}$ . Точки z_3 и z_4 — простые полюсы, так как числитель в этих точках не обращается в нуль и функцию можно представить в виде $f(z)= frac{varphi(z)}{z-z_0},~ varphi(z_0)ne0,~ z_0$ — точка z_3 или z_4 . В точках $z=pmfrac{1}{2}$ числитель обращается в нуль. Очевидно, это простые нули числителя, и поэтому его можно записать в виде cospi z= (z-z_0)cdot varphi(z),~ varphi(z_0)ne0,~ z_0 — точка z_1 или z_2 . Тогда для функции f(z) получаем

$f(z)= frac{(z-z_0)cdot varphi(z)}{4 left(z-dfrac{1}{2}right)!! left(z+ dfrac{1}{2}right)! (z^2+3)},.$

Так как $limlimits_{zto z_k} f(z)neinfty$ для $z_0=z_1=frac{1}{2}$ или $z_0=z_2=-frac{1}{2}$ , то эти точки — устранимые особые точки функции f(z) .

б) Особые точки функции: $z_{1,2}=pm1,~ z_{3,4}=pm i$ . Точки z_3=i и z_4=-i — простые полюсы.

Для точек z_1=1 и z_2=-1 проводим рассуждения, как в предыдущем пункте, и находим, что они — устранимые особые точки f(z) .

Пример 4.14. Определить тип особой точки z=0 для следующих функций: а) $f(z)= frac{e^z-1-z}{e^{z^5}-1}$ ; б) $f(x)= frac{cos z^2-1}{z^3sin^2z^2}$ .

Решение. В точке z=0 и числитель, и знаменатель каждой из функций обращается в нуль. Определим порядок нуля в каждом случае и используем п.3 утверждения 4.4.

а) Из разложений по степеням функций

$begin{gathered} e^z-1-z&= left(1+z+frac{z^2}{2!}+ldotsright)-1-z= frac{z^2}{2!}+frac{z^3}{3!}+ldots\ e^{z^5}-1&= left(1+z^5+frac{z^{10}}{2!}+ldotsright)-1= z^5+frac{z^{10}}{2!}+ldots end{gathered}$

находим, что z=0 — нуль второго порядка для числителя (0(2)) и нуль пятого порядка для знаменателя (0(5)) . Следовательно, z=0 — полюс третьего порядка для функции f(z) .

б) Используя правила определения порядка нуля, в частности, как и в предыдущем пункте, раскладывая функции в ряды по степеням , находим, что z=0 является 0(2) для числителя и 0(7) для знаменателя. Следовательно, z=0 -полюс пятого порядка для f(z) .

Пример 4.15. Найти конечные особые точки следующих функций и определить их тип:

а) $f(z)= frac{e^{2+2i}}{z^4-16}$ ; б) $f(z)= frac{(z+pi) sin frac{pi z}{2}}{zsin^2z}$ .

Решение

Пример 4.16. Определить тип особой точки z=0 для следующих функций:

а) $f(z)= frac{sin z-z}{cos z-1-dfrac{z^2}{2}}$ ; б) $f(z)= frac{sin z+z}{operatorname{ch}z-1-dfrac{z^2}{2}}$ ; в) $f(z)= frac{sin z-z}{cos z-1+dfrac{z^2}{2}}$ ; г) $f(z)= frac{sin z+z}{operatorname{ch}z-1+dfrac{z^2}{2}}$ .

Решение

Точка z=0 является нулем и знаменателя, и числителя для каждой из функций. Определим порядок нуля в каждом случае, используя правило определения порядка нуля (утверждение 3.5), в частности, раскладывая соответствующую функцию по степеням .

а) Из разложений

$begin{aligned}sin z-z&= left(z-frac{z^3}{3!}+ldotsright)-z=-frac{z^3}{3!}+ frac{z^5}{5!}+ldots\ cos z-1-frac{z^2}{2}= left(1-frac{z^2}{2!}+ frac{z^4}{4!}-ldotsright)-1-frac{z^2}{2}=-z^2+frac{z^4}{4!}-ldots end{aligned}$

находим, что z=0 является 0(3) для числителя и 0(2) — для знаменателя, поэтому она — устранимая особая точка. Так как

$limlimits_{zto0}f(z)= limlimits_{zto0} frac{z^3! left(-frac{1}{3}+ frac{z^2}{5!}+ ldotsright)}{z^2! left(-1+frac{z^2}{4!}-ldotsright)}=0,$

то, полагая f(0)=0 , можно считать, что z=0 — нуль для f(z) , причем 0(1) (см. замечания 4.4).

б) Из разложений

$sin z+z=2z-frac{z^3}{3!}+ldots$ и $operatorname{ch}z-1-frac{z^2}{2}= left(1+frac{z^2}{2!}+ frac{z^4}{4!}+ldotsright)-1-frac{z^2}{2}= frac{z^4}{4!}+ frac{z^6}{6!}+ldots$

находим, что z=0 является 0(1) для числителя и 0(4) — для знаменателя. Поэтому z=0 — полюс третьего порядка для f(z) .

в) Как и в предыдущих пунктах, находим, что z=0 является 0(3) для числителя и 0(4) — для знаменателя. Поэтому z=0 — простой полюс для f(z) .

г) Точка z=0 является простым нулем числителя, нулем второго порядка для знаменателя. Следовательно, это простой полюс для f(z) .

Определение порядка полюса в бесконечно удаленной точке

Рассмотрим бесконечно удаленную точку. Тип особой точки можно определить, вычисляя $limlimits_{ztoinfty}f(z)$ или раскладывая функцию в ряд Лорана (см. примеры 4.4, 4.7). Можно свести задачу к исследованию конечной точки $xi=0,left(frac{1}{z}= xiright)$ (см. утверждение 4.2 и пример 4.9). В двух последних случаях определяется и порядок полюса.

Практически удобное правило определения порядка полюса z=infty можно получить, используя п. 2 утверждения 4.2 и правила определения порядка полюса в конечной точке (утверждение 4.3). Действительно, пусть z=infty-Pi(n) для функции f(z) , тогда xi=0-Pi(n) для $f! left(frac{1}{xi}right)$ и можно записать $f! left(frac{1}{xi}right)= frac{F(xi)}{xi^n},~ F(xi)ne0$ (см. (4.14)). Поэтому, обозначив $f! left(frac{1}{z}right)= varphi(z)$ , для f(z) получим

$f(z)=z^ncdot varphi(z),qquad limlimits_{ztoinfty} varphi(z)ne0,qquad limlimits_{ztoinfty} varphi(z)neinfty.$

(4.15)

Представление функции в виде (4.15) является необходимым и достаточным условием полюса порядка функции f(z) в точке z=infty .

Замечание 4.5. Используя формулу (4.15), нетрудно убедиться, что если z=infty-Pi(m) для f_1(z) и Pi(k) для f_2(z) , то z=infty — полюс порядка (m-k) для функции $f(z)= frac{f_1(z)}{f_2(z)}$ .

Пример 4.17. Определить тип особой точки z=infty для функций: а) f(z)= z^2(z-2) ; б) $f(z)=frac{z^5+z^2+1}{z^3-2z}$ .

Решение

Так как $limlimits_{ztoinfty}f(z)=infty$ в обоих случаях, то z=infty для данных функций — полюс. Определим порядок полюса.

а) Точка z=infty является полюсом третьего порядка, в чем можно убедиться любым из следующих способов.

Первый способ. Разложение функции по степеням имеет вид f(z)=z^3-2z,~c_3ne0 , все c_n=0,~n>3 , и по определению (см. формулы (4.7), (4.11)) заключаем, что z=infty-Pi(3) .

Второй способ. Обозначим $z=frac{1}{xi}$ , получим функцию $f! left(frac{1}{xi}right)= frac{1-2xi}{xi^3}$ , для которой xi=0-Pi(3) . Поэтому, согласно п. 2 утверждения 4.2, точка z=infty-Pi(3) для f(z) .

Третий способ. Запишем функцию в виде $f(z)=z^3! left(1-frac{2}{z}right)$ и, так как функция $varphi(z)=left(1-frac{2}{z}right)$ — удовлетворяет условиям формулы (4.15), получим, что z=infty-Pi(3) для f(z) .

б) Разложение функции в ряд по степеням представляет некоторые трудности. Используем другие способы.

Первый способ. Обозначим $z=frac{1}{xi}$ , получим $f! left(frac{1}{xi}right)= frac{(xi^5+xi^3+1)cdotxi^3}{xi^5cdot(1-2xi^2)}$ , или $f! left(frac{1}{xi}right)= frac{xi^5+xi^3+1}{xi^2cdot(1-2xi^2)}$ .

Поэтому xi=0 является Pi(2) для $f!left(frac{1}{xi}right)$ и, следовательно, z=infty-Pi(2) для f(z) .

Второй способ. Представим функцию в виде $f(z)= frac{z^5cdot left(1+ dfrac{1}{z^3}+dfrac{1}{z^2}right)}{z^3cdot left(1-dfrac{2}{z^2}right)}$ или f(z)= z^2cdot varphi(z) , где $limlimits_{ztoinfty} varphi(z)=1$ , и, согласно формуле (4.15), z=infty-Pi(2) для f(z) .

Третий способ. Используем замечание 4.5. Можно определить порядок полюса z=infty для дроби $frac{f_1(z)}{f_2(z)}$ , зная соответствующие порядки полюсов числителя и знаменателя. Здесь, очевидно, z=infty-Pi(5) для числителя и Pi(3) — для знаменателя (см. формулы (4.7), (4.11)). Поэтому z=infty-Pi(2) для f(z) .

Пример 4.18. Определить порядок полюса в точке z=infty для следующих функций: а) $f(z)= frac{z^3}{z-1}$ ; б) $f(z)=z^2+1+frac{1}{z^2-1}$ .

Решение

Определение типа особых точек для суммы, разности, произведения и частного функций

Пусть z_0 — особая точка функций f_1(z) и f_2(z) и тип особой точки для каждой из функций известен. Требуется определить тип особой точки для функций $f_1(z)pm f_2(z);~ f_1(z)cdot f_2(z);~ frac{f_1(z)}{f_2(z)}$ . Рассмотрим следующие случаи.

Первый случай. Пусть точка го является полюсом порядка m~(Pi(m)) для функции f_1(z) и полюсом порядка k~(Pi(k)) для функции f_2(z) .

а) При исследовании суммы f(z)= f_1(z)+ f_2(z) воспользуемся формулой (4.14) (п.1 утверждения 4.3) и запишем слагаемые в виде

$f_1(z)=frac{varphi_1(z)}{(z-z_0)^m},~~ f_2(z)=frac{varphi_2(z)}{(z-z_0)^k}$ , где varphi_1(z_0)ne0,~varphi_2(z_0)ne0 .

При k=m для суммы f(z)= f_1(z)+ f_2(z) получаем $f(z)= frac{varphi_1(z)+varphi_2(z)}{(z-z_0)^m}$ или $f(z)=frac{varphi(z)}{(z-z_0)^m}$ , где varphi(z)= varphi_1(z)+ varphi_2(z) . Если varphi(z_0)ne0 , то z_0-Pi(m) для функции f(z) . Однако для функций f_1(z),, f_2(z) может выполняться условие varphi_1(z_0)+ varphi_2(z_0)=0 и’ следовательно, varphi(z_0)=0 . В этом случае формула (4.14) не применима и точка z_0 не будет полюсом порядка для f(z) . В соответствии с п.3 утверждения 4.3 порядок полюса будет меньше, чем , и равен (m-p) в случае m>p , где — порядок нуля функции varphi(z) . Если p=m , то z_0 — устранимая особая точка для f(z) .

Таким образом, при сложении функций порядок полюса в точке может оказаться равным или меньше, чем наибольший из порядков слагаемых.

б) Для исследования произведения f_1(z)cdot f_2(z) воспользуемся формулой связи нулей с полюсами (п.2 утверждения 4.3) и рассмотрим вспомогательные функции $F_1(z)= frac{1}{f_1(z)},~ F_2(z)= frac{1}{f_2(z)}$ . Для первой из этих функций z_0-0(m) , для второй соответственно z_0-0(k) . а поэтому для F(z)= F_1(z)cdot F_2(z) она будет 0(m+k) . Согласно п.2 утверждения 4.3, z_0 является Pi(m+k) для .

в) Аналогичные рассуждения для частного $frac{f_1(z)}{f_2(z)}$ приводят к результату: при m>k точка z_0 является Pi(m-k) для $frac{f_1(z)}{f_2(z)}$ .

Второй случай. Пусть точка z_0 является полюсом, устранимой особой точкой или не особой для f_1(z) и существенно особой для f_2(z) . Так как $limlimits_{zto z_0}f_2(z)$ не существует, то по свойству пределов он не существует для каждой из рассматриваемых комбинаций $f_1(z)pm f_2(z);~ f_1(z)cdot f_2(z);~ frac{f_1(z)}{f_2(z)}$ . Следовательно, для каждой из них z_0 — существенно особая точка. Заметим, что для функции $frac{1}{f_2(z)}$ эта точка является либо существенно особой точкой, либо не является изолированной особой точкой. Последнее проиллюстрировано в примере 4.5 для функции $frac{1}{sin z^{-1}}$ .

Третий случай. Пусть z_0 — полюс порядка для f_1(z) и устранимая особая точка для f_2(z) . Разложения этих функций в ряд в окрестности z_0 имеют вид (4.6) и (4.4) соответственно.

а) При сложении рядов в общей области сходимости получится ряд, главную часть которого будет составлять главная часть ряда функции f_1(z) . Следовательно, для f(z)= f_1(z)pm f_2(z) точка z_0 — полюс порядка .

б) Аналогичные рассуждения приводят к заключению, что такой же результат получится и для f(z)= f_1(z)cdot f_2(z) , если $limlimits_{zto z_0}f_2(z)ne0$ .

Если $limlimits_{zto z_0}f_2(z)=0$ и z_0-0(p),~ p<n для функции f_2(z) , то из равенства

$f_1(z)cdot f_2(z)= frac{varphi_1(z)}{(z-z_0)^n}cdot varphi_2(z)cdot (z-z_0)^p= frac{varphi(z)}{(z-z_0)^{n-p}}$ заключаем, что z_0-Pi(n-p) .

в) Для частного $frac{f_1(z)}{f_2(z)}$ при условии $limlimits_{zto z_0} f_2(z)ne0$ из равенства $f(z)= frac{f_1(z)}{f_2(z)}= frac{varphi_1(z)}{(z-z_0)^n f_2(z)}= frac{varphi(z)}{(z-z_0)^n}$ заключаем, что z_0-Pi(n) для f(z) .

Если $limlimits_{zto z_0}f_2(z)=0$ и z_0-0(p) для f_2(z) , то, используя условие кратного нуля, из равенства

$f(z)= frac{f_1(z)}{f_2(z)}= frac{varphi_1(z)}{(z-z_0)^n varphi_2(z) (z-z_0)^p}= frac{varphi(z)}{(z-z_0)^{n+p}}$

заключаем, что z_0 является Pi(n+p) для $frac{f_1(z)}{f_2(z)}$ , где — порядок полюса функции f_1(z),~p — порядок нуля функции f_2(z) в точке z_0 .

Подводя итог, запишем следующее утверждение.
Утверждение 4.4

1. Пусть точка z_0 является Pi(m) для функции f_1(z) и Pi(k) для функции f_2(z) . Тогда:

а) для f_1(z)pm f_2(z) она будет Pi(n),~ n leqslant max(m,k) , а при n=0 — устранимой особой точкой;

б) для f_1(z)cdot f_2(z) она является Pi(n),~ n=m+k ;

в) для $frac{f_1(z)}{f_2(z)}$ она будет Pi(n),~ n=m-k .

2. Пусть z_0 — существенно особая точка для функции f_2(z) и устранимая особая точка или полюс для функции f_1(z) . Тогда z_0 — существенно особая точка для $f_1(z)pm f_2(z);~ f_1(z)cdot f_2(z);~ frac{f_1(z)}{f_2(z)}$ .

3. Пусть точка z_0 является Pi(n) для функции f_1(z) и устранимой особой точкой для функции f_2(z) . Тогда:

а) для f_1(z)pm f_2(z) она будет Pi(n) ;

б) для f_1(z)cdot f_2(z) она является Pi(n) , если $limlimits_{zto z_0}f_2(z)ne0$ , и Pi(n-p) , если $limlimits_{zto z_0}f_2(z)=0$ и — порядок нуля f_2(z) в точке z_0 ;

в) для $frac{f_1(z)}{f_2(z)}$ она будет Pi(n) , если $limlimits_{zto z_0}f_2(z)ne0$ , и Pi(n+p) , если $limlimits_{zto z_0}f_2(z)=0$ и — порядок нуля f_2(z) в точке z_0 ;

4. Если точка z_0-Pi(n) для varphi(z) , то она существенно особая точка для сложной функции f(varphi(z)) . В этом можно убедиться, рассматривая ряды для и в окрестности z_0 .

Пример 4.19. Определить тип особой точки z=0 для функции f(z) , если f(z)= f_1(z)+ f_2(z) , где $f_1(z)= frac{1}{z^2}$ , а функция f_2(z) определяется следующим образом:

а) $f_2(z)= frac{1}{z}-frac{2}{z^2}$ ; б) $f_2(z)= frac{1}{z}-frac{1}{z^2}$ ; в) $f_2(z)=1-frac{1}{z}$ .

Решение

Пример 4.20. Найти особые точки функции $f(z)= frac{1}{e^z-1}-frac{1}{z}$ . Определить их тип.

Решение

Особыми точками функции являются особые точки первого слагаемого z=2kpi i,~ kinmathbb{Z} , особая точка второго слагаемого z=0 входит в это множество. Точки z_k=2kpi i,~kne0 являются простыми нулями знаменателя и поэтому простыми полюсами первой функции; для второго слагаемого эти точки не являются особыми. Поэтому точки -простые полюсы f(z) (см. п. 3 «а» утверждения 4.4).

Точка z=0 — простой полюс и для первого, и для второго слагаемого. Для f(z) — это или простой полюс, или устранимая особая точка (см. п.1 «а» утверждения 4.4). Преобразуем разность в дробь: $f(z)= frac{z-e^z+1}{(e^z-1)z}$ . Точка z=0 является нулем второго порядка и для числителя, и для знаменателя. Следовательно, это — устранимая особая точка, в чем можно убедиться, используя определение, т.е. находя $limlimits_{zto0}f(z)$ . Действительно,

$limlimits_{zto0}f(z)= limlimits_{zto0} frac{-1-z-dfrac{z^2}{2!}+ldots+z+ 1}{left(-1-z-dfrac{z^2}{2!}+ldots-1 right)!z}= limlimits_{zto0} frac{-dfrac{z^2}{2!}-dfrac{z^3}{3!}-ldots}{z^2! left(1+dfrac{z}{2!}+ldotsright)}= limlimits_{zto0} frac{-z^2! left(dfrac{1}{2!}+ dfrac{z}{3!}+ldotsright)}{ z^2!left(1+dfrac{z}{2!}+ldotsright)}=-frac{1}{2},.$

Точка z=infty для данной функции является неизолированной особой точкой, так как в любой ее окрестности |z|>R содержится бесконечное множество особых точек вида z_k=2kpi i . Эта точка- предельная точка полюсов. Заметим, что для знаменателя первого слагаемого функции она — существенно особая точка.

Пример 4.21. Найти особые точки следующих функций, определить их тип:

а) $f(z)= frac{z-pi}{sin^2z}cos frac{1}{z-2i}+ frac{1}{z^6+1}$ ; б) $f(z)= frac{1}{z^2-1} sin frac{pi z}{2z+1}+ frac{1}{e^z+i}$ .

Решение

Обозначим f_1(z) — первое слагаемое, f_2(z) — второе слагаемое функции f(z) , т.е. имеем f(z)=f_1(z)+f_2(z) .

а) Для f_1(z) точка z=2i является существенно особой точкой, так как это существенно особая точка для $cos frac{1}{z-2i}$ множителя этой функции. Поэтому она — существенно особая точка для f(z) (п. 2 утверждения 4.4).

Точки z_k=kpi,~kne1 — полюсы второго порядка функции f_1(z) , так как ее можно записать в виде $f_1(z)=frac{varphi(z)}{sin^2z}$ , где varphi(z_k)ne0 , а для знаменателя эти точки — нули второго порядка . Так как для f_2(z) эти точки не особые, то z_k=kpi,~znepi — полюсы второго порядка для f(z) (п. 3 утверждения 4.4).

С помощью аналогичных рассуждений получаем, что z=pi — простой полюс для f(z) .

Особыми точками f_2(z) являются корни уравнения z^6+1=0 , то есть $z_k=exp frac{(-pi+2kpi)i}{6},~ k=0,1,ldots,5$ . Все они — простые нули знаменателя- функции F(z) , а потому — простые полюсы для $f_2(z)= frac{1}{F(z)}$ . Так как эти точки не являются особыми для f_1(z) , то для f(z) — это простые полюсы.

Точка z=infty — неизолированная особая точка f(z) .

б) Точка $z=frac{-1}{2}$ — полюс дроби $frac{pi z}{2z+1}$ является существенно особой точкой для $sinfrac{pi z}{2z+1}$ (п.4 утверждения 4.4), поэтому она — существенно особая точка для f_1(z) и, следовательно, для f(z) .

Точка z=1 — простой полюс для f_1(z) , так как можно записать $f_2(z)= frac{varphi(z)}{z-1},~ varphi(z)ne0$ . Поскольку z=1 не является особой точкой для f_2(z) , то она — простой полюс для f(z) .

Точка z=-1 — устранимая особая точка для f_1(z) , так как она — простой нуль и для числителя, и для знаменателя дроби $frac{sindfrac{pi z}{2z+1}}{z^2-1}$ . Так как z=-1 не является особой точкой для f_2(z) , то она — устранимая особая точка для f(z) .

Особыми точками f_2(z) являются простые нули знаменателя — корни уравнения e^z+i=0 , или e^z=-i , то есть z=operatorname{Ln}(-i) . Все точки

z_k=ln|-i|+ibigl(arg(-i)+2kpibigr) , или $z_k=i! left(2kpi-frac{pi}{2}right)!,~ kin mathbb{Z}$

являются простыми полюсами для f_2(z) и, следовательно, простыми полюсами для f(z) .

Точка z=infty — неизолированная особая точка f(z) .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Теоретический минимум

Вычетом функции в особой точке по определению называется величина

Контур интегрирования должен охватывать только одну особую точку , причём она должна быть изолированной
и являться точкой однозначного характера.
Обычно по определению вычеты не вычисляют: это неудобно. Можно показать, что вычет функции в точке представляет собой
коэффициент при минус первой степени в разложении функции в ряд Лорана в окрестности данной точки. Это упрощает вычисление,
так как появляется возможность использовать приёмы разложения функции в ряд Лорана, не связанные с вычислением контурных
интегралов. Тут многое зависит от вида особой точки. В разложении функции в ряд Лорана в окрестности устранимой особой точки
отрицательные степени отсутствуют. Следовательно, и вычет в такой точке равен нулю. Разложение в ряд Лорана в окрестности полюса
содержит конечное число отрицательных степеней. В этом случае для полюса n-го порядка

Чаще всего применяется именно эта формула. Для простого полюса (полюса первого порядка) формула сильно упрощается:

Отдельно рассматривается вычет в бесконечно удалённой точке. Он равен взятому с противоположным знаком коэффициенту при
минус первой степени разложения функции в ряд Лорана в окрестности бесконечно удалённой точки.

Вычеты находят применение при вычислении интегралов по основной теореме о вычетах.

Примеры вычисления вычетов

Пример 1. Вычет функции в простом полюсе.
Найдём вычет функции в точке .

Пример 2. Вычет функции в полюсе третьего порядка.
Найдём вычет функции в точке .

Убедиться в том, что точка — полюс третьего порядка, достаточно просто. Котангенс в числителе сам по себе имеет в этой
точке простой полюс, функция в знаменателе делает данную точку полюсом именно третьего порядка.

Для вычисления этого предела раскладываем функции в числителе в ряд Тейлора. Причём так как в знаменателе
сразу получится третья степень — в первом же слагаемом, то и в числителе следует проводить разложение до кубических слагаемых:
.
Примечание. Этот расчёт приходится проделывать при вычислении значения дзета-функции Римана .

Пример 3. Вычет функции в полюсе второго порядка.
Найдём вычет функции в точке .

Хотя особая точка является полюсом второго порядка, пользоваться приведённой выше общей формулой для
вычетов в полюсах не будем. Проведём разложение в ряд Лорана:

Видно, что коэффициент при минус первой степени равен . Это и есть искомый вычет.

Пример 4. Вычет функции в бесконечно удалённой точке.
Найдём вычет функции в бесконечно удалённой точке.

Представим функцию в следующем виде:

Экспоненту можно разложить в ряд по известной формуле, для дроби используем разложение, представляющее собой сумму геометрической прогрессии:

Видно, что после перемножения скобок при минус первой степени останется число 2. Следовательно, вычет равен (-2).
BA3a
for love and rock-n-roll
VIP

Помнится, когда нам Теляковский рассказывал про вычеты, я сидел с открытым ртом и думал «вау, как красиво».
Реквестирую аналогичную тему про особые точки :huh: Завтра сдавать.
Sean33
агрессия и злоба
Модератор
VIP

Schufter, большое спасибо! Как раз во время!
panicdoctor, да, такая формула есть, конечно. Но на мой взгляд лучше помнить общую формулу для вычета в полюсе
любого порядка, чем помнить дополнительно ещё одну формулу. Тем более, что в простом полюсе вычет обычно находится легко. :huh:
Но подчеркну: формула есть, если есть желание — ей можно пользоваться. Просто высказал своё мнение.

Поделиться этой страницей

Источник

Вычисление вычетов

Пусть
f(z)
имеет полюс первого порядка. Тогда она
представляется в виде f(z)
=
и рядом Лоранаf(z)
=
.
Умножимf(z)
на (z
— a)
и перейдем к пределу

lim
f(z)
(z
— a)
= lim=( 49 )

т.е.
вычет функции с полюсом первого порядка
в точке а
равен пределу
произведения функции на множитель (z
— a)
при
.

При
вычислении предела в ( 49 ) используем
правило Лопиталя

lim=
lim=lim==res
f(z)

(
50 )

т.е.
для определения вычета достаточно
значение числителя функции в точке а
разделить
на значение производной от знаменателя
в этой точке.

Если
f(z)
имеет в точке а
полюс порядка
n,
то разложение этой функции в ряд Лорана
( 46 ) умножим на (z
— a)ⁿ

(z
— a)ⁿf(z)
=
+(z
— a)
+
…+(z
— a)^n

—¹+
(z
— a)ⁿ
,
( 51 )

(n
— 1) раз продифференцируем и получим (n
— 1)!

+
.

Переход
к пределу
исключает второе слагаемое и определит
вычет

=
( 52 )

Пр.
Найти вычеты функции f
(z)
=
.

Решение.
Полюсами являются точки z
= 1,
z
= 3 .

(z
— 1)
=
= -1/2

(z
— 3)
=
= 3/2

или
по формуле ( 47 ) :
, тогда

=
,

=

Пр.
Найти вычеты функции f(z)
=
.

Решение.
Здесь z
= 2 — полюс третьего порядка, тогда по (
52 ) имеем

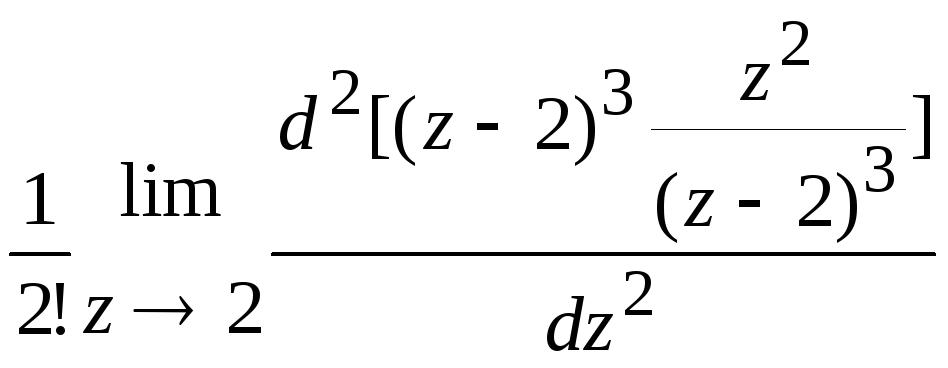
Определение порядка полюса

Пусть
f(z)
имеет в точке а
полюс порядка
n
и принимает вид

f(z)
=++
. . . ++(z).

Рассмотрим

f(z),
где k
произвольно, и перейдем к пределу
. Приk
< n
получим
,
при k
> n
получим 0
и только при
k
= n
получим
конечное число

, т.е. условие

(
53 )

определяет
порядок полюса для f(z)
в точке z
= a
путем подбора числа k
.

Перейдем
к обратной функции
.
Приz
= a
она обращается в 0 и её всегда можно
представить в виде

=
=

где

аналитическая функция и.
Числоn
определяет порядок
нуля для
приz
= a
и порядок полюса для f
(z).
Будем последовательно дифференцировать

и переходить к пределу.
Первый не нулевой результат появится
только после вычисленияn
– ой производной. Таким образом, для
определения порядка полюса функции f
(z),
имеющей вид дроби, достаточно выполнить
одно из следующих действий : 1) представить
её знаменатель в виде
;
2) вычислять значения производных её
знаменателя до первого ненулевого
результата.

Пр.

.

f(z)
=
приимеем полюс.

Определим его
порядок. Первый способ: проведем
разложение знаменателя в ряд

нуль
2 порядка.

Второй способ:
определим порядок нуля знаменателя
дифференцированием

Имеем полюс 2
порядка.

Пр.
Определить тип особой точки z
= 0 для функции

Решение.

f(z)=.
Определим порядок нуля числителя и
знаменателя.

имеет
ноль 2 порядка (см. выше).

=
= 0,

= 0,

= 32

имеем ноль 5 порядка.

=
,
т.е. функцияf(z)
при
имеет полюс 3 порядка.

Вычислим
производную от логарифма функции f(z)
=
=

вычет производной дает порядок полюса
функции.

Вычисление интегралов

A)
Пр. Вычислить J
=,
если-окружности:
1) |z
| = 1; 2)
| z
| = 3;
3)
| z
| = 5.

Решение.
Найдем вычеты относительно полюсов z
= 0 , z
= — 2 , z
= — 4

=

z
f(z)
=
= 1/8

=(z
+ 2) f(z)
== — ¼

=

(z
+ 4) f(z)
=
= 1/8

1)
Внутри окружности | z
| =1 находится
один полюс z
= 0

J₁=2i()
=i/4

2)
Внутри окружности | z
| = 3
находятся
полюсы z
= 0, z
=-2

J₂ = 2i()
= —i
/ 4.

3)
Внутри окружности |
z
| = 5 находятся
полюсы z
= 0, z
=-2, z
=-4

J₃
= 2i()
= 0 .

Б)
Рассмотрим
интегралы вида
.
Здесь от действительной переменнойх
легко перейти
к комплексной переменной z.
Тогда интегрирование будет производиться
вдоль замкнутой окружности с учетом
теоремы о вычетах.

Пусть
а
= 0 и
,т.е.z
является комплексной переменной с
модулем r
= 1 и аргументом
х (.
Ей соответствует окружность |z
| = 1 . Тогда
;
;

и
переходим к интегралу
.
Интервалприводит только к другой точке начала
движения по окружности.

Пр.

.
Пусть,
тогда,
,
,=
=.
Подынтегральная функция имеет две
изолированные особые точки, которые
являются полюсами 1 порядка. Но в
окружность радиуса 1 попадает только
полюси интеграл равен вычету в этой точке

В)
Пусть f
(z)
аналитическая
функция в верхней полуплоскости, включая
действительную ось, за исключением m
полюсов a_iрасположенных
над осью Ох.
Кроме того, lim
z²
f(z)
= C
– конечное
число при | z
|,
т.е. на
бесконечности функция становится
двукратной нулевой точкой (условие
Жордана). Построим замкнутый контур L,
состоящий из оси Ох
и полу-окружности радиуса R.
Тогда
=
+

, но

в
силу условия Жордана

= 0, и определенный интеграл от
функции
действительной
переменной
f(x)
будет
равен сумме
вычетов функции f
(z)
в a_i

J
=
=

(
54 )

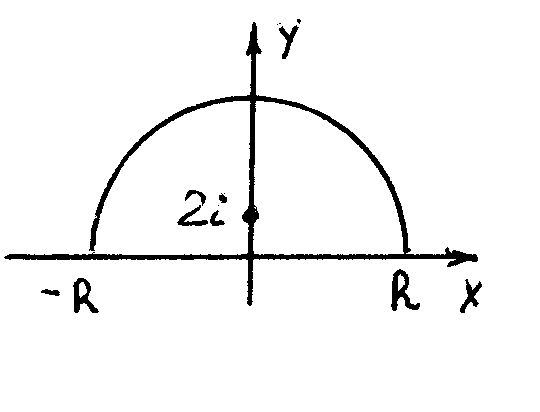
Пр.
Вычислить J
=
.

Решение.
Рассмотрим функцию f
(z)
=
,
аналитическую в верхней полуплоскости,
за исключением полюса 2 порядка в 2i.
Проверка
условия Жордана :

=

=

= { z
= r
e^it
} =

=

=
0 , т.е. конечное число
да.

Вычисление
вычета по формуле ( 52 )

====

Ответ.
J
= 2i

=
2i
()
=
.

Источник

Содержание

— Как узнать сколько полюсов у двигателя?
— Чему равна синхронная скорость асинхронного двигателя с одной парой полюсов?
— Чем больше пар полюсов?
— Как определить частоту вращения двигателя?
— Как определить синхронную скорость?
— Чему пропорционален вращающий момент?
— Как посчитать частоту вращения вала?
— Какое количество полюсов должно быть у синхронного генератора имеющего частоту тока 50 Гц?
— Как узнать мощность электродвигателя мультиметром?
— Как определить частоту вращения магнитного поля?

Как узнать сколько полюсов у двигателя?

Четырехскоростные двигатели бывают двенадцать на восемь на шесть и четыре полюса (12/8/6/4) то есть частоты вращения вала при этом пятьсот, семьсот пятьдесят, тысяча и полторы тысячи оборотов в минуту (500/750/1000/1500).

Чему равна синхронная скорость асинхронного двигателя с одной парой полюсов?

Из последней формулы видно, что скорость вращения двигателя n практически определяется значением его синхронной скорости, а последняя при стандартной частоте 50 Гц зависит от числа пар полюсов: при одной паре полюсов — 3000 об/мин, при двух парах — 1500 об/мин, при трёх парах — 1000 об/мин и т. д.

Чем больше пар полюсов?

И чем больше пар полюсов — тем меньшей будет синхронная частота вращения — частота вращения магнитного поля статора. Большинство современных асинхронных двигателей имеют от 1 до 3 пар магнитных полюсов, в редких случаях 4, ведь чем больше полюсов — тем ниже КПД асинхронного двигателя.

Как определить частоту вращения двигателя?

Исходя из формулы n = (1 — S)60f/p где n — скорость вращения ротора, S — скольжение, f- частота питающей сети, p — количество пар полюсов. Существует три способа регулирования скорости вращения асинхронного двигателя: — изменение скольжения. Этот способ используется в двигателях с фазным ротором.

Как определить синхронную скорость?

Синхронная скорость вращения обычных асинхронных двигателей выражается как:

n = 60*f *2 / p (1)
где
n = скорость вращения штока (об/мин, rpm)
f = частота (ГЦ=Hz; оборотов/с; 1/с)
p =число полюсов, !!! если формула дается в виде n = (60*f ) / p, то под p понимается число пар полюсов, а не число полюсов!!!

Чему пропорционален вращающий момент?

т. е. вращающий момент асинхронного двигателя пропорционален результирующему магнитному потоку и активной составляющей тока в обмотке ротора. Коэффициент пропорциональности с зависит от конструктивных параметров двигателя.

Как посчитать частоту вращения вала?

Определение частоты вращения вала электродвигателя n_эд = n₂ ∙ i, где i − передаточное отношение привода.

Какое количество полюсов должно быть у синхронного генератора имеющего частоту тока 50 Гц?

Ротор генератора, приводимого в движение водяной турбиной, делает 75 об/мин. Определить число полюсов генератора, если частота его тока 50 гц: Следовательно, генератор имеет 80 полюсов.

Как узнать мощность электродвигателя мультиметром?

Запишите показания до включения мотора, дайте ему поработать ровно 10 минут (лучше воспользоваться секундомером). Снимите новые показания счетчика и путем вычитания узнайте разницу. Умножьте эту цифру на 6. Полученный результат отображает мощность двигателя в кВт.

Как определить частоту вращения магнитного поля?

Как известно, частота тока в цепи ротора асинхронного двигателя зависит от скольжения, т. е. определяется разностью частот вращения ротора и поля статора. Указанное свойство позволяет использовать двигатель в качестве преобразователя частоты (рис.

Интересные материалы:

Можно ли обрезать герань на зиму?
Можно ли обрезать герань в ноябре?
Можно ли обрезать гибискус на зиму?
Можно ли обрезать Глоксинию?
Можно ли обрезать гнилые корни у цветущей орхидеи?
Можно ли обрезать гортензии?
Можно ли обрезать гортензию Метельчатую осенью?
Можно ли обрезать гортензию осенью?
Можно ли обрезать гортензию под корень?
Можно ли обрезать гортензию в августе?

Источник

Содержание

Глава 6. Вычеты функций и их применение

Вычет функции относительно изолированной особой точки. Основная теорема о вычетах

Вычетом функции $f(z)$ относительно изолированной особой точки $z_0$ называется коэффициент $c_{-1}$ при $(z-z_0)^{-1}$ в разложении в ряд Лорана функции $f(z)$ в окрестности $z_0$.
$$
mbox{Res }f(z_0) = c_{-1}.
$$

Вычетом функции $f(z)$ относительно изолированной особой точки $z_0$ называется интеграл
$$
mbox{Res }f(z_0) =frac1{2pi i}ointlimits_L f(z),dz,
$$ где $L$ — произвольный контур в кольце $0<|z-z_0|<R$, ориентированный против часовой стрелки ($L$ должен окружать точку $z_0$).

Основная теорема о вычетах (Коши)

Пусть функция $f(z)$ является аналитической всюду в замкнутой области $overline D$, за исключением конечного
числа изолированных особых точек $z_1,z_2,dots,z_N$, лежащих внутри области $D$. Тогда $$
ointlimits_L f(z),dz=2pi isumlimits_{k=1}^N
mbox{Res }f(z_k),
$$ где $L$ — полная граница области $D$, проходимая в положительном направлении.

Вычисление вычетов в конечных особых точках

Вычет в устранимой особой точке равен $0$.

Если $z_0$ — существенно особая точка, то имеется только один способ вычисления вычета — разложение функции в ряд Лорана и определение коэффициента $c_{-1}$.

Для нахождения вычета в полюсе есть несколько приемов.

* Для простого полюса можно воспользоваться формулой:
begin{equation}label{1}
mbox{Res }f(z_0)=limlimits_{zto z_0}
Big(f(z)(z-z_0)Big).
end{equation}
* Для полюса порядка $m$:
begin{equation}label{2}
mbox{Res }f(z_0)=frac1{(m-1)!}limlimits_{zto z_0}
frac{d^{m-1}}{dz^{m-1}}Big(f(z)(z-z_0)^mBig).
end{equation}
* Для простого полюса в случае функции $ f(z)=frac{g(z)}{varphi(z)}$, где
$g(z)$ и $varphi(z)$ — аналитические функции в окрестности точки $z_0$ и $g(z_0)neq 0$, а для $varphi(z)$ точка $z_0$ есть нуль первого порядка (для $f(z)$ же точка $z_0$ есть полюс первого порядка):
begin{equation}label{3}
mbox{Res }f(z_0)=frac{g(z_0)}{varphi'(z_0)}.
end{equation}

Вычислить
$$ I=ointlimits_{|z-i|=2}frac{z-7}{z^2(z-1)(z-5i)},dz. $$

Строим контур интегрирования — окружность $|z-i|=2$. Подынтегральная функция имеет особые точки $z_1=0$, $z_2=1$ и $z_3=5i$. Точка $5i$ не
лежит внутри контура интегрирования. Точка $z_1=0$ — полюс 2-го порядка, $z_2=1$ — полюс 1-го порядка. По основной теореме о вычетах получаем $$ I=2pi ibig(mbox{Res }f(0)+mbox{Res }f(1)big). $$ По формуле для вычисления вычета в полюсе 2-го порядка
$$
mbox{Res }f(0)=frac1{1!}limlimits_{zto0}left(
left(frac{(z-7)z^2}{z^2(z-1)(z-5i)}right)’right)=
$$ $$ =limlimits_{zto0}frac{(z-1)(z-5i)-(z-7)(2z-1-5i)} {(z-1)^2(z-5i)^2}=frac{7+30i}{25}. $$ Для простого полюса вычет равен $$
mbox{Res }f(1)
=limlimits_{zto1}frac{(z-7)(z-1)}{z^2(z-1)(z-5i)} =-frac6{1-i}. $$

Окончательно, $$ I=2pi ileft(frac{7+30i}{25}-frac6{1-i}right) =pileft(frac{24}5-frac{106}{25}iright). $$

О бесконечно удаленной точке $z=infty$

Выберем любое $r geqslant0$. Разложим функцию $f(z)$ по степеням $z$ во внешности круга $|z|> r$, которое иногда
называют окрестностью бесконечно удаленной точки, $$ f(z)=sumlimits_{-infty}^infty c_kz^k=F_1(z)+F_2(z) =sumlimits_{k=1}^infty
c_kz^k +sumlimits_{k=0}^inftyfrac{c_{-k}}{z^k}. $$ В этом случае $F_1(z)$ называют главной частью, а $F_2(z)$ — правильной частью.

В зависимости от поведения функции
$f(z)$ в окрестности $z=infty$ введена следующая классификация:

— Особенность в точке $z=infty$ устранимая, если все
$c_k=0$, $k=1,2,ldots$, т.е. если $f(z)=F_2(z)$ для $|z|>r$. В этом случае $$
limlimits_{ztoinfty}f(z)=c_0.
$$ Очевидно, что $$
frac1{2pi mathbf i }ointlimits_{L^-}f(z),dz=-c_{-1},
$$ где $L^-$ — произвольный контур, ориентированный по часовой стрелке, содержащий внутри себя окружность $|z|=r$.

Можно считать, что точка $z=infty$ находится внутри контура $L^-$. Если двигаться по контуру $L^-$ по часовой
стрелке, то точка $z=infty$ остается слева.

Видим, что в случае, когда $z=infty$ — устранимая особая точка, то вычет не обязательно
равен нулю!

— Точка $z=infty$ есть полюс порядка $m$, если
$f(z)=sumlimits_{k=1}^m c_k z^k+F_2(z)$ и $c_mne0$. В этом случае, очевидно, $$
limlimits_{ztoinfty}f(z)=infty.
$$

$$
ointlimits_{L^-}f(z),dz=sumlimits_{k=0}^infty c_{-k}
ointlimits_{L^-}frac{dz}{z^k}+sumlimits_{k=1}^m c_k
ointlimits_{L^-}z^k,dz=
$$ $$ =-c_{-1}intlimits_Lfrac{dz}z=-2pimathbf i c_{-1}, $$ потому, что $displaystyleointlimits_{L^-}z^k,dz=-ointlimits_L z^k,dz=0$, когда
$kne-1$;

— Точка $z=infty$ является существенно особой точкой, если
$f(z)=sumlimits_{k=1}^infty c_kz^k+F_2(z)$ и имеется бесконечное число чисел $c_k$, не равных нулю. В данном случае функция из-за первого слагаемого не имеет предела при $ztoinfty$.
$$
ointlimits_{L^-}f(z),dz=sumlimits_{k=-infty}^infty c_k
ointlimits_{L^-}z^k,dz=-2pi mathbf i c_{-1}.
$$

Вычетом функции $f(z)$ в бесконечно удаленной точке
называется $$
mbox{Res }f(infty)=frac1{2pi mathbf i }ointlimits_{L^-}f(z),dz,
$$ где $L^-$ — произвольный замкнутый контур, ориентированный по часовой стрелке, принадлежащий множеству $|z|>r$ (где функция $f(z)$
аналитична).

Кроме того, если $f(z)=sumlimits_{k=-infty }^infty c_kz^k$ — ряд Лорана функции во внешности окружности $|z|=r$, то
$$
mbox{Res }f(infty)=-c_{-1}.
$$

Теорема о сумме вычетов

Пусть функция $f(z)$ аналитична на всей плоскости $z$ за исключением конечного числа изолированных особых точек $z_1,z_2,dots,z_N$. Тогда сумма всех вычетов этой функции, включая вычет в бесконечно удаленной точке, равна нулю:
$$ sumlimits_{k=1}^Nmbox{Res }f(z_k)+mbox{Res }f(infty)=0. $$

Вычислить интеграл $ointlimits_{|z|=2}frac{z^{20},dz}{(2z^3+1)^2(z^4-1)^3}$.

Р е ш е н и е.

Все особые точки $z_k=sqrt[4]{1}$, $sqrt[3]{-0,5}$ лежат в круге $|z|=2$. Вычисление вычетов в этих точках довольно
затруднительно, поэтому воспользуемся формулой $$ I=2pi isumlimits_{k=1}^infty mbox{Res }f(z_k)=-2pi imbox{Res }f(infty). $$ Представим функцию в
виде $$
frac{z^{20}}{4z^6left(1+cfrac1{2z^3}right)^2z^{12}
left(1-cfrac1{z^4}right)^3}=
$$ $$ =frac{z^2}4left(1-frac1{2z^3}+frac1{4z^6}-dotsright)^2
left(1+frac1{z^4}+frac1{z^8}right)^3=frac{z^2}4-frac1{4z}
+dots . $$

Тогда $mbox{Res }f(infty)=dfrac14$ и интеграл равен $-2pi imbox{Res }f(infty)=-dfrac{pi i}2$.

О т в е т: $-dfrac{pi i}2$.

Вычисление определенных интегралов с помощью вычетов

Некоторые определенные интегралы от функций вещественного переменного удается преобразовать в интеграл по замкнутому контуру от функции комплексного переменного, что позволяет применить для вычисления этих интегралов основную теорему о вычетах. Часто удается достаточно просто получить ответ и в тех случаях, когда применение других методов анализа
оказывается затруднительным.

I. Интеграл вида $I=intlimits_0^{2pi}R(cos{x},sin{x}),dx,$

где $R(u,v)$ — рациональная функция двух переменных.

Подстановка $z=e^{itheta}$ даст для $$
begin{array}{l}
costheta=dfrac12left(e^{itheta}+e^{-itheta}right)
=dfrac12left(z+dfrac1zright), \
sintheta=dfrac1{2i}left(e^{itheta}-e^{-itheta}right)
=dfrac{-i}2left(z-dfrac1zright), \ dtheta=dfrac{dz}{iz}
end{array}
$$ и превратит вещественный интеграл в комплексный. При изменении $theta$ от $0$ до $2pi$ комплексная переменная пробегает
замкнутый контур — окружность $|z|=1$ в положительном направлении. Окончательно интеграл примет вид $$
I=frac1iointlimits_{|z|=1}Fleft(z+frac1z,z-frac1zright)
frac{dz}{z},.
$$

Вычислить интеграл
$$
intlimits_0^{2pi}frac{dx}{a+cos x},quad a>1.
$$

Р е ш е н и е.

Положим $e^{ix}=z$. При изменении $x$ от 0 до $2pi$ переменная $z$ пробегает окружность $|z|=1$ в положительном направлении.
Выразим $$
cos x=frac12left(e^{ix}+e^{-ix}right)=frac{z^2+1}{2z},
$$ и $$ dz=ie^{ix}dx=izdx,quadhbox{откуда}quad dx=frac{dz}{iz}. $$ Тогда $$
I=ointlimits_{|z|=1}frac{dz}{izleft(cfrac{z^2+1}{2z}+aright)} =frac2iointlimits_{|z|=1}frac{dz}{z^2+2az+1}. $$

Корни знаменателя $z_1=-a+sqrt{a^2-1}$, $z_2=-a-sqrt{a^2-1}$ — простые полюсы, $|z_1|<1$ и $z_1$ лежит внутри круга $|z|=1$: $$
mbox{Res }f(z_1)=frac1{z-z_2}Big|_{z=z_1}=frac1{2sqrt{a^2-1}}.
$$ Исходный интеграл равен $dfrac2icdotdfrac{2pi i}{2sqrt{a^2-1}} =dfrac{2pi}{sqrt{a^2-1}}$.

О т в е т:
$dfrac{2pi}{sqrt{a^2-1}}$.

II. Несобственный интеграл от рациональной функции $I=intlimits_{-infty}^infty R(x),dx=intlimits_{-infty}^infty frac{P_m(x)}{Q_n(x)},dx$,

где $P_m(x)$ и $Q_n(x)$ — многочлены степеней $m$ и $n$ соответственно.

Если знаменатель $Q_n(x)$ не имеет нулей на действительной оси, и $ngeqslant m+2$, тогда
begin{equation*}
intlimits_{-infty}^infty R(x),dx = 2pi mathbf i sumlimits_{k=1}^n mbox{Res }R(z_k),
end{equation*}
где вычеты берутся во всех полюсах $z_k$ функции $R(z)$, расположенных в верхней полуплоскости $mbox{Im }z>0$.

Вычислить интеграл $ I=intlimits_{-infty}^inftyfrac{dx}{x^4+1}.$

Р е ш е н и е.

Аналитическое продолжение подынтегральной функции в верхнюю полуплоскость, а именно функция $$ f(z)=frac1{z^4+1}, $$
удовлетворяет всем условиям, относящимся к вычислению интегралов с помощью вычетов. Особыми точками
функции в верхней полуплоскости являются точки $$ z_k=e^{tfrac{ipi}4(2k+1)},quad k=0,1, $$ причем обе эти точки — полюсы 1-го порядка.
Поэтому $$ I=2pi isumlimits_{k=0}^1 mbox{Res }f(z_k)=frac{pisqrt2}2. $$

III. Несобственные интегралы вида $I=intlimits_{-infty}^infty R(x)cos{lambda x},dx, ,, I=intlimits_{-infty}^infty R(x)sin{lambda x},dx$,

где $R(x)=P_m(x)/Q_n(x)$ — правильная рациональная дробь, не имеющая особых точек на действительной оси. Тогда
begin{equation*}
intlimits_{-infty}^infty R(x)cos{lambda x},dx = mbox{Re }left( 2pi mathbf i sumlimits_{k}
mbox{Res }R(z_k)e^{mathbf i lambda z_k}right),
end{equation*}
begin{equation*}
intlimits_{-infty}^infty R(x)sin{lambda x},dx = mbox{Im }left( 2pi mathbf i sumlimits_{k}
mbox{Res }R(z_k)e^{mathbf i lambda z_k}right),
end{equation*}
где вычеты берутся во всех полюсах $z_k$ функции $R(z)$, расположенных в верхней полуплоскости $mbox{Im }z>0$.

Интегралы вычисляются с помощью леммы Жордана:

Лемма Жордана

Пусть функция $f(z)$ аналитична в полуплоскости $mbox{Im }z>0$, за исключением конечного числа изолированных особых точек, и пусть
$M(R)$ есть максимум модуля $f(z)$ на полуокружности $gamma_{R}={zin mathbb C_{}: |z|=R, mbox{Im } z >0 }$.

Если $M(R)to0$ при $Rtoinfty$, то для любого действительного числа $lambda>0$
$$
intlimits_{gamma_R}f(z)e^{mathbf i lambda z},dzto0quadhbox{при}quad
Rtoinfty, $$

Для $lambda<0$ в условиях леммы нужно заменить верхнюю полуплоскость на нижнюю и соответственно верхнюю полуокружность на нижнюю.

Вычислить интеграл $ I=intlimits_{-infty}^inftyfrac{cosalpha x}{x^2+a^2},dx,, a>0, alpha>0$.

Р е ш е н и е.

Чтобы иметь возможность воспользоваться леммой Жордана, заметим, что в силу формулы Эйлера $$ I=mbox{Re }I_1
=mbox{Re}intlimits_{-infty}^infty frac{e^{mathbf i alpha x}} {x^2+a^2},dx. $$

Аналитическое продолжение подынтегральной функции интеграла $I_1$ — функция $dfrac{e^{mathbf i alpha z}}{z^2+a^2}$ имеет в верхней полуплоскости единственную особую точку $z_1=ia$, являющуюся простым полюсом. Поэтому по основной теореме о вычетах $$ I_1=2pi
mathbf i mbox{Res }left(frac{e^{mathbf i alpha z}}{z^2+a^2}Big|_{z=mathbf i a}
right)=fracpi{a}e^{-alpha a}quadhbox{и}quad
I=fracpi{a}e^{-alpha a}. $$

Логарифмический вычет. Принцип аргумента

Логарифмической производной функции $f(z)$ называется производная ее логарифма $left(ln {f(z)}right)’= frac{f'(z)}{f(z)}$.

Пусть $z_0$ — нуль порядка $n$, $z_1$ — полюс порядка $p$.
Запишем разложения в ряд Лорана логарифмической производной в окрестности нуля и полюса функции $f(z)$.
$$
left(ln {f(z)}right)’= frac{n}{z-z_0}+b_1+b_2(z-z_0)+dots quad Rightarrow
$$
$n$-кратный нуль функции $f(z)$ является для логарифмической производной простым полюсом, причем вычет логарифмической производной в этой точке равен кратности нуля, то есть $n$.
$$
left(ln {f(z)}right)’= frac{-p}{z-z_1}+c_1+c_2(z-z_1)+dots quad Rightarrow
$$
$p$-кратный полюс функции $f(z)$ является для логарифмической производной простым полюсом, причем вычет логарифмической производной в этой точке равен порядку полюса, взятому с обратным знаком, то есть $-p$.

Логарифмическим вычетом функции $f(z)$ в точке $z=a$ называется вычет ее логарифмической производной $ frac{f'(z)}{f(z)}$ в этой точке, т.е. значение
$$
mbox{Res }frac{f'(z)}{f(z)}=frac{1}{2pi mathbf i}ointlimits_{L} frac{f'(z)}{f(z)}dz,
$$
где в качестве контура $L$ интегрирования можно взять любую окружность с центром в точке $z=a$, целиком лежащую в указанной проколотой окрестности этой точки.

Если $f(z)$ является аналитической функцией на замкнутом контуре $L$ и не имеет нулей на этом контуре, то значение
$$
mbox{Res } frac{f'(z)}{f(z)}=frac{1}{2pi mathbf i}ointlimits_{L} frac{f'(z)}{f(z)}dz
$$
называют логарифмическим вычетом функции $f(z)$ относительно контура $L$.

Теорема о логарифмическом вычете

Логарифмический вычет многочлена $P_n(z)$ степени $n$ относительно контура $L$, на котором нет нулей $P_n(z)$, равен числу нулей многочлена (с учетом их кратности) внутри контура.

Принцип аргумента

Пусть непостоянная функция $f(z)$ аналитична всюду в односвязной области $D$ и на ее границе — кусочно-гладком контуре $L$, кроме, возможно, некоторого конечного числа полюсов. Пусть также функция имеет конечное число нулей, причем на контуре $L$ нет ни нулей, ни полюсов функции. Тогда приращение аргумента функции $f(z)$ при обходе в положительном направлении контура $L$ равно произведению $2pi$ на разность числа нулей и полюсов функции $f(z)$, расположенных в области $D$, причем каждый нуль следует считать сколько раз, какова его кратность, а каждый полюс — каков его порядок.
$$
Delta_Larg f(z)=2pi(N-P),
$$
$$
N=q_1+q_2+ldots+q_m, quad P=p_1+p_2+ldots+p_k,
$$
$q_i$ — кратность нуля $a_i$, $i=1,ldots,m$, $p_j$ — кратность полюса $b_j$, $j=1,ldots,k$.

Теорема Руше

Пусть функции $f(z)$ и $varphi(z)$ являются аналитическими в замкнутой области $D$, причем на границе $C$ этой области имеет место неравенство: $|f(z)|_{C}>|varphi(z)|_{C}$. Тогда полное число нулей (с учетом их кратности) в $D$ функции $F(z)=f(z)+varphi(z)$ равно полному числу нулей (с учетом их кратности) функции $f(z)$.

Найти число нулей функции $F(z)=z^8-4z^5+z^2-1$ в единичном круге.

Пусть $f(z)=-4z^5$, $varphi(z)=z^8+z^2-1$. Граница $C$ заданной области — единичный круг $|z|=1$.

$$
|z|=1: ,, begin{aligned} &|f(z)=|-4z^5|=4|z|^5=4, \ &|varphi(z)|leqslant|z|^8+|z|^2+1=3 ,, Rightarrow \ &|f(z)|>|varphi(z)| end{aligned}.
$$

Выполнены все условия теоремы Руше. Функция $f(z)$ имеет корень $z=0$ кратности $5$, лежащий в $|z|<1$. Значит, $F(z)=f(z)+varphi(z)$ имеет пять нулей в единичном круге.

Найти число корней уравнения $z^4-8z+10=0$ в кольце 1<|z|<3

Найдем число корней $N_1$ в области $|z|<1$ и число корней $N_2$ в области $|z|<3$. Тогда число корней в кольце 1<|z|<3 будет равно $N=N_2-N_1$.

а) $|z|<1$.

Пусть $F(z)=f(z)+varphi(z)$, где $f(z)=10$, $varphi(z)=z^4-8z$.
На границе $C$ единичного круга имеем:
$$
|z|=1: ,, |f(z)|=10, |varphi(z)|leqslant|z|^4+8|z|=9,, Rightarrow ,, |f(z)>|varphi(z)|.
$$
Выполнены все условия теоремы Руше. Функция $f(z)$ в области $|z|<1$ не имеет нулей. Следовательно и уравнение $F(z)=0$ не имеет корней в единичном круге. $N_1=0$.

б) $|z|<3$.

В итоге получаем: $N=N_2-N_1=4-0=4$

Источник

Изолированные особые точки функций и полюсы

Классификация особых точек

Типы особых точек функции

Теоремы Сохоцкого и Пикара

Ряд Лорана в окрестности особой точки

Правила определения порядка полюса

Определение порядка полюса в бесконечно удаленной точке

Определение типа особых точек для суммы, разности, произведения и частного функций

BA3a
for love and rock-n-roll
VIP

Sean33
агрессия и злоба
Модератор
VIP

Поделиться этой страницей

Вычисление вычетов

Определение порядка полюса

Вычисление интегралов

Как узнать сколько полюсов у двигателя?

Чему равна синхронная скорость асинхронного двигателя с одной парой полюсов?

Чем больше пар полюсов?

Как определить частоту вращения двигателя?

Как определить синхронную скорость?

Чему пропорционален вращающий момент?

Как посчитать частоту вращения вала?

Какое количество полюсов должно быть у синхронного генератора имеющего частоту тока 50 Гц?

Как узнать мощность электродвигателя мультиметром?

Как определить частоту вращения магнитного поля?

Содержание

Глава 6. Вычеты функций и их применение

Вычет функции относительно изолированной особой точки. Основная теорема о вычетах

Вычисление вычетов в конечных особых точках

О бесконечно удаленной точке $z=infty$

Вычисление определенных интегралов с помощью вычетов

I. Интеграл вида $I=intlimits_0^{2pi}R(cos{x},sin{x}),dx,$

II. Несобственный интеграл от рациональной функции $I=intlimits_{-infty}^infty R(x),dx=intlimits_{-infty}^infty frac{P_m(x)}{Q_n(x)},dx$,

III. Несобственные интегралы вида $I=intlimits_{-infty}^infty R(x)cos{lambda x},dx, ,, I=intlimits_{-infty}^infty R(x)sin{lambda x},dx$,

Лемма Жордана

Логарифмический вычет. Принцип аргумента

Теорема Руше

Изолированные особые точки функций и полюсы

Классификация особых точек

Типы особых точек функции

Теоремы Сохоцкого и Пикара

Ряд Лорана в окрестности особой точки

Правила определения порядка полюса

Определение порядка полюса в бесконечно удаленной точке

Определение типа особых точек для суммы, разности, произведения и частного функций

BA3a for love and rock-n-roll VIP

Sean33 агрессия и злоба Модератор VIP

Поделиться этой страницей

Вычисление вычетов

Определение порядка полюса

Вычисление интегралов

Как узнать сколько полюсов у двигателя?

Чему равна синхронная скорость асинхронного двигателя с одной парой полюсов?

Чем больше пар полюсов?

Как определить частоту вращения двигателя?

Как определить синхронную скорость?

Чему пропорционален вращающий момент?

Как посчитать частоту вращения вала?

Какое количество полюсов должно быть у синхронного генератора имеющего частоту тока 50 Гц?

Как узнать мощность электродвигателя мультиметром?

Как определить частоту вращения магнитного поля?

Содержание

Глава 6. Вычеты функций и их применение

Вычет функции относительно изолированной особой точки. Основная теорема о вычетах

Вычисление вычетов в конечных особых точках

О бесконечно удаленной точке $z=infty$

Вычисление определенных интегралов с помощью вычетов

I. Интеграл вида $I=intlimits_0^{2pi}R(cos{x},sin{x}),dx,$

II. Несобственный интеграл от рациональной функции $I=intlimits_{-infty}^infty R(x),dx=intlimits_{-infty}^infty frac{P_m(x)}{Q_n(x)},dx$,

III. Несобственные интегралы вида $I=intlimits_{-infty}^infty R(x)cos{lambda x},dx, ,, I=intlimits_{-infty}^infty R(x)sin{lambda x},dx$,

Лемма Жордана

Логарифмический вычет. Принцип аргумента

Теорема Руше

BA3a
for love and rock-n-roll
VIP

Sean33
агрессия и злоба
Модератор
VIP