D
= seqpdist(Seqs)
D
=
seqpdist
(Seqs,
…’Method’, MethodValue, …)
Описание
D
=
seqpdist
(Seqs)
возвращает вектор D,
содержащий
биологического
расстояния
между
каждой парой
последовательностей
хранятся
в
М
последовательностей массива данных
Seqs.
D
состоит
из 1-by-(M*(M-1)/2)
строк,
соответствующих
M*(M-1)/2
парам
последовательностей
в
массиве Seqs.
Выходной
параметр
D
ранжирован
по следующему порядку
((2,1),
(3,1
),…,
(M,
1), (3,2
),…(
М,
2
),…(
М,
М-1)).
Это
левый
нижний
треугольник
полной
дистанционной
матрицы. Чтобы
получить
расстояние
между
I-ой
и
J-ой
последовательностями
для
I>
J,
необходимо использовать формулу
расчёта расстояний
D((J-1)*(M-J/2)+I-J).
D
=
seqpdist
(Seqs,
…’Method’,
MethodValue,
…) указывается
метод
вычисления
расстояний
между
каждой
последовательности
пары.
Варианты
методов
представлены
в
следующих
таблицах 6 – 9.
Таблица
6
|
Аргумент |
Описание |
|
MethodValue |
Строка, |
|
IndelsValue |
Строка, |
|
PairwiseAlignmentValue |
Управление
true false |
|
AlphabetValue |
Строка, |
|
ScoringMatrixValue |
Строка ‘BLOSUM62’ ‘BLOSUM30’ ‘BLOSUM100’
‘PAM10 ‘DAYHOFF’ ‘GONNET’
По
‘BLOSUM50’ ‘NUC44’ |
Таблица
7
Методы,
используемые для нуклеотидных и
аминокислотных последовательностей
|
Метод |
Описание |
|
p-distance |
Количественное |
|
Jukes-Cantor |
Оценка
d
Для
d |
|
alignment-score |
Расстояние Это |
Таблица
8
Методы,
используемые только для нуклеотидных
последовательностей
|
Метод |
Описание |
|
Kimura |
Отдельно |
|
Tamura |
Отдельно |
Таблица
9
Методы,
используемые только для аминокислотных
последовательностей
|
Метод |
Описание |
|
Poisson |
Расчёт |
|
Gamma |
Расчёт |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
�������
��� �������� ���������� ����� �������� ������� � ������������
����� 1. ������� ���������� �� ����� �� ���� ����� �� ���������,
������������ ����� �������.
�������
����� A , B , C � D – �����, �������� ���������� ����� ��������
����� 1. ���������� ����������� �������� ABCD � �������� D . �
��������� – �������������� ����������� ABC . ������� ң��� DA , DB
� DC ���� �������� ����� ����� �����, ������� ţ ������ DO ��������
����� ����� O ���������� ��������� ����� ��������� ABC , �.�. �����
����� ��������������� ������������ ABC �� �������� 1.
����� M – �������� ������� BC . �����
AM = AB sin ABM = AB sin 60o = 1·
= ,
AO = AM =
·
=
.
��������� DO – ������ ��������, ���������� �� ����� D �� ���������
ABC ����� ����� ������� DO . �� �������������� ������������ AOD
�������, ���
DO = =
=
=
.
����, ��� ��������� ������� ���������� ����� ����� .
�����
.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 8179 |
pdist
Pairwise distance between pairs of observations
Syntax
Description
example
D = pdist(X)
returns the Euclidean distance between pairs of observations in
X.
example
D = pdist(X,Distance)
returns the distance using the method specified by Distance.
example
D = pdist(X,Distance,DistParameter)
returns the distance using the method specified by Distance and
DistParameter. You can specify
DistParameter only when Distance is
'seuclidean', 'minkowski', or
'mahalanobis'.
example
D = pdist(X,Distance,CacheSize=cache)
or
D = pdist(X,Distance,DistParameter,CacheSize=cache)
uses a cache of size cache megabytes to accelerate the
computation of Euclidean distances. This argument applies only when
Distance is 'fasteuclidean',
'fastsquaredeuclidean', or
'fastseuclidean'.
Examples
collapse all
Compute Euclidean Distance and Convert Distance Vector to Matrix
Compute the Euclidean distance between pairs of observations, and convert the distance vector to a matrix using squareform.
Create a matrix with three observations and two variables.
rng('default') % For reproducibility X = rand(3,2);
Compute the Euclidean distance.
D = 1×3
0.2954 1.0670 0.9448
The pairwise distances are arranged in the order (2,1), (3,1), (3,2). You can easily locate the distance between observations i and j by using squareform.
Z = 3×3
0 0.2954 1.0670
0.2954 0 0.9448
1.0670 0.9448 0
squareform returns a symmetric matrix where Z(i,j) corresponds to the pairwise distance between observations i and j. For example, you can find the distance between observations 2 and 3.
Pass Z to the squareform function to reproduce the output of the pdist function.
y = 1×3
0.2954 1.0670 0.9448
The outputs y from squareform and D from pdist are the same.
Compute Minkowski Distance
Create a matrix with three observations and two variables.
rng('default') % For reproducibility X = rand(3,2);
Compute the Minkowski distance with the default exponent 2.
D1 = pdist(X,'minkowski')
D1 = 1×3
0.2954 1.0670 0.9448
Compute the Minkowski distance with an exponent of 1, which is equal to the city block distance.
D2 = pdist(X,'minkowski',1)
D2 = 1×3
0.3721 1.5036 1.3136
D3 = pdist(X,'cityblock')
D3 = 1×3
0.3721 1.5036 1.3136
Compute Pairwise Distance with Missing Elements Using a Custom Distance Function
Define a custom distance function that ignores coordinates with NaN values, and compute pairwise distance by using the custom distance function.
Create a matrix with three observations and two variables.
rng('default') % For reproducibility X = rand(3,2);
Assume that the first element of the first observation is missing.
Compute the Euclidean distance.
If observation i or j contains NaN values, the function pdist returns NaN for the pairwise distance between i and j. Therefore, D1(1) and D1(2), the pairwise distances (2,1) and (3,1), are NaN values.
Define a custom distance function naneucdist that ignores coordinates with NaN values and returns the Euclidean distance.
function D2 = naneucdist(XI,XJ) %NANEUCDIST Euclidean distance ignoring coordinates with NaNs n = size(XI,2); sqdx = (XI-XJ).^2; nstar = sum(~isnan(sqdx),2); % Number of pairs that do not contain NaNs nstar(nstar == 0) = NaN; % To return NaN if all pairs include NaNs D2squared = sum(sqdx,2,'omitnan').*n./nstar; % Correction for missing coordinates D2 = sqrt(D2squared);
Compute the distance with naneucdist by passing the function handle as an input argument of pdist.
D2 = pdist(X,@naneucdist)
D2 = 1×3
0.3974 1.1538 0.9448
Accelerate Euclidean Distance Computation Using fasteuclidean Distance
Create a large matrix of points, and then measure the time used by pdist with the default «euclidean" distance metric.
rng default % For reproducibility N = 10000; X = randn(N,1000); D = pdist(X); % Warm up function for more reliable timing information tic D = pdist(X); standard = toc
Next, measure the time used by pdist with the "fasteuclidean" distance metric. Specify a cache size of 10.
D = pdist(X,"fasteuclidean",CacheSize=10); % Warm up function tic D2 = pdist(X,"fasteuclidean",CacheSize=10); accelerated = toc
Evaluate how many times faster the accelerated computation is compared to the standard.
The accelerated version computes about three times faster for this example.
Input Arguments
collapse all
X — Input data
numeric matrix
Input data, specified as a numeric matrix of size
m-by-n. Rows correspond to
individual observations, and columns correspond to individual
variables.
Data Types: single | double
Distance — Distance metric
character vector | string scalar | function handle
Distance metric, specified as a character vector, string scalar, or
function handle, as described in the following table.
| Value | Description |
|---|---|
'euclidean' |
Euclidean distance (default) |
'squaredeuclidean' |
Squared Euclidean distance. (This option is provided |
'seuclidean' |
Standardized Euclidean distance. Each coordinate difference between observations is |
'fasteuclidean' |
Euclidean distance computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. Algorithms starting with 'fast' do not support sparse data. For details, see Algorithms. |
'fastsquaredeuclidean' |
Squared Euclidean distance computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. Algorithms starting with 'fast' do not support sparse data. For details, see Algorithms. |
'fastseuclidean' |
Standardized Euclidean distance computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. Algorithms starting with 'fast' do not support sparse data. For details, see Algorithms. |
'mahalanobis' |
Mahalanobis distance, computed using the sample covariance of |
'cityblock' |
City block distance |
'minkowski' |
Minkowski distance. The default exponent is 2. Use |
'chebychev' |
Chebychev distance (maximum coordinate difference) |
'cosine' |
One minus the cosine of the included angle between points (treated as |
'correlation' |
One minus the sample correlation between points (treated as sequences of |
'hamming' |
Hamming distance, which is the percentage of coordinates that differ |
'jaccard' |
One minus the Jaccard coefficient, which is the percentage of nonzero coordinates that |
'spearman' |
One minus the sample Spearman’s rank correlation between observations |
@ |
Custom distance function handle. A distance function has the form function D2 = distfun(ZI,ZJ) % calculation of distance ... where
If your data is not sparse, you can generally |
For definitions, see Distance Metrics.
When you use 'seuclidean',
'minkowski', or 'mahalanobis', you
can specify an additional input argument DistParameter
to control these metrics. You can also use these metrics in the same way as
the other metrics with the default value of
DistParameter.
Example:
'minkowski'
Data Types: char | string | function_handle
Distance metric parameter values, specified as a positive scalar, numeric vector, or
numeric matrix. This argument is valid only when you specify
Distance as 'seuclidean',
'minkowski', or 'mahalanobis'.
-
If
Distanceis'seuclidean',
DistParameteris a vector of scaling factors for
each dimension, specified as a positive vector. The default value is
std(X,'omitnan'). -
If
Distanceis'minkowski',
DistParameteris the exponent of Minkowski
distance, specified as a positive scalar. The default value is 2. -
If
Distanceis'mahalanobis',
DistParameteris a covariance matrix, specified as
a numeric matrix. The default value iscov(X,'omitrows').
DistParametermust be symmetric and positive
definite.
Example:
'minkowski',3
Data Types: single | double
cache — Size of Gram matrix in megabytes
1e3 (default) | positive scalar | "maximal"
Size of the Gram matrix in megabytes, specified as a positive scalar or
"maximal". The pdist
function can use CacheSize=cache only when the
Distance argument is
'fasteuclidean',
'fastsquaredeuclidean', or
'fastseuclidean'.
If cache is "maximal",
pdist tries to allocate enough memory for an
entire intermediate matrix whose size is
M-by-M, where M
is the number of rows of the input data X. The cache
size does not have to be large enough for an entire intermediate matrix, but
must be at least large enough to hold an M-by-1 vector.
Otherwise, pdist uses the standard algorithm for
computing Euclidean distances.
If the distance argument is 'fasteuclidean',
'fastsquaredeuclidean', or
'fastseuclidean' and the cache
value is too large or "maximal",
pdist might try to allocate a Gram matrix
that exceeds the available memory. In this case, MATLAB® issues an error.
Example: "maximal"
Data Types: double | char | string
Output Arguments
collapse all
D — Pairwise distances
numeric row vector
Pairwise distances, returned as a numeric row vector of length
m(m–1)/2, corresponding to pairs
of observations, where m is the number of observations in
X.
The distances are arranged in the order (2,1), (3,1), …,
(m,1), (3,2), …, (m,2), …,
(m,m–1), i.e., the lower-left
triangle of the m-by-m distance matrix
in column order. The pairwise distance between observations
i and j is in
D((i-1)*(m-i/2)+j-i) for i≤j.
You can convert D into a symmetric matrix by using
the squareform function.
Z = squareform(D) returns an
m-by-m matrix where
Z(i,j) corresponds to the pairwise distance between
observations i and j.
If observation i or j contains
NaNs, then the corresponding value in
D is NaN for the built-in
distance functions.
D is commonly used as a dissimilarity matrix in
clustering or multidimensional scaling. For details, see Hierarchical Clustering and the function reference pages for
cmdscale, cophenet, linkage, mdscale, and optimalleaforder. These
functions take D as an input argument.
More About
collapse all
Distance Metrics
A distance metric is a function that defines a distance between
two observations. pdist supports various distance
metrics: Euclidean distance, standardized Euclidean distance, Mahalanobis distance,
city block distance, Minkowski distance, Chebychev distance, cosine distance,
correlation distance, Hamming distance, Jaccard distance, and Spearman
distance.
Given an m-by-n data matrix
X, which is treated as m
(1-by-n) row vectors
x1,
x2, …,
xm, the various distances between
the vector xs and
xt are defined as follows:
-
Euclidean distance
The Euclidean distance is a special case of the Minkowski distance,
where p = 2. -
Standardized Euclidean distance
where V is the
n-by-n diagonal matrix whose
jth diagonal element is
(S(j))2,
where S is a vector of scaling factors for each
dimension. -
Mahalanobis distance
where C is the covariance matrix.
-
City block distance
The city block distance is a special case of the Minkowski distance,
where p = 1. -
Minkowski distance
For the special case of p = 1, the Minkowski distance gives the city block distance.
For the special case of p = 2, the Minkowski distance gives the Euclidean distance.
For the special case of p = ∞, the Minkowski distance gives the Chebychev
distance. -
Chebychev distance
The Chebychev distance is a special case of the Minkowski distance,
where p = ∞. -
Cosine distance
-
Correlation distance
where
x¯s=1n∑jxsj and x¯t=1n∑jxtj.
-
Hamming distance
-
Jaccard distance
-
Spearman distance
where
-
rsj is the rank
of xsj taken over
x1j,
x2j,
…xmj, as
computed bytiedrank. -
rs and
rt are the
coordinate-wise rank vectors of
xs and
xt, i.e.,
rs = (rs1,
rs2,
… rsn). -
r¯s=1n∑jrsj=(n+1)2.
-
r¯t=1n∑jrtj=(n+1)2.
-
Algorithms
collapse all
Fast Euclidean Distance Algorithm
The values of the Distance argument that begin
fast (such as 'fasteuclidean' and
'fastseuclidean') calculate Euclidean distances using an
algorithm that uses extra memory to save computational time. This algorithm is named
«Euclidean Distance Matrix Trick» in Albanie [1] and elsewhere.
Internal testing shows that this algorithm saves time when the number of predictors
is at least 10.
To find the matrix D of distances between all the points
xi and
xj, where each
xi has n
variables, the algorithm computes distance using the final line in the following
equations:
The matrix xiTxj in the last line of the equations is called the Gram
matrix. Computing the set of squared distances is faster, but
slightly less numerically stable, when you compute and use the Gram matrix instead
of computing the squared distances by squaring and summing. For a discussion, see
Albanie [1].
To store the Gram matrix, the software uses a cache with the default size of
1e3 megabytes. You can set the cache size using the
cache argument. If the value of cache is
too large or "maximal", pdist might
try to allocate a Gram matrix that exceeds the available memory. In this case,
MATLAB issues an error.
References
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
-
The distance input argument value (
Distance) must
be a compile-time constant. For example, to use the Minkowski distance,
includecoder.Constant('Minkowski')in the
-argsvalue ofcodegen. -
The distance input argument value (
Distance)
cannot be a custom distance function. -
pdistdoes not support code generation for fast Euclidean
distance computations, meaning those distance metrics whose names begin with
fast(for example,'fasteuclidean'). -
The generated code of
pdistusesparfor(MATLAB Coder) to create loops that run in
parallel on supported shared-memory multicore platforms in the generated code. If your compiler
does not support the Open Multiprocessing (OpenMP) application interface or you disable OpenMP
library, MATLAB
Coder™ treats theparfor-loops asfor-loops. To find supported compilers, see Supported Compilers.
To disable OpenMP library, set theEnableOpenMPproperty of the
configuration object tofalse. For
details, seecoder.CodeConfig(MATLAB Coder).
For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
-
The supported distance input argument values
(Distance) for optimized CUDA code are
'euclidean',
'squaredeuclidean',
'seuclidean','cityblock',
'minkowski','chebychev',
'cosine','correlation',
'hamming', and
'jaccard'. -
Distancecannot be a custom distance
function. -
Distancemust be a compile-time constant.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes and limitations:
-
The distance input argument value (
Distance) cannot
be a custom distance function.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2023a: Fast Euclidean distance using a cache
The 'fasteuclidean', 'fastseuclidean', and
'fastsquaredeuclidean' distance metrics accelerate the
computation of Euclidean distances by using a cache and a different algorithm (see
Algorithms). Set the size
of the cache using the cache argument.
#python-3.x #scipy #geometry
#python-3.x #scipy #геометрия
Вопрос:
Я ищу помощь в рабочем процессе, который, учитывая произвольное количество точек в плоскости (x, y), может найти все отрезки, которые соединяют 2 (и только 2) точки. Моя первая мысль — использовать scipy.spatial.distance.pdist() , чтобы получить все уникальные попарные расстояния, затем для каждого расстояния между двумя точками проверить, являются ли какие-либо другие точки коллинеарными. Я могу представить, что этот подход становится неэффективным при большом количестве точек, поэтому я хочу знать, знает ли кто-нибудь более эффективный способ решения этой проблемы.
Вопрос громоздкий, поэтому я приведу пример. У меня есть список из 3 (x, y) координатных точек coords = [(1,1), (2,1), (3,1)] , которые образуют прямую линию, и я хочу найти длины всех отрезков, которые соединяют 2 (и только 2) точки. Для этого примера у меня есть только два отрезка длиной 1, которые соответствуют моим критериям (от (1,1) до (2,1) и (2,1) до (3,1) ). Я могу получить все попарные расстояния между точками, используя scipy.spatial.distance.pdist() , но результат этой функции включает расстояние между (1,1) и (3,1) , чего я не хочу.
Мой предпочтительный язык — Python, но я открыт для ответов на других языках программирования.
Комментарии:
1. Если я правильно понимаю, вам нужно расстояние для всех пар, которые являются соседями в списке? Или в этом есть что-то еще?
2. @user3184950 Вы могли бы так выразиться, да. Я не сформулировал это таким образом, потому что «соседи» обычно предполагают ближайших соседей, что не входило в мои намерения. Вы можете рассматривать это как идентификацию соседних точек, если линия между этими двумя точками не пересекает третью точку.
3. Мне все еще неясно, есть ли какая-либо разница, если 10 точек находятся на прямой линии или случайной прогулке. Есть ли какая-либо разница в выборе пар, по которым вы хотите рассчитать расстояние?
4. @user3184950 Меня интересуют смежные пары точек в 2 измерениях, независимо от расстояния между этими точками. Для 10 точек на прямой я бы получил 9 расстояний. Если эти 10 точек случайным образом разбросаны по 2D-сетке, и ни одна линия не соединит более двух точек, то каждая точка может рассматривать любую другую точку как соседнюю.
5. bowdoin.edu /~ltoma/обучение / cs3250-CompGeom /spring17 /Лекции / … Алгоритм 2 кажется простым в реализации, надеюсь, достаточно быстрым для вашего набора данных
Законы больших чисел показывают, во-первых, что медиана Кемени обладает устойчивостью по отношению к незначительному изменению состава экспертной комиссии; во-вторых, при увеличении числа экспертов она приближается к некоторому пределу. Его естественно рассматривать как истинное мнение экспертов, от которого каждый из них несколько отклонялся по случайным причинам. Рассматриваемый здесь закон больших чисел является обобщением известного в статистике «классического» закона больших чисел. Он основан на иной математической базе — теории оптимизации, в то время как «классический» закон больших чисел использует суммирование. Упорядочения и другие бинарные отношения нельзя складывать, поэтому приходится применять иную математику.
Вычисление медианы Кемени — задача целочисленного программирования. В частности, для ее нахождения используется различные алгоритмы дискретной математики, в частности, основанные на методе ветвей и границ. Применяют также алгоритмы, основанные на идее случайного поиска, поскольку для каждого бинарного отношения нетрудно найти множество его соседей.
Рассмотрим упрощенный пример вычисления медианы Кемени. Пусть дана квадратная матрица (порядка 9) попарных расстояний для множества бинарных отношений из 9 элементов 
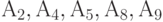
| 0 | 2 | 13 | 1 | 7 | 4 | 10 | 3 | 11 |
| 2 | 0 | 5 | 6 | 1 | 3 | 2 | 5 | 1 |
| 13 | 5 | 0 | 2 | 2 | 7 | 6 | 5 | 7 |
| 1 | 6 | 2 | 0 | 5 | 4 | 3 | 8 | 8 |
| 7 | 1 | 2 | 5 | 0 | 10 | 1 | 3 | 7 |
| 4 | 3 | 2 | 5 | 0 | 10 | 1 | 3 | 7 |
| 4 | 3 | 7 | 4 | 10 | 0 | 2 | 1 | 5 |
| 10 | 2 | 6 | 3 | 1 | 2 | 0 | 6 | 3 |
| 3 | 5 | 5 | 8 | 3 | 1 | 6 | 0 | 9 |
| 11 | 1 | 7 | 8 | 7 | 5 | 3 | 9 | 0 |
В соответствии с определением медианы Кемени следует ввести в рассмотрение функцию
рассчитать ее значения для всех 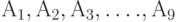
Из всех вычисленных сумм наименьшая равна 13, и достигается она при 


Контрольные вопросы и задачи
- Почему необходимо применение экспертных оценок при решении технических, организационных, экономических, экологических и иных проблем?
- Какие стадии экспертного исследования выделяет менеджер — организатор такого исследования?
- По каким основаниям классифицируют различные варианты организации экспертных исследований?
- Какова роль диссидентов в различных видах экспертиз?
- Какой вид могут иметь ответы экспертов?
- Чем метод средних арифметических рангов отличает от метода медиан рангов?
- Почему необходимо согласование кластеризованных ранжировок и как оно проводится?
- В чем состоит проблема согласованности ответов экспертов?
- Как бинарные отношения используются в экспертизах?
- Как бинарные отношения описываются матрицами из 0 и 1?
- Что такое расстояние Кемени и медиана Кемени?
- Чем закон больших чисел для медианы Кемени отличается от «классического» закона больших чисел, известного в статистике?
-
В табл. 14.4 приведены упорядочения 7 инвестиционных проектов, представленные 7 экспертами.
Таблица
14.4.
Упорядочения проектов экспертамиЭксперты Упорядочения 1 1 < {2,3} < 4 < 5 < {6,7} 2 {1,3} < 4 < 2< 5< 7 < 6 3 1 < 4 < 2 < 3 < 6 < 5 < 7 4 1 < {2, 4} < 3 < 5 < 7 <6 5 2 < 3 < 4 < 5 <1 <6 <7 6 1 < 3 < 2 < 5 < 6 < 7 < 4 7 1 < 5 < 3 < 4 < 2 < 6 < 7 Найдите:
а) итоговое упорядочение по средним арифметическим рангам;
б) итоговое упорядочение по медианам рангов;
в) кластеризованную ранжировку, согласующую эти два упорядочения.
- Выпишите матрицу из 0 и 1, соответствующую бинарному отношению (кластеризованной ранжировке)
.
- Найдите расстояние Кемени между бинарными отношениями — упорядочениями
и
.
-
Дана квадратная матрица (порядка 9) попарных расстояний (мер различия) для множества бинарных отношений из 9 элементов
(табл.14.5). Найдите в этом множестве медиану для множества из 5 элементов
.
Таблица
14.5.
Попарные расстояния между бинарными отношениями0 5 3 6 7 4 10 3 11 5 0 5 6 10 3 2 5 7 3 5 0 8 2 7 6 5 7 6 6 8 0 5 4 3 8 8 7 10 2 5 0 10 8 3 7 4 3 7 4 10 0 2 3 5 11 7 7 8 7 5 3 9 0
Темы докладов и рефератов
- Роль экспертных методов в менеджменте.
- Организация различных видов экспертных исследований.
- Сравнение очных и заочных вариантов работы экспертов.
- Методы средних баллов.
- Согласование кластеризованных ранжировок.
- Методы теории люсианов в экспертных оценках.
- Классификация мнений экспертов и проверка согласованности.
- Использование люсианов в теории и практике экспертных оценок.
- Формирование итогового мнения комиссии экспертов.
- Расстояние по Кемени и медиана Кемени в экспертных оценках.
- Законы больших чисел в пространствах нечисловой природы.



 .
.![А = [3< 2 <1< {4,5}]](https://intuit.ru/sites/default/files/tex_cache/ed401eebd7560b8beb892784d0f6d93b.png) и
и ![B = [1 < {2 ,3} < 4 < 5 ]](https://intuit.ru/sites/default/files/tex_cache/a60ac96a1fb4e798eadbfc10b78e466f.png) .
.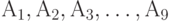 (табл.14.5). Найдите в этом множестве медиану для множества из 5 элементов
(табл.14.5). Найдите в этом множестве медиану для множества из 5 элементов 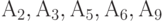 .
.