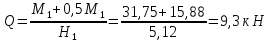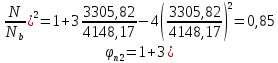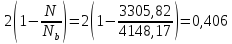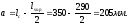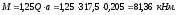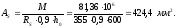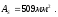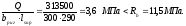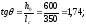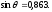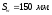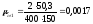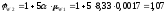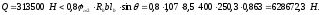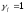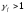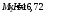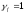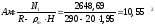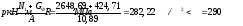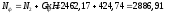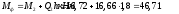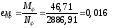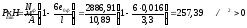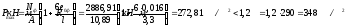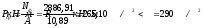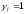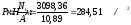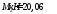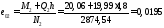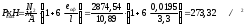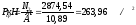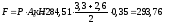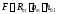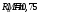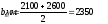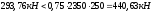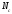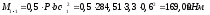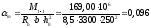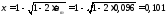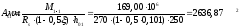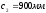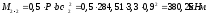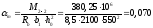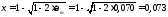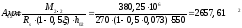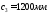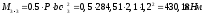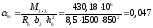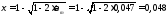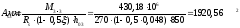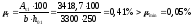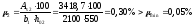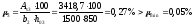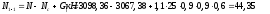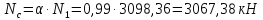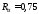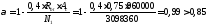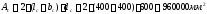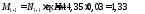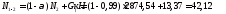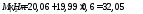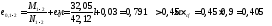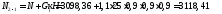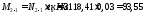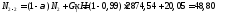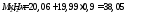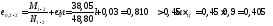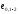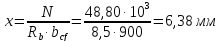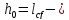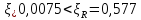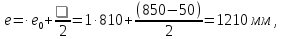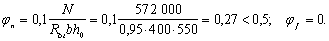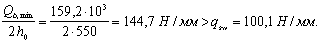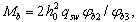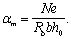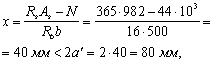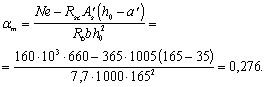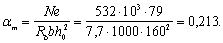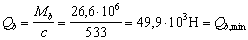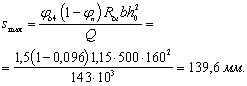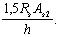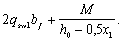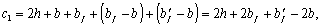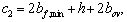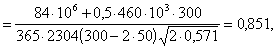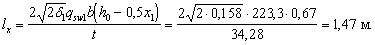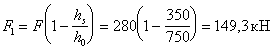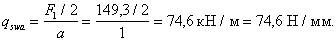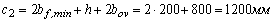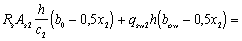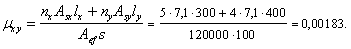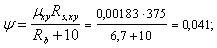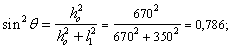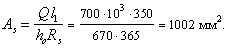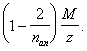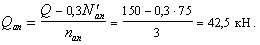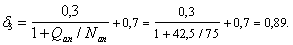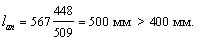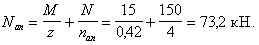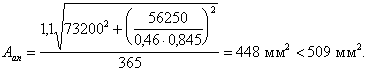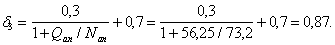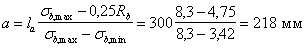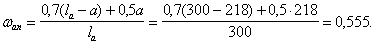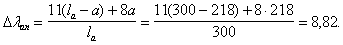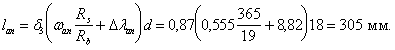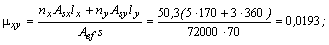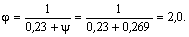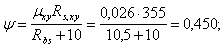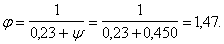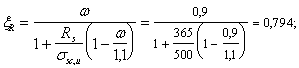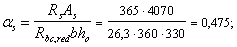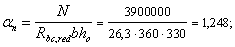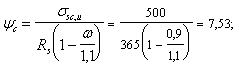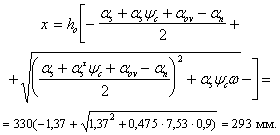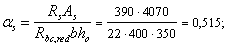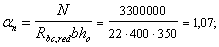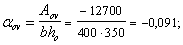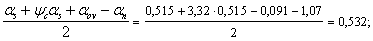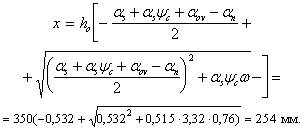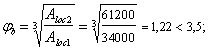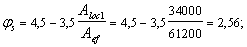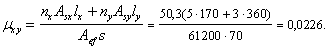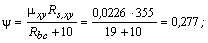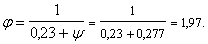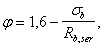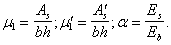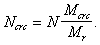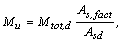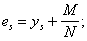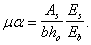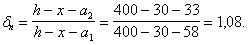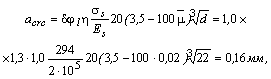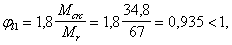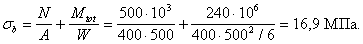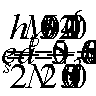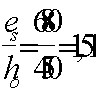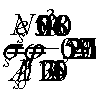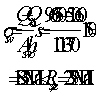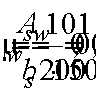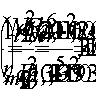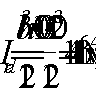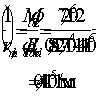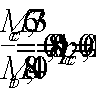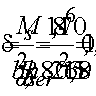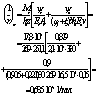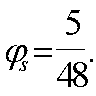Поперечная
сила в колонне равна:
Поскольку
Q
постоянна по высоте колонны С
= Сmax=
= 3∙h0
=3∙350=1050мм
< H1
= 5,12м
Поскольку
C=Cmax
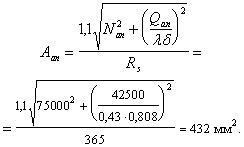
Nb
= Rb·A+RSC·
As,tot
=8,5∙4002+
355·7854 =4148,17 кН
> N
Qb,min
= 0,5Rbtbh0
= 0,5∙0,75∙400∙350 = 52500 Н
= 52,5кН
>
>
Q
= 9,3 кН
Прочность
по наклонному сечению обеспечена.
Поперечная арматура принимается по
конструктивным требованиям, то есть Ø
8 А 240 с шагом Sw
= 350мм (Sw

и Sw
Расчёт
по бетонной полосе между наклонными
сечениями:
Q=9,3
кН<0,3Rbbh0φn1
= 0,3∙8,5∙400∙350∙0,406 = 145 кН
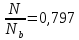
поэтому
φn1
=
Прочность
по бетонной полосе обеспечена.
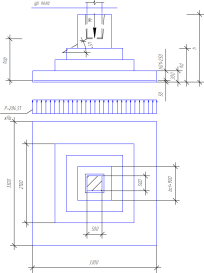
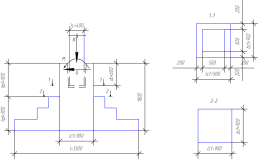
3.3. Расчет консоли колонны.
Консоль
колонны предназначены для опирания
ригеля рамы. Консоли колонны бетонируются
одновременно с её стволом, поэтому
выполняется также из тяжелого бетона
класса В15 имеем расчетное сопротивление
бетона
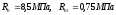
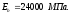
расчетное сопротивление
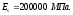
выполняется в виде горизонтальных
двухветвевых хомутов из стержней
диаметром 6 мм класса А240.
Рабочая
высота опорного сечения консоли
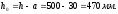
опорного сечения консоли будет:
QbЛ<Qb=φb2xRbtxbxh02/c,
где с=а=205 мм.
Qb,min=0,5Rbtxbxh0<Qb<Qmax=2,5xRbtxbxh0
Qb=790243H>480∙103H
Qb,max=2,5∙0,75∙400∙600=450∙103
H
Определяем
площадь продольной арматуры
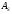
Момент в опорном сечении, взятый с
коэффициентом 1,25 равен:
Площадь
сечения арматуры будет равна:
Принимаем
2
Расчет
консоли по СНиП2.03.01-84
h1=650-350=300
мм >h/3=200 мм
h0=h-a=650-50=600
мм
Проверяем
условие прочности по наклонной сжатой
полосе:
Принимаем
шаг горизонтальных хомутов
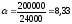
Проверяем
условие прочности:
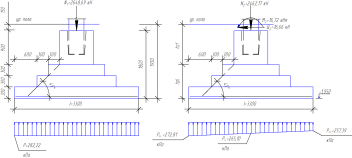
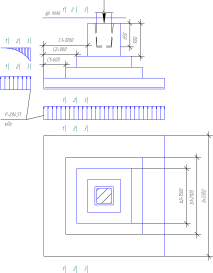
4. Расчет фундаментов под колонны
Требуется
рассчитать железобетонный фундамент
под среднюю колонну.
Исходные
данные: Бетон В15, арматура А400,
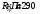
h=1,8м, H=1,95 м.
Усилия:
—
первая схема загружения
—
вторая схема загружения
6.1.
Определение размеры подошвы фундамента
от усилий при
—
первая схема загружения
Принимаем
b=l=3,3м, A=10,89 м2, Gф=20·10,89·1,95=424,71 кН.
—
вторая схема загружения
Принятые
размеры подошвы фундамента удовлетворяют
обеим схемам загружения.
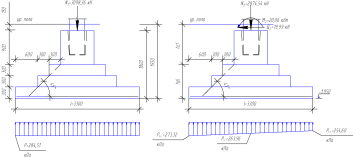
Рисунок
17 – Эпюры напряжений под подошвой
фундамента от нагрузок при
6.2.
Расчет фундамента на прочность
6.2.1.Определение
напряжений в грунте под подошвой
фундамента
От
первого сочетания усилий
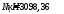
М1=0
От
второго сочетания усилий
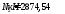
Q2=19,99
кН
Рисунок
18 — Эпюры напряжений под подошвой
фундамента от расчетных нагрузок
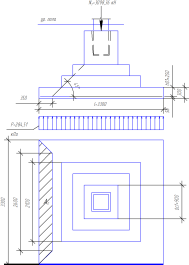
6.2.2
Расчет на продавливание плитной части
фундамента
Анализируя
полученные эпюры давления Р, дальнейший
расчет плитной части производим от
первого сочетания усилий.
Рисунок
19 — Схема образования пирамиды продавливания
плитной части фундамента
Продавливающая
сила:
Условие
прочности:
Прочность
нижней ступени на продавливание
достаточна.
6.2.3
Проверка фундамента по прочности на
продавливание колонной
от
дна стакана
Условие
выполнения расчета – боковая грань
пирамиды продавливания от дна стакана
проходит ниже боковой грани пирамиды
продавливания плитной части.
hcf-dp=900-0
> 0,5( lcf-lc)=0,5(900-400)
= 250 мм — расчет нетребуется.
Рисунок
20 — Схема продавливания фундамента от
дна стакана
6.2.4
Проверка фундамента на раскалывание
от действия продольной силы
Не
требуется, так как обеспечена его
прочность на продавливание колонной
от дна стакана.
6.2.5
Расчет плитной части фундамента на
поперечную силу.
При
b/l = 3,3/3,3 = 1 ˃ 0,5 не требуется.
6.2.6
Расчет плитной части фундамента на
обратный момент.
Не
требуется по причине однозначной эпюры
напряжений под подошвой фундамента.
6.2.7
Определение площади сечения арматуры
плитной части фундамента
Сечение
1-1 (по грани верхней ступени)
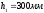
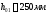
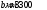
Сечение
2-2 (по грани второй ступени)
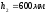

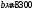
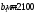
Сечение
3-3 (по грани подколонника)
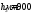
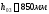
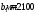
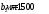
По
большей площади 2657,61 мм2
принимаем 4 сетки двух типоразмеров:
—
1,6 х 3,2 с 9
As =
1810мм2
—
1,4 х 3,2 с 8
As =
1608 мм2
Суммарная
площадь арматуры в одном направлении
в 17
As
= 3418 мм2
(+28,61%).
Процент
армирования сечений:
Рисунок
21 — Расчетные сечения при определении
арматуры в подошве фундамента
6.2.8
Расчет подколонника
В
данном случае подколонник рассматривается
как короткая сжатая колона с поперечным
сечением 900х900мм.
Рисунок
22 – Расчетное сечение подколонника
Случайный
эксцентриситет
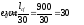
Расчетные
усилия в сечении 1-1
Первое
сочетание усилий
Принимаем
α=0,99
Так
как
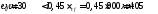
усилий, можно проектировать бетонным.
Второе
сочетание усилий
Следовательно,
подколонник, исходя из второго сочетания
усилий, можно принять железобетонным
с вертикальной арматурой.
Расчетные
усилия в сечении 2-2
Первое
сочетание усилий
Так
как
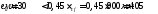
усилий, можно проектировать бетонным.
Второе
сочетание усилий
Следовательно,
подколонник, исходя из второго сочетания
усилий, можно принять железобетонным
с вертикальной арматурой. Для его расчета
принимаем второе сочетание усилий в
расчетном сечении 2-2, так как
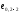
Так
как подколонник железобетонный, то
вертикальная арматура рассчитывается
по формуле:
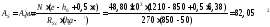
где
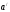
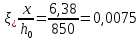
где
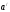
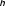
Принимаем
вертикальную арматуру
с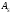
Рисунок
23 — Вертикальное армирование подколонника
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Межрегиональная ассоциация архитекторов и проектировщиков |
Библиотека СРО
-
05 августа 2009
ПОСОБИЕ
ПО ПРОЕКТИРОВАНИЮ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ИЗ ТЯЖЕЛЫХ И ЛЕГКИХ БЕТОНОВ БЕЗ ПРЕДВАРИТЕЛЬНОГО НАПРЯЖЕНИЯ АРМАТУРЫ
(к СНиП 2.03.01-84)
ЧАСТЬ 3
РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ
Пример 41. Дано: колонна многоэтажного каркаса с сечением размерами b = 400 мм, h = 600 мм; а = аў = 50 мм; бетон тяжелый класса В25 (Rbt = 0,95 МПа при gb2 = 0,9); хомуты, расположенные по граням колонны, из арматуры класса A-III, диаметром 10 мм (Rsw = 255 МПа; Asw = 157 мм2), шагом s = 400 мм; изгибающие моменты в верхнем и нижнем опорных сечениях равны Msup = 350 кН·м, Minf = 250 кН·м и растягивают соответственно левую и правую грани колонн; продольная сила N = 572 кН; длина колонны (расстояние между опорными сечениями) l = 2,8 м.
Требуется проверить прочность наклонных сечений колонны по поперечной силе.
Расчет. h0 = h – a = 600 – 50 = 550 мм. Расчет производим согласно п. 3.31 с учетом рекомендаций п. 3.53.
Поперечная сила в колонне равна:
Поскольку поперечная сила постоянна по длине колонны, длину проекции наклонного сечения принимаем максимально возможной, т. е. равной
Определим коэффициент jn:
Поскольку с = сmax, Qb = Qb,min = jb3 (1 + jn)Rbtbh0 = 0,6 (1 + 0,27)0,95 · 400 · 550 = 159,2 · 103 H < Q = 214 кН, т. е. хомуты требуются по расчету.
Значение qsw определим по формуле (55):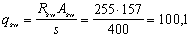
Проверим условие (57):
Поскольку условие (57) не выполняется, определим значение Mb по формуле
откуда
с0 принимаем равным с0 = 2h0 = 2 · 550 = 1100 мм, тогда Qsw = qswc0 = 100,1 · 1100 = 110,1 · 103 Н.
Проверим условие (50):
т. е. прочность сечений по поперечной силе обеспечена.
Центрально- и внецентренно растянутые элементы
ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
3.77 (3.26). При расчете сечений центрально-растянутых железобетонных элементов должно соблюдаться условие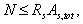
где As,tot ѕ площадь сечения всей продольной арматуры.
ВНЕЦЕНТРЕННО РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
РАСЧЕТ ПРЯМОУГОЛЬНЫХ СЕЧЕНИЙ, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА, ПРИ РАСПОЛОЖЕНИИ ПРОДОЛЬНОЙ СИЛЫ В ПЛОСКОСТИ ОСИ СИММЕТРИИ
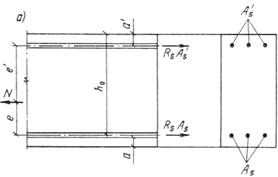
3.78 (3.27). Расчет прямоугольных сечений внецентренно растянутых элементов с арматурой, сосредоточенной у наиболее растянутой и у сжатой (наименее растянутой) граней, должен производиться в зависимости от положения продольной силы N:
а) если продольная сила N приложена между равнодействующими усилий в арматуре S и Sў (черт. 51, а), т. е. при еў Ј h0 – aў, ѕ из условий: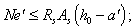
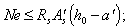
б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и Sў (черт. 51, б), т. е. при еў > h0 – aў, ѕ из условия
при этом высота сжатой зоны х определяется по формуле
Черт. 51. Схема усилий и эпюра напряжений в сечении, нормальном
к продольной оси внецентренно растянутого железобетонного элемента,
при расчете его по прочности
а ѕ продольная сила N приложена между равнодействующими усилий в арматуре S и Sў;
б ѕ то же, за пределами расстояния между равнодействующими усилий в арматуре S и Sў
Если полученное из расчета по формуле (160) значение х > xRh0, в условие (159) подставляется х = xRh0, где xR определяется по табл. 18 и 19.
Если х < 0, прочность сечения проверяется из условия (157).
При симметричном армировании прочность независимо от значения еў проверяется из условия (157).
Примечание. Если при eў > h0 – aў высота сжатой зоны, определенная без учета сжатой арматуры 
3.79. Требуемое количество продольной арматуры определяется следующим образом:
а) при eў Ј h0 – aў определяется площадь сечения арматуры S и Sў соответственно по формулам:

б) при eў > h0 – aў определяется площадь сечения растянутой арматуры As по формуле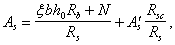
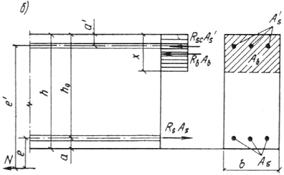
где x принимается по табл. 20 в зависимости от значения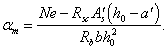
При этом должно удовлетворяться условие am Ј aR (см. табл. 18 и 19). В противном случае следует увеличить сечение сжатой арматуры 
Если am < 0, площадь сечения растянутой арматуры As определяется по формуле (161).
Площадь симметричной арматуры независимо от значения еў подбирается по формуле (161).
Примечание. При еў > h0 – aў необходимое количество арматуры, определенное по формуле (161), можно несколько снизить, если значение x, определенное по табл. 20 без учета сжатой арматуры, т. е. по значению 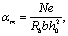

где z определяется по табл. 20 в зависимости от значения
ОБЩИЙ СЛУЧАЙ РАСЧЕТА НОРМАЛЬНЫХ СЕЧЕНИЙ ВНЕЦЕНТРЕННО РАСТЯНУТОГО ЭЛЕМЕНТА (ПРИ ЛЮБЫХ СЕЧЕНИЯХ, ВНЕШНИХ УСИЛИЯХ И ЛЮБОМ АРМИРОВАНИИ)
3.80. Расчет сечений внецентренно растянутого элемента в общем случае (см. черт. 45) должен производиться из условия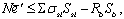
где 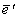
Sb ѕ статический момент площади сжатой зоны бетона относительно указанной оси;
Ssi ѕ статический момент площади сечения i-го стержня продольной арматуры относительно указанной оси;
ssi ѕ напряжение в i-м стержне продольной арматуры.
Высота сжатой зоны х и напряжения ssi определяются из совместного решения уравнений (154) и (155) с заменой перед N знака „минус” знаком „плюс”.
При косом внецентренном растяжении для определения положения границы сжатой зоны кроме использования формул (154) и (155) требуется соблюдение дополнительного условия, чтобы точки приложения внешней продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и равнодействующей усилий в растянутой арматуре лежали на одной прямой (см. черт. 45).
РАСЧЕТ СЕЧЕНИЙ, НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
3.81. Расчет наклонных сечений внецентренно растянутых элементов на действие поперечной силы производится как для изгибаемых элементов согласно пп. 3.28ѕ3.41. При этом значение Mb в п. 3.31 определяется по формуле
где 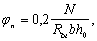
значение Qb,min принимается равным jb3 (1 + jf – jn)Rbtbh0. Кроме того, во всех формулах пп. 3.29, 3.40 и 3.41 коэффициент jb4 заменяется на jb4 (1 – jn).
Расчет наклонных сечений внецентренно растянутых элементов на действие изгибающего момента производится как для изгибаемых элементов согласно пп. 3.42ѕ3.45. При этом высота сжатой зоны в наклонном сечении определяется с учетом растягивающей силы N по формуле (160) или согласно п. 3.80.
В случае выполнения условия eў < h0 – aў расчетный момент в наклонном сечении допускается определять как момент всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно оси, проходлящей через центр тяжести арматуры Sў.
ПРИМЕРЫ РАСЧЕТА
Пример 42. Дано: растянутая ветвь двухветвевой колонны с поперечным сечением размерами b = 500 мм, h = 200 мм; а = аў = 40 мм; продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь ее сечения As = Aўs = 982 мм2 (2 Æ 25); бетон тяжелый класса В25 (Rb = 16 МПа при gb2 = 1,1); продольная сила N = 44 кН; максимальный изгибающий момент М = 43 кН · м.
Требуется проверить прочность нормального сечения.
Расчет. h0 = 200 – 40 = 160 мм;


Поскольку арматура симметричная, прочность проверим из условия (157):
т. е. условие (157) не удовлетворяется. Так как еў = 1037 мм > h0 – aў = 120 мм, а высота сжатой зоны х, определенная по формуле (160) без учета сжатой арматуры:
согласно примечанию к п. 3.78 проверим прочность из условия (159), принимая х = 40 мм и Aўs = 0:
т. е. прочность нормального сечения обеспечена.
Пример 43. Дано: прямоугольное сечение размерами b = 1000 мм, h = 200 мм; а = аў = 35 мм; бетон тяжелый класса В15 (Rb = 7,7 МПа при gb2 = 0,9); продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь сечения арматуры Sў Aўs = 1005 мм2; растягивающая сила N = 160 кН; изгибающий момент М = 116 кН·м.
Требуется определить площадь сечения арматуры S.
Расчет. h0 = 200 – 35 = 165 мм;

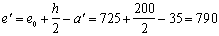
Так как еў = 790 мм h0 – аў = 165 – 35 = 130 мм, определим необходимую площадь сечения растянутой арматуры согласно п. 3.796.
Вычислим значение
Так как 0 < am < aR = 0,44 (см. табл. 18), значение As определим по формуле (163). Для этого по табл. 20 при am = 0,276 находим x = 0,33.
Принимаем As = 3079 мм2 (5 Æ 28).
Пример 44. Дано: прямоугольное сечение размерами b = 1000 мм, h = 200 мм; а = аў = 40 мм; бетон тяжелый класса В15 (Rb = 7,7 МПа при gb2 = 0,9); продольная арматура класса A-III (Rs = Rsc = 365 МПа); растягивающая сила N = 532 кН; изгибающий момент М = 74 кН·м.
Требуется определить площадь сечения симметричной продольной арматуры.
Расчет. h0 = h – a = 200 – 40 = 160 мм;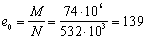
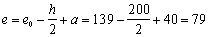

Поскольку арматура симметричная, площадь сечения арматуры определим по формуле (161):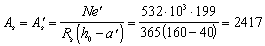
Так как еў = 199 мм > h0 – аў = 120 мм, согласно примечанию к п. 3.79 значение As можно снизить.
Определим значение x без учета сжатой арматуры. Для этого вычислим значение am:
Из табл. 20 при am = 0,213 находим x = 0,24 и z = 0,88. Так как 

Принимаем As = Aўs = 2281 мм2 (6 Æ 22).
Пример 45. Дано: растянутая ветвь двухветвевой колонны с сечением размерами b = 500 мм, h = 200 мм; а = аў = 40 мм; бетон тяжелый класса В25 (Rbt = 1,15 МПа при gb2 = 1,1); хомуты, расположенные по граням ветви, из арматуры класса A-III (Rsw = 285 МПа); продольная растягивающая сила N = 44 кН; поперечная сила Q = 143 кН; расстояние между перемычками двухветвевой колонны l = 600 мм.
Требуется определить диаметр и шаг хомутов.
Расчет. h0 = h – а = 200 – 40 = 160 мм. Расчет производим согласно п. 3.33а с учетом рекомендаций п. 3.81.
Значение Mb определим по формуле (167), приняв jb2 = 2 (см. табл. 21), jf = 0 и 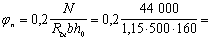
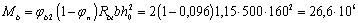
Поскольку в пределах между перемычками поперечная сила постоянна, длину проекции наклонного сечения принимаем максимально возможной, т. е.
Тогда
Так как 2h0 = 2 · 160 = 320 мм < с = 533 мм, принимаем с0 = 2h0 = 320 мм.
Определим коэффициент æ :
æ
Поскольку 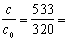


Максимально допустимый шаг хомутов, согласно п. 3.30, равен:
Кроме того, шаг хомутов, согласно п. 5.58, не должен превышать 2h = 2 · 200 = 400 мм.
Принимаем шаг хомутов s = 100 мм < smax, тогда
Принимаем два хомута диаметром по 10 мм (Asw = 157 мм2).
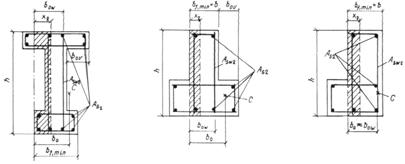
Элементы, работающие на кручение с изгибом (расчет пространственных сечений)
ЭЛЕМЕНТЫ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
3.82 (3.37). При расчете элементов на кручение с изгибом должно соблюдаться условие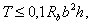
где b, h ѕ соответственно меньший и больший размеры граней элемента.
При этом значение Rb для бетона класса выше В30 принимается как для бетона класса В30.
3.83. Пространственные сечения рассчитываются на совместное действие крутящих и изгибающих моментов, располагая сжатую зону у грани элемента, перпендикулярной плоскости действия изгибающего момента (1-я схема, черт. 52).
Кроме того, пространственные сечения рассчитываются на совместное действие крутящих моментов и поперечных сил, расоплагая сжатую зону у грани элемента, параллельно плоскости действия изгибающего момента (2-я схема, черт. 53).
Черт. 52. Схема усилий в пространственном сечении
1-й схемы
Черт. 53. Схема усилий в пространственном сечении
2-й схемы
3.84. Расчет пространственного сечения по 1-й схеме производится из условия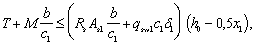
при этом значение RsAs1 принимается не более 
В условии (169):
с1 ѕ длина проекции на продольную ось элемента линии, ограничивающей сжатую зону пространственного сечения; невыгоднейшее значение с1 в общем случае определяется последовательными приближениями и принимается не более 2h + b и не более 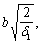
As1 ѕ площадь сечения всех продольных стержней, расположенных у растянутой от изгиба грани шириной b;
qsw1 ѕ усилие в поперечных стержнях, расположенных у растянутой от изгиба грани шириной b на единицу длины элемента, равное: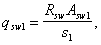
где Asw1 ѕ площадь сечения одного поперечного стержня;
s1 ѕ расстояние между поперечными стержнями;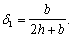
Моменты крутящий Т и изгибающий М принимаются в поперечном сечении, проходящем через середину пространственного сечения (черт. 54, а).
Высота сжатой зоны х1 определяется по формуле
где 
Если х1 < 2аў, в условии (169) принимается х1 = 2аў. Если х1 > xRh0 (где xR ѕ см. п. 3.14), должна быть проверена прочность нормального сечения согласно п. 3.15.
Условие (169) также должно выполняться, если в качестве значений As1 и Asw1 принимать площади сечения продольной и поперечной арматуры, расположенной в сжатой от изгиба зоне; в этом случае значение М подставляется со знаком „минус”.
Примечание. Ограничение, вводимое на значение RsAs1 при использовании условия (169), допускается учитывать и при использовании формулы (172), что может привести к некоторому увеличению расчетной несущей способности.
Черт. 54. Определение изгибающего и крутящего моментов
поперечной силы, действующих в пространственном сечении
а ѕ 1-й схемы; б ѕ 2-й схемы
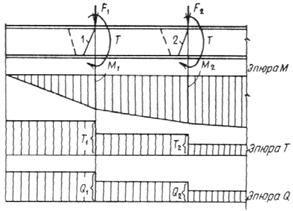
3.85. Прочность по продольной арматуре, расположенной у растянутой от изгиба грани (1-я схема), рекомендуется проверять:
а) для неразрезных балок и консолей, располагая пространственное сечение у опоры, а также для любых элементов, нагруженных сосредоточенными силами и крутящими моментами, располагая пространственные сечения у мест приложения этих сил и моментов со стороны участка с большими крутящими моментами (черт. 55), ѕ из условия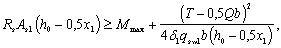
где Mmax ѕ наибольший изгибающий момент в начале пространственного сечения;
T, Q ѕ соответственно крутящий момент и поперечная сила в сечении с наибольшим изгибающим моментом.
При этом qsw1 b(h0 – 0,5x1) принимается не более
Черт. 55. Расположение расчетных пространственных сечений
1-й схемы в балке, нагруженной сосредоточенными силами
1, 2 ѕ расчетные пространственные сечения;
M1, T1, Q1 ѕ расчетные усилия для пространственного сечения 1;
М2, Т2, Q2 ѕ то же, для пространственного сечения 2
б) для элементов, нагруженных только равномерно распределенной нагрузкой q, если в пролетном сечении с наибольшим изгибающим моментом Mmax имеет место крутящий момент Т0, ѕ из условия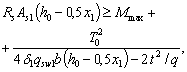
где t ѕ равномерно распределенный крутящий момент на единицу длины элемента.
Прочность по продольной арматуре, расположенной у сжатой от изгиба грани, рекомендуется проверять для свободно опертых балок из условия (173), принимая усилия Т и Q в опорном сечении при Mmax = 0.
Если на рассматриваемых участках выполняется условие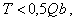
продольную арматуру можно проверить только из условия чистого изгиба (см. п. 3.15).
Прочность по поперечной арматуре, расположенной у любой грани шириной b, рекомендуется проверять из условия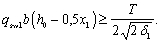
Примечание. Подобранную из условия (173) продольную арматуру можно несколько уменьшить, если невыгоднейшее пространственное сечение длиной проекции с1, равной:
выходит за пределы длины элемента или его участка с однозначными и ненулевыми значениями Т. В этом случае расчет производится общим методом согласно п. 3.84 при соответственно уменьшенной длине проекции с1.
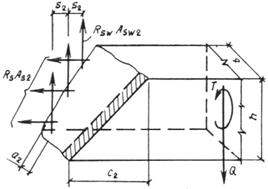
3.86. Расчет пространственного сечения по 2-й схеме (см. черт. 53) производится из условия
при этом значение RsAs2 принимается не более 2qsw2h, а значение qsw2 ѕ не более
В условии (178):
As2 ѕ площадь сечения всех растянутых продольных стержней, расположенных у грани шириной h, параллельной плоскости изгиба;
с2 ѕ длина проекции на продольную ось элемента линии, ограничивающей сжатую зону пространственного сечения; невыгоднейшее значение с2 определяется по формуле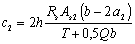
и принимается не более 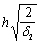

где Asw2 ѕ площадь сечения одного поперечного стержня, расположенного у грани шириной h;
s2 ѕ расстояние между поперечными стержнями, расположенными у грани шириной h;
а2 ѕ расстояние от грани шириной h до оси продольных стержней, расположенных у этой грани.
Крутящийся момент Т и поперечная сила Q принимаются в поперечном сечении, проходящем через середину пространственного сечения (см. черт. 54, б).
В случае, когда удовлетворяется условие (175), расчет пространственного сечения по 2-й схеме не производится. Вместо него производится расчет наклонных сечений согласно пп. 3.31ѕ3.38 без учета отогнутых стержней. При этом в соответствующих формулах к поперечной силе Q добавляется величина 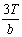
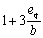
3.87. Необходимую из расчета пространственного сечения по 2-й схеме интенсивность хомутов 
при 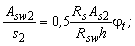
при 1,75 і jt > 1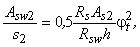
где T, Q ѕ максимальные значения соответственно крутящего момента и поперечной силы на рассматриваемом участке.
При jt > 1б75 следует увеличить площадь сечения арматуры As2 или размер сечения b так, чтобы было выполнено условие j t Ј 1,75.
Если поперечная нагрузка приложена в пределах высоты сечения и действует в сторону растянутой зоны, интенсивность вертикальных хомутов должна быть увеличена по сравнению с вычисленной по формулам (182) и (183) в соответствии с расчетом на отрыв согласно п. 3.97.
ЭЛЕМЕНТЫ ТАВРОВОГО, ДВУТАВРОВОГО И ДРУГИХ СЕЧЕНИЙ, ИМЕЮЩИХ ВХОДЯЩИЕ УГЛЫ
3.88. Поперечное сечение элемента следует разбивать на ряд прямоугольников (черт. 56), при этом, если высота свесов полок или ширина ребра переменны, принимаются их средние значения.
Черт. 56. Разделение на прямоугольники сечений,
имеющих входящие углы, при расчете на кручение с изгибом
Размеры поперечного сечения должны удовлетворять условию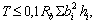
где hi, bi ѕ соответственно больший и меньший размеры каждого из составляющих сечение прямоугольников.
Кроме того, необходимо соблюдать требование п. 3.30.
Если в пределах высоты сечения имеются полки (выступы), нижние или верхние грани которых не являются продолжение соответствующих граней элемента, расчет пространственных сечений ведется без учета этих полок как для элемента прямоугольного сечения согласно пп. 3.83ѕ3.87.
3.89. Расчет пространственного сечения на совместное действие крутящего и изгибающего моментов (1-я схема, черт. 57) производится из условия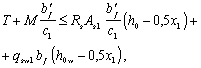
при этом значение RsAs1 принимается не более
В условии (185):
bўf, bf ѕ ширина соответственно сжатой грани и растянутой грани, нормальной к плоскости изгиба;
с1 ѕ длина проекции на продольную ось элемента линии, ограничивающей сжатую зону пространственного сечения; значение с1 принимается соответствующим значению угла наклона пространственной трещины к оси элемента 45° на всех гранях элемента и определяется (без учета х1) по формуле
при этом длина с1 не должна выходить за пределы элемента и его участка с однозначными и ненулевыми значениями Т;
As1 ѕ площадь сечения всех продольных стержней, расположенных в растянутой от изгиба зоне;
х1 ѕ высота сжатой зоны, определяемая как для плоского поперечного сечения изгибаемого элемента (см. п. 3.20);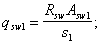
Asw1, s1 ѕ площадь поперечных стержней, расположенных в одной плоскости в растянутой от изгиба зоне, и шаг этих стержней;
h0w ѕ расстояние от сжатой грани до равнодействующей усилий в поперечных стержнях растянутой зоны.
Черт. 57. Схемы расположения сжатой зоны в пространственном
сечении 1-й схемы железобетонного элемента двутаврового
и таврового сечений, работающего на кручение с изгибом
С ѕ центр тяжести продольной растянутой арматуры
Моменты крутящий Т и изгибающий М в условии (185) принимаются в поперечном сечении, проходящем через середину пространственного сечения.
В случае изменения шага поперечных стержней s1 в пределах длины с1 учитывается средний шаг на участке длиной bf, расположенном симметрично относительно поперечного сечения, проходящего через середину пространственного сечения.
Кроме того, следует проверить прочность нормального сечения согласно п. 3.20.
Примечание. Ограничение, вводимое на значение RsAs1 при использовании условия (185), допускается учитывать и при вычислении высоты сжатой зоны х1, что приведет к некоторому увеличению расчетной несущей способности.
3.90. Расчет пространственного сечения на совместное действие крутящего момента и поперечной силы (2-я схема, черт. 58) производится из условия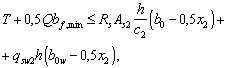
при этом значение RsAs2 принимается не более 2qsw2h.
В условии (187):
bf,min ѕ меньшая ширина полки элемента или при одной полке ширина ребра;
As2 ѕ площадь всех продольных стержней, расположенных в растянутой зоне при данной схеме;
с2 ѕ длина проекции на продольную ось элемента линии, ограничивающей сжатую зону пространственного сечения, определяемая по формуле
где bov ѕ ширина свеса полки, расположенного в растянутой зоне, при этом длина с2 не должна выходить за пределы элемента или его участка с однозначными и ненулевыми значениями Т;
х2 ѕ высота сжатой зоны, определяемая как для плоского поперечного сечения изгибаемого элемента при данной схеме расположения сжатой зоны, при этом не учитывается сжатый свес полки, выступающий за грань полки меньшей ширины или за грань ребра при одной полке;
Asw2, s2 ѕ соответственно площадь сечения одного поперечного стержня, расположенного в растянутой зоне при данной схеме на всю высоту h, и его шаг;
b0, b0w ѕ расстояния от боковой сжатой грани полки (или ребра) шириной bf,min до равнодействующей усилий соответственно в продольных стержнях площадью As2 и в поперечных стержнях площадью Asw2.
Черт. 58. Схемы расположения сжатой зоны в пространственном сечении 2-й схемы железобетонного элемента двутаврового, таврового и Г-образного сечений, работающего на кручение с изгибом
С ѕ центр тяжести продольной растянутой арматуры
Крутящий момент Т и поперечная сила Q в условии (187) принимаются в поперечном сечении, проходящем через середину пространственного сечения.
В случае изменения шага поперечных стержней s2 в пределах длины с2 учитывается средний шаг на участке длиной h, расположенном симметрично относительно поперечного сечения, проходящего через середину пространственного сечения.
Кроме того, следует проверить прочность наклонного сечения согласно п. 3.31.
ЭЛЕМЕНТЫ КОЛЬЦЕВОГО СЕЧЕНИЯ С ПРОДОЛЬНОЙ АРМАТУРОЙ, РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ОКРУЖНОСТИ
3.91. Размеры поперечного кольцевого сечения элемента должны удовлетворять условию
где r1, r2 ѕ соответственно внутренний и наружный радиусы кольцевого сечения.
Расчет пространственного сечения (черт. 59) производится из условия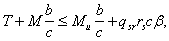
где b, c ѕ длина проекции линии, ограничивающей сжатую зону, соответственно на поперечное сечение элемента и на его продольную ось (см. черт. 59). Значение b принимается равным
значение с определяется согласно п. 3.91;
Черт. 59 Пространственное сечение железобетонного элемента кольцевого поперечного сечения, работающего на кручение с изгибом

Мu — предельный изгибающий момент при чистом изгибе, принимаемый равным правой части условий (138) или (139);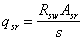
Аsr,s — соответственно площадь сечения стержня спиральной (кольцевой)арматуры и шаг навивки спирали (шаг колец);
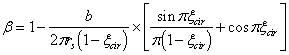
или по черт. 60.
Черт. 60. График для определения коэффициента 
Моменты крутящий Т и изгибающий М в условии (190) принимаются в поперечном сечении, проходящем через середину пространственного сечения.
Кроме того, должно быть проверено условие (190) как при чистом кручении с умножением величины Мu на отношение 
Значение qsr в условии (190) принимается не более 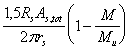
3.92. Условие (190) проверяется для пространственных сечений, в которых длина проекции с не выходит за пределы участка с однозначными и ненулевыми значениями Т и не превышает 
Для элементов с постоянным сечением по длине рекомендуется проверять пространственные сечения, начинающиеся от нормального сечения с наибольшим значением Т, а при постоянных значениях Т — от сечения с наибольшим значением М=Ммах. В последнем случае невыгоднейшее значение с равно: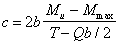
Для элементов с переменным сечением по длине рекомендуется проверять несколько пространственных сечений, расположенных в разных местах по длине, и при значениях с, равных:
при этом длина проекции с не должна выходить за пределы длины элемента. Размеры поперечного сечения принимаются соответствующими середине пространственного сечения.
ПРИМЕРЫ РАСЧЕТА
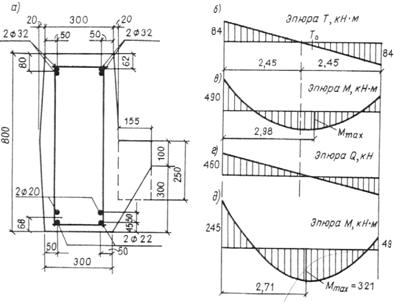
Пример 46. Дано: ригель перекрытия торцевой рамы многоэтажного промышленного здания, нагруженный равномерно распределенной нагрузкой q=154,4 кН/м и равномерно распределенными крутящими моментами t=34,28 кН·м/м; поперечное сечение ригеля у опоры — по черт. 61, а; эпюра крутящих моментов от вертикальных постоянных и длительных нагрузок — по черт. 61, б; эпюры изгибающих моментов и поперечных сил от невыгоднейшей для опорного сечения комбинации вертикальных нагрузок и ветровой нагрузки — по черт. 61, в, г; эпюра изгибающих моментов от невыгоднейшей для пролетного сечения комбинации вертикальных нагрузок — по черт. 61, д; бетон тяжелый класса В25; продольная и поперечная арматура класса А-III (Rs=Rsc=365 МПа; Rsw=290 МПа).
Черт. 61. К примеру расчета 46
Требуется подобрать вертикальные и горизонтальные поперечные стержни и проверить прочность ригеля на совместное действие кручения и изгиба.
Расчет. Поскольку сечение имеет входящие углы, проверим условие (184), разбив сечение на два прямоугольника размерами 800х320 и 155х250 мм и приняв Rb = 13 МПа (т.е. при 

т.е. условие (184) удовлетворяется.
Расчет пространственных сечений производим как для прямоугольного сечения размерами b = 300 мм и h = 800 мм, так как нижняя грань ригеля и выступающая полка образуют угол.
Так как для опорного сечения 0,5Qb = 0,5·460·0,3 = 69 кН·м < Т = 84 кН·м, согласно пп. 3.85 и 3.86, расчет приопорного участка по 1-й и 2-й схемам необходим.
Необходимую из расчета по 2-й схеме интенсивность вертикальных стержней определяем согласно п. 3.87.
Предварительно вычислим коэффициенты 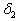


где Аs2 = 1609 + 314 + 380 = 2304 мм2 (2Æ32 + Æ20 + Æ22).
Поскольку 
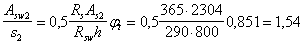
Принимая шаг вертикальных хомутов s2 = 100 мм, находим площадь сечения одного хомута:
Asw2 = 1,54 · 100 = 154 мм2.
Принимаем хомуты диаметром 14 мм (Asw2 = 154 мм2).
Проверим прочность по продольной арматуре, установленной у верхней растянутой грани приопорного участка ригеля согласно п. 3.85а (1-я схема).
Из черт. 61, а находим As1 = 3217 мм2 (4Æ32) и 
По формуле (172) определим высоту сжатой зоны х1, принимая Rb = 16 МПа (т.е. при 

= 136 мм.
Шаг и диаметр горизонтальных поперечных стержней приопорного участка принимаем такими же, как для вертикальных хомутов, т.е. s1=100 мм, Asw1=154 мм2, отсюда
h0 = 800 — 80 = 720 мм.
Проверим выражение qsw1b(h0-0,5x1) = 446,6·300(720-0,5·139)=
= 87,2·106 Н·мм < 
Проверим условие (173):
= 365·3217(720-0,5·139)=763,8·106 Н·мм,
т.е. верхней продольной арматуры из условия прочности установлено достаточно.
Из условия (176) проверим прочность по горизонтальной поперечной арматуре, расположенной на приопорном участке:
qsw1b(h0 — 0,5x1) = 446,6·300(720-0,5·139)=
= 87,2·106 Н·мм > 
т.е. горизонтальной поперечной арматуры на приопорном участке установлено достаточно.
Как видно из черт. 61, б, д, в сечении с наибольшим пролетным изгибающим моментом имеет место крутящий момент, поэтому следует проверить прочность по продольной арматуре, установленной у нижней растянутой грани в средней части пролета ригеля, из условия (174).
Для этой части ригеля, два верхних стержня Æ 32 оборваны, и поэтому, согласно черт: 61, а, имеем A/sw = 1609 мм2 (2 Æ 32); а/ = 62 мм; As1 = 1388 мм2 (2 Æ 20 + 2 Æ22); а = 68 мм.
Определим высоту сжатой зоны х1, принимая Rb = 13 МПа (т.е. при 
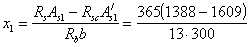
Принимаем х1 = 2а’, отсюда h0 — 0,5 x1 = h — a — a’ = 800 — 68 — 62 = 670 мм.
Горизонтальные поперечные стержни в средней части пролета принимаем диаметром 14 мм (Аsw1 = 154 мм2) и с шагом s1 = 200 мм, отсюда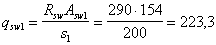
Из черт. 61, б, д имеем: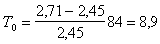
Мmax = 321 кН·м.
Проверим условие (174):
+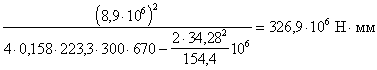
< RsAs1 (h0 — 0,5x1) = 365·1388·670=339,4·106 Н·мм,
т.е. нижней продольной арматуры из условия прочности установлено достаточно.
Определим, на каком расстоянии lх от нулевой точки эпюры Т можно допустить шаг горизонтальных поперечных стержней 200 мм, используя условие (176). Принимая Т=tlx, имеем qsw1b(h0 — 0,5 x1) = 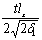
Следовательно, шаг горизонтальных стержней 100 мм можно допустить на приопорных участках ригеля длиной 2,45-1,47 
Пример 47. Дано: балка перекрытия с поперечным сечением — по черт. 62, а; расположение нагрузок, эпюры изгибающих и крутящих моментов, а также эпюра поперечных сил — по черт. 62, б; бетон тяжелый класса В25 (Rb = 13 МПа при 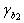
Требуется проверить прочность балки на совместное действие кручения и изгиба.
Расчет. Разбиваем поперечное сечение на два прямоугольника размерами 200х400 и 350х400 мм и проверяем условие (184):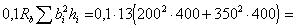
Черт. 62. К примеру расчета 47
Из черт. 62, а имеем h0=800-50=750 мм.
Сначала проверим прочность пространственного сечения по 2-й схеме согласно п. 3.90. При этом, поскольку сосредоточенные силы, приложенные посередине высоты сечения, вызывают отрыв растянутой зоны балки, учтем, что часть вертикальных хомутов воспринимает отрывающую силу, равную согласно п. 3.97:
(где hs = 400 — 50 = 350 мм).
Усилие на единицу длины балки в вертикальных хомутах, расположенных у правой грани, от действия отрывающей силы F определим, распределяя отрывающую силу на две ветви хомутов и принимая ширину площадки опирания силы F b = 300 мм, тогда
а = 2hs + b = 2·350 + 300 = 1000 мм = 1 м,
т.е.
Таким образом, учитываемая при расчете пространственного сечения величина qsw2 при Аsw2 = 154 мм2 (1Æ14) и s2 = 100 мм (см. черт. 62, а) будет равна:
Согласно черт. 58, в и 62, а, принимаем bf,min = 200 мм, h = 800 мм, bov=0, As2 = 1071 мм2 (1Æ32 + 1Æ12+1Æ14).
Тогда значение с2 будет равно:
Пространственное сечение располагаем у опоры балки. Поскольку с2 < 1,94 м, т. е. пространственное сечение не выходит за пределы участка с ненулевыми значениями Т, оставляем с2 = 1,2 м.
Расчетные значения Q и T принимаем на расстоянии 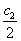

Поскольку RsAs2 = 365·1071 = 391·103 Н < 2qsw2h = 2·372·800=595·103 Н, оставляем RsAs2 = 391 кН.
Высоту сжатой зоны х2 определяем как для прямоугольного сечения согласно п. 3.20, принимая для данной схемы h0 = b0 = 200 -50 = 150 мм и b = h = 800 мм (сжатый свес полки не учитывается).
Поскольку а’ = 50 мм составляет значительную долю от h0 = 150 мм, значение х2 определяем без учета сжатой арматуры: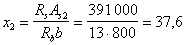
Проверяем условие (187), принимая bow = bo = 150 мм: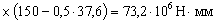
> Т + 0,5 Qbf,min = 40 + 0,5 × 293,5 × 0,2 = 69,35 кН×м,
т. е. прочность по 2-й схеме обеспечена.
Проверяем прочность пространственного сечения по 1-й схеме согласно п. 3.89. Принимаем b’f = b = 200мм; bf= 350мм; Аs1 = 2526 мм2 (3Æ32 + 1Æ12); Аўs1 = 308 мм2 (2Æ14); Аsw1 = 154 мм2 (1Æ14); s1 = 200 мм.
Определяем длину проекции c1:
c1 = 2h + 2bf + b’f ‑ 2b = 2 × 800 + 2 × 350 + 200 ‑ 2 × 200 = 2100 мм.
Пространственное сечение располагаем на участке между опорой и первым грузом у места приложения этого груза. Поскольку c1 > 1,94 м, т.е. пространственное сечение выходит за пределы балки, принимаем c1 = 1,94м. Расчетные значения М и Т принимаем на расстоянии 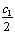
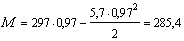
Высоту сжатой зоны определяем как для прямоугольного сечения: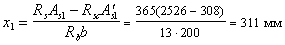
при этом х1 = 311 мм < xR ho = 0,604 × 750 = 453 мм (где xR ‑ см. табл. 18);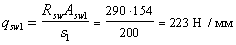
Поскольку 2qsw1 bf + 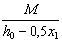
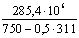
Проверяем условие (185), приняв how = ho = 750 мм:
т. е. прочность сечения по 1-й схеме обеспечена.
Расчет железобетонных элементов на местное действие нагрузок
РАСЧЕТ НА МЕСТНОЕ СЖАТИЕ
3.93(3.39). При расчете на местное сжатие (смятие) элементов без поперечного армирования должно удовлетворяться условие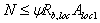
где N — продольная сжимающая сила от местной нагрузки;
Aloc1 — площадь смятия (см. черт. 63);
y — коэффициент, принимаемый равным:
при равномерном распределении местной нагрузки на площади смятия — 1,0;
при неравномерном распределении местной нагрузки на площади смятия (под концами балок, прогонов, перемычек) — 0,75;
Rb, loc ѕ расчетное сопротивление бетона смятию, определяемое по формуле
Rb, loc = ajb Rb, (195)
здесь ajb і 1,0;
a = 1,0 для бетона класса ниже В25;
a = 13,5 Rbt /Rb для бетона класса В25 и выше;
jb = 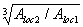
но не более следующих значений:
при схеме приложения нагрузки по черт. 63, а, в, г, е, и для бетона:
тяжелого, мелкозернистого и легкого классов:
выше В7,5 ………………….. 2,5
В3,5; В5; В7,5 …………….. 1,5
легкого класса В2,5 …….. 1,2
при схеме приложения нагрузки по черт. 63, б, д, ж независимо от вида и класса бетона ѕ 1,0;
Rb, Rbt — принимаются как для бетонных конструкций (см. поз. 5 табл. 9);
Aloc2 — расчетная площадь смятия, определяемая в соответствии с п. 3.94.
Если условие (194) не удовлетворяется, рекомендуется применять косвенное армирование в виде сварных сеток и рассчитывать элемент в соответствии с п. 3.95.
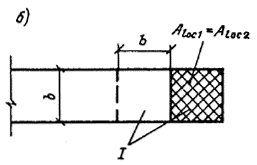
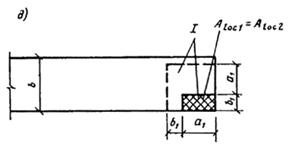
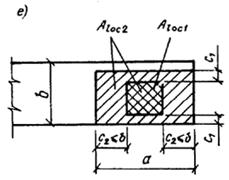
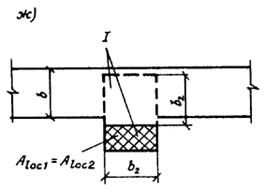
3.94(3.40). В расчетную площадь Aloc2 включается участок, симметричный по отношению к площади смятия (черт. 63). При этом должны выполняться следующие правила:
при местной нагрузке по всей ширине элемента b в расчетную площадь включается участок длиной не более b в каждую сторону от границы местной нагрузки (черт. 63, а);
при местной краевой нагрузке по всей ширине элемента расчетная площадь Aloc2 равна площади смятия Aloc1 (черт. 63, б);
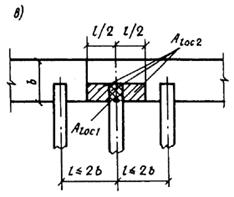
при местной нагрузке в местах опирания концов прогонов и балок в расчетную площадь включается участок шириной, равной глубине заделки прогона или балки, и длиной не более расстояния между серединами пролетов, примыкающих к балке (черт. 63, в);
если расстояние между балками превышает двойную ширину элемента, длина расчетной площади определяется как сумма ширины балки и удвоенной ширины элемента (черт. 63, г);
при местной краевой нагрузке на угол элемента (черт. 63, д) расчетная площадь Aloc2 равна площади смятия Aloc1;
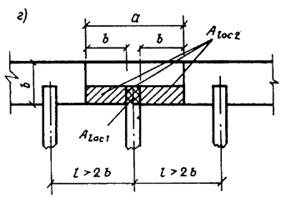
Черт. 63. Определение расчетной площади Aloc2 при расчете на местное сжатие при местной нагрузке
а ѕ по всей ширине элемента; б ѕ краевой по всей ширине элемента; в, г ѕ в местах опирания концов прогонов и балок; д — краевой на угол элемента; е — на часть длины и ширины элемента; ж — краевой в пределах выступа стены (пилястры); и — на сечение сложной формы; I — минимальная зона армирования сетками, при которой косвенное армирование учитывается в расчете
при местной нагрузке, приложенной на части длины и ширины элемента, расчетная площадь принимается согласно черт. 63, е. При наличии нескольких нагрузок указанного типа расчетные площади ограничиваются линиями, преходящими через середину расстояний между точками приложения двух соседних нагрузок;
при местной краевой нагрузке, расположенной в пределах выступа стены (пилястры) или простенка таврового сечения, расчетная площадь Aloc2 равна площади смятия Aloc1 (черт. 63, ж);
при определении расчетной площади для сечений сложной формы не должны учитываться участки, связь которых с загруженным участком не обеспечена с необходимой надежностью (черт. 63, и).
Примечание. При местной нагрузке от балок, прогонов, перемычек и других элементов, работающих на изгиб, учитываемая в расчете глубина опоры при определении Aloc1 и Aloc2 принимается не более 20 см.
3.95(3.41). При расчете на местное сжатие элементов из тяжелого бетона с косвенным армированием в виде сварных поперечных сеток должно удовлетворяться условие
N Ј R*b,loc Aloc1, (196)
где Aloc1 ѕ площадь смятия;
R*b,loc — приведенная призменная прочность бетона при расчете на местное сжатие, определяемая по формуле
R*b,loc = Rb jb + jmxy Rs,xy js, (197)
здесь Rs,xy , j, mxy ѕ обозначения те же, что в п. 3.57;
jb = 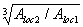
js — коэффициент, учитывающий влияние косвенного армирования в зоне местного сжатия; для схем черт. 63, б, д, ж принимается js = 1,0, при этом косвенное армирование учитывается в расчете при условии, что поперечные сетки установлены на площади не менее ограниченной пунктирными линиями на соответствующих схемах черт. 63; для схем черт. 63, а, в, г, е, и коэффициент js определяется по формуле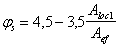
Aef — площадь бетона, заключенного внутри контура сеток косвенного армирования, считая по их крайним стержням, для которой должно удовлетворяться условие Aloc1 < Aef Ј Aloc2.
Если контур площади смятия выходит за пределы контура сеток косвенного армирования [например, на величину защитного слоя бетона арматуры сеток при расположении площади смятия у краев элемента (см. черт.63, а ‑ д, ж, и)], при определении значений Aloc1 и Aloc2 не учитывается площадь, занимаемая защитным слоем.
Наименьшую глубину заложения сеток косвенного армирования следует определять по формулам:
для схем загружения по черт. 63, в ‑ е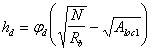
для схем загружения по черт. 63, а, б, ж, и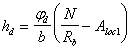
В формулах (198) и (199):
jd = 0,5 — при схемах загружения по черт. 63, а, е, и;
jd = 0,75 ѕ при схемах загружения по черт. 63, в, г;
jd = 1,0 — при схемах загружения по черт. 63, б, д, ж.
Число сеток принимается не менее двух. Кроме того, должны выполняться конструктивные требования п. 5.79. При этом, если в каком-либо направлении размеры ячейки сетки превышают 100 мм или 1/4 меньшей стороны сечения, стержни сетки этого направления не учитываются при определении коэффициента mху.
ПРИМЕРЫ РАСЧЕТА
Пример 48. Дано: стальная стойка, опираемая на железобетонный фундамент и центрально-нагруженная силой N = 1000 кН (черт. 64); фундамент из тяжелого бетона класса В 12,5 (Rb = 6,7 МПа при gb2 = 0,9).
Требуется проверить прочность бетона под стойкой на местное сжатие (смятие).
Черт. 64. К примеру расчета 48
Расчет производим в соответствии с указаниями пп. 3.93 и 3.94.
Расчетную площадь Аloc2 определяем в соответствии с черт. 63, е.
Согласно черт. 64, имеем c1 = 200 мм < b = 800 мм; a1 = 200 × 2+300 = 700 мм; b1 = 200 × 2+200 = 600 мм; Аloc2 = a1 b1 = 700 × 600 = 420000 мм2.
Площадь смятия равна Аloc1 = 300 × 200 = 60000 мм2. Поскольку класс бетона ниже В25, a = 1,0.
Коэффициент jb равен:
Определяем расчетное сопротивление бетона смятию по формуле (195), принимая rb с учетом gb9 = 0,9 (см. табл. 9) как для бетонной конструкции: rb = 6,7 × 0,9 = 6,03 МПа:
Rb, loc = ajb Rb = 1 × 9 × 6,03 = 11,5 МПа
(где ajb = 1 × 1,9 = 1,9 > 1,0).
Проверяем условие (194), принимая y = 1,0 как при равномерном распределении местной нагрузки, тогда
т. е. прочность бетона на местное сжатие не обеспечена, и поэтому необходимо применить косвенное армирование. Принимаем косвенное армирование в виде сеток из арматурной проволоки класса Вр-1, диаметром 3 мм, ячейкой 100ґ100 мм и шагом по высоте s = 100 мм (Rs,xy = 375 МПа).
Проверяем прочность согласно п. 3.95. Так как jb = 1,9 < 3,5, в расчет вводим jb = 1,9.
Коэффициент косвенного армирования сетками mxу определяем по формуле (99).
Из черт. 64 имеем: пx = 5; lx = 300 мм; пy = 4; ly = 400мм; Аsx = Аsy = 7,1 мм2 (Æ3); Аef = lx lу = 300 × 400 = 120000 мм2 > Aloc1 = 60 000 мм2, тогда
По формулам (101) и (100) определяем y и j:
Коэффициент js равен:
js = 4,5 ‑ 3,5 Aloc1/Aef = 4,5 ‑ 3,5 × 60000/120000 = 2,75.
Приведенную прочность бетона R*b,loc определяем по формуле (197):
R*b,loc = Rb jb + jmxy Rs,xy js =
= 6,7 × 1,9+ 3,69 × 0,00183 × 375 × 2,75 = 19,7 МПа.
Проверяем условие (196):
R*b,loc Aloc1 = 19,7 × 60000 = 1182 × 103 H > N = 1000 кН,
т. е. прочность бетона обеспечена.
Определяем наименьшую глубину заложения сеток по формуле (198), принимая jd = 0,5:
т. е. достаточно установить две сетки.
РАСЧЕТ НА ПРОДАВЛИВАНИЕ
3.96(3.42). Расчет на продавливание плитных конструкций (без поперечной арматуры) от действия сил, равномерно распределенных на ограниченной площади, должен производиться из условия
F Ј aRbt um ho, (200)
где F ѕ продавливающая сила;
a — коэффициент, принимаемый равным для бетона:
тяжелого …………………… 1,00
мелкозернистого ………. 0,85
легкого …………………….. 0,80
um ѕ среднеарифметическое значение периметров верхнего и нижнего оснований пирамиды, образующейся при продавливании в пределах рабочей высоты сечения.
При определении um и F предполагается, что продавливание происходит по боковой поверхности пирамиды, меньшим основанием которой служит площадь действия продавливающей силы, а боковые грани наклонены под углом 45° к горизонтали черт.65, а).
Продавливающая сила F принимается равной силе, действующей на пирамиду продавливания, за вычетом нагрузок, приложенных к большему основанию пирамиды продавливания (считая по плоскости расположения растянутой арматуры) и сопротивляющихся продавливанию.
Если схема опирания такая, что продавливание может происходить только по поверхности пирамиды с углом наклона боковых граней более 45° [например, в свайных ростверках (черт. 65, б)], тогда правая часть условия (200) определяется для фактической пирамиды продавливания с умножением на ho/с (где с — длина горизонтальной проекции боковой грани пирамиды продавливания). При этом значение несущей способности принимается не более значения, соответствующего пирамиде при с = 0,4hо.
Черт. 65. Схема пирамиды продавливания при угле наклона ее боковых граней к горизонтали
а ѕ 45°; б ѕ более 45°
При установке в пределах пирамиды продавливания хомутов, нормальных к плоскости плиты, расчет должен производиться из условия
F Ј Fb + 0,8 Fsw, (201)
но не более 2Fb,
где Fb — правая часть условия (200);
Fsw =175SAsw ѕ сумма всех поперечных усилий, воспринимаемых хомутами, пересекающими боковые грани пирамиды продавливания (175 МПа ѕ предельное напряжение в хомутах).
При учете поперечной арматуры значение Fsw должно быть не менее 0,5 Fb.
Допускается учитывать в расчете и меньшее значение Fsw при замене правой части условия (201) на 2,8Fsw, но не менее Fb.
При расположении хомутов на ограниченном участке вблизи сосредоточенного груза производится дополнительный расчет на продавливание пирамиды с верхним основанием, расположенным по контуру участка, с поперечной арматурой, из условия (200) без учета поперечной арматуры.
Поперечная арматура должна удовлетворять требованиям п. 5.75.
РАСЧЕТ НА ОТРЫВ
3.97(3.43). Расчет железобетонных элементов на отрыв от действия нагрузки, приложенной к его нижней грани или в пределах высоты его сечения (черт. 66), должен производиться из условия
где F — отрывающая сила;
hs ѕ расстояние от уровня передачи отрывающей силы на элемент до центра тяжести сечения продольной арматуры S; при передаче нагрузки через монолитно связанные балки или консоли принимается, что нагрузка передается на уровне центра тяжести сжатой зоны элемента, вызывающего отрыв;
SRswАsw ѕ сумма поперечных усилий, воспринимаемых хомутами, устанавливаемыми дополнительно сверх требуемых по расчету наклонного или пространственного сечения согласно пп. 3.31ѕ3.39, 3.86, 3.87 и 3.90; эти хомуты располагаются по длине зоны отрыва, равной:
а = 2 hs + b, (203)
здесь b ѕ ширина площадки передачи отрывающей силы F.
При равномерно распределенной нагрузке q, приложенной в пределах высоты сечения, необходимая интенсивность хомутов увеличивается на величину q(1 ‑ hs/ho)/Rsw.
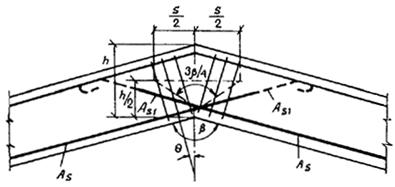
3.98. Входящие углы в растянутой зоне элементов, армируемые пересекающимися продольными стержнями (черт. 67), должны иметь поперечную арматуру, достаточную для восприятия:
а) равнодействующей усилий в продольных растянутых стержнях, не заведенных в сжатую зону, равной: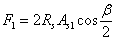
б) 35 % равнодействующей усилий во всех продольных растянутых стержнях, равных:
Необходимая по расчету из этих условий поперечная арматура должна быть расположена по длине s = h tg 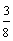
Сумма проекций усилий в поперечных стержнях (хомутах), располагаемых по этой длине, на биссектрису угла должна составлять не менее суммы F1 + f2,
т. е. SRsw Asw cosq і F1 + F2. (206)
В формулах (204) ѕ (206):
As ѕ площадь сечения всех продольных растянутых стержней;
Аs1 ѕ площадь сечения продольных растянутых стержней, не заанкеренных в сжатой зоне;
b ѕ входящий угол в растянутой зоне элемента;
SAsw ѕ площадь сечения поперечной арматуры в пределах длины s;
q — угол наклона поперечных стержней к биссектрисе угла b.
Черт. 66. Схема для определения длины зоны отрыва
а ѕ при примыкании балок; б ѕ то же, консолей; I ѕ центр тяжести сжатой зоны сечения примыкающего элемента
Черт. 67. Армирование входящего угла, расположенного в растянутой зоне железобетонного элемента
Расчет коротких консолей
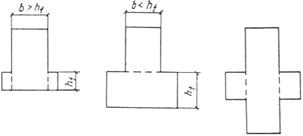
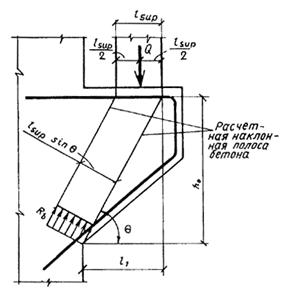
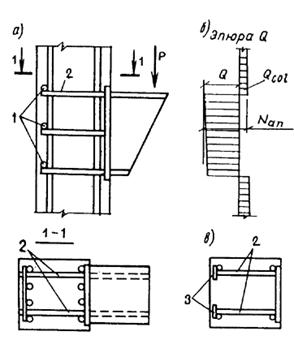
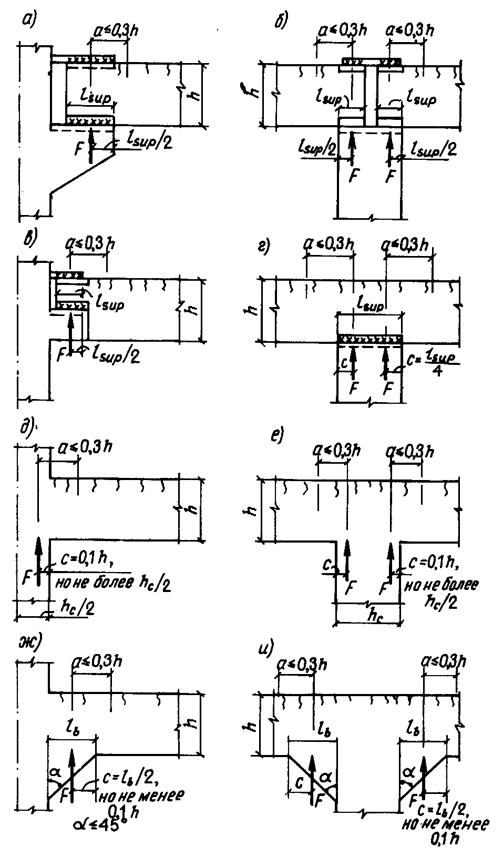
3.99 (3.34). Расчет коротких консолей колонн [l1 Ј 0,9 h0; (черт. 68)] на действие поперечной силы для обеспечения прочности по наклонной сжатой полосе между грузом и опорой должен производиться из условия
Q Ј 0,8 Rb b lsup sin2 q (1 + 5 amw), (207)
в котором правая часть принимается не более 3,5 Rbt b ho и не менее 2,5 Rbt b ho.
В условии (207):
lsup ѕ длина площадки опирания нагрузки вдоль вылета консоли;
q — угол наклона расчетной сжатой полосы к горизонтали 

здесь sw — расстояние между хомутами, измеренное по нормали к ним.
При расчете учитываются хомуты горизонтальные и наклонные под углом не более 45° к горизонтали.
Напряжение сжатия в местах передачи нагрузки на консоль не должно превышать Rb,loc (см. п. 3.93).
Для коротких консолей, входящих в жесткий узел рамной конструкции с замоноличиванием стыка, значение lsup в выражении (207) принимается равным вылету консоли l1, если при этом выполняются условия М/Q і 0,3 м и lsup/l1 і 2/3 (где М и Q — соответственно момент, растягивающий верхнюю грань ригеля, и поперечная сила в нормальном сечении ригеля по краю консоли). В этом случае правая часть условия (207) принимается не более 5Rbtbho.
Черт. 68. Расчетная схема для короткой консоли при действии поперечной силы
При шарнирном опирании на короткую консоль сборной балки, идущей вдоль вылета консоли, при отсутствии специальных выступающих закладных деталей, фиксирующих площадку опирания (черт. 69), значение lsup в условии (207) принимается равным 2/3 длины фактической площадки опирания.
Поперечное армирование коротких консолей должно удовлетворять требованиям п. 5.77.
Черт. 69. Расчетная схема для короткой консоли при шарнирном опирании сборной балки, идущей вдоль вылета консоли
3.100. При шарнирном опирании балки на консоль колонны продольная арматура консоли проверяется из условия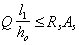
где l1, ho ѕ см. черт. 68.
При этом продольная арматура консоли должна быть доведена до свободного конца консоли и иметь надлежащую анкеровку (см. пп. 5.44 и 5.45).
При жестком соединении ригеля и колонны с замоноличиванием стыка и привариванием нижней арматуры ригеля к арматуре консоли через закладные детали продольная арматура консоли проверяется из условия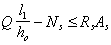
где l1, ho — соответственно вылет и рабочая высота короткой консоли;
Ns — горизонтальное усилие, действующее на верх консоли от ригеля, равное: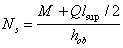
и принимаемое не более 1,4 kf lw Rwf + 0,3 Q (где kf и lw — соответственно высота и длина углового шва приваривания закладных деталей ригеля и консоли; Rf ѕ расчетное сопротивление угловых швов срезу по металлу шва, определяемое согласно СНиП II-23-81, при электродах Э42 Rwf = 180 МПа; 0,3 — коэффициент трения стали по стали), а также не более Rsw аsw (где Rsw и аsw — соответственно расчетное сопротивление и площадь сечения верхней арматуры ригеля).
В формулах (209) и (210):
M, Q — соответственно изгибающий момент и поперечная сила в нормальном сечении ригеля по краю консоли; если момент М растягивает нижнюю грань ригеля, значение М учитывается в формуле (210) со знаком «минус»;
lsup — фактическая длина площадки опирания нагрузки вдоль вылета консоли;
hob — рабочая высота ригеля.
ПРИМЕРЫ РАСЧЕТА
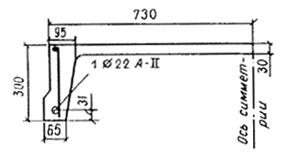
Пример 49. Дано: на короткую консоль колонны опирается свободно лежащая сборная балка (черт. 70), идущая вдоль вылета консоли; длина площадки опирания lsup,f = 300 мм; ширина консоли (колонны) b = 400 мм; соответственно высота и вылет консоли h = 700 мм, l1 = 350 мм; бетон колонны тяжелый класса В25 (Rb = 13 МПа, Rbt = 0,95 МПа при gb2 = 0,9; Еb = 27 × 103 МПа); продольная арматура класса А-III (Rs = 365 МПа); нагрузка на консоль Q = 700 кН.
Требуется проверить прочность консоли на действие поперечной силы и определить площадь сечения продольной арматуры и хомутов.
Черт. 70. К примеру расчета 49
Расчет. ho = h ‑ а = 700 ‑ 30 = 670 мм. Поскольку 3,5 Rbt bho = 3,5 × 0,95 × 400 × 670 = 891,1 × 103 H = 891,1 кН > Q = 700 кН и в то же время 2,5 Rbt bho = 2,5 × 0,95 × 400 × 670 = 636,5 кН <Q = 700 кН, прочность консоли проверяем из условия (207).
Согласно п. 3.99, расчетную длину площадки опирания нагрузки принимаем равной:
lsup = 2/3 lsup, f = 2/3 × 300 = 200 мм.
Согласно п. 5.77, принимаем шаг хомутов равным
sw = 150 мм < 
При двухветвевых хомутах диаметром 10 мм имеем Аsw = 157 мм2, тогда
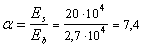
0,8 Rb blsup sin2q (1 + 5 amw) = 0,8 × 13 × 400 × 200 ґ
ґ 0,786 (1+5×7,4 × 2,62 × 10-3) = 717 × 103 H > Q = 700 кН,
т. е. прочность консоли по поперечной силе обеспечена.
Из условия (208) определим необходимую площадь сечения продольной арматуры консоли:
Принимаем 3 Æ 22 (As = 1140 мм2).
Расчет закладных деталей и соединений элементов
РАСЧЕТ ЗАКЛАДНЫХ ДЕТАЛЕЙ
3.101 (3.44). Расчет нормальных анкеров, приваренных в тавр к плоским элементам стальных закладных деталей, на действие изгибающих моментов, нормальных и сдвигающих сил от статической нагрузки, расположенных в одной плоскости симметрии закладной детали (черт. 71), должен производиться по формуле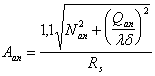
где Aan — суммарная площадь поперечного сечения анкеров наиболее напряженного ряда;
Nan ѕ наибольшее растягивающее усилие в одном ряду анкеров, равное:
Qan ѕ сдвигающее усилие, приходящееся на один ряд анкеров, равное:
Nўan — наибольшее сжимающее усилие в одном ряду анкеров, определяемое по формуле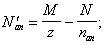
В формулах (211) ѕ (214):
М, N, Q — соответственно момент, нормальная и сдвигающая силы, действующие на закладную деталь; момент определяется относительно оси, расположенной в плоскости наружной грани пластины и проходящей через центр тяжести всех анкеров;
z ѕ расстояние между крайними рядами анкеров;
nan — число рядов анкеров вдоль направления сдвигающей силы; если не обеспечивается равномерная передача сдвигающей силы Q на все ряды анкеров, то при определении сдвигающего усилия Qan учитывается не более четырех рядов;
l — коэффициент, определяемый для анкерных стержней диаметром 8 — 25 мм для тяжелого и мелкозернистого бетонов классов В12,5 — В50 и легкого бетона классов В12,5 — В30 по формуле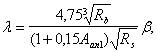
но принимаемый не более 0,7; для тяжелого и мелкозернистого бетонов класса выше В50 коэффициент l принимается как для класса В50, а для легкого бетона класса выше В30 — как для класса В30. Для тяжелого бетона коэффициент l можно определять по табл. 28.
В формуле (215):
Rb, Rs, ѕ в МПа;
при определении Rb коэффициент gb2 (см. п. 3.1) принимается равным 1,0;
Aan1 ѕ площадь сечения анкерного стержня наиболее напряженного ряда, см2;
b ѕ коэффициент, принимаемый равным для бетона:
тяжелого ………………………….. 1,0
мелкозернистого групп:
А ……………………………………… 0,8
Б и В ………………………………… 0,7
легкого ……………………………. rm/2300
(rm ѕ средняя плотность
бетона, кг/м3);
d ѕ коэффициент, определяемый по формуле
но принимаемый не менее 0,15;
здесь w = 0,3 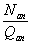
w = 0,6 
если растягивающие усилия в анкерах отсутствуют, то коэффициент d принимается равным 1,0.
Площадь сечения анкеров остальных рядов должна приниматься равной площади сечения анкеров наиболее напряженного ряда.
В формулах (212) и (214) нормальная сила N считается положительной, если направлена от закладной детали (см. черт. 71), и отрицательной — если направлена к ней. В случаях, когда нормальные усилия Nan и Nўan, а также сдвигающее усилие Qan при вычислении по формулам (212) ѕ (214) получают отрицательные значения, в формулах (211), (213) и (216) их принимают равными нулю. Кроме того, если Nan получает отрицательное значение, в формуле (213) принимается Nўan =N.
При расположении закладной детали на верхней (при бетонировании) поверхности изделия коэффициент l уменьшается на 20 %, а значение Nўan в формуле (213) принимается равным нулю.
Черт. 71. Схема усилий, действующих на закладную деталь
3.102. Расчет нормальных анкеров закладных деталей на действие расположенных в двух плоскостях симметрии закладной детали изгибающих моментов и сдвигающих сил, а также нормальной силы и крутящих моментов выполняется в соответствии с «Рекомендациями по проектированию стальных закладных деталей для железобетонных конструкций» (М., Стройиздат, 1984).
3.103(3.45). В закладной детали с анкерами, приваренными внахлестку под углом от 15 до 30° (см. п. 5.111), наклонные анкера, располагаемые симметрично относительно плоскости действия сдвигающей силы, рассчитываются на действие этой сдвигающей силы (при Q > N, где N ѕ отрывающая сила) по формуле
где Aan,inc ѕ суммарная площадь поперечного сечения наклонных анкеров;
Nan ѕ см. п. 3.101.
При этом должны устанавливаться нормальные анкера, рассчитываемые по формуле (211) при d = 1,0 и при значениях Qan, равных 0,1 сдвигающего усилия, определяемого по формуле (213). Допускается уменьшать площадь сечения наклонных анкеров за счет передачи на нормальные анкера части сдвигающей силы, равной Q ‑ 0,9 Rs Aan,inc. В этом случае d определяется по формуле (216).
Таблица 28
| Диаметр | Значения коэффициента l для расчета нормальных анкеров закладных деталей в зависимости от класса тяжелого бетона и арматуры | |||||||||||||||||
| анкера, | В15 | B20 | B25 | B30 | B40 | і B50 | ||||||||||||
| мм | А-I | A-II | A-III | А-I | A-II | A-III | А-I | A-II | A-III | А-I | A-II | A-III | А-I | A-II | А-III | А-I | A-II | A-III |
| 8 | 0,60 | ѕ | 0,48 | 0,66 | ѕ | 0,53 | 0,70 | ѕ | 0,57 | 0,70 | ѕ | 0,60 | 0,70 | ѕ | 0,66 | 0,70 | ѕ | 0,70 |
| 10 | 0,58 | 0,52 | 0,45 | 0,64 | 0,57 | 0,50 | 0,69 | 0,62 | 0,54 | 0,70 | 0,65 | 0,57 | 0,70 | 0,70 | 0,63 | 0,70 | 0,70 | 0,66 |
| 12 | 0,55 | 0,50 | 0,43 | 0,61 | 0,55 | 0,48 | 0,66 | 0,59 | 0,52 | 0,70 | 0,62 | 0,55 | 0,70 | 0,69 | 0,60 | 0,70 | 0,70 | 0,63 |
| 14 | 0,53 | 0,47 | 0,41 | 0,58 | 0,52 | 0,46 | 0,63 | 0,56 | 0,49 | 0,66 | 0,59 | 0,52 | 0,70 | 0,65 | 0,57 | 0,70 | 0,69 | 0,60 |
| 16 | 0,50 | 0,45 | 0,39 | 0,55 | 0,49 | 0,43 | 0,59 | 0,53 | 0,47 | 0,63 | 0,56 | 0,49 | 0,69 | 0,62 | 0,54 | 0,70 | 0,65 | 0,57 |
| 18 | 0,47 | 0,42 | 0,37 | 0,52 | 0,46 | 0,41 | 0,56 | 0,50 | 0,44 | 0,59 | 0,53 | 0,46 | 0,65 | 0,58 | 0,51 | 0,68 | 0,61 | 0,54 |
| 20 | 0,44 | 0,39 | 0,34 | 0,49 | 0,44 | 0,38 | 0,52 | 0,47 | 0,41 | 0,55 | 0,50 | 0,43 | 0,61 | 0,54 | 0,48 | 0,64 | 0,58 | 0,50 |
| 22 | 0,41 | 0,37 | 0,32 | 0,46 | 0,41 | 0,36 | 0,49 | 0,44 | 0,39 | 0,52 | 0,46 | 0,41 | 0,57 | 0,51 | 0,45 | 0,60 | 0,54 | 0,47 |
| 25 | 0,37 | 0,33 | 0,29 | 0,41 | 0,37 | 0,32 | 0,44 | 0,40 | 0,35 | 0,47 | 0,42 | 0,37 | 0,51 | 0,46 | 0,40 | 0,54 | 0,49 | 0,43 |
Примечания: 1. Для бетона класса В 12,5 коэффициент l следует уменьшать на 0,02 по сравнению с коэффициентом l для бетона класса В15.
2. Значения коэффициента l приведены при gbi = 1,00.
3.104. На приваренные к пластине упоры из полосовой стали или арматурных коротышей (см. п. 5.114) можно передавать не более 30% сдвигающей силы, действующей на деталь при напряжениях в бетоне под упорами, равных Rb. При этом значение сдвигающей силы, передаваемой на анкера закладной детали, соответственно снижается.
3.105(3.46). Конструкция сварных закладных деталей с приваренными к ним элементами, передающими нагрузку на закладные детали, должна обеспечивать включение в работу анкерных стержней в соответствии с принятой расчетной схемой. Внешние элементы закладных деталей и их сварные соединения рассчитываются согласно СНиП II-23-81. При расчете пластин и фасонного проката на отрывающую силу рекомендуется принимать, что они шарнирно соединены с нормальными анкерными стержнями. Если элемент, передающий нагрузку, приваривается к пластине по линии расположения одного из рядов анкеров, при расчете отрывающую силу рекомендуется уменьшать на величину пaАan1Rs (где na — число анкеров в данном ряду).
Кроме того, толщину пластины t расчетной закладной детали, к которой привариваются втавр анкера, следует проверять из условия
t і 0,25 
где dan — диаметр анкерного стержня, требуемый по расчету;
Rsq — расчетное сопротивление прокатной стали закладной детали сдвигу, равное 0,58 Ry (где Ry ѕ см. СНиП II-23-81).
Для типов сварных соединений, обеспечивающих большую зону включения пластины в работу при вырывании из нее анкерного стержня (см. поз. 6 табл. 52), возможна корректировка условия (218) с целью уменьшения толщины пластины. При действии на закладную деталь с уменьшенной толщиной пластины сдвигающей силы Q суммарная площадь сечения (перпендикулярного действию этой силы) пластины с приваренными к ней элементами в зоне расположения анкерных стержней вдоль силы Q принимается не менее площади сечения пластины толщиной, определяемой по формуле (218)
3.106. При выполнении условия
Nўan Ј 0, (219)
где Nўan — см. п. 3.101, т. е. когда все нормальные анкера растянуты, производят расчет на выкалывание бетона следующим образом:
а) для нормальных анкеров с усилением на концах (см. п. 5.113) ѕ из условия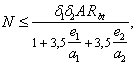
где А — площадь проекции на плоскость, нормальную к анкерам, поверхности выкалывания, идущей от усилений анкеров (краев анкерных пластин или высаженных головок) под углом 45° к осям анкеров; при эксцентриситете силы N относительно центра тяжести анкеров eo = M/N размер проекции поверхности выкалывания в направлении этого эксцентриситета уменьшается на величину, равную 2eo, при соответствующем смещении наклонной грани поверхности выкалывания (черт. 72); площади анкерных пластин или высаженных головок, расположенных на поверхности выкалывания, не учитываются;
d1 ѕ коэффициент, принимаемый равным: для тяжелого и мелкозернистого бетонов — 0,5; для легкого бетона — 0,4;
d2 — коэффициент, принимаемый равным:
при 

при 
При этом, если часть стержня длиной а расположена в зоне бетона при 0,25 Ј sbc/Rb Ј 0,75, d2 определяется по формуле
d2 = 1 + 0,2 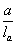
здесь la — длина анкерного стержня;
сжимающие напряжения в бетоне sbc, перпендикулярные нормальному анкеру и распределенные по всей длине, определяются как для упругого материала по приведенному сечению от постоянно действующих нагрузок при коэффициенте надежности по нагрузке, равном 1,0;
a1, a2 — размеры проекции поверхности выкалывания;
e1, e2 — эксцентриситеты силы N относительно центра тяжести площади А в направлении соответственно размеров а1 и a2;
Черт. 72. Схема выкалывания бетона анкерами закладной детали с усилениями на концах при Nўan Ј 0
1 ѕ точка приложения нормальной силы N; 2 ѕ поверхность выкалывания; 3 — проекция поверхности выкалывания на плоскость, нормальную к анкерам
б) для анкеров без усиления на концах расчет производится из условия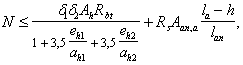
где Ah — то же, что и А, если поверхность выкалывания проходит на расстоянии h от пластины закладной детали (черт. 73);
ah1, ah2 ѕ размеры проекции поверхности выкалывания;
eh1, eh2 — эксцентриситеты силы N относительно центра тяжести площади Ah, в направлении соответственно размеров ah1 и ah2;
Аan,a ѕ площадь сечения всех анкеров, пересекающих поверхность выкалывания;
lan — длина зоны анкеровки (см. п. 5.44).
Условие (222) проверяется при различных значениях h, меньших длины анкеров или равных ей.
Черт. 73. Схема выкалывания бетона анкерами закладной детали без усилений на концах при N’an Ј 0
1 ѕ точка приложения нормальной силы N; 2 ѕ поверхность выкалывания; 3 ѕ проекция поверхности выкалывания на плоскость, нормальную к анкерам
Если число анкеров в направлении эксцентриситета больше двух, в условиях (220) и (222) силу N можно уменьшить на величину
Если концы анкеров находятся вблизи поверхности бетона, противоположной пластине закладной детали, необходимо произвести дополнительную проверку условия (222) без учета последнего члена правой части условия при h, равном расстоянию от пластины до противоположной грани элемента, при этом часть площади Ah, расположенная между крайними рядами анкеров, не учитывается.
3.107. При выполнении условия Nўan > 0 и наличии усиления на концах анкеров расчет бетона на выкалывание (черт. 74) производится из условия
где Nan ѕ см. формулу (212);
A1 ѕ то же, что А в формуле (220), если поверхность выкалывания начинается от места усиления анкеров наиболее растянутого ряда (см. черт. 74);
е — эксцентриситет усилия N относительно центра тяжести площади А1 в направлении размера а.
Расчет на выкалывание можно не производить, если концы анкеров заведены за продольную арматуру, расположенную у противоположной от закладной детали грани колонны, а усиления анкеров в виде пластин или поперечных коротышей зацепляются за стержни продольной арматуры диаметром: при симметричном зацеплении — не менее 20 мм, при несимметричном — не менее 25 мм (черт. 75). В этом случае участок колонны между крайними рядами анкеров проверяется, согласно пп. 3.31 и 3.53, на действие поперечной силы, равной:
Q = Nan 
где Qcol ѕ поперечная сила на участке колонны, прилежащем к наиболее растянутому ряду анкеров закладной детали, определяемая с учетом усилий, действующих на закладную деталь.
Черт. 74. Схема выкалывания бетона растянутыми анкерами закладной детали при Nўan > 0
1 — проекция поверхности выкалывания на плоскость, нормальную к анкерам; 2 — анкерная пластина; 3 — точка приложения усилия Nan
Черт. 75. Конструкция закладной детали, не требующей расчета на выкалывание
а — закладная деталь с коротышами, симметрично зацепленными за продольную арматуру колонны; б ѕ эпюра Q участка колонны с закладной деталью; в ѕ анкера закладной детали с анкерными пластинами, несимметрично зацепленными за продольную арматуру колонны; 1 — поперечные коротыши, приваренные контактной сваркой к анкерам; 2 ѕ анкера; 3 ѕ анкерные пластины
3.108. Если сдвигающая сила Q действует на закладную деталь по направлению к краю элемента (черт. 76), при отсутствии наклонных анкеров расчет на откалывание бетона производится из условия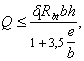
где d1 ѕ см. п. 3.106; при расположении закладной детали на верхней (при бетонировании) поверхности изделий из легких бетонов коэффициент d1 уменьшается на 20 %,
b ѕ ширина элемента, равная b = c1 + c2 + s (где c1 и c2 ѕ расстояния от крайних рядов анкеров до ближайших краев элемента в направлении, нормальном к сдвигающей силе, принимаемые не более h, s ѕ расстояние между крайними рядами анкеров в том же направлении);
h ѕ расстояние от наиболее удаленного ряда анкеров до края элемента в направлении сдвигающей силы Q, принимаемое не более толщины элемента b1 (см. черт. 76);
е ѕ эксцентриситет силы Q относительно середины ширины элемента b.
В случае приложения к закладной детали кроме сдвигающей силы Q отрывающей силы N правая часть условия (224) умножается на коэффициент 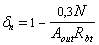
Черт. 76. Схема для расчета на откалывание бетона нормальными анкерами закладной детали
В случае приложения сдвигающей силы к закладной детали с наклонными анкерами, приваренными внахлестку и имеющими на концах усиления (см. п. 5.113), расчет на откалывание бетона производится в соответствии с Рекомендациями, упомянутыми в п. 3.102.
3.109. Если на концах анкеров закладной детали имеются усиления в виде анкерных пластинок или высаженных головок (см. п. 5.113), бетон под этими усилениями проверяется на смятие из условия
где a, jb — коэффициенты определяемые согласно п. 3.93;
Аloc1 ѕ площадь анкерной пластины или сечения высаженной головки за вычетом площади сечения анкера;
Nloc — сила смятия, определяемая следующим образом:
а) для анкеров, приваренных втавр, при la і 15d:
если вдоль анкера возможно образование трещин от растяжения бетона или в случае применения гладких анкерных стержней ѕ по формуле
Nloc = Nan1; (226)
если образование этих трещин невозможно — по формуле
Nloc = Nan1 
б) для анкеров, приваренных втавр, при la < 15d значение Nloc определенное по формулам (226) и (227), увеличивается на 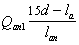
в) для анкеров, приваренных внахлестку, Nloc определяется по формуле
nloc = Qinc. (228)
В формулах (226) ѕ (228):
Nan1, Qan1 ѕ соответственно наибольшее растягивающее и сдвигающее усилия, приходящиеся на один нормальный анкер (см. п. 3.101);
Qinc ѕ усилие в наклонном анкере.
Формулой (225) можно пользоваться, если толщина анкерной пластины составляет не менее 0,2 ее длины.
3.110. Определение перемещений сварных закладных деталей, расчет наклонных анкеров, приваренных под слоем флюса к пластине под углом более 45°, и расчет штампованных закладных деталей производятся согласно Рекомендациям, упомянутым в п. 3.102.
ПРИМЕРЫ РАСЧЕТА
Пример 50. Дано: закладная деталь колонны с приваренным столиком для опирания обвязочных балок, а также расположение и величины нагрузок от обвязочных балок — по черт. 77; анкера из арматуры класса А-III (Rs = 365 МПа); бетон колонны тяжелый класса В20; пластина из стали марки ВСт3кп2 (Ry = 215 МПа).
Требуется запроектировать нормальные анкера закладной детали и определить толщину пластины.
Черт. 77. К примеру расчета 50
Расчет. Принимаем расположение анкеров, как показано на черт. 77. Поскольку все нагрузки действуют в одном направлении и не вызывают кручения, определяем суммарную площадь поперечного сечения анкеров наиболее напряженного верхнего ряда по формуле (211).
Для этого вычислим момент внешних сил:
М = Ql = 150 × 0,15 = 22,5 кН×м.
Принимая z = 0,3м и N = 0, определим наибольшее растягивающее усилие в одном ряду анкеров по формуле (212):
На черт. 77 сдвигающая сила Q = 150 кН, число рядов анкеров nan = 3.
Сдвигающее усилие, приходящееся на один ряд анкеров, вычислим по формуле (213), принимая Nўan = Nan = 75 кН:
Коэффициент d определим по формуле (216).
Так как Nўan > 0, w = 0,3
отсюда
Задаваясь диаметром анкеров 16 мм, по табл. 28 при классе бетона В20 и классе арматуры А-III находим l = 0,43, тогда
Принимаем по два анкера в каждом ряду диаметром 18 мм (Aan = 509 мм2).
Проверим значение Aan при коэффициенте, соответствующем принятому диаметру 18 мм, т. е. при l = 0,41:
Оставляем 2Æ18.
Определим минимально допустимую длину анкеров без усилений lan согласно п. 5.112. Для этого вычислим коэффициент d3:
Значение Rb принимаем с учетом gb2 = 0,9 (нагрузки непродолжительного действия отсутствуют), т.е. Rb = 10,5 МПа.
Определим lan, предполагая „в запас» sbc < 0,25 Rb, т. е. принимая wan = 0,7, Dlan = 11:
Учитывая, что площадь Aan принята с запасом, уточним значение lan:
Поскольку при такой длине анкеров размещение их в колонне невозможно, требуется уменьшить длину анкеров с устройством на концах усилений. Согласно п. 5.113, концы анкеров усиливаем высаженными головками диаметром dh = 54 мм і 3d и проверяем бетон на смятие под головкой и на выкалывание, приняв длину анкеров равной la = 250 мм > 10d = 10 × 18 = 180 мм.
Расчет на смятие производим согласно п. 3.109.
Площадь смятия Аloc1 под высаженной головкой одного анкера равна:
Предположим «в запас», что в колонне со стороны закладной детали возможно образование трещин. Тогда, согласно п. 3.109, при la = 250 мм < 15 d = 15 × 18 = 270 мм сила смятия будет равна:
Принимаем максимальное значение jb = 2,5, поскольку расчетная площадь бетона Аloc2 здесь неопределенно велика; a = 1,0.
Проверим условие (225):
т. е. прочность на смятие обеспечена.
Поскольку Nўan > 0, расчет на выкалывание производим согласно п. 3.107. Концы анкеров с усилениями не заведены за продольную арматуру колонны, расположенную у противоположной от закладной детали грани колонны, поэтому расчет производим из условия (223).
Вычислим значение A1 (см. черт. 77):
A1 = (2 × 250 + 54) 400 ‑ 2 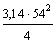
Усилие Nan = 75 кН приложено в центре тяжести площади А1, следовательно, е = 0. Для тяжелого бетона d1 = 0,5.
Проверим условие (223), пренебрегая ,,в запас» сжимающими напряжениями бетона (т. е. d2 = 1,0) и учитывая gb2 = 0,9 (т. е. Rbt = 0,8 МПа):
d1d2A1Rbt = 0,5 × 1 × 217000 × 0,80 = 86800 Н > Nan = 75000 Н,
т. е. прочность бетона на выкалывание обеспечена.
Принятые расстояния между анкерами в направлении поперек и вдоль сдвигающей силы, соответственно равные 260 мм > 5d = 5 × 18 = 90 мм и 150 мм > 7d = 7 × 18 = 126 мм, удовлетворяют требованиям п. 5.111. Расстояние от оси анкера до грани колонны, равное 70 мм > 3,5d = 3,5 × 18 = 63 мм, также удовлетворяет требованиям п. 5.111.
Конструкция столика, приваренного к закладной детали, обеспечивает равномерное распределение усилий между растянутыми анкерами и равномерную передачу сжимающих напряжений на бетон, не вызывая изгиба пластины закладной детали. Поэтому толщину этой пластины определим из условия (218), принимая Rsq = 0,58 Ry = 0,58 × 215 = 125 МПа, а диаметр анкера, требуемый по расчету, равным 
t = 0,25 

Из условия механизированной дуговой сварки под флюсом (см. табл. 52, поз. 1) толщина пластины должна быть не менее 0,65d = 0,65 × 18 = 11,7 мм.
Принимаем толщину пластины t = 14 мм.
Пример 51. Дано: закладная деталь колонны с приваренным раскосом стальных связей — по черт. 78, а; растягивающая сила в раскосе от действия ветровых нагрузок 270 кН; анкера закладной детали из арматуры класса A-III (Rs = 365 МПа); пластина закладной детали из стали марки ВСт3сп2 (Ry = 215 МПа); бетон колонны тяжелый класса В30; армирование колонны — по черт. 78, б, минимальная продольная сила в колонне 1100 кН; изгибающий момент в колонне на уровне закладной детали в плоскости анкеров 40 кН × м.
Требуется запроектировать анкера закладной детали, определить толщину пластины и проверить прочность окружающего бетона на выкалывание.
Расчет. Принимаем расположение рядов анкеров по вертикали, как показано на черт. 78, в. Усилие в раскосе раскладываем на нормальную силу N, приложенную к закладной детали с эксцентриситетом e0 = 100 мм, и сдвигающую силу Q:
N = 270 cos 56°20ў = 270 × 0,555 = 150 кН;
Q = 270 sin 56°20ў = 270 × 0,832 = 225 кН.
При z = 0,42 м и M = Neo = 150 × 0,1 = 15 кН×м определим наибольшее растягивающее усилие в одном ряду анкеров по формуле (212):
Наибольшее сжимающее усилие в одном ряду анкеров вычислим по формуле (214):
т. е. прижатие пластины к бетону отсутствует.
Сдвигающее усилие Qan, приходящееся на один ряд анкеров, определим по формуле (213), принимая Nўan = 0:
Так как N’an = 0,
w = 0,6 

отсюда 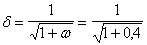
Черт. 78. К примеру расчета 51
По табл. 28, задаваясь диаметром анкеров 16 мм, при классе бетона В30 и анкерах из арматуры класса А-III находим l = 0,49, тогда
Принимаем по два анкера в каждом ряду диаметром 18 мм (Aan = 509 мм2). Проверим необходимое значение Aan при коэффициенте l, соответствующем принятому диаметру 18 мм, т. е. при l = 0,46:
Оставляем по два анкера диаметром 18 мм. Располагаем анкера на минимальном расстоянии один от другого в горизонтальном направлении, равном 5d = 5 × 18 = 90 мм (см. п. 5.111). Расстояния между анкерами в вертикальном направлении (т. е. в направлении сдвигающей силы Q), равные 140 мм > 7d = 7 × 18 = 126 мм, также удовлетворяют требованию п. 5.111.
Определим толщину пластины закладной детали. Поскольку фасонка, передающая отрывающую силу на закладную деталь, располагается посредине расстояния между вертикальными рядами анкеров, толщину пластины определим из расчета на прочность пластины как консольной балки с вылетом 35 мм (см. черт. 78) на действие растягивающего усилия в одном анкере, равного: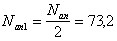
Ширину консольной балки принимаем b = 80 мм. Расчет производим из условия М Ј RyW, где М = 36600 × 35 = 1×280000 H×мм, 
откуда 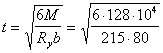
Принимаем пластину из полосовой стали толщиной 22 мм, при этом выполняются условие (218):
0,25 
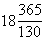
Определим минимально допустимую длину анкеров без усилений по формуле (316) с учетом п. 5.112. Для этого вычислим коэффициент d3:
Значение Rb принимаем с учетом gb2 = 1,1, поскольку нагрузка на закладную деталь вызвана только ветровой нагрузкой, т. е. Rb = 19 МПа.
Для определения коэффициентов wan и Dl вычислим максимальное и минимальное напряжения бетона в пределах длины анкера. Для этого вычислим приведенные площадь Ared и момент инерции Ired сечения колонны, принимая по черт. 78, б Аs = Аўs = 1232 мм (2Æ28):
Аred = bh + 2Аs (a ‑ 1) = 400 × 400 + 2 × 1232 (6,9 ‑ 1) = 174,5 × 103 мм2;
Ired = 
= 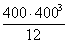
здесь 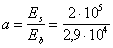
Максимальное напряжение бетона в конце анкера длиной la = 300 мм (т. е. на расстоянии у = 300 + 22 — 400/2 = 122 мм от центра тяжести сечения):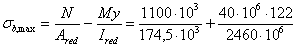
= 6,31 + 1,98 = 8,3 МПа < 0,75 Rb = 14,3 МПа.
Минимальное напряжение бетона в начале анкера, т. е. при у = 

= 3,42 МПа < 0,25 Rb = 4,75 МПа.
Поскольку анкер не расположен полностью в зоне с напряжением от 0,25Rb до 0,757Rb, определим длину части анкера а, расположенную в этой зоне:
Тогда, согласно формуле (317),
Dlan определяем аналогично wan с заменой коэффициентов 0,7 и 0,5 соответственно на 11 и 8 (см. табл. 44):
Допустимая длина анкера равна:
Учитывая, что площадь Aan принята с запасом, уточняем lan : lan = 305
Принимаем длину анкера la = 300 мм.
Проверим бетон на выкалывание.
Поскольку все анкера растянуты и не имеют усилений, расчет производим из условия (222). Определим площадь проекции поверхности выкалывания аh с учетом смещения наклонной грани на 2eo = 2 × 100 = 200 мм. При h = la = 300 мм
Ah = (420 ‑ 200 + 2 × 300) 400 = 32,8 × 104 мм2.
Так как сила N приложена в центре тяжести площади Ah, eh1 = еh2 = 0, d1 = 0,5 (как для тяжелого бетона).
По формуле (221) получим
d2 = 1 + 0,2 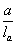
Поскольку la = h, RsАап,а (la ‑ h)/lan = 0. Учитывая, что gb2 = 1,1, Rbt = 1,3 МПа.
d1d2AhRbt = 0,5 × 1,145 × 32,8 × 104 × 1,3 = 244300 Н > N = 150 кН.
Проверим условие (222) при h = 200 мм < la. Так как на расстоянии h от пластины поверхность выкалывания пересекает только две пары анкеров,
Aan1 = 1018 мм2 (4Æ18);
Аh = (420 ‑ 200 + 2 × 200) 400 = 24,2 × 104 мм2,
d1d2AhRbt + RsАап,а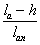
= 0,5 × 1,145 × 24,2 × 104 × 1,3 + 365 × 1018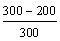
= 304 × 103 Н > N = 150 кН.
Поскольку с уменьшением h несущая способность бетона на выкалывание повышается, расчет при меньших значениях h не производим.
Проверим условие (222) при значении h, равном высоте сечения колонны, т. е. h = 400 мм, без учета площади, расположенной между анкерами [(420 ‑ 200) 90 = 19800 мм2]:
Аh = (420 ‑ 200 + 2 × 400) 400 ‑ 19800 = 388 000 мм2 > 328000 мм2,
т. е. площадь Аh превышает площадь, вычисленную при h = 300 мм. Следовательно, прочность бетона на выкалывание обеспечена.
РАСЧЕТ СТЫКОВ СБОРНЫХ КОЛОНН
3.111. Стыки колонн, выполняемые ванной сваркой выпусков продольной арматуры, расположенных в специальных подрезках, при последующем замоноличивании этих подрезок (см. п. 5.90) рассчитываются для двух стадий работы:
1-я до замоноличивания стыка — на нагрузки, действующие на данном этапе возведения здания; при определении усилий такие стыки условно принимаются шарнирными;
2-я после замоноличивания стыка ѕ на нагрузки, действующие на данном этапе возведения здания и при эксплуатации; при определении усилий такие стыки принимаются жесткими.
3.112. Расчет незамоноличенных стыков колонн, указанных в п. 3.111 (черт. 79), производится на местное сжатие бетона колонны центрирующей прокладкой из условия (196) с добавлением в его правую часть усилия, воспринимаемого арматурными выпусками и равного:
Nout = 0,5 jRsc As (229)
где j ѕ коэффициент продольного изгиба для выпусков, определяемый в соответствии со СНиП II-23-81 (табл. 72) при расчетной длине lo, равной фактической длине свариваемых выпусков;
Аs ѕ площадь сечения всех выпусков.
При этом значение R*b,loc умножается на коэффициент yloc = 0,75, учитывающий неравномерность распределения нагрузки под центрирующей прокладкой, а за расчетную площадь Аloc2 принимается часть площади сечения торца колонны Aef в пределах контура сеток косвенного армирования размерами, не превышающими соответствующих утроенных размеров площади смятия Аloc1.
За площадь Аloc1 принимается площадь центрирующей прокладки или, если центрирующая прокладка приваривается при монтаже к распределительному листу (см. черт. 79), площадь этого листа. При этом его учитываемые размеры не должны превышать соответствующих размеров площади Aef, а толщина листа должна быть не менее 1/3 максимального расстояния от края листа до центрирующей прокладки.
Черт. 79. Незамоноличенный стык колонны
1 ѕ центрирующая прокладка; 2 ѕ распределительный лист; 3 ѕ ванная сварка арматурных выпусков; 4 — сетки косвенного армирования торца колонны
3.113. Расчет замоноличенных стыков колонн, указанных в п. 3.111, производится как для сечения колонны на участке с подрезками согласно пп. 3.50ѕ3.76 с учетом следующих рекомендаций:
а) при наличии косвенного армирования сетками как в бетоне колонн, так и в бетоне замоноличивания расчет ведется согласно пп. 3.57 и 3.60, при этом рассматривается цельное сечение, ограниченное стержнями сеток, расположенными у граней замоноличенного участка колонны (черт. 80);
Черт. 80. Расчетное сечение замоноличенного стыка колонны с сетками косвенного армирования в бетоне колонны и в бетоне замоноличивания
1 ѕ бетон колонны; 2 ѕ бетон замоноличивания; 3 ѕ сетки косвенного армирования
б) при наличии косвенного армирования только в бетоне колонн расчет производится или с учетом этого косвенного армирования, но без учета бетона замоноличивания, или с учетом бетона замоноличивания, но без учета косвенного армирования колонн; прочность стыка считается обеспеченной при выполнении условия прочности хотя бы по одному из этих расчетов;
в) расчетные сопротивления бетона колонн и бетона замоноличивания (Rb или Rb,red) умножаются на коэффициенты условий работы, соответственно равные gbc = 0,9 и gbs = 0,8;
г) при расчете с учетом замоноличивания значение w определяется по формулам (15) или (104) по классу бетона замоноличивания, если он располагается по всей ширине наиболее сжатой грани, и по наибольшему классу бетона, если по сжатой грани располагается частично бетон замоноличивания и частично бетон колонны; в формуле (104) всегда учитывается минимальное значение mxy.
При расчете стыка с учетом бетона замоноличивания площадь сечения замоноличивания аbs рекомендуется приводить к площади сечения колонны умножением ее на отношение расчетных сопротивлений бетона замоноличивания и бетона колонны при неизменных высотах сечения замоноличивания.
Для симметрично армированных колонн прямоугольного сечения расчет замоноличенного стыка можно производить по формулам пп. 3.67 и 3.68, принимая за hўf = hf высоту сечений подрезок, а за bўf = bf ѕ ширину сечения, приведенного к бетону колонны, по наиболее сжатой стороне сечения.
Коэффициент h, учитывающий прогиб колонны (см. п. 3.54), определяется по геометрическим характеристикам сечения колонны вне зоны стыка.
3.114. Стыки колонн, выполняемые сопряжением торцов через слой цементного или полимерного раствора с обрывом продольной арматуры (см. п. 5.91, стыки 1-го и 2-го типов), в стадии эксплуатации рассчитываются как внецентренно сжатые бетонные элементы согласно п. 3.6 с учетом косвенного армирования сетками согласно пп. 3.57 и 3.60. При этом расчетное сопротивление бетона rb,red умножается на коэффициент условий работы gb, равный 0,9 или 1,0, при заполнении шва соответственно цементным или полимерным раствором. При отсутствии раствора между торцами колонн (например, в сферических стыках, в стыках с приторцованными поверхностями) указанный коэффициент условий работы принимается равным gb = 0,65.
ПРИМЕРЫ РАСЧЕТА
Пример 52. Дано: стык колонны — по черт. 81; бетон колонны класса В30 (Rbc = 15,5 МПа при gb2 = 0,9; Rb,ser = 22 МПа); бетон замоноличивания класса B20 (Rbs = 10,5 МПа при gb2 = 0,9; Rb,ser = 15 МПа); арматурные выпуски класса А-III (Rs = Rsc = 365 МПа; Rs,ser = 390 МПа), площадь их сечения Аs = А’s = 4070 мм2 (4Æ36); сетки косвенного армирования их стержней класса А-III, диаметром 8 мм (Rs,xy = 355 МПа) с шагом s = 70 мм как в бетоне колонны, так и в бетоне замоноличивания; продольная сила в стадии эксплуатации N = 3900 кН при gf > 1,0 и N = 3300 кН при gf = 1,0, ее эксцентриситет в перпендикулярном подрезкам направлении с учетом прогиба колонны eo = 55 мм.
Требуется проверить прочность стыка в стадии эксплуатации и определить предельную продольную силу в стыке в стадии возведения здания.
Черт. 81. К примеру расчета 52
1 ѕ арматурные выпуски; 2 — распределительный лист; 3 ѕ центрирующая прокладка
Расчет в стадии эксплуатации. В соответствии с п. 3.113a принимаем размеры сечения по осям крайних стержней сеток, т. е. b = h = 360 мм, ho = 330 мм (см. черт. 81).
Определим расчетное сопротивление бетона колонны и замоноличивания с учетом сеток косвенного армирования согласно п. 3.57.
Для бетона колонн:
Aef = 360 × 200 = 72 000 мм2 (см. черт. 81);
nx = 5; lx = 170 мм; пy = 3; ly = 360 мм; Asx = Asy = 50,3 мм2 (Æ8);
Отсюда значение Rbc,red с учетом коэффициента условий работы gbc = 0,9 (см. п. 3.113 в) равно:
Rbc,red = gbc (Rbc + jmхуRs,ху) =
= 0,9(15,5 + 2,0 × 0,0193 × 355) = 26,3 МПа.
Для бетона замоноличивания в одной из подрезок
Aef = 360 × 80 = 28 800 мм2 (см. черт. 81);
Asx = Asy = 50,3 мм2 (Æ8); lx = 65 мм; ly = 360 мм;
Значение Rbs,red с учетом коэффициента условий работы gbs = 0,8 равно:
Rbs,red = gbs (Rbs + jmхуRs,ху) =
= 0,8(10,5 + 1,47 × 0,026 × 355) = 19,3 МПа.
Определим значение w по формуле (104) по классу бетона замоноличивания, поскольку подрезка располагается по всей ширине наиболее сжатой грани колонны, при этом принимаем минимальное значение mxy = 0,0193:
d2 = 10mxy = 10 × 0,0193 = 0,19 > 0,15, принимаем d2 = 0,15;
w = 0,85 ‑ 0,008Rbs + d2 = 0,85 ‑ 0,008 × 10,5 + 0,15 = 0,916 > 0,9, принимаем w = 0,9.
Приводим сечение стыка к бетону колонны, при этом ширина подрезки становится равной: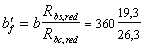
высота подрезки hўf = 80 мм (см. черт. 81).
Прочность стыка проверим согласно п. 3.67.
Для этого по формуле (14) определим значение xR, принимая ssc,и = 500 МПа:
Aov = (b’f ‑ b) hўf = (264 ‑ 360)80 = ‑ 7680 мм2.
Высота сжатой зоны равна:
Так как х = 433 мм > xR ho = 0,794 × 330 = 260 мм, высоту сжатой зоны определим по формуле (132).
Для этого вычислим:
Значение е равно e = eo + 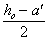

Прочность стыка проверим по условию (131):
Rbc,redbx (ho ‑ x/2) + Rbc,redAov (ho ‑ hўf/2) + Rsc Aўs (ho ‑ aў) =
= 26,3 × 360 × 293 (330 ‑ 293/2) ‑ 26,3 × 7680 (330 ‑ 80/2) +
+ 365 × 4070 (330 ‑ 30) = 896,1 × 106 H × мм > Ne = 3900 × 0,205 = 800 кН × м,
т. е. прочность стыка в стадии эксплуатации обеспечена.
Проверим трещиностойкость защитного слоя замоноличенного участка колонны согласно п. 3.60 по аналогии с расчетом по прочности стыка в стадии эксплуатации:
ho = h ‑ a = 400 ‑ 50 = 350 мм;
w = 0,85 ‑ 0,006Rbs,ser = 0,85 ‑ 0,006 × 15 = 0,76;
Aov = (b’f ‑ b) hўf = (273 ‑ 400) 100 = ‑12700 мм2;
Rs = Rsc = Rs,ser = 390 МПа;
e = eo + 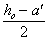

Rbc,serbx (ho ‑ x/2) + Rbc,serAov (ho ‑ hўf/2) + RscAўs (ho ‑ aў) =
= 22 × 400 × 254 (350 ‑ 254/2) ‑ 22 × 12700 (350 ‑ 100/2) + 390 × 4070 (350 ‑ 50) =
= 890,8 × 106 H×мм > Ne = 3300 × 0,205 = 677 кН×м.
Расчет незамоноличенного стыка в стадии возведения. Определяем расчетное сопротивление бетона смятию с учетом косвенного армирования согласно пп. 3.93 и 3.112.
Площадь части сечения торца колонны, ограниченная контуром сеток, равна:
Aef = 170 × 360 = 61200 мм2.
За площадь смятия принимаем площадь распределительного листа, поскольку его толщина 20 мм превышает 1/3 расстояния от края листа до центрирующей прокладки (50 × 1/3 = 17 мм), при этом ширину площади смятия принимаем равной ширине сетки — 170 мм.
Aloc1 = 200 × 170 = 34 000 мм2.
Поскольку 360 мм < 3 × 200 мм, принимаем Aloc2 = Aef = 61200 мм2,
отсюда
Поскольку расчет производим на нагрузки в стадии возведения, принимаем Rbc = 19 МПа (т. e. при gb2 = 1,1):
Значение R*b,loc определяем по формуле (197), учитывая коэффициент yloc = 0,75:
R*b,loc = yloc (Rbс jb + jmxy Rs,xy js) = 0,75 (19 × 1,22 +
+ 1,97 × 0,0226 × 355 ×2,56) = 47,7 МПа.
По формуле (229) определим усилие в арматурных выпусках.
Радиус инерции арматурного стержня Æ36 равен:
Длина сваренных выпусков l = lo = 400 мм.
Согласно табл. 72 СНиП II-23-81 при l = 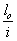
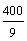
Предельная продольная сила, воспринимаемая незамоноличенным стыком, равна:
N = R*b,loc Aloc1 + Nоut = 47,7 × 34000 + 1245 × 103 = 2867 × 103 H.
РАСЧЕТ БЕТОННЫХ ШПОНОК
3.115. Размеры бетонных шпонок, передающих сдвигающие усилия между сборным элементом и дополнительно уложенным бетоном или раствором (черт. 82), рекомендуется определять по формулам :

где Q — сдвигающая сила, передающаяся через шпонки;
tk, hk, lk ѕ глубина, высота и длина шпонки;
пk — число шпонок, вводимое в расчет и принимаемое не более трех.
Черт. 82. Схема для расчета шпонок, передающих сдвигающие усилия от сборного элемента монолитному бетону
1 ѕ сборный элемент; 2 ѕ монолитный бетон
При наличии сжимающей силы N высоту шпонок допускается определять по формуле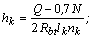
и принимать уменьшенной по сравнению с высотой, определяемой по формуле (231), не более чем в 2 раза.
При соединении шпонками элементов настила длина шпонки, вводимая в расчет, должна составлять не более половины пролета элемента, при этом величина Q принимается равной сумме сдвигающих усилий по всей длине элемента.
По условиям (230) ѕ (232) следует проверять шпонки сборного элемента и шпонки из дополнительно уложенного бетона, принимая расчетные сопротивления бетона шпонок Rb и Rbt как для бетонных конструкций.
Примечание. При расчете на выдергивание растянутой ветви двухветвевой колонны из стакана фундамента допускается учитывать работу пяти шпонок.
4. РАСЧЕТ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ОБРАЗОВАНИЮ ТРЕЩИН
4.1(4.1). Железобетонные элементы рассчитываются по образованию трещин:
нормальных к продольной оси элемента;
наклонных к продольной оси элемента.
Расчет по образованию трещин производится:
а) для выявления необходимости проверки по раскрытию трещин;
б) для выяснения случая расчета по деформациям.
В железобетонном элементе или на его участках трещины отсутствуют, если усилия, вызванные действием полной нагрузки (или ее части, когда нагрузки вызывают усилия разных знаков) и вводимые в расчёт с коэффициентом надежности по нагрузке gf = 1,0, меньше усилий, воспринимаемых сечением при образовании трещин. Полная нагрузка включает постоянные, длительные и кратковременные нагрузки.
Допускается принимать без расчета, что изгибаемые элементы сечений прямоугольного и таврового со сжатыми полками имеют на наиболее напряженных участках трещины, нормальные к продольной оси, если требуемый по расчету коэффициент армирования m > 0,005.
4.2(4.5). Расчет железобетонных элементов по образованию нормальных трещин производится из условия
Мr < Мcrc, (233)
где Мr ѕ момент внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно оси, параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется;
Мcrc — момент, воспринимаемый сечением, нормальным к продольной оси элемента при образовании трещин, и определяемый по формуле
Mcrc = Rbt,serWpl 
здесь Mshr ѕ момент усилия Nshr вызванного усадкой бетона, относительно той же оси, что и для определения Мr; знак момента определяется направлениями вращения («плюс» ѕ когда направления противоположны, «минус» ѕ когда направления моментов Мshr и Мr совпадают).
Для свободно опертых балок и плит момент Мcrc определяется по формуле
Mcrc = Rbt,serWpl ‑ Nshr (eop + r). (235)
Усилие Nshr рассматривается как внешняя растягивающая сила; его величина и эксцентриситет относительно центра тяжести приведенного сечения определяются по формулам:
Nshr = sshr (As + Aўs); (236)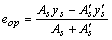
где sshr ѕ напряжение в арматуре, вызванное усадкой бетона, равное: для тяжелого бетона класса В35 и ниже — 40 МПа при естественном твердении и 35 МПа ѕ при тепловой обработке; для других видов и классов бетона sshr принимается согласно СНиП 2.03.01-84 (табл. 5, поз. 8);
уs, уўs ѕ расстояния от центра тяжести приведенного сечения до центров тяжести сечений соответственно арматуры S и Sў.
Если коэффициент армирования m < 0,01, допускается в формулах (234) и (235) величины Wpl и r определять как для бетонного сечения, принимая Nshr = 0 и As = A’s = 0.
Значение Mr определяется по формулам:
для изгибаемых элементов (черт. 83, а)
Мr = М;
для внецентренно сжатых элементов (черт. 83, б)
Mr = N(eo ‑ r), (238)
для центрально- и внецентренно растянутых элементов (черт. 83, в)
Mr = N(eo + r), (239)
В формулах (234), (235), (238) и (239):
r — расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
Значение r определяется для элементов:
изгибаемых — по формуле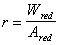
внецентренно сжатых — по формуле
здесь
но принимается не менее 0,7 и не более 1,0;
sb — максимальное напряжение в сжатом бетоне, вычисляемое как для упругого тела по приведенному сечению;
центрально- и внецентренно растянутых — по формуле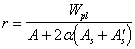
Wpl ѕ момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона, определяемый согласно п.4.3.
Примечание. Приведенное сечение включает сечение бетона, а также сечение всей продольной арматуры, умноженное на отношение соответствующих модулей упругости арматуры и бетона.
4.3 (4.7). Момент сопротивления приведенного сечения для крайнего растянутого волокна Wpl (с учетом неупругих деформаций растянутого бетона) определяется в предположении отсутствия продольной силы N по формуле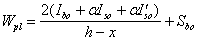
где Ibo, Iso, Iўso — моменты инерции соответственно площадей сечения сжатой зоны бетона, арматуры S и Sў относительно нулевой линии;
Sbo — статический момент площади сечения растянутой зоны бетона относительно нулевой линии.
Положение нулевой линии в общем случае определяется из условия
где Sўbo, Sso, Sўso ѕ статические моменты соответственно площади сечения сжатой зоны бетона, арматуры S и Sў относительно нулевой линии;
Abt — площадь сечения растянутой зоны бетона.
Для прямоугольных, тавровых и двутавровых сечений условие (244) принимает вид
где 

Условием (245) можно пользоваться, если найденная по нему нулевая линия пересекает ребро таврового или двутаврового сечения.
Черт. 83. Схемы усилий и эпюры напряжений в поперечном сечении элемента при расчете его по образованию трещин, нормальных к продольной оси элемента
а ѕ при изгибе; б ѕ при внецентренном сжатии; в ѕ при центральном и внецентренном растяжении; 1 ѕ ядровая точка; 2 ѕ центр тяжести приведенного сечения
Значение Wpl допускается определять по формуле
Wpl = [0,292 + 0,75 (g1 + 2m1a) + 0,075(gў1 + 2mў1a)] bh2; (246)
где
При известном значении Wred (см. п. 4.2) величину Wpl можно также определить по формуле
Wpl = g Wred, (247)
где g ѕ см. табл. 29.
Таблица 29
| Сечение | Коэффициент g | Форма поперечного сечения |
| 1. Прямоугольное | 1,75 |  |
| 2. Тавровое с полкой, расположенной в сжатой зоне |
1,75 |
 |
| 3. Тавровое с полкой (уширением), расположенной, в растянутой зоне: а) при bf/b Ј 2 независимо от отношения hf/h б) bf/b > 2 и hf/h і 0,2 в) bf/b > 2 и hf/h < 0,2 |
1,75 1,75 |
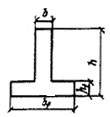 |
| 4. Двутавровое симметричное (коробчатое): а) при bўf/b = bf/b Ј 2 независимо от отношений hўf/h = hf/h б) при 2 < bўf/b = bf/b Ј 6 независимо от отношений hўf/h = hf/h в) при b’f/b = bўf/b > 6 и hўf/h = hўf/h > 0,2 г) при 6 < bўf/b = bf/b Ј 15 и hўf/h = hf/h < 0,2 д) при bўf/b = bf/b > 15 и hўf/h = hf/h < 0,2 |
1,75 1,50 1,50 1,25 1,10 |
 |
| Двутавровое несимметричное, удовлетворяющее условию bўf/b Ј 3: а) при bf/b Ј 2 независимо от отношения hf/h б) при 2 < bf/b Ј 6 независимо от отношения hf/h в) при bf/b > 6 и hf/h > 0,1 |
1,75 1,50 1,50 |
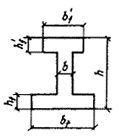 |
| 6. Двутавровое несимметричное, удовлетворяющее условию 3 < bўf/b < 8: а) при bўf/b Ј 4 независимо от отношения hf/h б) при bf/b > 4 и hf/h і 0,2 в) при bf/b > 4 и hf/h < 0,2 |
1,50 1,50 |
 |
| 7. Двутавровое несимметричное, удовлетворяющее условию bўf/b і 8: а) при hf/h > 0,3 б) при hf/h Ј 0,3 |
1,50 |
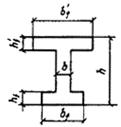 |
|
8. Кольцевое и круглое |
2-0,4D1/D |
 |
| 9. Крестовое: а) при bўf/b і 2 и 0,9 і hўf/h > 0,2 б) в остальных случаях |
2,00 1,75 |
 |
Примечания: 1. В табл. 29 обозначения bf и hf соответствуют размерам полки, которая при расчете по образованию трещин растянута, a bўf и hўf — размерам полки, которая для этого случая расчета сжата.
2. Wpl = g Wred, где Wred ѕ момент сопротивления для растянутой грани приведенного сечения, определяемый по правилам сопротивления упругих материалов.
4.4. Участки по длине элемента, на которых отсутствуют наклонные трещины, определяются из условия
Q Ј jb3 Rbt.serbho, (248)
где jb3 — см. табл. 21.
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ ТРЕЩИН
(4.13). Железобетонные элементы рассчитываются по раскрытию трещин:
нормальных к продольной оси элемента;
наклонных к продольной оси элемента.
Проверка ширины раскрытия трещин не требуется, если, согласно расчету по пп. 4.1ѕ4.4, они не образуются от действия постоянных, длительных и кратковременных нагрузок, вводимых в расчет с коэффициентом надежности по нагрузке gf = 1,0.
Для изгибаемых и внецентренно сжатых элементов статически определимых систем при однорядном армировании, указанных в табл. 1, поз. 4, проверка ширины раскрытия нормальных трещин не требуется в следующих случаях:
а) для арматуры классов А-I и А-II:
при любых коэффициентах армирования m, если диаметр d Ј 20 мм;
при m і 0,01, если диаметр d = 22 ѕ 40 мм;
б) для арматуры класса А-III:
при любых коэффициентах армирования m, если диаметр d Ј 8 мм;
при m і 0,01, если диаметр d = 10 — 25 мм;
при m і 0,015, если диаметр d = 28 ѕ 40 мм;
в) для арматуры класса Вр-1 ѕ при m і 0,006 при любых диаметрах.
При расчете по ракрытию трещин усилие от усадки бетона Nshr принимается равным нулю.
4.6. В общем случае расчет по раскрытию трещин производится два раза: на непродолжительное и продолжительное раскрытие трещин (см. п. 1.15).
Для элементов, указанных в табл. 1, поз. 4 и выполняемых из тяжелого и легкого бетонов, при проверке раскрытия трещин, нормальных к продольной оси элемента, допускается расчет производить только один раз:
если 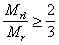
если 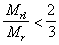
здесь Mrl, Mr — момент Mr (см. п. 4.2) соответственно от суммы постоянных и длительных нагрузок и от всех нагрузок.
Расчет по раскрытию трещин, нормальных к продольной оси элемента
4.7(4.14). Ширину раскрытия трещин, нормальных к продольной оси элемента, acrc, мм, следует определять по формуле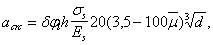
где d ѕ коэффициент, принимаемый равным для элементов:
изгибаемых и внецентренно сжатых….. 1,0
растянутых …………………………………….. 1,2
jl — коэффициент, принимаемый равным при учете:
кратковременных нагрузок и непродолжительного
действия постоянных и длительных нагрузок…………… 1,00
продолжительного действия постоянных и
длительных нагрузок для конструкций из бетона:
тяжелого:
естественной влажности………………….
в водонасыщенном состоянии (элементы,
воспринимающие давление жидкостей, а
также эксплуатируемые в грунте ниже
уровня грунтовых вод) ………………………………………..1,20
при попеременном водонасыщении и высушивании 1,75
мелкозернистого групп:
А ………………………………………………………………………1,75
Б ……………………………………………………………………… 2,00
В ……………………………………………………………………… 1,50
легкого класса В12,5 и выше ………………………………. 1,50
поризованного …………………………………………………… 2,00
значения jl для мелкозернистого, легкого и поризованного бетонов в водонасыщенном состоянии умножаются на коэффициент 0,8, а при попеременном водонасыщении и высушивании ѕ на коэффициент 1,2;
h — коэффициент, принимаемый равным для арматуры классов: А-II и А-III ѕ 1,0; А-I — 1,3; Вр-1 ѕ 1,2;
ss ѕ напряжение в стержнях крайнего ряда арматуры S, определяемое согласно п. 4.9;
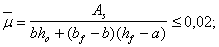
если hf < а, растянутые свесы при вычислении 
если во внецентренно растянутых элементах сила N расположена между центрами тяжести арматуры S и Sў, при определении 
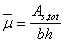
d — диаметр растянутой арматуры, мм; при различных диаметрах стержней значение d принимается равным: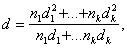
здесь d1, …, dk ѕ диаметр стержней растянутой арматуры;
п1, …, nk ѕ число стержней диаметрами соответственно d1, …, dk..
Кроме того, следует учитывать указания п. 4.8.
4.8 (4.14). Ширина раскрытия трещин асrc, определенная согласно п. 4.7, корректируется в следующих случаях:
а) если центр тяжести сечения стержней крайнего ряда арматуры S изгибаемых, внецентренно сжатых, внецентренно растянутых при eо і 0,8ho элементов отстоит от наиболее растянутого волокна бетона на расстоянии a2 > 0,2h, значение acrc должно быть увеличено умножением на коэффициент da, равный: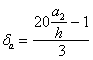
и принимаемый не более 3;
б) для слабоармированных изгибаемых и внецентренно сжатых элементов из тяжелого и легкого бетонов (например, фундаментов) при 

jb = jf1 jl1, (253)
но не более 1,0,
где jf1 — коэффициент, учитывающий уровень нагружения и равный:
jl1 — коэффициент, учитывающий длительность действия нагрузки и равный при учете:
кратковременных нагрузок и непродолжительного действия постоянных и длительных нагрузок 1,0;
продолжительного действия постоянных и длительных нагрузок
но не менее 1,0;
Мo ѕ момент, при котором растянутый бетон над трещинами практически выключается из работы, равный:
Мо = Мсrс + ybh2Rbt,ser, (256)
где 
если Mо < Mr, коэффициент jb не вычисляется;
Mr ѕ момент, определяемый, согласно п. 4.2, от полной нагрузки, включающей постоянную, длительную и кратковременную нагрузки;
Mcrc ѕ см. п. 4.2;
При использовании коэффициента jb и при 
в) для статически неопределимых систем, а также для свободно опертых балок при l/h < 7, вблизи мест приложения сосредоточенных сил и опорных реакций при m Ј 0,02 ширину раскрытия трещин acrc, вычисленную по формуле (249), допускается уменьшать умножением на коэффициент jloc, учитывающий местные особенности напряженного состояния в железобетонных конструкциях и определяемый по формуле
но не менее 0,8 и не более 1,0,
где F — абсолютное значение сосредоточенной силы или опорной реакции;
М — абсолютное значение изгибающего момента в нормальном сечении, проходящем через точку приложения сосредоточенной силы или опорной реакции (черт. 84);
а — расстояние от точки приложения сосредоточенной силы или опорной реакции до рассматриваемого сечения, принимаемое в соответствии с черт. 84, но не более 0,3h;
h — расстояние от грани элемента, к которой приложена сила F, до растянутой грани;
ho — то же, до растянутой арматуры (черт. 85);
г) для элементов из легкого бетона класса В7,5 и ниже величина acrc должна быть увеличена на 20 %.
Черт. 84. Положение опорных реакций в жестких узлах, принимаемое для определения коэффициента jloc
а — г ѕ стыки сборных элементов; д — и ѕ монолитные сопряжения
Черт. 85. Расчетные схемы для определения коэффициента jloc
а ѕ при приложении силы к сжатой грани элемента; б ѕ то же, к уширениям (полкам) элемента; в ѕ то же, по длине статически неопределимой балки
4.9 (4.15). Напряжения в растянутой арматуре ss (определяются по формулам для элементов:
центрально-растянутых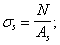
изгибаемых
внецентренно сжатых и внецентренно растянутых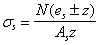
В формуле (260) знак «плюс» принимается при внецентренном растяжении, знак «минус» ѕ при внецентренном сжатии. При расположении растягивающей продольной силы N между центрами тяжести арматуры S и Sў значение еs принимается со знаком «минус».
В формулах (259) и (260) :
z — расстояние от центра тяжести площади сечения арматуры S до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной, определяемое согласно п. 4.16, при этом для внецентренно растянутых элементов при ео < 0,8ho z принимается равным zs — расстоянию между центрами тяжести арматуры S и Sў, коэффициент v в формуле (277) принимается всегда равным vsh = 0,45 (как при непродолжительном действии нагрузки); допускается z принимать таким же, как при расчете по деформациям на те же нагрузки, если
В случае, когда Mr < Mcrc (см. п. 4.2), значение ss, определяется по формуле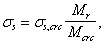
где ss,crc ѕ напряжение в арматуре при действии нагрузки, соответствующей образованию трещин, определяемое по формулам (259) и (260) с заменой М на
Mcrc и N на
При определении Ncrc моменты Mcrc и Mr допускается вычислять при r = 0,8Wred /Ared.
При расположении растянутой арматуры в несколько рядов по высоте сечения в изгибаемых, внецентренно сжатых, а также внецентренно растянутых элементах при eo > 0,8ho напряжения ss необходимо умножать на коэффициент dn, равный: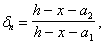
где х = xho; значение x определяется по формуле (274); для изгибаемых элементов допускается принимать значение х таким же, как и при расчете по прочности;
а1, a2 — расстояния от центра тяжести площади сечения соответственно всей арматуры S и крайнего ряда стержней до наиболее растянутого волокна бетона.
Значение напряжения ss от действия полной нагрузки, определенное с учетом коэффициента dn, не должно превышать Rs,ser. Это условие допускается не проверять для статически определимых конструкций с арматурой одного класса при ее однорядном расположении.
Упрощенные способы определения ss. Для изгибаемых элементов допускается определять ss по формуле
где Ми — предельный момент по прочности, равный:
при проверке прочности сечений ѕ правой части неравенств (17) — (21), (28), (30)
при подборе сечения арматуры
здесь Mtot,d — момент от действия полной нагрузки с коэффициентом надежности по нагрузке gf > 1,0;
Аs,fact — фактическая площадь принятой арматуры;
Asd — площадь арматуры, требуемая по расчету прочности.
При применении арматуры разных классов в формулу (263) вводится расчетное сопротивление арматуры для предельных состояний первой группы Rs по более прочной арматуре.
Для внецентренно сжатых элементов из тяжелого и легкого бетонов при Mr і Mcrc допускается вычислять ss по формуле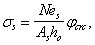
где jcrc — коэффициент, определяемый по табл. 30.
Таблица 30
| jf |  |
Коэффициенты jcrc при значениях ma, равных | |||||||||||
| 0,01 | 0,02 | 0,03 | 0,05 | 0,07 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,40 | 0,50 | ||
|
0 |
Ј0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,04 0,18 0,31 0,44 0,59 0,74 0,81 |
0,07 0,22 0,34 0,48 0,62 0,77 0,84 |
0,10 0,25 0,37 0,50 0,64 0,79 0,86 |
0,15 0,29 0,40 0,53 0,67 0,82 0,89 |
0,18 0,31 0,43 0,56 0,70 0,84 0,91 |
0,22 0,34 0,46 0,58 0,72 0,86 0,94 |
0,26 0,38 0,49 0,62 0,75 0,89 0,97 |
0,31 0,42 0,55 0,65 0,78 0,92 1,00 |
0,34 0,45 0,55 0,67 0,81 0,95 1,02 |
0,37 0,47 0,57 0,69 0,82 0,96 1,03 |
0,41 0,50 0,60 0,72 0,85 0,99 1,06 |
0,45 0,52 0,62 0,74 0,87 1,01 1,08 |
|
0,05 |
Ј0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,04 0,17 0,30 0,44 0,59 0,74 0,82 |
0,04 0,20 0,33 0,46 0,61 0,76 0,84 |
0,07 0,22 0,35 0,48 0,63 0,78 0,85 |
0,11 0,26 0,38 0,51 0,65 0,80 0,86 |
0,14 0,28 0,40 0,53 0,67 0,82 0,90 |
0,18 0,31 0,43 0,56 0,70 0,84 0,92 |
0,22 0,34 0,46 0,59 0,72 0,87 0,94 |
0,26 0,38 0,49 0,61 0,75 0,89 0,97 |
0,29 0,40 0,51 0,64 0,77 0,91 0,99 |
0,32 0,42 0,53 0,66 0,79 0,93 1,00 |
0,36 0,46 0,56 0,68 0,82 0,95 1,03 |
0,38 0,48 0,58 0,70 0,83 0,97 1,04 |
|
0,10 |
Ј0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,03 0,16 0,30 0,44 0,59 0,75 0,83 |
0,04 0,19 0,32 0,46 0,61 0,76 0,84 |
0,05 0,21 0,33 0,47 0,62 0,77 0,85 |
0,09 0,24 0,36 0,50 0,64 0,79 0,87 |
0,11 0,26 0,38 0,52 0,66 0,81 0,88 |
0,14 0,28 0,40 0,54 0,68 0,83 0,90 |
0,16 0,31 0,43 0,56 0,70 0,85 0,92 |
0,22 0,34 0,46 0,59 0,73 0,87 0,94 |
0,25 0,37 0,48 0,61 0,75 0,89 0,96 |
0,28 0,39 0,50 0,63 0,76 0,90 0,98 |
0,31 0,42 0,53 0,65 0,79 0,93 1,00 |
0,34 0,44 0,55 0,67 0,80 0,94 1,02 |
|
0,20 |
Ј0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,03 0,15 0,29 0,44 0,59 0,75 0,83 |
0,04 0,17 0,31 0,45 0,60 0,76 0,84 |
0,05 0,19 0,32 0,46 0,61 0,77 0,85 |
0,06 0,21 0,34 0,48 0,63 0,78 0,86 |
0,07 0,23 0,35 0,49 0,64 0,79 0,87 |
0,10 0,25 0,37 0,51 0,65 0,81 0,88 |
0,13 0,27 0,40 0,53 0,67 0,82 0,90 |
0,16 0,30 0,42 0,55 0,69 0,84 0,91 |
0,19 0,32 0,44 0,57 0,71 0,85 0,93 |
0,21 0,34 0,45 0,58 0,72 0,87 0,94 |
0,25 0,37 0,48 0,61 0,75 0,89 0,96 |
0,28 0,39 0,50 0,63 0,76 0,90 0,98 |
|
0,30 |
Ј0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,03 0,15 0,29 0,44 0,59 0,75 0,84 |
0,04 0,16 0,30 0,45 0,60 0,76 0,85 |
0,05 0,17 0,31 0,46 0,61 0,77 0,85 |
0,05 0,19 0,33 0,47 0,62 0,78 0,86 |
0,06 0,21 0,34 0,48 0,63 0,78 0,86 |
0,07 0,23 0,35 0,49 0,64 0,79 0,87 |
0,10 0,25 0,37 0,51 0,66 0,81 0,89 |
0,12 0,27 0,39 0,53 0,67 0,82 0,90 |
0,15 0,29 0,41 0,54 0,68 0,83 0,91 |
0,17 0,30 0,42 0,55 0,70 0,84 0,92 |
0,20 0,33 0,45 0,58 0,72 0,86 0,94 |
0,23 0,35 0,46 0,59 0,73 0,88 0,95 |
|
0,50 |
Ј0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,04 0,15 0,29 0,44 0,60 0,77 0,85 |
0,04 0,16 0,30 0,45 0,61 0,77 0,85 |
0,04 0,16 0,30 0,45 0,61 0,77 0,85 |
0,04 0,18 0,31 0,46 0,62 0,77 0,86 |
0,04 0,19 0,32 0,47 0,62 0,78 0,86 |
0,04 0,20 0,33 0,48 0,63 0,79 0,87 |
0,06 0,22 0,35 0,49 0,64 0,79 0,87 |
0,08 0,23 0,36 0,50 0,65 0,80 0,88 |
0,10 0,24 0,37 0,51 0,66 0,81 0,89 |
0,12 0,26 0,38 0,52 0,67 0,82 0,89 |
0,15 0,28 0,40 0,54 0,68 0,83 0,91 |
0,17 0,30 0,42 0,55 0,69 0,84 0,92 |
|
0,70 |
Ј0,8 1,0 1,2 1,5 2,0 3,0 4,0 |
0,04 0,15 0,29 0,45 0,61 0,77 0,85 |
0,04 0,15 0,30 0,45 0,61 0,77 0,85 |
0,04 0,16 0,30 0,45 0,61 0,77 0,85 |
0,04 0,17 0,31 0,46 0,61 0,77 0,86 |
0,04 0,18 0,32 0,46 0,62 0,78 0,86 |
0,04 0,19 0,32 0,47 0,62 0,78 0,86 |
0,04 0,20 0,34 0,48 0,63 0,79 0,87 |
0,06 0,21 0,34 0,49 0,64 0,79 0,87 |
0,07 0,22 0,35 0,49 0,64 0,80 0,88 |
0,08 0,23 0,36 0,50 0,65 0,80 0,88 |
0,11 0,25 0,38 0,52 0,66 0,81 0,89 |
0,13 0,27 0,39 0,53 0,67 0,82 0,90 |
Найденные по формулам (263) и (264) значения ss в случае расположения арматуры в несколько рядов по высоте сечения умножаются на коэффициент dn.
4.10 (4.14). Ширина непродолжительного раскрытия трещин от действия всех нагрузок определяется как сумма ширины продолжительного раскрытия от действия постоянных и длительных нагрузок (при jl > 1,0) и приращения ширины раскрытия от действия кратковременных нагрузок (при jl = 1,0). Этому соответствует определение ширины непродолжительного раскрытия трещин по формуле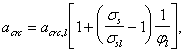
где acrс,l — ширина продолжительного раскрытия трещин от действия постоянных и длительных нагрузок;
jl > 1,0— см. п. 4.7; если величина acrс,l определена с учетом формулы (253), то коэффициент jl в формуле (265) заменяется произведением jl jl1 (где jl1 ѕ см. п. 4.8б);
ssl, ss — определяются согласно п. 4.9 соответственно от суммы постоянных и длительных нагрузок и от всех нагрузок.
Расчет по раскрытию трещин, наклонных к продольной оси элемента
4.11(4.17). Ширина раскрытия трещин, наклонных к продольной оси элемента, при армировании хомутами, нормальными к продольной оси, должна определяться по формуле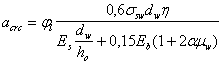
где jl ѕ коэффициент, принимаемый равным при учете:
кратковременных нагрузок и непродолжительного
действия постоянных и длительных нагрузок…………….. 1,00
продолжительного действия постоянных и длительных
нагрузок для конструкций из бетонов:
тяжелого:
естественной влажности……………………………………….. 1,50
в водонасыщенном состоянии……………………………….. 1,20
при попеременном водонасыщении и высушивании… 1,75
мелкозернистого и легкого ѕ то же, что в формуле (249);
h ѕ то же, что в формуле (249);
dw ѕ- диаметр хомутов;
ssw — напряжение в хомутах, определяемое по формуле
значение напряжения ssw не должно превышать Rs,ser;
Qb1 ѕ правая часть условия (72) с коэффициентом jb4, умноженным на 0,8, при этом, Rbt заменяется на значение Rbt,ser, принимаемое не более значения, соответствующего бетону класса В30;
Q — поперечная сила в конце наклонного сечения с проекцией длиной с.
Значение с принимается не более 2hо. Если при расчете элемента на действие равномерно распределенной нагрузки выполняется условие
(где q1 ѕ см. п. 3.32), значение с можно принимать равным только 2hо.
Для элементов из легкого бетона класса В7,5 и ниже значение acrc, вычисленное по формуле (266), должно быть увеличено на 30 %.
При определении ширины непродолжительного раскрытия наклонных трещин от действия всех нагрузок должны учитываться указания п. 4.10. При этом в формуле (265) коэффициент jl назначается согласно настоящему пункту, а отношение ssl/ss заменяется на отношение напряжений sswl/ssw, определяемых по формуле (267) соответственно от суммы постоянных и длительных нагрузок и от всех нагрузок.
Допускается уменьшать величину асrc в 1,5 раза по сравнению с определенной по формуле (266), если элемент армирован продольными стержнями того же диаметра, что и хомуты, и с расстояниями по высоте сечения, равными шагу хомутов s.
Примеры расчета
Пример 53. Дано: железобетонная плита перекрытия с размерами поперечного сечения (для половины сечения плиты) по черт. 86: b = 85 мм, h = 400 мм, bўf = 725 мм, hўf= 50 мм; бетон тяжелый класса В25; рабочая арматура класса A-III (Rs = 365 МПа; Еs = 2×105 МПа), расположенная в два ряда (a1 = 58 мм; a2 = 33 мм); площадь ее сечения Аs = 760 мм2 (2Æ22) ; полный момент в середине пролета Мtot = 69 кН×м; все нагрузки постоянные и длительные; из расчета по прочности известно, что Ми = 92,3 кН×м и х = 30 мм.
Требуется произвести расчет по раскрытию трещин, нормальных к продольной оси элемента.
Черт. 86. К примеру расчета 53
Расчет. ho = h ѕ а = 400 ѕ 58 = 342 мм. Так как 
Для определения продолжительного раскрытия трещин вычислим напряжение в арматуре ss. Согласно формуле (263), величина ss на уровне центра тяжести арматуры равна:
Поскольку арматура расположена в два ряда, вычислим по формуле (262) коэффициент dn:
Напряжение в нижнем стержне арматуры равно:
ss = 273×1,08 = 294МПа.
Ширину раскрытия трещин находим по формуле (249). Так как 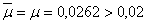


что меньше предельно допустимой ширины раскрытия трещин acrc2 = 0,3 мм.
Пример 54. Дано: железобетонная плита фундамента с размерами поперечного сечения h = 300 мм, b = 1150 мм; a = 42 мм; бетон тяжелый класса В15 (Rbt,ser = 1,15 МПа; Eb = 2,05×104 МПа); рабочая арматура класса A-III (Rs = 365 МПа; Еs = 2×105 МПа); площадь ее сечения Аs = 923 мм2 (6 Æ14); момент в расчетном сечении от постоянных и длительных нагрузок Ml = 63 кН×м, от кратковременных нагрузок Msh = 4 кН×м; предельный момент по прочности Мu = 80,5 кН×м; фундамент расположен выше уровня грунтовых вод.
Требуется произвести расчет по раскрытию нормальных трещин.
Расчет. ho = h ‑ а = 300 ‑ 42 = 258 мм. Определим необходимость вычисления ширины раскрытия трещин согласно п. 4.5. Для этого найдем момент трещинообразования Mcrc.
Так как 
Mcrc = Rbt,serWpl = 0,292bh2Rbt,ser = 0,292×1150×3002×1,15 = 34,75×106 Н×мм = 34,8 кН×м.
Так как Mr = Мtot = Ml + Мsh = 63 + 4 = 67 кН×м > Mcrc = 34,8 кН×м, проверка ширины раскрытия трещин необходима.
Поскольку фундамент расположен выше уровня грунтовых вод, допустимая ширина продолжительного раскрытия трещин, согласно табл. 1, поз. 4, acrc2 = 0,3 мм, поэтому при 
Ширину раскрытия трещин определим по формуле (249).
Напряжение в арматуре ss вычислим по упрощенной формуле (263):
Коэффициенты, вводимые в формулу (249), принимаем равными: d = 1,0; h = 1,0; 
что больше допустимого значения acrc2 = 0,3 мм, в связи с чем целесообразно произвести корректировку значения acrc в меньшую сторону согласно п. 4.8б. Поскольку 
По формуле (256) определим значение Мо, предварительно вычислив:
Mo = Mcrс + ybh2Rbt,ser = 34,8×106 + 0,454×1150×3002×1,15 = 88,8×106 Н×мм = 88,8 кН×м.
Поскольку Мо = 88,8 кН×м > Mr = 67 кН×м, вычислим коэффициент jb по формуле (253) :
принимаем jl1 = 1;
jb = jf1jl1 = 0,79 < 1.
С учетом коэффициента jb, ширина раскрытия трещин равна acrc = 0,34×0,79 = 0,269 мм < 0,3 мм, т. е. меньше предельно допустимого значения.
Пример 55. Дано: железобетонная колонна промышленного здания с размерами поперечного сечения h = 500 мм, b = 400 мм; a = aў = 50 мм; бетон тяжелый класса В15 (Rb,ser = 11 МПа; Rbt,ser = 1,15 МПа; Eb = 2,05×104 МПа); рабочая арматура класса A-III (Еs = 2×105 МПа); площадь ее сечения As = Aўs = 1232 мм2 (2 Æ28); продольная сжимающая сила N = Nl = 500 кН; момент от полной нагрузки Mtot = 240 кН×м, в том числе момент от постоянных и длительных нагрузок Ml = 150 кН×м.
Требуется рассчитать колонну по раскрытию трещин.
Расчет. ho = h ‑ a = 500 ‑ 50 = 450 мм. Определим необходимость расчета по раскрытию трещин. Для этого проверим условие (233). Так как 
Mcrc = 0,292bh2Rbt,ser = 0,292×400×5002×1,15 = 33,6×106 Н×мм.
Ядровое расстояние r определим по формуле (241). Для этого вычислим sb как для упругого тела (влиянием арматуры пренебрежем):
принимаем j = 0,7;
По формуле (238) определим момент Mr:
т. е. условие (233) не выполняется. Следовательно, проверка раскрытия трещин обязательна.
Поскольку 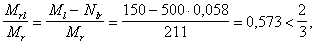
По вычисленным значениям jf = 0,074, ma = 0,067 и 
Согласно п. 4.7, d = 1,0; h = 1,00;
Напряжение в арматуре ss от действия всех нагрузок так же определим по формуле (264).
При jf = 0,074,ma = 0,067 и 
Тогда, согласно формуле (265),
что меньше предельно допустимого значения acrcl = 0,4 мм (см. табл. 1, поз. 4).
Пример 56. Дано: свободно опертая балка перекрытия пролетом l = 5,5 м, нагруженная равномерно распределенными нагрузками: временной длительно действующей эквивалентной нагрузкой v = 30 кН/м и постоянной нагрузкой g = 12,5 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм, hо = 370 мм; бетон тяжелый класса В 15 (Rbt,ser = 1,15 МПа; Eb = 2,05×104 МПа); хомуты двухветвевые из арматуры класса А-I (Еs = 2,1×105 МПа) с шагом s = 150 мм, диаметром 8 мм (Аsw = 101 мм2).
Требуется произвести расчет по раскрытию наклонных трещин.
Расчет. Определим сначала необходимость расчета по раскрытию наклонных трещин, проверив условие (248).
Наибольшая поперечная сила в опорном сечении равна:
Согласно табл. 21, jb3 = 0,6.
jb3Rbt,serbho = 0,6×1,15×200×370 = 51060 H < Qmax = 117 кН,
т. е. наклонные трещины образуются и расчет по их раскрытию необходим.
Расчет производим согласно п. 4.11. Определим значения Q и Qb1.
q1 = g + v/2 = 12,5 + 30/2 = 27,5 кН/м;
jb4 = 1,5 (см. табл. 21).
Поскольку 0,2jb4Rbt,serb = 0,2×1,5×1,15×200 = 56,9 Н/мм > q1 = 27,5 Н/мм, значение с при определении Qb1 и Q принимаем равным с = 2h о = 2×370 = 740 мм.
Отсюда
Q = Qmax ѕ q1 с = 117 ѕ 27,5 · 0,740 = 96,65 кН .
Определим напряжение в хомутах по формуле (267):
Согласно пп. 4.7 и 4.11, jl = 1,5; h = 1,3; dw = 8 мм.
Определим ширину раскрытия наклонных трещин по формуле (266):
что меньше предельно допустимого значения асrc = 0,3 мм (см. табл. 1).
РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ДЕФОРМАЦИЯМ
4.12(4.22) Деформации (прогибы, углы поворота) элементов железобетонных конструкций следует вычислять по формулам строительной механики, определяя входящие в них значения кривизны в соответствии с указаниями пп.4.13 — 4.21.
4.13(4.23). Кривизна определяется:
а) для участков элемента, где в растянутой зоне не образуются трещины, нормальные к продольной оси элемента (см. п. 4.1), ѕ как для сплошного тела;
б) для участков элемента, где в растянутой зоне имеются трещины, нормальные к продольной оси, — как отношение разности средних деформаций крайнего волокна сжатой зоны бетона и продольной растянутой арматуры к рабочей высоте сечения элемента.
При расчете по деформациям усилие от усадки бетона Nshr принимается равным нулю.
Определение кривизны железобетонных элементов на участках без трещин в растянутой зоне
4.14(4.24). На участках, где не образуются нормальные к продольной оси трещины, полная величина кривизны должна определяться по формуле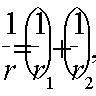
где 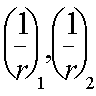
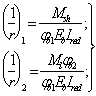
jb1 — коэффициент, учитывающий влияние кратковременной ползучести бетона и принимаемый для бетонов:
тяжелого, мелкозернистого и легкого при плотном
мелком заполнителе…………………………………………… 0,85
легкого при пористом мелком заполнителе и
поризованного…………………………………………………… 0,70
jb2 ѕ коэффициент, учитывающий влияние длительной ползучести бетона на деформации элемента без трещин и принимаемый по табл. 31.
Таблица 31 (34, 35)
| Коэффициенты jb2 и vl при влажности воздуха окружающей среды, % | ||||||
| Вид бетона | 40ѕ75 (нормальной) | ниже 40 (пониженной) | св. 75 (повышенной) | |||
| jb2 | vl | jb2 | vl | jb2 | vl | |
| Тяжелый, легкий | 2,0 | 0,15 | 3,0 | 0,10 | 1,6 | 0,19 |
| Поризованный | 2,0 | 0,07 | 3,0 | 0,04 | 1,6 | 0,09 |
| Мелкозернистый | ||||||
| групп: | ||||||
| А | 2,6 | 0,10 | 3,9 | 0,07 | 2,1 | 0,125 |
| Б | 3,0 | 0,08 | 4,5 | 0,05 | 2,4 | 0,10 |
| В | 2,0 | 0,15 | 3,0 | 0,10 | 1,6 | 0,19 |
Примечания: 1. Влажность воздуха окружающей среды принимается согласно указаниям п. 1.8.
2. Группы мелкозернистого бетона см. п. 2.1.
3. При попеременном водонасыщении и высушивании бетона значения jb2, следует умножать, а значения vl ѕ делить на коэффициент 1,2.
Определение кривизны железобетонных элементов на участках с трещинами в растянутой зоне
4.15 (4.27). На участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых, внецентренно сжатых, а также внецентренно растянутых при eо і 0,8ho элементов прямоугольного, таврового и двутаврового (коробчатого) сечений должна определяться по формуле
Для изгибаемых элементов последнее слагаемое правой части формулы (271) принимается равным нулю. Знак «минус» в этой формуле принимается при внецентренном сжатии, знак «плюс» — при внецентренном растяжении.
В формуле (271):
Мs — момент относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести площади сечения арматуры S, от всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, равный:
для изгибаемых элементов Мs = М;
для внецентренно сжатых и внецентренно растянутых элементов Мs = Nes;
z ѕ расстояние от центра тяжести площади сечения арматуры S до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной (плечо внутренней пары сил), определяемое согласно указаниям п. 4.16;
ys — коэффициент, учитывающий работу растянутого бетона на участке с трещинами и определяемый согласно указаниям п. 4.17;
yb — коэффициент, учитывающий неравномерность распределения деформаций крайнего сжатого волокна бетона по длине участка с трещинами и принимаемый равным:
для тяжелого, мелкозернистого и легкого бетонов
класса В10 и выше ………………………………………………………0,9
для легкого и поризованного бетонов класса В7,5 и ниже… 0,7
jf ѕ коэффициент, определяемый по формуле (277);
x = x/ho — определяется согласно указаниям п. 4.16;
v ѕ коэффициент, характеризующий упруго-пластическое состояние бетона сжатой зоны и принимаемый равным:
при непродолжительном действии нагрузки ѕ коэффициенту vsh = 0,45;
при продолжительном действии нагрузки ѕ коэффициенту vl, определяемому по табл. 31.
Для изгибаемых и внецентренно сжатых элементов из тяжелого бетона при Mr < Mo кривизну допускается определять с учетом работы растянутого бетона над трещинами по формуле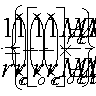
где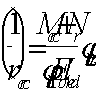

равном:
для изгибаемых элементов Мs = Мo;
для внецентренно сжатых элементов Ms = Мo + Nуsr;
уsr = yo ‑ а + r — расстояние от центра тяжести растянутой арматуры до оси, проходящей через наиболее удаленную ядровую точку (см. п. 4.2);
Мr — момент, определяемый согласно п. 4.2 от полной нагрузки, включающей постоянную, длительную и кратковременные нагрузки;
Мo ѕ момент, при котором растянутый бетон над трещинами выключается из работы, определяемый по формуле (256), в которой y уменьшается вдвое при учете продолжительного действия постоянных и длительных нагрузок;
Mcrc,r ѕ см. п. 4.2;
M, Mtot — моменты внешних сил относительно оси, проходящей через центр тяжести сечения, соответственно от рассматриваемой и от полной нагрузки;
jb1, jb2 — см. п. 4.14; при непродолжительном действии нагрузки jb2 = 1,0.
4.16(4.28). Значение x вычисляется по формуле
но принимается не более 1,0, при этом es/ho принимается не менее 0,5.
Для изгибаемых элементов последнее слагаемое правой части формулы (274) принимается равным нулю.
В формуле (274) верхние знаки принимаются при сжимающем, а нижние — при растягивающем усилии N.
В формуле (274):
b — коэффициент, принимаемый равным для бетона:
тяжелого и легкого………………………………………… 1,8
мелкозернистого……………………………………………. 1,6
поризованного……………………………………………….. 1,4
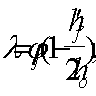
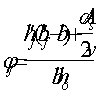
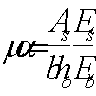
Значение z вычисляется по формуле
Для элементов прямоугольного сечения и таврового сечения с полкой в растянутой зоне в формулы (276) и (279) вместо hўf подставляются значения 2a’ или hўf = 0 соответственно при наличии или отсутствии арматуры Sў.
Если 
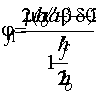

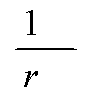

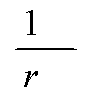
Расчет сечений, имеющих полку в сжатой зоне, при 
Расчетная ширина полки bўf определяется согласно указаниям п. 3.23.
Для внецентренно сжатых элементов значение z должно приниматься не более 0,97es.
(4.29). Коэффициент ys определяется по формуле
но не более 1,0, при этом следует принимать es/ho і 1,2/jls.
Для изгибаемых элементов последний член в правой части формулы (280) принимается равным нулю.
В формуле (280):
jls ѕ коэффициент, учитывающий влияние длительности действия нагрузки и принимаемый по табл. 32;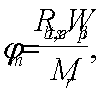
Таблица 32(36)
| Длительность действия | Коэффициент jls при классе бетона | |
| нагрузки | В 10 и выше | В7,5 и ниже |
| Непродолжительное действие при арматуре классов: | ||
| А-II, А-III | 1,1 | 0,8 |
| А-I, Вр-I | 1,0 | 0,7 |
| 2. Продолжительное действие | 0,8 | 0,6 |
но не более 1,0;
здесь Wpl ѕ см. п. 4.3;
Mr — см. п. 4.2.
4.18. Кривизна внецентренно растянутых элементов с продольной силой N, приложенной между центрами тяжести площадей арматуры S и Sў, на участках с нормальными трещинами в растянутой зоне определяется по формуле
где zs = ho ‑ aў — расстояние между центрами тяжести площадей арматуры S и Sў;
ys, yўs — коэффициенты, учитывающие работу растянутого бетона соответственно для арматуры S и Sў и определяемые по формулам: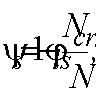
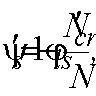
здесь jls ѕ коэффициент, принимаемый равным при действии нагрузки:
непродолжительном……………………………………. 0,70
продолжительном……………………………………….. 0,35
Ncrc, Nўcrc ѕ усилия, приложенные в той же точке, что и сила N, и соответствующие образованию трещин соответственно в более и менее растянутой зонах сечения; значения Ncrc и Nўcrc определяются по формулам:
и принимаются не более N; кроме того, при r’ < ео значение Nўcrc принимается равным N.
В формулах (285):
Wpl, Wўpl ѕ значения Wpl, определенные согласно п. 4.3 соответственно для более и менее растянутой сторон сечения;
r, rў ѕ расстояния от центра тяжести приведенного сечения до ядровых точек, наиболее удаленных соответственно от более и менее растянутой сторон сечения; значения r и rў определяются по формуле (242).
4.19. Кривизна внецентренно растянутых элементов с продольной силой N, приложенной вне расстояния между центрами тяжести площадей арматуры S и Sў, и при eо < 0,8hо определяется линейной интерполяцией между кривизной 


4.20. Для элементов прямоугольного сечения с симметричной арматурой, испытывающих косое внецентренное сжатие, кривизны вычисляются по формуле
где 
jb — коэффициент, учитывающий влияние угла наклона силовой плоскости на величину деформаций кососжимаемых элементов и определяемый по формуле

здесь 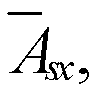
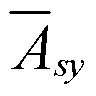
hх, hy — размеры сечения в направлении осей соответственно х и у;
b — угол наклона силовой плоскости (плоскости эксцентриситета силы N) к плоскости оси х, рад.
Плоскость деформирования составляет с плоскостью оси х угол g, определяемый из равенства
где Ix, Iy ѕ моменты инерции приведенного сечения относительно осей соответственное y и х.
Кривизны в плоскостях х и у при косом внецентренном сжатии равны:
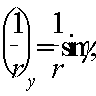
где 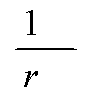
4.21 (4.30). Полная кривизна 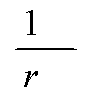

где 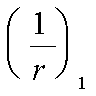


Кривизны 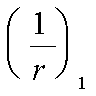


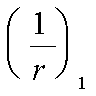




Определение прогибов
4.22 (4.31). Прогиб fm, обусловленный деформацией изгиба, определяется по формуле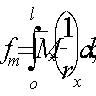
где 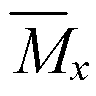

При определении прогиба в середине пролета формула (293) может быть приведена к виду
где 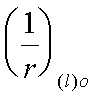


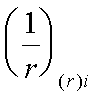

п — четное число равных участков, на которое разделяется пролет элемента; число п рекомендуется принимать не менее 6.
Черт. 87. Эпюра кривизны в железобетонном элементе с переменным по длине сечением
В формулах (293) и (294) кривизны 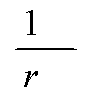
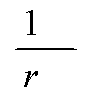
При определении прогибов статически неопределимых конструкций рекомендуется учитывать перераспределение моментов, вызванных образованием трещин и неупругими деформациями бетона.
Для изгибаемых элементов постоянного сечения, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знака, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента (черт. 88).
Черт. 88. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения
а — схема расположения нагрузки; б — эпюра изгибающих моментов; в ѕ эпюра кривизны
4.23 (4.32, 4.33). Для изгибаемых элементов при 
Прогиб fq, обусловленный деформацией сдвига, определяется по формуле 1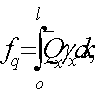
где 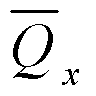
gx ѕ деформация сдвига, определяемая по формуле
здесь Qx ѕ поперечная сила в сечении х от действия внешней нагрузки;
jb2 ѕ коэффициент, учитывающий влияние длительной ползучести бетона и принимаемый по табл. 31; при непродолжительном действии нагрузки jb2 = 1,0;
G — модуль сдвига бетона (см. п. 2.12);
jcrc — коэффициент, учитывающий влияние трещин на деформации сдвига и принимаемый равным:
на участках по длине элемента, где
отсутствуют нормальные и наклонные
к продольной оси элемента трещины……………….. 1,0;
на участках, где имеются только наклонные к
продольной оси элемента трещины………………….. 4,8;
на участках, где имеются только нормальные или нормальные и наклонные к продольной оси элемента трещины, — по формуле
здесь Mx, 
(4.34). Для сплошных плит толщиной менее 250 мм, армированных плоскими сетками, с трещинами в растянутой зоне значения прогибов, подсчитанные по формуле (293), умножаются на коэффициент 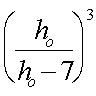
Определение продольных деформаций
4.25. Относительные деформации eo (удлинения или укорочения) в направлении продольной оси элементов определяются следующим образом.
1. Относительные деформации внецентренно сжатых и внецентренно растянутых элементов с однозначной эпюрой напряжений:
а) для внецентренно сжатых элементов или их отдельных участков — по формуле
б) для внецентренно растянутых элементов или их участков при отсутствии трещин — по формуле
В формулах (298) и (299) знак «плюс» соответствует деформациям укорочения, знак «минус» — деформациям удлинения;
в) для внецентренно растянутых элементов или их участков при наличии трещин (т. е. для элементов, указанных в п. 4.18), — по формуле
где esm, eўsm — средние величины удлинения арматуры соответственно S и S’, определяемые по формулам:
здесь zs, ys, yўs ѕ см. п. 4.18.
2. Относительные деформации изгибаемых, внецентренно сжатых и внецентренно растянутых элементов с двухзначной эпюрой напряжений в сечении:
а) для элементов или их отдельных участков, не имеющих трещин в растянутой зоне, — по формуле
Правило знаков то же, что для формул (298) и (299);
б) для участков элементов, указанных в п. 4.15, имеющих трещины в растянутой зоне, — по формуле
где esm, ebm — средние величины соответственно относительного удлинения арматуры и относительного укорочения крайнего сжатого волокна бетона на участке между трещинами, определяемые по формулам:

где Ms, ys, z, jf, x ѕ см. пп. 4.15 — 4.17; правило знаков — см. п. 4.15;
в) для участков внецентренно растянутых элементов, указанных в п. 4.19, — линейной интерполяцией между значением eо, определенным по формуле (300) при еs = 0 (т. е. при еo = yso), и значением еo, определенным по формуле (303) при еs = 0,8ho (т. е. при при еo = 0,8 ho + yso), где yso ѕ см. п. 4.19.
В формулах (298) ѕ (305):
ys — расстояние от рассматриваемого волокна до центра тяжести арматуры S;
уо — то же, до центра тяжести приведенного сечения;
jb1, jb2 — см. п. 4.14; при непродолжительном действии нагрузки jb2 = 1,0;
v — см. п. 4.15.
Деформации eо, определенные по формулам (298) — (303), со знаком «плюс» отвечают укорочению, со знаком «минус» — удлинению.
При одновременном действии постоянных, длительных и кратковременных нагрузок порядок вычисления eо аналогичен определению полной кривизны по п. 4.21.
4.26. Укорочение (удлинение) элементов на уровне рассматриваемого волокна определяется по формуле
где eоi ѕ относительные продольные деформации в сечении, расположенном посредине участка длиной li;
п — число участков, на которые разбивается длина элемента.
Приближенные методы расчета деформаций
4.27. Прогибы железобетонных изгибаемых элементов из тяжелого бетона постоянного сечения, эксплуатируемых при нормальной и повышенной влажности (влажность воздуха окружающей среды свыше 40 %), заведомо меньше предельно допустимых, если выполняется условие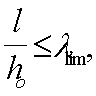
где llim — граничное отношение пролета к рабочей высоте сечения, менее которого проверка прогибов не требуется (табл. 33).
При 

Значения llim, приведенные в табл. 33, отвечают продолжительному действию равномерно распределенной нагрузки на свободно опертую балку при предельном прогибе, равном 
Таблица 33
|
Сечения |
Коэффициенты jf, jft |
Значения llim для определения случаев, когда проверка прогибов элементов из тяжелого бетона не требуется, при значениях ma, равных | ||||||||
| 0,02 | 0,04 | 0,07 | 0,10 | 0,15 | 0,20 | 0,30 | 0,40 | 0,50 | ||
 |
jf = jft = 0 | 25 17 |
17 12 |
14 10 |
12 9 |
10 8 |
9 8 |
10 10 |
11 11 |
11 11 |
 |
jf = 0,2; jft = 0 |
31 22 |
22 16 |
18 13 |
16 11 |
12 9 |
10 8 |
10 10 |
11 11 |
11 11 |
 |
jf = 0,4; jft = 0 |
42 25 |
25 17 |
23 15 |
18 12 |
14 10 |
11 8 |
10 9 |
10 9 |
11 11 |
| jf = 0,6; jft = 0 |
45 30 |
28 30 |
24 17 |
19 14 |
16 12 |
13 9 |
11 9 |
10 10 |
11 11 |
|
| jf = 0,8; jft = 0 |
48 32 |
30 21 |
25 18 |
20 15 |
18 13 |
15 10 |
12 9 |
10 9 |
10 10 |
|
| jf = 1,0; jft = 0 |
50 35 |
33 22 |
26 19 |
23 17 |
20 14 |
17 12 |
14 9 |
11 9 |
10 10 |
|
 |
jft = 0,2; jf = 0 |
28 18 |
17 12 |
14 10 |
12 9 |
10 8 |
9 8 |
10 10 |
11 11 |
11 11 |
| jft = 0,6; jf = 0 |
32 20 |
20 13 |
15 10 |
13 9 |
10 8 |
9 9 |
10 10 |
11 11 |
12 12 |
|
| jft = 1,0; jf = 0 |
36 22 |
23 14 |
16 10 |
13 9 |
10 8 |
9 9 |
10 10 |
11 11 |
12 12 |
|
 |
jf = jft = 0,2 | 34 23 |
25 17 |
19 14 |
16 11 |
12 9 |
10 8 |
10 10 |
11 11 |
11 11 |
| jf = jft = 0,6 | 48 33 |
34 25 |
26 18 |
21 14 |
16 12 |
15 9 |
11 8 |
10 10 |
11 11 |
|
| jf = jft = 1,0 | 55 42 |
44 36 |
36 21 |
26 17 |
20 14 |
17 12 |
14 9 |
11 9 |
10 9 |
|
| As = Aўs |  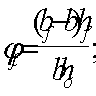  |
Примечание. Значения llim, приведенные над чертой, применяются при расчете элементов, армированных сталью класса А-II, под чертой ѕ класса A-III.
Если предельно допустимые прогибы f (см. п. 1.17) меньше 

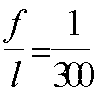

Для сплошных плит толщиной менее 250 мм, армированных плоскими сетками, значения llim уменьшаются делением на коэффициент, указанный в п. 4.24.
Примечание. Значения llim могут быть увеличены в следующих случаях:
а) если прогиб определяется от действия момента Ml, составляющего часть полного момента Мtot (поз. 2 ѕ 4 табл. 2), ѕ умножением llim табл. 33 на отношение Мtot/ Ml;
б) если нагрузка отличается от равномерно распределенной ѕ умножением значений llim табл. 33 на отношение 
в) если прогиб определяется от совместного действия кратковременных, длительных и постоянных нагрузок — умножением значений llim табл. 33 на коэффициент jq, определяемый по формуле
где q ѕ отношение деформации от длительного действия нагрузки к деформации от кратковременного действия той же нагрузки, принимаемое равным для элементов: прямоугольного сечения q = 1,8; таврового сечения с полкой в сжатой зоне q = 1,5; таврового сечения с полкой в растянутой зоне q = 2,2.
ОПРЕДЕЛЕНИЕ КРИВИЗНЫ
4.28. Для изгибаемых элементов из тяжелого бетона постоянного сечения, указанных в п. 4.15 и эксплуатируемых при влажности воздуха окружающей среды свыше 40 %, кривизна 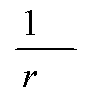
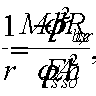
где j1, j2 — см. табл. 34.
При одновременном действии постоянных, длительных и кратковременных нагрузок кривизна 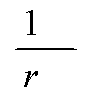
где j1sh — коэффициент j1 при непродолжительном действии нагрузки;
j1l, j2l — коэффициенты j1 и j2 при продолжительном действии нагрузки.
ОПРЕДЕЛЕНИЕ ПРОГИБОВ
4.29. Для изгибаемых элементов при 
а) для элементов постоянного сечения, работающих как свободно опертые или консольные балки, ѕ по формуле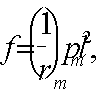
где 
рm — коэффициент, принимаемый по табл. 35;
Таблица 34
| Коэффициенты | Коэффициент j1 при значениях ma, равных | Коэффициент j2 при значениях ma, равных | ||||||||||||||||||||||
| jft | jf | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,10 | 0,13 | 0,15 | 0,17 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 | <0,04 | 0,04-0,08 | 0,08-0,15 | 0,15-0,30 | 0,30-0,50 |
| Продолжительное действие нагрузки | ||||||||||||||||||||||||
| 0,0 0,0 0,0 0,0 0,0 0,0 |
0,0 0,2 0,4 0,6 0,8 1,0 |
0,43 0,49 0,52 0,54 0,56 0,57 |
0,39 0,46 0,49 0,51 0,53 0,54 |
0,36 0,44 0,47 0,49 0,51 0,52 |
0,34 0,42 0,46 0,48 0,49 0,51 |
0,32 0,41 0,45 0,47 0,48 0,50 |
0,30 0,39 0,44 0,46 0,47 0,49 |
0,28 0,37 0,42 0,44 0,46 0,48 |
0,26 0,35 0,40 0,43 0,45 0,47 |
0,23 0,31 0,38 0,42 0,44 0,46 |
0,22 0,29 0,35 0,39 0,42 0,44 |
0,21 0,27 0,33 0,37 0,40 0,42 |
0,19 0,25 0,31 0,35 0,38 0,41 |
0,16 0,21 0,26 0,31 0,35 0,38 |
0,14 0,19 0,24 0,28 0,32 0,35 |
0,13 0,17 0,22 0,25 0,29 0,32 |
0,12 0,16 0,20 0,23 0,27 0,30 |
0,11 0,14 0,18 0,22 0,25 0,28 |
0,10 0,13 0,17 0,20 0,23 0,26 |
0,10 0,12 0,13 0,13 0,14 0,15 |
0,07 0,09 0,10 0,11 0,12 0,13 |
0,04 0,05 0,06 0,08 0,09 0,10 |
0,00 0,00 0,02 0,02 0,04 0,06 |
0,00 0,00 0,00 0,00 0,00 0,00 |
| 0,2 0,4 0,6 0,8 1,0 |
0,0 0,0 0,0 0,0 0,0 |
0,47 — — — — |
0,40 0,42 0,43 — — |
0,36 0,36 0,37 0,38 0,40 |
0,33 0,33 0,33 0,33 0;33 |
0,31 0,31 0,31 0,30 0,30 |
0,30 0,30 0,30 0,29 0,29 |
0,28 0,28 0,27 0,27 0,27 |
0,26 0,26 0,25 0,24 0,24 |
0,23 0,22 0,22 0,22 0,22 |
0,22 0,21 0,21 0,21 0,20 |
0,21 0,20 0,20 0,20 0,19 |
0,19 0,19 0,18 0,17 0,17 |
0,16 0,16 0,15 0,15 0,15 |
0,14 0,14 0,14 0,14 0,14 |
0,13 0,13 0,12 0,12 0,12 |
0,11 0,11 0,11 0,11 0,11 |
0,11 0,10 0,10 0,10 0,10 |
0,10 0,10 0,10 0,10 0,10 |
0,15 0,18 0,20 0,23 0,25 |
0,12 0,16 0,19 0,22 0,24 |
0,08 0,13 0,17 0,20 0,23 |
0,03 0,06 0,09 0,12 0,14 |
0,00 0,02 0,03 0,05 0,06 |
| 0,2 0,4 0,6 0,8 1,0 |
0,2 0,4 0,6 0,8 1,0 |
0,51 — — — — |
0,45 0,53 — — — |
0,43 0,49 0,53 — — |
0,40 0,47 0,50 0,53 0,61 |
0,38 0,45 0,48 0,50 0,53 |
0,37 0,43 0,46 0,48 0,50 |
0,36 0,42 0,44 0,46 0,48 |
0,34 0,39 0,41 0,44 0,45 |
0,30 0,37 0,39 0,41 0,43 |
0,28 0,35 0,38 0,39 0,40 |
0,26 0,33 0,36 0,38 0,39 |
0,24 0,30 0,34 0,37 0,38 |
0,21 0,26 0,31 0,34 0,36 |
0,19 0,23 0,28 0,31 0,34 |
0,17 0,21 0,25 0,29 0,32 |
0,16 0,20 0,23 0,26 0,29 |
0,14 0,18 0,21 0,25 0,27 |
0,13 0,17 0,20 0,23 0,26 |
0,16 0,20 0,24 — — |
0,13 0,19 0,22 0,25 0,26 |
0,08 0,14 0,20 0,24 0,25 |
0,04 0,07 0,12 0,19 0,20 |
0,00 0,03 0,04 0,08 0,12 |
| Непродолжительное действие нагрузки | ||||||||||||||||||||||||
| 0,0 0,0 0,0 0,0 0,0 0,0 |
0,0 0,2 0,4 0,6 0,8 1,0 |
0,64 0,72 0,76 0,79 0,82 0,84 |
0,59 0,66 0,69 0,71 0,73 0,74 |
0,56 0,63 0,66 0,69 0,70 0,71 |
0,53 0,61 0,65 0,67 0,68 0,69 |
0,51 0,59 0,63 0,65 0,67 0,68 |
0,50 0,58 0,62 0,64 0,66 0,67 |
0,49 0,57 0,61 0,63 0,65 0,66 |
0,46 0,56 0,60 0,63 0,65 0,66 |
0,43 0,53 0,59 0,62 0,64 0,66 |
0,41 0,51 0,57 0,61 0,63 0,65 |
0,40 0,49 0,56 0,60 0,63 0,65 |
0,37 0,46 0,53 0,58 0,61 0,63 |
0,34 0,43 0,49 0,55 0,58 0,61 |
0,32 0,40 0,46 0,52 0,56 0,59 |
0,30 0,37 0,44 0,49 0,53 0,56 |
0,28 0,35 0,41 0,46 0,50 0,54 |
0,26 0,33 0,39 0,44 0,48 0,52 |
0,25 0,31 0,37 0,42 0,46 0,50 |
0,17 0,21 0,23 0,25 0,26 0,27 |
0,14 0,18 0,20 0,21 0,23 0,24 |
0,09 0,11 0,14 0,16 0,17 0,18, |
0,02 0,03 0,04 0,05 0,06 0,07 |
0,00 0,00 0,00 0,00 0,00 0,00 |
| 0,2 0,4 0,6 0,8 1,0 |
0,0 0,0 0,0 0,0 0,0 |
0,74 — — — — |
0,60 0,63 0,81 — — |
0,56 0,57 0,59 0,63 0,84 |
0,53 0,54 0,54 0,55 0,57 |
0,51 0,51 0,51 0,51 0,52 |
0,49 0,49 0,49 0,49 0,49 |
0,47 0,47 0,47 0,47 0,47 |
0,44 0,44 0,44 0,44 0,44 |
0,42 0,42 0,42 0,42 0,42 |
0,40 0,40 0,40 0,40 0,40 |
0,39 0,39 0,39 0,39 0,39 |
0,37 0,37 0,37 0,37 0,37 |
0,34 0,34 0,34 0,34 0,34 |
0,32 0,32 0,32 0,32 0,32 |
0,30 0,30 0,30 0,30 0,30 |
0,28 0,28 0,28 0,28 0,28 |
0,26 0,26 0,26 0,26 0,27 |
0,25 0,25 0,25 0,25 0,25 |
0,28 0,35 0,36 0,45 0,50 |
0,23 0,31 0,39 0,40 0,46 |
0,16 0,25 0,32 0,38 0,44 |
0,07 0,14 0,20 0,25 0,29 |
0,00 0,03 0,08 0,12 0,15 |
| 0,2 0,4 0,6 0,8 1,0 |
0,2 0,4 0,6 0,8 1,0 |
0,79 — — — — |
0,67 0,77 — — — |
0,63 0,69 0,76 — — |
0,61 0,66 0,70 0,76 0,92 |
0,59 0,64 0,67 0,71 0,76 |
0,58 0,62 0,65 0,68 0,71 |
0,56 0,61 0,64 0,66 0,69 |
0,55 0,58 0,61 0,64 0,66 |
0,52 0,56 0,58 0,61 0,63 |
0,50 0,55 0,57 0,59 0,61 |
0,48 0,54 0,56 0,58 0,60 |
0,46 0,52 0,55 0,57 0,58 |
0,42 0,48 0,53 0,56 0,57 |
0,39 0,45 0,50 0,53 0,56 |
0,37 0,43 0,47 0,51 0,54 |
0,35 0,40 0,45 0,49 0,52 |
0,33 0,38 0,43 0,47 0,50 |
0,31 0,37 0,41 0,45 0,48 |
0,27 0,39 0,50 — — |
0,24 0,37 0,46 0,60 0,72 |
0,17 0,30 0,44 0,57 0,70 |
0,08 0,16 0,28 0,41 0,55 |
0,00 0,04 0,11 0,21 0,31 |
при схеме загружения свободно опертой или консольной балки, не приведенной в табл. 35, прогиб определяется по формулам сопротивления материалов при жесткости, равной отношению наибольшего момента к наибольшей кривизне;
б) если прогиб, определенный по подпункту «а», превышает допустимый, то для слабоармированных элементов (m Ј 0,5 %) его значение рекомендуется уточнять за счет учета повышенной жесткости на участках без трещин при переменной жесткости на участке с трещинами; для свободно опертых балок, загруженных равномерно распределенной нагрузкой, это соответствует формуле
где рcrc — коэффициент, принимаемый по табл. 36 в зависимости от отношения Mcrc/Mtot (Mcrc ѕ см. пп. 4.2 и 4.3) ;
Для иных схем загружения величина f может быть определена по формуле (314) ;
в) для изгибаемых элементов с защемленными опорами прогиб в середине пролета определяется по формуле
где 
рm ѕ коэффициент, определяемый по табл. 35 как для свободно опертой балки;
г) для элементов переменного сечения, а также в тех случаях, когда требуется более точное, чем по формулам (311) и (313), определение прогибов, а сами элементы и нагрузка симметричны относительно середины пролета, прогиб определяется по формуле
Таблица 35
| Схема загружения консольной балки | Коэффициент рm | Схема загружения свободно опертой балки | Коэффициент рm |
 |
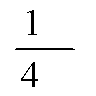 |
 |
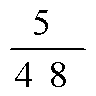 |
 |
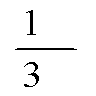 |
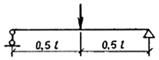 |
 |
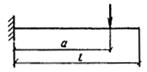 |
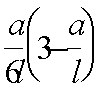 |
 |
 |
Примечание. При загружении элемента одновременно по нескольким схемам 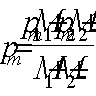

Таблица 36
| Mcrc/Mtot | 1,00 | 0,99 | 0,98 | 0,96 | 0,94 | 0,92 | 0,90 | 0,85 | 0,80 |
| Pcrc | 0,104 | 0,088 | 0,082 | 0,073 | 0,067 | 0,062 | 0,058 | 0,049 | 0,042 |
Продолжение табл. 36
| Mcrc/Mtot | 0,75 | 0,70 | 0,60 | 0,50 | 0,40 | 0,30 | 0,20 | 0,10 | 0,00 |
| Pcrc | 0,036 | 0,032 | 0,024 | 0,018 | 0,013 | 0,008 | 0,005 | 0,002 | 0,000 |
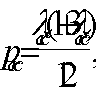

где 


В остальных случаях прогиб в середине пролета рекомендуется определять по формуле (294).
Входящие в формулы (311) ѕ (314) значения кривизн определяются по формулам (271), (272), (282), (286), (309) и (310) при наличии трещин в растянутой зоне и по формулам (269) и (270) — при их отсутствии.
Для сплошных плит толщиной менее 250 мм необходимо учитывать указания п. 4.24.
4.30. Для коротких элементов (l/h < 10) постоянного сечения, работающих как свободно опертые балки, прогиб вычисляется согласно п. 4.29 и умножается на коэффициент Pq, учитывающий влияние деформаций сдвига. Коэффициент Pq определяется по формуле
где jq = 0,5 — при отсутствии как нормальных, так и наклонных трещин, т.е. при выполнении условий (233) и (248);
jq = 1,5 — при наличии нормальных или наклонных трещин;
рm — см. табл. 35.
Примеры расчета
Пример 57. Дано: железобетонная плита перекрытия гражданского здания прямоугольного сечения размерами h = 120 мм, b = 1000 мм, ho = 105 мм; пролет l = 3,1 м; бетон тяжелый класса В25 (Eb =2,7×104 МПа; Rbt.ser = 1,6 МПа); растянутая арматура класса А-II (Еs = 2,1×105 МПа), площадь ее поперечного сечения Аs = 393 мм2 (5 Æ10); полная равномерно распределенная нагрузка qtot = 7 кН/м, в том числе ее часть от постоянных и длительных нагрузок ql = 6 кН/м; прогиб ограничивается эстетическими требованиями.
Требуется рассчитать плиту по деформациям.
Расчет. Определим необходимость расчета плиты по деформациям согласно п. 4.27:
Из табл. 33 по ma = 0,029 и jf = jft = 0 находим llim = 21. Так как h < 250 мм, то llim корректируем путем деления на коэффициент 
Учитывая примечание к п. 4.27 (случай «а»), имеем
Поскольку —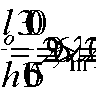
Определим кривизну в середине пролета от действия момента Мl (так как прогиб ограничивается эстетическими требованиями).
Принимаем без расчета, что элемент имеет трещины в растянутой зоне, в связи с чем кривизну определим по формуле (309).
Из табл. 34 по ma = 0,028 и jf = jft = 0 находим значения j1 = 0,393 и j2 = 0,10, соответствующие продолжительному действию нагрузки.
Прогиб определим согласно п. 4.29а, принимая, согласно табл. 35, 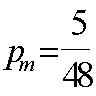
Так как h < 250 мм, полный прогиб равен f = 13,5 × 1,23 = 16,6 мм, что больше предельно допустимого прогиба 
Поскольку m = 0,00375 < 0,005, согласно п. 4.296 уточним значение f по формуле (312). Для этого вычислим величины 
Так как рассчитывается слабоармированный элемент (m < 0,01), Ired и Мcrc определим как для бетонного сечения (см. пп. 4.2 и 4.3):
jb1 = 0,85 (как для тяжелого бетона);
Коэффициент рсrс определим по табл. 36 при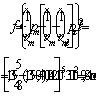
С учетом поправки на малую высоту сечения (h < 250 мм) f = 9,84×1,23 = 12,1 мм, что меньше предельно допустимого прогиба f = 15,5 × мм.
Поскольку l/h > 10, влиянием деформаций сдвига пренебрегаем.
Пример 58: Дано: ригель перекрытия общественного здания прямоугольного сечения размерами b = 200 мм, h = 600 мм; a = 80 мм; пролет ригеля l = 4,8 м; бетон тяжелый класса В25 (Еb = 2,7 ґ 104 МПа; Rbt,ser = 1,6 МПа); рабочая арматура класса А-III (Es = 2 × 105 МПа), площадь ее поперечного сечения Аs = 2463 мм (4 Æ28); полная равномерно распределенная нагрузка qtot = 85,5 кН/м, в том числе ее часть от постоянных и длительных нагрузок ql = 64 кН/м; прогиб ограничивается эстетическими требованиями; влажность воздуха в помещении свыше 40 %.
Требуется рассчитать ригель по деформациям.
Расчет. Определим необходимость расчета по деформациям согласно п. 4.27.
ho = 600 ‑ 80 = 520 мм ;
Так как l/h = 4,8/0,6 = 8 < 10, необходимо учитывать влияние деформаций сдвига на прогиб элемента: l/ho = 4,8/0,52 = 9,3. По табл. 33 при ma = 0,176 и jf = jft = 0 находим llim = 8.
т. е. расчет по деформациям необходим.
Поскольку m = 0,238 > 0,005, согласно п. 4.1 кривизну определим с учетом наличия трещин в растянутой зоне. Так как прогиб ограничивается эстетическими требованиями, расчет производим на действие момента Мl. Кривизну в середине пролета 
По табл. 34 при ma = 0,176 и jf = jft = 0 находим j1 = 0,206 и j2 = 0.
Полный прогиб определим согласно пп. 4.29а и 4.30 с учетом влияния деформаций сдвига. Согласно табл. 35,
т. е. прогиб ригеля меньше предельно допустимого (см. табл. 2).
Пример 59. Дано: железобетонная плита покрытия с расчетным пролетом 5,7 м; размеры поперечного сечения (для половины сечения плиты) — по черт. 89; бетон легкий класса В25 (Rb,ser = 18,5 МПа; Rbt,ser = 1,6 МПа), марки по средней плотности D1600 (Eb =16,5×103 МПа); рабочая арматура класса А-II (Es = 2,1×105 МПа), площадь ее сечения As = 380 мм2 (1Æ22); постоянная и длительная равномерно распределенные нагрузки на плиту ql = 8,75 кН/м; прогиб плиты ограничивается эстетическими требованиями; помещение, перекрываемое плитой, имеет нормальную влажность воздуха (40 ѕ 75 %).
Требуется рассчитать плиту по деформациям.
Черт. 89. К примеру расчета 59
Расчет. Момент в середине плиты от постоянных и длительных нагрузок для половины сечения равен:
Из черт. 89 имеем: ho = 300 ‑ 31 = 269 мм; b = (95 + 65) /2 = 80 мм; b’f = 730 мм; hf = 30 мм.
Поскольку приближенные методы расчета по деформациям не относятся к конструкциям из легкого бетона, расчет кривизны производим по формулам пп. 4.15 ѕ 4.17 как для элементов с трещинами в растянутой зоне (
Определим кривизну плиты в середине пролета по формуле (271). Момент Ms при действии постоянных и длительных нагрузок равен Ms = М = 17,8 кН×м.
Относительную высоту сжатой зоны бетона x находим по формуле (274). Для этого вычислим величины:
b = 1,8 (как для легкого бетона), подставив которые в формулу (274), получим
Так как 
Определим коэффициент ys согласно п. 4.17. Для этого находим по формуле (246) величину Wpl:
Коэффициент jm определим по формуле (281), учитывая, что для изгибаемого элемента Mr = М:
Из табл. 32 имеем jls = 0,8; ys = 1,25 ѕ jlsjm = 1,25 ѕ 0,8 × 0,464 = 0,879 < 1,0.
Кривизну плиты в середине пролета определим по формуле (271), принимая коэффициенты v= vl = 0,15 (см. табл. 31) и yўb = 0,9:
Так как l/h = 5700/300 = 19 > 10, согласно п. 4.29, прогиб f = fm, который определим по формуле (311). Согласно табл. 35,
т. е. прогиб плиты меньше предельно допустимого (см. табл. 2).
5. КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ
ОБЩИЕ ПОЛОЖЕНИЯ
5.1(5.1). При проектировании бетонных и железобетонных конструкций и изделий для обеспечения условий их экономичного и качественного изготовления, требуемой долговечности и совместной работы арматуры и бетона надлежит выполнять конструктивные требования настоящего раздела.
5.2. Конструкции следует принимать простого очертания. Рекомендуется использовать арматуру, закладные детали и строповочные петли, выпускаемые в виде товарной продукции по нормалям и государственным стандартам. Арматуру следует проектировать в виде укрупненных блоков и пространственных каркасов для сокращения времени укладки в форму (опалубку).
Распалубочную и отпускную прочность бетона следует назначать минимально возможной для ускорения оборота форм (опалубки) и интенсивного использования производственных площадей.
Необходимо стремиться к унификации арматуры и закладных деталей в отдельных конструкциях и их сериях, к небольшому числу разных марок и диаметров стали, типов арматурных элементов ѕ сеток и каркасов, шагов продольных и поперечных стержней.
МИНИМАЛЬНЫЕ РАЗМЕРЫ СЕЧЕНИЯ ЭЛЕМЕНТОВ
5.3(5.2). Минимальные размеры сечения бетонных и железобетонных элементов, определяемые из расчета по действующим усилиям и соответствующим группам предельных состояний, должны назначаться с учетом экономических требований, необходимости унификации опалубочных форм и армирования, а также условий принятой технологии изготовления конструкций.
Кроме того, размеры сечения элементов железобетонных конструкций необходимо принимать такими, чтобы соблюдались требования в части расположения арматуры в сечении (толщины защитных слоев бетона, расстояния между стержнями и т. п.) и анкеровки арматуры.
5.4(5.3). Толщина1 монолитных плит должна приниматься, мм, не менее:
для покрытий…………………………………………………………………….. 40
для междуэтажных перекрытий жилых и общественных
зданий. ……………………………………………………………………………… 50
для междуэтажных перекрытий производственных зданий…….. 60
для плит из легкого бетона класса В7,5 и ниже во всех
случаях…………………………………………………………………………….. 70
1Здесь и далее по тексту величины размеров сечений, толщины защитного слоя бетона и др., приведенные в настоящем Пособии, относятся к номинальным значениям, назначаемым при проектировании и указываемым в чертежах. От этих номинальных значений возможны отклонения в натуре, не превышающие величин, указанных в соответствующих государственных стандартах, технических условиях и др.
Минимальная толщина сборных плит должна определяться из условия обеспечения требуемой толщины защитного слоя бетона и условий расположения арматуры по толщине плиты (см. пп. 5.32-5.41).
Размеры сечений внецентренно сжатых элементов должны приниматься такими, чтобы их гибкость lo/i в любом направлении, как правило, не превышала:
для железобетонных
элементов……………………………………….. 200 (для прямоугольных
сечений при lo/h Ј 60)
для колонн, являющихся элементами
зданий…………………………………………….. 120 (при lo/h Ј 35)
для бетонных элементов…………………….. 90 (для прямоугольных
сечений при lo/h Ј 26)
ГАБАРИТЫ И ОЧЕРТАНИЯ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
5.5. Размеры сборных бетонных и железобетонных элементов следует назначать с учетом грузоподъемности и габаритных ограничений технологического, транспортного и монтажного оборудования на заводах-изготовителях и на строительных площадках. В необходимых случаях следует учитывать возможность подъема железобетонного изделия вместе с формой.
5.6. Во избежание повреждений от местных концентраций напряжений при резком изменении направлений граней изделия (например, во внутренних углах) рекомендуется предусматривать смягчение очертания в виде уклонов, фасок или закруглений по возможности небольшой величины (до 50 мм), чтобы не требовалось местное армирование (черт. 90, а, б, в).
Во внешних острых углах во избежание откалывания бетона следует устраивать скосы или закругления (черт. 90, г).
Черт. 90. Закругления и фаски
а ѕ закругления в ребристой плите; б ѕ- фаска между полкой и стенкой в тавровой балке; в ѕ сочетание фаски и закругления в узле фермы; г ѕ смягчение острого угла в ригеле; д ѕ закругления в отверстии для пропуска коммуникаций, строповки и т. д.
5.7. Отверстия в железобетонных элементах для пропуска коммуникаций, строповки и т. п. следует принимать по возможности небольшими и располагать в пределах ячеек арматурных сеток и каркасов так, чтобы не нужно было перерезать арматуру и армировать по месту. Углы отверстий желательно делать плавными (черт. 90, д).
5.8. При проектировании бетонных и железобетонных конструкций их очертание следует принимать с учетом устройства и способа использования форм (опалубки).
При применении форм с откидными бортами очертание изделия не должно препятствовать повороту борта (черт. 91, а) при распалубке.
При применении неразъемных форм для возможности извлечения изделия из них должны предусматриваться технологические уклоны не менее 1:10 (черт. 91, б, в). В случае применения неразъемных форм с использованием выпрессовывания уклон должен быть не менее 1:15 (черт. 91, г).
При немедленной распалубке с обеспечением фиксированного (во избежание нарушения бетона) вертикального перемещения формующего элемента оснастки (черт. 91, д, е) уклон должен быть не менее 1:50.
При использовании форм с одним неподвижным и одним откидным бортом для возможности вертикального подъема конструкции при распалубке следует переход от большей ширины изделий к меньшей [например, от нижней полки к стенке (черт. 91, ж)] принимать плавным под углом не менее 45°. Это требование можно не учитывать, если форма снабжена выпрессовывающим устройством (черт. 91, з).
Применение выпрессовывания и немедленной распалубки должно согласовываться с изготовителем изделия.
Черт. 91. Технологические уклоны
а ѕ в форме с откидными бортами; б, в ѕ в неразъемной форме; г — то же, с применением выпрессовщика; д, е — при немедленной распалубке; ж ѕ в форме с глухим бортом; з ѕ то же, с выпрессовщиком; 1 — изделие; 2 ѕ форма; 3 ѕ откидной борт; 4 ѕ выпрессовщик; 5 ѕ вкладыш; 6 ѕ формующая рамка
От действующих во внецентренно сжатой сквозной колонне расчетных усилий N и М в ее ветвях возникают только продольные усилия (как в ферме с параллельными поясами). Поперечную силу воспринимает решетка. Несущая способность такой колонны может быть исчерпана или в результате потери устойчивости колонны в целом, или в результате потери устойчивости какой-либо ветви.
Усилия в отдельных ветвях колонны определяют по формуле (рисунок ниже):
N1 = Ny/h0 ± M/h0
где h0 — расстояние между центрами тяжести ветвей; у — расстояние от центра тяжести колонны до оси ветви, противоположной рассматриваемой.
К расчету сквозной внецентренно сжатой колонны
После определения усилий в ветвях наиболее напряженную из них проверяют на устойчивость в обеих плоскостях как центрально сжатый элемент. За расчетную длину принимают: в плоскости действия момента — расстояние между узлами крепления решетки, из плоскости действия момента — длину ветви.
Устойчивость колонны в целом в плоскости действия момента проверяют по формуле выше, при этом коэффициент φе определяют в зависимости от условной приведенной гибкости λef = λef √Ry/Е и относительного эксцентриситета m. Приведенную гибкость λef вычисляют, как для центрально-сжатых колонн, по формуле выше.
Относительный эксцентриситет для сквозных колонн
m = Mx/N Ay/Ix
где А — площадь сечения ветвей колонны; у — расстояние от центра тяжести сечения колонны до оси наиболее сжатой ветви; Ix — момент инерции сечения.
Устойчивость сквозной колонны как единого целого из плоскости действия момента проверять не нужно, так как она обеспечивается проверкой устойчивости в этом направлении каждой из ветвей.
Расчет и конструирование соединительных решеток в сквозных колоннах. В сжатых колоннах всегда бывают некоторые неучитываемые расчетом случайные или конструктивные эксцентриситеты, под влиянием которых в центрально-сжатых колоннах возникают изгибающие моменты и перерезывающие силы. Интенсивность этих изгибающих моментов и поперечных сил неизвестна, так как неизвестна величина эксцентриситетов, возникающих в реальных колоннах.
Поэтому для определения расчетной поперечной силы в центрально-сжатых составных сквозных колоннах пользуются результатами исследований, которые показали, что поперечная сила зависит от геометрических размеров колонны и материала. Элементы соединительной решетки составных сжатых стержней (колонн) рассчитывают на условную поперечную силу Qfic, принимаемую постоянной по всей длине стержня:
где N— продольное усилие в составном стержне; φ — коэффициент продольного изгиба, принимаемый для составного стержня в плоскости соединительных элементов.
Условную поперечную силу Qfic прикладывают в каждом узле составного стержня. Она равномерно распределяется между плоскостями решеток. Таких плоскостей обычно две, в результате чего на каждую плоскость действует сила (рисунок ниже):
Qx = Qs/sinβ
где β — угол между раскосом и ветвью.
Во внецентренно сжатых сквозных колоннах элементы решетки рассчитывают на поперечную силу, равную большему из значений, определенному при статическом расчете Q или условному Qfic
Сжимающие усилия в раскосе находят при раскосной решетке так же, как и в элементах фермы (рисунок ниже):
Nad = Qx/sin (3
где Р — угол между раскосом и ветвью.
Схемы для расчета соединительных решеток
Раскосы обычно выполняют из одиночного уголка, прикрепляемого к ветви одной полкой, в результате чего возникает конструктивный эксцентриситет и, соответственно, изгибающий момент. Это находит отражение при проверке устойчивости сжатого раскоса, напряжение в котором не должно превосходить расчетного сопротивления:
где γс = 0,75 — коэффициент условий работы, учитывающий одностороннее прикрепление раскоса из уголка; φ — коэффициент продольного изгиба, определяемый по гибкости раскоса λd =ld/imin; ld — длина раскоса; imin — минимальный радиус инерции одиночного уголка; A’d — площадь сечения одного раскоса.
Наименьший профиль элементов раскосной решетки, применяемый в сварных колоннах, равнополочный уголок 45×5. Предельная гибкость элементов решетки [λ] = 150.
В составных стержнях с безраскосной решеткой планки жестко связаны с ветвями. В результате такой стержень можно рассматривать как безраскосную ферму. Расчет планок заключается в определении их сечения и расчете прикрепления к ветвям. Расстояние между планками определяется принятой гибкостью ветви (при подборе сечения) и ее радиусом инерции относительно оси 1—1 (см. рисунок выше). В свету это расстояние равно:
l1=λ1i1
Планки работают на изгиб от перерезывающей силы F, которая возникает в результате действия условной поперечной силы. Значение F можно получить из условия равновесия вырезанного узла стержня (рисунок выше):
F = Qsl /bef
где l — расстояние между центрами планок; bef— расстояние между осями ветвей.
Момент, изгибающий планку в месте ее крепления (там же действует и сила F как реактивная),
М = Qsl/2.
В сварных конструкциях планки крепят к ветвям внахлестку угловыми швами, причем значение нахлестки обычно составляет до 30 мм (см. рисунок выше).
Ширину планок d назначают из условия ее прикрепления. Кроме того, она должна быть достаточно жесткой, поэтому обычно принимают d = (0,5 — 0,75)b, где b — ширина стержня. Толщину планок назначают конструктивно 6-10 мм в пределах (1/10 — 1/25)d.
Прочность угловых швов проверяют только по металлу шва (так как сварка — ручная) по равнодействующему напряжению от момента М и перерезывающей силы F.
В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).


Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:

Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Рассчитываем первый участок:
Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:


Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
4.3. Расчет и конструирование сквозной колонны
Пример 4.3. Подобрать сквозную колонну из двух швеллеров, соединенных планками (рис. 4.5), по данным примера 4.2.
Рис. 4.5. Составной стержень колонны на планках
Расчетом сквозных колонн относительно материальной оси x—x определяют номер профиля, а расчетом относительно свободной оси y—y, производимым так же, как сплошных колонн, но с заменой гибкости стержня приведенной гибкостью, назначают расстояние между ветвями, при котором обеспечивается равноустойчивость стержня в двух взаимно перпендикулярных плоскостях.
4.3.1. Расчет колонны на устойчивость относительно
материальной оси x—x
Рекомендуют предварительно задаться гибкостью: для средних по длине колонн 5 – 7 м с расчетной нагрузкой до 2500 кН принимают гибкость l = 90 – 50; с нагрузкой 2500 – 3000 кН – l = 50 – 30, для более высоких колонн необходимо задаваться гибкостью несколько большей.
Предельная гибкость колонн 

Рекомендуемые материалы
Задаемся гибкостью l = 50.
Условная гибкость
По табл. 3.12 определяем тип кривой в соответствии с типом принятого сечения (тип ′′b′′). Согласно табл. 3.11 условной гибкости 
Находим требуемую площадь поперечного сечения по формуле

Требуемая площадь одной ветви
Требуемый радиус инерции относительно оси x-x
По требуемым площади Ab и радиусу инерции ix выбираем из сортамента (ГОСТ 8240-93) два швеллера №36, имеющих следующие характеристики сечения:
Ab = 53,4 см2; A = 2Ab = 53,4 × 2 = 106,8 см2; Ix = 10820 см4; I1 = 513 см4;
ix = 14,2 см; i1 = 3,1 см; толщину стенки d = 7,5 мм; ширину полки bb = 110 мм; привязку к центру тяжести zо = 2,68 см; линейную плотность (массу 1 м пог.) 41,9 кг/м.
Если максимальный швеллерный профиль [40 не обеспечивает требуемую несущую способность сквозной колонны, переходят на проектирование
ветвей колонны из прокатных двутавров, принимаемых по ГОСТ 8239–89.
Определяем:
– гибкость колонны

– условную гибкость
– для кривой устойчивости ′′b′′ коэффициент устойчивости φ = 0,833. Проверяем общую устойчивость колонны относительно материальной
оси x—x:
Общая устойчивость колонны обеспечена.
Недонапряжение в колонне
Если устойчивость колонны не обеспечена или получен большой запас, то изменяют номер профиля и вновь делают проверку.
4.3.2. Расчет колонны на устойчивость относительно свободной оси y—y
Расчет на устойчивость центрально-сжатой колонны сквозного сечения, ветви которой соединены планками или решетками, относительно свободной оси (перпендикулярной плоскости планок или решеток) производят по приведенной гибкости lef :
– для колонны с планками

и 
– для колонны с треугольной решеткой
где 


I1 – момент инерции ветви относительно оси 1-1 (по сортаменту);
lb – расстояние между планками по центрам тяжести;
lob – расстояние между планками в свету;
bo – расстояние между центрами тяжести ветвей колонн;

A – площадь сечения всего стержня колонны;
Ad1 – суммарная площадь поперечных сечений раскосов решеток, лежащих в плоскостях, перпендикулярных оси у-у;
α1 = 10a3/(b2l) – коэффициент, зависящий от угла наклона раскоса к ветви β (a, b, l – размеры, определяемые по рис. 4.6).
Рис. 4.6. Схема треугольной решетки
Подбор сечения колонн относительно оси y—y производится из условия ее равноустойчивости (равенства гибкости λx относительно x—x и приведенной гибкости λef относительно оси y—y), которая достигается за счет изменения расстояния между ветвями bo.
4.3.3. Сквозная колонна с планками
Расчет колонны относительно свободной оси y—y. Приравнивая 
где l1 = 33 – предварительно принятая гибкость ветви (гибкость ветви назначают в пределах l1 = 30 – 40 и обеспечивают ее при последующем конструировании колонны путем выбора соответствующего расстояния между планками lo = λ1i1).
По λy находим радиус инерции:
Воспользовавшись приближенными значениями радиусов инерции, приведенными в табл. 4.1, определяем ширину сечения:
b = iy/0,44 = 17,38 / 0,44 = 39,5 см.
Принимаем b = 400 мм и определяем расстояние между ветвями:
Проверяем расстояние в свету между полками швеллеров:
а = b – 2bb = 400 – 2 · 110 = 180 мм > 100 мм.
Расстояние между ветвями увеличивать не требуется.
Проверка колонны на устойчивость относительно оси у-у. До проверки устойчивости колонны нужно скомпоновать сечение стержня, установить расстояние между планками, назначить их размеры.
Расчетная длина ветви
Принимаем расстояние в свету между планками lob = 100 см.
Длину планки bпл принимают равной расстоянию в свету между ветвями с напуском на ветви по 20…30 мм:
Высоту планок hпл обычно устанавливают в пределах (0,5 – 0,75)b =
= 200 – 300 мм, где b = 400 мм – ширина колонны. Принимаем hпл = 240 мм.
Толщину планок принимают tnл = 6 – 12 мм и по условиям местной устойчивости она должна быть:

Окончательно принимаем планки из листов 240´240´8 мм.
Момент инерции стержня колонны относительно оси у-у
Радиус инерции
iy = 
Гибкость стержня колонны
λy = ly/iy = 813 / 17,6 = 46,19.
Для вычисления приведенной гибкости λef относительно свободной оси проверяется отношение погонных жесткостей планки и ветви:
где
Гибкость ветви колонны
Приведенная гибкость
Условная приведенная гибкость
По табл. 3.11 в зависимости от 
Производим проверку:
Устойчивость колонны обеспечена.
Недонапряжение в колонне
Сечение принято.
Расчет планок.
Проверяем принятое сечение планок. Расчет соединительных элементов (планок, решетки) сжатых составных стержней выполняется на условную поперечную силу Qfic, принимаемую постоянной по всей длине стержня колонны и определяемую по формуле
Qfic = 7,15·10-6 (2330 – E/Ry)N/φ =
= 7,15·10-6(2330 – 2,06 · 104 / 24) 2067,18 / 0,833 = 26,3 кН,
где j = 0,833 – коэффициент устойчивости при сжатии, принимаемый для составного стержня в плоскости соединительных элементов.
Поперечная сила, приходящаяся на планку одной грани (рис. 4.7) вычисляется по формуле
Сдвигающая сила в месте прикрепления планки к ветви колонны
Рис. 4.7. К расчету планок
Момент, изгибающий планку в ее плоскости:
Приварку планок толщиной tпл = 8 мм к полкам швеллеров производим механизированной сваркой в среде углекислого газа, принимая катет сварного шва k = 6 мм.
Учитывая, что несущая способность планки больше, чем несущая способность сварного шва с катетом kf ≤ tпл, достаточно проверить прочность сварного шва. Расчет производится на равнодействующую напряжений в шве от изгибающего момента M1 и поперечной силы F (см. рис. 4.5).
Так как для механизированной сварки
прочность шва проверяем по металлу границы сплавления.
Напряжение в шве от изгиба
Напряжение от поперечной силы
где 
Проверяем прочность шва:
Прочность шва обеспечена, следовательно, несущая способность планки достаточна.
4.3.4. Сквозная колонна с треугольной решеткой
Расчет колонны относительно свободной оси y—y. Чтобы определить приведенную гибкость в колоннах с треугольной решеткой, задаемся сечением двух раскосов Ad1 = 2Ad (начиная с равнополочного уголка ∟50´50´5/ГОСТ 8509-93 с площадью Ad = 4,8 см2, в ходе расчета треугольной решетки размеры сечения при необходимости уточняются).
Для треугольной решетки, состоящей из одних раскосов, угол между раскосом и направлением поперечной силы α = 35о (рис. 4.8), для треугольной решетки с дополнительными распорками – α = 45о.
Рис. 4.8. К расчету треугольной решетки
Приравнивая λx = λef = 
λy =
где α1 = 10ld3/(bo2l1) = 10/(cos2α sinα) = 10 / (0,8192 ∙ 0,574) = 26 при α = 35о.
По λy находим радиус инерции:
iy = ly/λy = 813 / 54,67 = 14,87 см.
Воспользовавшись приближенными значениями радиусов инерции по табл. 4.1, определяем ширину сечения:
Принимаем b = 340 мм и проверяем расстояние в свету между полками швеллеров:
Расстояние достаточно.
Определяем расстояние между ветвями:
Проверка колонны на устойчивость относительно оси у-у. Момент инерции сечения колонны относительно оси у-у
Iy = 2[I1 + Ab(bо/2)2] = 2 [513 + 53,4 (28,64 / 2)2] = 22926,7 см4.
Радиус инерции
Гибкость стержня колонны
λy = ly/iy = 813 / 14,65 = 55,49.
Приведенная гибкость
Условная приведенная гибкость
По табл. 3.11 в зависимости от 
Производим проверку:
Устойчивость колонны относительно оси y—y обеспечена.
Недонапряжение в колонне
что допустимо в составном сечении согласно СНиП [6].
В колоннах с решеткой должна быть также проверена устойчивость отдельной ветви на участке между смежными узлами решетки.
Расчетное усилие
Nb = N/2 = 2067,18 / 2 =1033,59 кН.
Расчетная длина ветви (см. рис. 34)
l1 = 2botgα = 2 · 28,64 · 0,7 = 40,1 см.
Площадь сечения ветви Ab = 53,4 см2.
Радиус инерции сечения [36 относительно оси 1-1 i1 = 3,1 см.
Гибкость ветви
Условная гибкость ветви
Коэффициент устойчивости при центральном сжатии для типа кривой устойчивости ″b″ φ = 0,984.
Проверяем устойчивость отдельной ветви:
Ветвь колонны на участке между смежными узлами решетки устойчива.
Расчет треугольной решетки. Расчет треугольной решетки сквозной колонны выполняется как расчет решетки фермы, элементы которой рассчитываются на осевое усилие от условной поперечной силы Qfic (см. рис. 4.8). При расчете перекрестных раскосов крестовой решетки с распорками следует учитывать дополнительное усилие, возникающее в каждом раскосе от обжатия ветвей колонны. Усилие в раскосе определяем по формуле
Сечение раскоса из равнополочного уголка ∟50×50×5, предварительно принятое при расчете стержня сквозной колонны (Ad = 4,8 см2), проверяем на устойчивость, для этого вычисляем:
– расчетную длину раскоса
ld = bo/cosα = 28,64 / 0,819 = 34,97 см;
– максимальную гибкость раскоса
где iyo = 0,98 см – минимальный радиус инерции сечения уголка относительно оси yо—yо (по сортаменту);
– условную гибкость раскоса
– φmin = 0,925 – минимальный коэффициент устойчивости для типа кривой устойчивости ″b″;
– γс = 0,75 – коэффициент условий работы, учитывающий одностороннее прикрепление раскоса из одиночного уголка (см. табл. 1.3).
Производим проверку сжатого раскоса на устойчивость по формуле
Устойчивость раскоса обеспечена.
Распорки служат для уменьшения расчетной длины ветви колонны и рассчитываются на усилие, равное условной поперечной силе в основном сжатом элементе (Qfic/2). Обычно они принимаются такого же сечения, как и раскосы. Рассчитываем узел крепления раскоса к ветви колонны механизированной сваркой на усилие в раскосе Nd = 16,37 кН. Расчет сварного шва производим по металлу границы сплавления.
Усилия, воспринимаемые швами, вычисляются по следующим формулам
– у обушка
Nоб = (1 – α)Nd = (1 – 0,3) 16,37 = 11,46 кН;
– у пера
Nп = αNd = 0,3 · 16,37 = 4,91 кН.
Задаваясь минимальным катетом шва у пера kf = tуг – 1 = 5 – 1 = 4 мм, находим расчетные длины шва:
– у обушка
lw,об = Nоб/(βzRwzγwzγc) = 11,46 / (1,05 · 0,4 · 16,65 · 1 · 1) = 1,64 см;
– у пера
Рекомендуем посмотреть лекцию «Введение».
lw,п = Nп/(βzRwzγwzγc) = 4,91 / (1,05 · 0,4 · 16,65 · 1 · 1) = 0,7 см.
Принимаем минимальную конструктивную длину сварного шва у обушка и пера lw,об = lw,п = 40 + 1 = 50 мм.
Если не удается разместить сварные швы в пределах ширины ветви, то для увеличения длины швов возможно центрирование раскосов на грань колонны.
При делении колонны на отправочные марки, вызванном условиями транспортирования, отправочные элементы сквозных колонн с решетками в двух плоскостях следует укреплять диафрагмами, располагаемыми у концов отправочного элемента. В сквозных колоннах с соединительной решеткой в одной плоскости диафрагмы следует располагать по всей длине колонны не реже, чем через 4 м. Толщину диафрагмы принимают 8 – 14 мм (рис. 4.9).
Рис. 4.9. Диафрагма жесткости