У Вас с содержательной точки зрения почти всё уже сделано, но есть ряд терминологических неточностей. Понятие порядка элемента даётся не для колец, а для групп. С кольцом связана аддитивная группа, о которой здесь речь не идёт, и мультипликативная группа, которая и имеется в виду, так как сказано про умножение. Но не уточнено, из каких элементов она состоит. Если $%R$% — кольцо с единицей, то все его обратимые элементы образуют группу относительно умножения, обозначаемую $%R^{ast}$%, и называемую группой обратимых элементов кольца, или его мультипликативной группой.
Для колец вычетов $%mathbb Z_n$% группа $%mathbb Z_n^{ast}$% состоит из $%varphi(n)$% элементов — тех остатков, которые взаимно просты с $%n$%.
Кольцо $%mathbb Z_{546}$% в самом деле изоморфно прямому произведению, но не групп, а колец вычетов. В то же время, его мультипликативная группа изоморфна прямому произведению мультипликативных групп сомножителей, то есть $$Z_{546}^{ast}cong Z_2^{ast}times Z_3^{ast}times Z_7^{ast}times Z_{13}^{ast}.$$ Известно, что для простого $%p$% группа $%mathbb Z_p^{ast}$% является циклической, то есть обладает элементом порядка $%varphi(p)=p-1$%. Такие элементы для каждой из компонент Вы указали верно.
Для нахождения элемента порядка 12 в группе $%mathbb Z_{456}^{ast}$% можно поступить чуть проще (правда, его не следует называть «максимальным по умножению» — максимален ведь не сам элемент, а его порядок в группе). Берём сначала элемент 2: он имеет требуемый порядок по модулю 13, но его брать нельзя, так как он не взаимно прост с 546. Однако, прибавляя к нему несколько раз 13, мы получаем элемент с тем же свойством. Он имеет порядок 12 по модулю 13, а потому и по «старшему» модулю 546 он не уменьшится. Увеличиться он также не может, так как значение 12 максимально. Итого имеем 2, 15, 28, 41, и на последнем элементе можно остановиться, так как он не делится ни на одно из чисел 2, 3, 7, 13.
Тем не менее, если продолжать Ваше рассуждение, то надо решить систему линейных сравнений $%xequiv1pmod2$%; $%xequiv2pmod3$%; $%xequiv3pmod7$%; $%xequiv2pmod{13}$%.
Способы решения таких систем описаны в учебниках по теории чисел. См., например у Бухштаба. Здесь можно сразу заменить второе и последнее сравнение на условие $%xequiv2pmod{39}$%, записать решение в виде $%x=39y+2$%, и подставить в третье сравнение. Также надо будет учесть нечётность. В итоге должно получиться значение $%x=353$%. Такой остаток существует и единственен по известной теореме (китайская теорема об остатках).
При определении
бинарных операций на множествах
произвольной природы удобно сохранить
термины умножение
и произведение
и записывать
бинарную операцию в виде
или же (в некоторых случаях)сложение
и
сумма
и использовать аддитивную запись:
.
Определение.
Множество
называетсягруппой,
если выполнены следующие условия:
-
на множестве
введена бинарная операция
;
-
введенная бинарная
операция является ассоциативной:
;
-
множество
содержитединичный
элемент
,
обладающий свойством
для всех
;
-
для любого элемента
существуетобратный
элемент
такой, что
.
Пример 3. Пусть
.
В качестве бинарной операции на множестве
целых чисел рассмотрим обычное сложение.
Эта операция удовлетворяет всем трем
необходимым условиям группы:
-
ассоциативность
—
;
-
единичным элементом
является
;
-
обратным элементом
к
будет элемент
(
).
Следовательно,
множество целых чисел
является группой с бинарной операцией
– сложение.
Определение.
Два элемента
и
группы
коммутируют
друг с
другом, если
.
Определение.
Если все элементы группы
коммутируют друг с другом, то такая
группа называется
коммутативной или
абелевой.
Если какие-либо элементы группы не
коммутируют друг с другом, то такая
группа называется неабелевой.
Определение.
Число
элементов в группе
называетсяпорядком
этой
группы.
Определение.
Если число
элементов в группе конечно, то такая
группа называется конечной
группой.
Если же группа содержит счетное число
элементов, то ее называют бесконечной
дискретной группой
(например,
).
Наряду с дискретными
группами в современной физике часто
рассматриваются непрерывные
группы (топологические
группы или
группы Ли).
Определение.
Если все
элементы группы (включая единичный
элемент) представимы в виде степени
одного элемента, то группа называется
циклической
и обозначается
,
где— порядок группы. Группа
может быть реализована вращениями
вокруг своего центра многоугольника в
его плоскости, совмещающими многоугольник
с самим с собой. Обозначим элемент группы(вращение на угол
)
через.
Закон композиции в группе введем правилом.
Очевидно, что— единичный элемент группы, а элемент
является обратным элементом к элементу
.
Любое рассматриваемое вращение
многоугольника представимо в виде
некоторой степени вращения на угол,
где— число углов рассматриваемого
многоугольника, т.е..
Определение.
Симметрической
группой степени
называется группа перестановок множества
из
элементов.
Под перестановкой
же понимается взаимно однозначное
отображение множества на себя, при этом
элементы множества меняются местами
(или именами). Поскольку для перестановки
не важна природа элементов множества,
а только их порядок (или их номера)
перестановку можно задать таблицей.
Например, перестановка, заданная таблицей
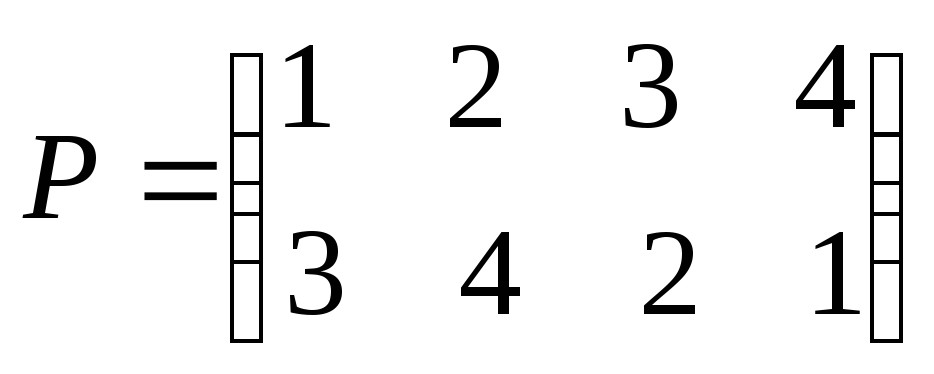
говорит нам, что
первый элемент становится третьим,
второй – четвертым, третий – вторым, а
четвертый – первым. Закон композиции
в симметрической группе задается
следующим образом. Пусть заданы две
перестановки
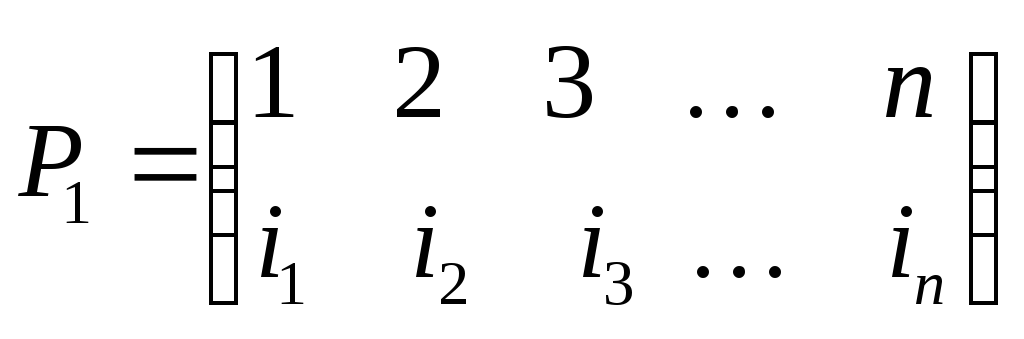
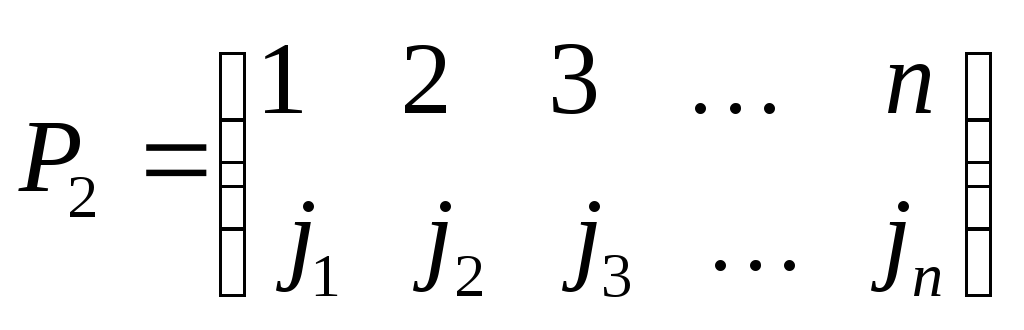
Переставим столбцы таблицы, соответствующей
второй перестановке, так, чтобы ее
верхняя строчка совпала бы с нижней
строчкой таблицы первой перестановки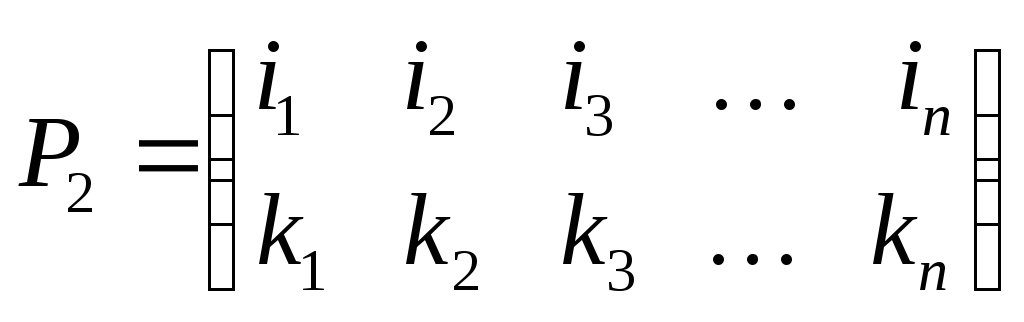
Тогда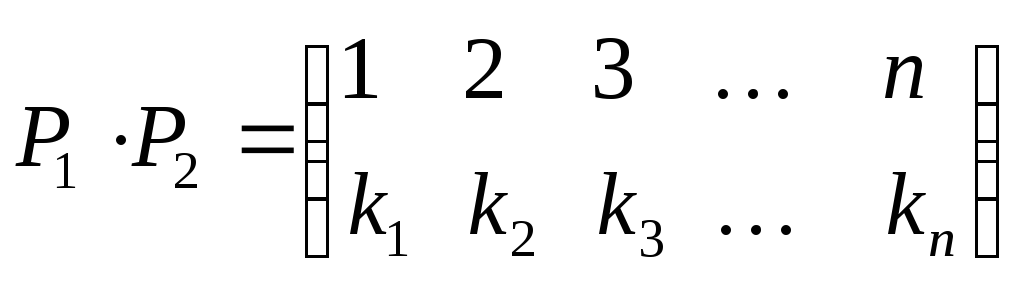
Заметим, что перестановка столбцов
таблицы, не меняет саму перестановку.
Пример 4. Пусть
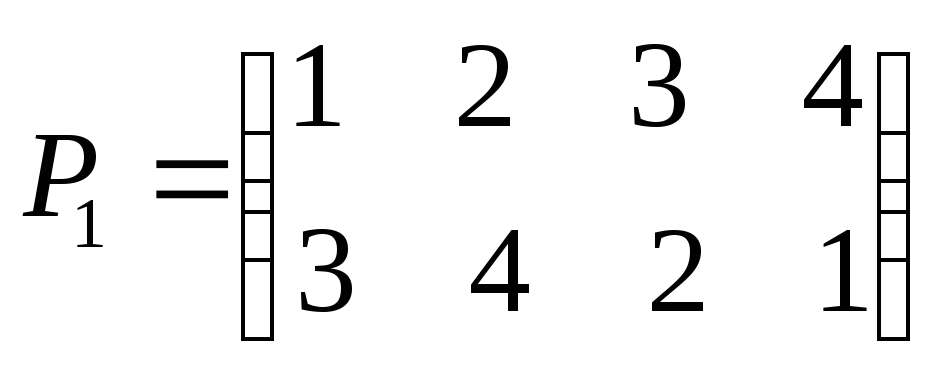

Тогда
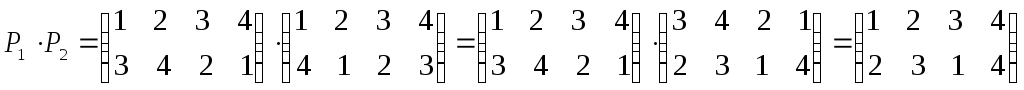
II.
Таблица умножения группы.
Для задания той
или иной группы достаточно построить
ее таблицу
умножения.
Она похожа на привычную арифметическую
таблицу умножения. Элементы группы
располагаются в верхней строке и в том
же порядке в левом столбце таблицы, а
внутри нее размещаются произведения
элементов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5.
Рассмотрим симметрическую
группу
,
элементами которой являются перестановки: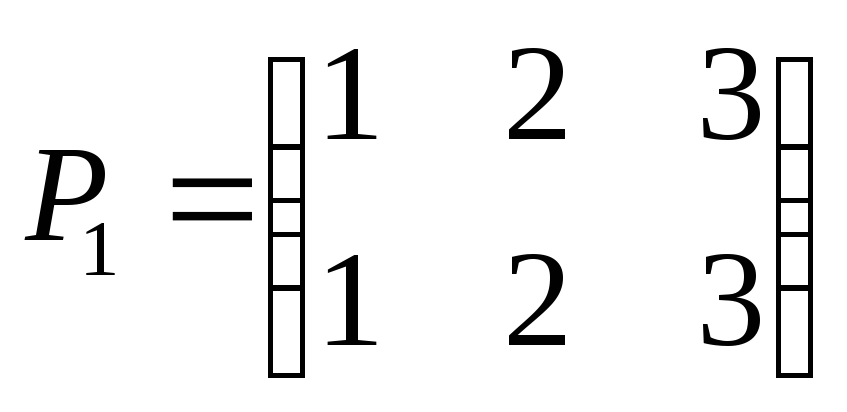
элемент группы),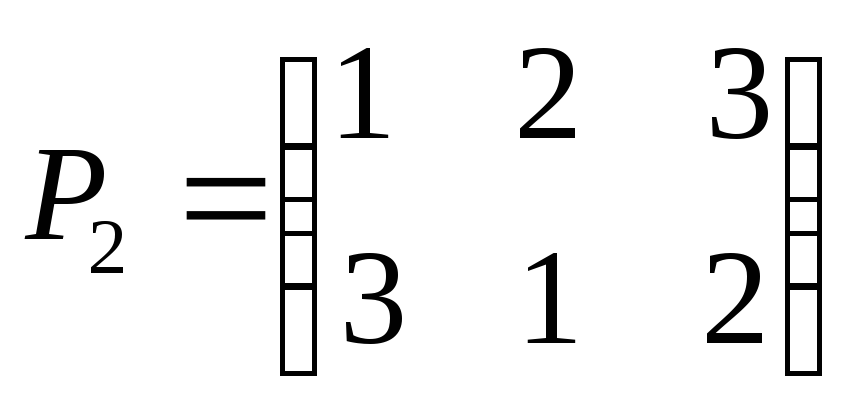
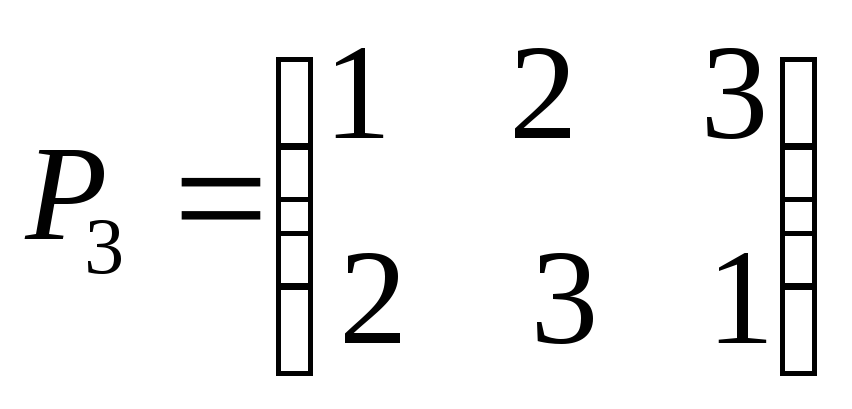
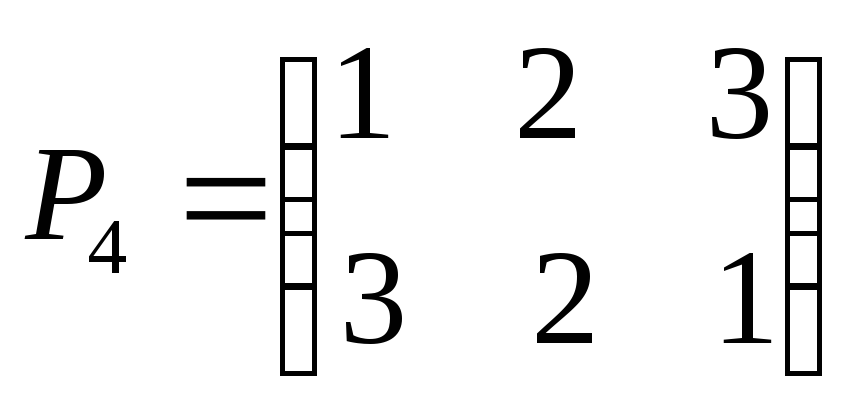
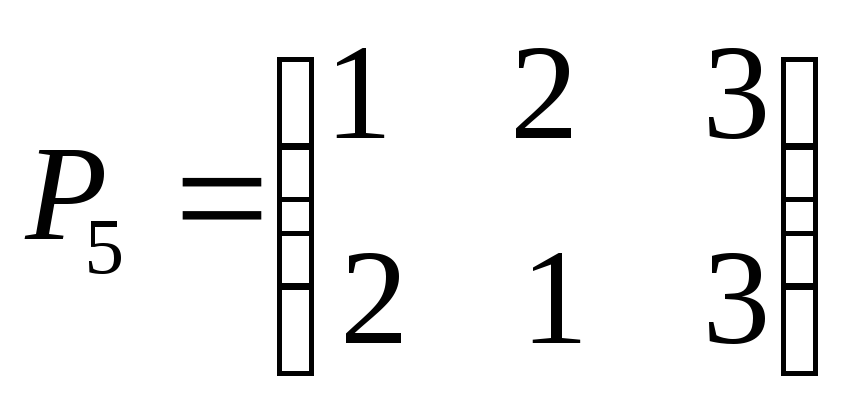
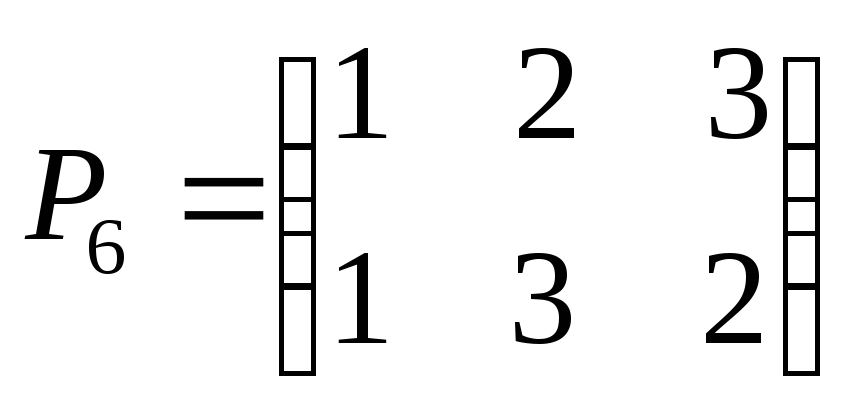
Таблица умножения этой группы имеет
вид
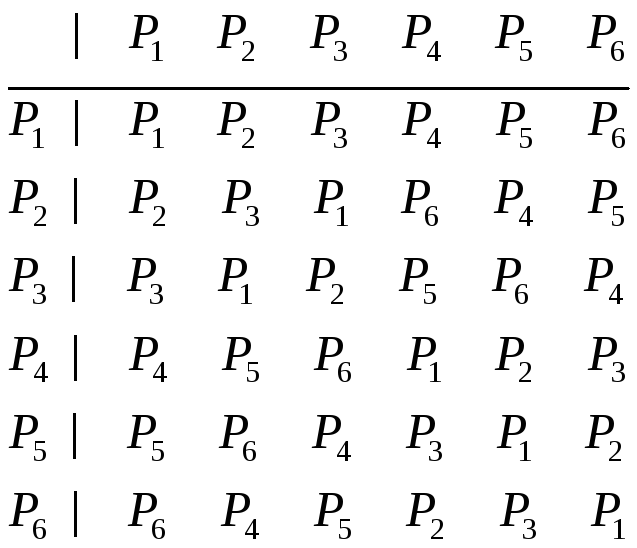
Отметим основные
свойства таблицы умножения любой группы
(для группыих легко увидеть в приведенном выше
примере):
-
Если группа имеет
элементов, то ее таблица умножения
имеетстрок и
столбцов, т.е. является квадратной с
общим числом символов.
-
Таблица содержит
только элементы группы, причем в каждой
строке и в каждом столбце эти элементы
различные. Следовательно, каждая строка
и каждый столбец содержит все элементы
группы. -
Имеются только
одна строка и один столбец, в которых
элементы группы стоят в том же порядке,
в котором они стоят над таблицей или
левее таблицы (эти строка и столбец
задаются единичным элементом группы
и отражают свойства единичного
элемента).
-
Таблица умножения
абелевой группы симметрична относительно
главной диагонали (симметрическая
группа
не является абелевой:
,
в то время как).
-
Возьмем какую-либо
строку таблицы умножения группы (скажем
под номером
)
и найдем в ней единичный элемент. Пусть
он принадлежит столбцу под номером.
Тогда на пересечении строки с номероми столбца с номером
стоит также единичный элемент группы,
т.е. единичные элементы группы стоят
в таблице умножения либо на главной
диагонали, либо симметрично относительно
нее. Это свойство таблицы отражает
свойство обратного элементаи позволяет легко находить обратные
элементы. Например, элементстоит в третьей строке, а единичный
элемент в этой строке находится во
втором столбце, следовательно, элементыи
взаимно обратны.
Определение.
Пусть
и
.Порядком
элемента
называется наименьшее положительное
число,
удовлетворяющее условию.
Очевидно, что для циклических групп
порядок элемента равен порядку группы.
Определение.
Если
— множество элементов, принадлежащих
группе,
таких, что все элементы группымогут быть выражены в виде произведений
элементов из(и их обратных), то множество
называетсясистемой
образующих группы
(сами же элементы множества
называютсяобразующими
группы
).
Поскольку каждый
элемент циклической группы представляется
степенью одного элемента этой группы,
то эта группа имеет одну образующую.
Симметрическая группа
имеет две образующие, например,
.
Определение.
Множество
называетсяподгруппой
группы
,
если
-
каждый элемент
множества
является элементом группы
;
-
есть группа
относительно закона композиции,
определенного в группе
.
Проверка факта,
что подмножество
,
является подгруппой группы,
сводится к проверке трех условий:
-
;
-
;
-
.
Любая группа имеет
две тривиальные подгруппы – единичный
элемент
и сама группа
.
Эти две подгруппы называютсянесобственными
подгруппами группы
,
остальные ее подгруппы (если они
существуют) называютсясобственными
подгруппами.
Пример 6. Множества
и
являются собственными подгруппами
симметрической группы.
III.
Отображения групп. Теорема Кэли.
Определение.
Пусть мы
имеем две группы
и
,
а также отображениегруппы
на группу
.
Если это отображение сохраняет групповую
операцию –образ
произведения двух элементов равен
произведению их образов,
т. е.
,
то отображениеназываетсягомоморфным
отображением или
гомоморфизмом.
Пример 7.
Рассмотрим две циклические группы
и
.
Гомоморфизмом будет отображение,
заданное правилом.
Определение.
Взаимно однозначное гомоморфное
отображение одной группы на другую
называется изоморфным
отображением или
изоморфизмом.
Сами группы при этом называют изоморфными.
Изоморфные группы
имеют одинаковое число элементов и
одинаковую групповую структуру.
Пример 8. Группа
вращений пятиугольника
изоморфна группе
,
в которой закон композиции – сложение
по модулю пять. Таблица умножения такой
группы имеет вид

Изоморфизмом
является отображение
,
заданное правилом
.
Симметрические
группы
играют особую роль в теории групп, о чем
говорит теорема Кэли.
Теорема Кэли.
Всякая группа
порядка
изоморфна некоторой подгруппе
симметрической группе.
Следовательно,
задачу изучения структуры всех конечных
групп можно перевести в плоскость
изучения подгрупп симметрических групп.
IV.
Смежные классы. Теорема Лагранжа.
Рассмотрим группу
порядка
,
которая имеет собственную подгруппупорядка
.
Пустьсостоит из элементов
.
Так как,
то в группенайдется элемент
,
не принадлежащий подгруппе.
Образуем множество произведений элементасо всеми элементами подгруппы
:
.
Все элементы множества
различны и не
принадлежат подгруппе
.
Если в группенайдется элемент
,
не принадлежащий множествами
,
то образуем множество.
Все элементы множества
различны и не
принадлежат множествам
и
.
Повторяем эту процедуру до тех пор, пока
на исчерпаем все элементы группы.
Пусть последним мы образовали множество.
Множества вида(включая саму подгруппу
)
называютлевыми
смежными классами
подгруппы
в группе
.
При этом справедливо равенство
.
Более точно левые
смежные классы образуют разбиение
группы
.
Следовательно,.
Это равенство формулируется в виде
теоремы.
Теорема Лагранжа.
Порядок
подгруппы конечной группы есть делитель
порядка группы.
Пример 9.
Рассмотрим симметрическую группус ее отмеченной выше подгруппой
.
Образуем левый смежный класс.
Классыи
полностью исчерпывают группу.
Следовательно,.
Возможен другой вариант.
Аналогичным образом
можно построить правые
смежные классы
.
В общем случае.
Если порядок группы
– простое число, то она не имеет
собственных подгрупп. Все группы такого
порядка – циклические группы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача про группу перестановок
Sn — группа перестановок длины n.
An — группа чётных подстановок длины n.
Задача:
а) Найти максимально возможный порядок элемента в этой группе.
б) Найти число различных циклических подгрупп максимального порядка в этой группе.
Задачу решить как для Sn, так и для An.
Народ, помогите, пожалуйста! Наш преподаватель категорически отказывается объяснять, как решается эта задача, а без неё я не смогу получить допуск к зачёту. Если не можете написать решение целиком — хотя бы выскажите идею.
Заранее благодарю, Сергей.
Или я чего-то не понимаю, или это зверская задача.
Если воспользоваться теоремой о разложении перестановки в произведение циклов, то легко видеть, что порядок некоторой перестановки есть наименьшее общее кратное длин циклов, на которые она разлагается.
Т. е. если некоторая перестановка длины n разложена в произведение r циклов длины n_1, n_2, n_3, . n_r, то порядок этой перестановки есть НОК(n_1, n_2, n_3, . n_r).
Как максимизировать это число, сходу совершенно не понятно.
Или я что-то прочно забыл?
Надо найти НАИБОЛЬШЕЕ среди всех наименьших общих кратных длин циклов, на которые разлагается перестановка. Но как это сделать — ума не приложу.
А по пункту «б» — вообще не понятно, как подступиться к этой задаче.
К пункту «б».
У кто-то вывел формулу:
N = k * n! / (f(m)*m), где
n — длина перестановки;
m — максимальный порядок подгруппы;
k — количество различных разложений перестановки длины n на циклы, при которых (при разложениях) НОК максимально.
f(n) — функция Эйлера.
Однако есть две неприятные вещи:
1. Формула работает не всегда.
2. Непонятно, откуда в ней взялась функция Эйлера.
Лично у меня есть следующие соображения.
1. Надо найти разложение: k1+k2+. +ks = n, такое что, НОК(k1, k2, . ks) — максимально.
2. Найти, сколькими способами можно заполнить БЕЗ ПОВТОРЕНИЙ s циклов (длины k1, . ks соответственно) n натуральными числами — это и будет количеством различных циклических подгрупп максимального порядка.
Поправьте меня, если я не прав.
Никаких идей нет 🙁
Сергей, но если формула работает не всегда, то это уже не формула :(.
Или у Вас есть надежда ее подправить? Но тогда нужно бы знать, как она получена.
Цитата
Лично у меня есть следующие соображения.
1. Надо найти разложение: k1+k2+. +ks = n, такое что, НОК(k1, k2, . ks) — максимально.
2. Найти, сколькими способами можно заполнить БЕЗ ПОВТОРЕНИЙ s циклов (длины k1, . ks соответственно) n натуральными числами — это и будет количеством различных циклических подгрупп максимального порядка.
Поправьте меня, если я не прав.
Первое — несомненно (но что это дает? — все равно ведь неясно, как считать НОК неизвестных чисел и, тем более, как его максимизировать), второе — сомнительно. Вы уверены ли ли, что разные заполнения соответствуют разным подгруппам?
P.S. Это где ж такой зачет? %(( Это ж ужас! 🙁
В МГТУ им. Либермана, тьфу, Баумана на кафедре «Информационная безопасность». 🙂
Кстати, отдельное «спасибо» Чашкину А.В. за то, что он очень хорошо нам «объяснил» алгебру, а также за то, что мы очень хорошо «умеем» решать задачи. 🙂
Такая задача ставится для небольших n.
n<=20.
В общем случае она явно нерешаемая. 🙂
Сергей, для небольших n все подсчитать несложно.
Просто вручную, перебором (нужно только его верно организовать).
Во всяком случае для пункта а). Про б) я еще не успел подумать, но и там, похоже, все не сложно.
P.S. Не надо больше так, хорошо? А то я вчера весь вечер только и думал, как решить Вашу задачку в общем случае.
Приведена таблица для группы S_n. m — максимальный порядок, f(m) — функция Эйлера. (немного странная запись чисел в таблице вызвана желанием выравнять столбцы)
_n | _m_ |f(m)| соответствующие разбиения n на слагаемые
01 | 001 | 01 | [1]
02 | 002 | 01 | [2]
03 | 003 | 02 | [3]
04 | 004 | 02 | [4]
05 | 006 | 02 | [2, 3]
06 | 006 | 02 | [6], [1, 2, 3]
07 | 012 | 04 | [3, 4]
08 | 015 | 08 | [3, 5]
09 | 020 | 08 | [4, 5]
10 | 030 | 08 | [2, 3, 5]
11 | 030 | 08 | [1, 2, 3, 5], [5, 6]
12 | 060 | 16 | [3, 4, 5]
13 | 060 | 16 | [1, 3, 4, 5]
14 | 084 | 24 | [3, 4, 7]
15 | 105 | 48 | [3, 5, 7]
16 | 140 | 48 | [4, 5, 7]
Для вычисления количества циклических подгрупп максимального порядка при n <=16 можно использовать формулу k*n!/(m * f(m))
Метод разумного перебора, я думаю, позволяет добраться и до 20, но на это мне надо еще где-то час времени, а времени нынче не хватает 🙂 Вот до 16 доходится быстро и легко.
Извините, забыл.
Но решение задачи в общем случае также представляет интерес. 🙂
Кстати, а как быть для An?
Для начала по пункту а).
Нужно, чтобы элемент максимального порядка оказался четной перестановкой — тогда он лежит в A_n. Здесь можно использовать два правила: 1) при перемножении перестановок их четности складываются; 2) четность цикла длины k равна четности числа (k-1).
С учетом этих правил теперь надо искать таки наборы k_1, . k_s, что сумма k_1 + . + k_s = n, НОК(k_1, . k_s) максимально и еще количество четных чисел среди k_1, . k_s само четно (это даст четность перестановки, получаемой перемножением циклов с длинами k_1, . k_s). Т.е. снова получится перебор, только с большим числом условий.
Пусть n — длина перестановки, m — максимальный порядок элемента, и пусть есть k наборов (k_1, . k_s) на которых реализуется максимум.
Для определенности рассмотрим одни такой набор. Посмотрим, сколько из него можно организовать элементов максимального порядка. Фактически нам надо расставить произвольно без повторений числа от 1 до n — это n! способов. Вот только мы некоторые элементы получили по несколько раз из-за того, что циклы (234), (342), (423) — это на самом деле один и тот же цикл. Вообще, цикл длины t был посчитан t раз. Таким образом, каждый максимальный элемент мы посчитали k_1*k_2*. *k_s раз (первый цикл можно «представить» k_1 способами, независимо от него второй цикл можно «представить» k_2 способами и т.д.). Таким образом, число элементов максимального порядка будет равно n!/(k_1*. *k_s) — это для одного набора k_1, . k_s.
Надо такое проделать для каждого из имеющихся k наборов — так мы посчитаем вообще все элементы максимального порядка в группе S_n — получится сумма по всем максимизирующим наборам k_1, . k_s выражения n!/(k_1*. *k_s).
Теперь рассмотрим все циклические группы подгруппы максимального порядка. Каждая такая группа порождена каким-то элементом максимального порядка, причем элементы максимального порядка из разных подгрупп не могут совпадать (иначе совпадали бы сами подгруппы). Но количество порождающих элементов в циклической группе порядка m равно f(m), поскольку если элемент g — порождающий, то элемент g^x будет порождающим если и только если x и m взаимно просты, а количество элементво, взаимно простых с m равно f(m). Итак, если N — число групп, то число элементов максимального проядка равно N*f(m).
Значит, N*f(m) = сумма(n!/(k_1*. *k_s)) по всем максимизирующим (k_1, . k_s).
Заметим теперь еще, что если все k_1, . k_s — попарно взаимно просты, то m = HOK(k_1, . k_s) = k_1*. *k_s. Значит, если в каждом максимизирующем наборе все k_i попарно взаимно просты, то сумма(n!/(k_1*. *k_s)) = k*n!/m, где k — число максимизирующих наборов.
Таким образом, получаем написанную ранее вами формулу
N = k*n!/(m*f(m))
и получаем условия, когда ею можно пользоваться
теория-групп — Элемент с максимальным порядком в кольце
Дано кольцо $%Z_$%. Необходимо найти максимальный порядок элемента по умножению. На данный момент результат следующий: $$ Z_ cong Z_ times Z_ times Z_ times Z_$$ То есть, исходное кольцо изоморфно прямому произведению соответствующих групп. Также получена оценка сверху максимального порядка изоморфной группы: $$ НОК(varphi(2), varphi(3), varphi(7), varphi(13)) = 12 $$ После исследования каждого кольца по отдельности, я сделал следующий вывод: в $% Z_, Z_ $% максимальный порядок 2 (элементы 1 и 2 соответственно), в $% Z_ $% — это 6 (элемент 3), в $% Z_ $% — это 12 (элемент 2). делаем вывод, что элемент $% (1, 2, 3, 2) $% является максимальным по умножению, но я не понимаю, как найти соответствующий элемент в $% Z_ $%? Буду рад, если укажете на неправильные рассуждения, скорее всего, они присутствуют.
задан 25 Фев ’19 1:35
1 ответ
У Вас с содержательной точки зрения почти всё уже сделано, но есть ряд терминологических неточностей. Понятие порядка элемента даётся не для колец, а для групп. С кольцом связана аддитивная группа, о которой здесь речь не идёт, и мультипликативная группа, которая и имеется в виду, так как сказано про умножение. Но не уточнено, из каких элементов она состоит. Если $%R$% — кольцо с единицей, то все его обратимые элементы образуют группу относительно умножения, обозначаемую $%R^$%, и называемую группой обратимых элементов кольца, или его мультипликативной группой.
Для колец вычетов $%mathbb Z_n$% группа $%mathbb Z_n^$% состоит из $%varphi(n)$% элементов — тех остатков, которые взаимно просты с $%n$%.
Кольцо $%mathbb Z_$% в самом деле изоморфно прямому произведению, но не групп, а колец вычетов. В то же время, его мультипликативная группа изоморфна прямому произведению мультипликативных групп сомножителей, то есть $$Z_^cong Z_2^times Z_3^times Z_7^times Z_^.$$ Известно, что для простого $%p$% группа $%mathbb Z_p^$% является циклической, то есть обладает элементом порядка $%varphi(p)=p-1$%. Такие элементы для каждой из компонент Вы указали верно.
Для нахождения элемента порядка 12 в группе $%mathbb Z_^$% можно поступить чуть проще (правда, его не следует называть «максимальным по умножению» — максимален ведь не сам элемент, а его порядок в группе). Берём сначала элемент 2: он имеет требуемый порядок по модулю 13, но его брать нельзя, так как он не взаимно прост с 546. Однако, прибавляя к нему несколько раз 13, мы получаем элемент с тем же свойством. Он имеет порядок 12 по модулю 13, а потому и по «старшему» модулю 546 он не уменьшится. Увеличиться он также не может, так как значение 12 максимально. Итого имеем 2, 15, 28, 41, и на последнем элементе можно остановиться, так как он не делится ни на одно из чисел 2, 3, 7, 13.
Тем не менее, если продолжать Ваше рассуждение, то надо решить систему линейных сравнений $%xequiv1pmod2$%; $%xequiv2pmod3$%; $%xequiv3pmod7$%; $%xequiv2pmod$%.
Способы решения таких систем описаны в учебниках по теории чисел. См., например у Бухштаба. Здесь можно сразу заменить второе и последнее сравнение на условие $%xequiv2pmod$%, записать решение в виде $%x=39y+2$%, и подставить в третье сравнение. Также надо будет учесть нечётность. В итоге должно получиться значение $%x=353$%. Такой остаток существует и единственен по известной теореме (китайская теорема об остатках).
отвечен 25 Фев ’19 3:12
@falcao, подскажите пожалуйста, а как поступать в такой ситуации(звездочки чего-то не показываются, имеются в виду только обратимые элементы):
С первыми двумя множителями прямого произведения все ясно, но вот с третьим как «руками» подобрать элемент порядка $%varphi(7^2)=42$% не очень понятно.
@Квантиль: для построения элемента порядка 42 достаточно построить элементы взаимно простых порядков 2, 3, 7 и перемножить. Для начала берём первообразный корень по модулю 7 — число a=3. Его порядок по модулю 7 равен 6. По модулю 49 порядок делится на 6. Прямая проверка показывает, что здесь он равен 42, то есть нам случайно повезло, и это уже ответ. В общем случае, если вышло 6k, то берём a^k, и это элемент порядка 6. Примером элемента порядка p=7 по модулю p^2 будет 1+p, что проверяется через биномиальную формулу. В конце берём a^k(1+p) mod p^2.
@falcao, добрый вечер. Подскажите, пожалуйста, в примере от Квантиль каким образом поступать далее? Получается, наибольший порядок элемента = 42. Для первой группы из суммы образующий элемент g = 1 (mod 2), для второй – g = 2 (mod 3) , для третьей – g = 3 (mod 49). Итого получаем систему из трёх линейных сравнений. Решением является число x = 101 (mod 294). Но при проверке и возведении икса в степень 42 по модулю 294 не получается единицы… не понимаю, где допускаю ошибку в рассуждениях.
@Kai: ответ 101 правильный. Я только что это проверил. Думаю, Вы просто ошиблись при возведении в степень.
@falcao, благодарю! Если рассматривать вопрос о перечислении всех элементов степени 42, нужно поступить следующим образом: взять 3, имеющую степень 42 по модулю 49, и прибавлять к ней 49. Получается ряд: 52, 101, 150, 199, 248. Из этих чисел только два (101, 199) являются искомыми, так как взаимно просты с модулем. Поправьте, пожалуйста, если допустила ошибку.
@Kai: задача нахождения всех элементов кольца, порядок которых в мультипликативной группе равен 42, достаточно сложна. Таких элементов много (по-моему, штук 36), и их не так просто выписать. И сам метод надо обосновывать — почему выписаны будут все такие элементы? Оба числа 101 и 199 годятся, но это явно не весь «улов».
@falcao, можете рассказать, как Вы получили 36?
Проверил на компьютере. Наверное, можно к этому числу прийти и как-то вручную при помощи стандартной техники. Но выписывать все эти значения — задача явно громоздкая.
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Научный форум dxdy
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву , правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Максимальный порядок элемента группы подстановок
Задача следующая:
Доказать, что порядок любого элемента группы 








Вот тут я застрял — судя по условию задачи, наибольшая возможная длина цикла равна 
Заранее благодарен за любые идеи!
Возьмём, например, 



Будьте добры, вот этот момент поясните пожалуйста: 
Не получается: ![$left[left(frac<n><x>right)^xright]'=-frac<n><x^2>left(frac<n><x>right)^x ln frac<n><x>$» /><br />Приравниваем к нулю и потенциируем: <img decoding=](https://dxdy-01.korotkov.co.uk/f/c/0/d/c0dd9c997e3ef8f8391d47c69fdc11de82.png)


|
25 / 25 / 11 Регистрация: 13.12.2011 Сообщений: 818 |
|||||
|
1 |
|||||
Найти порядок элемента группы12.11.2013, 06:57. Показов 41565. Ответов 6
в теории групп ничего не понимаю, а нужно делать. что означают S5,S6, C*, GL4(R), GL2(C), GLn(C). и как находить порядок элемента группы?
0 |
|
4526 / 3520 / 358 Регистрация: 12.03.2013 Сообщений: 6,038 |
|
|
12.11.2013, 19:38 |
2 |
|
Sn — группа перестановок на множестве из n элементов (симметрическая группа)
0 |
|
Модератор 35427 / 19452 / 4071 Регистрация: 12.02.2012 Сообщений: 32,488 Записей в блоге: 13 |
|
|
15.11.2013, 20:20 |
3 |
|
Придется «попотеть»… Берем, например, матрицу з). Возводим в квадрат: Умножаем результат на исходную матрицу еще раз (т.е. получаем куб исходной матрицы): Поскольку получилась единичная матрица, то степень элемента = 3…
0 |
|
28 / 28 / 0 Регистрация: 12.11.2013 Сообщений: 55 |
|
|
16.11.2013, 21:06 |
4 |
|
0 |
|
4265 / 2239 / 203 Регистрация: 26.08.2011 Сообщений: 3,802 Записей в блоге: 5 |
|
|
16.11.2013, 21:11 |
5 |
|
MathYa, все намного проще. Раскладываем перестановку в независимые циклы
2 |
|
28 / 28 / 0 Регистрация: 12.11.2013 Сообщений: 55 |
|
|
16.11.2013, 21:22 |
6 |
|
Thinker Спасибо!
0 |
|
4265 / 2239 / 203 Регистрация: 26.08.2011 Сообщений: 3,802 Записей в блоге: 5 |
|
|
16.11.2013, 21:26 |
7 |
|
MathYa, не за что) д) множество матриц такого вида изоморфно группе S4. В частности, данная матрица соответствует перестановке
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
16.11.2013, 21:26 |
|
Помогаю со студенческими работами здесь
порядок группы равен 4 и в ней только 1 элемент имеет порядок 4. какой порядок имеют остальные элементы? сколько в ней подгрупп? Найти порядок группы, таблицу (Кэли) умножений элементов
Доказать, что порядок и индекс подгруппы конечной группы являются делителями порядка самой группы Найти порядок элемента в группе Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 7 |
Содержание
- 1 Постановка задачи
- 2 Решение
- 2.1 Алгоритм
- 2.2 Алгоритмическая сложность
Постановка задачи
Пусть — группа, . Требуется найти порядок элемента .
Решение
По следствию из теоремы Лагранжа порядок элемента является делителем порядка группы.
Таким образом достаточно рассмотреть , где , — делители порядка группы.
Алгоритм
- Найти все делители перебором от 1 до
- Для каждого делителя проверить значение . Наименьший , такой что , является порядком элемента в группе.
Алгоритмическая сложность
Перебор от до выполняется за . Возведение в степень выполняется за . Следовательно время выполнения .




 Найдите порядок элемента мультипликативной группы
Найдите порядок элемента мультипликативной группы