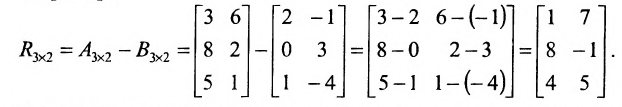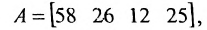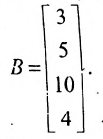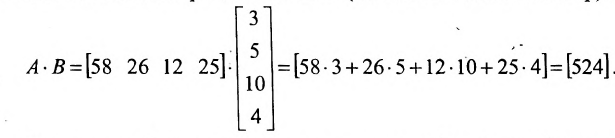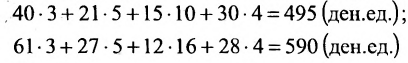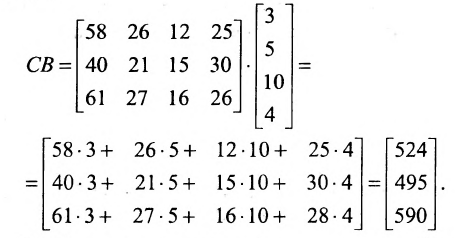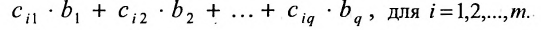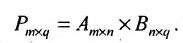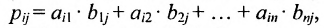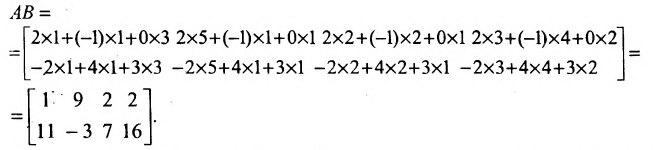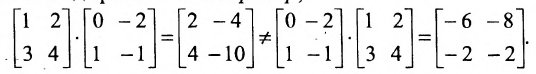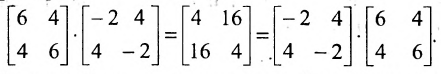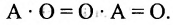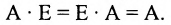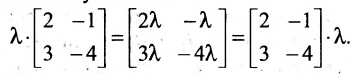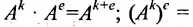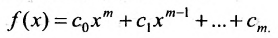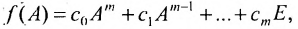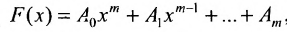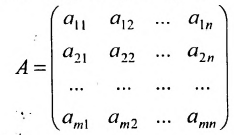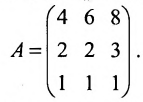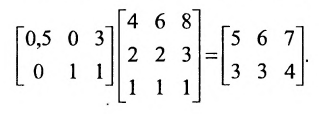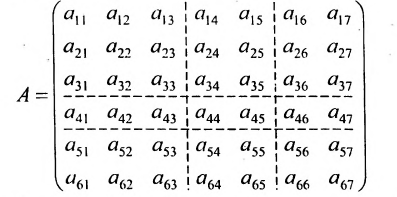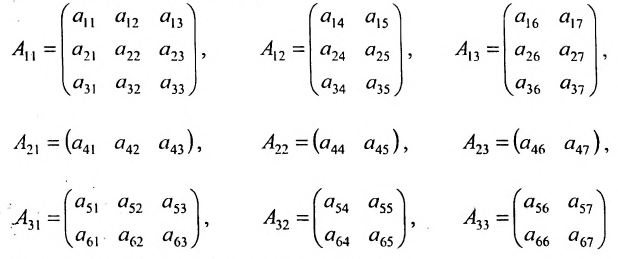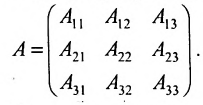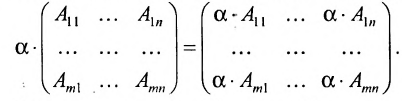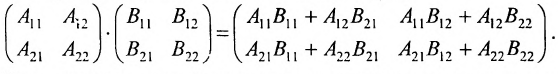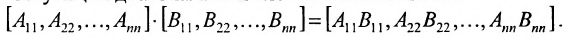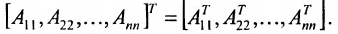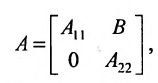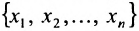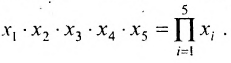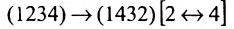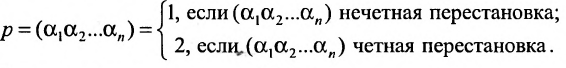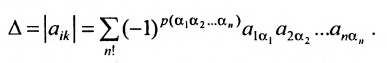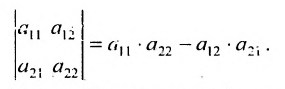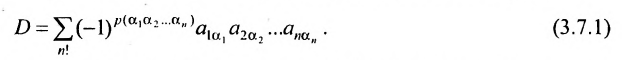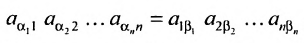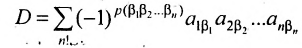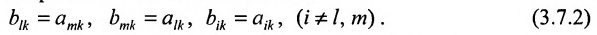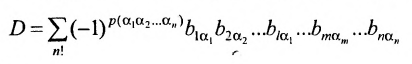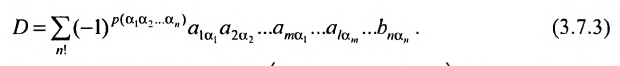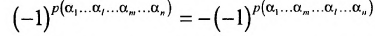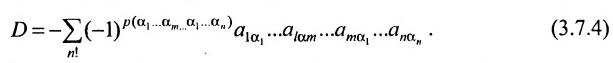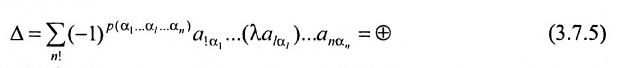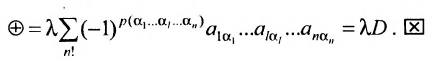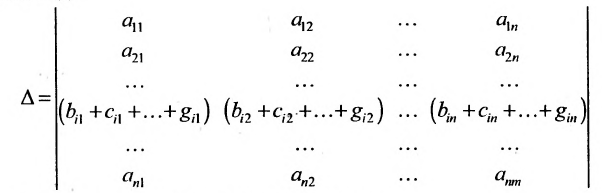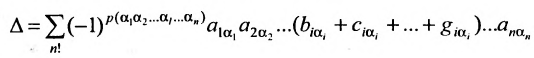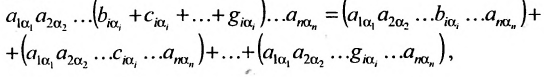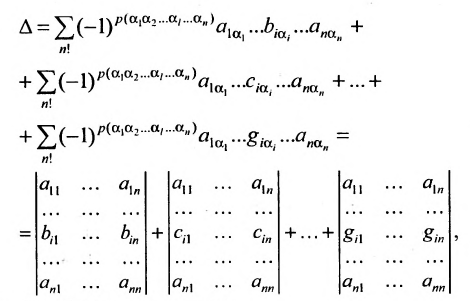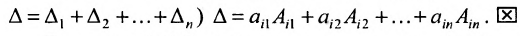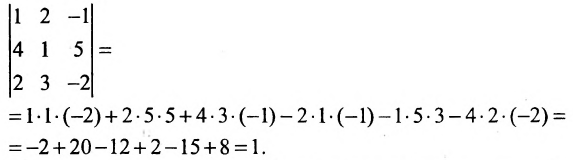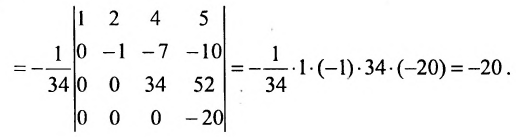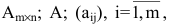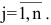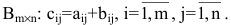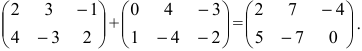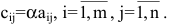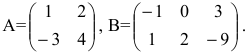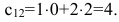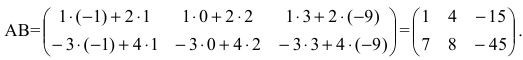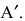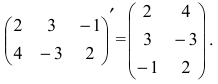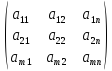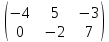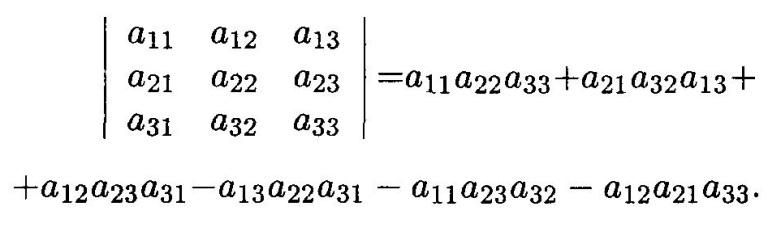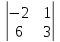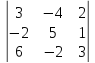Before we learn about the Order of a Matrix let us know What is a Matrix. Matrices are defined as a rectangular array of numbers or functions. It is a rectangular array and two- dimensional. A Matrix is a rectangular array of numbers or symbols which are generally arranged in rows and columns. The plural of matrix is matrices. The entries are the numbers in the matrix and each number is known as an element.
Order a Matrix – Definition
Basically, a two-dimensional matrix consists of the number of rows and the number of columns. The order of the matrix is defined as the number of rows and columns. The number of rows is represented by ‘m’ and the number of columns is represented by ‘n’. Therefore the order of the matrix is equal to m x n, and it is also called as ‘m by n’.
The size of the matrix is written as m x n, where m is the number of rows and n is the number of columns. For example, we have a 3 x 2 matrix, the number of rows is equal to 3, and the number of columns is equal to 2.
Different Types of Matrices
There are different types of matrices, basically categorized on the basis of the value of their elements, their order, number of rows and number of columns, etc. Now, using different conditions, the various matrix types are categorized along with their definition.
- Row Matrix
- Column Matrix
- Null Matrix
- Square Matrix
- Diagonal Matrix
- Upper Triangular Matrix
- Lower Triangular Matrix
- Symmetric Matrix
- Anti- Symmetric Matrix
- Equal Matrix
- Singular Matrix
- Non Singular Matrix
- Horizontal Matrix
- Vertical Matrix
- Unity or identity Matrix.
Row Matrix: A Matrix having only one row is called a Row Matrix. A= [aij]mxn is a row matrix , if m=1 then row matrix is represented as A= [aij]1xn . It has only one row and the order of a matrix will be 1 x n. For example, A= [1 2 4 5] is row matrix of order 1 x 4.
Column Matrix: A Matrix having only one column is called a Column Matrix. A= [aij]mxn is a column matrix, if n=1 then column matrix is represented as A= [aij]mx1 . It has only one column and the order of a matrix will be m x 1. Just like row matrices had only one row, column matrices have only one column. Thus the value of the column matrix will be 1.
Null Matrix: Null Matrix is also called Zero Matrix. In a matrix all the elements are zero then it is called a Zero Matrix or Null Matrix and it is generally denoted by 0. Thus, A = [aij]mxn is a Zero or Null Matrix.
Unity or Identity Matrix: If a square matrix has all elements 0 and each diagonal element is non-zero, it is called an identity matrix. It is denoted by I.
Equal Matrix: If two matrices are said to be equal if they are same order if their corresponding elements are equal to the square matrix.
Square Matrix: If the number of rows and the number of columns in a matrix are equal, then it is called Square Matrix.
How to find Order of a Matrix?
A Two- Dimensional matrix consists of the number of rows (m) and a number of columns (n). The order of the matrix is equal to m x n (also pronounced as ‘m by n’).
Order of Matrix = Number of Rows x Number of Columns.
In the above, you can see, the matrix has 2 rows and 4 columns. Therefore, the order of the matrix is 2 x 4.
How will you Determine the Order of Matrix?
If a matrix has m number of rows and n number of columns, now let’s know how to find the order of the matrix.
Here few examples, how to find the order of a matrix,
[1 2 3] is an example, in this, the order of the matrix is (1 x 3), which means the number of rows (m) is 1 and the number of columns (n) is 3.
[7 5] is an example of (1 x 2) matrix, in this number of rows are (m) is 1 and number of columns (n) is 2.
( A =left[
begin{matrix}
6 & 2 & 3cr
12 & 15 & 35 cr
end{matrix}
right]
)
The order of the above matrix is (2 x 3), in this number of rows is (m) is 2, and the number of columns (n) is 3.
A matrix of the order m x n has mn elements. Hence we say that if the number of elements in a matrix is prime, then it must have one row or one column. Usually, we denote a matrix by using capital letters such as A, B, C, D, M, N, X, Y, Z, etc.
The product of m and n can be obtained in more than one ways, some of the ways are,
- mn x 1
- 1 x mn
- m x n
- n x m
Number of Elements in Matrix
Suppose, A is the order of 2 x 3. Therefore, the number of elements present in a matrix will also be 2 times 3, i.e 6.
Similarly, the other matrix order is 4 x 3, thus the number of elements will be 12 i.e. 4 times 3. If we know the order of a matrix, we can easily determine the total number of elements that the matrix has,
If a matrix is of m x n order, it will have mn element.
Order of a Matrix Examples
Example 1.
If matrix A has an 8 number of elements, then determine the order of the matrix.
Solution:
We know that number of elements is 8
Let’s write all the possible factors of the number 8
8 = 1 x 8
8 = 4 x 2
8 = 2 x 4
8 = 8 x 1
we can get the number 8 is four ways.
Therefore, there are four possible ways or orders of the matrix with 8 number of elements are 1 x 8, 2 x 4, 4 x 2, and 8 x 1.
Example 2.
If a matrix X has 7 number of elements, find the order of the matrix.
Solution:
We know that number of elements is 7
Let’s write all the possible factors of the number 7
7 = 1 x 7
7= 7 x 1
we can get the number 7 in two ways.
Therefore, there are two possible ways or orders of the matrix with 7 number of elements are 1 x 7, 7 x 1.
Example 3.
What is the order of a matrix given below?
( A =left[
begin{matrix}
1 & 2 & 9cr
18 & 12 & 15 cr
end{matrix}
right]
)
Solution:
The number of rows in a given matrix is A = 2
The number of columns in a given matrix is A = 3
Therefore, the order of matrix is 2 x 3.
Example 4.
What is the order of a matrix given below?
( A =left[
begin{matrix}
4 & 5 & 7cr
11 & 14 & 18 cr
21 & 24 & 8 cr
end{matrix}
right]
)
Solution:
The number of rows in a given matrix is A = 3
The number of columns in a given matrix is A = 3
Therefore, the order of the matrix is 3 x 3.
FAQ’s on Order of Matrix
1. What is Matrix and Types?
A Matrix can be defined as a rectangular array of numbers or functions. A matrix consists of rows (m) and columns (n) that is m x n. Types of Matrices are :
- Row Matrix
- Column Matrix
- Null Matrix
- Equal Matrix
- Unity or Identity Matrix
- Square Matrix
- Rectangular Matrix
- Horizontal Matrix
- Vertical Matrix
- Scalar Matrix
2. What is the Null Matrix?
Null Matrix is also called Zero Matrix. In a matrix all the elements are zero then it is called a Zero Matrix or Null Matrix and it is generally denoted by 0. Thus, A = [aij]mxn is a Zero or Null Matrix.
3. What is another name of Unity Matrix?
Another name of the unity matrix is Identity Matrix. If a square matrix has all elements 0 and each diagonal element is non-zero, it is called an Identity Matrix. It is denoted by I.
4. What is the order of Square Matrix?
A Matrix that has a number of rows is equal to a number of columns is called Square Matrix. In this matrix, all the elements are arranged in m number of rows and n number of columns . So the order of the matrix is denoted by mxn.
5. Explain a Scalar Matrix?
Scalar Matrix is similar to a square matrix. In the scalar matrix, all off-diagonal elements are equal to zero and all on diagonal elements happen to be equal. In other words, the Scalar Matrix is an identity matrices multiple.
|
7 / 5 / 4 Регистрация: 02.06.2012 Сообщений: 248 |
|
|
1 |
|
Как найти ранг и порядок матрицы?15.12.2012, 20:13. Показов 46754. Ответов 5
Порядок матрицы 3×3 = 3, а порядок матрицы 4×3 = 4? Как найти ранг матрицы? Лучший способ? Примечание: никакого способа не знаю. Добавлено через 14 минут
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
15.12.2012, 20:13 |
|
Ответы с готовыми решениями: Найти ранг матрицы В В =( 1 3 5 1 Найти ранг матрицы. Найти ранг матрицы
5 |
|
1891 / 1472 / 173 Регистрация: 16.06.2012 Сообщений: 3,342 |
|
|
15.12.2012, 21:19 |
2 |
|
Как найти ранг матрицы? Метод элементарных преобразований.
порядок матрицы? О порядке говорят лишь применительно к квадратным матрицам. Это число строк (столбцов).
1 |
|
7 / 5 / 4 Регистрация: 02.06.2012 Сообщений: 248 |
|
|
15.12.2012, 22:41 [ТС] |
3 |
|
количество ступеней будет рангом. Количество элементов по главной диагонали, исключая нули, будут показывать ранг. Добавлено через 57 минут Код a11 = 7 a12 = 7 a21 = 7 a22 = 7 Добавлено через 15 минут
0 |
|
2525 / 1751 / 152 Регистрация: 11.08.2012 Сообщений: 3,349 |
|
|
16.12.2012, 09:33 |
4 |
|
«Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице». Да. Но вы неверно поняли утверждение.
Количество элементов по главной диагонали, исключая нули, будут показывать ранг. Только для треугольных матриц
0 |
|
7 / 5 / 4 Регистрация: 02.06.2012 Сообщений: 248 |
|
|
16.12.2012, 11:57 [ТС] |
5 |
|
Строки вашей матрицы линейно зависимы Но разве линейно зависимые строки это не тогда когда все элементы столбца равны нулю?
0 |
|
2525 / 1751 / 152 Регистрация: 11.08.2012 Сообщений: 3,349 |
|
|
16.12.2012, 13:41 |
6 |
|
Но разве линейно зависимые строки это не тогда когда все элементы столбца равны нулю? То, что вы написали, лишь частный случай. Столбцы (строки) матрицы, можно рассматривать как самостоятельные матрицы-векторы. Обозначу через
0 |
Содержание:
Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов:
В дальнейшем будем писать матрицу в сокращенном виде
Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой
Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом
Пример:
Следующие таблицы являются матрицами
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы
Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы — на соответствующие строки.
Замечание: Согласно свойству 1. для определителей (см. Лекцию № 1) для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы.
Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной
Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной
Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю:
Действия над матрицами
1. Суммой (разностью) двух матриц 
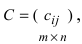
Пример:
Найти сумму (разность) матриц
Решение:
Из приведенных матриц складывать (вычитать) можно только матрицы А и С, которые имеют одинаковую структуру. Найдем сумму:
и разность этих матриц:
2. При умножении вещественного числа k на матрицу 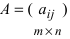
Пример:
Умножить (-2) на матрицу
Решение:
Результат умножения имеет вид
3. Произведением матриц 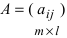
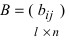
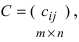
Замечание: Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы.
Пример:
Найти (возможные) произведения матриц
Решение:
Матрица А имеет структуру 2×3, матрица В — 2×2, матрица С — 3×2. Согласно определению можно найти произведения 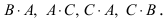
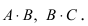
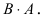
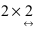
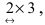
Остальные возможные произведения найти самостоятельно.
Замечание: Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е.
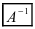
Определение: Обратной матрицей к исходной квадратной матрице 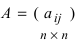
Рассмотрим схему построения обратной матрицы
Замечание: Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде.
Пример:
Найти обратную матрицу к матрице
Решение:
Вычислим детерминант данной матрицы 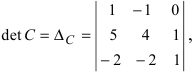
Вычислим алгебраические дополнения всех элементов определителя: 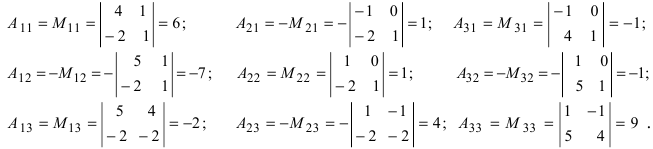
Проверим правильность нахождения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
Таким образом, 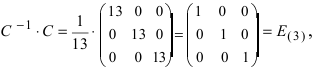
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Матрицей размера 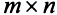
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 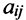
Например, матрица
или, в сокращенной записи,
Например, 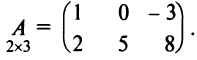
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. 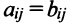
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.)
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
В этой записи, например, матричный элемент 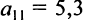
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца — матрицей (вектором)-столбцом: 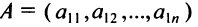
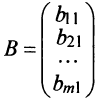
Матрица называется квадратной 
Например, 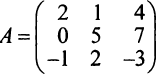
Элементы матрицы 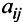
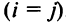
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
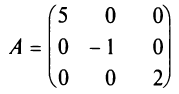
Если у диагональной матрицы 

Например,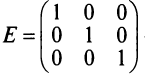
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю:
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.
Умножение матрицы на число
Произведением матрицы А на число 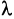
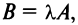
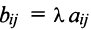
Например, если 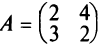
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например,
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е.
Сложение матриц
Суммой двух матриц А и В одинакового размера 
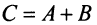
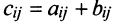
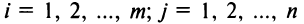
Например,
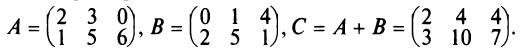
Вычитание матриц
Разность двух матриц одинакового размера определяется через предыдущие операции:
Умножение матриц
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй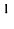
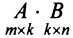
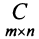
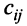

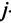
Пример №1
Вычислить произведение матриц 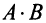
Решение:
1. Найдем размер матрицы-произведения (если умножение матриц возможно):
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом:
Получаем 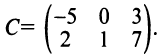
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а)Если произведение матриц 
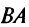
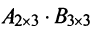
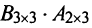
б)Если даже произведения 

Пример №2
Найти произведения матриц 

Решение:
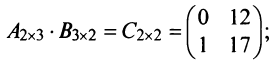
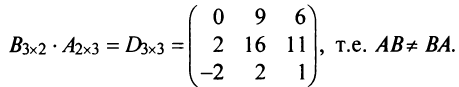


Пример №3
Найти произведения матриц 

Решение:
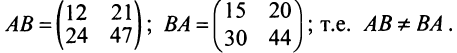
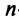
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 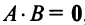
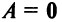
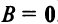
Возведение в степень
Целой положительной степенью 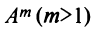
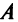
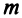

Заметим, что операция возведения в степень определяется только для квадратных матриц.
По определению полагают 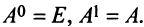
Пример №4
Найти 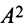
Решение:
Обращаем внимание на то, что из равенства 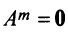
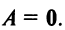
Транспонирование матрицы
Транспонирование матрицы — переход от матрицы 



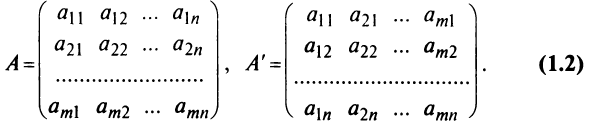

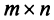

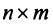
Например,
В литературе встречаются и другие обозначения транспонированной матрицы, например, 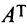
Свойства операции транспонирования:
Рекомендуем читателю доказать их самостоятельно. Рассмотренные выше операции над матрицами позволяют упростить решения некоторых экономических задач.
Пример №5
Предприятие выпускает продукцию трех видов: 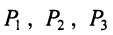
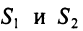
где каждый элемент 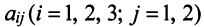
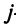
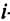
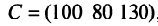
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение:
Затраты 1-го сырья составляют 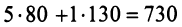
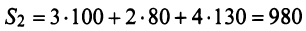
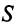
Тогда общая стоимость сырья 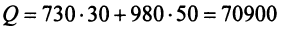
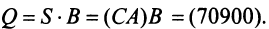
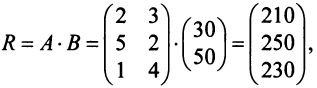
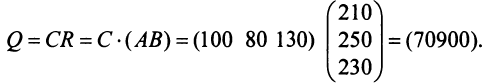
На данном примере мы убедились в выполнении свойства 7 (см. с. 13) — ассоциативного закона произведения матриц:
Определители квадратных матриц
Необходимость введения определителя — числа, характеризующего квадратную матрицу 
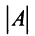
Определителем матрицы первого порядка 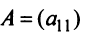
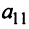
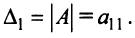
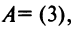
Определителем матрицы второго порядка 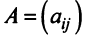
Произведения а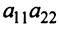
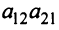
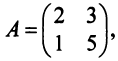
Пусть дана квадратная матрица третьего порядка: 
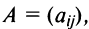
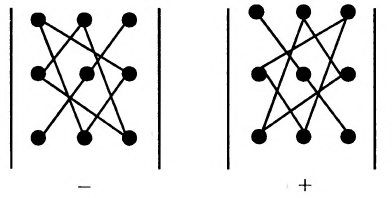
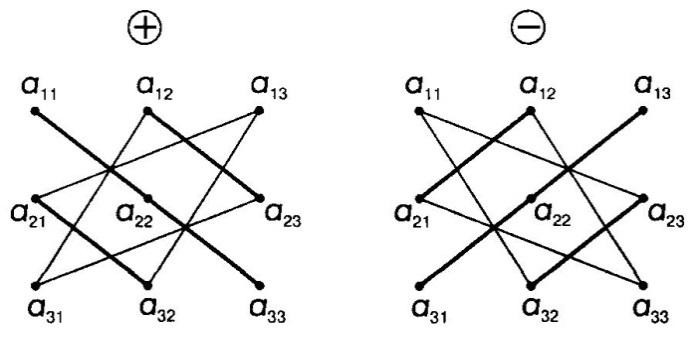
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников или правилом Сарруса.
Пример №6
Вычислить определитель третьего порядка
Решение:
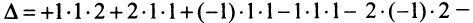
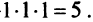
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия. Рассмотрим квадратную матрицу 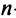
Из общего числа 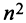
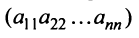
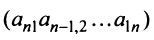
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.
Номера столбцов 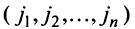
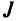
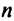

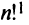
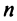
Введем понятие беспорядка, или инверсии, в перестановке 
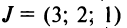
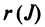
Возвращаясь к наборам (1.5) из элементов матрицы 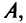
и число 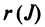
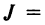
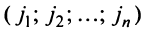
Определение. Определителем квадратной матрицы 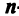
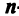
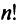
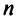
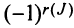
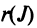
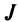
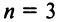
то же число, что и по формуле (1.4).
Заметим, что с ростом 
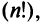
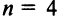
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
Пусть дана квадратная матрица 

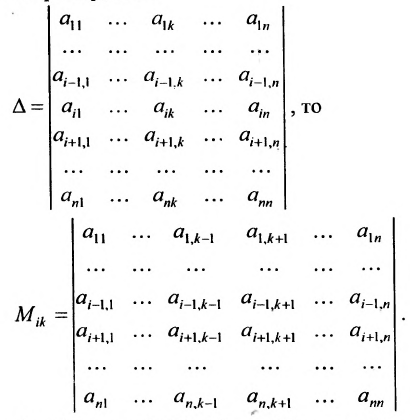
Минором 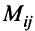
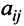

определитель матрицы 

Например, минором элемента 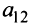

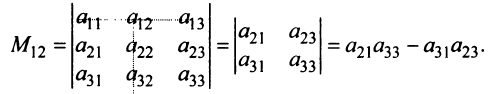

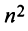
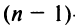
Алгебраическим дополнением 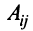
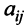

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца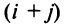
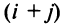
Например,
Пример №7
Найти алгебраические дополнения всех элементов матрицы (из примера 1.6):
Решение:
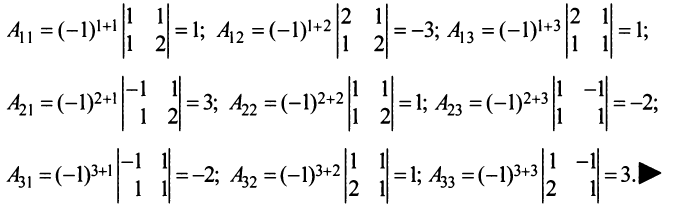
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам 
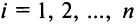
(разложение по элементам 
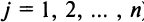

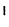
После преобразований (представляем их сделать читателю) нетрудно убедиться в том, что полученное выражение совпадает с определением (1.4). Аналогичный результат получаем разложением определителя матрицы по любой строке или столбцу.
Пример №8
Вычислить определитель треугольной матрицы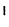
Решение:
Раскладывая по первому столбцу, получаем:
На частном примере мы убедились в том, что определитель треугольной (и, очевидно, диагональной) матрицы равен произведению элементов главной диагонали.
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей 
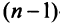
Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 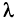

Пусть определитель исходной матрицы равен 

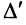
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов. Например, 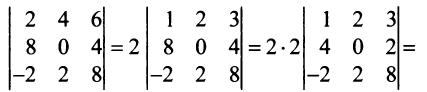
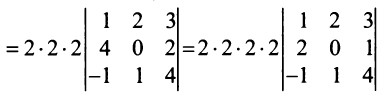
3. При транспонировании матрицы ее определитель не изменяется:
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
□ Предположим вначале, что переставлены две соседние строки матрицы: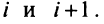


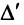
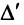
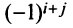
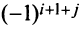
Если переставить не соседние строки, а, скажем, 
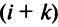

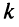
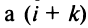
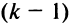
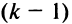
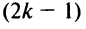
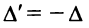
Доказательство для столбцов аналогично.
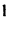
5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.
□Действительно, переставим эти строки (столбцы). С одной стороны, определитель не изменится, но, с другой стороны, по свойству 4 поменяет знак, т.е.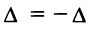
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
□ Пусть для определенности пропорциональны первая и вторая строки. Тогда, вынося коэффициент пропорциональности 
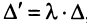

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
Рассмотрим квадратную матрицу 
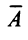



т.е. матрица 

Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:
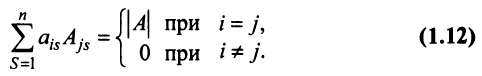
Пусть для определенности к элементам 


где 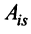

Используя формулу (1.12), получаем, что первая сумма равна определителю исходной матрицы, а вторая — 0, т.е.
9. Сумма произведений произвольных чисел 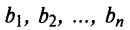
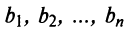
Свойство вытекает непосредственно из теоремы Лапласа.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 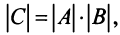
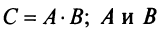
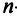
Замечание. Из свойства 10 следует, что даже если 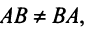
Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1—9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
Пример №9
Вычислить определитель четвертого порядка:
Решение:
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим, например, элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем 
Раскладывая по элементам множители, получаем:
Обратная матрица
Для каждого числа
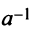
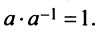
Определение. Матрица 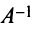

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную. Если 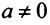
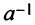

Если определитель матрицы отличен от нуля 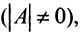
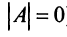
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 
Необходимость. Пусть матрица 

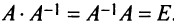
Достаточность. Пусть 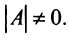
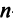
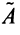


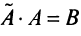
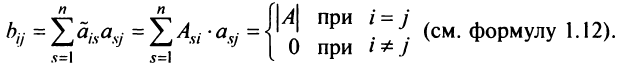
Аналогично доказывается, что произведение 
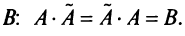
то произведения 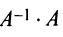
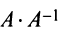
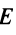
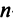
Докажем единственность обратной матрицы. Предположим, что существуют еще матрицы 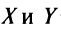
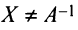
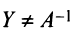

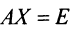
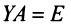

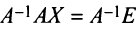
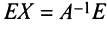
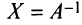

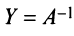
Алгоритм вычисления обратной матрицы:
Пример №10
Найти матрицу, обратную к данной:
Решение:
1°. Определитель матрицы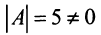


2°. Находим матрицу 

3°. Находим алгебраические дополнения элементов матрицы 
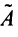
4° . Вычисляем обратную матрицу
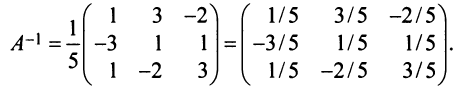
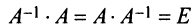
Для невырожденных матриц выполняются следующие свойства:
Ранг матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице 
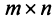
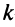
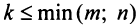
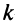

Например, из матрицы 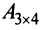
Определение. Рангом матрицы 
Ранг матрицы 
Из определения следует: а) ранг матрицы 
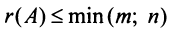
б) 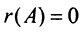
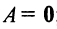
в) для квадратной матрицы 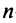
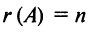

Пример №11
Вычислить ранг матрицы
Решение:
Матрица 
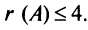
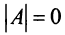

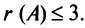
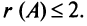
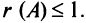

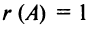
Пример №12
Вычислить ранг матрицы
Решение:
Для матрицы 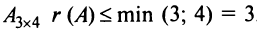
Проверим, равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычеркивании одного из столбцов матрицы):
Поскольку все миноры третьего порядка нулевые,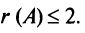
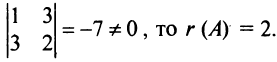
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.
Назовем элементарными преобразованиями матрицы следующие:
- Отбрасывание нулевой строки (столбца).
- Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
- Изменение порядка строк (столбцов) матрицы.
- Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
- Транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица 
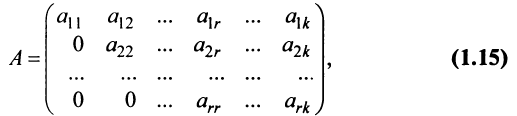
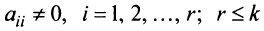
Замечание. Условие 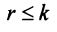
Очевидно, что ранг ступенчатой матрицы равен 
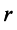
Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример №13
Найти ранг матрицы
Решение:
1°. Если 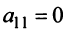
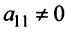
2°. Если 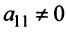
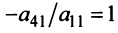
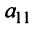
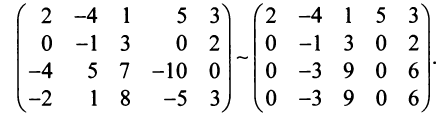
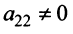
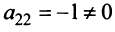
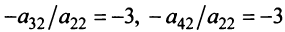
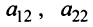
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например,
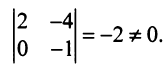
Для рангов матриц справедливы следующие соотношения:
5)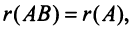

6) 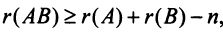
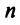


Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.


Две строки матрицы называются равными, если равны их соответствующие элементы: 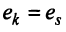
Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка е называется линейной комбинацией строк 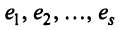
где 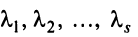
Строки матрицы 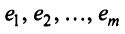
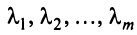
где 0 = (0 0…0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.

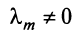
где
Таким образом, строка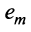
Если линейная комбинация строк (1.17) равна нулю тогда и только тогда, когда все коэффициенты 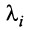
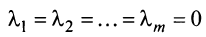
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы).


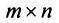
Это означает, что существует отличный от нуля минор 

Тогда строки матрицы 
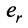
Вычтем из элементов 
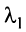
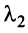
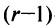
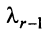

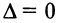

Строки 
Покажем, что любые 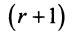
Рассмотрим минор 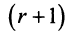
при дополнении рассматриваемого минора элементами еще одной строки 
Этот минор равен нулю, так как ранг матрицы равен 
Раскладывая его по элементам последнего (добавленного) столбца, получаем 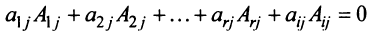
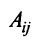

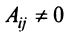
Разделив последнее равенство на 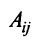
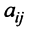
где
Фиксируем значение 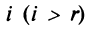
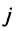
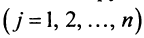
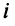
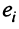

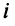
Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
Матрицы в линейной алгебре
Прямоугольная таблица:
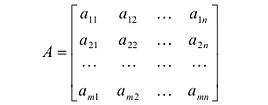
состоящая из m строк и n столбцов, называется матрицей размера m х n или (n,m)-матрицей.
Матрицу (9.1) будем обозначать А или 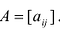
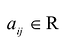
Если m = n, то матрица (9.1) называется квадратной матрицей порядка n.
В квадратной матрице n-го порядка диагональ, состоящая из элементов 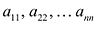
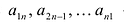
Квадратная матрица:
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 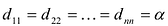
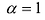
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы А и В называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 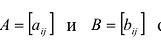
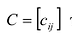
Сложение матриц обладает следующими свойствами:
- Коммутативность, т.е. А + В = В + А.
- Ассоциативность, т.е. (А + B)+ С = А + (В + С).
- Для любых двух матриц А и В одинакового размера существует единственная матрица X такая, что А + X = В. Матрица X обозначается X = В-А и называется разностью матриц В и А. Урав-=нение А + Х = 0 имеет решение Х = 0-А, получающаяся при этом матрица называется противоположной А и обозначается — А.
Произведением матрицы 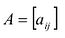
Умножение матрицы на действительное число обладает следующими свойствами:
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. В этом случае произведением матрицы 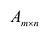
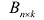
т.е. элемент, стоящий в n -той строке и j-том столбце матрицы произведения равен сумме произведений элементов n’-той строки матрицы А на соответствующие элементы j -го столбца матрицы В.
Свойства умножения:
- Если матрица А согласована с матрицей В, а матрица В согласована с матрицей С, то А • В• С = (А
В)- С = А
(В
С) — ассоциативность умножения;
- (А + ВС = АС + ВС, А-(В + С)= АВ + АС — свойство дистрибутивности;
- Умножение матриц не коммутативно, т.е., как правило,
Транспонированием матрицы А называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. i-я строка матрицы А становится i -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице А обозначается 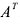
Свойства транспонирования:
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 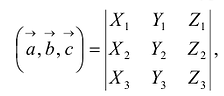
Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу n -го порядка
Для записи определителя n-го порядка матрицы А будем применять обозначения 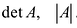
Минором 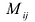

Пример №14
Найти минор 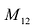
По определению, минор 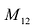
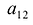
Алгебраическим дополнением элемента 
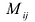
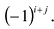

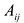
Пример №15
Найти алгебраическое дополнение элемента 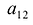
Определителем квадратной матрицы А n-го порядка 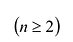
где аи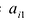
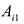
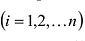
Запись по формуле (9.3) называется разложением определителя но первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы А n-го порядка 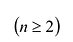
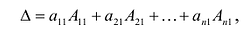
где 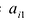
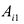
Свойство 2. Если поменять местами две строки или два столбца матрицы А, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы n-го порядка (будем в дальнейшем говорить определитель n-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
Свойство 3. Определитель, y которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе 
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя 
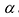
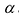
Умножим элементы i-той строки на 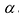
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пронорциональныу равен нулю.
Пусть i-я строка пропорциональна j-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя 

Разложив определитель 
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам i-той строки определителя 
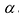
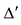


Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель 


Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 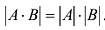
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы А обозначают rankA или rА.
Если все миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы А) равны нулю, то rankA = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то rankA = 1. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка к, окаймляющие ненулевой минор (A-l)-ro порядка равны нулю, либо таких миноров нет. Тогда rankA = к -1.
Пример №16
Вычислить ранг матрицы
Минор первого порядка (элемент 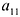
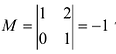
Далее рассмотрим миноры, окаймляющие минор М :
Все эти миноры равны нулю, значит rankA = 2. Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
- > умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
- > прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:
с разрешающим элементом 
- > k первой строке прибавить k-ю, умноженную на число
и т.д.;
> k последней строке прибавить k — го, умноженную на число 
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 
После выполнения этих преобразований получается матрица:
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя. Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример №17
Вычислить ранг матрицы
Применим к матрице А элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.
Вычитая далее вторую строку из третьей и последней, имеем:
Последняя матрица содержит отличный от нуля минор 
Отметим два важных свойства ранга матрицы:
- Ранг матрицы не меняется при ее транспонировании;
- Если ранг матрицы равен г, то любые ее г + 1 строк (столбцов) линейно зависимы.
Обратная матрица
Пусть А — квадратная матрица порядка n. Матрица В называется обратной матрицей к матрице А, если выполняются равенства А-В = В■ А = Е, где Е — единичная матрица порядка n.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 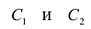
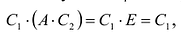
Откуда 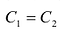

Теорема 2. Матрица А имеет обратную матрицу тогда и только тогда, когда 
Пусть А имеет обратную матрицу. Тогда 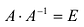
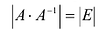
Следовательно, 
Пусть 

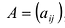
здесь 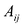
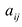
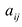
Непосредственное умножение А на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) — матрица, обратная к А.
Пример №18
Найти обратную матрицу к матрице
Так как 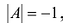

Матрицу 
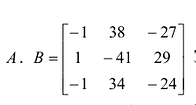
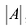
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если А и В — невырожденные матрицы одинакового порядка, то:
Матрицы и определители
Определение и типы матриц
Определение 3.1.1. Прямоугольная таблица 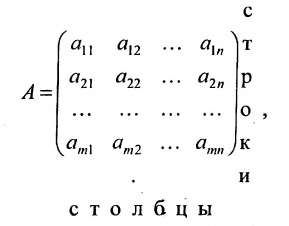
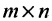
Числа 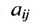
Матрицы удобно обозначать в виде 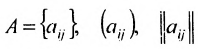
Превратим в матрице (3.1.1) строки в столбцы, а столбцы в строки, получим матрицу 
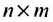
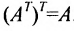
Пример №19
Рассмотрим матрицу
элементы которой характеризуют зависимость средних розничных цен на автомобили от срока их службы в 1998, 1999 и 2000 гг. Строки матрицы соответствуют продолжительности эксплуатации автомобиля, а столбцы — годам. Содержательное значение каждого элемента матрицы определяется его местом в данном массиве чисел. Например, число 3100 во второй строке и втором столбце, элемент с/22> представляет среднюю розничную цену автомобиля прослужившего два года в 1999 г. Следовательно, числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и гот же срок службы в разные годы 1998-2000 гг., а числа в столбце — цены автомобилей различного срока службы в данном году.
В той мере, в какой это связано с характеристикой цен па автомобили, такой выбор строк матрицы полностью произволен, и мы могли бы сразу же поменять местами строки и столбцы без какой-либо потери информации, получив строки для отдельных лет и столбцы для сроков службы, т.е. получили бы транспонированную матрицу по отношению к матрице Р:
Хотя элементы матрицы 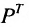
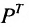
Если, элементы 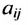
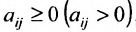
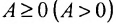
Матрица Р в примере 3.1.1 является положительной матрицей, так как её элементы положительные действительные числа.
Матрица, состоящая из одной строки 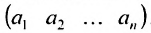
называется матрицей-столбцом. Транспонированием переводят матрицу-строку в матрицу-столбец, и наоборот.
Если m=n, то матрица называется квадратной, при этом число строк (столбцов) называется порядком квадратной матрицы.
Рассмотрим некоторые виды квадратных матриц.
Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной. Она обозначается символом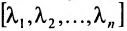
Если в диагональной матрице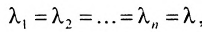
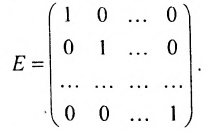
Например,
Матрица A — верхнеугольная, а В — нижнетреугольная. Квадратная матрица называется ленточной, если все её элементы, не стоящие на главной диагонали и в соседних с ней косых строках, равны нулю. Например,
В ленточной матрице не равные нулю элементы заполняют «ленту», осью которой служит главная диагональ. Ленточная матрица называется модулированной, если в каждой косой строке стоят одинаковые элементы:
Квадратная матрица называется симметрической, если её элементы, расположенные симметрично относительно главной диагонали, одинаковы: 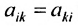
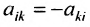
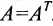
Например, матрица, характеризующая влияние факторов на инвестиции и запасы, является симметрической матрицей вида:
Элемент 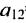
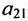
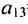
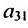
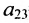
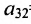
Очевидно, что транспонированная симметричная матрица равна самой матрице.
Квадратная матрица, у которой на главной диагонали стоит одно и го же число 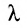
Матрица, у которой на главной диагонали стоят любые клетки Жордана, а все элементы вне этих клеток равны нулю, называется Жордаповой матрицей. Например, матрица является Жордановой.
Она содержит четыре клетки Жордана: две клетки второго порядка с числом 3 на диагонали, одну клетку третьего порядка с числом нуль на диагонали и одну клетку первого порядка с числом нуль на диагонали.
Из приведенных примеров следует, что понятие матрицы широко используется в экономике. Кроме того, можно подчеркнуть, что планирование производства должно основываться на надлежащим образом упорядоченной системе информации, записанной в виде матрицы, с помощью которой просто и сжато описываются зависимости, имеющие место в материальном производстве. Так, например, планирование на предприятии основывают, пользуясь нормами как системой информации. Если на предприятии производится четыре продукта 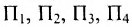
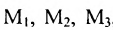
где 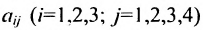
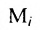
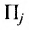
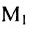
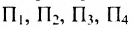
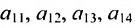
Можно привести следующий пример использования матриц: два предприятия передают свою продукцию на три оптовых склада, причём расходы на перевозку единицы продукции с предприятия 1 на отдельные склады соответственно равняются 2,3,4; а с предприятия 2 они составляют 1,5,2. Тогда матрица
есть матрица удельных транспортных расходов.
Следует отметить использование матриц в межотраслевом балансе производства (матрица технологических коэффициентов производства), в определении совокупных затрат труда (матрица коэффициентов материальных затрат) и т.д.
Пример №20
Продавец мороженого решает вопрос о том, сколько пакетов мороженого ему следует закупить. К покупке пакетов мороженого он может прибегнуть один раз. Каждый пакет стоит 10 ден.ед. и может быть продан за 12 ден.ед. Пакеты мороженого, оставшиеся не распроданными, никакой стоимости не представляют. Известно, что количество пакетов мороженого, которое он сможет продать, колеблется от 1 до 5. Составим матрицу денежных сумм, выручаемых в зависимости от его решения и от результатов продажи. По строкам расположим результаты того или иного решения продавца мороженого, а по столбцам — возможный исход продаж.
Решение:
Предположим, что продавец мороженого закупает один пакет. Тогда он его продаст и получает прибыль в 2 ден.ед.
Следовательно, первая строка матрицы будет иметь вид: 2 2 2 2 2. Сели он закупит 2 пакета, то продав один, он потеряет 8 ден.ед.; продав 2 пакета, он получит прибыль 4 ден.ед. Следовательно, вторая строка примет вид: -8 4 4 4 4. Рассуждая аналогичным образом, получаем матрицу:
Арифметические операции над матрицами
Матрицы А и В считаются равными, если они одинаковой размерности и всс элементы 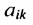
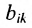
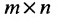
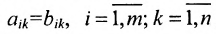
Определение 3.2.1. Суммой матриц А а В размерности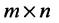
Из определения следует, что складывают матрицы с одинаковыми размерами, при этом сумма будет матрицей с теми же размерами.
Например,
Определение 3.2.2. Произведением матрицы А на скаляр 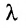
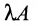
Матрица (-1)A записывается -А и называется матрицей, противоположной матрице А. Если все элементы матрицы равны нулю, го она называется нуль-матрицей и обозначается 0.
Введенные операции сложения матриц и умножения матрицы на скаляр 
- А + В = В + А — (перемсстительный) коммутативный закон.
- (А + В) + С = А + (B + C);
.
.
.
.
Определение 3.2.3. Разностью матриц одинаковой размерности называется матрица той же размерности: 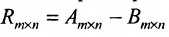
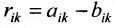
Например,
Как и при операции сложения, можно вычитать друг из друга только те матрицы, которые имеют одинаковую размерность.
Прежде чем вводить произведение матриц, рассмотрим произведение векторов. И для пояснения общего метода воспользуемся числовыми примерами.
Предположим, что объем различных продаж за месяц некоторого товара некоторой компании «а» составил 58, 26, 12, 25 единиц за первую, вторую, третью и четвертую недели соответственно, и что цена этого товара по неделям соответственно равна 3, 5, 10, 4 ден.ед. Следовательно, общий доход за месяц от продажи товара равен 58-3 + 26-5+ 12-10 + 25-4 = 524ден.ед. Представим данные
о продажах при помощи матрицы-строки:
а соответствующие цены с помощью матрицы-столбца:
Тогда общий доход от продажи товара, равный 524 ден.ед., представляет собой сумму произведений элементов матрицы-строки A (количество проданного товара по неделям) на соответствующие элементы матрицы-столбца В (цены по неделям на товар):
Приведенный пример помогает уяснить общую методику вычисления произведения матрицы-строки на матрицу-столбец: для этого каждый элемент матрицы-строки А нужно умножить на соответствующий элемент матрицы-столбца В и сложить полученные произведения.
Предположим теперь, что компания «а» имеет отделения в трёх различных регионах. Данные о количестве проданного товара по регионам запишем в виде матрицы С:
Цена по неделям за месяц была такой же. Доход от розничной продажи в первом регионе был вычислен; аналогичные расчёты могут быть произведены и по двум другим регионам:
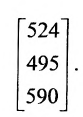
Представим итоговые данные по выручке в виде матрицы-столбца:
Взглянув на вычисления, можно убедиться в том, что элементы этой матрицы-столбца получаются так же, как и описанное ранее произведение матрицы-строки А на матрицу-столбец В, причем в качестве матрицы-строки А в каждом случае взята последующая строка матрицы С. Полученный результат представляет произведение СВ:
В общем случае произведение матрицы С на матрицу-столбец В, это вектор-столбец,i-Й элемент которого представляет сумму произведений каждого из элементов i-й строки матрицы С на соответствующие элементы вектора-столбца В.
Из этого примера следует, что произведение 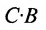
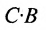
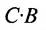
Аналогичным образом определяется произведение матрицы-строки 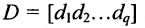
если число элементов матрицы-строки D равно числу элементов в столбцах матрицы Р (т.е. равно числу строк этой матрицы). В этом случае произведении 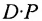
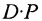
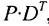
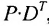
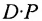
Пример №21
Пусть матрица
характеризует переход подписчика от одной газеты к другой в зависимости от продолжительности подписки. В этой матрице перехода данные сгруппированы по строкам и столбцам в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулирование подписки. Элементы первой строки характеризуют состояние подписчиков газет с продолжительностью подписки до одного года; второй строки — с продолжительностью подписки от одного года до двух лет; третья строка — с продолжительностью подписки более двух лет; элементы четвертой строки характеризуют аннулирование подписки. Элементы первого столбца характеризуют возможность остаться в категории подписчиков до одного года; элементы второго столбца — возможность продолжить подписку от одного до двух лет, если подписчик имеет продолжительность подписки до одного года; элементы третьего столбца- возможность продолжить подписку более двух лет: элементы четвертого столбца — возможность аннулировать подписку.
Предположим, что известно распределение 5000 подписчиков по продолжительности подписки на газеты: 3000 имеют продолжительность подписки до одного года (категория 1), 800 — имеют продолжительность подписки от одного до двух лет (категория 2), 1200 подписчиков имеют, продолжительность подписки более двух лет (категория 3). Представим эти данные в виде матрицы-строки Q =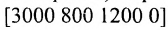
Для того чтобы определить возможное количество подписчиков в каждой из этих категорий через год, умножим матрицу-строку Q на матрицу Р:
Матрица-строка, полученная в результате умножения, показывает, что из I категории через год возможно 2100 подписчиков будут принадлежать к категории II, 1720- к категории III, и 1180 возможно аннулируют подписку.
Учитывая введенные операции, умножение двух матриц А и В можно представить как многократное умножение матрицы А на матрицы-столбцы, рассматривая вторую матрицу В как набор мат-риц-столбцов. При этом произведение матриц А и В может иметь смысл только в том случае, когда j-й столбец матрицы В (а, следовательно, и все ее столбцы) насчитывают тоже число элементов, что и i-я строка матрицы А (а, следовательно, и все ее строки). Поскольку количество элементов в столбце матрицы равно числу строк в ней (а количество элементов в строке равно количеству столбцов) это означает, что в матрице В должно быть столько же строк, сколько столбцов содержит матрица А.
Таким образом, произведение матрицы 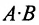
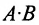
Если число столбцов в А равно числу строк в В, то матрицы называются согласованными для умножения А на В. При этом если А размерности т * п, а В размерность 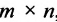
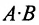
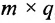
Определение 3.2.4. Произведением матрицы А размерности 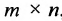
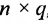
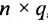
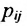
, при 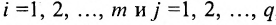
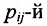
- Заказать решение задач по высшей математике
Пример №22
Пусть 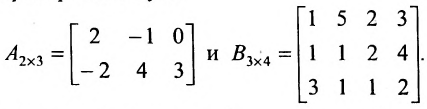
Произведение матриц, вообще говоря, не коммутативно, т.е. А В не всегда равно 
Из приведенного примера следует, что, перемножая матрицы А и В, можно получить два произведения 
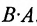
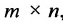
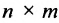
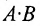
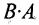
Из сказанного не следует, что АВ и ВА всегда должны различаться между собой, в отдельных случаях они могут быть равны. Например,
В двух случаях, имеющих особо важное значение, произведение матриц обладает свойством коммутативности:
1) в случае умножения на нулевую матрицу: если 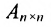
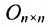
Нулевая матрица выполняет роль нуля в матричной алгебре;
2) в случае умножения на единичную матрицу: если 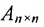
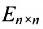
Единичная матрица того же порядка служит единицей в матричной алгебре. Например,
Отметим, что произведение матрицы на скалярную величину так же коммутативно:
Матрицу А можно умножить саму на себя тогда и только тогда, когда она квадратная. Если n — натуральное число, больше единицы, то 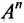
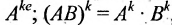
Значением многочлена
с числовыми коэффициентами 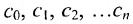
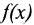
где Е- единичная матрица.
Многочленной матрицей называется прямоугольная (в частности квадратная) матрица А, элементы которой являются многочленами от одной переменной х с числовыми коэффициентами. Матричным многочленом называется выражение вида
где х- переменное и 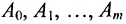
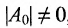
Два матричных многочлена одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами, с той разницей, что умножение числовых матриц, а потому и матричных многочленов не обязательно коммутативно.
Операцию умножения для матриц можно ввести иначе. Пусть задана матрица размерности 
Обозначим столбцы матрицы А следующим образом:
их называют векторами-столбцами; а строки:
которые называют векторами-строками.
Пример №23
Пусть число трёх типов игрушек, которые нужно изготовить, равно соответственно 20, 30, 40. Определим число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа на них.
Решение:
Составим матрицу А, в которой по строкам укажем число деталей одного вида, необходимых для производства трёх типов игрушек, а по столбцам — число деталей трех видов, необходимых для производства одной игрушки трёх типов:
Число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа определим умножением матрицы А на матрицу-столбец, характеризующую число игрушек:
Зная количество деталей, необходимых для производства одной игрушки, можно определить потребность в сырье для производства одной игрушки, если известны нормы расхода сырья для производства одной детали, которые приведены в таблице 3.2.2.
Эти потребности в сырье определяются умножением матриц
Умножив результат произведения матриц на количество игрушек, определим потребности в сырье для выполнения заказа
Приведенный пример иллюстрирует простоту решения задачи при помощи умножения матриц.
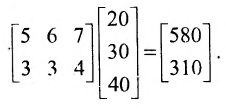
Пример №24
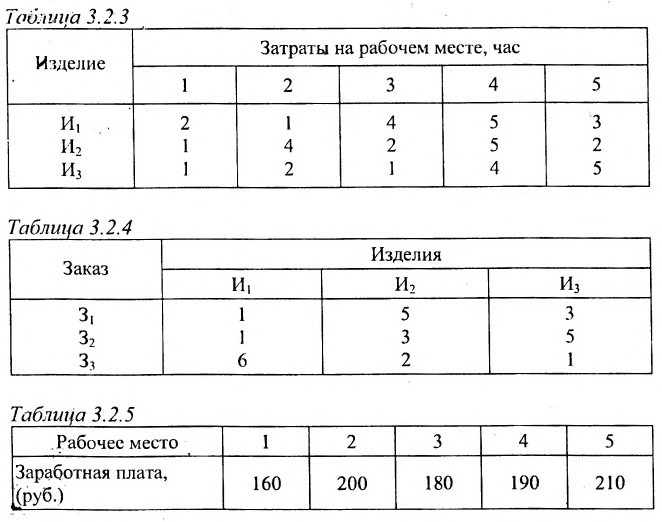
Предположим, что затраты рабочего времени в часах на каждом рабочем месте и на каждое изделие заданы в таблице 3.2.3. Количество изделий (в штуках) в каждом заказе задано в таблице 3.2.4. Часовая заработная плата (в рублях) на каждом рабочем месте задана в таблице 3.2.5
Решение:
Рассчитаем заработную плату, приходящуюся при производстве различных изделий на каждый заказ.
Решение. Введем в рассмотрение следующие матрицы:
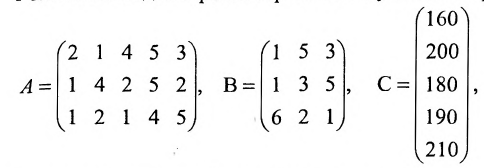
Так как матрица С задает зависимость между величиной заработной платы и затратами рабочего времени на каждом рабочем месте, а матрица А — между затратами времени на каждом рабочем месте и выпуском изделий, то произведение АС задает линейную зависимость между выпуском одного изделия и величиной заработной платы. Поскольку матрица В определяет количество изделий в каждом заказе, то произведение В(АС) определяет выполнение каждого заказа. Поэтому, вычислив произведение В (АС):

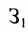
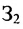
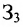
Блочные матрицы и действия над ними
Для упрощения действий над матрицами больших размеров выполняют переход к матрицам меньших размеров путём разбиения их на клетки горизонтальными и вертикальными прямыми, пересекающими всю матрицу.
Например, проведём в матрице А две горизонтальные и две вертикальные прямые:
Получим 9 клеток, каждая из которых будет некоторой матрицей. Введём для них обозначения:
Тогда матрицу А можно записать в виде:
Полученную матрицу называют блочной, или клеточной. Любую матрицу множеством способов можно представить в блочной форме. Особый интерес представляют блочные матрицы, имеющие квадратные диагональные клетки. Например,
В матрице В клетки 
Если у блочных матриц число диагональных клеток одинаково, причём соответственные диагональные клетки имеют один и тот же порядок, то такие матрицы называются конформными.
Блочная матрица, у которой все клетки, кроме стоящих на главной диагонали, являются нуль-матрицами, называется квазидиагональной. Примером квазидиагональной матрицы является матрица
вида: 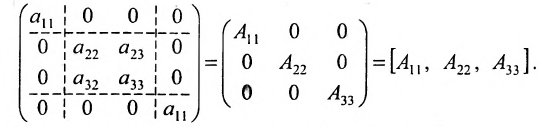
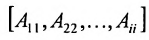
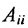
Если к квадратной матрице а добавить снизу матрицу-строку, справа — матрицу-столбец и в правом нижнем углу добавить элемент, то полученная блочная матрица называется окаймлённой.
Арифметические операции над блочными матрицами выражаются через операции над клетками матриц. Такое выражение возможно для конформных матриц.
1) Сложение блочных матриц производится аналогично правилу сложения обычных матриц: 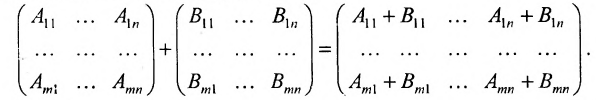
2) При умножении блочной матрицы на скаляр все клетки блочной матрицы умножаются на этот скаляр:
3) Произведение конформных блочных матриц формально совпадает с правилом умножения обычных матриц:
При умножении матриц соответственные диагональные клетки умножаемых матриц должны иметь одинаковый порядок. В противном случае блочные матрицы не будут конформными и их умножать нельзя.
Произведением конформных квазидиагональных матриц является квазидиагональная матрица с той же структурой, причём каждая диагональная клетка произведения является произведением соответствующих диагональных клеток сомножителей:
При транспонировании квазидиагональной матрицы получаем квазидиагональную матрицу, диагональные клетки которой являются транспонированными матрицами:
Матрица А, которую одновременной перестановкой строк и столбцов можно привести к блочному виду
где 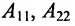
Матрица неразложима если для неё не существует таких одновременных перестановок строк и столбцов, которые приводили бы сё к разложимой форме.
Оператор суммирования и его свойства
В экономических исследованиях часто употребляются переменные, определенные на дискретных множествах
или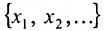
суммирования служит заглавная греческая буква 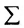
например, сумму 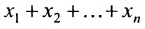
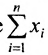
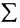
Для оператора суммирования справедливы следующие тождества:
Существует также способ записи операции умножения с помощью прописной греческой буквы «пи» — П : Так, например, произ-ведение пяти множителей можно сокращенно записать:
Перестановки
Рассмотрим n целых чисел (элементов) 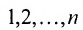
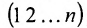
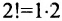
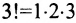
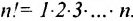
Назовем беспорядком (или инверсией) в перестановке тот факт, что большее число стоит перед меньшим. Если перестановка имеет четное число инверсий, то она называется четной, в противном случае — нечетной. Обмен местами двух элементов в перестановке называется транспозицией. Например:
Транспозиция переводит одну перестановку в другую и меняет четность перестановки.
Определение определителя
Рассмотрим квадратную матрицу размерности п и составим из ее элементов таблицу вида
или более компактно: 
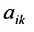
Этой таблице соотнесем число, называемое определителем, вычисляемое по правилу, сформулированному в следующем определении.
Определение 3.6.1. Определителем n-го порядка называется алгебраическая сумма n! членов, каждый из которых представляет собой произведение n элементов 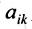
строки и каждого столбца; при этом член определителя берется со знаком «+», если вторые индексы его элементов образуют чётную перестановку, и со знаком «—», если эта перестановка нечетная, а первые индексы образуют натуральную перестановку.
Определитель n-то порядка обозначается в виде таблицы (3.6.1), где горизонтали — строки, а вертикали — столбцы.
Введем величину:
Тогда в силу определения 3.6.1 определитель n-то порядка запишется в виде:
Суммирование распространяется на все перестановки 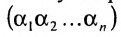
В частности, определителем второго порядка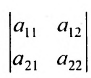
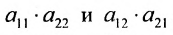
Таким образом, каждой квадратной матрице А можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое 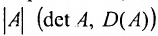
Свойства определителя n-го порядка
Свойствами, сформулированными ниже, обладают определители любого порядка, в частности второго и третьего порядков.
Доказательство. Рассмотрим определитель 
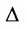
В каждом слагаемом формулы (4.1) переставим сомножители таким образом, чтобы их первые индексы составили натуральную перестановку; вторые индексы образуют произвольную перестановку:
Перестановки 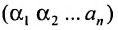
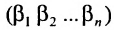
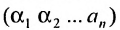
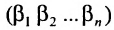
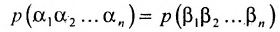
Так как 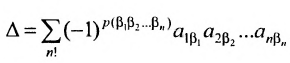
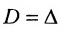
Из свойства 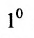
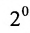
Доказательство. Рассмотрим определитель 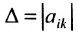
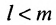
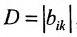

В силу равенств (3.7.2) преобразуем определитель
к виду
Выполним в перестановке 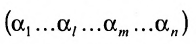
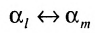
Затем поменяем местами сомножители 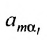
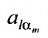
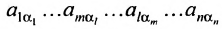
В равенстве (3.7.4) первые индексы элементов образуют натуральную перестановку 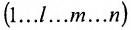
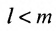
вторых индексов такая же, как и в выражении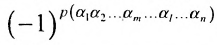
Доказательство. Так как по условию две строки одинаковы, то их перестановка не меняет величины 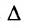
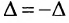
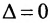
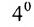
Доказательство. Пусть в определителе 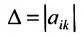
Из (3.7.5) следует, что каждое слагаемое содержит множителем число 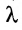
Из свойства 
Следствие 3.7.1. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Действительно, по свойству 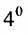
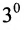
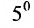
Доказательство. Пусть все элементы 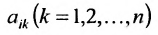

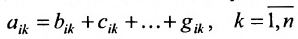
В силу определения его можно записать:
но так как
то
что и требовалось доказать.
Следствие 3.7.2. Величина определителя не изменится, если /с элементам любой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умножив их предварительно на один и тот же множитель.
Действительно, если мы рассмотрим определитель
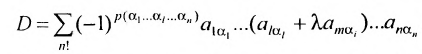
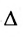
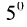
так как второе слагаемое равно 0 как определитель с двумя пропорциональными строками.
Миноры и алгебраические дополнения
Определение 3.8.1. Если в определителе n-го порядка вычеркнем i-ую строку и k-ый столбец, на пересечении которых находится элемент 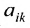

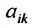
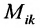
Определение 3.8.1. Минор 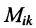
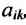
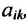

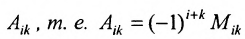
С помощью алгебраических дополнений определитель порядка п может быть выражен через определители порядка n-1. Этот факт справедлив для определителей имеющих специальную структуру, т. е. имеют место
Лемма 3.8.1. Если в определителе порядка n все элементы последней строки (столбца), кроме элемента, стоящего в правом нижнем углу, равны нулю, то определитель равен произведению этого элемента на соответствующий ему минор.
Лемма 3.8.2. Если в определителе порядка n все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
Из сформулированных лемм вытекают следующие теоремы:
Теорема 3.8.1. (теорема разложения). Определитель порядка п равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения: 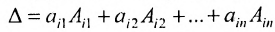
Доказательство. Так как строки и столбцы равносильны, то достаточно проверить справедливость равенства:
Представим каждый элемент i-й строки определителя
тогда его можно представить в виде суммы определителей (по свойству 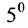
Определитель 
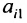

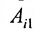
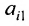
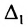
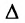
Следовательно,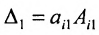
Аналогично 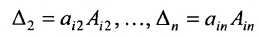
Теорема 3.8.2. (теорема аннулирования). Сумма парных произведений элементов любой строки (столбца) определителя на алгебраические дополнения параллельной строки (столбца) равна нулю:
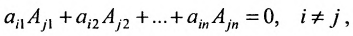
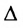
Вычисление определителей
Укажем некоторые способы вычисления определителей.
1) По теореме 3.8.1 определитель любого порядка п выражается через n определителей (n-1)-го порядка. Применяя эту теорему несколько раз, можно преобразовать исходный определитель к некоторому числу определителей третьего порядка, вычисление которых не представляет труда. Однако для упрощения вычислений целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведется к определителю более низкого порядка, и т. д.
2) Пользуясь свойствами определителя, приводят его к треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали, равны нулю. Полученный определитель треугольного вида равен произведению элементов главной диагонали, т. е.
Если удобнее получить нули по одну сторону от побочной диагонали, то 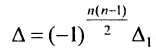
3) Если определитель 
Определитель квазидиагональной матрицы равен произведению определителей её диагональных клеток:
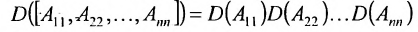
Определитель второго порядка, согласно определению 3.6.1 равен произведению диагональных элементов минус произведение элементов побочной диагонали. Например,
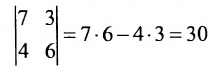
Определитель третьего порядка по определению 3.6.1. равен алгебраической сумме шести слагаемых. Построение этой суммы можно выполнить по правилу Саррюса. Со знаком «+» и рассматривая произведение элементов определителя, обозначенных на схеме точками
Hстример,
Определители выше третьего порядков вычисляются либо сведением к треугольному виду, либо используя теорему разложения или используя рекуррентную формулу. Например,
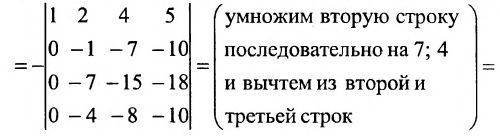
(последовательно умножим первую строку на 2; 4; 3 и вычтем получающиеся при этом строки из второй, третьей и четвертой строк)
(умножим третью строку на 20/34 и вычтем из четвертой строки; сомножитель четвертой строки 1/34 вынесем за знак определителя; в результате получим определитель верхнетреуголыюго вида, который равен произведению элементов, стоящих на главной диагонали) .
Матрицы и операции над матрицами
Матрицей размера 
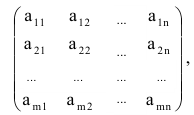
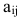
Например, элемент 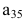
Суммой двух матриц одинакового размера 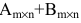
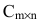
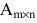
Например,
Произведением матрицы 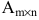
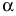
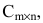
Например,
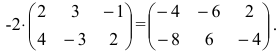
Внимание! Умножаются только согласованные матрицы.
Произведением матрицы А размера 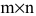
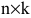
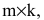
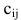
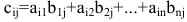
Пример:
Даны матрицы
Найти то из произведений АВ, В А, которое существует.
Решение:
Найдем произведение матриц АВ. Оно существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно двум.
Например, элемент произведения матриц с индексом 12 равен по определению сумме произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В:
Тогда
Рассмотрим произведение матриц ВА. Число столбцов матрицы В (n=3) не совпадает с числом строк матрицы А (m=2). Произведение матриц ВА не существует.
Вывод. В общем случае произведение матриц не коммутативно, т.е. не всегда АВ=ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: 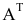
Например,
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
Содержание
Матрица
Определение, обозначения
Матрица1) – прямоугольная таблица
$$ A=
left(begin{array}{llll}
3 & -7 & dots & sqrt{pi} \
&&& \
C_n^1 & 101.(66) & dots & frac{5}{7} \
dots & & & dots \
aleph_0 & 0 & dots & e
end{array}right) ,
$$
в каждой ячейке которой располагается некоторое число (или, в общем случае, элемент из некоторого множества – лишь бы только были определены те операции, что нам потребуются ниже), называемое элементом матрицы.
Будем обозначать матрицы прописными латинскими буквами $ , A_{},B,dots, {mathfrak A},{mathfrak B},dots $, а – при необходимости – их элементы буквами строчными $ a_{},b,dots,{mathfrak a},{mathfrak b},dots $ Сами таблицы условимся ограничивать скобками – либо круглыми $ ( quad )_{} $, либо квадратными $ [ quad ]_{} $.
В матрице $ A_{} $ естественным образом выделяются строки и столбцы, при этом отсчет строк и столбцов уславливаются вести, начиная от левого верхнего угла матрицы. Упорядоченная пара чисел
(количество строк, количество столбцов)
матрицы называется порядком (или размерностью) матрицы. Так, если матрица имеет $ m_{} $ строк и $ n_{} $ столбцов, то о ней говорят как о матрице порядка $ mathbf m_{} $ на $ mathbf n_{} $, и записывают порядок в виде $ mtimes n_{} $.
Любая $ mtimes n_{} $-матрица содержит всего $ ,mn_{} $ элементов, и каждому из этих элементов можно поставить в соответствие «координаты его местоположения» в матрице, т.е. упорядоченную пару натуральных чисел $ (j,k)_{} $, в которой первое число отвечает за номер строки элемента, а второе — за номер его столбца.
Часто будет возникать необходимость записи матрицы общего вида, т.е. матрицы с элементами, числовые значения которых могут быть переменными. В самом общем случае — когда все элементы матрицы $ A_{} $ могут быть произвольными — будем их записывать в виде $ a_{jk}^{} $ или же, когда необходимо избежать недоразумения, в виде $ a_{j,k}^{} $. Так, $ a_{11}^{} $ означает элемент матрицы $ A_{} $, стоящий в ее левом верхнем углу; $ b_{10,3}^{} $ – элемент матрицы $ B, $, стоящий в $ 10_{} $-й строке и $ 3_{} $-м столбце; $ {mathfrak c}_{m-3,2n-7}^{} $ – элемент матрицы $ {mathfrak C}_{} $, стоящий в $ (m-3)_{} $-й строке и $ (2n-7)_{} $-м столбце. Такая договоренность позволяет записывать компактно матрицы, для элементов которых имеется функциональная зависимость от местоположения в таблице. К примеру, совершенно произвольную $ mtimes n_{} $-матрицу
$$
A=
left( begin{array}{lllll}
a_{11} & a_{12} & a_{13}& dots & a_{1n} \
a_{21} & a_{22} & a_{23}& dots & a_{2n} \
dots & & & & dots \
a_{m1} & a_{m2} & a_{m3}& dots & a_{mn}
end{array}
right)
$$
мы можем записать в виде $ A_{}=left [a_{jk} right ]_{j=1,dots,m atop k=1,dots,n} $.
П
Пример.
$$
A=left [frac{1}{j+k-1}
right ]_{j=1,2,3,4 atop k=1,2,3}
=
left(begin{array}{rrr}
1 & frac{1}{2} & frac{1}{3} \
&& \
frac{1}{2} & frac{1}{3} & frac{1}{4} \
&& \
frac{1}{3} & frac{1}{4} & frac{1}{5} \
&& \
frac{1}{4} & frac{1}{5} & frac{1}{6}
end{array}right)
.
$$
?
Найти развернутое выражение для матриц, представленных в компактной форме
a) $ A_{} =left [ max (j,k) right ]_{j=1,2,3,4 atop k=1,2quad} $ ;
б) $ B_{} =left [ |j-k| right ]_{j=1,2,3 atop k=1,2,3 } $ ;
в) $ C_{}=left [delta_{jk} right ]_{j=1,dots,5 atop k=1,2,3 } $,
где $ delta_{jk}^{} $ означает символ Кронекера.
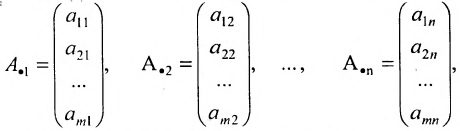
В принятых обозначениях $ j_{} $-й строкой произвольной матрицы $ A_{} $ будет матрица
$$ A^{[j]}=left(a_{j1},a_{j2},dots,a_{jn} right) , $$
а ее $ k_{} $-м столбцом – матрица
$$
A_{[k]}=left( begin{array}{c} a_{1k} \ a_{2k} \ vdots \ a_{mk} end{array} right) .
$$
Матрицы $ A_{} $ и $ B_{} $ называются равными если равны их порядки и совпадают элементы на соответствующих местах:
$$ A=left[a_{jk} right]_{j=1,dots,m atop k=1,dots,n} ,
B=left[b_{jk} right]_{j=1,dots,m atop k=1,dots,n} ,
$$
$$
quad Rightarrow quad A=B iff a_{jk} =b_{jk} forall jin {1,dots,m },
kin {1,dots,n } .
$$
Матрицы разных порядков не считаются равными.
Еще одно упрощение записи – часто применяемое для матриц заранее не специфицированного порядка – заключается в том, что если некоторый участок матрицы занят равными нулю элементами, то они либо не указываются вовсе, либо вся их совокупность обозначается $ {mathbb O}_{} $.
Матрица, состоящая только из нулей, называется нулевой матрицей соответствующего порядка.
Ее будем записывать в виде $ {mathbb O}_{mtimes n}^{} $.
П
Пример.
$$
left(begin{array}{rrrr}
0 & 0 & 0 & 0 \
0 & 0 & 0 & 0
end{array}right) = {mathbb O}_{2times 4} .
$$
Элементарные операции
умножение на число
Произведением матрицы $ A_{} $ на число (скаляр) $ c_{} $ называется матрица, каждый элемент которой равен произведению соответствующего элемента матрицы $ A_{} $ на число $ c_{} $:
$$
A=left[a_{jk} right ]_{j=1,dots,m atop k=1,dots,n} {color{RubineRed} Rightarrow }
ccdot A = left [ca_{jk} right]_{j=1,dots,m atop k=1,dots,n} .
$$
$$
3cdot
left(begin{array}{rrr}
1& 0 & 1 \
-1 & 1 & 0 \
0 & 1 & 2
end{array}
right) =
left(begin{array}{rrr}
3& 0 & 3 \
-3 & 3 & 0 \
0 & 3 & 6
end{array}
right) , quad
2cdot
left(
begin{array}{r}
1 \ 0 \ -1
end{array}
right) =
.
$$
сложение
Для матриц $ A_{} $ и $ B_{} $ одного порядка их суммой называется матрица, каждый элемент которой равен сумме соответствующих элементов складываемых матриц:
$$A =left[a_{jk} right]_{j=1,dots,m atop k=1,dots,n}, B=left[b_{jk} right]_{j=1,dots,m atop k=1,dots,n} quad{color{RubineRed} Rightarrow } quad A+B = left[a_{jk} + b_{jk} right]_{j=1,dots,m atop k=1,dots,n} , .$$
$$
left(
begin{array}{rrr}
1& -2 & -1 \
2 & -1 & -2 \
1 & 2 & sqrt{3} \
0 & 1 & 7
end{array}
right)
+
left(
begin{array}{rrr}
-1& 3 & 2 \
1 & 0 & 1 \
-1 & -2 & 3 \
-1 & 1 & -5
end{array}
right)=
$$
Т
Теорема. Множество матриц фиксированного порядка $ m times n_{} $ образует линейное пространство относительно двух этих введенных операций.
Будем обозначать это пространство $ mathbb R^{m times n} $ в случае, когда рассматриваются только числа (элементы матрицы и скаляры, на которые допускается их домножение) вещественные, и $ mathbb C^{m times n} $ если рассматриваются и мнимые.
транспонирование
Преобразование матрицы, при котором ее строки становятся столбцами новой матрицы, называется транспонированием матрицы:
$$
left( begin{array}{lllll}
a_{11} & a_{12} & a_{13}& dots & a_{1n} \
a_{21} & a_{22} & a_{23}& dots & a_{2n} \
dots & & & & dots \
a_{m1} & a_{m2} & a_{m3}& dots & a_{mn}
end{array}
right)^{top}=
left(begin{array}{llll}
a_{11} & a_{21} & dots & a_{m1} \
a_{12} & a_{22} & dots & a_{m2} \
a_{13} & a_{23} & dots & a_{m3} \
vdots & & & vdots \
a_{1n} & a_{2n} & dots & a_{mn}
end{array}
right)
$$
В компактном виде:
$$
left( left[a_{jk} right]_{j=1,dots,m atop k=1,dots,n} right)^{top}=left[a_{kj} right]_{k=1,dots,n atop j=1,dots,m}
,
$$
а в схематичном:
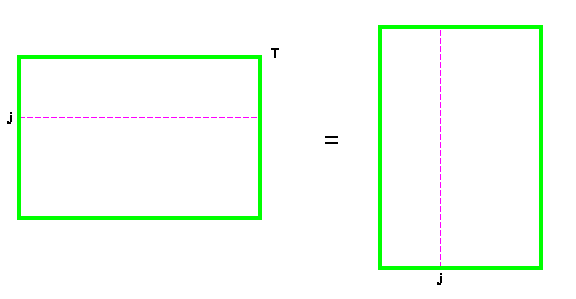
§
В литературе для операции транспонирования используются также обозначения $ A^{t}=mbox{ }^{t}A=A^{prime}=A^{ast} $.
?
Показать справедливость следующих свойств операции транспонирования:
а) $ left( A^{top} right)^{top} = A $;
б) $ (A+B)^{top}=A^{top} + B^{top} $;
в) $ (cA)^{top}=c A^{top} $, где $ c_{} $ — число;
г) $ (AB)^{top}= B^{top} A^{top} $
при условии, что все операции в левых частях равенств определены (операция умножения матриц определяется
☟
НИЖЕ ).
конкатенация
Для матриц $ A_{} $ и $ B_{} $ с одинаковым количеством строк можно определить операцию $ Amid B_{} $ (будем также использовать обозначение $ [A mid B] $) конкатенации2) матриц:
$$ A=
left(begin{array}{llll}
a_{11} & a_{12} & dots & a_{1n} \
a_{21} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{m1} & a_{m2} & dots & a_{mn}
end{array}right) ,
B=
left(begin{array}{llll}
b_{11} & b_{12} & dots & b_{1k} \
b_{21} & b_{22} & dots & b_{2k} \
dots & & & dots \
b_{m1} & b_{m2} & dots & b_{mk}
end{array}right) Rightarrow
$$
$$
Rightarrow Amid B=
left(begin{array}{llllllll}
a_{11} & a_{12} & dots & a_{1n} & b_{11} & b_{12} & dots & b_{1k} \
a_{21} & a_{22} & dots & a_{2n} & b_{21} & b_{22} & dots & b_{2k} \
dots & & & &&& & dots \
a_{m1} & a_{m2} & dots & a_{mn} & b_{m1} & b_{m2} & dots & b_{mk}
end{array}right).
$$
Проще говоря: к матрице $ A_{} $ «приписывается» справа матрица $ B_{} $. В этом смысле саму матрицу $ A_{} $ можно считать результатом конкатенации ее столбцов:
$$ A= A_{[1]}mid A_{[2]} mid dots mid A_{[m]}=left[ A_{[1]}mid A_{[2]} mid dots mid A_{[m]} right] . $$
Можно также производить конкатенацию матриц «по вертикали», т.е. по строкам3). Одновременную конкатенацию — когда к матрице $ A_{mtimes n}^{} $ приписывается столбец $ U_{mtimes 1 } $ справа и строка $ V_{1times (n+1)} $ снизу — называют окаймлением4) матрицы.
векторизация
матрицы5) произвольного порядка образно означает «вытягивание» ее в вектор-столбец. Если
представить матрицу как результат конкатенации ее столбцов:
$$ A=left[A_{[1]} mid A_{[2]} mid dots mid A_{[n]}right] , $$
то
$$ operatorname{Vec}(A)=left(begin{array}{c}
A_{[1]} \ A_{[2]}\ vdots \ A_{[n]}
end{array}
right) , .
$$
Так, например
$$
operatorname{Vec}left(begin{array}{ccc}
a_1 & b_1 & c_1 \
a_2 & b_2 & c_2
end{array}
right)=
left(begin{array}{c}
a_1 \
a_2 \
b_1 \
b_2 \
c_1 \
c_2
end{array}
right), .
$$
перезагрузка
Умножение матриц
Для матрицы-строки $ U=(u_{1},dots,u_n) $ и матрицы-столбца $ V=left(begin{array}{c} v_{1}\ vdots\ v_n end{array}right) $ определим произведение $ Ucdot V_{} $ как число
$$ Ucdot V= u_1v_1+dots+u_nv_n . $$
Для произвольных матриц $ A_{} $ и $ B_{} $ произведение матрицы $ A_{} $ на матрицу $ B_{} $ определяется тогда и только тогда, когда их порядки связаны ограничением:
количество столбцов матрицы $ A_{} $ = количество строк матрицы $ B_{} $
т.е. если матрица $ A_{} $ имеет порядок $ mtimes n_{} $, то матрица $ B_{} $ может иметь порядок $ ntimes k_{} $ при $ forall kin{mathbb N}_{} $. В этом случае произведение матрицы $ A_{} $ на матрицу $ B_{} $ обозначается6) $ Acdot B_{} $ и представляет собой матрицу $ C_{} $ порядка $ mtimes k_{} $:
$$
begin{array}{ccccc}
C&=&A&cdot&B ,\
{mtimes k}&&{mtimes n}&&{ntimes k}
end{array}
$$
элементы которой вычисляются по следующему правилу
$$
C=[c_{jell}]_{_{j=1,dots,matop
ell=1,dots,k
}},quad
c_{jell}= A^{[j]}B_{[ell]}=a_{j1}b_{1ell}+a_{j2}b_{2ell}+dots+a_{jn}b_{nell} .
$$
Таким образом, элемент, стоящий в $ j_{} $-й строке и $ ell_{} $-м столбце матрицы $ C_{} $, равен произведению $ j_{} $-й строки матрицы $ A_{} $ на $ ell_{} $-й столбец матрицы $ B_{} $.
В схематичном виде:
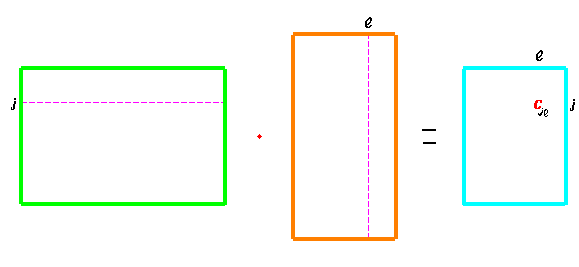
Порядок («размеры») матрицы $ C_{} $ определяется следующим образом: высота берется от первого сомножителя, а ширина — от второго.
При этом произведение $ B cdot A_{} $ может и не быть определено!
П
Пример.
$$
A=left(begin{array}{rr}
1&2\
-1&0\
3&7
end{array}right),B=left(begin{array}{rrrr}
mathbf i&0&0&-1\
4&2&0&-2
end{array}right) color{Red}{Longrightarrow} Acdot B=left(begin{array}{rrrr}
8+ mathbf i&4&0&-5\
-mathbf i&0&0&1\
28+3mathbf i&14&0&-17
end{array}right)
$$
П
Пример.
$$
A=left(
begin{array}{rrr}
3&-1&-1\
2&0&1\
1&1&1
end{array}right),B=left(begin{array}{rr}
2&1\
-1&0\
0&1
end{array}right) color{Red}{Longrightarrow} Acdot B= left(begin{array}{rr}
7&2\
4&3\
1&2
end{array}right)
$$
П
Пример.
$$
A=left(begin{array}{c}
1\ 0\ 1\ 1
end{array}right), B=(1,2,-1,-2) color{Red}{Longrightarrow} Acdot B=
left(begin{array}{rrrr}
1&2&-1&-2\
0&0&0&0\
1&2&-1&-2\
1&2&-1&-2
end{array}right)
$$
$$
B cdot A = ( — 2 ) .
$$
Т
Теорема. Операция умножения матриц подчиняется ассоциативному закону:
$$ (Acdot B) cdot D = Acdot (B cdot D) $$
если хотя бы в одной части равенства произведение определено.
Доказательство
☞
ЗДЕСЬ.
Операция умножения матриц
некоммутативна
: даже если определены оба произведения $ Acdot B_{} $ и $ B cdot A_{} $, то, как правило, $ Acdot B ne B cdot A $.
Что послужило причиной введения такой операции умножения?
Ответ и дальнейшие свойства операции умножения
☞
ЗДЕСЬ.
В приложениях используются и другие определения произведения двух матриц. Например, для матриц $ A_{} $ и $ B_{} $ одинакового порядка их адамаровым произведением называется матрица того же порядка, состоящая из поэлементных произведений: $ C=left[ a_{jk} b_{jk} right] $. См. также и
☞
КРОНЕКЕРОВО ПРОИЗВЕДЕНИЕ.
Квадратные матрицы
Матрица $ A_{} $ называется квадратной, если количество ее строк равно количеству ее столбцов. О квадратной $ ntimes n_{} $-матрице будем говорить как о матрице порядка $ mathbf n $, а записывать ее компактно в виде
$$A=left[ a_{jk} right]_{j,k=1}^n$$
Если матрицы $ A_{} $ и $ B_{} $ – квадратные порядка $ n_{} $, то обе матрицы $ AB_{} $ и $ BA_{} $ являются тоже квадратными порядка $ n_{} $. Тем не менее, и в этом случае, как правило, $ ABne BA_{} $.
П
Пример.
$$
A=
begin{pmatrix}
1 & 2 \
3 & 4
end{pmatrix}
,quad
B=
begin{pmatrix}
1 & 2 \
5 & 3
end{pmatrix} color{Red}{Longrightarrow}
AB=
begin{pmatrix}
11 & 8 \
23 & 18
end{pmatrix},
BA=
begin{pmatrix}
7 & 10 \
14 & 22
end{pmatrix}
.
$$
Говорят, что квадратные матрицы $ A $ и $ B $ коммутируют (или перестановочны), если $ AB=BA $.
симметричная
Главной диагональю квадратной матрицы $ A_{} $ называется ее диагональ, идущая из левого верхнего в правый нижний угол, т.е. эта диагональ совпадает с вектором $ (a_{11},dots,a_{jj},dots,a_{nn}^{}) $.
Матрица $ A_{} $ называется симметричной если она удовлетворяет соотношению
$$A=A^{top} .$$
Из определения следует, что симметричная матрица может быть только квадратной, а ее элементы должны удовлетворять соотношению:
$$ a_{jk}=a_{kj} quad npu {j,k } subset {1,dots, n} . $$
Иными словами, симметричная матрица — это такая матрица, которая симметрична относительно своей главной диагонали.
?
Сколько элементов надо задать, чтобы однозначно определить симметричную матрицу порядка $ n_{} $?
Частным случаем симметричной матрицы является диагональная матрица:
$$
D=left(
begin{array}{cccc}
a_{11} & & & \
& a_{22} & & {mathbb O} \
{mathbb O} & & ddots & \
& & & a_{nn}
end{array}
right) .
$$
§
Подробнее о симметричной матрице
☞
ЗДЕСЬ.
единичная
Матрица $$
E_n =
left(
begin{array}{cccc}
1 & & & \
& 1 & & {mathbb O} \
{mathbb O} & & ddots & \
& & & 1
end{array}
right)_{n}=
left[delta_{jk} right]_{j,k=1}^n
$$ называется единичной матрицей порядка $ n_{} $.
кососимметричная
Матрица $ A_{} $ называется кососимметричной если она удовлетворяет соотношению
$$A=-A^{top} .$$
Из определения следует, что кососимметричная матрица может быть только квадратной, а ее элементы должны удовлетворять соотношению:
$$ a_{jk}=-a_{kj} quad , {j,k } subset {1,dots, n} . $$
Отсюда вытекает, что все элементы главной диагонали кососимметричной матрицы должны быть равны 0.
П
Пример. Векторное произведение вектора $ X=(x_{1},x_2,x_3) $ на вектор $ Y=(y_{1},y_2,y_3) $ может быть задано с помощью кососимметричной матрицы:
$$
Xtimes Y = (x_{1},x_2,x_3) left(begin{array}{rrr}
0 & -y_3 & y_2 \
y_3 & 0 & -y_1 \
-y_2 & y_1 & 0
end{array}
right)
, .
$$
?
Указать все элементы кососимметричной матрицы
$$
left(
begin{array}{rrr}
color{Red}{Box} & 1 & color{Red}{Box} \
color{Red}{Box} & color{Red}{Box} & 3 \
-2 & color{Red}{Box} & color{Red}{Box}
end{array}
right)_{3times 3} .
$$
?
Доказать, что при любой квадратной матрице $ A_{} $
а) матрицы $ A_{}+A^{top} $ и $ A_{}A^{top} $ будут симметричными;
б) матрица $ A_{}-A^{top} $ будет кососимметричной.
Т
Теорема. Для любой квадратной матрицы $ A_{} $ существует и единственно ее представление в виде суммы симметричной и кососимметричной матриц, а именно:
$$ A = frac{1}{2} (A+A^{top}) + frac{1}{2} (A-A^{top}) . $$
§
Свойства кососимметричной матрицы
☞
ЗДЕСЬ
обратно симметричная матрица
Не очень удачный перевод на русский выражения reciprocal symmetric matrix. Формально определяется как квадратная матрица с ненулевыми элементами, удовлетворяющая соотношению
$$ A=[a_{jk}]_{j,k=1}^n , a_{jk}=1/a_{kj} . $$
Из этого определения следует, что все элементы главной диагонали такой матрицы равны $ 1_{} $.
Обычно рассматриваются положительные обратно симметричные матрицы.
П
Пример.
$$
left( begin{array}{rrr}
1 & sqrt{2} & 3 \
1/sqrt{2} & 1 & 1/4 \
1/3 & 4 & 1
end{array}
right) .
$$
Матрицы встречаются в теории принятия решений. Пусть имеется $ n_{} $ различных критериев $ C_1,C_2,dots, C_n $ и человек, принимающий решения (эксперт), может оценить во сколько раз критерий $ C_j $ важнее (предпочтительней) критерия $ C_k $; соответствующую величину $ a_{jk} $ называют интенсивностью (мощностью) предпочтения7). Особенно удачно, если эксперт оказывается достаточно квалифицированным (или самоуверенным) и в состоянии ранжировать набор критериев, придав каждому определенные веса $ w_1,w_2,dots, w_n $. Тогда матрица
$$
left[frac{w_j}{w_k} right]_{j,k=1}^n
$$
представляет собой обратно симметричную матрицу, обладающую свойством
$$ a_{jk}=a_{jell}a_{ell k} . $$
В этом случае про обратно симметричную матрицу говорят, что она мощностно-транзитивная 
треугольная
Так называется квадратная матрица, у которой все элементы выше главной диагонали или ниже ее равны нулю.
Различают верхнетреугольную9)
$$
U=left(begin{array}{ccccc}
a_{11} & a_{12} &a_{13} & dots & a_{1n} \
& a_{22} & a_{23} & dots & a_{2n} \
& & ddots & & \
& mathbb O & & ddots & vdots \
& & & & a_{nn}
end{array}
right)
$$
и нижнетреугольную
$$
L=left(begin{array}{ccccc}
a_{11} & & & & \
a_{21} & a_{22} & & & \
& & ddots & mathbb O & \
vdots & & & ddots & \
a_{n1} & a_{n2} & dots & & a_{nn}
end{array}
right)
$$
матрицы. Часто эти матрицы называют право— и левотреугольными соответственно и обозначают тогда $ R_{} $ и $ L_{} $. В одной и той же книге можно встретить одновременно
LU-разложение матрицы и QR-разложение матрицы; при этом вторые буквы означают именно верхнетреугольные матрицы. Так исторически сложилось: неудобно, но привычно!
Хессенберга
Матрица вида
$$
left(begin{array}{llllll}
a_{11} & a_{12} & a_{13} & dots & a_{1,n-1} & a_{1n} \
a_{21} & a_{22} & a_{23} & dots & a_{2,n-1} & a_{2n} \
0 & a_{32} & a_{33} & dots & a_{3,n-1} & a_{3n} \
vdots & & ddots & & & \
0 & 0 & 0 & dots & a_{n,n-1} & a_{nn}
end{array}
right) ,
$$
т.е. с элементами $ a_{ij}=0 $ при $ i<j+1 $ называется верхней матрицей Хессенберга.
ортогональная
матрица — это квадратная матрица $ A_{} $ с вещественными элементами, удовлетворяющая соотношению:
$$ A cdot A^{top} = E , $$
здесь $ E_{} $ — единичная матрица того же порядка, а $ {}^{top} $ означает транспонирование. Иными словами, строки матрицы $ A_{} $ удовлетворяют условию
$$ A^{[j]}cdot left( A^{[k]} right)^{top} = a_{j1}a_{k1}+a_{j2}a_{k2} + dots + a_{jn}a_{kn}= delta_{jk} , $$
где $ delta_{jk}^{} $ — символ Кронекера. Если определить скалярное произведение для строк $ X=(x_1,x_2,dots,x_{n}) $ и $ Y=(y_1,y_2,dots,y_{n}) $ по правилу, естественно обобщающему определение скалярного произведения в двух- и трехмерном пространстве:
$$ langle X,Y rangle =x_1y_1+x_2y_2+dots+x_ny_n , $$
то определение ортогональной матрицы оправдано тем, что ее строки оказываются взаимно ортогональными. К тому же, они все имеют «единичную длину»: сумма квадратов элементов любой строки равна 1.
В литературе под ортогональной матрицей иногда понимают и матрицу с комплексными элементами, удовлетворяющую соотношению
$ A cdot A^{top} = E $. Тогда для матрицы из приведенного выше случая используют название вещественная ортогональная матрица.
П
Пример. Матрица
$$
left(
begin{array}{rr}
cos theta & — sin theta \
sin theta & cos theta
end{array}
right)
$$
— ортогональная.
Т
Теорема. Если матрица $ A_{} $ — ортогональная, то и матрица $ A_{}^{top} $ — ортогональная, т.е. у ортогональной матрицы взаимно ортогональны не только строки, но и столбцы.
§
Подробнее об ортогональной матрице
☞
ЗДЕСЬ
Следующий класс матриц не относится ко множеству ортогональных, но близок к нему по смыслу.
Матрица $ A_{} $ называется матрицей Адамара10) если любой ее элемент равен либо $ +1_{} $ либо $ — 1_{} $ и ее строки взаимно ортогональны. Иными словами для матрицы Адамара порядка $ n_{} $ должно быть выполнено:
$$ A^{top} cdot A = n E , $$
где $ E_{} $ — единичная матрица того же порядка.
П
Пример. Матрицы
$$
left(
begin{array}{rr}
1 & 1 \
1 & -1
end{array}
right) quad u quad
left(
begin{array}{rrrr}
1 & 1 & 1 & 1 \
1 & -1 &1 & -1 \
1 & 1 & -1 & -1 \
1 & -1 & -1 & 1
end{array}
right)
$$
— матрицы Адамара. С помощью последней матрицы и следующего результата можно сконструировать матрицу Адамара порядка $ 2^{n} $.
Т
Теорема. Если $ H_{} $ — матрица Адамара порядка $ n_{} $, то блочная матрица $$ left[ begin{array}{rr}
H & H \
H & -H
end{array}
right]
$$
является матрицей Адамара порядка $ 2,n $.
Если при $ n> 2 $ матрица Адамара существует, то $ n_{} $ должно быть кратно $ 4_{} $. Обратное утверждение составляет содержание следующей гипотезы:
Гипотеза Адамара: для любого натурального $ n_{} $ кратного $ 4_{} $ существует матрица Адамара порядка $ n_{} $. Не доказана.11)
§
Применение матрицы Адамара:
☞
КОДИРОВАНИЕ.
☞
Максимальное значение определитедя матрицы порядка $ n $, элементы которой по модулю не превосходят $ 1 $ достигается на матрицах Адамара (в случае их существования для данного $ n $); оно равно $ n^{n/2} $. См.
☞
Неравенство Адамара
ганкелева
матрица — это квадратная матрица вида
$$
left(begin{array}{lllll}
h_0 & h_1 & h_2 & dots & h_{n-1} \
h_1 & h_2 & h_3 & dots & h_n \
h_2 & h_3 & h_4 & dots & h_{n+1} \
vdots & & & ddots & vdots \
h_{n-1} & h_{n} & h_{n+1} & dots & h_{2n-2}
end{array}
right)_{ntimes n}= left[ h_{j+k}right]_{j,k=0}^{n-1}
$$
Симметричная матрица, на каждой диагонали которой, перпендикулярной главной, стоят одинаковые элементы. Таким образом, ганкелева12) матрица полностью определяется заданием своих крайних элементов:
$$ h_0,h_1,dots, h_{2n-2} $$
— они называются образующими ганкелевой матрицы.
§
Подробнее о ганкелевой матрице
☞
ЗДЕСЬ.
тёплицева
Так называется квадратная матрица вида
$$
left(begin{array}{lllll}
t_0 & t_{-1} & t_{-2} & dots & t_{-n+1} \
t_1 & t_0 & t_{-1} & dots & t_{-n+2} \
t_2 & t_1 & t_0 & dots & t_{-n+3} \
vdots & & & & vdots \
t_{n-1} & t_{n-2} & t_{n-3} & dots & t_{0}
end{array}
right)= left[ t_{j-k}right]_{j,k=0}^{n-1} .
$$
Элементы каждой диагонали, параллельной главной, одинаковы. В отличие от ганкелевой матрицы, теплицева13) матрица не обязательно симметрична.
Частным случаем тёплицевой матрицы является циклическая матрица:
$$
left(begin{array}{lllll}
a_1 & a_2 & a_3 & dots & a_n \
a_n & a_1 & a_2 & dots & a_{n-1} \
a_{n-1} & a_n & a_1 & dots & a_{n-2} \
vdots & & & & vdots \
a_2 & a_3 & a_4 & dots & a_1
end{array}
right) ;
$$
(иногда называется циркулянтом, хотя в отечественной литературе циркулянтом чаще называют ее определитель).
Каждая строка, начиная со второй, получается сдвигом предыдущей вправо на один элемент; тот элемент, что при этом сдвиге «вываливается» за пределы матрицы, переставляется в начало строки.
§
Подробнее о циклической матрице
☞
ЗДЕСЬ
положительная
Так называется матрица $ A_{} $ все элементы которой положительны (определяется для матриц произвольного порядка — не обязательно квадратных). Обозначается $ A > 0 $ или $ A > mathbb O $. По аналогии определяются неотрицательная ( $ A ge 0 $), отрицательная и неположительная матрицы.
стохастическая
Неотрицательная матрица, в которой сумма элементов каждой строки равна $ 1 $:
$$
left(begin{array}{cccc}
p_{11} & p_{12} & dots & p_{1n} \
p_{21} & p_{22} & dots & p_{2n} \
& & & \
p_{n1} & p_{n2} & dots & p_{nn}
end{array}
right)
$$
$$sum_{j=1}^n p_{kj}=1 npu k in {1,dots,n } . $$
П
Пример.
$$
left(begin{array}{cccc}
1/3 & 1/2 & 1/6 & 0 \
0 & 1 & 0 & 0\
0.13 & 0.35 & 0.21 & 0.31 \
1/4 & 1/4 & 1/4 & 1/4
end{array}
right)
$$
Используется в теории вероятностей, см.
☞
цепи Маркова.
элементарных преобразований
Для квадратной матрицы $ A_{} $ умножение ее на единичную матрицу $ E_{} $ того же порядка не приводит к изменению матрицы: $ A cdot E = Ecdot A=A_{} $. Теперь «испортим» матрицу $ E_{} $ хотя бы в одном ее элементе и понаблюдаем за результатами аналогичных умножений.
П
Пример. а) Изменяется элемент вне главной диагонали: $ 0_{} $ меняется на какое-то число $ {color{Red}{ alpha} } in mathbb A_{} $.
$$
left(
begin{array}{ccc}
1 & 0 & 0 \
0 & 1 & 0 \
0 & {color{Red}{ alpha} } & 1
end{array}
right)
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)=
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} + {color{Red}{ alpha} } a_{21} & a_{32} + {color{Red}{ alpha} } a_{22} & a_{33} + {color{Red}{ alpha} } a_{23}
end{array}
right) ;
$$
$$
left(
begin{array}{ccc}
1 & 0 & 0 \
0 & 1 & {color{Red}{ alpha} } \
0 & 0& 1
end{array}
right)
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)=
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} + {color{Red}{ alpha} } a_{31} & a_{22} + {color{Red}{ alpha} } a_{32} & a_{23} + {color{Red}{ alpha} } a_{33} \
a_{31} & a_{32} & a_{33}
end{array}
right) .
$$
Вывод. Умножение матрицы такого вида ( $ 0_{} $ в $ j_{} $-й строке и $ k_{} $-м столбце матрицы $ E_{} $ меняется на $ {color{Red}{ alpha} } $) слева на матрицу $ A_{} $ эквивалентно прибавлению к $ j_{} $-й строке матрицы $ A_{} $ ее $ k_{} $-й строки, домноженной на $ {color{Red}{ alpha} } $.
б) Изменяется элемент главной диагонали: $ 1_{} $ меняется на какое-то число $ {color{Red}{ alpha} } in mathbb A_{} $.
$$
left(
begin{array}{ccc}
1 & 0 & 0 \
0 & {color{Red}{ alpha} } & 0 \
0 & 0& 1
end{array}
right)
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)=
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
{color{Red}{ alpha} } a_{21} & {color{Red}{ alpha} } a_{22} & {color{Red}{ alpha} } a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)
$$
Вывод. Умножение матрицы такого вида ( $ 1_{} $ в $ j_{} $-й строке матрицы $ E_{} $ меняется на $ {color{Red}{ alpha} } $) слева на матрицу $ A_{} $ эквивалентно домножению на $ {color{Red}{ alpha} } $ соответствующей строки матрицы $ A_{} $.
в) Произведем еще одну «экзекуцию» с матрицей $ E_{} $: переставим местами две ее строки. Такая матрица иногда называется матрицей перестановки (и, кстати, является ортогональной ) , что оправдано следующим ее свойством: умножим ее на $ A_{} $:
$$
left(
begin{array}{ccc}
1 & 0 & 0 \
0 & 0 & 1 \
0 & 1& 0
end{array}
right)
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)=
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{31} & a_{32} & a_{33} \
a_{21} & a_{22} & a_{23}
end{array}
right)
$$
Вывод. Умножение матрицы такого вида (переставляются $ j_{} $-я и $ k_{} $-я строки матрицы $ E_{} $) слева на матрицу $ A_{} $ эквивалентно перестановке соответствующих строк матрицы $ A_{} $.
♦
Для общего случая матриц порядка $ n_{} $ матрицы, построенные по аналогии с предыдущим примером, называются матрицами элементарных преобразований.
?
Показать, что умножение матриц преобразований справа на матрицу $ A_{} $ эквивалентно соответствующим преобразованиям столбцов матрицы $ A_{} $.
?
Какое действие с матрицей $ A_{} $ оказывает умножение ее на матрицу
$$
left(
begin{array}{ccccc}
0 & 0 & dots & 0 & 1 \
0 & 0 & dots & 1 & 0 \
vdots & & & & vdots \
0 & 1 & dots & 0 & 0 \
1 & 0 & dots & 0 & 0
end{array}
right) ?
$$
Последняя матрица относится к классу матриц, обобщающих класс матриц элементарных преобразований. Матрица $ P_{} $ называется матрицей перестановки если в любой ее строке и любом ее столбце в точности один элемент равен $ 1_{} $ при всех остальных равных $ 0_{} $. Она тесно связана с понятием перестановки элементов. Пусть имеются различные числа14) $ {alpha_1,dots, alpha_n} $. Любое их упорядочивание называется перестановкой. Если имеются две перестановки одного и того же набора чисел, записываемые в виде векторов-строк: $ (x_1,dots,x_{n}) $ и $ (y_1,dots,y_n) $, то они связаны между собой посредством умножения на матрицу перестановки $ P_{} $ порядка $ n_{} $:
$$ (y_1,dots,y_n) =(x_1,dots,x_n)P . $$
Так, к примеру, если $ (y_1,y_2,y_3,y_4)=(x_2,x_4,x_3,x_1) $, то
$$(y_1,y_2,y_3,y_4)=(x_1,x_2,x_3,x_4)
left(begin{array}{cccc}
0 & 0 & 0 & 1 \
1 & 0 & 0 & 0 \
0 & 0 & 1 & 0 \
0 & 1 & 0 & 0
end{array}
right) .
$$
Очевидно действие матрицы перестановки при умножении на произвольную квадратную матрицу $ A_{} $; также очевидно, что результат этого действия эквивалентен последовательным действиям матриц элементарных преобразований, т.е. любая матрица перестановки может быть представлена как произведение матриц элементарных преобразований.
Матрицы элементарных преобразований используются при анализе метода Гаусса решения систем линейных уравнений.
ленточная
Пронумеруем диагонали квадратной матрицы, начиная с главной — в обе стороны. Если все диагонали, начиная с некоторого их номера, будут заполнены нулевыми элементами, то такая матрица называется ленточной. Аналитически:
$$ a_{jk}=0 quad npu quad |j-k| ge L .$$
Минимальное из возможных значений $ L $, при которых последнее будет выполнено, называется шириной ленточной матрицы: в этом случае матрица имеет не более $ 2L-1 $ диагоналей, которые могут содержать ненулевые элементы.
П
Пример. Ленточная матрица ширины $ 1_{} $ является диагональной матрицей; ленточная матрица ширины $ 2_{} $ является трехдиагональной:
$$
left(
begin{array}{lllllllll}
a_{11} & a_{12} & 0 & 0 & 0 & 0 & dots & 0 & 0 \
a_{21} & a_{22} & a_{23} & 0 & 0 & 0 & dots & 0 & 0 \
0 & a_{32} & a_{33} & a_{34} & 0 & 0 & dots & 0 & 0 \
0 & 0 & a_{43} & a_{44} & a_{45} & 0 & dots & 0 & 0 \
vdots & & & & ddots & & & & vdots \
0 & 0 & 0 & 0 & 0 & 0 & dots & a_{n,n-1} & a_{n,n}
end{array}
right).
$$
§
Ленточные матрицы возникают в численных методах решения граничных задач для обыкновенных дифференциальных уравнений; см.
☞
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ.
Часто встречающиеся («именные») матрицы
Вандермонда
$$ mathbf V(x_1,dots,x_n)= left[ x_j^{k-1} right]_{j,k=1}^{n}=
left(begin{array}{ccccc}
1 &x_1&x_1^2&ldots&x_1^{n-1}\
1 &x_2&x_2^2&ldots&x_2^{n-1}\
vdots& &&& vdots\
1 &x_n&x_n^2&ldots&x_n^{n-1}
end{array}right)_{ntimes n}
$$
или ей транспонированная. Иногда рассматривают неквадратные матрицы Вандермонда.
§
Подробнее о матрице Вандермонда
☞
ЗДЕСЬ.
Частным случаем матрицы Вандермонда является матрица дискретного преобразования Фурье:
$$
F=left[ varepsilon_j^{k} right]_{j,k=0}^{n-1}=
left( begin{array}{lllll}
1 & 1 & 1 & dots & 1 \
1 & varepsilon_1 & varepsilon_1^2 & dots & varepsilon_1^{n-1} \
1 & varepsilon_2 & varepsilon_2^2 & dots & varepsilon_2^{n-1} \
1 & varepsilon_3 & varepsilon_3^2 & dots & varepsilon_3^{n-1} \
vdots & & & & vdots \
1 & varepsilon_{n-1} & varepsilon_{n-1}^{2} & dots & varepsilon_{n-1}^{n-1}
end{array}
right)_{ntimes n}
quad npu quad varepsilon_j = cos frac{2 pi j}{n} + {mathbf i} , sin frac{2 pi j}{n}
$$
— корне n-й степени из 1. Основываясь на свойстве $ varepsilon_j=varepsilon_1^j $, матрицу часто записывают в эквивалентном виде
$$
F=
left[ varepsilon^{jk} right]_{j,k=0}^{n-1}=
left( begin{array}{lllll}
1 & 1 & 1 & dots & 1 \
1 & varepsilon & varepsilon^2 & dots & varepsilon^{n-1} \
1 & varepsilon^2 & varepsilon^4 & dots & varepsilon^{2(n-1)} \
1 & varepsilon^3 & varepsilon^6 & dots & varepsilon^{3(n-1)} \
vdots & & & & vdots \
1 & varepsilon^{n-1} & varepsilon^{2(n-1)} & dots & varepsilon^{(n-1)^2}
end{array}
right)_{ntimes n} quad npu quad varepsilon = cos frac{2 pi}{n} + {mathbf i} , sin frac{2 pi}{n} .
$$
§
Свойства матрицы дискретного преобразования Фурье
☞
ЗДЕСЬ; ее применение
☞
ТРИГОНОМЕТРИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ.
Гессе
Матрица, составленная из частных производных второго порядка функции $ f(x_1,dots,x_{ell}) $
$$
H (f) = left(
begin{array}{cccc}
{partial^2 f}/{partial x_1^2} & {partial^2 f}/{partial x_1 partial x_2} & dots & {partial^2 f}/{partial x_1 partial x_{ell}} \
{partial^2 f}/{partial x_2 partial x_1} & {partial^2 f}/{partial x_2^2} & dots & {partial^2 f}/{partial x_2 partial x_{ell}} \
dots & && dots \
{partial^2 f}/{partial x_{ell} partial x_1} & {partial^2 f}/{partial x_{ell} partial x_2} & dots & {partial^2 f}/{partial x_{ell}^2}
end{array}
right)= left[ frac{partial^2 f}{partial x_j partial x_k} right]_{j,k=1}^{ell}
$$
(в предположении, что эти производные существуют). Определитель матрицы Гессе называется гессианом.
§
Подробнее о применениях матрицы Гессе к задачам исследования стационарных точек функции на экстремум, а также самой функции на выпуклость
☞
ЗДЕСЬ.
Грама
Пусть в линейном пространстве $ mathbb E $ определено скалярное произведение векторов, которое обозначим $ langle X,Y rangle $.
Матрицей Грама системы векторов $ {X_1,dots,X_{m} } $ называется квадратная матрица
$$
G(X_1,dots,X_m)=
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right)
= left[ langle X_j,X_k rangle right]_{j,k=1}^m
.
$$
Если векторы $ {X_1,dots,X_{n} } $ составляют базис линейного пространства, то задание их матрицы Грама сведет вычисление скалярного произведения произвольных векторов пространства к действию с их координатами:
если
$$X=x_1X_1+ dots +x_nX_n quad u quad Y=y_1X_1+ dots +y_nX_n ,
$$
то
$$
langle X,Y rangle=left(x_1,x_2,dots,x_n right)
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \
dots & & & dots \
langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle
end{array}
right)
left(
begin{array}{c}
y_1 \
y_2 \
vdots \
y_n
end{array}
right)
.
$$
§
Подробнее о свойствах матрицы Грама и ее применении к задачам вычисления расстояний
☞
ЗДЕСЬ.
Фробениуса
Матрица
$$
{mathfrak F}=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n}
$$
или ей транспонированная. Ее характеристический полином имеет вид
$$ det ({mathfrak F} — x E) = (-1)^n(x^n-a_1x^{n-1}-dots-a_{n}) , . $$
Тем самым, матрица Фробениуса является решением задачи построения матрицы простейшего вида, имеющей заданный характеристический полином. Исходя из этого соображения, матрицу $ {mathfrak F} $ часто называют сопровождающей матрицей полинома15) $ f(x)=x^n-a_1x^{n-1}-a_2x^{n-2}- dots — a_n $.
§
Применение матрицы Фробениуса
☞
РЕШЕНИЕ ЛИНЕЙНОГО РАЗНОСТНОГО УРАВНЕНИЯ.
Якоби
Матрицей Якоби системы из $ m_{} $ функций
$ {f_1(x_1,dots,x_n),dots,f_{m}(x_1,dots,x_n)} $ по переменным $ x_{1},dots,x_n $ называется матрица,
составленная из всевозможных частных производных:
$$
mathbf J = left[ frac{partial f_j}{partial x_k} right]_{j=1,dots,m, atop k=1,dots,n} =
left(
begin{array}{cccc}
{partial f_1}/{partial x_1} & {partial f_1}/{partial x_2} & dots & {partial f_1}/{partial x_n} \
{partial f_2}/{partial x_1} & {partial f_2}/{partial x_2} & dots & {partial f_2}/{partial x_n} \
dots & && dots \
{partial f_m}/{partial x_1} & {partial f_m}/{partial x_2} & dots & {partial f_m}/{partial x_n}
end{array}
right)_{mtimes n} .
$$
В частном случае $ m=1_{} $ матрица Якоби состоит из одной строки:
этот вектор в $ mathbb R_{}^{n} $ или в $ mathbb C^{n} $ называется градиентом функции $ f_{} $ (в точке $ (x_1,dots,x_{n}) $):
$$
operatorname{grad} (f) = left( frac{partial f}{partial x_1},dots, frac{partial f}{partial x_n} right) .
$$
§
Применение матрицы Якоби
☞
ЗДЕСЬ
f
Функции от матрицы
определитель
или детерминант16) определяется для произвольной квадратной матрицы $ A_{} $, и представляет из себя полином от всех ее элементов. Обозначается — либо $ det (A_{}) $, либо $ det A_{} $, либо — в развернутом виде —
$$
left|
begin{array}{cccc}
a_{11} & a_{12} & dots & a_{1n} \
a_{21} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{n1} & a_{n2} & dots & a_{nn}
end{array}
right|
$$
(матрица ограничивается вертикальными чертами). Имея в виду порядок матрицы $ A_{} $, о ее определителе говорят как об определителе порядка $ n_{} $.
Для $ n=1_{} $:
$$
det (A) = a_{11} ;
$$
для $ n=2_{} $:
$$
det (A) = left|
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right|=a_{11}a_{22}-a_{12}a_{21} ;
$$
для $ n=3_{} $:
$$
det (A) =
left|
begin{array}{lll}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right| =
$$
$$
=a_{11}a_{22}a_{33}+a_{12}a_{23} a_{31} +
a_{21}a_{32} a_{13} — a_{31} a_{22} a_{13} — a_{21}a_{12}a_{33} —
a_{11} a_{32} a_{23} ;
$$
для $ n=4_{} $ формула становится громоздкой.
Понятие определителя вводится с целью компактной записи критерия разрешимости системы линейных уравнений
$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=b_1,\
a_{21}x_1 &+a_{22}x_2&+ ldots&+a_{2n}x_n &=b_2,\
dots & & & dots & \
a_{n1}x_1 &+a_{n2}x_2&+ ldots&+a_{nn}x_n &=b_n.
end{array} right.
$$
и представления ее решения.
Т
Теорема. Если определитель матрицы, составленной из коэффициентов $ a_{jk} $, отличен от нуля, то система имеет единственное решение относительно неизвестных $ x_{1},dots,x_n $.
§
Определение, свойства и применения определителя
☞
ЗДЕСЬ
Для неквадратных матриц понятие определителя не вводится, но имеется понятие миноров матрицы.
Если выбрана подматрица матрицы $ A_{} $ — т.е. взяты ее элементы, стоящие на пересечении
строк с номерами $ i_1,i_2,dots,i_{k} $ и столбцов с номерами $ j_1,dots,j_{ell} $ (номера указаны строго в порядке возрастания) и эта подматрица — квадратная, т.е. $ k=ell $, то ее определитель называется минором матрицы (k-го порядка). Обозначать будем
$$ Aleft( begin{array}{llll} i_1 & i_2 & dots & i_{k} \
j_1 & j_2 & dots & j_{k}
end{array}
right) . $$
след
определяется для произвольной квадратной матрицы $ A_{} $ как сумма элементов ее главной диагонали;
обозначается17) $ operatorname{Sp}(A_{}) $ или $ operatorname{tr}(A_{}) $:
$$ operatorname{Sp}(A)=a_{11}+a_{22}+dots+a_{nn} . $$
Свойства. Для квадратных матриц одинакового порядка имеют место равенства:
a) $ operatorname{Sp}(A+B) = operatorname{Sp}(A) + operatorname{Sp}(B_{}) $;
б) $ operatorname{Sp}(alpha A_{}) = alpha operatorname{Sp}(A) $ для любого числа $ alpha_{} $;
в) $ operatorname{Sp}(AB) = operatorname{Sp}(BA_{}) $;
г) $ operatorname{Sp} (A^{top}) = operatorname{Sp} (A_{}) $
д) $ operatorname{Sp}(A^{top} B) = sum_{j,l=1}^n a_{jk} b_{jk} $
характеристический полином
определяется для произвольной квадратной матрицы $ A_{} $ как $ det (A_{}- x E) $, где $ E_{} $ – единичная матрица одинакового с $ A_{} $ порядка. Если порядок матрицы равен $ n_{} $, то указанный определитель является полиномом степени $ n_{} $ по $ x_{} $.
П
Пример. Для $ n=2_{} $:
$$ det (A-x E)=
begin{vmatrix}
a_{11}-x & a_{12}\
a_{21}& a_{22}-x
end{vmatrix}=x^2-(a_{11}+a_{22})x + (a_{11}a_{22}-a_{12}a_{21}) ;
$$
для $ n=3 $:
$$
det (A-x E)=
begin{vmatrix}
a_{11}-x & a_{12} & a_{13}\
a_{21}& a_{22}-x & a_{23} \
a_{31}& a_{32} & a_{33}-x
end{vmatrix}=
$$
$$
=-x^3+(a_{11}+a_{22}+a_{33})x^2 — left {
begin{vmatrix}
a_{11}& a_{12}\
a_{21}& a_{22}
end{vmatrix}
+begin{vmatrix}
a_{22}& a_{23}\
a_{32}& a_{33}
end{vmatrix}+
begin{vmatrix}
a_{11}& a_{13}\
a_{31}& a_{33}
end{vmatrix}
right }x+
$$
$$
+det A .
$$
§
Структура, свойства и методы вычисления характеристического полинома
☞
ЗДЕСЬ
ранг
определяется для произвольной (не обязательно квадратной) матрицы $ A_{} $ как наибольший порядок ее отличных от нуля миноров. Иначе говоря: $ operatorname{rank} (A_{}) ={mathfrak r}in {mathbb N} $ тогда и только тогда, когда существует ее минор порядка $ {mathfrak r} $, отличный от нуля, а все миноры более высокого порядка равны нулю. Кроме того, полагают ранг нулевой матрицы равным нулю: $ operatorname{rank} ({mathbb O}_{mtimes n}) = 0_{} $.
§
Методы вычисления, свойства и применения ранга матрицы
☞
ЗДЕСЬ
норма
Функция, ставящая в соответствие произвольной квадратной матрице $ A_{} $ порядка $ n_{} $ вещественное число, называется матричной нормой если для нее выполняются следующие аксиомы:
-
$ || A_{} || geq 0 $ (неотрицательность);
-
$ || A_{} || = 0 $ тогда и только тогда, когда $ A_{}=mathbb{O} $ (положительность);
-
$ || alpha A_{} ||=|alpha|cdot || A || $ для всех $ alpha_{}in mathbb{C} $ (абсолютная однородность);
-
$ || A + B_{} || le ||A||+||B|| $ (неравенство треугольника);
-
$ ||AB||le ||A|| cdot ||B_{}|| $.
§
Норма вводится не только для квадратных матриц. Подробнее
☞
ЗДЕСЬ.
Обращение матрицы
Для квадратной матрицы $ A_{} $ матрица $ B_{} $ называется левой обратной, если $ BA=E_{} $, где $ E_{} $ – единичная матрица одинакового порядка с $ A_{} $. Отсутствие свойства коммутативности умножения приводит к необходимости определения еще одной обратной матрицы — правой обратной, т.е. матрицы $ C_{} $ такой, что $ AC= E_{} $. К счастью, необходимость в этом «дублировании» практически сразу пропадает:
Т
Для того, чтобы существовала левая обратная матрица для матрицы $ A_{} $ необходимо и достаточно, чтобы $ det A_{} ne 0 $. В этом случае, левая обратная матрица будет единственной, и будет совпадать с правой обратной.
Для обратной к матрице $ A_{} $ закреплено обозначение $ A_{}^{-1} $, а сама процедура нахождения обратной матрицы называется обращением. Матрица, определитель которой отличен от нуля, называется неособенной или невырожденной или обратимой.
Доказательство. Необходимость условия $ det A_{} ne 0 $ для существования, например, левой обратной матрицы следует из условия
$$ det (B cdot A)= det E quad iff quad (det B) (det A) =1 . $$
Покажем достаточность. Вычислим все алгебраические дополнения к элементам матрицы $ A_{} $, составим из них новую матрицу порядка $ n_{} $ и транспонируем ее. Полученная матрица
$$
operatorname{adj}(A) =left(left[A_{jk} right]_{jk}^n right)^{top} =
left(
begin{array}{llll}
A_{11} &
A_{21}& dots &
A_{n1} \
A_{12} &
A_{22} & dots &
A_{n2} \
dots & & & dots \
A_{1n} &
A_{2n} & dots &
A_{nn}
end{array}
right)
$$
называется взаимной или союзной матрице $ A_{} $. Для любой матрицы $ A_{} $ имеет место равенство
$$
A cdot operatorname{adj}(A) =
left(
begin{array}{cccc}
det A & & & \
& det A & & {mathbb O} \
{mathbb O} & & ddots & \
& & & det A
end{array}
right) = det A cdot E .
$$
Справедливость этого факта следует из теории определителей: сумма произведений элементов строки матрицы на их алгебраические дополнения равна определителю матрицы; а на алгебраические
дополнения к элементам любой другой строки — нулю (см.
☞
ЗДЕСЬ ).
При выполнении условия $ det A_{} ne 0 $ можем взять
$$
A^{-1}=frac{ operatorname{adj}(A) }{det A}=
left(
begin{array}{llll}
frac{A_{11}}{det A} &
frac{A_{21}}{det A} & dots &
frac{A_{n1}}{det A} \
&&& \
frac{A_{12}}{det A} &
frac{A_{22}}{det A} & dots &
frac{A_{n2}}{det A} \
&&& \
vdots & & & vdots \
frac{A_{1n}}{det A} &
frac{A_{2n}}{det A} & dots &
frac{A_{nn}}{det A}
end{array}
right) .
$$
Пока что мы получили правую обратную матрицу: доказано, что она удовлетворяет условию $ A C = E_{} $. Проверка того, что полученная матрица будет являться и левой обратной, т.е. удовлетворяет условию $ C A=E $, производится снова с использованием теоремы о сумме произведений элементов столбца матрицы $ A_{} $ на алгебраические дополнения к другому столбцу той же матрицы (см.
☞
ЗДЕСЬ ). Теперь покажем, единственность полученной обратной матрицы. Предположим, что каким-то другим способом найдена еще одна матрица $ C_1 $ обладающая тем же самым свойством $ A C_1 = E $. Домножим это равенство слева на матрицу $ C_{} $:
$$ C(AC_1) = C E . $$
Операция умножения матриц подчиняется ассоциативному закону, поэтому
$$ (CA) C_1 = C , $$
но, по доказанному ранее, $ CA=E_{} $. И мы получили равенство $ C_1 = C $, доказывающее единственность правой обратной матрицы. Аналогично доказывается единственность и левой обратной.
♦
П
Пример. Вычислить
$$
left( begin{array}{rrr}
4 & 8 & -5\
-4 & 7 &-1 \
-3 & 5 & 1
end{array}
right)^{-1} .
$$
Решение. Вычисляем определитель этой матрицы: $ det A = 99 ne 0 $. Обратная матрица существует. Вычисляем алгебраические дополнения элементов:
$$
overbrace{left| begin{array}{rr}
7 &-1 \
5 & 1
end{array}
right|}^{A_{11}}=12,
overbrace{-left| begin{array}{rrr}
-4 &-1 \
-3 & 1
end{array}
right|}^{A_{12}}=7,
overbrace{left| begin{array}{rrr}
-4 & 7 \
-3 & 5
end{array}
right|}^{A_{13}}=1,
$$
$$
overbrace{-left| begin{array}{rr}
8 &-5 \
5 & 1
end{array}
right|}^{A_{21}}=-33,
overbrace{left| begin{array}{rr}
4 &-5 \
-3 & 1
end{array}
right|}^{A_{22}}=-11,
overbrace{-left| begin{array}{rr}
4 &8 \
-3 & 5
end{array}
right|}^{A_{23}}=-44,
$$
$$
overbrace{left| begin{array}{rr}
8 &-5 \
7 & -1
end{array}
right|}^{A_{31}}=27,
overbrace{-left| begin{array}{rr}
4 &-5 \
-4 & -1
end{array}
right|}^{A_{32}}=24,
overbrace{left| begin{array}{rr}
4 &8 \
-4 & 7
end{array}
right|}^{A_{33}}=60 .
$$
Cоставляем из них матрицу:
$$
left( begin{array}{rrr}
12 & 7 & 1\
-33 & -11 &-44 \
27 & 24 & 60
end{array}
right)
$$
и не забываем ее транспонировать, а также поделить на определитель!
Ответ.
$$
left( begin{array}{rrr}
frac{scriptstyle 4}{scriptstyle 33} &
-frac{scriptstyle 1}{scriptstyle 3} &
frac{scriptstyle 3}{scriptstyle 11} \
&& \
frac{scriptstyle 7}{scriptstyle 99} &
-frac{scriptstyle 1}{scriptstyle 9} &
frac{scriptstyle 8}{scriptstyle 33} \
&& \
frac{scriptstyle 1}{scriptstyle 99} &
-frac{scriptstyle 4}{scriptstyle 9} &
frac{scriptstyle 20}{scriptstyle 33}
end{array}
right) .
$$
?
Показать справедливость следующих свойств операции обращения :
a) $ (A^{-1})^{-1}=A_{} $;
б) $ (Acdot B)^{-1} = B^{-1}A_{}^{-1} $;
в) $ (A_{}^{top})^{-1}=(A^{-1})^{top} $;
г) $ det A_{}^{-1} = (det A)^{-1} $.
Предполагается, что в левой части каждого равенства операции определены.
§
Методы вычисления, свойства и применения обратной матрицы
☞
ЗДЕСЬ
Полином от матрицы и матричный полином
Для квадратной матрицы $ A_{} $ ее $ k_{} $-й степенью ($ k_{}in mathbb N $) называют результат умножения ее на себя $ k_{} $ раз:
$$ A^k = underbrace{Atimes dots times A}_k . $$
В виду ассоциативности операции умножения, скобки в этом произведении можно расставить произвольным образом. Дополнительно полагают $ A^{0} = E $ при ненулевой матрице $ A_{} $ и, в случае существования обратной матрицы, определяют и отрицательную степень:
$$ A^{-k} = (A^{-1})^k . $$
?
Показать, что
a) cтепени матрицы $ A_{} $ коммутируют: $ A^{k} A^{ell}= A^{ell} A^k $;
б) $ det (A^k) = left( det A right)^{k} $.
П
Пример. Вычислить
$$
left( begin{array}{rrr}
-3 & 2 & -3 \
-2 & 3 & -3 \
1 &-1 & 1
end{array}
right)^9
$$
Решение. Чтобы сэкономить на количестве матричных умножений, будем осуществлять их по схеме
$$
left(left(A^2 right)^2right)^2 A .
$$
Имеем
$$
A^2=left( begin{array}{rrr}
2 & 3 & 0 \
-3 & 8 & -6 \
0 &-2 & 1
end{array}
right) quad Rightarrow quad left(A^2 right)^2=
left( begin{array}{rrr}
-5 & 30 & -18 \
-30 & 67 & -54 \
6 &-18 & 13
end{array}
right) quad Rightarrow quad left(left(A^2 right)^2right)^2=
left( begin{array}{rrr}
-983 & 2184 & -1764 \
-2184 & 4561 & -3780 \
588 & -1260 & 1033
end{array}
right)
$$
и окончательно
$$
left(left(A^2 right)^2right)^2A=
left( begin{array}{rrr}
-3183 & 6350 & -5367 \
-6350 & 13095 & -10911 \
1789 & -3637 & 3049
end{array}
right) .
$$
♦
?
Проверить, что для матрицы из предыдущего примера, любая ее степень
$$ B=A^n $$
будет подчиняться условиям: $ b_{12}=-b_{21}^{} $ и $ b_{23}^{}=3 b_{32} $.
Обобщением возведения в степень является операция вычисления полинома от матрицы. Если $ g(x)=b_0x^m+b_1x^{m-1}+dots+b_{m} $ — полином по переменной $ x_{} $, то значением этого полинома на квадратной матрице $ A_{} $ называется матрица
$$ g(A)=b_0A^m +b_1A^{m-1}+dots+b_m E , $$
где $ E_{} $ — единичная матрица того же порядка, что и $ A_{} $.
П
Пример. Вычислить $ g(A)_{} $ для
$$ g(x)= 3,x^4-x^3+2,x^2-4,x-1 quad u quad
A=left( begin{array}{rrr}
1 & -3 & 4 \
3& 1 &8 \
-4 & -8 & 1
end{array}
right) .
$$
Решение. Можно было бы производить вычисления напрямую, но мы снова попытаемся сэкономить на количестве операций, действуя по схеме Хорнера:
$$
g(A)=(((3A-E)A+2E)A-4E)A-E .
$$
$$
B_1 = 3A-E =
left( begin{array}{rrr}
2 & -9 & 12 \
9& 2 & 24 \
-12 & -24 & 2
end{array}
right) ;
$$
$$
B_2=B_1A+2E=
left( begin{array}{rrr}
-71 & -111 & -52 \
-81& -215 & 76 \
-92 & -4 & -236
end{array}
right) ;
$$
$$
B_3=B_2A-4E=
left( begin{array}{rrr}
-200 & 518 & -1224 \
-1030& -584 & -1968 \
840 & 2160 & -640
end{array}
right) ;
$$
$$
g(A)=B_4=B_3A-E=
left( begin{array}{rrr}
6249 & 10910 & 2120 \
5090& 18249 & -10760 \
9880 & 4760 & 19999
end{array}
right)
$$
♦
§
Более подробный анализ структуры и изложение способов вычисления полинома от матрицы (а также таких функций как $ e^x, cos x , sin x ,
sqrt{x} $)
☞
ЗДЕСЬ.
Следующее определение сходно по звучанию с предыдущим, но не совпадает с ним по смыслу. Имеются разночтения в определении matrix polynomial — см. статьи Википедии Polynomial matrix и Matrix polynomial.
Рассмотрим квадратную матрицу, элементами которой являются полиномы над множеством $ mathbb A_{} $ (мы ограничимся случаями, когда это множество совпадает с одним из множеств $ mathbb Z_{},mathbb Q, mathbb R $ или $ mathbb C_{} $).
П
Пример.
$$
A(x)=left(
begin{array}{ccc}
3x^2+4x+1 & x^3 — sqrt{3} & -2,x +1 \
x^2-1 & 7,x^3-x+4 & 6,x^2-3,x+1 \
4,x^3-7,x^2+3,x-2 & 2,x-17 & x^2
end{array}
right) .
$$
Такую матрицу можно представить в виде полинома по $ x_{} $ с матричными коэффициентами:
$$
A(x)= left(
begin{array}{ccc}
0 & 1 & 0 \
0 & 7 & 0 \
4 & 0 & 0
end{array}
right) x^3 +
left(
begin{array}{rcc}
3 & 0 & 0 \
1 & 0 & 6 \
-7 & 0 & 1
end{array}
right) x^2 +
left(
begin{array}{rrr}
4 & 0 & -2 \
0 & -1 & -3 \
3 & 2 & 0
end{array}
right) x
+left(
begin{array}{rrr}
1 & — sqrt{3} & 1 \
-1 & 4 & 1 \
-2 & -17 & 0
end{array}
right) .
$$
В общем случае полиномиальная матрица имеет вид
$$
A(x)=A_0 x^m + A_1 x^{m-1}+dots+A_m ,
$$
где $ A_0,dots,A_{m} $ — квадратные числовые матрицы одинакового порядка $ n_{} $.
Часто полиномиальная матрица называется матричным полиномом по $ x_{} $ (или же полиномом по $ x_{} $ с матричными коэффициентами).
Если при этом $ A_0 ne mathbb O $, то $ n_{} $ называют степенью полиномиальной матрицы. Если,
вдобавок, матрица $ A_{0} $
невырожденная, то матричный полином называется регулярным.
Матричные уравнения
Матрица может быть определена не только явным образом, но и заданием соотношения, которому она должна удовлетворять. Так, к примеру обратная матрица для квадратной матрицы $ A $ фактически определялась как решение матричного уравнения $ AX= E $. Отсутствие свойства коммутативности умножения порождает причудливые комбинации, не имеющие аналогов в скалярном случае.
Уравнение Ляпунова
имеет вид
$$ A^{top}X+XA=C $$
при заданной матрице $ A_{} $ и заданной симметричной матрице $ C_{} $ (обе — квадратные одинакового порядка $ n_{} $),
относительно неизвестной матрицы $ X_{} $, которая разыскивается также во множестве симметричных матриц порядка $ n_{} $.
Имеет важное значение в теории управления.
Уравнение является частным случаем матричного уравнения Сильвестра
$$ AX+XB=C $$
при произвольных квадратных матрицах $ A,B,C_{} $.
!
Далее идет сложный для понимания материал!
Пример. Решить матричное уравнение Сильвестра для матриц второго порядка:
$$ A=left(
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right) ,
B=left(
begin{array}{cc}
b_{11} & b_{12} \
b_{21} & b_{22}
end{array}
right) ,
C=left(
begin{array}{cc}
c_{11} & c_{12} \
c_{21} & c_{22}
end{array}
right) .
$$
Решение. Подставляя в уравнение матрицу
$$
X=left(
begin{array}{cc}
x_{11} & x_{12} \
x_{21} & x_{22}
end{array}
right) ,
$$
с пока неопределенными элементами, получаем систему линейных уравнений, которую тоже запишем в матричном виде:
$$
left( begin{array}{cccc}
a_{11}+b_{11} & a_{12} & b_{21} & 0 \
a_{21} & a_{22}+b_{11} & 0 & b_{21} \
b_{12} & 0 & a_{11}+b_{22} & a_{12} \
0 & b_{12} & a_{21} & a_{22}+b_{22}
end{array}
right)
left( begin{array}{c}
x_{11} \ x_{21} \ x_{12} \ x_{22}
end{array}
right)=
left( begin{array}{c}
c_{11} \ c_{21} \ c_{12} \ c_{22}
end{array}
right)
$$
(матрицы $ X_{} $ и $ C_{} $ «вытянули» в строки). Матрица в левой части имеет порядок $ 4_{} $ и может быть представлена в виде суммы двух матриц:
$$
left( begin{array}{cccc}
a_{11}+b_{11} & a_{12} & b_{21} & 0 \
a_{21} & a_{22}+b_{11} & 0 & b_{21} \
b_{12} & 0 & a_{11}+b_{22} & a_{12} \
0 & b_{12} & a_{21} & a_{22}+b_{22}
end{array}
right)=
left( begin{array}{cccc}
a_{11} & a_{12} & 0 & 0 \
a_{21} & a_{22} & 0 & 0 \
0 & 0 & a_{11} & a_{12} \
0 & 0 & a_{21} & a_{22}
end{array}
right)
+
left( begin{array}{cccc}
b_{11} & 0 & b_{21} & 0 \
0 & b_{11} & 0 & b_{21} \
b_{12} & 0 & b_{22} & 0 \
0 & b_{12} & 0 & b_{22}
end{array}
right) .
$$
Для формализации записи этих двух слагаемых придумана специальная операция
☞
КРОНЕКЕРОВО ПРОИЗВЕДЕНИЕ. Пока не останавливаясь на этом формализме, вычислим определитель: получим крайне громоздкий полином $ 4_{} $-й степени относительно элементов матриц $ A_{} $ и $ B_{} $. Оказывается, этот полином совпадает
с результантом характеристического полинома матрицы $ A_{} $ и характеристического полинома матрицы $ (-B_{}) $:
$$ mathcal R (det(A-lambda E), det(-B-lambda E)) . $$
Если это выражение отличо от нуля, то матричное уравнение $ AX+XB=C $ имеет решение при любой матрице $ C_{} $.
♦
Квадратные уравнения
?
Уравнение $ x^2=-1 $ не имеет решения в вещественных числах. Можно ли утверждать аналогичное для уравнения матричного:
$$X^2=-
left(
begin{array}{rr}
1 & 0 \
0 & 1
end{array}
right) ?
$$
Эта задача — вычисления квадратного корня из матрицы — является частью общей задачи о вычислении аналитической функции от матрицы, т.е. произвольной функции $ g(x) $, представимой в виде сходящегося ряда. Частным случаем задачи является рассмотренная выше задача вычисления полинома от матрицы. Подробнее об этой задаче
☞
ЗДЕСЬ.
Уравнение
$$ A^{top}X+XA-X^{top}BX=C $$
называется матричным уравнением Риккати. Уравнение Ляпунова получается из него при нулевой матрице $ B $.
Матрица квадратичной формы
рассматривается
☞
ЗДЕСЬ
Матрица преобразования координат
— это матрица, связывающая координаты произвольного
вектора $ X_{} $ из $ n_{} $—мерного линейного пространства в двух различных базисах $ {X_1,dots,X_n} $ и $ {{mathfrak X}_1,dots,{mathfrak X}_n} $ этого пространства:
$$X=x_1X_1+dots+x_nX_n={mathfrak x}_1{mathfrak X}_1+dots+{mathfrak x}_n{mathfrak X}_n
.$$
Называется также матрицей перехода от базиса к базису. Подробнее
☞
ЗДЕСЬ.
Матрица линейного отображения
— это матрица, связывающая координаты произвольного вектора $ X_{} $ из линейного пространства $ mathbb V_{} $ с координатами его образа $ Y_{} $ в линейном пространстве $ mathbb W_{} $ при выборе некоторых фиксированных базисов этих пространств.
Подробнее
☞
ЗДЕСЬ.
Задачи
Источники
Вопрос 1. Основные сведения о матрицах.
Матрицей
размерности m×n
называется прямоугольная
таблица чисел,
состоящая из m–
строк
и n–
столбцов.
Числа,
составляющие матрицу, называются ее
элементами.
Элемент,
стоящий на пересечении строки с номером
i(i‒
той строки),
i
=
1, 2…m
и столбца с номером j(j‒
того столбца),
j
=
1, 2…n
– обозначается aij.
Матрица
обозначается заглавными буквами A,B,C…,
а их элементы ‒ соответствующими
прописными буквами.
Am×
n=
Пример:
A3×2
=
А11
=
3
А21
=
–
2
А22
=
5
А32
=
–1
Виды матриц
1.
Матрица, состоящая из одной строки,
называется матрицей ‒ строкой или
вектором – строкой. В1×n=
(b11
b12…b1n)
2.
Матрица, состоящая из одного столбца,
называется матрицей ‒ столбцом или
вектором – столбцом. Сm×1
=
3.
Матрица называется квадратной n‒
го порядка, если у нее число строк равно
числу столбцов и равноn.
A
=
квадратная матрица третьего порядка
Главная
диагональ
Элементы
квадратной матрицы, у которых совпадает
номер строки и столбца, образуют главную
диагональ.
Квадратная
матрица, все элементы главной диагонали
которой равны 1, а остальные элементы
равны 0, называется единичной
матрицей.
E=

единичная матрица второго порядка.
E=
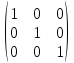
единичная матрица третьего порядка.
Вопрос 2. Операции над матрицами и их свойства.
1.Произведение
матрицы на число.
Произведением
матрицы A
на число λназывается
такая матрица B,
каждый элемент которой находится по
формуле:
bij=λ
×
aij
Пример:
A=
‒
3A=

2.
Сумма
матриц.
Суммой
матриц A
и B
одинаковой размерности называется
матрица C,
каждый элемент которой находится по
формуле: (Cij=
Aij
+Bij),
т.е. матрицы складываются поэлементно.
Пример:
+


3.
Разность
матриц.
А
‒ В = А + (‒1)
×
В
Пример:
‒


4.
Произведение
матриц.
Произведением
матрицы Аm×lна
матрицу Вl×nназывается
матрица Сm×n,
каждый
элемент которой cijравен
сумме произведений всех элементов i
– ой строки матрицы A
на соответствующие элементыj
‒ того столбца матрицы B.
Пример:
A2×3=

=
=
=
5.
Возведение в степень с натуральным
показателем квадратных матриц.
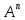
A×A….A
n
‒ раз.
Пример:
A=

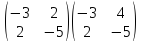


6.
Транспонирование матриц.
Матрица
АТ
(или
АI)
называется транспонированной к матрице
A,
если строки матрицы A
заменены соответствующими столбцами
матрицы B,
т.е. при транспонировании строки и
столбцы меняются местами.
А3×2
=

7.
Свойства операций.
1.
Коммутативность (переместительный
закон)
A
+ B
= B
+ A;
т. е. сумма матриц коммутативна.
A
× BB
× A;
т. е. произведение не коммутативно.
2.
Ассоциативность (сочетательный закон)
A
+ (B
+ С) = (A
+ B)
+ С;
A
× (B
× С) = (A
× B)
× С;
3.
Дистрибутивность (распределительный
закон)
(A
+ B) × С
= A×C + B×C;
4.
A × E = A.
ЛЕКЦИЯ
№ 2.
Вопрос
1. Определители квадратных матриц и
способы их вычисления.
Определителем
квадратной матрицы называется число,
характеризующее эту матрицу.
Определители
обозначаются двумя вертикальными
чертами:
│A│
или ∆ (дельта).
Определителем
первого порядка квадратной матрицы
первого порядка A
= (а11)
называется число,
равное элементу этой матрицы.
│а11│=
а11.
Определителем
второго порядка квадратной матрицы A
=

вычисляемое по формуле:
Пример:

– 3 × 7 – 6 × (– 5) = – 21+30 = 9.
Определителем
третьего порядка квадратной матрицы
третьего порядка называется число,
вычисляемое по формуле:
Правило
Сарруса (правило треугольника).
Пример
1:

–
2×1×
(–5)
+ 5×4×(–
4)
+ 3×2×(–
3)
–
(–
3)
×1× (–
4)
–
4×2×
(–
2)
–
5×3 × (–
5)
= 10 –
80
–18
–12
+16 +75 = –
9.
Пример
2:

45 + 8 ‒ 24 ‒ 60 + 6 ‒ 24 = ‒ 49.
Минором
Mij
элемента aijквадратной
матрицы n
‒ го порядка называется определитель
(n
‒ 1) ‒ го порядка, полученный из данной
матрицы вычеркиванием i
‒ й
строки и j
‒ го
столбца, на пересечении которых стоит
данный элемент.
Пример:

M11
=
= 15 + 2 = 17;
M12
=
= –
6
–
6
= –12;
и т. д. всего 9 миноров.
Алгебраическим
дополнением Aijэлемента
aij
квадратной матрицы называется его
минор,
взятый со знаком (‒1)i+j.
Пример:
А
11 =
(–1)1+1
×
M11
=
17.
А
12 =
(–1)1+2
×
M12
=
‒ 1×M12
= 12.
А
13 =
(–1)1+3
×

4 ‒ 30= – 26; и т.д.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

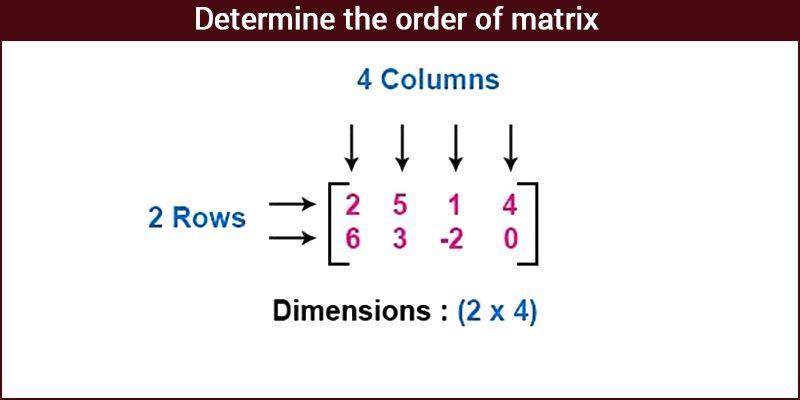

 Найти ранг матрицы
Найти ранг матрицы

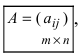
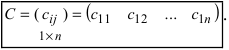
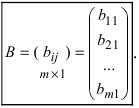
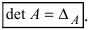


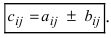
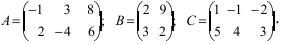
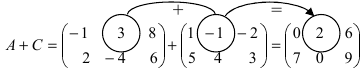
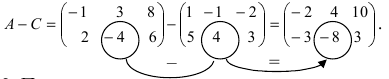

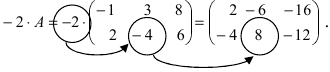
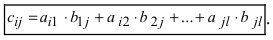
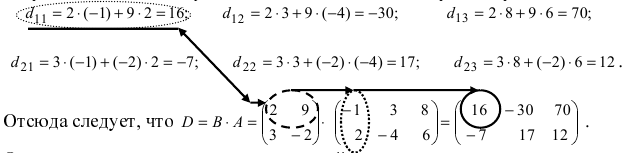
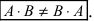
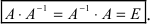
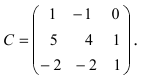
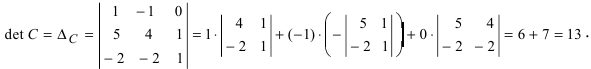
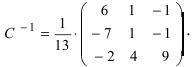
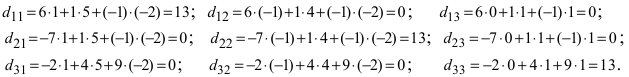
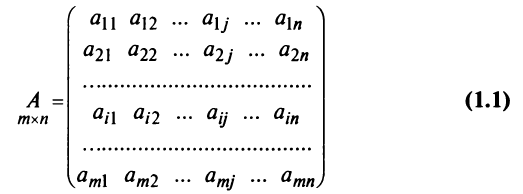
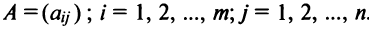

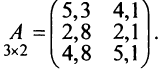
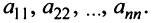

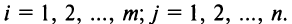
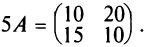
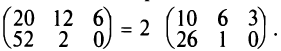
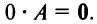
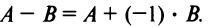
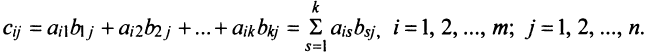
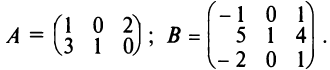
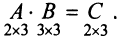
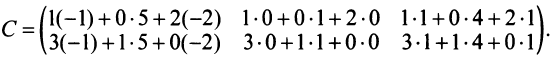
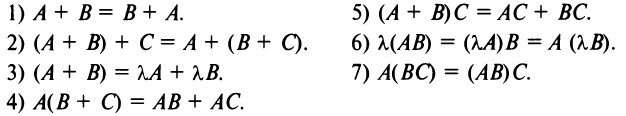
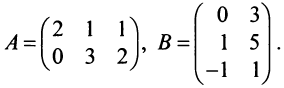
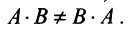
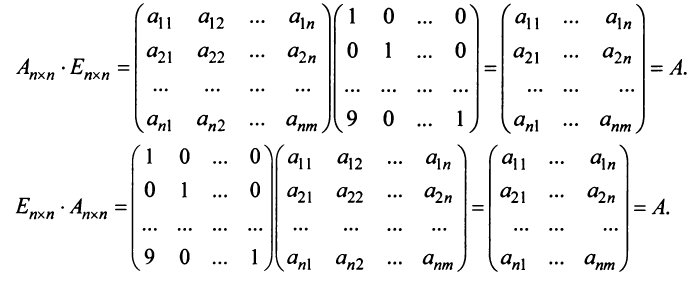
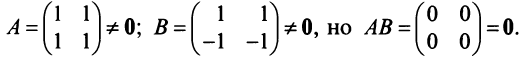
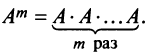
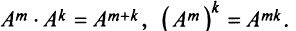
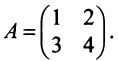
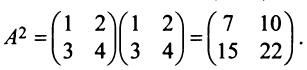

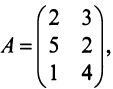
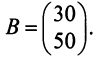
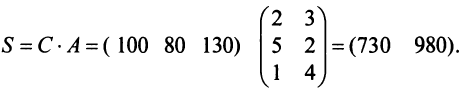

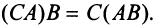

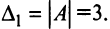
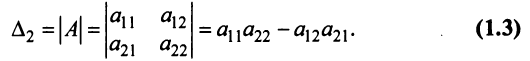
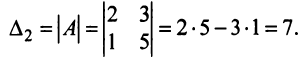
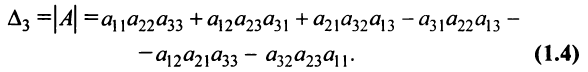

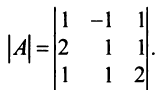



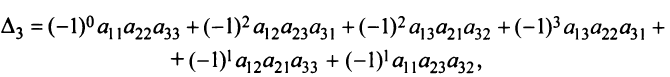
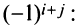

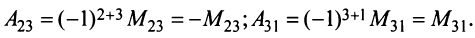
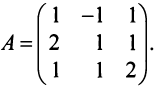
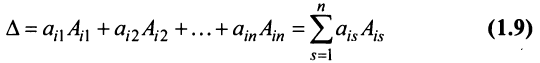
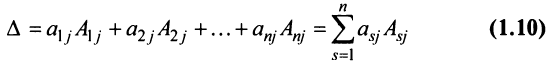
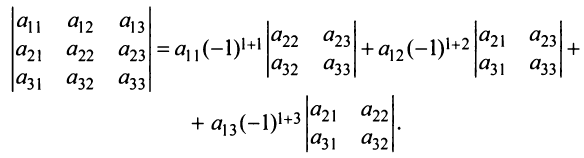

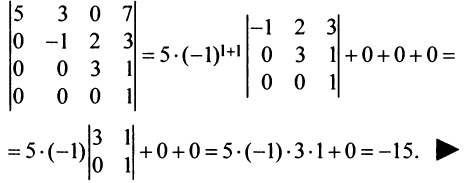
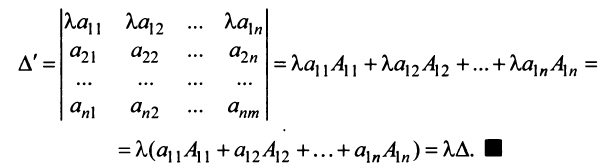
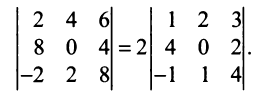
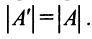
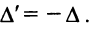

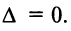
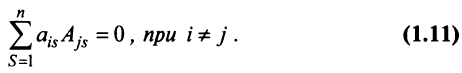
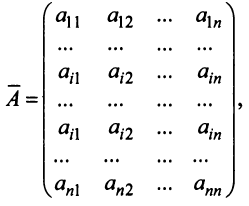
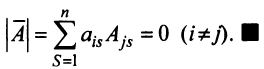
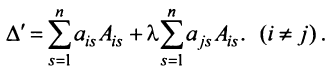
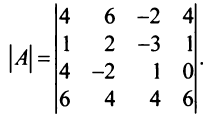
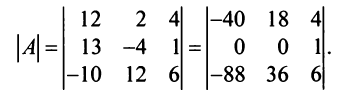
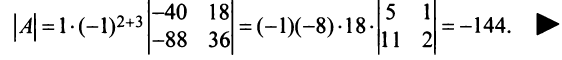

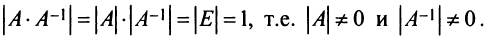
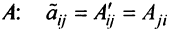
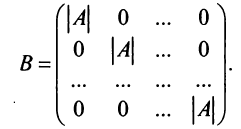
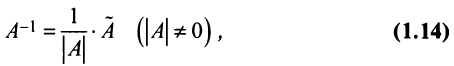
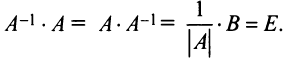

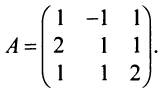
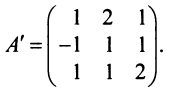
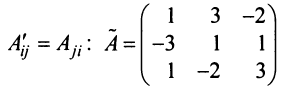
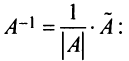
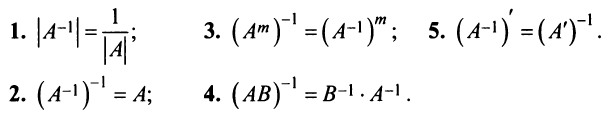
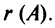
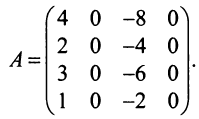

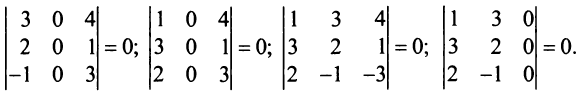

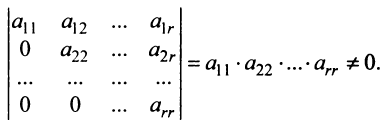
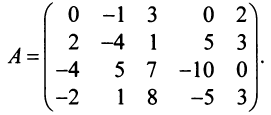
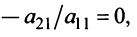
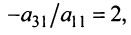
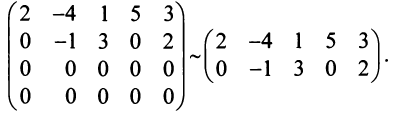

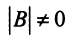
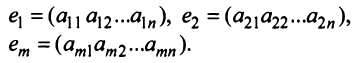
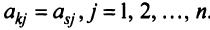
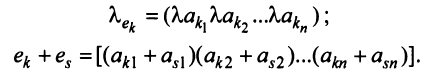
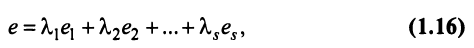
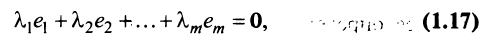
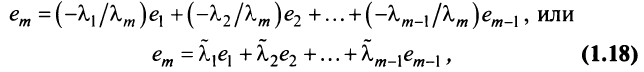
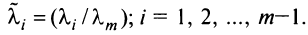

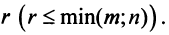

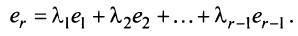


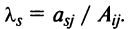
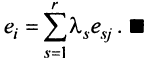
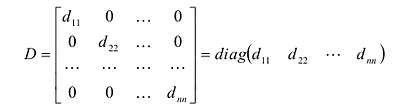
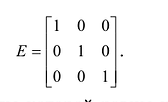
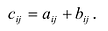
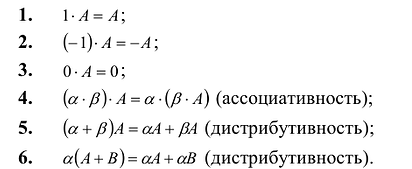
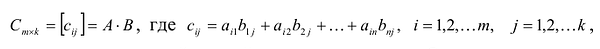
 В)- С = А
В)- С = А  (В
(В  С) — ассоциативность умножения;
С) — ассоциативность умножения;
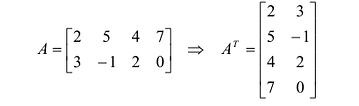
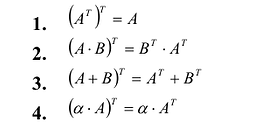
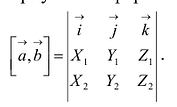
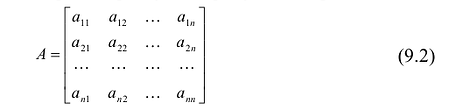
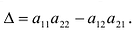
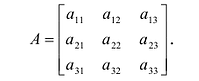
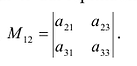
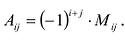
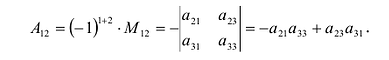
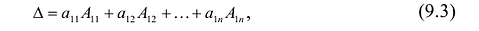
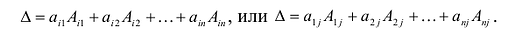
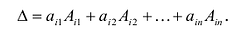
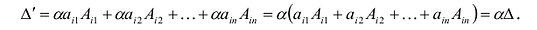
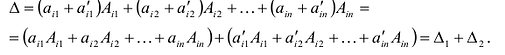

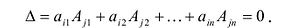
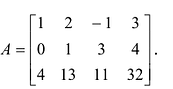
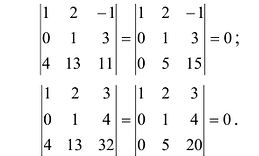

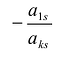 и т.д.;
и т.д.;

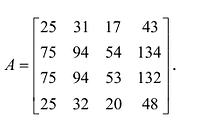


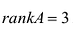
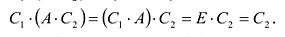
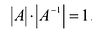
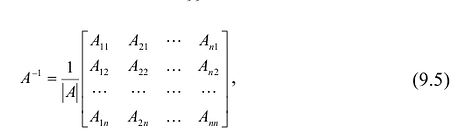
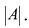

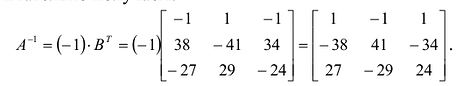
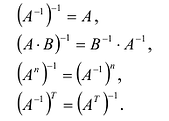


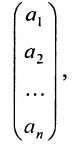
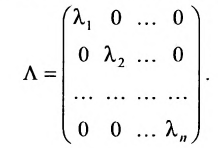
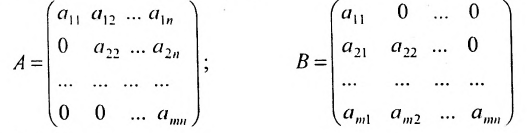

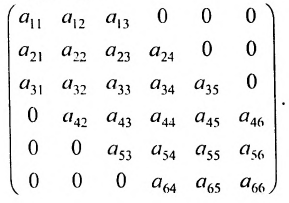
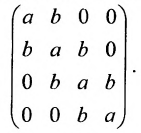




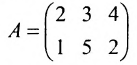

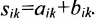
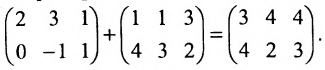
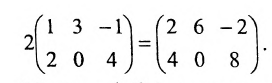
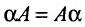 .
.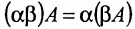 .
.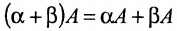 .
.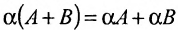 .
.