Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
порядок касания кривых и каков его геометрический смысл?
|
|
01/12/11 |
Объясните, пожалуйста, доходчиво, что такое порядок касания . Заранее благодарна! З. Ы.
|
|
|
|
|
ИСН |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
18/05/06 |
Обычно это объясняют на примере рельсов. Порядки выше второго, впрочем, не отличить ни глазом, ни на ощупь. Бесконечный порядок возможен, но вряд ли кому нужен.
|
||
|
|
|||
|
Ktina |
Re: Что такое порядок касания и каков его геометрический смысл?
|
|
01/12/11 |
Обычно это объясняют на примере рельсов.
|
|
|
|
|
nnosipov |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
20/12/10 |
Может ли он быть бесконечным для двух несовпадающих кривых? Вот стандартный пример:
|
||
|
|
|||
|
wallflower |
Re: Что такое порядок касания и каков его геометрический смысл?
|
|
24/12/11 |
|
|
|
|
|
Padawan |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
13/12/05 |
И ещё, где вся эта канитель применяется? Я лично применял эту канитель для вывода условий, при которых кривая, заданная кривизной и кручением, лежит на сфере. Вот в этой теме кривая на сфере.
|
||
|
|
|||
|
ИСН |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
18/05/06 |
Про дороги — ну вот topic41983.html — Ср, 2012-03-21, 20:03 — там говорят про «скачок кривизны», а не «порядок касания», но суть та же.
|
||
|
|
|||
|
svv |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
23/07/08 |
Пособие «Как определить порядок касания с помощью WolframAlpha (Maple, MathCAD, Mathematica, MATLAB, …)». Даны функции Пример. Определить порядок касания кривых
Ответ: касание третьего порядка.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
1.Понятие кривизны и ее вычисление.
Рассмотрим концентрические
окружности. Будем определять кривизну
окружности радиуса Rкак величину k=1/R.
Центром кривизны назовем центр окружности,
а ее радиус – радиусом кривизны. Обобщим
эти понятия на произвольную гладкую
кривую. Рассмотрим гладкую кривую с
параметризацией x(t),y(t),для
краткости будем использовать обозначения:
x0=x(t0),x=x(t),y0=y(t0),y=y(t),u0=x(t0),u=x(t),v0=y(t0),v=y(t).
В процессе рассмотрения
t0будет
фиксирована, а t
будет рассматриваться, как текущая
точка. Составим уравнения нормалей в
точках (x0,y0),
(x,y).

.
Найдем точку пересечения этих прямых.

Умножим первое
уравнение на u,
а второе на –vи
сложим.
(uv0 -vu0)p=u(x0-x)
+v(y0–y)откуда
.
Далее перейдем к
пределу при tt0(uu0,vv0).Получим
.
Подставляя найденной значение параметра
для предельной точки пересечения
нормалей, получим координаты предельной
точки
,
.
Полученная таким образом точка называется
центром кривизны кривой в заданной
точке, а расстояние от этой точки до
центра кривизны называется радиусом
кривизны.
.
Величина обратная радиусу кривизны
называется кривизной
.
Окружность с центром
в (X0,Y0)и радиуса R0называется
соприкасающейся окружностью.
2.Выражение центра и радиуса кривизны для явно заданной кривой.
Рассмотрим кривую , заданную в виде y=f(x),x[a,b].В качестве
параметризации выберем x=t,y=f(t),t[a,b].Тогда
,
,
.
3.Порядок соприкосновения кривых.
Пусть 1,2представлены
функциями y=f1(x),y=f2(x)и пересекаются
в точке (x0,y0).Кривые
1,2имеют порядок
соприкосновения nв точке (x0,y0),если
,
для всех k=0,1,…,n,и
.
Достаточными условиями
для того, чтобы кривые имели порядок
касания nявляются
следующие условия:
Функции n+1непрерывно
дифференцируемы в окрестности точки
x0и
,
k=0,…,n,
.
Для доказательства
обозначим f(x)=f2(x)
-f1(x).Тогда в окрестности
точки x0имеет
место разложение по формуле Тейлора с
остатком в форме Лагранжа
,
тогда

k=0,1,…,n+1.
Таким образом, будут выполнены условия
из определения порядка касания.
Ответ.
80
Конспект лекций
Логинов А.С. ЭТФ 1 семестр loginov_1999@mail.ru
Соседние файлы в папке ma
- #
- #
- #
- #
- #
- #
Касание
Касание — свойство двух линий или линии и поверхности иметь в некоторой точке общую касательную прямую или свойство двух поверхностей иметь в некоторой точке общую касательную плоскость.
Точка в которой две геометрические фигуры имеют касание, называется точкой касания или точкой соприкосновения.
Порядок касания
Порядок касания является характеристикой близости двух линий, линии и поверхности или двух поверхностей в окрестности их общей точки.
Связанные определения
См. также
- Дифференциальная геометрия кривых
Соприкасающиеся плоскости и окружности
Говорят, что кривые (y = fleft( x right)) и (y = gleft( x right)) имеют в точке (left( <,> right)) касание (n)-го порядка , если выполняются следующие условия: [ > right) = gleft( <> right),>;; > right) = g’left( <> right),>;; > right) = g»left( <> right),;ldots,;> <>left( <> right) = >left( <> right),>;; <right)>>left( <> right) ne right)>>left( <> right).> ] В частности, если (n = 1,) то кривые (y = fleft( x right)) и (y = gleft( x right)) имеют общую касательную .
Случай (n = 0) означает, что кривые имеют общую точку (left( <,> right):) (fleft( <> right) = gleft( <> right),) но их первые производные при этом не совпадают: (f’left( <> right) ne g’left( <> right).) В этом случае кривые просто пересекаются в точке (.)
Можно рассмотреть разность функций (varphi left( x right) = gleft( x right) — fleft( x right)) в окрестности точки () и разложить ее в ряд Тейлора с остаточным членом в форме Пеано. Если кривые (gleft( x right)) и (fleft( x right)) имеют порядок касания (n,) то первые (n) членов ряда равны нулю и разность (varphi left( x right)) представляется в виде [ <varphi left( x right) = frac<<<varphi ^<left( right)>>left( <> right) + alpha >> <<left( right)!>><left( > right)^> > = <frac<<right)>>left( <> right) — right)>>left( <> right) + alpha >> <<left( right)!>><left( > right)^>,> ] т.е. пропорциональна (<left( > right)^>.) Следовательно, при четном значении (n) разность (varphi left( x right)) имеет разные знаки слева и справа от точки касания (,) т.е. в этом случае кривые пересекаются в точке (.) Частный случай (n = 0) рассмотрен выше.
При нечетном (n) кривые (y = fleft( x right)) и (y = gleft( x right)) касаются друг друга в точке () без взаимного пересечения.
Рассмотрим следующую задачу. Дано уравнение кривой (y = fleft( x right)) и семейство кривых [Gleft( right) = 0] с (n + 1) параметрами (.) Требуется, изменяя значения параметров, выбрать из данного семейства такую кривую, которая с кривой (y = fleft( x right)) в точке (left( <,> right)) имела бы наивысший возможный порядок касания. Такая кривая будет называться соприкасающейся кривой .
Введем обозначение [Phi left( right) = Gleft( right).] Условия касания записываются в виде: [left< begin Phi left( <,a,b, ldots ,ell> right) = 0\ <Phi’_x>left( <,a,b, ldots ,ell> right) = 0\ <Phi»_>left( <,a,b, ldots ,ell> right) = 0\ cdots cdots cdots cdots cdots cdots cdots \ Phi _<>^<left( n right)>left( <,a,b, ldots ,ell> right) = 0 end right..] В результате мы получаем систему из (n + 1) уравнений с (n + 1) неизвестными значениями параметров. Решая эту систему, находим параметры () и уравнение соприкасающейся кривой. Обычно ее порядок касания будет не ниже, чем (n) (в случае (n + 1) параметров). Таким образом, порядок касания соприкасающейся кривой, как правило, на единицу меньше числа параметров.
Выведем уравнение соприкасающейся окружности. Пусть задана функция (y = fleft( x right),) которая является по меньшей мере дважды дифференцируемой. Семейство окружностей описывается уравнением [ <left( right)^2> + <left( right)^2> = .] Как видно, здесь мы имеем дело с тремя параметрами − координатами центра окружности (a, b) и ее радиусом (R.) Ясно, что в данном случае максимально возможный порядок касания равен (2.)
Будем считать, что парабола задана уравнением (y = gleft( x right) = a + bx + c.) Данная функция содержит (3) параметра. Поэтому можно предположить, что порядок касания кривых равен (2.) Тогда коэффициенты (a, b, c) находятся из следующих условий: [left< begin fleft( <> right) = gleft( <> right)\ f’left( <> right) = g’left( <> right)\ f»left( <> right) = g»left( <> right) end right..] Производные функций (fleft( x right) = ) и (gleft( x right) = a + bx + c) выражаются формулами [ > right)^prime > = ,>;;; > right)^prime > = ;> ] [ + bx + c> right)^prime > = 2ax + b,>;;; right)^prime > = 2a.> ] Тогда система уравнений принимает такой вид: [left< begin >> = ax_0^2 + b + c\ >> = 2a + b\ >> = 2a end right..] Подставляя ( = 0,) получаем: [ left< begin c = 1\ b = 1\ 2a = 1 end right. ;;text<или>;; left< begin a = frac<1><2>\ b = 1\ c = 1 end right.. ] Итак, парабола, соприкасающаяся с экспоненциальной функцией в точке ( = 0,) имеет второй порядок касания и определяется формулой [y = frac<<>> <2>+ x + 1.] Если записать ее уравнение в виде [ >> <2>+ x + 1 > = <frac<1><2>left( <+ 2x> right) + 1 > = <frac<1><2>left( <+ 2x + 1 — 1> right) + 1 > = <frac<1><2> <left( right)^2> + frac<1><2>,> ] то видно, что вершина параболы находится в точке (left( < — 1,largefrac<1><2>normalsize> right).) Схематически обе соприкасающиеся кривые показаны на рисунке (2.)
Полагая, что семейство парабол является трехпараметрическим, т.е. описывается уравнением [y = a + bx + c] с тремя параметрами (a, b) и (c,) введем функцию [Phi left( right) = a + bx + c — fleft( x right)] и запишем условие касания в точке () в виде [left< begin Phi left( <,a,b,c> right) = 0\ <Phi ‘_x>left( <,a,b,c> right) = 0\ <Phi »_>left( <,a,b,c> right) = 0 end right..] В нашем случае (fleft( x right) = cos x.) Следовательно, [ right)^prime > = — sin x,>;;; right)^prime > = — cos x.> ] В результате имеем следующую систему для определения коэффициентов (a, b, c:) [left< begin ax_0^2 + b + c — cos = 0\ 2a + b + sin = 0\ 2a + cos = 0 end right..] Подставляя ( = 0,) получаем: [left< begin c — 1 = 0\ b = 0\ 2a + 1 = 0 end right.,;; Rightarrow left< begin a = — frac<1><2>\ b = 0\ c = 1 end right..] Таким образом, парабола, соприкасающаяся с функцией косинус в точке ( = 0,) описывается уравнением [y = — frac<<>> <2>+ 1.] Как видно, это уравнение соответствует первым двум членам разложения косинуса в ряд Маклорена .
Здесь мы имеем дело с семейством функций, содержащих (4) параметра. Следовательно, наивысший возможный порядок касания кривых равен (3.) Для определения коэфициентов (a, b, c) и (d) запишем следующие условия касания: [left< begin fleft( <> right) = gleft( <> right)\ f’left( <> right) = g’left( <> right)\ f»left( <> right) = g»left( <> right)\ f»’left( <> right) = g»’left( <> right) end right..] Производные кубической функции имеют такой вид: [g’left( x right) = <left( + b + cx + d> right)^prime > = 3a + 2bx + c,] [g»left( x right) = <left( <3a+ 2bx + c> right)^prime > = 6ax + 2b,] [g»’left( x right) = <left( <6ax + 2b>right)^prime > = 6a.] Вычислим производные тангенса: [f’left( x right) = <left( <tan x>right)^prime > = frac<1><<<<cos >^2>x>>,] [ <<<<cos >^2>x>>> right)^prime > > = <<left[ <<<left( <cos x>right)>^< — 2>>> right]^prime > > = < — 2<left( <cos x>right)^< — 3>> cdot left( < — sin x>right) > = <frac<<2sin x>><<<<cos >^3>x>>,> ] [ ><<<<cos >^3>x>>> right)^prime > > = <frac<<<<left( <2sin x>right)>^prime ><<cos >^3>x — 2sin x<<left( <<<cos >^3>x> right)>^prime >>><<<<cos >^6>x>> > = <frac<<2,cos x,<<cos >^3>x — 2sin x cdot 3,<<cos >^2>x cdot left( < — sin x>right)>><<<<cos >^6>x>> > = <frac<<2,<<cos >^3>x + 6,<<sin >^2>x,<<cos >^2>x>><<<<cos >^6>x>> > = <frac<<<<cos >^2>xleft( <2,<<cos >^2>x + 2,<<sin >^2>x + 4,<<sin >^2>x> right)>><<<<cos >^6>x>> > = <frac<<2 + 4,<<sin >^2>x>><<<<cos >^4>x>>.> ] Тогда система уравнений принимает вид: [left< begin tan = ax_0^3 + bx_0^2 + c + d\ frac<1><<<<cos >^2>>> = 3ax_0^2 + 2b + c\ frac<<2sin >><<<<cos >^3>>> = 6a + 2b\ frac<<2 + 4<<sin >^2>>><<<<cos >^4>>> = 6a end right..] Подставляя значение ( = 0,) получаем: [left< begin d = 0\ c = 1\ 2b = 0\ 6a = 2 end right.,;; Rightarrow left< begin a = frac<1><3>\ b = 0\ c = 1\ d = 0 end right..] Таким образом, соприкасающаяся кубическая функция записывается как [y = frac<<>> <3>+ x.] Данная кривая имеет третий порядок касания с кривой тангенса в начале координат.
Заметим, что найденная кубическая функция представляет собой разложение тангенса в ряд Маклорена до третьего порядка.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end
Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.
Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).
Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:
Если расписать покоординатно, то получим следующее уравнение:
begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:
Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$
Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end
begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end
begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$
— правая). Изменим направление одного из векторов. Например, пусть
Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end
begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.
Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через касательную и главную нормаль в данной точке кривой, называют соприкасающейся плоскостью.
Отсюда и из определения главной нормали следует, что соприкасающаяся плоскость определена для точек кривой, в которых кривизна (kneq 0).
Если гладкая кривая (Gamma=<textbf=textbf(t),;alphaleq tleqbeta>) дважды дифференцируема и ее кривизна в точке (M_<0>=M(t_<0>)) не равна нулю, то уравнение соприкасающейся плоскости (Q) в точке (M_<0>) имеет вид
$$
(r-r(t_0),r'(t_0),r″(t_0))=0.label
$$
(circ) Если (s=s(t)) — переменная длина дуги кривой (Gamma), то дифференцируя (r(t)) как сложную функцию и используя эту и эту формулы, получаем
$$
textbf_’=textbf_’s_’=s_’tau,quad textbf_″=frac
$$
где индексы указывают, по каким переменным производится дифференцирование. Отсюда следует, что векторы (textbf_’) и (textbf_″) параллельны плоскости (Q). По условию (kneq 0), и поэтому ([textbf_’,textbf_″]neq 0). Следовательно, векторы (textbf_’) и (textbf_″) не коллинеарны.
Рис. 22.8
Так как векторы (textbf-textbf(t_<0>), textbf'(t_<0>)=textbf_'(t_<0>), textbf″(t_0)=textbf_″(t_<0>)) параллельны плоскости (Q) (рис. 22.8), то их смешанное произведение равно нулю, то есть во всех точках плоскости (Q) (и только в этих точках) должно выполняться условие eqref. (bullet)
Запишем уравнение eqref в координатной форме:
$$
beginx-x(t_0)&y-y(t_0)&z-z(t_0)\x'(t_0)&y'(t_0)&z'(t_0)\x″(t_0)&y″(t_0)&z″(t_0)end=0nonumber
$$
http://vmath.ru/vf5/diffgeom/seminar1
http://univerlib.com/mathematical_analysis/derivative/osculating_plane/
Тогда получатся тождества относительноxm+1 , …, xn :F1 (ϕ1 , …, ϕm , xm+1 , …, xn ) = 0, …, Fm (ϕ1 , …, ϕm , xm+1 , …, xn ) = 0.4. Условный экстремум93Дифференцируя эти тождества в точке M0 и используя инвариантность формы первого дифференциала, приходим к равенствам⎧∂F∂F11⎪(M)dϕ+…+(M)dϕ +⎪m100⎪∂x∂x⎪1mMM0⎪0⎪⎪∂F1∂F1⎪⎪(M)dx+…+(M0 ) dxn = 0,+⎪m+10⎨∂x1∂xn. . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . .⎪∂Fm∂Fm⎪⎪⎪(M(M)dϕ+…+)dϕ +m100⎪⎪∂x∂x1mMM0⎪0⎪⎪∂F∂F⎪⎩+ m (M0 ) dxm+1 + … + m (M0 ) dxn = 0.∂x1(10.52)∂xnЭти равенства представляют собой системуурав m линейныхнений относительно дифференциалов dϕ1 M , …, dϕm M , причем0 0D (F1 , …, Fm ) определитель системы равен якобиану, отличD (x1 , …, xm ) M0ному от нуля в силу (10.40).Следовательно, из этой системы однозначно находятся искомые дифференциалы dϕi M (i = 1, …, m), как функции от0dxm+1 , …, dxn . Подставляя выражения для dϕi вместо dxiM0(i = 1, …, m) в формулу (10.51), получаем искомую квадратичную формуd2 g M = Q (dxm+1 , …, dxn ) .(10.53)0Пример.
Найдем экстремумы функции u = x + y при условиисвязи xy − 1 = 0.В данном случае для решения задачи можно было бы использовать первый метод, поскольку из условия связи можно выразить в явном виде один из аргументов функции через другой (на1пример, y = ), после чего задача сводится к отысканию точекx1безусловного экстремума функции одной переменной u = x +x(решите задачу этим методом), но мы применим для решенияметод Лагранжа.Введем функцию ЛагранжаΦ = x + y + λ(xy − 1),94Гл.
10. Неявные функциигде λ — пока не определенный множитель, и составим системууравнений (10.49), которая в нашем примере имеет вид⎧F1 := xy − 1 = 0,⎪⎪⎪⎨ ∂Φ= 1 + λy = 0,∂x⎪⎪∂Φ⎪⎩= 1 + λx = 0.∂yЭта система имеет два решения:x = 1, y = 1, λ = −1иx = −1, y = −1, λ = 1.Таким образом, имеем две точки возможного условного экстремума функции u = x + y при условии связи xy − 1 = 0:точка M1 (1; 1), при этом Φ = x + y − (xy − 1), иточка M2 (−1; −1), при этом Φ = x + y + (xy − 1).Далее в соответствии с описанным алгоритмом вычислимвторой дифференциал функции Лагранжа, причем так, как еслибы x и y были независимыми переменными.
Для точки M1 (1; 1)имеем:dΦ = dx + dy − ydx − xdy ,d2 Φ = −2dxdy.Выразим теперь dy через dx, используя условие связи F1 := xy −− 1 = 0. Система уравнений (10.52) состоит в нашем примере изодного уравнения:∂F1∂F(M1 ) · dx + 1 (M1 ) · dy = 0, то есть dx + dy = 0,∂x∂yоткуда dy = −dx. Подставляя это выражение для dy в равенствоd2 Φ = −2dxdy , находим квадратичную форму Q (см. (10.53)):d2 g x=1 = Q(dx) = 2(dx)2 .Так как Q(dx) — положительно определенная квадратичная форма, то в точке M1 (1; 1) функция u = x + y имеет условныйминимум (u (M1 ) = 2) при условии связи xy − 1 = 0.Аналогично доказывается, что в точке M2 (−1; −1) функцияu = x + y имеет условный максимум (u (M2 ) = −2) при условиисвязи xy − 1 = 0 (проведите доказательство самостоятельно).Рассмотренный пример имеет наглядную геометрическую иллюстрацию.
Линиями уровня функции u = x + y (то есть лини-4. Условный экстремум95Рис. 10.5.ями на плоскости (x, y), на которых функция имеет постоянноезначение) являются прямые x + y = c = const, а условие связиxy − 1 = 0 является уравнением гиперболы. На рис. 10.5 изображены линии уровня для нескольких значений c (c < −2, c = −2,c = 0, c = 2, c > 2) и гипербола xy − 1 = 0, в точках которойищутся экстремумы функции u = x + y .Через точку M1 (1; 1) гиперболы проходит линия уровняx + y = 2, а через любую другую точку гиперболы в окрестноститочки M1 проходит линия уровня x + y = c, где c > 2.
Такимобразом, в точке M1 функция u = x + y имеет наименьшеезначение (u (M1 ) = 2) по отношению ко всем другим точкамгиперболы из окрестности точки M1 (разумеется, окрестностьточки M1 должна быть не слишком большой, чтобы в нее непопали точки другой ветви гиперболы).Также наглядно видно, что в точке M2 (−1; −1), через которую проходит линия уровня x + y = −2, функция u = x + yимеет наибольшее значение (u (M2 ) = −2) по отношению ко всемдругим точкам гиперболы из окрестности точки M2 .Г л а в а 11ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГОИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ПЛОСКИХКРИВЫХС помощью дифференциального исчисления мы умеем находить точки локального экстремума функции, промежутки монотонности, направление выпуклости, точки перегиба и асимптотыграфиков функций.
Здесь мы рассмотрим применение дифференциального исчисления к другим геометрическим вопросам: касание плоских кривых, огибающая семейства кривых, кривизнаплоской кривой.§ 1. Касание плоских кривыхРис. 11.1. Прямая L —общая касательная ккривым L1 и L2 в точке M0 .Если две плоские кривые имеют общую точку M0 и в этой точке — общуюкасательную, то говорят, что эти кривыекасаются (соприкасаются) в точке M0(рис.
11.1).Пусть кривые L1 и L2 являются графиками функций y = f1 (x) и y = f2 (x), ипусть они касаются в точке M0 (x0 , f1 (x0 ))(рис. 11.2). Пусть n — натуральное число.Рис. 11.2.Говорят, что порядок касания кривых L1 и L2 в точке M0равен n, если существует отличный от нуля пределlimx→x0|f2 (x) − f1 (x)|.|x − x0 |n+1(11.1)1. Касание плоских кривых97Если предел (11.1) равен нулю, то говорят, что порядок касаниякривых L1 и L2 в точке M0 выше n.Если порядок касания выше любого n, то говорят, что порядок касания бесконечный.Примеры.1) Графики функций y = x4 и y = x3 касаются в точке O(0; 0),общей касательной графиков⎧является ось Ox (докажите это).
3x − x4 ⎨ 0, n < 2,Так как lim= 1, n = 2,⎩x→0 |x|n+1∞, n > 2,то порядок касания данных кривых вточке O равен 2.2e−1/x , x = 0,2) Рассмотрим функции y = 0 и y =0,x = 0.Нетрудно доказать (сделайте это), что порядок касания графиковэтих функций в точке O(0; 0) — бесконечный.Теорема 1. Пусть кривые L1 и L2 являются графиками функций y = f1 (x) и y = f2 (x) и пусть функции f1 (x) и f2 (x) (n + 1)раз дифференцируемы в точке x0 . Тогда:10 .
если f1 (x0 ) = f2 (x0 ), f1 (x0 ) = f2 (x0 ), . . . ,(n)(n)(n+1)f1 (x0 ) = f2 (x0 ), f1(n+1)(x0 ) = f2(x0 ),(11.2)то порядок касания кривых L1 и L2 в точке M0 (x0 , f1 (x0 )) равенn;20 . обратно: если порядок касания кривых L1 и L2 в точкеM0 равен n, то выполнены соотношения (11.2).Доказательство. 10 . Пусть выполнены соотношения (11.2). Используя формулу Тейлора и эти соотношения, получаем:f2 (x) − f1 (x) = f2 (x0 ) + · · · +1 (n)f (x0 )(x − x0 )n +n! 21(n+1)f2+(x0 )(x − x0 )n+1 + o (x − x0 )n+1 −(n + 1)!1 (n)− f1 (x0 ) + · · · + f1 (x0 )(x − x0 )n +n!1(n+1)n+1n+1+f(x0 )(x − x0 )+ o (x − x0 )=(n + 1)! 11(n+1)(n+1)=(x0 ) − f1(x0 ) (x − x0 )n+1 + o (x − x0 )n+1 ,f2(n + 1)!1(n+1)(n+1)f2(x0 ) − f1(x0 ) = 0.причем число A =(n + 1)!4 В.Ф.
Бутузов98 Гл. 11. Приложения диф. исчисления к исследованию плоских кривыхОтсюда следует:limx→x0|f2 (x) − f1 (x)|= |A| = 0,|x − x0 |n+1а это и означает, согласно определению, что порядок касаниякривых L1 и L2 в точке M0 равен n. Утверждение 10 доказано.20 . Пусть порядок касания кривых L1 и L2 в точке M0 равенn. Если предположить, что цепочка равенств в (11.2) нарушаетсяпри некотором k n, то получим, в силу доказанного в п.10 , чтопорядок касания кривых L1 и L2 в точке M0 равен k − 1 < n, аесли допустить, что в (11.2) выполняются все равенства и, кроме(n+1)(n+1)того, f1(x0 ) = f2(x0 ), то получим, что порядок касаниявыше n.
И то, и другое противоречит условию. Следовательно,выполнены соотношения (11.2). Теорема доказана.Примеры. 1) Рассмотрим графики функций y = x и y = sin x,они имеют общую точку O(0; 0) (рис. 11.3). В данном примереf1 (x) = x, f2 (x) = sin x. Несложные вычисления (проделайте их)приводят к соотношениям:f1 (0) = f2 (0) = 0, f1 (0) = f2 (0) = 1, f1 (0) = f2 (0) = 0,f1 (0) = 0 = f2 (0) = −1.Отсюда по теореме 1 следует, что порядок касания графиковданных функций в точке O(0; 0) равен 2.2) Пусть криваяL1 является графикомфункции y = f (x), аL2 — касательная кграфику этой функциив точке M0 (x0 , f (x0 )),и пусть существуетf (x0 ).
Докажите, что:если f (x0 ) = 0, тоРис. 11.3.порядок касания кривыхL1 и L2 в точке M0равен 1;если f (x0 ) = 0 и существует f (x0 ), то порядок касания кривыхL1 и L2 в точке M0 не ниже 2.2. Огибающая однопараметрического семейства кривых99§ 2. Огибающая однопараметрического семействакривыхОсобые точки кривыхПусть Oxy — прямоугольная система координат на плоскости.Кривая на плоскости Oxy может быть задана:явно, то есть уравнением вида y = f (x) или x = f (y);неявно, то есть уравнением вида F (x, y) = 0;параметрически, то есть уравнениями x = ϕ(t), y = ψ(t), где t —параметр, принимающий значения из некоторого промежутка.В дальнейшем будем считать, что функции, входящие в уравнения кривых, непрерывно дифференцируемы, то есть имеютнепрерывные производные первого порядка.Пусть кривая L задана неявно уравнением F (x, y) = 0, ипусть точка M0 (x0 , y0 ) ∈ L (то есть F (x0 , y0 ) = 0) и Fx2 (x0 , y0 ) ++ Fy2 (x0 , y0 ) = 0.
Пусть, например, Fy (x0 , y0 ) = 0. Тогда в некоторой окрестности точки M0 в силу теоремы о неявной функциикривая L может быть задана явным уравнением вида y = f (x),причем функция y = f (x) (решение уравнения F (x, y) = 0 относительно y ) дифференцируема и ее производная выражаетсяформулойFx (x, y) f (x) = −(11.3)Fy (x, y)y=f (x)Если же Fx2 (x0 , y0 ) + Fy2 (x0 , y0 ) = 0, то есть Fx (x0 , y0 ) == Fy (x0 , y0 ) = 0, то в окрестности точки M0 (x0 , y0 ) кривая Lможет не иметь явного уравнения.Точку M0 (x0 , y0 ) кривой L, длякоторой Fx2 (x0 , y0 ) + Fy2 (x0 , y0 ) = 0 (== 0) будем называть особой (обыкновенной) точкой этой кривой.Пример. Уравнение x2 − y 2 = 0(здесь F (x, y) = x2 − y 2 ) задаеткривую, состоящую из двух прямых, пересекающихся в точке O(0; 0)(рис.

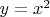 и
и  с одной стороны, и
с одной стороны, и  и
и  и
и  и
и  . Известно, что они касаются в точке
. Известно, что они касаются в точке  , но порядок касания неизвестен, и его надо найти.
, но порядок касания неизвестен, и его надо найти. («микроскоп») в окрестности
(«микроскоп») в окрестности  («порядок увеличения микроскопа»). Последнее значение
(«порядок увеличения микроскопа»). Последнее значение  , при котором функция-микроскоп при
, при котором функция-микроскоп при  и
и  в точке
в точке 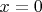 .
. для
для  :
: . При
. При 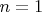 . Глубокий нуль.
. Глубокий нуль.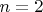 . Нуль.
. Нуль. . Нуль.
. Нуль. . Какое-то конечное число.
. Какое-то конечное число. . Бесконечность.
. Бесконечность.