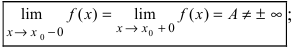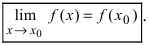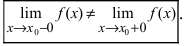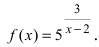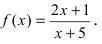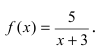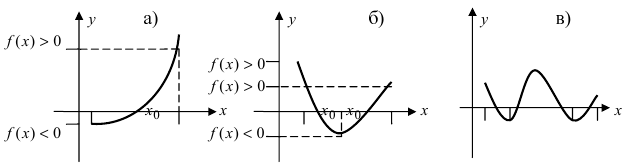Функция f(x) называется непрерывной в точке х = а если:
1) она определена в этой точке;
2) существует предел функции в этой точке
3) значение предела равно значению функции в точке х = а, т.е.
Если одно из условий нарушается то функция называется разрывной в точке х = а, а сама точка х = а называется точкой разрыва. Все элементарные функции являются непрерывными на интервалах определенности.
Классификация точек разрыва
Точка х0 называется точкой разрыва первого рода функции у = f(x) если существуют конечные односторонние пределы справа
и слева
Если, кроме этого, выполняется хотя бы одно из условий
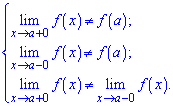
то функция в точке х = а имеет неустранимый разрыв первого рода.
Если пределы равны, однако функция не существует
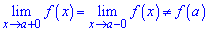
то имеем устранимый разрыв первого рода.
Точка х0 называется точкой разрыва второго рода функции у= f(x) если граница справа 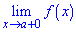
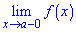
Скачком функции в точке разрыва х = х0 называется разность ее односторонних границ
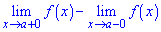
если они разные и не равны бесконечности.
При нахождении точек разрыва функции можно руководствоваться следующими правилами:
1) элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной на определенном интервале.
2) элементарная функция может иметь разрыв в точке где она не определена при условии, что она будет определена хотя бы с одной стороны от этой точки.
3) Неэлементарные функция может иметь разрывы как в точках где она определена, так и в тех где она определена.
Например, если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов, то на границе стыка может быть разрывной.
Рассмотрим несколько задач по данной теме.
Задача 1.
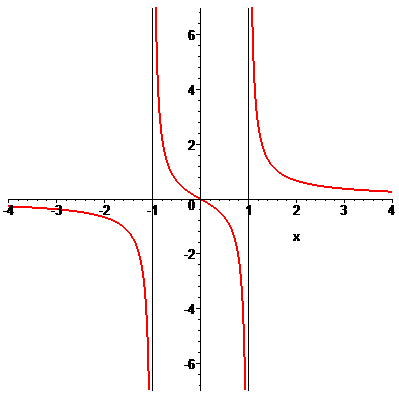
Найти точки разрыва функции
а)
Решение:
Функция определена во всех точках кроме тех где знаменатель обращается в нуль x = 1, x = 1. Область определения функции следующая
Найдем односторонние пределы в точках разрыва
При нахождении односторонних границ подобного вида достаточно убедиться в знаке функции и в том, что знаменатель стремится к нулю. В результате получим границу равную бесконечности или минус бесконечности.
Поскольку в точках x = 1, x = -1 функция имеет бесконечные односторонние пределы, то аргументы 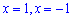
——————————————————-
б)
Решение:
Задача достаточно простая. В первую очередь находим нули знаменателя
Таким образом функция определена на всей действительной оси за исключением точек 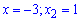
Пределы бесконечны поэтому, по определению, имеем точки разрыва 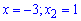
Из графиков приведенных функций видим что для ряда из них отыскания точек разрыва сводится до нахождения вертикальных асимптот. Но бывают функции которые и без вертикальных асимптот имеют разрывы первого или второго рода.
——————————————————-
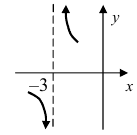
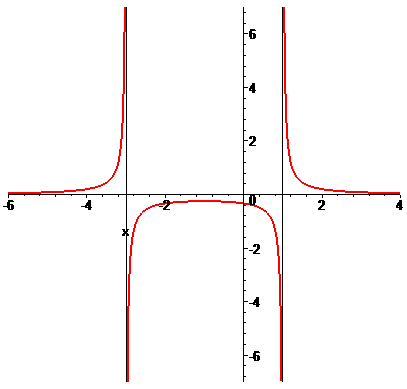
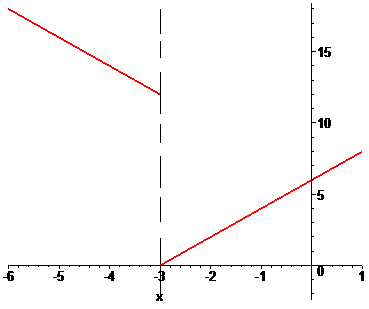
в)
Решение:
Заданная функция непрерывна на всей числовой оси кроме точки x = -3. Вычислим односторонние границы в этой точке
Они различаются по значениям, однако есть конечными. Итак точка x = -3 является неустранимой точкой разрыва І рода.
——————————————————-
Задача 2.
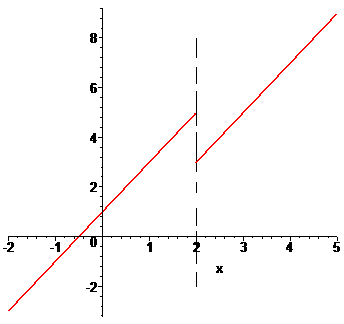
Найти точки разрыва функции если они существуют. Вычислить скачок функции в точке разрыва. Построить график функции.
а)
Решение:
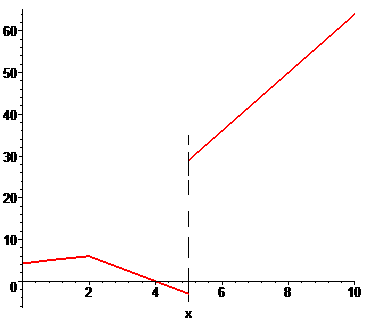
Для заданной функции точка x = 2 является точкой разрыва. Найдем предел функции , чтобы определить характер разрыва
По определению, точка x = 2 является неустранимой точкой разрыва первого рода. Вычислим скачок функции при x=2
График функции на интервале который нас интересует приведен далее
——————————————————-
б)
Решение:
Неэлементарная функция y (x) определена для всех положительных значений аргумента. Точки которые разбивают функцию на интервалы могут быть разрывами. Для проверки найдем соответствующие пределы
Поскольку предел функции в точке x = 2 равен значению функции в этой точке то функция — непрерывная.
Отсюда также следует, что для непрерывной функции скачок равен 6-6 = 0.
Исследуем на непрерывность вторую точку
По определению функция в точке x = 2 имеет неустранимый разрыв І рода.
Прыжок функции равен 29 — (- 3) = 31.
По условию задания построим график функции.
Из приведенного материала Вы должны научиться находить разрывы первого и второго рода, а также различать их. Для этого подобрано немного примеров, которые в полной мере раскрывают все важные вопросы темы. Все остальное сводится к нахождению простых односторонних пределов и не должно быть для Вас сложным.
Точки разрыва функции
Назначение
Сервис предназначен для определения типа точек разрыва функции.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Решение сохраняется в формате MS Word
Классификация точек разрыва
Для точек разрыва принята следующая классификация.
Если в точке имеются конечные пределы, но они не равны
f(x0+0)≠f(x0-0), то x0 называется точкой разрыва первого рода, при этом разрыв называют скачком функции.Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.
Точка x=x0 называется точкой устранимого разрыва, если
f(x0+0)=f(x0-0)≠f(x0). Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) функцию и функция станет непрерывной в точке x0.
см. также Непрерывность функции: основные понятия и свойства (разрывы функции и их классификации с подробными примерами).
Пример №1. Установить непрерывность или определить характер точек разрыва. Нарисовать график функции f(x) в окрестностях этих точек:
Решение. Найдем точки разрыва функции внутри указанной области.
Находим переделы в точке x=1.
В этой точке функция терпит разрыв. Предел равен ∞, поэтому это точка разрыва II-го рода.
Находим переделы в точке x=0
В этой точке функция терпит разрыв. Пределы существуют, но не равны, поэтому это точка разрыва I-го рода.
Ответ: точка x1=1 является точкой разрыва II-го рода, точка x2=0 является точкой разрыва I-го рода.
Пример №2. Найти точки разрыва функции, если они существуют. Сделать чертеж.
Решение. Исследуем точку стыка промежутков x=π/2
В этой точке пределы существуют и они равны, поэтому функция в этой точке непрерывна.
Исследуем поведение функции на отрезке (π/2;π).
Пределы существуют, на указанном промежутке функция непрерывна.
Исследуем точку стыка промежутков x=π
В этой точке пределы существуют, но они разные, поэтому это точка разрыва I-го рода.
Исследуем поведение функции на отрезке (pi;∞).
Пределы существуют, на указанном промежутке функция непрерывна.
Ответ: Точка x=π является точкой разрыва I-го рода.
Пример №3. Найти точки разрыва функции и определить их тип.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Содержание:
- Определение точки разрыва
- Точка разрыва первого рода
- Точка разрыва второго рода
- Точка устранимого разрыва
- Примеры решения задач
Определение точки разрыва
Определение
Точка $a$, в которой нарушено хотя бы одно
из трех условий непрерывности функции, а именно:
- функция $f(x)$ определена в точке и ее окрестности;
- существует конечный предел функции $f(x)$
в точке $a$; - это предел равен значению функции в точке $a$,
т.е. $lim _{x rightarrow a} f(x)=f(a)$
называется точкой разрыва функции.
Пример
Функция $y=sqrt{x}$ не определена в точке
$x=-1$, а значит, эта точка является точкой
разрыва указанной функции.
Точка разрыва первого рода
Определение
Если в точке $a$ существуют конечные
пределы $f(a-0)$ и
$f(a+0)$, такие, что
$f(a-0) neq f(a+0)$, то точка
$a$ называется точкой разрыва первого рода.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Функция $f(x)=left{begin{array}{l}{0, x>1} \ {1, x leq 1}end{array}right.$ в точке
$x=1$ имеет разрыв первого рода, так как
$f(1-0)=1$, а
$f(1+0)=0$
Точка разрыва второго рода
Определение
Если хотя б один из пределов $f(a-0)$ или
$f(a+0)$ не существует или равен бесконечности, то
точка $a$ называется точкой разрыва второго рода.
Пример
Для функции $y=frac{1}{x}$ точка
$x=0$ — точка разрыва второго рода, так как
$f(0-0)=-infty$ .
Точка устранимого разрыва
Определение
Если существуют
левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением
функции $f(x)$ в точке
$a$:
$f(a) neq f(a-0)=f(a+0)$ или функция
$f(x)$ не определена в точке
$a$, то точка
$a$ называется точкой устранимого разрыва.
Пример
Рассмотрим функцию $f(x)=left{begin{array}{l}{3 x+1, x lt 0} \ {1-4 x, x>0} \ {e^{2}, x=0}end{array}right.$ .
Найдем односторонние пределы и значение функции в точке $x=0$:
$f(0)=e^{2}$
$f(0-0)=lim _{x rightarrow 0-} f(x)=lim _{x rightarrow 0-}(3 x+1)=1$
$f(0+0)=lim _{x rightarrow 0+} f(x)=lim _{x rightarrow 0+}(1-4 x)=1$
Так как $f(0-0)=f(0+0)$ и не равны значению функции в
точке, то точка $x=0$ — точка устранимого разрыва.
Примеры решения задач
Пример
Задание. Исследовать функцию $f(x)=left{begin{array}{l}{x^{2}, x lt 1} \ {(x-1)^{2}, 1 leq x leq 2} \ {3-x, x>2}end{array}right.$ на непрерывность.
Решение. Рассматриваемая функция определена и
непрерывна на промежутках
$(-infty ; 1)$,
$(1 ; 2)$ и
$(2 ;+infty)$, на которых она задана непрерывными
элементарными функциями $y_{1}(x)=x^{2}$,
$y_{2}(x)=(x-1)^{2}$ и
$y_{3}(x)=3-x$ соответственно. А тогда, разрыв возможен
только на концах указанных промежутков, то есть в точках
$x=1$ и
$x=2$ .
Найдем односторонние пределы и значение функции в каждой из точек.
1) Рассмотрим точку $x=1$ . Для нее
$f(1)=left.(x-1)^{2}right|_{x=1}=0$
$f(1-0)=lim _{x rightarrow 1-} f(x)=lim _{x rightarrow 1-} y_{1}(x)=lim _{x rightarrow 1-} x^{2}=1$
$f(1+0)=lim _{x rightarrow 1+} f(x)=lim _{x rightarrow 1+} y_{2}(x)=lim _{x rightarrow 1+}(x-1)^{2}=0$
Так как $f(1-0) neq f(1+0)$ , то в точке
$x=1$ функция терпит разрыв первого рода.
2) Для точки $x=2$ имеем:
$f(2)=left.(x-1)^{2}right|_{x=2}=1$
$f(2-0)=lim _{x rightarrow 2-} f(x)=lim _{x rightarrow 2-} y_{2}(x)=lim _{x rightarrow 2-}(x-1)^{2}=1$
$f(2+0)=lim _{x rightarrow 2+} f(x)=lim _{x rightarrow 2+} y_{3}(x)=lim _{x rightarrow 2+}(3-x)=1$
Так как односторонние пределы и значение функции в этой точке равны, то это означает, что в точке
$x=2$ функция непрерывна.
Ответ. В точке $x=1$ функция
терпит разрыв первого рода, а в точке $x=2$ непрерывна.
Пример
Задание. Исследовать функцию $y=e^{frac{1}{x-1}}$
на непрерывность в точках $x_{1}=1$ и
$x_{2}=0$ .
Решение. 1) Исследуем функцию на
непрерывность в точке
$x_{1}=1$:
$f(1-0)=lim _{x rightarrow 1-} e^{frac{1}{x-1}}=e^{-infty}=0$
$f(1+0)=lim _{x rightarrow 1+} e^{frac{1}{x-1}}=e^{+infty}=infty$
Так как один из односторонних пределов бесконечен, то точка $x_{1}=1$
— точка разрыва второго рода.
2) Для точки $x_{2}=0$ получаем:
$f(0-0)=lim _{x rightarrow 0-} e^{frac{1}{x-1}}=e^{-1}=frac{1}{e}$
$f(0+0)=lim _{x rightarrow 0+} e^{frac{1}{x-1}}=e^{-1}=frac{1}{e}$
и значение функции в точке
$f(0)=e^{frac{1}{x-1}}=frac{1}{e}$
Таким образом, в точке $x_{2}=0$ заданная
функция является непрерывной.
Ответ. $x_{1}=1$
— точка разрыва второго рода, а в точке $x_{2}=0$
функция непрерывна.
Читать дальше: основные теоремы о непрерывности функций.
Функция
является непрерывной в некоторой точке
,
если выполняются следующие условия:
Т.е.
предел функции
при стремлении
(слева), равен пределу функции при стремлении
(справа) и равен значению функции в точке
.
Если хотя бы одно из условий нарушается, тогда говорят, что функция
имеет разрыв в точке
.
Все
точки разрыва функции
делят на точки разрыва первого рода и точки разрыва второго рода.
Eсли существуют конечные односторонние пределы
и
, тогда точка
называется точкой разрыва
первого рода.
Точки разрыва первого рода в свою очередь подразделяются на точки устранимого разрыва и скачки.
Если
— является точкой разрыва первого рода и при этом
, точка
называется точкой
устранимого разрыва.
График соответствующей функции приведён на рисунке ниже:
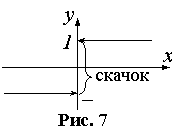
Eсли же
, тогда в точке
.
происходит скачок функции
Величина скачка определяется по формуле
. Соответствующий график приведён на рисунке:
Если хотя бы один из пределов
или
равен
, точка
называется точкой разрыва
второго рода. Пример соответствующего графика функции представлен на рисунке ниже:
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha вычисляет точки разрыва заданной функции с описанием подробного хода решения.
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
- — она определена в этой точке и ее некоторой
-окрестности;
- — существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
— предел функции в точке 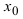
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 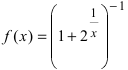
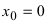
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 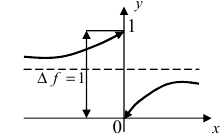
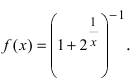
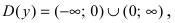
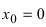
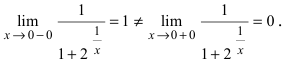
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция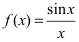
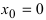
Решение:
В точке 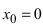
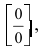
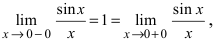
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 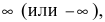
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 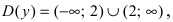
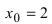
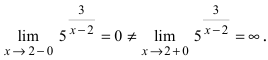
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 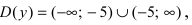
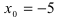
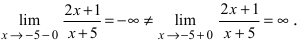
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 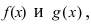
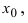
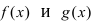
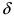
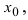
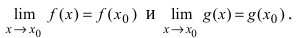
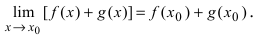
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 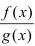
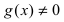
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 
Из рисунка видно, что график функции 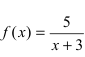
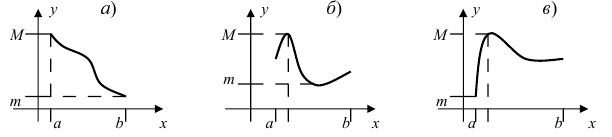
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 
Определение: Замкнутый интервал 
Приведем без доказательства свойства непрерывных функций на сегменте 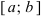
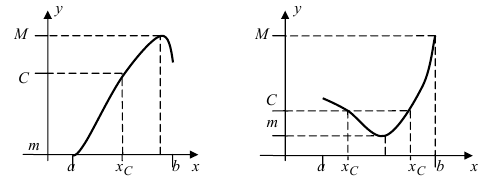
Теорема: Если функция 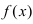
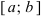
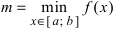
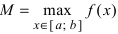
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 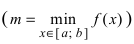
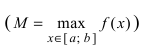
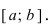
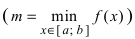
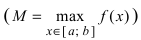
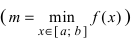
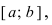
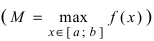
Тб. Если функция 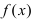
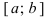
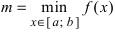
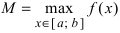
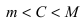
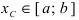
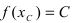
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 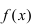
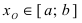
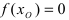
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы

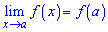
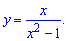
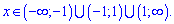
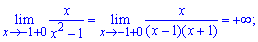
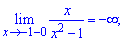
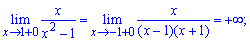
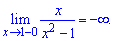
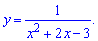
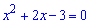
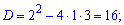
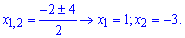
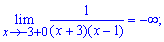
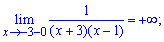
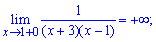
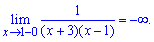
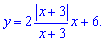
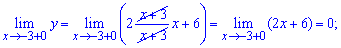
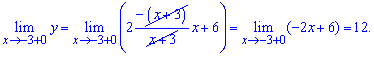
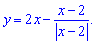
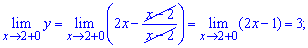
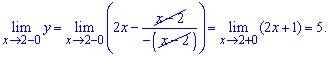
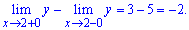
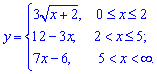
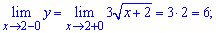
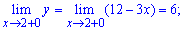
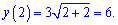
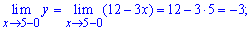
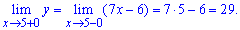
 Если в точке имеются конечные пределы, но они не равны
Если в точке имеются конечные пределы, но они не равны 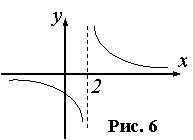 Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.
Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует. Точка x=x0 называется точкой устранимого разрыва, если
Точка x=x0 называется точкой устранимого разрыва, если 
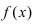
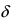 -окрестности;
-окрестности;