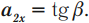Как найти порядок в физике

У этого термина существуют и другие значения, см. Порядок.

Поря́дком в физике называют, как правило, упорядоченное в пространстве расположение объектов, часто атомов или молекул. Более аккуратно можно сказать, что порядок в этом смысле слова — это состояние системы, с достаточной степенью точности инвариантное относительно некоторых определённых сдвигов в пространстве.

При описании строения кристаллического твёрдого тела обычно говорят о позиционном и ориентационном порядке. Позиционный порядок означает, что объекты расположены на более-менее одинаковом расстояния друг относительно друга. Ориентационный порядок означает, что пространственная ориентация объектов скоррелирована.

Порядок различается также по степени охвата системы. Часто говорят о трёх типах порядка:

• дальний порядок означает, что не только соседние, но и сколько угодно удалённые объекты системы находятся в коррелированном состоянии.
• квазидальний порядок означает, что удалённые объекты системы коррелируют, но слабо. Более точно: степень корреляции между удалёнными объектами уменьшается с ростом расстояния между ними очень медленно, по степенному закону с небольшим показателем степени.
• ближний порядок означает, что заметная корреляция есть только между самыми ближайшими соседями. Степень корреляции между удалёнными объектами уменьшается с ростом расстояния экспоненциально быстро.

Примечания

См. также

• Порядок
• Параметр порядка
• Энтропия
• Хаос
• Теория вероятностей

Ссылки

• Хаос и порядок дискретных систем в свете синергетической теории информации

Порядок (физика)

Связанные понятия

Специа́льная тео́рия относи́тельности (СТО; также называемая ча́стная тео́рия относи́тельности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света (в рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей). Фактически СТО описывает геометрию четырёхмерного пространства-времени и базируется на плоском…

Интервал в теории относительности — аналог расстояния между двумя событиями в пространстве-времени, являющийся обобщением евклидового расстояния между двумя точками. Интервал лоренц-инвариантен, то есть не меняется при переходе от одной инерциальной системы отсчёта к другой, и, даже более, является инвариантом (скаляром) в специальной и общей теории относительности.

Динами́ческий ха́ос — явление в теории динамических систем, при котором поведение нелинейной системы выглядит случайным, несмотря на то, что оно определяется детерминистическими законами. В качестве синонима часто используют название детерминированный хаос; оба термина полностью равнозначны и используются для указания на существенное отличие хаоса как предмета научного изучения в синергетике от хаоса в обыденном смысле.

Простра́нство-вре́мя (простра́нственно-временно́й конти́нуум) — физическая модель, дополняющая пространство равноправным временны́м измерением и таким образом создающая теоретико-физическую конструкцию, которая называется пространственно-временным континуумом. Пространство-время непрерывно и с математической точки зрения представляет собой многообразие с лоренцевой метрикой.

Упоминания в литературе

Связанные понятия (продолжение)

Теория катастроф — раздел математики, включающий в себя теорию бифуркаций дифференциальных уравнений (динамических систем) и теорию особенностей гладких отображений.

Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания состояния механической системы. Строгое теоретико-механическое определение: число степеней свободы механической системы есть размерность пространства её состояний с учётом наложенных связей.

Ось вре́мени — философский термин, используемый для краткого именования направленности и необратимости времени. Наглядно иллюстрируется как временна́я ось (именуемая также в контексте термодинамики стрелою времени) — концепция, описывающая время как прямую (то есть математически одномерный объект), протянутую из прошлого в будущее. Из любых двух несовпадающих точек оси времени одна всегда является будущим относительно другой. Выделяют три основные стрелы времени: термодинамическую, космологическую…

Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано…

Электри́ческий ди́польный моме́нт — векторная физическая величина, характеризующая, наряду с суммарным зарядом (и реже используемыми высшими мультипольными моментами), электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ею поля и действия на неё внешних полей. Главная после суммарного заряда и положения системы в целом (её радиус-вектора) характеристика конфигурации зарядов системы при наблюдении её издали.

Время Ляпунова — время, за которое система приводится к полному хаосу. Определяется как число, обратное к наибольшей из экспонент Ляпунова системы. Названо в честь математика А. М. Ляпунова.

Тео́рия ха́оса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных при определённых условиях явлению, известному как хаос (динамический хаос, детерминированный хаос). Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированной. Для акцентирования особого характера изучаемого в рамках этой теории явления обычно принято использовать название теория динамического хаоса.

Одноро́дность простра́нства — одинаковость свойств пространства во всех его точках. Она означает, что нет такой точки в пространстве, относительно которой существует некоторая «выделенная» симметрия, все точки пространства равноправны. Все физические явления в одних и тех же условиях, но в различных местах пространства протекают одинаково.

Переход Костерлица — Таулеса или переход Березинского — Костерлица — Таулеса (БКТ-переход) или топологический фазовый переход — фазовый переход в двумерной XY-модели. Это переход из состояния связанных пар вихрь-антивихрь при низких температурах в состояние с неспаренными вихрями и антивихрями при некоторой критической температуре. Переход назван в честь занимающихся конденсированными средами физиков Вадима Львовича Березинского, Джона М. Костерлица и Дэвида Дж. Таулеса. БКТ-переходы можно наблюдать…

Вре́мя — форма протекания физических и психических процессов, условие возможности изменения. Одно из основных понятий философии и физики, мера длительности существования всех объектов, характеристика последовательной смены их состояний в процессах и самих процессов, изменения и развития, а также одна из координат единого пространства-времени, представления о котором развиваются в теории относительности.

Лоренцево сокращение, Фицджеральдово сокращение, также называемое релятивистское сокращение длины движущегося тела или масштаба — предсказываемый релятивистской кинематикой эффект, заключающийся в том, что с точки зрения наблюдателя, движущиеся относительно него предметы имеют меньшую длину (линейные размеры в направлении движения), чем их собственная длина. Множитель, выражающий кажущееся сжатие размеров, тем сильнее отличается от 1, чем больше скорость движения предмета.

Реше́ние Ке́рра — Нью́мена — точное решение уравнений Эйнштейна, описывающее невозмущённую электрически заряженную вращающуюся чёрную дыру без космологического члена. Астрофизическая значимость решения неясна, так как предполагается, что встречающиеся в природе коллапсары не могут быть существенно электрически заряжены.

Эргодичность — специальное свойство некоторых динамических систем, состоящее в том, что в процессе эволюции почти каждое состояние с определённой вероятностью проходит вблизи любого другого состояния системы.

Теория среднего поля или теория самосогласованного поля — подход к изучению поведения больших и сложных стохастических систем в физике и теории вероятностей через исследование простых моделей. Такие модели рассматривают многочисленные малые компоненты, которые взаимодействуют между собой. Влияние других индивидуальных компонент на заданный объект аппроксимируется усредненным эффектом, благодаря чему задача многих тел сводится к одночастичной задаче.

Многомерное время — гипотезы существования времени с размерностью T > 1. Эти гипотезы имеют определённое распространение в физике, философии и фантастике.

Порядок Шарковского — упорядочение натуральных чисел, связанное с исследованием периодических точек динамических систем на отрезке или на вещественной прямой.

Фазовые переходы второго рода — фазовые переходы, при которых вторые производные термодинамических потенциалов по давлению и температуре изменяются скачкообразно, тогда как их первые производные изменяются постепенно. Отсюда следует, в частности, что энергия и объём вещества при фазовом переходе второго рода не изменяются, но изменяются его теплоёмкость, сжимаемость, различные восприимчивости и т. д.

Сфера Блоха — способ представления чистых состояний кубита в виде точек на сфере.

В квантовой механике, частица в одномерном периодическом потенциале — это идеализированная задача, которая может быть решена точно (при некоторых специального вида потенциалах), без упрощений. Предполагается, что потенциал бесконечен и периодичен, то есть обладает трансляционной симметрией, что, вообще говоря, не выполняется для реальных кристаллов, и всегда существует как минимум один дефект — поверхность (это приводит к другой задаче о поверхностных состояниях или таммовских уровнях).

Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число компонентов, фаз и термодинамических степеней свободы в равновесной термодинамической системе. Роль правила фаз особенно велика при рассмотрении гетерогенных равновесий в многофазных многокомпонентных системах.

Теоре́ма о сложе́нии скоросте́й — одна из теорем кинематики, связывает между собой скорости материальной точки в различных системах отсчёта. Утверждает, что при сложном движении материальной точки её абсолютная скорость равна сумме относительной и переносной скоростей.

При́нцип наиме́ньшего де́йствия Га́мильтона (также просто принцип Гамильтона), точнее при́нцип стациона́рности де́йствия — способ получения уравнений движения физической системы при помощи поиска стационарного (часто — экстремального, обычно, в связи со сложившейся традицией определения знака действия, наименьшего) значения специального функционала — действия. Назван в честь Уильяма Гамильтона, использовавшего этот принцип для построения так называемого гамильтонова формализма в классической механике…

Одноро́дность времени — означает, что все моменты времени равноправны, то есть что если в два любые момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то начиная с этих моментов все явления в ней будут проходить совершенно одинаково. Однородность — одно из ключевых свойств времени в классической механике. Является фундаментальным обобщением опытных фактов.Все известные законы природы, в том числе для живой материи, подтверждают равномерность хода времени. Например…

Макроскопи́ческий масшта́б представляет собой масштаб длины, на котором объекты или процессы имеют размеры, поддающиеся измерению и наблюдению невооруженным глазом.

Говорят, что возникло математическое совпадение, если два выражения дают почти одинаковые значения, хотя теоретически это совпадение никак объяснить нельзя.

Центр масс, центр ине́рции, барице́нтр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр) — (в механике) — геометрическая точка, характеризующая движение тела или системы частиц как целого. В общем случае центр масс не совпадает с центром тяжести, совпадение происходит только у систем материальных точек и тел с однородной по объёму плотностью в однородном гравитационном поле.

Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное соображение (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых, описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного полей). Более доступно он звучит так: чем точнее измеряется одна характеристика частицы, тем менее точно можно измерить вторую…

Пространство состояний — в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение её состояний.

Число Стралера, число Хортона — Стралера или число Стралера — Философова математического дерева — это численная мера сложности ветвления.

Локализация Андерсона, сильная локализация или переход Андерсона — утверждение о том, что в упорядоченном кристалле при определенной величине разброса энергий состояний на определенных узлах решетки все электронные состояния являются локализованными.

Сюрреальные числа (англ. surreal number — название принадлежит американскому математику Дональду Кнуту) впервые были использованы под другим названием («числа» — англ. number) в работах английского математика Джона Конвея для описания ряда аспектов теории игр.

Вселе́нная Фри́дмана (метрика Фридмана — Леметра — Робертсона — Уокера) — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием…

Дихотоми́я (греч. διχοτομία: δῐχῆ, «надвое» + τομή, «деление») — раздвоенность, последовательное деление на две части, более связанные внутри, чем между собой. Способ логического деления класса на подклассы, который состоит в том, что делимое понятие полностью делится на два взаимоисключающих понятия. Дихотомическое деление в математике, философии, логике и лингвистике является способом образования подразделов одного понятия или термина и служит для образования классификации элементов.

Аттра́ктор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Аттрактором может являться притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением о воздух), периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью), или некоторая ограниченная область с неустойчивыми…

Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — длину, ширину и высоту, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.

Элементарный клеточный автомат — это клеточный автомат с одномерным массивом ячеек в форме бесконечной в обе стороны ленты, который имеет два возможных состояния ячеек (0 и 1, «мёртвые» и «живые», «пустые» и «заполненные») и правило для определения состояния ячейки на следующем шаге, использующее только состояние ячейки и её двух соседей на текущем шаге. В целом такие автоматы являются одними из наиболее простых возможных клеточных автоматов, однако при некоторых правилах они показывают сложное поведение…

Циклический порядок — способ расположения множества объектов на окружности. В отличие от большинства структур, в теории порядка циклический порядок не моделируется бинарным отношением, таким как «a < b». Нельзя сказать, что восток «больше по часовой стрелке», чем запад. Вместо этого циклический порядок определяется как тернарное отношение , означающее, что «после a дoстигаем b раньше, чем c». Например, . Тернарное отношение называется циклическим порядком, если оно является циклическим, асимметричным…

Преде́л — одно из основных понятий математического анализа. Различают предел последовательности и предел функции.

Упоминания в литературе (продолжение)

Порядок (физика)

Материал из Большого Справочника

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( S )​ — перемещение тела относительно неподвижной системы отсчета;
​( S_1 )​ — перемещение тела относительно подвижной системы отсчета;
​( S_2 )​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( v )​ — скорость тела относительно неподвижной системы отсчета;
​( v_1 )​ — скорость тела относительно подвижной системы отсчета;
​( v_2 )​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​( alpha )​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​( v )​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​( a )​, единица измерения — м/с².
В векторном виде:

где ​( v )​ – конечная скорость; ​( v_0 )​ – начальная скорость;
​( t )​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​( a_n )​ – нормальное ускорение, ​( a_{tau} )​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ​( v )​ ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​( t )​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​( t )​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

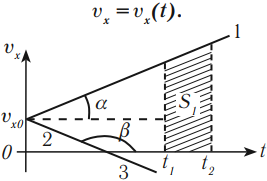
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​( x=x(t) )​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​( a_x )​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​( v_{0x} )​ > 0, ​( a_x )​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​( t_2-t_1 )​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​( n )​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​( g )​, единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​( v_0 )​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​( v )​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​( v_0=v_{0x} )​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​( g )​ и без начальной скорости ​( v_{0y}=0 )​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​( v_0 )​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​( alpha )​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​( a_{цс} )​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​( T )​, единицы измерения – с.

где ​( N )​ – количество оборотов, ​( t )​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​( nu )​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​( v )​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​( omega )​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​( v_1 )​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​( (m) )​ равна нулю, мгновенная скорость в верхней точке ​( (n) )​ равна удвоенной скорости ​( v_1 )​, мгновенная скорость точки ​( (p) )​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​( (c) )​ – по теореме косинусов.

Основные формулы по теме «Кинематика»

Предоставленные сами себе, события
имеют тенденцию развиваться от плохого к худшему
(из законов Мерфи)

Когда я сказал, что в следующий раз мы поговорим либо об эволюции, либо о втором законе термодинамики, я, конечно же, слукавил, потому что уже тогда точно знал, чему будет посвящён следующий выпуск. Но чего не сделаешь, ради красного словца? Раз уж говорил о случайных событиях, о вероятностях, о предсказании будущего, то почему бы и не поиграть в интригу? А ну, угадайте, о чём будет следующая серия? Ставки принимаются.

На самом деле, я уже тогда точно знал, что в следующий раз я буду говорить именно о втором законе термодинамики. Тут может, кто-то спросит, а почему сразу второй? А где же первый? А первый закон термодинамики у нас уже был. Это ни что иное, как закон сохранения энергии в применение к тепловым системам. Есть глобальный закон сохранения, а есть его частный случай – первый закон термодинамики, который говорит о том, что полная энергия тепловой системы остаётся постоянной при любых процессах внутри этой системы. Или ещё есть такая его формулировка, что количество теплоты, полученное системой, идёт на изменение её внутренней энергии и на совершение этой системой работы. Ещё из первого закона (или, как его ещё называют, первого начала) термодинамики следует невозможность вечного двигателя, который бы совершал работу только за счёт своей внутренней энергии, без участия внешних источников.

Что вообще даёт нам первый закон (или первое начало) термодинамики? Он задаёт определённые рамки, в которых могут происходить тепловые процессы. Но и не только тепловые, закон сохранения энергии применим к любым физическим процессам. Есть замкнутая система, и полная энергия этой системы не меняется. Если мы хотим выйти за эти рамки, нам надо разомкнуть систему. Об этом мы уже говорили, затрагивая, в том числе, и процессы экономические. Поэтому на первом законе термодинамики задерживаться больше не будем, перейдём, наконец, ко второму.

У второго закона (или второго начала) термодинамики тоже есть несколько формулировок. Пожалуй, самая короткая из них звучит так: энтропия замкнутой системы не может уменьшаться. Самая короткая, но при этом непонятная, да? Потому как не понятно, что такое энтропия? Может, слово это вы где-то и слышали, но что оно означает?

Прежде, чем на этот вопрос ответить, я отойду немного в сторону. В школе изучение предмета физики начинается с того, что есть физические тела и физические явления. Я специально обращу ваше внимание, что в школе изучают не науку физику, а предмет физику. Чем одно отличается от другого, подумайте самостоятельно. Так вот, изучение предмета физики начинается, обычно, с того, что физика изучает физические тела и физические явления. А потом рассказывается, что у физических тел есть определённые свойства. Например, такое свойство как инертность – свойство тела сохранять свою скорость, или неподвижность. Но в физике мало говорить о свойствах тел, потому как, если изучать просто свойства, то это будет не физика, а природоведение. Физика начинается там, где возникает понятие меры. Есть тело, у тела есть свойство, у свойства есть мера. Если говорить об инертности, то её мера называется массой. Мера – это количественное выражение свойства, мера нам нужна для того, чтобы сравнивать тела по их свойствам. Более инертное тело обладает большей массой, менее инертное – меньшей массой. Массы можно количественно оценивать и измерять.

Но вот, о чём на первых уроках физики не говорят, а, по мере изучения предмета, часто забывают сказать, так это о том, что помимо физических тел, физика изучает ещё и системы тел. И у систем тоже есть определённые свойства, а у этих свойств – свои меры. Система – это не просто набор тел, это – нечто большее, и свойства системы не всегда состоят из свойств тех тел, которые в неё входят. Некоторые свойства систем те же, что и у отдельных тел, а некоторые – принципиально другие.

Все мы знаем, что тела состоят из молекул, а потому физическое тело – это одновременно и система тел. И если, например, массу тела можно рассматривать как общую массу всех молекул, из которых оно состоит, то температура тела не является общей температурой молекул. У молекул вообще нет температуры, у молекул есть кинетическая энергия, а температура – это свойство системы молекул, объединённых в физическое тело.

Температура – это, пожалуй, самое простое системное свойство,  а есть и более сложные. Вот одним из таких более сложных (конечно же, не самых сложных) системных свойств является энтропия. Если температура – это мера средней кинетической энергии молекул, входящих в систему, то энтропия – это мера беспорядка в системе.

Помните, ещё в первой главе я говорил, что есть понятия в узком смысле и в широком смысле? Тогда мы это рассматривали на примере пути. Путь в физическом смысле, путь в бытовом смысле, в литературном. Так вот, слово «беспорядок» тоже имеет несколько смысловых уровней. Есть беспорядок в бытовом смысле, как мы его понимаем, а есть строгий физический термин. В физике беспорядок – это количество возможных состояний системы. Чем их больше, тем больше беспорядок в системе, и тем больше её энтропия.

Теперь о том, что значит это самое количество возможных состояний? К примеру, если мы бросаем монету, то там всего два возможных состояния: орёл и решка. Если – игральную кость, то там – шесть возможных состояний. В колоде карт – уже намного больше. Если кто знает такую игру как покер, то там смысл заключается в том, чтобы собирать определённые комбинации из 5 карт. Чем меньше возможных состояний для комбинации, тем она сильнее. Самая сильная – роял-флеш – имеет всего 4 возможных состояния. Если кто не знает, то роял-флеш – это 5 самых старших карт одной масти, от туза до десятки. Поскольку мастей – четыре, то и возможных вариантов роял-флеш – четыре. Стрит-флеш – это просто 5 карт одной масти подряд, не самых старших, имеет 32 возможных состояния, карэ – 4 карты одного ранга плюс любая пятая — 13×12=156 возможных состояний. Ну, и так далее, до пары и нулёвки. Вообще на примере игры в покер очень хорошо изучать комбинаторику и теорию вероятностей.

Но что оно всё значит, с точки зрения энтропии? Что, чем случай более уникальный, тем энтропия системы меньше. А чем случай заурядней, тем энтропия больше. А чтобы наглядно понять, как работает второе начало термодинамики, давайте возьмём колоду карт, карты в которой расположены в строгом порядке. Сначала пики от двойки до туза, потом трефы в таком же порядке, бубны и черви (джокеры мы брать не будем, чтобы не создавать лишних трудностей). Такое состояние, которое соответствует абсолютному порядку, для колоды всего одно, соответственно энтропия данной системы (то есть, нашей колоды) минимальна. А теперь начнём её тасовать. Что произойдёт? Порядок в системе будет разрушен. И, в конце концов, после перемешивания колода утратит всякие остатки начального порядка. По ходу перемешивания энтропия будет неуклонно расти, и в конце нашего эксперимента придёт к максимально возможному значению.

Кстати, максимальная энтропия колоды карт имеет вполне определённое значение, есть формула, по которой её можно рассчитать, желающие могут найти, но предупреждаю, что формула не простая. Студенты технических специальностей, пожалуй, смогут посчитать, а вот у школьников и гуманитариев могут возникнуть трудности. Формула Больцмана, если кому интересно.

Так вот, вернёмся к тому состоянию, при котором всякий порядок в колоде карт будет окончательно и бесповоротно утрачен. Почему окончательно и бесповоротно? Потому что есть второе начало термодинамики, которое говорит о том, что энтропия замкнутой системы не может уменьшаться. Раз она достигла максимального значения, то и впредь будет оставаться на этом максимальном значении. Не верите? Можете сами проверить, тасуя колоду карт, вернётся ли она, как бы долго вы не тасовали, к изначальному состоянию порядка? Нет. Только если вы вмешаетесь и своим волевым решением разложите карты в нужном вам порядке, но в таком случае, это будет уже не замкнутая система, вы своим волевым вмешательством её размокнёте и влезете туда. А пока колода карт отдана воле случая, порядка в ней больше не станет.

Это, как вы понимаете, касается не только колоды карт, это касается любых замкнутых систем. Пока система замкнута, её энтропия может либо расти, либо оставаться неизменной. А если мы хотим понизить энтропию системы, нам придётся её разомкнуть, то есть, вмешаться в систему извне.

Возникает вопрос, а если вдруг нам невероятно повезёт, и в ходе случайных процессов, возникнет какой-то порядок? К примеру, по мере случайного тасования, карты выстроятся в строгом порядке? Может такое быть? В принципе, может, но вероятность такого события настолько мала, что на практике её можно не учитывать. А учёные по этому поводу говорят, что законы термодинамики говорят нам не о полном запрете некоторых событий, а лишь о ничтожной их вероятности. Например, существует ничтожная вероятность, что чайник, поставленный нами на горячую конфорку остынет, а конфорка ещё больше нагреется. Как такое может произойти с точки зрения физики? А так, что все быстрые молекулы случайно окажутся в конфорке, а все медленные – в чайнике. Но вероятность такого события настолько мала, что даже если бы вся наша Вселенная состояла из чайников, вряд ли бы мы за все миллиарды лет её существования где-то такое увидели.

Впрочем, ещё раз подчеркну, что всё это касается только замкнутых систем. В открытых системах всё это возможно. Холодильники, кондиционеры работают именно по такому принципу. Если вы обращали внимание, то задняя стенка холодильника всегда горячая, так же как и наружный блок кондиционера. Кондиционер разделяет холод и тепло, холод – в комнату, тепло – на улицу. Но всё это происходит только за счёт того, что мы подводим к этим приборам электроэнергию, которая и работает на разделение холода и тепла. Само по себе такое разделение происходить не может.

И вот тут мы подходим к одному интересному, я бы даже сказал, зловещему понятию термодинамики. Называется оно тепловая смерть Вселенной. Что это такое? Раз само по себе разделение холода и тепла невозможно, само по себе происходит только смешение одного и второго, то, что всё это значит для нашей Вселенной?

Чтобы наглядно это представить, возьмите опять колоду карт, чтобы карты в ней были разложены в две группы – красные и чёрные. Пусть красные это будет тепло, то есть, быстрые молекулы, а чёрные – холод, то есть медленные молекулы. И начните их тасовать. Что произойдёт? Произойдёт естественное смешение красных и чёрных. А что должно произойти во Вселенной? За миллиарды лет быстрые и медленные молекулы должны окончательно перемешаться, и во всей Вселенной установится тепловое равновесие. Или, иными словами, энтропия Вселенной достигнет максимального значения. А раз значение энтропии станет максимальным, то, согласно второму началу термодинамики, меньше оно уже не станет. То есть, разделение на холодные и горячие места станет невозможным. Если вы не поняли, то это будет означать, что остынут все звёзды, и больше никаких горячих звёзд не появится. Это значит, что прекратятся все тепловые процессы во Вселенной. Вселенная превратится в равномерную тепловую пустыню. Вот это и будет её тепловая смерть.

Печально, да? А я думаю, печалиться не стоит. Ведь мы видим, что ничего подобного не происходит. И мало того, что Вселенная не приходит в состояние тепловой смерти, так ещё и на протяжении её существования происходит постоянно усложнение форм. Формируются новые звёзды, вокруг звёзд появляются планеты, на планетах зарождается жизнь (по крайней мере, на одной планете точно, но вполне возможно, что и на многих других тоже), которая, в свою очередь, тоже постоянно усложняется от простейших одноклеточных до самого человека. И некоторые плохо образованные граждане, в связи с этим, ставят под сомнение сам принцип не убывания энтропии, то есть, второе начало термодинамики. Но, как мы помним, у всякого закона есть своя область применения, и там, где надо, второе начало термодинамики работает безукоризненно. А там, где не надо…

А вот о том, где не надо, уже в следующий раз.