From Wikipedia, the free encyclopedia
In mathematics, the order of a finite group is the number of its elements. If a group is not finite, one says that its order is infinite. The order of an element of a group (also called period length or period) is the order of the subgroup generated by the element. If the group operation is denoted as a multiplication, the order of an element a of a group, is thus the smallest positive integer m such that am = e, where e denotes the identity element of the group, and am denotes the product of m copies of a. If no such m exists, the order of a is infinite.
The order of a group G is denoted by ord(G) or |G|, and the order of an element a is denoted by ord(a) or |a|, instead of 
Lagrange’s theorem states that for any subgroup H of a finite group G, the order of the subgroup divides the order of the group; that is, |H| is a divisor of |G|. In particular, the order |a| of any element is a divisor of |G|.
Example[edit]
The symmetric group S3 has the following multiplication table.
-
• e s t u v w e e s t u v w s s e v w t u t t u e s w v u u t w v e s v v w s e u t w w v u t s e
This group has six elements, so ord(S3) = 6. By definition, the order of the identity, e, is one, since e 1 = e. Each of s, t, and w squares to e, so these group elements have order two: |s| = |t| = |w| = 2. Finally, u and v have order 3, since u3 = vu = e, and v3 = uv = e.
Order and structure[edit]
The order of a group G and the orders of its elements give much information about the structure of the group. Roughly speaking, the more complicated the factorization of |G|, the more complicated the structure of G.
For |G| = 1, the group is trivial. In any group, only the identity element a = e has ord(a) = 1. If every non-identity element in G is equal to its inverse (so that a2 = e), then ord(a) = 2; this implies G is abelian since 
.
The relationship between the two concepts of order is the following: if we write
for the subgroup generated by a, then
For any integer k, we have
- ak = e if and only if ord(a) divides k.
In general, the order of any subgroup of G divides the order of G. More precisely: if H is a subgroup of G, then
- ord(G) / ord(H) = [G : H], where [G : H] is called the index of H in G, an integer. This is Lagrange’s theorem. (This is, however, only true when G has finite order. If ord(G) = ∞, the quotient ord(G) / ord(H) does not make sense.)
As an immediate consequence of the above, we see that the order of every element of a group divides the order of the group. For example, in the symmetric group shown above, where ord(S3) = 6, the possible orders of the elements are 1, 2, 3 or 6.
The following partial converse is true for finite groups: if d divides the order of a group G and d is a prime number, then there exists an element of order d in G (this is sometimes called Cauchy’s theorem). The statement does not hold for composite orders, e.g. the Klein four-group does not have an element of order four). This can be shown by inductive proof.[1] The consequences of the theorem include: the order of a group G is a power of a prime p if and only if ord(a) is some power of p for every a in G.[2]
If a has infinite order, then all non-zero powers of a have infinite order as well. If a has finite order, we have the following formula for the order of the powers of a:
- ord(ak) = ord(a) / gcd(ord(a), k)[3]
for every integer k. In particular, a and its inverse a−1 have the same order.
In any group,
There is no general formula relating the order of a product ab to the orders of a and b. In fact, it is possible that both a and b have finite order while ab has infinite order, or that both a and b have infinite order while ab has finite order. An example of the former is a(x) = 2−x, b(x) = 1−x with ab(x) = x−1 in the group 
Counting by order of elements[edit]
Suppose G is a finite group of order n, and d is a divisor of n. The number of order d elements in G is a multiple of φ(d) (possibly zero), where φ is Euler’s totient function, giving the number of positive integers no larger than d and coprime to it. For example, in the case of S3, φ(3) = 2, and we have exactly two elements of order 3. The theorem provides no useful information about elements of order 2, because φ(2) = 1, and is only of limited utility for composite d such as d = 6, since φ(6) = 2, and there are zero elements of order 6 in S3.
In relation to homomorphisms[edit]
Group homomorphisms tend to reduce the orders of elements: if f: G → H is a homomorphism, and a is an element of G of finite order, then ord(f(a)) divides ord(a). If f is injective, then ord(f(a)) = ord(a). This can often be used to prove that there are no homomorphisms or no injective homomorphisms, between two explicitly given groups. (For example, there can be no nontrivial homomorphism h: S3 → Z5, because every number except zero in Z5 has order 5, which does not divide the orders 1, 2, and 3 of elements in S3.) A further consequence is that conjugate elements have the same order.
Class equation[edit]
An important result about orders is the class equation; it relates the order of a finite group G to the order of its center Z(G) and the sizes of its non-trivial conjugacy classes:
where the di are the sizes of the non-trivial conjugacy classes; these are proper divisors of |G| bigger than one, and they are also equal to the indices of the centralizers in G of the representatives of the non-trivial conjugacy classes. For example, the center of S3 is just the trivial group with the single element e, and the equation reads |S3| = 1+2+3.
See also[edit]
- Torsion subgroup
Notes[edit]
- ^ Conrad, Keith. «Proof of Cauchy’s Theorem» (PDF). Retrieved May 14, 2011.
- ^ Conrad, Keith. «Consequences of Cauchy’s Theorem» (PDF). Retrieved May 14, 2011.
- ^ Dummit, David; Foote, Richard. Abstract Algebra, ISBN 978-0471433347, pp. 57
References[edit]
- Dummit, David; Foote, Richard. Abstract Algebra, ISBN 978-0471433347, pp. 20, 54–59, 90
- Artin, Michael. Algebra, ISBN 0-13-004763-5, pp. 46–47
Как найти порядок элементов в группе?
Порядок элемента A группы G — это минимальное положительное число k, для которого справедливо равенство Ak=J (где J — единичный элемент группы). То есть — порядок элемента группы — это минимальная положительная степень, в которой данный элемент равен единице. Теорема.
Чему равен порядок группы?
Порядок группы делится на порядок ее любой подгруппы, в частности, на порядок любой циклической подгруппы. Этот порядок равен порядку образующего элемента.
Кто придумал теорию групп?
История У теории групп три исторических корня: теория алгебраических уравнений, теория чисел и геометрия. Математики, стоящие у истоков теории групп, — это Леонард Эйлер, Карл Фридрих Гаусс, Жозеф Луи Лагранж, Нильс Хенрик Абель и Эварист Галуа.
Как доказать что подгруппа нормальная?
Подгруппа H называется нормальной подгруппой (или нормальным делителем) группы G, если для каждого элемента a ∈ S его левые и правые смежные классы совпадают, т. е. если ∀a ∈ S aH = Ha. Заметим, что каждая подгруппа абелевой группы нормальна.
Как доказать что группа циклическая?
называется циклической, если она порождена одним элементом a, то есть все её элементы являются степенями a (или, если использовать аддитивную терминологию, представимы в виде na, где n — целое число.) }. Иначе говоря, группа G циклическая, если в G любая подгруппа, содержащая a, совпадает с G.
Как делятся группы?
В короткопериодном варианте периодической системы группы подразделяются на подгруппы — главные (или подгруппы A), начинающиеся с элементов первого и второго периодов, и побочные (подгруппы В), содержащие d-элементы.
Что такое группа факторов?
Факторгруппа — множество смежных классов группы по её нормальной подгруппе, само являющееся группой с определённой специальным образом групповой операцией. Образ группы при гомоморфизме изоморфен её факторгруппе по ядру этого гомоморфизма.
Кто дал определение группа?
Понятие группы ввёл Эварист Галуа, изучая многочлены в 1830-е годы. Современная теория групп является активным разделом математики.
Почему математика называется математикой?
Термин «математика» используется в русском языке с конца XVII в. Слово пришло из западноевропейских языков, хотя первоосновой является греческое слово, обозначающее «познающий». Математика — это «наука, которая изучает величины, их количественные отношения, а также пространственные формы».
Какая подгруппа называется нормальной?
Норма́льная подгру́ппа (также инвариа́нтная подгру́ппа или нормальный делитель) — подгруппа особого типа, левый и правый смежные классы по которой совпадают. Такие группы важны, поскольку позволяют строить факторгруппу.
Какая подгруппа у меди?
Подгру́ппа ме́ди — химические элементы 11-й группы периодической таблицы химических элементов (по устаревшей классификации — элементы побочной подгруппы I группы). В группу входят переходные металлы, из которых традиционно изготавливают монеты: медь Cu, серебро Ag и золото Au.
Что такое левый смежный класс?
Левые смежные классы по подгруппе либо не пересекаются, либо совпадают. Достаточно доказать, что если классы пересекаются, то они совпадают.
Какие бывают группы людей?
Виды групп
- Первичная (члены группы непосредственно взаимодействуют друг с другом, взаимоотношения отличаются интимностью, взаимной симпатией и пониманием. Примеры: семья, группа друзей)
- Вторичная (члены группы связаны между собой опосредованно, деятельностью по достижению общей цели.
Как разделяются химические элементы?
Классификация по ИЮПАК Щелочные металлы — металлы первой группы: Li, Na, K, Rb, Cs, Fr. Щелочноземельные металлы — металлы второй группы: Be, Mg, Ca, Sr, Ba, Ra. Пниктогены (пниктиды) — элементы пятой группы: N, P, As, Sb, Bi, Mc.
Что такое управляемые факторы риска?
Управляемые факторы риска – это, напротив те факторы, которые вы можете изменить, приняв соответствующие меры или внеся коррективы в свой образ жизни. Курящие люди умирают от Курение. ишемической болезни сердца в 2 раза чаще, чем те, кто никогда не курил.
Что относится к факторам риска?
Факторы риска – это обстоятельства (внешние или внутренние), отрицательно влияющие на здоровье человека и создающие благоприятную среду для возникновения и развития заболеваний….Среди ведущих факторов, негативно влияющих на здоровье, следует отметить:
- Курение. …
- Злоупотребление алкоголем. …
- Переедание. …
- Гиподинамия. …
- Стрессы.
14 мар. 2016 г.
Что означает понятие группа?
ГРУППА – объединение людей, соответствующее состоянию общности (см. ОБЩНОСТЬ), наиболее узкая форма общества, в котором отношение общности определяет характер целого.
Материал из Викиконспекты
Перейти к: навигация, поиск
| Определение: |
| Порядком элемента группы называется наименьшее , что . Если такого не существует, то говорят, что порядок бесконечен. |
Примеры
- Порядок любого ненулевого элемента в группе целых чисел по сложению равен бесконечности.
- Порядок элемента в группе вычетов по модулю конечен и равен двум, поскольку .
Свойства
| Утверждение: |
| Действительно, необходимо при некоторых совпадение степеней (иначе получится бесконечное число различных элементов в группе). Но тогда порядок не больше : . |
| Определение: |
| -группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа . Порядок разных элементов может быть разным. |
Примеры
- Группа вычетов по модулю простого числа относительно сложения: .
- Циклическая группа порядка .
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Найти порядок группы
|
||
11/04/08 |
|||
|
|
|||
|
Профессор Снэйп |
|
||
18/12/07 |
Из
Далее, для любого
Получается, что возможностей для
1)
В этом перечислении только 3 циклических группы:
|
||
|
|
|||
|
Хет Зиф |
|
||
20/05/06 |
|||
|
|
|||
|
Профессор Снэйп |
|
||
18/12/07 |
Хет Зиф писал(а): Вот это не совсем понял. Почему эти элементы должны быть различны?
|
||
|
|
|||
|
Хет Зиф |
|
||
20/05/06 |
Да, я и не говорю что они не различны, по крайней мере все другие элементы, выражаются через них.
|
||
|
|
|||
|
Профессор Снэйп |
|
||
18/12/07 |
Вроде понял. Возьмём группу
Кроме того, Ну и ясно, что второй вариант — это искомая группа. Значит, правильный ответ: не циклическая. Добавлено спустя 1 минуту 40 секунд: Хет Зиф писал(а): Да, я и не говорю что они не различны, по крайней мере все другие элементы, выражаются через них.
Тогда я не понял фразу «уже 16 порядок». Может, Вы хотели сказать: «уже порядок
|
||
|
|
|||
|
Хет Зиф |
|
||
20/05/06 |
Профессор Снэйп Да я именно это и хотел сказать. Цитата: остаётся лишь 2 варианта: Ну да, это сразу следует если из перечисленных мной элементов нет равных. Ну а также что если мы не считаем возможность
|
||
|
|
|||
|
ShMaxG |
|
||
11/04/08 |
|||
|
|
|||
|
Профессор Снэйп |
|
||
18/12/07 |
Хет Зиф писал(а): Профессор Снэйп Да я именно это и хотел сказать. Цитата: остаётся лишь 2 варианта: Ну да, это сразу следует если из перечисленных мной элементов нет равных. Ну а также что если мы не считаем возможность То, что среди перечисленных Вами элементов нет равных, надо доказывать. Вы, когда делали своё утверждение, этого не доказали. Добавлено спустя 51 секунду: ShMaxG писал(а): Профессор Снэйп писал(а): Почему? А что значат обозначения
Что именно у Вас вызывает затруднение. То, что
|
||
|
|
|||
|
Хет Зиф |
|
||
20/05/06 |
Профессор Снэйп Да, можно доказать это пристальным всматриванием
|
||
|
|
|||
|
Профессор Снэйп |
|
||
18/12/07 |
Хет Зиф писал(а): Профессор Снэйп Да, можно доказать это пристальным всматриванием
Пристальный взгляд к делу не пришьёшь
На самом деле, конечно, пример
|
||
|
|
|||
|
ShMaxG |
|
||
11/04/08 |
Профессор Снэйп писал(а): Хет Зиф писал(а): Профессор Снэйп То, что Да, а как порядок элемента связан с порядком группы?
|
||
|
|
|||
|
Хет Зиф |
|
||
20/05/06 |
Профессор Снэйп Не ну группа может быть и меньшего порядка . Добавлено спустя 2 минуты 29 секунд: ShMaxG Порядок элемента делит порядок группы
|
||
|
|
|||
|
Профессор Снэйп |
|
||
18/12/07 |
Хет Зиф писал(а): Профессор Снэйп Не ну группа может быть и меньшего порядка .
Бр… Вы порядок немножко у себя на чердаке наведите (без обид
Правильно сказать так: то, что в моём примере из определяющих соотношений. И, значит,
|
||
|
|
|||
|
ShMaxG |
|
||
11/04/08 |
Так, ребят, простите меня за тормознутость, я за вами не успеваю) Скажите пожалуйста только что за обозначения во втором сообщении и какой отсев происходит
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы






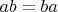 следует, что группа абелева и что любой её элемент представляется в виде
следует, что группа абелева и что любой её элемент представляется в виде  . Из остальных двух соотношений вытекает, что можно считать
. Из остальных двух соотношений вытекает, что можно считать  и
и  . Таким образом, порядок группы уже
. Таким образом, порядок группы уже  .
.
 справедливо
справедливо  . Значит, порядок группы есть степень двойки и, следовательно,
. Значит, порядок группы есть степень двойки и, следовательно,  .
.
 не так уж и много.
не так уж и много.
 ,
,  ;
; ,
,  ;
; ;
; ;
; .
.
 ,
,  и
и  . Наверное, надо просто посмотреть, что ни одна из них не подходит (или, наоборот, какая-то подходит).
. Наверное, надо просто посмотреть, что ни одна из них не подходит (или, наоборот, какая-то подходит). ,
,  и
и  . Все соотношения выполняются… Группа явно порождается этими двумя элементами.
. Все соотношения выполняются… Группа явно порождается этими двумя элементами.
 . Значит, из определяющих соотношений не следует
. Значит, из определяющих соотношений не следует  и остаётся лишь 2 варианта:
и остаётся лишь 2 варианта:  и
и  .
. .
.  не говорит например о том что
не говорит например о том что  не может быть равен
не может быть равен  .
.  говорит о том, что
говорит о том, что 