Как найти последовательность в вероятности

Определение последовательности испытаний

До сих пор мы в основном рассматривали случайные эксперименты, состоящие как бы из одного этапа. Хотя встречались примеры и ’’многоступенчатых” экспериментов. В этом разделе мы дадим описание математической модели эксперимента, который состоит из нескольких шагов или этапов.

Пусть — некоторые конечные множества. Элементы множества— это возможные результаты эксперимента на -м шаге. Тогда в качестве элементарного исхода такого эксперимента, состоящего из шагов, естественно взять , где . В этом случае . Чтобы полностью задать вероятностью модель, необходимо задать вероятности элементарных исходов.

Определение 1 . Вероятностное пространство , где = , называется последовательностью испытаний с множеством значений на -м шаге.

В этом определении вероятность задана сразу для всей последовательности . Но в реальных задачах результаты эксперимента появляются последовательно шаг за шагом. Поэтому и вероятностную структуру естественно задавать с помощью вероятностей появления , если мы знаем, что на предыдущих шагах уже появились . Используя теорему умножения,

мы можем записать

называется начальным распределением, а вероятностями переходов на соответствующих шагах для последовательности изиспытаний.

Пример (модель Эренфестов). Пусть мы имеем две урны. В начальный момент в первой урне два белых шара, во второй — два черных. Сначала мы выбираем случайно один шар из первой урны, отмечаем его цвет и кладем его во вторую урну. Затем выбираем случайно один шар из второй урны, отмечаем его цвет и кладем в первую урну и т.д. Пусть проводим п испытаний. На каждом шаге . На первом шаге с вероятностью 1 выбирают белый шар. После шагов мы знаем состав очередной урны и можем найти вероятность появления белого или черного шара, используя классическое определение вероятностей.

Если в этом примере отмечать не цвет появившегося шара, а вновь полученный состав урн (что эквивалентно), то вероятности перехода будут зависеть от результата эксперимента только на последнем шаге, а не на всех предыдущих шагах. Это свойство имеет место для многих реальных задач. Поэтому целесообразно выделить этот случай отдельно.

Определение 2 . Последовательность испытаний называется цепью Маркова, если для всех и всех

Еще более простую ситуацию мы получаем, если вообще не зависят от условий

Определение 3 . Говорят, что мы имеем последовательность п независимых испытаний, если

Нетрудно проверить, что в этом случае для любого имеет место

1. 
2. 

Определение 4 . Вероятностное пространство называется последовательностью независимых и одинаковых испытаний, если это последовательность независимых испытаний,

Можно показать, что события, связанные с разными испытаниями, являются независимыми.

Простейшим является случай, когда , т.е. множество исходов на каждом шаге состоит из двух элементов. Модель такого эксперимента называется схемой Бернулли и изучается подробно в следующем разделе.

Схема Бернулли. Биномиальное распределение

Начнем с неформального определения. Схемой Бернулли или последовательностью независимых одинаковых испытаний с двумя исходами называется случайный эксперимент, в котором:

1. Проводится независимых испытаний;
2. каждое испытание кончается одним из двух исходов (один исход называется ’’успех” и обозначается 1, а второй — ’’неуспех” и обозначается 0);
3. вероятность появления ’’успеха” одна и та же в каждом испытании и равна .

Числа и называются параметрами схемы Бернулли. Формальное описание модели такого эксперимента дано в следующем определении.

Определение 5 . Схемой Бернулли с параметрами и называется дискретное вероятностное пространство , где состоит из элементарных исходов вида,= 0,1, , а вероятности элементарных исходов задаются по правилу

Где — число единиц в исходе .

Выпадение герба будем считать ’’успехом”. Это схема Бернулли с параметрами

Обычно в рамках схемы Бернулли мы хотим вычислить вероятность не отдельного элементарного исхода, а некоторого более сложного события. Например, в предыдущем примере нас может интересовать вероятность того, что выпало ровно 3 герба. Такой вопрос является наиболее типичным для схемы Бернулли. Пусть есть событие, состоящее в том, что в независимых испытаниях мы получили ровно успехов. По определению вероятности события

,

где мы воспользовались тем, что вероятности элементарных исходов в все одинаковые и вычисляются по формуле (3), а число различных исходов равно размещению единиц по мест без учета порядка.

Если нас интересует число успехов, а не когда именно они появились, то мы можем построить менее подробную модель.

Определение 6 . Биномиальной моделью с параметрами п и называется вероятностное пространство , где

и

,

Вероятности , вычисляемые по формуле (4), образуют

так называемое биномиальное распределение. Нетрудно проверить, что они обладают обычными свойствами вероятностей:

1. 
2. 

и, кроме того,

Часто в прикладных задачах нас интересует, какое число успехов имеет наибольшую вероятность. Для этого сравним вероятность двух соседних значений.

Последнее выражение больше 1 при и меньше 1 при . Это приводит нас к следующим свойствам биномиальных вероятностей:

1. если , то при переходе от к вероятность возрастает,
2. если, то при переходе от к вероятность убывает,
3. если число — целое, то имеем два наиболее вероятных значения для числа успехов: и ,
4. если число — дробное, то имеем одно наиболее вероятное значение

Полезно нарисовать графики изменения вероятностей с изменением для разных и .

Пример 2 . Симметричную игральную кость подбрасывают 6 раз. Найти вероятность того, что выпадут ровно два герба и наиболее вероятное число появлений шестерки.

В этой задаче. Тогда

Число является дробным, поэтому наиболее вероятное число появлений шестерки есть

Предельные теоремы в схеме Бернулли

Выше мы получили формулу, по которой можно рассчитать вероятность того, что в серии из испытаний Бернулли с вероятностью успеха будет получено ровно успехов. А именно

В реальных задачах число испытаний бывает достаточно большим, и производить расчеты по этой формуле становится затруднительным. В этих случаях обычно стараются найти более простые выражения, которые асимптотически эквивалентны точным формулам, когда те или иные параметры меняются определенным образом. Для нашей модели существуют две аппроксимации, которые находят широкие приложения в практических задачах и, как мы увидим позднее, имеют и самостоятельное значение.

Теорема Пуассона. Пусть мы имеем схему Бернулли с параметрами и . Пусть ,так, что ,

Тогда для любого фиксированного т

Доказательство. Зафиксируем некоторое целое неотрицательное . Тогда

Более аккуратный анализ позволяет доказать, что

5

Если идля

Пример 3 . На некоторой телефонной станции 10 ООО номеров. В день через станцию поступает в среднем 30 ООО вызовов. Найти вероятность того, что по некоторому конкретному номеру будет ровно два звонка.

Предположим, что вызов по любому номеру является равновероятным и при каждом вызове номер выбирается независимо от других вызовов. Тогда мы имеем схему Бернулли с параметрами . Используя теорему Пуассона, получаем

Для распределения Пуассона составлены таблицы.

Другой асимптотический результат получается, если , а выбрано так, что , но величина лежит в некотором фиксированном интервале , где —

Локальная теорема Муавра-Лапласа. Пусть мы имеем схему Бернулли с параметрами и . Тогда при и фиксированном

равномерно по всем т, для которых —

Здесь

Для функции составлены таблицы. Отметим, что =

Пример 4 . Симметричную монету подбрасывают 100 раз. Найти вероятность того, что герб выпадет ровно 50 раз.

В этой задаче . Тогда

Используя локальную теорему Муавра-Лапласа, получаем

Как видно из последнего примера, при больших и фиксированном вероятности для всех значений очень малы. Поэтому обычно интересуются не тем, какое конкретное число успехов будет в нашем эксперименте, а в каких пределах оно окажется. Например, мы может вычислить вероятность того, что число появлений герба при 100 подбрасываниях будет лежать в пределах от 40 до 60. В таких задачах оказывается полезной следующая теорема.

Интегральная теорема Муавра-Лапласа. Пусть мы имеем схему Бернулли с параметрами и . Если , а — фиксировано, то равномерно по всем

5

Где — число успехов в п испытаниях, а

Более того, для любых имеет место оценка

Для функции , называемой функцией распределения стандартного нормального закона, составлены таблицы. Она обладает свойствами:

1. 
2. 

В силу свойства 2 таблицы обычно составляют только для положительных или только для отрицательных . Так как , то для можно считать, что . Очень часто вместо используют функцию, которая называется функцией Лапласа или интегралом вероятностей. Она обладает следующими свойствами:

1)

2)

3)

Для нее также составлены таблицы (для ). В силу свойства 3 ее можно использовать в интегральной теореме Муавра-Лапласа вместо функции

Пример 5 . Симметричную монету подбрасывают 100 раз. Найти вероятность того, что число появившихся гербов будет лежать в пределах от 40 до 60.

В этой задаче . В силу интегральной предельной теоремы Муавра-Лапласа

5

,

Применяя эту аппроксимацию, мы допускаем ошибку, которая не превышает величины

Более точный анализ показывает, что эта ошибка гораздо меньше.

Интегральная предельная теорема Муавра-Лапласа является частным случаем более общего результата, называемого центральной предельной теоремой, доказательство которого будет приведено позднее.

Полиномиальное распределение

Последняя модель, а именно биномиальное распределение, имеет очевидное обобщение на случай, когда число исходов в каждом испытании одинаково, но, возможно, отлично от двух.

Пусть мы имеем последовательность независимых испытаний, каждое из которых кончается одним из исходов, вероятности которых равны соответственно , и они одни и те же во всех испытаниях. Пусть, далее, есть число появлений -го исхода в этих испытаниях. Тогда вектор дает нам описание того, чем закончился такой эксперимент. Используя те же рассуждения, что и в биномиальной модели, нетрудно доказать, что вероятность такого исхода вычисляется по формуле

Суммируя все вышеизложенное, приходим к определению.

Определение 7 . Вероятностное пространство , в котором элементарные исходы имеют вид , где — целые неотрицательные числа такие, что , а их вероятности вычисляются по формуле

, называется полиномиальным распределением.

Пример 6 . Симметричный игральный кубик подбрасывают 10 раз. Найти вероятность события, состоящего в том, что выпадут 2 шестерки и одна пятерка.

В этом эксперименте проводится 10 испытаний, в которых естественно фиксировать три различных исхода: выпали шестерка, пятерка и другая цифра, вероятности которых равны и соответственно. Тогда

При больших п расчеты по формуле (5) становятся затруднительными. В этом случае применяются асимптотические формулы, аналогичные тем, что мы рассматривали для биномиального распределения.

Задача 1 . Пусть мы провели испытаний с тремя исходами, вероятности которых равны и соответственно. Предположим, что ,, таким образом, что ,. Тогда при фиксированных и

Теория вероятности — подробнее

Что такое вероятность?

Рассмотрим пример. Допустим, мы бросаем игральную кость. Что это за кость такая, знаешь? Так называют кубик с цифрами на гранях. Сколько граней, столько и цифр: от ( 1) до ( 6).

Итак, мы бросаем кость и хотим, чтобы выпало ( 5) или ( 6). И нам выпадает ( 5).

В теории вероятностей говорят, что произошло благоприятное событие.

Если бы выпало ( 6), событие тоже было бы благоприятным. Итого может произойти всего два благоприятных события.

А сколько неблагоприятных?

Раз всего возможных событий ( 6), значит, неблагоприятных из них ( 6-2=4) события (это если выпадет ( 1,text{ }2,text{ }3) или ( 4)).

Вероятностью называется отношение количества благоприятных событий к количеству всех возможных событий.

То есть вероятность показывает, какая доля из всех возможных событий приходится на благоприятные.

Обозначают вероятность латинской буквой ( p) (видимо, от английского слова probability — вероятность).

Принято измерять вероятность в процентах (см. темы «Дроби, рациональные числа» и «Проценты»).

Для этого значение вероятности нужно умножать на ( 100%).

В примере с игральной костью вероятность ( p=frac{благоприятных}{всего}=frac{2}{6}=frac{1}{3}).

А в процентах: ( p=frac{1}{3}cdot 100%=frac{100}{3}%approx 33,3%).

И еще события бывают зависимыми друг от друга и независимыми. Начнем с зависимых событий.

Зависимые события

Например, ты решил зайти к знакомому, помнишь подъезд и даже этаж на котором он живет. А вот номер и расположение квартиры забыл. И вот стоишь ты на лестничной клетке, а перед тобой ( 3) двери на выбор.

Каков шанс (вероятность) того, что если ты позвонишь в первую дверь, тебе откроет твой друг? Всего квартиры ( 3), а друг живет только за одной из них. С равным шансом мы можем выбрать любую дверь.

Но каков этот шанс?

Дверей ( 3), нужная дверь ( 1). Вероятность угадать, позвонив в первую дверь: ( frac{1}{3}). То есть один раз из трех ты точно угадаешь.

Мы хотим узнать, позвонив ( 1) раз, как часто мы будем угадывать дверь? Давай рассмотри все варианты:

1. Ты позвонил в 1-ю дверь
2. Ты позвонил в 2-ю дверь
3. Ты позвонил в 3-ю дверь

А теперь рассмотрим все варианты, где может находиться друг:

а. За 1ой дверью
б. За 2ой дверью
в. За 3ей дверью

Сопоставим все варианты в виде таблицы. Галочкой обозначены варианты, когда твой выбор совпадает с местоположением друга, крестиком – когда не совпадает.

Как видишь, всего возможно ( 9) вариантов местоположения друга и твоего выбора, в какую дверь звонить.

А благоприятных исходов всего ( 3). То есть ( 3) раза из ( 9) ты угадаешь, позвонив в дверь ( 1) раз, т.е. ( frac{3}{9}=frac{1}{3}).

Это и есть вероятность – отношение благоприятного исхода (когда твой выбор совпал с местоположение друга) к количеству возможных событий.

Определение – это и есть формула. Вероятность принято обозначать p, поэтому:

( displaystyle p=frac{text{благоприятных}}{всего})

Поскольку математики называют различные действия (у нас такое действие – это звонок в дверь) экспериментами, то результатом таких экспериментов принято называть исход.

Ну а исходы бывают благоприятные и неблагоприятные.

Давай вернемся к нашему примеру. Допустим, мы позвонили в одну из дверей, но нам открыл незнакомый человек. Мы не угадали. Какова вероятность, что если позвоним в одну из оставшихся дверей, нам откроет наш друг?

Если ты подумал, что ( displaystyle frac{1}{3}), то это ошибка. Давай разбираться.

У нас осталось две двери. Таким образом, у нас есть возможные шаги:

1. Позвонить в 1-ую дверь
2. Позвонить во 2-ую дверь

Друг, при всем этом, точно находится за одной из них (ведь за той, в которую мы звонили, его не оказалось):

а. Друг за 1-ой дверью
б. Друг за 2-ой дверью

Давай снова нарисуем таблицу:

Как видишь, всего есть ( 4) варианта, ( 2) из которых – благоприятны. То есть вероятность равна ( displaystyle frac{2}{4}=frac{1}{2}).

А почему не ( displaystyle frac{1}{3})?

Рассмотренная нами ситуация – пример зависимых событий. Первое событие – это первый звонок в дверь, второе событие – это второй звонок в дверь.

А зависимыми они называются потому что влияют на следующие действия. Ведь если бы после первого звонка в дверь нам открыл друг, то какова была бы вероятность того, что он находится за одной из двух других?

Правильно, ( 0%).

Но если есть зависимые события, то должны быть и независимые? Верно, бывают.

Правило умножения вероятностей независимых событий

Что такое независимые события ты уже знаешь.

А если нужно найти вероятность того, что два (или больше) независимых события произойдут подряд?

Можно конечно посчитать, но есть способ проще.

Допустим мы хотим знать, какова вероятность того, что бросая монетку ( 2) раза, мы два раза увидим орла?

Мы уже считали: ( p=0,25).

А если бросаем монетку ( 3) раза? Какова вероятность увидеть орла ( 3) раза подряд?

Всего возможных вариантов ( 8):

• Орел-орел-орел
• Орел-орел-решка
• Орел-решка-орел
• Орел-решка-решка
• Решка-орел-орел
• Решка-орел-решка
•  Решка-решка-орел
• Решка-решка-решка

Не знаю, как ты, но я ( 3) раза ошибся, составляя этот список. Ух! А подходит нам только ( 1) вариант (первый).

( displaystyle p=frac{{{N}_{б}}}{N}=frac{1}{8})

Для 5 бросков можешь составить список возможных исходов сам. Но математики не столь трудолюбивы, как ты.

Поэтому они сначала заметили, а потом доказали, что вероятность определенной последовательности независимых событий каждый раз уменьшается на вероятность одного события.

Другими словами,

Вероятность определенной последовательности независимых событий равна произведению вероятностей каждого из событий

Рассмотрим на примере все той же, злосчастной, монетки.

Вероятность выпадения орла в ( 1) испытании? ( displaystyle frac{1}{2}). Теперь мы бросаем монетку ( 5) раз.

Какова вероятность выпадения ( 5) раз подряд орла?

( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}={{left( frac{1}{2} right)}^{5}}=frac{1}{32})

Это правило работает не только, если нас просят найти вероятность того, что произойдет одно и то же событие несколько раз подряд.

Если бы мы хотели найти последовательность РЕШКА-ОРЕЛ-РЕШКА, при ( 3) бросках подряд, мы поступили бы также.

Вероятность выпадения решка – ( displaystyle frac{1}{2}), орла – ( displaystyle frac{1}{2}).

Правило сложения вероятностей несовместных событий

Так стоп! Новое определение.

Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента.

Ряд несовместных событий образуют полную группу событий.

Давай разбираться. Возьмем нашу изношенную монетку и бросим её ( 3) раза. Возможные варианты:

• Орел-орел-орел
• Орел-орел-решка
• Орел-решка-орел
• Орел-решка-решка
• Решка-орел-орел
• Решка-орел-решка
•  Решка-решка-орел
• Решка-решка-решка

Так вот, несовместные события – это определенная, заданная последовательность событий. ( 1),text{ }2),text{ }3),text{ }4)ldots text{ }8)) – это несовместные события.

Вероятности несовместных событий складываются.

Если мы хотим определить, какова вероятность двух (или больше) несовместных событий, то мы складываем вероятности этих событий.

Нужно понять, что выпадение орла или решки – это два независимых события.

Если мы хотим определить, какова вероятность выпадения последовательности ( 1)) (или любой другой), то мы пользуемся правилом умножения вероятностей.

Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?

( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}=frac{1}{8})

Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно ( 1) раз, т.е. варианты ( 4),text{ }6)) и ( 7)), то мы должны сложить вероятности этих последовательностей.

Правило, помогающее не запутаться, когда умножать, а когда складывать:

Опишите, что должно произойти, используя союзы «И» или «ИЛИ». Затем вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения.

Возвратимся к примеру, когда мы подбросили монетку ( 3) раза, и хотим узнать вероятность увидеть орла ( 1) раз.

Что должно произойти?

Должны выпасть:

(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).

Виды сходимости
последовательности случайных величин.

Закон больших
чисел

Центральная
предельная теорема

Виды сходимости случайных величин

Пусть {Х_n
, n
≥ 1} = Х₁
, Х₂
,… , Х_n
,… – последовательность случайных
величин

Определение.
Случайные величины Х₁
, Х₂
,… , Х_n
,… сходятся при n
→∞ к случайной величине Х

С вероятностью
1, если Р{ω:
X_n
(ω)
→ X(ω)}
= 1

в среднеквадратичном,
если Е (X_n
− X)²
→ 0

по вероятности,
если для любого ε > 0 Р( |X_n
− X|
<ε) → 1

по распределению,
если функции распределения случайных
величин F_Xn
сходятся к F_X

Замечание.
Из сходимости в среднем квадратичном
следует сходимость по вероятности

Из сходимости по
вероятности следует сходимость по
распределению

Из сходимости с
вероятностью 1 следует сходимость по
вероятности.

Отступление.
Сходимость последовательности.

Последовательность
функций Х₁
(ω), Х₂
(ω) ,… , Х_n
(ω) сходится
на пространстве Ω к некоторому Х, если
при любом фиксированном ω числовая
последовательность {Х_n
} сходится к Х(ω).

Число a
называется пределом
числовой последовательности
{a_n},
если для любого положительного числа
ε, как бы мало оно ни было, существует
такой номерN,
что для всех a_n
c номерами n>N
справедливо неравенство a-ε
<a_n<a+
ε. Неравенство | a_n-a|
< ε. эквивалентное неравенству a-ε
<a_n<a+
ε , означает, что для любого ε.>0 существует
такой номерN
, что все a_n
номерами n>N
расположены между a-ε
и a+
ε. Последовательность a_n,
предел которой — конечное число a,
называется сходящейся,
и ее предел обозначают lim
a_n
= a
при n∞.
Если изобразить элементы последовательности
a_n
на плоскости точками с координатами
(n,
a_n),
то неравенства a-ε
<a_n<a+
ε означают, что все точки (n,
a_n)
с номерами n>N
расположены между параллельными оси
абсцисс прямыми a-ε
и a+
ε.

Закон больших чисел

Пусть у нас имеется
случайная величина Х с математическим
ожиданием а и дисперсией σ²
. Проведем n
независимых опытов, находя значения Х,
и рассмотрим среднее арифметическое
всех наблюденных значений Х. Рассмотрим
значение математического ожидания и
дисперсии этой величины. Пусть Х —
значение Х ₁в
первом эксперименте, Х₂
— во втором,…, Х_n
– в n,
и т.д. Соответственно, Х₁
, Х₂
,… , Х_n
,… — это последовательность независимых,
одинаково распределенных случайных
величин (Термин «одинаково распределенные»
означает, что величины имеют общее
распределение (и, соответственно,
совпадают их математические ожидания,
дисперсии и пр.), которое не обязательно
должно быть указано). По свойствам
математического ожидания и дисперсии
математическое ожидание среднего
арифметического (Х₁
+ Х₂
+… + Х_n
) / n
будет равно а, а дисперсия σ²/n.
То есть, математическое ожидание среднего
арифметического равно математическому
ожиданию самой величины Х и не зависит
от количества испытаний, а дисперсия с
ростом их числа убывает. Иными словами,
при большом числе экспериментов n
среднее арифметическое оказывается
практически неслучайной величиной. В
таком случае говорят об устойчивости
среднего
арифметического.

Рассмотрим теперь
формулировку закона
больших чисел:

Пусть {Х_i
, i
≥ 1} – последовательность независимых,
одинаково распределенных случайных
величин. (Иными словами, проводится
большое количество независимых
экспериментов, в каждом из которых
наблюдается случайная величина одной
и той же природы). Предполагается, что
среднее и дисперсия каждой из Х_i
конечны.
Они обозначаются a
и σ²
соответственно.

S_n
= Х₁
+ Х₂
+… + Х_n
, n
≥ 1

ES_n
= na

DS_n
= nσ²

Тогда случайная
величина S_n
/ n,
равная среднему арифметическому n
первых величин из последовательности,
сходится в среднеквадратичном, по
вероятности и с вероятностью 1 к
математическому ожиданию а.

Е (S_n
/ n
— a)²
→ 0 ,

P
(|S_n
/ n
— a
|
< ε ) 
1 и

Р{ω:
S_n
/ n
(ω)
→ а} = 1

при n

∞

Пример.

Пусть эксперимент
состоит в n-кратном
подбрасывании монеты. Пусть Х_n
– случайная величина, равная 1, если
выпал «герб», и 0 – если «решка» в n
бросании. Величины Х_i
независимы,
поскольку независимы эксперименты
(подбрасывания). Вероятности выпадения
«герба» и «решки» совпадают и равны ½.
Тогда математическое ожидание EХ_i
= а = ½ , а дисперсия DX=
σ²=1/4.
Величина (Х₁
+ Х₂
+… + Х_n
) / n
равна доле выпавших гербов при n
бросаниях монеты и согласно закону
больших чисел должна стремиться к ½.Если
бы монета была несимметричной и
вероятность выпадения Герда была p

½, то по закону больших чисел доля гербов
стремилась бы к а = р

Обобщение закона
больших чисел (закон больших чисел в
форме Чебышева)

Рассмотренное
выше утверждение можно обобщить на
случай, когда мы не можем гарантировать
одинаковое распределение случайных
величин, то есть когда закон распределения
случайной величины Х от эксперимента
к эксперименту не остается одним и тем
же, а изменяется. Тогда вместо среднего
арифметического наблюденных значений
одной и той же величины Х с постоянными
математическим ожиданием а и дисперсией
σ²
рассматривается
среднее арифметическое n различных
случайных величин с различными
математическими ожиданиями a_i
и дисперсиями σ²_i
. Обобщенный закон больших чисел
утверждает, что и в этом случае среднее
арифметическое (Х₁
+ Х₂
+… + Х_n
) / n
сходится к среднему их математических
ожиданий (a₁
+ a₂
+… + a_n)
/ n
.

Замечание.
Выполнение закона больших чисел отражает
предельную устойчивость средних
арифметических случайных величин: при
большом числе испытаний они практически
перестают быть случайными и совпадают
со своими средними значениями

Замечание.
Именно Закон больших чисел является
основанием для использования в статистике
среднего арифметического выборки
(выборочного среднего) для оценки
математического ожидания генеральной
совокупности.

Ни в одной из форм
закона больших чисел не идет речь о
законах распределения. Предельные
законы распределения составляют предмет
другой группы теорем — центральной
предельной теоремы, которую иногда
называют «количественной формой закона
больших чисел».

Соседние файлы в папке Модуль 1. Лекции

• #
• #
• #
• #
• #
• #

Предположим, что некоторый эксперимент можно проводить неоднократно при одних и тех же условиях. Пусть этот опыт производится N раз, т. е. проводится последовательность из N испытаний.

Определение. Последовательность N Испытаний называют Взаимно независимой, если любое событие, связанное с данным испытанием, не зависит от любых событий, относящихся к остальным испытаниям.

Допустим, что некоторое событие A может произойти с вероятностью P в результате одного испытания или не произойти с вероятностью Q=1—P.

Определение. Последовательность из N Испытаний образует схему Бернулли, если выполняются следующие условия:

1) последовательность N испытаний взаимно независима,

2) вероятность события A не изменяется от испытания к испытанию и не зависит от результата в других испытаниях.

Событие A называют “ успехом” испытания, а противоположное событие — “неудачей”. Рассмотрим событие

={ в N испытаниях произошло ровно M “успехов”}.

Для вычисления вероятности этого события справедлива формула Бернулли

P() = , M = 1, 2, …, N , (1.6)

где — число сочетаний из N элементов по M :

= = .

Пример 1.16. Три раза подбрасывают кубик. Найти:

а) вероятность того, что 6 очков выпадет два раза;

б) вероятность того, что число шестерок не появится более двух раз.

Решение. “Успехом” испытания будем считать выпадение на кубике грани с изображением 6 очков.

А) Общее число испытаний – N =3, число “успехов” – M = 2. Вероятность “успеха” — P=, а вероятность “неудачи” — Q= 1 — = . Тогда по формуле Бернулли вероятность того, что результате трехразового бросания кубика два раза выпадет сторона с шестью очками, будет равна

.

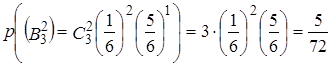
Б) Обозначим через А событие, которое заключается в том, что грань с числом очков 6 появится не более двух раз. Тогда событие можно представить в виде Суммы трех несовместных событий А= ,

Где В30 – событие, когда интересующая грань ни разу не появится,

В31 — событие, когда интересующая грань появится один раз,

В32 — событие, когда интересующая грань появится два раза.

По формуле Бернулли (1.6) найдем

P(А) = р () = P()=++=

=.

< Предыдущая		Следующая >

Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Найти вероятность того что — не просто. И  как решать задачи на вероятность?. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Таким образом подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов. Например, шанс получить решку при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.

Как мы уже с вами увидели, вероятность может быть выражена как в процентах, так и в обычных числах. Важно: на ЕГЭ вам нужно будет записать ответ в числах, не в процентах. Принято, что вероятность изменяется от 0 (никогда не произойдет) до 1 (абсолютно точно произойдет). Также можно сказать, что всегда

Вероятность подходящих событий + вероятность неподходящих событий = 1

Теперь мы точно понимаем, как считать вероятность отдельного события, и даже такие задачи есть в банке ФИПИ, но понятно, что на этом всё не заканчивается. Чтобы жизнь была веселее, в задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.

Вероятность нескольких событий

Подсчитываем вероятность каждого события в отдельности, затем между дробями ставим знаки:

1. Если нужно первое И второе событие, то умножаем.

2. Если нужно первое ИЛИ второе событие, то складываем.

Задачи и решения задач на вероятность

Задача 1. Среди натуральных чисел от 23 до 37 случайно выбирают одно число. Найдите вероятность того, что оно не делится на 5.

Решение:

Вероятность, это отношение благоприятных вариантов к общему их количеству.

Всего в этом промежутке 15 чисел. Из них на 5 делится всего 3, значит не делится 12.

Вероятность тогда: 

Ответ: 0,8.

Задача 2. Для дежурства в столовой случайно выбирают двух учащихся класса. Какова вероятность того, что дежурить будут два мальчика, если в классе обучается 7 мальчиков и 8 девочек?

Решение: Вероятность, это отношение благоприятных вариантов к общему их количеству. В классе 7 мальчиков, это благоприятные варианты. А всего 15 учеников.

Вероятность что первый дежурный мальчик:

Вероятность что второй дежурный мальчик:

Раз оба должны быть мальчики, вероятности перемножим:

Ответ: 0,2.

Задача 3. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.

Решение: Пассажиру В. удобны 30 мест (12 + 18 = 30), а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30/300, т. е. 0,1.

Задача 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам.

Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.

Решение: Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна 15/25, т. е. 0,6.

Задача 5. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам.

Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.

Решение: Из 35 билетов 28 не содержат вопроса по кислотам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам, равна 28/35, т. е. 0,8.

Задача 6. В среднем из 500 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Решение: Если из 500 насосов 2 подтекают, то 498 не подтекают. Следовательно, вероятность выбора хорошего насоса — 498/500, т. е. 0,996.

Задача 7. Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,065. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 70 штук.

На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

Решение: Частота события «гарантийный ремонт» равна 70/1000, т. е. 0,07. Она отличается от предсказанной вероятности на 0,005 (0,07 – 0,065 = 0,005).

Задача 8. В чемпионате по гимнастике участвуют 50 спортсменок: 18 из России, 14 из Украины, остальные — из Белоруссии. Порядок, в котором выступают гимнастки, определяется жребием.

Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии.

Решение: Всего участниц на чемпионате 50, а спортсменок из Белоруссии — 18 (50 – 18 – 14 = 18).

Вероятность того, что первой будет выступать спортсменка из Белоруссии — 18 из 50, т. е. 18/50, или 0,36.

Задача 9. Научная конференция проводится в 5 дней. Всего запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой.

Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

Решение: За первые три дня будут прочитаны 36 докладов (12 ∙ 3 = 36), на последние два дня планируется 44 доклада. Поэтому на последний день запланировано 22 докладов (44 : 2 = 22). Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 22/80, т. е. 0,275.

Задача 10.

Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 14 участников из России, в том числе Егор Косов.

Найдите вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России?

Решение: В первом туре Егор Косов может сыграть с 25 шахматистами (26 – 1 = 25), из которых 13 ― из России. Значит, вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России, равна 13/25, или 0,52.

Задача 11.

В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.

Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

Решение: Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек, т. е. 4/16, или 0,25.

Задача 12.  В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?

Решение: Выбирают двоих туристов из пяти. Следовательно, вероятность быть выбранным равна 2/5, т. е. 0,4.

Задача 13. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.

Решение: На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист полетит первым рейсом вертолёта, равна 6/30, или 0,2.

Задача 14. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?

Решение: Натуральных чисел от 10 до 19 десять, из них на 3 делятся три числа: 12, 15 и 18. Следовательно, искомая вероятность равна 3/10, т. е. 0,3.

Вероятность нескольких событий

Задача 1. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Стратор». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.

Решение: 

Тип вопроса: совмещение событий.

Нас устроит следующий вариант: «Статор» не начинает первую игру, начинает вторую игру, не начинает третью игру. Вероятность такого развития событий равна произведению вероятностей каждого из этих событий. Вероятность каждого из них равна 0,5, следовательно: 0,5 · 0,5 · 0,5 = 0,125.

Задача 2. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей ― 1 очко, если проигрывает ― 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.

Решение: 

Тип вопроса: совмещение событий.

Задачу выполняют несколько вариантов:

Игра №1	Игра №2	Вероятность данного варианта
3	1	0,4 · 0,2 = 0,08
1	3	0,2 · 0,4 = 0,08
3	3	0,4 · 0,4 = 0,16

Вероятность происхождения какого-либо их этих 3-х вариантов равна сумме вероятностей каждого из вариантов: 0,08 + 0,08 + 0,16 = 0,32.

Задача 3. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того что Аня и Нина окажутся в одной группе.

Решение: 

Тип вопроса: уменьшение групп.

Вероятность попадания Ани в одну из групп равна 1. Вероятность попадания Нины в ту же группу равна 2 из 20 (2 оставшихся места в группе, а человек осталось 20). 2/20 = 1/10 = 0,1.

Задача 4. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.

Решение:

Способ №1

Тип задачи: уменьшение групп.

Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая однорублевая монета попадет в один из карманов (групп) = 1.

Вероятность, что две двухрублевые монеты попадут в этот же карман = количество оставшихся мест в этом кармане/на количество оставшихся мест в обоих карманах = 2/5 = 0,4.

Способ №2

Тип вопроса: совмещение событий.

Задачу выполняют в несколько вариантов:

Если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):

Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 

Задача 5. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.

Решение:

Тип задачи: уменьшение групп.

Способ №1

Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая двухрублевая монета попадет в один из карманов (групп) = 1. Вероятность, что вторая монета попадет в другой карман = количество оставшихся мест в другом/ на количество оставшихся мест в обоих карманах = 3/5 = 0,6.

Способ №2

Тип вопроса: совмещение событий.

Задачу выполняют несколько вариантов:

Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):

Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 

Задача 6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно два раза.

Решение: Тип вопроса: нахождение желаемого и действительного совмещение событий Нас устраивают три варианта:

Орёл ― решка ― орёл;

Орёл ― орёл ― решка;

Решка ― орёл ― орёл;

Вероятность каждого случая ― 1/2, а каждого варианта ― 1/8 (1/2 ∙ 1/2 ∙ 1/2 = 1/8)

Нас устроит либо первый, либо второй, либо третий вариант. Следовательно, складываем их вероятности и получаем 3/8 (1/8 + 1/8 + 1/8 = 3/8), т. е. 0,375.

Задача 7. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение: 

Тип вопроса: совмещение событий.

В любом случае А. будет играть как белыми, так и черными, поэтому нас устроит вариант, когда гроссмейстер А. выиграет, играя белыми (вероятность ― 0,5), а также играя чёрными (вероятность ― 0,34). Поэтому надо перемножить вероятности этих двух событий: 0,5 ∙ 0,34 = 0,17.

Задача 8. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

Решение: 

Тип вопроса: совмещение событий.

Вероятность того, что батарейка исправна, равна 0,98. Покупателю надо, чтобы и первая, и вторая батарейка были исправны: 0,98 · 0,98 = 0,9604.

Задача 9. На рок-фестивале выступают группы ― по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из США будет выступать после группы из Канады и после группы из Китая? Результат округлите до сотых.

Решение: 

Тип вопроса: совмещение событий.

Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (КИТ — Китай, КАН = Канада):

… США, КАН, КИТ …

… США, КИТ, КАН …

… КИТ, США, КАН …

… КАН, США, КИТ …

… КАН, КИТ, США …

… КИТ, КАН, США …

США находится после Китая и Канады в двух последних случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна:

≈ 0,33.

Дополняющая вероятность

Задача 1. 

Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05.

Найдите вероятность того, что случайно выбранная батарейка будет забракована.

Решение: 

Существуют 2 варианта, которые нам подходят:

Вариант А: батарейка забракована, она неисправна;

Вариант Б: батарейка забракована, она исправна.

Вероятность варианта А: 0,02 ∙ 0,97 = 0,0194;

Вероятность варианта Б: 0,05 ∙ 0,98 = 0,049;

Нас устроит либо первый, либо второй вариант: 0,0194 + 0,049 = 0,0684.

Задача 2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая — 40%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение: 

Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,6 · 0,03 = 0,018.

Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,4 · 0,05 = 0,02.

Вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,018 + 0,02 = 0,038.

Задача 3. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных.

Решение: 

Предположим, у нас х тарелок изначально (ведь мы постоянно имеем дело с процентами, поэтому нам ничего не мешает оперировать конкретными величинами).

Тогда 0,1х — дефектные тарелки, а 0,9х — нормальные, которые поступят в магазин сразу. Из дефектных убирается 80%, то есть 0,08х, и остаётся 0,02х, которые тоже пойдут в магазин. Таким образом, общее количество тарелок на полках в магазине окажется: 0,9х + 0,02х = 0,92х. Из них нормальными будет 0,9х. Соответственно, по формуле вероятность будет 0,9х/0,92х ≈ 0,978.

Задача 4. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,91. Вероятность того, что этот товар доставят из магазина Б, равна 0,89. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.

Решение. Вероятность того, что первый магазин не доставит товар, равна 1 − 0,91 = 0,09. Вероятность того, что второй магазин не доставит товар, равна 1 − 0,89 = 0,11. Вероятность происхождения двух этих событий одновременно равна произведению вероятностей каждого из них: 0,09 · 0,11 = 0,0099.

Задача 5. При изготовлении подшипников диаметром 70 мм вероятность того, что диаметр будет отличаться от заданного меньше чем на 0,01 мм, равна 0,961. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 69,99 мм или больше чем 70,01 мм.

Решение: Нам дана вероятность события, при котором диаметр будет в пределах между 69,99 мм и 70,01 мм, и она равна 0,961. Вероятность всех остальных вариантов мы можем найти по принципу дополняющей вероятности: 1 − 0,961 = 0,039.

Задача 6. Вероятность того, что на тесте по истории учащийся верно решит больше 9 задач, равна 0,68. Вероятность того, что верно решит больше 8 задач, равна 0,78. Найдите вероятность того, что верно решит ровно 9 задач.

Решение: Вероятность того, что Т. верно решит более 8 задач, включает в себя вероятность решения ровно 9 задач. При этом, события, при которых О. решит больше 9 задач, нам не подходят. Следовательно, отняв от вероятности решения более 9 задач вероятность решения более 8 задач, мы и найдём вероятность решения только 9 задач: 0,78 – 0,68 = 0,1.

Задача 7. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,88. Вероятность того, что окажется меньше 12 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 12 до 20.

Решение. Вероятность того, что в автобусе окажется меньше 21 пассажира, включает в себя вероятность, что в нём окажутся от 12 до 20 пассажиров. При этом события, при которых пассажиров будет меньше 12, нам не подходят. Следовательно, отняв от первой вероятности (менее 21) вторую вероятность (менее 12), мы и найдём вероятность того, что пассажиров будет от 12 до 20 : 0,88 – 0,66 = 0,22.

Задача 8. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 10 апреля погода в Волшебной стране хорошая. Найдите вероятность того, что 13 апреля в Волшебной стране будет отличная погода.

Решение:

Задачу выполняют несколько вариантов («Х» — хорошая погода, «О» — отличная погода):

11 апреля	12 апреля	13 апреля	Вероятность данного варианта
X – 0,9	X – 0,9	O – 0,1	0,9 ·0,9 ·0,1 = 0,081
X – 0,9	O – 0,1	O – 0,9	0,9 ·0,1 ·0,9 = 0,081
O – 0,1	O – 0,9	O – 0,9	0,1 ·0,9 ·0,9 = 0,081
O – 0,1	X – 0,1	O – 0,1	0,1 ·0,1 ·0,1 = 0,001

Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 0,081 + 0,081 + 0,081 + 0,001 = 0,244.

Задача 9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

Решение:

Задачу выполняют несколько вариантов («Х» ― хорошая погода, «О» ― отличная погода):

4 июля	5 июля	6 июля	Вероятность данного варианта
X – 0,8	X – 0,8	O – 0,2	0,8 · 0,8 · 0,2 = 0,128
X – 0,8	O – 0,2	O – 0,8	0,8 · 0,2 · 0,8 = 0,128
O – 0,2	O − 0,8	O − 0,8	0,2 · 0,8 · 0,8 = 0,128
O – 0,2	X – 0,2	O – 0,2	0,2 · 0,2 · 0,2 = 0,008

Вероятность происхождения какого-либо их этих 4 ― х вариантов равна сумме вероятностей каждого из вариантов: 0,128 + 0,128 + 0,128 + 0,008 = 0,392.