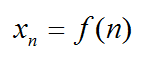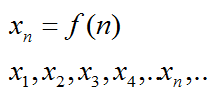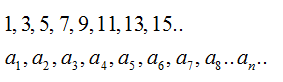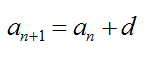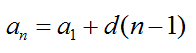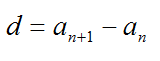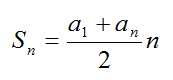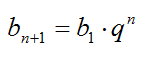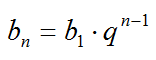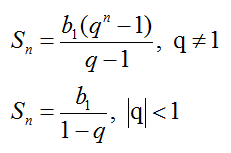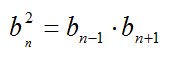Как найти последовательные числа 5 класс

Дети используют математические навыки ежедневно, будь то в школе или дома, во время занятий или игр. Изучение математики необходимо для детей с раннего возраста. Вы можете привить своим детям позитивное отношение к математике, упростив им задачу. Математика — это не то, что вы можете просто читать и изучать. В математике существуют различные формулы и выводы. Чтобы сделать математику легкой для ваших детей, вам нужно, чтобы они понимали каждую концепцию математики. Давайте начнем с последовательных чисел стимулирующим образом.

Что такое последовательные числа?
Те числа, которые следуют друг за другом непрерывно, от возрастающего к убывающему порядку, называются последовательными числами. Числа всегда записываются в виде ряда, где числа не должны пропускать какие-либо промежуточные, и разница между числами, по-видимому, фиксирована. Обычно они имеют разницу в 1 между каждыми двумя числами.

Пример последовательного числа:
Что такое 7 последовательных чисел?
1, 2, 3, 4, 5, 6, 7 это 7 последовательных чисел. Не обязательно начинать его с числа 1. Концепция 7 последовательных чисел может быть применена к 55, 56, 57, 58, 59, 60, 61, 62 как хорошо. Давайте проверим еще несколько примеров из 7 последовательных чисел.

Такие как :

11, 12, 13, 14, 15, 16, 17
-3, -2, -1, 0, 1, 2, 3
45, 46, 47, 48, 49, 50, 51
37, 38, 39, 40, 41, 42, 43

Что такое последовательные составные числа?
Последовательные составные числа состоят из более чем двух множителей, и список чисел без пропуска какого-либо промежуточного числа называется последовательным составным числом. Все натуральные числа, которые не являются простыми числами, кроме 1, называются составными числами.

Примеры последовательных составных чисел.
4, 6, 8, 9, 10
95, 96, 98, 99, 100

Что такое последовательные натуральные числа?
Последовательные натуральные числа
Подмножество действительных чисел, которое включает только положительные целые числа, такие как 1, 2, 3, 4, 5, 6, и так далее называются натуральными числами. Числа, которые непрерывно следуют друг за другом в порядке от наименьшего числа до наибольшего числа, называются последовательными натуральными числами. Это исключает ноль, дроби, десятичные дроби и отрицательные числа.

Примеры последовательных натуральных чисел
1,2,3,4,5,6,7,8,9 до бесконечности

Здесь ноль не является натуральным числом, потому что 0 не является ни положительным, ни отрицательным.

Что такое последовательные нечетные числа?
Нечетные последовательные числа — это те целые числа, которые можно разделить на 2, оставив остаток равным 1. Непрерывный поток четных чисел в списке называется четными последовательными числами.Непрерывный поток четных чисел в списке называется четными последовательными числами.

Примеры последовательных нечетных чисел
1, 3, 5, 7, 9, 11
53, 55, 57, 59, 61
Что такое последовательные четные числа?
Четные последовательные числа — это те целые числа, которые нельзя полностью разделить на 2. Непрерывный поток четных чисел в списке называется четными последовательными числами.

Примеры последовательных четных чисел
0, 2, 4, 6, 8, 10
28, 30, 32, 34, 36
Что такое последовательные простые числа?
Числа, состоящие ровно из 2 множителей, 1 и самого числа, называются простыми числами. Ряд простых чисел называется последовательными простыми числами.

Примеры последовательных простых чисел
2, 3, 5, 7, 11, 13, 17
73, 79, 83, 89, 97
Как найти последовательные числа?
Предположим, n — целое число.

Следовательно, (n + 1) и (n + 2) будут следующими двумя последовательными целыми числами.

Часто задаваемые вопросы 
1. Что такое два последовательных четных числа?
Ответ: Любое четное число, которое следует за другим числом в последовательности, называется двумя последовательными четными числами.

Два последовательных четных числа: 2, 4 или 8, 10

2. Что такое два последовательных нечетных числа?
Ответ: Любое нечетное число, которое следует за другим числом в последовательности, называется двумя последовательными нечетными числами.

Два последовательных нечетных числа: 7, 9 или 13, 15

3. Найдите среднее значение первых 6 последовательных четных чисел.
Ответ: Первая сумма из n четных чисел будет:

=n(n+1)

Среднее

=n(n+1)/n

=n+1

Предположим, что первые шесть последовательных нечетных чисел 2, 4, 6, 8, 10, 12

следовательно, n = 6

=n(n+1)

=6(6+1)

=42

Сумма первых шести последовательных чисел равна 42

Среднее,

= n+1

= (6+1)

= 7

4. Найдите среднее значение первых 7 последовательных четных чисел.
Ответ: Первая сумма из n четных чисел будет:

= n (n+1)

Среднее

= n (n+1) / n

= n+1

Предположим, что первые шесть последовательных нечетных чисел 2, 4, 6, 8, 10, 12, 14

следовательно, n = 7

= n (n+1)

= 7 (7+1)

= 56

Сумма первых шести последовательных чисел равна 56

Среднее,

= n+1

= (7+1)

= 8

5. Какова формула последовательных нечетных чисел?
Ответ: Формула нечетных последовательных чисел:

Сумма n нечетных чисел = n 2

Вывод суммы нечетных чисел

Нечетное число = 1, 3, 5 ……..( 2n-1)

Здесь первое число (a) = 1

Последнее число (l) = (2n-1)

Сумма AP (арифметическая прогрессия) = n/2 (a +l)

= n/2 (1 + 2n -1)

= 2n 2/2
= n2

Формула: Сумма нечетных чисел = n 2

По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.

Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.

Последовательности чисел

Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной. 

Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.

Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.

Что такое числовая последовательность? 

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N. 

Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.

На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.

Какие бывают последовательности

Различают:

• постоянную, или монотонную последовательность: 1, 1, 1, 1, 1… 
• возрастающую последовательность, в которой каждый следующий элемент больше предыдущего
• убывающую последовательность, в которой каждый следующий элемент меньше предыдущего

Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.

Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Посмотрим на числа:

Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.

Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:

Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.

Сумма первых n членов прогрессии вычисляется по формуле:

Также африфметическая прогрессия обладает характреристическим свойством:

Геометрическая прогрессия

Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:

Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:

Сумма первых n членов прогрессии:

Характеристическое свойство геометрической прогрессии:

Способы задания последовательностей

Последовательность можно задать несколькими способами:

1. Аналитически или, проще говоря, формулой.
2. Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие.
3. Описательно, простым перечислением всех элементов последовательности.

Предел последовательности

Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.

Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.

Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.

Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел. 

Что нужно помнить, вычисляя пределы последовательностей

Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.

1. Последовательность может иметь только один предел.
2. Если последовательность имеет предел, то она ограничена. Обратное верно не всегда!
3. Если члены некоторой последовательности zn заключены между соответствующими членами двух последовательностей xn, yn, сходящихся к одному пределу, то и эта последовательность сходится к тому же пределу.
4. Предел постоянной последовательности равен ее постоянному.
5. Если две последовательности x и y равны между собой, то пределы этих последовательностей также равны между собой, если они существуют.
6. Если каждый член сходящейся последовательности не превосходит соответствующего члена другой сходящейся последовательности, то и предел первой не превосходит предела второй.
7. Предел суммы (разности) двух последовательностей равен сумме (разности) их пределов. При условии, что обе последовательности имеют пределы.
8. Предел произведения двух последовательностей, имеющих пределы, существует и равен произведению пределов последовательностей. 
9. Постоянный множитель можно выносить за знак предела.
10. Предел частного двух последовательностей, имеющих пределы, равен частному пределов этих последовательностей, если предел знаменателя не равен нулю.

Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором. 

Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.

План урока:

Понятие числовой последовательности

Способы задания последовательностей

Возрастающие и убывающие последовательности

Ограниченные и неограниченные последовательности

Последовательности в жизни

Понятие числовой последовательности

Попытаемся записать в ряд все четные числа, начиная с двойки:

2, 4, 6, 8, 10, 12

Ясно, что запись можно продолжать бесконечно. Мы получили некоторый ряд чисел, в данном случае бесконечный. Любой такой ряд называется бесконечной числовой последовательностью

Приведем примеры бесконечных числовых послед-тей:

Заметим, что числа в послед-ти могут повторяться. Так, известно, что число π – это бесконечная десятичная дробь 3,1415926… Выписывая в ряд эти цифры, можно получить послед-ть, в которой будут повторяющиеся числа:

3, 1, 4, 1, 5, 9, 2, 6

Числа, входящие в состав послед-ти, называют членами послед-ти. Всегда можно указать, какое число является первым членом послед-ти, какое – вторым и т. д. Для их обозначения используются буквы с индексами. Например, есть послед-ть четных чисел 2, 4, 6, 8… Выпишем первые ее члены, обозначая их буквой а:

Получается, что каждому натуральному числу n соответствует какой-то единственный член послед-ти, который обозначается как а_n. То есть послед-ть задает некое правило, с помощью которого для каждого числа n можно вычислить число a_n. Отсюда можно сформулировать более сложное определение бесконечной числовой послед-ти – это функция, областью определения которой является множество натуральных чисел.

Способы задания последовательностей

Чтобы задать послед-ть, необходимо указать способ, с помощью которого можно вычислить любой ее член. Проще всего это сделать, записав формулу, в которой в качестве переменной использует номер члена послед-ти n.Такая формула называется формулой n-ого члена последовательности.

Пример. Послед-ть задается формулой а_n = 3n. Выпишите первые пять членов этой послед-ти.

Решение. Чтобы найти первый член послед-ти, то есть а₁, просто подставим в формулу единицу:

Аналогично можно вычислить и следующие четыре члена послед-ти:

Итак, послед-ть имеет вид:

3, 6, 9, 12, 15…

Ответ: 3, 6, 9, 12, 15

Пример:Запишите формулу n-ого члена для послед-ти

1, 3, 5, 7, 9…

состоящей из положительных нечетных чисел.

Решение. Каждое нечетное число можно представить в виде 2n– 1. Тогда получаем:

Получаются как раз члены послед-ти, указанной в условии. Поэтому формула n-ого члена будет выглядеть как а_n = 2n– 1.

Ответ: а_n = 2n– 1.

Стоит обратить внимание, что для вычисления n-ого члена послед-ти НЕ нужно вычислять все предшествующие члены.

Пример. Запишите 38-й член послед-ти, заданной формулой а_n = 2n² + 1.

Решение. Подставим n = 38 в формулу и получим:

Ответ: 1445

Теперь рассмотрим послед-ть, в которой первые два числа равны единице, а каждый следующий член равен сумме двух предыдущих. Она называется последовательностью Фибоначчи и начинается так:

1, 1, 2, 3, 5, 8, 13, 21…

Действительно, по условию, первые два члена – это единица:

а каждый следующий равен сумме предыдущих:

Формулу n-ого члена записать для послед-ти Фибоначчи очень сложно (хотя и возможно). Вместо этого здесь удобнее использовать рекуррентный способ задания последовательности. Записываются первые несколько членов послед-ти, а после дается формула (ее называют рекуррентной), которая позволяет вычислить следующие члены по предыдущим:

При использовании рекуррентного способа для вычисления n-ого члена обычно необходимо вычислить все предыдущие члены послед-ти.

Пример. Найдите пятый член послед-ти, заданной рекуррентной формулой а_n= 3•а_n–1– 1, если а₁ = 2.

Решение. Будем последовательно вычислять все члены послед-ти, вплоть до пятого:

Ответ: 5

Надо понимать, что одну и ту же послед-ть можно задать по-разному. Так, послед-ть четных чисел можно задать формулой n-ого члена а_n = 2n, так и рекуррентной формулой а_n = a_n–1 + 2, если а₁ = 1.

Пример. Дана послед-ть, заданная формулой а_n = n². Задайте ее рекуррентным способом.

Решение. Сначала вычислим первый член послед-ти:

Чтобы записать рекуррентную формулу, попытаемся найти разницу между членами, имеющими номера n и (n– 1):

Итак, получили равенство

Перенесем в нем слагаемое (– a_{n– 1}) вправо и получим рекуррентную формулу:

Наконец, некоторые послед-тине получается задать ни формулой n-ого члена, ни рекуррентным способом. Их можно только описать. Таковой является, например, послед-ть простых чисел:

2, 3, 5, 7, 11…

Мы не будем это доказывать, однако не существует такой формулы, которая позволяла бы вычислить n-ое простое число либо по самому числу n, либо по предыдущим простым числам. Действительно, для построения такой послед-ти используют особый алгоритм, известный как решето Эратосфена. Если бы существовала формула n-ого члена, то потребность в использовании решета Эратосфена отпала бы.

Возрастающие и убывающие последовательности

Рассмотрим послед-ть, заданную формулой а_n = 5n:

5, 10, 15, 20, 25…

Очевидно, что каждый следующий член больше предыдущего. Это значит, что мы имеем дело с возрастающей последовательностью.

Теперь изучим послед-ть, заданной рекурсивным способом:

Выглядеть он будет так:

50, 48, 46, 44, 42…

Ясно, что каждый следующий член послед-ти меньше предыдущего. Такой ряд чисел называется убывающей последовательностью.

Убывающие и возрастающие послед-ти называют также монотонными последовательностями.

Для того, чтобы определить характер послед-ти, достаточно найти разность членов а_nи а_n+1. Если получается положительное выражение, то послед-ть возрастает, а если выражение отрицательно, то послед-ть убывает. Если получилось выражение, которое может иметь различный знак, то послед-ть вовсе не является монотонной.

Пример. Послед-ть задана формулой a_n = n/(n + 1). Является ли она убывающей либо возрастающей?

Решение. Запишем выражения для вычисления n-ого и (n+ 1)-ого члена послед-ти:

Осталось найти их разницу:

При натуральных значениях n полученная разница является положительным числом. Это значит, что каждый следующий член больше предыдущего, то есть послед-ть является возрастающей.

Ответ: возрастающая.

Пример. Исследуйте на монотонность послед-ть, заданную формулой

Решение. Если выписать первые члены послед-ти, может показаться, что она – убывающая:

-7, -12, -15, -16…

Но это не так. Запишем выражения для n-ого и (n + 1)-ого члена послед-ти:

Теперь найдем их разность:

Получили выражение (2n– 7), которое может быть как отрицательным, так и положительным (при n≥ 4). Это значит, что послед-ть немонотонна. В этом можно убедиться, вычислив четвертый и пятый член послед-ти:

Получаем, что у₅>у₄, поэтому послед-ть не является убывающей

Ответ: послед-ть немонотонна.

 Ограниченные и неограниченные последовательности

Изучим послед-ть, заданную с помощью формулы b_n = 1/n. Её первые члены будут выглядеть так:

Очевидно, что она является убывающей, ведь каждая следующая дробь меньше предыдущей. Вместе с тем все члены послед-ти являются положительными числами. Это значит, что для каждого n выполняется неравенство b_n> 0. То есть последовательность ограничена числом 0. В математике такие послед-ти называют ограниченными снизу.

Существует и послед-ти, ограниченные сверху. Это такие послед-ти, каждый член которых меньше какого-то постоянного числа.

В качестве примера можно привести послед-ть, заданную формулой с_n = 1 – 1/n. Каждый следующий ее член все ближе к единице, но ни один из них не достигает ее. Покажем, как строго доказать это. Для этого используют метод рассуждений «от противного».

Предположим, что послед-ть с_n = 1 – 1/n не ограничена числом 1 сверху. Тогда существует такой ее член с_n, для которого выполняется условие

Попытаемся найти номер этого члена:

Полученное нер-во выполняется только для отрицательных n. Но n – это натуральное, то есть положительное число. Это говорит о том, что не существует такого натурального n, для которого справедливо нер-во 0 ≥ 1/n. Значит, и не существует такого с_n, для которого верно нер-во с_n ≥ 1. Из этого следует, что послед-ть ограничена сверху числом 1.

Пример. Докажите, что послед-ть m_n = n² – 6n + 4 ограничена снизу числом (– 6).

Решение. Предположим, что на самом деле послед-ть не ограничена снизу числом (– 6). Тогда хотя бы для одного ее члена будет выполняться нер-во

Найдем номер этого члена:

Получили неравенство второй степени. Для его решения следует найти корни квадратного трехчлена. Начнем с вычисления дискриминанта:

Дискриминант отрицательный, а ветви параболы смотрят вверх. Поэтому схематично парабола относительно оси Ох будет располагаться так:

Видно, что нер-во решений не имеет. Значит, не существует такого номера n, для которого верно условие m_n ≤ – 6. Следовательно, послед-ть ограничена снизу числом (– 6).

Если послед-ть ограничена одновременно и снизу, и сверху, то ее называют просто ограниченной послед-тью.

Примером ограниченной последовательности является b_n = 1/n. С одной стороны, она ограничена нулем снизу. С другой стороны, она ограничена сверху числом 2, так как первый ее член равен единице, а вся послед-ть – убывающая.

Примером неограниченной последовательности является v_n = 5n, ведь ее невозможно ограничить сверху.

Примером ограниченной последовательности является b_n = 1/n. С одной стороны, она ограничена нулем снизу. С другой стороны, она ограничена сверху числом 2, так как первый ее член равен единице, а вся послед-ть – убывающая.

Примером неограниченной последовательности является v_n = 5n, ведь ее невозможно ограничить сверху.

1, 3, 5, 7, 9…

Начнем вычислять сумму первых n членов двумя способами: просто складывая и используя формулу S_n= n². Посмотрим, будут ли получаться одинаковые результаты.

Видно, что формула работает. Однако, сколько бы раз мы не проверяли ее, это не будет служить строгим доказательством ее справедливости. Возможно, что она будет работать для первого миллиона члена послед-ти, а для 1000001-ого даст ошибку. Поэтому поступим иначе. Предположим, что фор-ла S_n= n² верна хотя бы для одного значения n, равного k:

Докажем, что тогда она будет верна и для следующего числа k + 1. То есть нужно доказать равенство

Ясно, что сумму (k + 1) членов послед-ти можно получить, прибавив к сумме k членов (то есть к S_k )ещё одно слагаемое a_n+1, то есть справедлива запись:

При этом мы предположили, что верно равенство

а число a_n+1 можно посчитать по формуле n-ого члена:

Тогда можно записать

Получили формулу сокращенного умножения – квадрат суммы. Его можно «свернуть»:

Итак, если для формула S_k= k² верна для k = 1 (а в этом мы убедились в самом начале), то она верна и для k = 2. Но если она верна для k = 2, то она верна и для k = 3 и т.д. Получаем цепочку утверждений, каждое из которых подтверждает истинность формулы для конкретного натурального числа k, а все вместе они подтверждают ее истинность для всех натуральных чисел. Таким образом, нам удалось доказать справедливость формулы S_n= n².

Сформулируем принцип математической индукции:

То есть сначала надо доказать, что утверждение выполняется при n = 1. Это действие называют шагом индукции. Далее предполагают, что утверждение верно при n = k, и из этого выводят, что оно верно и для n =k + 1.

Пример. Докажите с помощью математической индукции, что сумма квадратов первых n натуральных чисел вычисляется по формуле:

Решение. Докажем базис индукции, то есть то, что утверждение верно при n = 1. Действительно, подставив единицу в формулу, получим:

Получили один и тот же результат. Базис индукции доказан.

Теперь предположим, что формула верна для произвольного n = k:

Тогда сумма (k + 1) квадратов может быть найдена по формуле

Подставим в нее выражение для S_k и получим:

С другой стороны, нам надо доказать, что величина S_k+1определяется по формуле

Приравняем выражения (1) и (2) и покажем, что они тождественно равны:

Умножим обе части на 6 и получим:

Получили одинаковые выражения в обоих частях рав-ва, поэтому оно является верным при любом значении k. Значит, мы смогли доказать шаг индукции, и следовательно, всё исходное утверждение.

Пример. Докажите, что любую сумму, большую 7 копеек, можно оплатить, используя только два типа монет: по 3 и 5 копеек.

Это утверждение, очевидно, верно сумм в 8, 9 и 10 копеек:

Добавив к этим суммам ещё одну трехкопеечную монету, мы сможем получить выражения для следующих трех чисел:

С помощью ещё одной монетки в три копейки можно уплатить следующие 3 суммы:

Ясно, что продолжая подобные рассуждения, можно для любого натурального числа записать эквивалентную ему сумму пятерок и троек, что доказывает утверждение из условия.

Последовательности в жизни

Порою, изучая математические объекты, люди задумываются – а какое отношение все эти формулы имеют к реальной жизни? Встречаются ли последовательности в природе и обществе, или они являются лишь плодом фантазии математиков?

На самом деле последовательности имеют большое практическое приложение. Так, Фибоначчи сформулировал свою последовательность тогда, когда изучал скорость размножения кроликов. Если каждая пара кроликов рожает в месяц ещё одну пару, а через месяц и старая, и новая пара рожает ещё кроликов, то их численность будет расти также, как и последовательность Фибоначчи! Аналогично протекают процессы роста популяций других животных.

Большое значение последовательности имеют в программировании. Дело в том, что порою программам нужно получить некоторое случайное число, чтобы имитировать случайные события. Однако по ряду причин компьютеру тяжело сгенерировать истинно случайное число, поэтому часто используют генераторы псевдослучайных чисел. Это особые алгоритмы, порождающие последовательности чисел, которые кажутся случайными, хотя таковыми на самом деле не являются.

Встречаются последовательности и в астрономии. В частности, расстояние от планет до Солнца примерно можно рассчитать с помощью особой последовательности Тициуса-Боде. Последние исследования показывают, что и расположение планет в других планетных системах хорошо описывается этой последовательностью.

Шаяхметов Адил Бейсенович, учитель математики, информатики, ГУ «Амангельдинская средняя школа» отдела образования акимата Карасуского района, Костанайская область. Карасуский район, село Амангельды

Последовательности натуральных чисел и их закономерности

5 класс

Математика _5 класс _Последовательности натуральных чисел и их закономерности.Разработка урока  

Математика _5 класс _Последовательности натуральных чисел и их закономерности .Приложения к уроку 

Математика _5класс _Последовательности натуральных чисел . Презентация

Раздел долгосрочного плана: 5.1 А  Натуральные числа и ноль	Школа: ГУ Амангельдинская средняя школа
Дата:	ФИО учителя: Шаяхметов Адил Бейсенович
Класс: 5 класс	Количество присутствующих:	отсутствующих:
Тема урока	Последовательности натуральных чисел и их закономерности
Тип урока	Изучения новой темы
Цели обучения, которые достигаются на данном  уроке (ссылка на учебную программу)	5.2.3.1 устанавливать закономерности в последовательности из натуральных чисел 5.2.3.2 находить недостающие элементы в последовательностях из натуральных чисел
Цели урока	Рассмотреть закономерности последовательностей  натуральных чисел. Обеспечить усвоение нахождения закономерностей  и элементов в последовательности из натуральных чисел
Критерии оценивания	Знание и понимание Знает  и понимает ,что члены последовательности могут быть подчинены определенной закономерности ;     Критическое мышление Устанавливает  закономерности в последовательности из натуральных чисел ; Находит недостающие элементы в последовательностях из натуральных чисел; Оценка Обосновывает свой выбор подкрепляя записями и устными коментариями ;
	Языковые цели	Лексика и терминология, специфичная для предмета: Натуральные числа ,числовые последовательности , закономерность ,члены последовательности ,недостающие элементы последовательности . Полезные выражения для диалогов и письма: Установить закономерность в последовательности из натуральных чисел , найти недостающий элемент последовательности , обоснуйте свой выбор данного элемента последовательности
Привитие ценностей	Привитие уважения и академической честности через организацию парной работы
Межпредметные связи	Связь с физкультурой
Навыки использования ИКТ	Использование презентаций
Предварительные знания	Последовательности из натуральных чисел ,текстовые задачи
Запланиро ванные этапы урока
Начало  урока  4   мин	Приветствие .Позитивный  настрой на урок Постановка цели урока	Презентация Слайды 1-3
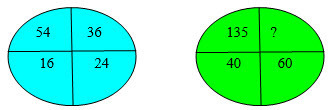
Середина  урока                                      6  мин 15 мин 3  мин 7 мин 2 мин	2.Индивидуальная работа . Устно.  Найдите недостающее число в таблице  и в круге: 3.Изучение новой темы (фронтальная работа) Обсуждение  с учащимися примеров  из жизни, связанные с числовыми закономерностями. Например, обратить внимание учащихся: на нумерацию домов на улице (по одной стороне улицы номера домов чётные, по другой – нечётные); на нумерацию квартир одного подъезда (на лестничной площадке по 3 квартиры; каковы номера квартир, расположенных посередине на всех этажах дома?); на расположение пакетов с макаронами на полке, начиная от пакетов по 1 кг до пакетов по 10 кг. Для каждого примера мы можем записать числовую последовательность :  а) 1,3,5,7,9, … в)   2,4,6,8,10,12, …  с )1,4,7,10,13,…  d)  5,10,15,20,25,…      Посмотрите внимательно на последовательности и установите какая закономерность выполняется для каждого случая      А теперь приведите примеры числовых последовательностей, которые вы  встречали в повседневной жизни. Рассмотрим примеры : Установите закономерность и найдите следующий член последовательности : ) 6,4,10,8,14,… 2) 3,6,12,24,48,… 3)0,3,8,15,24,… 4)5,8,11,15,19… Физкультминутка 4. Работа в парах  Задание    1 уровень 1) Установить  закономерность  и  определить 2 последующих элемента последовательности 1)21,20,18,15,11,… 2)1,4,9,16,25,36…  2 Продвинутый уровень Найдите неправильное число последовательности :   1) 2,6,18,52,162,486;   2) 120,115,105,90,70,50,15; 5 . Самооценивание  по готовым ответам . Обратная связь	Презентация Слайды 4-5 nazva.net/rubric/4 Раздаточный материал Приложение 1 Презентация Слайд 6 Приложение 2 panda_convert.mp4 Раздаточный материал Приложение 3
Конец  урока 5  мин 3 мин	6.Подведение итогов урока Рефлексия Стратегия  Анкета 1. На уроке я работал 2. Своей работой на уроке я 3. Урок для меня показался 4. За урок я 5. Материал урока мне был 6. Домашнее задание мне кажется активно / пассивно доволен / не доволен коротким / длинным не устал / устал понятен / не понятен полезен / бесполезен интересен / скучен легким / трудным интересным / неинтересным Домашнее заданиие 1) Установить закономерности и записать 2 недостающих элемента: 1)3,5,10,12,24,26,… 2)1,2,2,4,8,32… 2) Придумать 2 последовательности с определенной закономерностью	Раздаточный материал Приложение 4 Раздаточный материал Приложение 5
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?	Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?	Здоровье и соблюдение техники безопасности
Учащиеся в течение урока будут работать в парах, индивидуально. Более способным ученикам будет предоставлена возможность оказать помощь менее способным.	Проверка уровня усвоения материала будет проведена в форме фронтальной работы учащихся, в форме индивидуальной работы.	В начале урока учащиеся ознакомлены с правилами поведения и техникой безопасности на уроке.
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему?
Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?