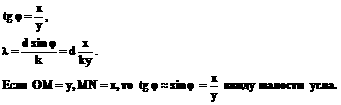Как найти постоянную дифракционной решетки формула

1. Цель работы:

С
помощью измерений и последующего
использования формулы для главных
максимумов дифракционной решетки
определить постоянную дифракционной
решетки и оценить допущенную погрешность.

2. Теоретическая часть

Такие
простейшие
оптические явления, как прямолинейность
распространения в однородной среде,
отражение и преломление света можно
объяснить с помощью как корпускулярных,
так и волновых представлений о природе
света. И те, и другие содержат ряд
парадоксов. Однако понять и объяснить
такие явления, как интерференция,
дифракция и поляризация света можно
только в том случае, если считать, что
свет — волна. Х. Гюйгенс сформулировал
принцип, согласно которому каждая точка
оптической среды, которой в данный
момент времени достигла световая волна,
представляет собой элементарный источник
сферических световых волн, а волновой
фронт в любой следующий момент времени
представляет собой огибающую (результат
сложения) волн от элементарных источников.

В этом случае
малое препятствие на пути волнового
фронта не приведет к возникновению
геометрической тени, поскольку свет от
элементарных источников, расположенных
на волновом фронте в стороне от
препятствия, будет попадать в область
тени. Эффективно это выглядит как
огибание светом препятствия. Такое
явление называется дифракцией.

Э

лементарные
источники на одном и том же сферическом
фронте F
когерентны. Если они расположены на
разных расстояниях от выбранной точки
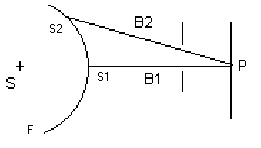
наблюдения Р (рис.1), то в общем случае
свет от них будет приходить в эту точку
в разных фазах. Результат сложения
когерентных волн будет

Рис.1

определяется
разностью их фаз.

Если
расстояния В₁
(кратчайшее расстояние от фронта волны,
испускаемой источником S,
до точки наблюдения Р) и В₂
различаются
на половину длины волны света, то
колебания от соответствующих элементарных
источников S₁
и S₂
приходят в точку Р в противофазе и гасят
друг друга. То же самое происходит, если
эти расстояния различаются на любое
нечетное число полуволн. Если же разность
расстояний равна длине волны излучения
или кратна ей, то волны от двух источников
приходят в точку Р в одинаковых фазах
и усиливают друг друга при сложении.

Сферический
волновой фронт может быть разбит на
зоны Френеля, которые представляют
собой такие кольцевые области, что свет
от любой пары соседних зон будет приходить
в точку наблюдения в противофазе. Это
возможно тогда, когда расстояние от
краев соседних зон до точки наблюдения
будут отличаться друг от друга на
половину длины волны. Если между
источником и экраном имеется преграда
в виде отверстия, то суммарная освещенность
в точке Р будет зависеть от того, четное
или нечетное число зон Френеля
соответствуют волновому фронту,
достигшему этого отверстия. В первом
случае произойдет практически полное
гашение света, во втором случае останется
нескомпенсированный вклад одной из
зон.

Если вырезать
специальную преграду в виде концентрических
колец, перекрывающих путь свету только
от четных или только от нечетных зон
Френеля для данного взаимного расположения
источника, преграды и экрана, то
компенсации света от соседних зон, как
это имеет место, когда никакой преграды
нет, происходить не будет. Поэтому будет
иметь место усиление освещенности в
данной точке экрана.

Эти
соображения позволяют установить, где
будут находиться минимумы засветки
экрана при дифракции плоскопараллельного
пучка света на щели. После прохождения
щели свет попадает на экран под разными
углами φ к первоначальному направлению.
Если ширина b
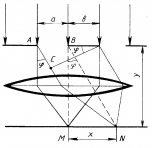
щели (рис. 2) такова, что в направлении φ
на ней укладывается четное число зон
Френеля, то в данном направлении
произойдет взаимное гашение света, и
на экране будет минимум засветки. Для
того чтобы узнать, сколько зон Френеля
укладывается на щели, необходимо
определить разность хода двух лучей,
проходящих через границы щели.

Рис.2

Если
окажется, что разность хода равна четному
числу полуволн, то и зон Френеля будет
четное число, что соответствует минимуму
засветки экрана в данном направлении.
Из рисунка видно, что упомянутая разность
хода равна bsin.
Поэтому условие минимума освещенности
на щели имеет вид

,

(1)

где
k
— целые числа 1, 2, 3… .

Дифракционной
решеткой называется система параллельных
щелей, ширина которых и промежутки между
которыми сравнимы с длиной волны
падающего света. Расстояние d,
равное сумме ширины b
щели и промежутка a
между щелями, называется постоянной
решетки (или периодом решетки, или шагом
решетки), d
= a
+ b.
При дифракции света на дифракционной
решетке максимумы засветки для различных
длин волн оказываются в разных местах
экрана, белый свет разлагается в спектр.
Каждое вещество обладает своими
спектральными характеристиками, поэтому
дифракционную решетку можно использовать
для спектрального анализа.

Условие, определяющее
положение максимумов или минимумов
засветки экрана при дифракции на решетке,
нельзя записать так же просто, как
соответствующее условие для щели,
поскольку эта преграда устроена более
сложным образом. Формула, описывающая
положение главных максимумов дифракционной
решетки, имеет вид

,
(2)

где
d
— постоянная решетки, 
— угол между нормалью к решетке и
направлением на точку, в которой имеется
максимум засветки,


— длина волны падающего света.

В
некоторых случаях может оказаться, что
не все главные максимумы из тех, что
описываются формулой, видны. Это
происходит в тех случаях, когда ширина
щели в целое число раз отличается от
расстояния между щелями. В общем же
случае можно точно указать, какое
количество К
главных
максимумов можно наблюдать при заданных
условиях. Полагая sin
= 1, что соответствует максимальному
значению левой части формулы, а, значит,
и максимальному значению номера k
в правой части, получим

.
(3)

Однако
величина в правой части получившегося
соотношения не всегда является целой,
в то время как число максимумов — целое
число. Поэтому следует взять целую часть
(не округлить!) получившегося выражения.
Учитывая, что и с другой стороны от
нулевого главного максимума имеется
столько же главных максимумов, а также
включая в общее их число нулевой главный
максимум, получим

.
(4)

При
исследовании спектров веществ с помощью
дифракционной решетки важное значение
имеет ее разрешающая способность, т. е.
возможность наблюдать две близкие линии
спектра раздельно. Эта величина
характеризуется отношением малой
разности длин волн этих линий 
к длине волны 
любой из них и равна

.
Можно показать, что разрешающая
способность равна

,

(5)

где
k
— номер главного максимума, в котором
проводится измерение, N
— полное число линий решетки, на которые
падает излучение. Увеличение обоих
последних параметров повышает разрешающую
способность решетки.

В
современной физике (и в данной учебной
лабораторной работе) большую роль играет
лазерный источник света. Принцип работы
лазера состоит в том, что из двух известных
механизмов излучения света атомом —
спонтанного и вынужденного — специально
используется последний. При спонтанном
излучении возбужденный тем или иным
способом атом испускает фотон в
произвольном направлении, с произвольными
поляризацией и фазой. При вынужденном
излучении возбужденный атом испускает
фотон под воздействием еще одного
фотона, принадлежащего полю излучения,
в котором находится атом. В последнем
случае излучаемый фотон имеет те же
импульс, поляризацию и фазу, что и тот,
который стимулировал его излучение.
Поскольку вместо одного налетевшего
фотона теперь появляется два, происходит
усиление излучения, которое является
когерентным.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Дифракция света
Характерным проявлением волновых свойств света является дифракция света — отклонение света от прямолинейного рас­пространения на резких неоднородностях среды. Дифракция была открыта Ф.Гримальди в конце XVII в. Объяснение яв­ления дифракции света дано Т. Юнгом и О. Френелем, которые не только дали описание экспериментов по наблюдению явлений интерференции и дифракции света, но и объяснили свойство пря­молинейности распространения света с позиций волновой теории.
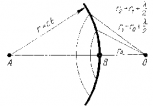
Зоны Френеля Принцип Гюйгенса — Френеля: волновая поверх­ность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции. Для того чтобы найти амплитуду световой волны от точечного моно­хроматического источника света А в произвольной точке О изо­тропной среды, надо источник света окружить сферой радиусом r=ct. Интерференция волны от вторичных источников, располо­женных на этой поверхности, определяет амплитуду в рассмат­риваемой точке О, т. е. необходимо произвести сложение коге­рентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах. Наименьшее расстояние от точки О до волновой поверхности В равно r0. Первая зона Френеля ограничивается точками волновой поверхности, рассто­яния от которых до точки О равны: , где λ — длина световой волны. Вторая зона . Аналогично определяются границы других зон. Если разность хода  от двух соседних зон равна половине длины волны, то коле­бания от них приходят в точку О в противоположных фазах и на­блюдается интерференционный минимум, если разность хода равна длине волны, то наблю­дается интерференционный максимум. Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно). Расчеты позволили понять, каким образом свет от точечного источника, испускающего сферические волны, достигает про­извольной точки О пространства.
Дифракция от различных препятствий: от тонкой прово­лочки; от круглого отверстия; от круглого непрозрачного экрана.
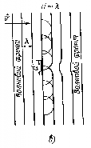
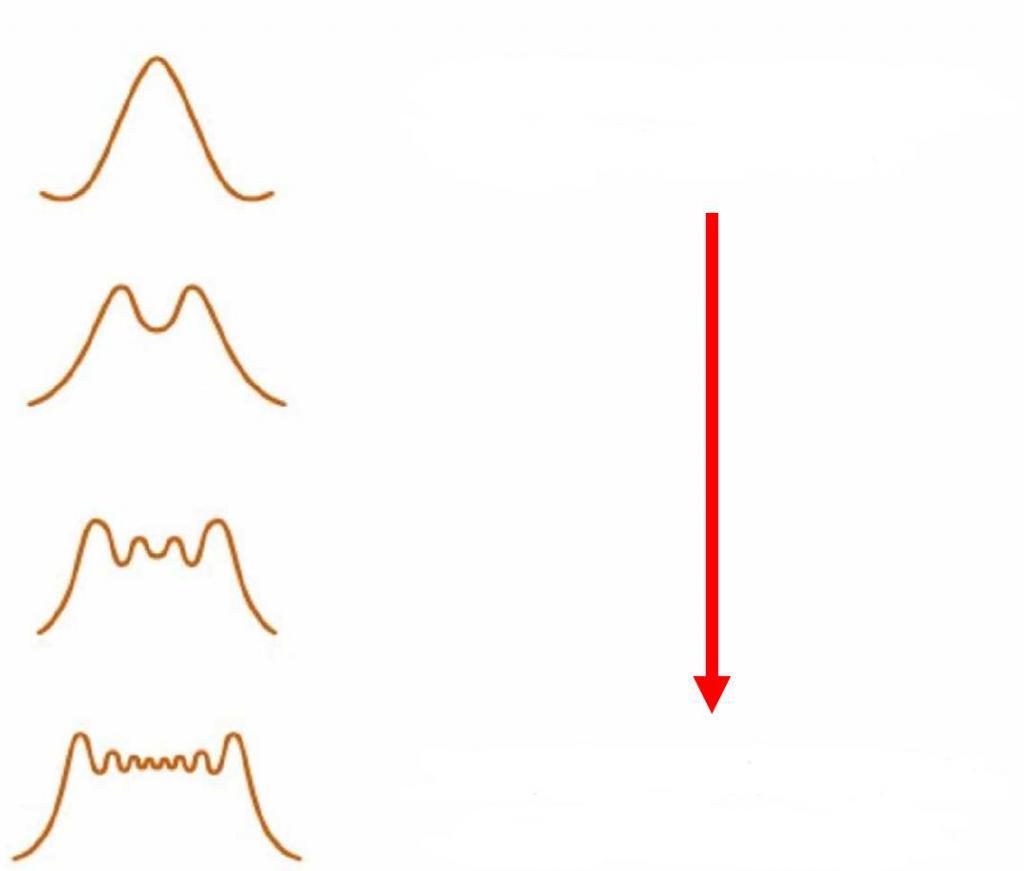
Дифракция происходит на предметах любых размеров, а не только соизмеримых с длиной волны λ. Трудности наблюдения заключаются в том, что вследствие малости длины световой волны интерференционные максиму­мы располагаются очень близко друг к другу, а их интенсив­ность быстро убывает.
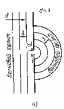
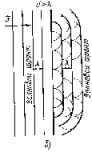
Дифракция наблюдается хорошо на расстоянии . Если , то дифракция невидна и получается резкая тень (d — диаметр экрана). Эти соотношения определяют границы применимости геометрической оптики. Если наблюдение ведется на расстоянии , где d—размер предмета, то начинают проявляться волновые свойства света. На рис. показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны.
Интерференционные картины от разных точек предмета пе­рекрываются, и изображение смазывается, поэтому прибор не выделяет отдельные детали предмета. Дифракция устанавлива­ет предел разрешающей способности любого оптического при­бора. Разрешающая способность человеческого глаза приблизите­льно равна одной угловой минуте: , где D — диаметр зрач­ка; телескопа α=0,02» микроскопа: увеличение не более 2-103 раз. Можно видеть предметы, размеры которых соизмеримы с длиной световой волны.
Дифракционная решетка
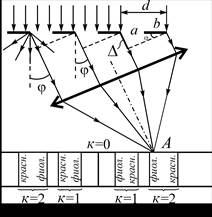
Дифракционная решетка — система препятствий (параллельных штрихов), сравнимых по размерам с длиной волны. Величина d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части. Угол φ — угол отклонения световых волн вследствие дифракции. Наша задача — определить, что будет наблюдаться в произвольном направлении φ — максимум или минимум. Оптическая разность хода  Из условия максимума интерференции получим: . Следовательно:  — формула дифракционной решетки. Величина k — порядок дифракцион­ного максимума ( равен 0, ± 1, ± 2 и т.д.).
Определение λ с помощью дифракционной решетки

5.5. Дифракционная решетка

Широкое распространение в научном эксперименте и технике получили дифракционные решетки, которые представляют собой множество параллельных, расположенных на равных расстояниях одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. Дифракционные решетки изготавливаются с помощью делительной машины, наносящей штрихи (царапины) на стекле или другом прозрачном материале. Там, где проведена царапина, материал становится непрозрачным, а промежутки между ними остаются прозрачными и фактически играют роль щелей.

Рассмотрим сначала дифракцию света от решетки на примере двух щелей. (При увеличении числа щелей дифракционные максимумы становятся лишь более узкими, более яркими и отчетливыми.)

Пусть а — ширина щели, a b — ширина непрозрачного промежутка (рис. 5.6).

Рис. 5.6. Дифракция от двух щелей

Период дифракционной решетки — это расстояние между серединами соседних щелей:

Разность хода двух крайних лучей равна

Если разность хода равна нечетному числу полуволн

то свет, посылаемый двумя щелями, вследствие интерференции волн будет взаимно гаситься. Условие минимумов имеет вид

Эти минимумы называются дополнительными.

Если разность хода равна четному числу полуволн

то волны, посылаемые каждой щелью, будет взаимно усиливать друг друга. Условие интерференционных максимумов с учетом (5.36) имеет вид

Это формула для главных максимумов дифракционной решетки.

Кроме того, в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, то есть главные минимумы решетки будут наблюдаться в направлениях, определяемых условием (5.21) для одной щели:

Если дифракционная решетка состоит из N щелей (современные решетки, применяемые в приборах для спектрального анализа, имеют до 200 000 штрихов, и период d = 0.8 мкм, то есть порядка 12 000 штрихов на 1 см), то условием главных минимумов является, как и в случае двух щелей, соотношение (5.41), условием главных максимумов — соотношение (5.40), а условие дополнительных минимумов имеет вид

Здесь k’ может принимать все целочисленные значения, кроме 0, N, 2N, . . Следовательно, в случае N щелей между двумя главными максимумами располагается (N–1) дополнительных минимумов, разделенных вторичными максимумами, создающими относительно слабый фон.

Положение главных максимумов зависит от длины волны l. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный — наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Заметим, что в то время как спектральная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, наоборот, сильнее отклоняет красные лучи.

Важной характеристикой всякого спектрального прибора является разрешающая способность.

Разрешающая способность спектрального прибора — это безразмерная величина

Дифракционная решётка

Дифракциейназывается любое отклонение распространения света от прямолинейного, не связанное с отражением и преломлением. Качественный метод расчета дифракционной картины предложил Френель. Основной идеей метода является принцип Гюйгенса — Френеля:

Каждая точка, до которой доходит волна, служит источником когерентных вторичных волн, а дальнейшее распространение волны определяется интерференцией вторичных волн.

Геометрическое место точек, для которых колебания имеют одинаковые фазы, называют волновой поверхностью. Волновой фронт также является волновой поверхностью.

Дифракционная решеткапредставляет собой совокупность большого числа параллельных щелей или зеркал одинаковой ширины и отстоящих друг от друга на одинаковом расстоянии.Периодом решетки (d)называется расстояние между серединами соседних щелей, или что то же самое сумма ширины щели (а) и непрозрачного промежутка (b)между ними (d = a + b).

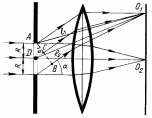
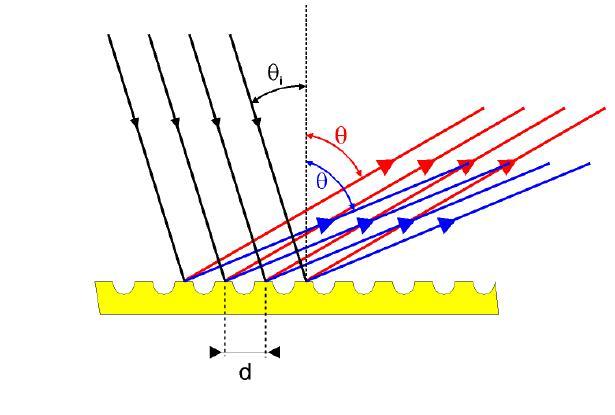
Рассмотрим принцип действия дифракционной решетки. Пусть на решетку нормально к её поверхности падает параллельный пучок лучей белого света (рис. 1). На щелях решетки, ширина которых соизмерима с длиной волны света, происходит дифракция.

Рис. 1. Ход лучей в дифракционной решетке

В результате за дифракционной решеткой согласно принципу Гюйгенса-Френеля от каждой точки щели световые лучи будут распространяться во всех возможных направлениях, которым можно сопоставить углы отклонения φ световых лучей (углы дифракции) от первоначального направления. Параллельные между собой лучи (дифрагирующие под одинаковым углом φ) можно сфокусировать, установив за решеткой собирающую линзу. Каждый пучок параллельных лучей соберется в задней фокальной плоскости линзы в определённой точке А. Параллельные лучи, соответствующие другим углам дифракции, соберутся в других точках фокальной плоскости линзы. В этих точках будет наблюдаться интерференция световых волн, исходящих от разных щелей решетки. 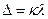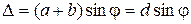Если оптическая разность хода между соответствующими лучами монохроматического света будет равна целому числу длин волн , κ = 0, ±1, ±2, …, то в точке наложения лучей будет наблюдаться максимум интенсивности света для данной длины волны, Из рисунка 1 видно, что оптическая разность хода Δ между двумя параллельными лучами, выходящими из соответствующих точек соседних щелей, равна

, (1)

где φ – угол отклонения луча решеткой.

Следовательно, условие возникновения главных интерференционных максимумов решетки или уравнение дифракционной решетки

, (2)

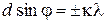
где λ – длина световой волны.

В фокальной плоскости линзы для лучей, не испытавших дифракции, наблюдается центральный белый максимум нулевого порядка (φ = 0, κ = 0), справа и слева от которого располагаются цветные максимумы (спектральные линии) первого, второго и последующих порядков (рис. 1). Интенсивность максимумов уменьшается с ростом их порядка, т.е. с увеличением угла дифракции.

Уравнение (1) позволяет рассчитать длину волны падающего света, если измерен угол дифракции φ, для данной спектральной линии, известны период дифракционной решетки d и порядок спектра k.

Зная период решетки, можно рассчитать число штрихов n, нанесенных на 1 мм ширины решетки:

. (3)

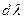
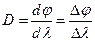
Одной из основных характеристик дифракционной решетки является её угловая дисперсия. Угловая дисперсия решетки определяет угловое расстояние dφ между направлениями для двух спектральных линий, отличающихся по длине волны на 1 нм ( = 1 нм), и характеризует степень растянутости спектра вблизи данной длины волны:

. (4)

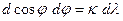
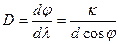
Формула для расчета угловой дисперсии решетки может быть получена при дифференцировании уравнения (2) . Тогда

. (5)

Из формулы (5) следует, что угловая дисперсия решетки тем больше, чем больше порядок спектра.

Для решеток с разными периодами ширина спектра больше у решетки, характеризующейся меньшим периодом. Обычно в пределах одного порядка 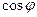меняется незначительно (особенно для решеток с небольшим числом штрихов на миллиметр), поэтому дисперсия в пределах одного порядка почти не меняется. Спектр, полученный при постоянной дисперсии, растянут равномерно во всей области длин волн, что выгодно отличает спектр решетки от спектра, даваемого призмой.

Угловая дисперсия связана с линейной дисперсией . Линей­ную дисперсию можно также вычислить по формуле

, (6) где – линейное расстояние на экране или фотопластинке между спектральными линиями, f – фокусное расстояние линзы.

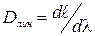
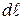
Дифракционная решетка также характеризуется разрешающей способностью. Этавеличина, характеризующая способность дифракционной решетки давать раздельное изображение двух близких спектральных линий

R = 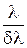, (7)

где l – средняя длина волны разрешаемых спектральных линий; dl – разность длин волн двух соседних спектральных линий.

Зависимость разрешающей способности от числа щелей дифракционной решетки N определяется формулой

R = 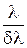= kN, (8)

где k – порядок спектра.

Из уравнения для дифракционной решетки (1) можно сделать следующие выводы:

1. Дифракционная решетка будет давать заметную дифракцию (значительные углы дифракции) только в том случае, когда период решетки соизмерим с длиной световой волны, то есть d »l» 10 –4 см. Решетки с периодом меньше длины волны не дают дифракционных максимумов.

2. Положение главных максимумов дифракционной картины зависит от длины волны. Спектральные составляющие излучения немонохроматического пучка отклоняются решеткой на разные углы (дифракционный спектр). Это позволяет использовать дифракционную решетку в качестве спектрального прибора.

3. Максимальный порядок спектра, при нормальном падении света на дифракционную решетку, определяется соотношением:

Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем и частотой штрихов, что позволяет перекрыть область спектра от ультрафиолетовой его части (l » 100 нм) до инфракрасной (l » 1 мкм). Широко используются в спектральных приборах гравированные решетки (реплики), которые представляют собой отпечатки решеток на специальных пластмассах с последующим нанесением металлического отражательного слоя.

Дата добавления: 2015-06-10 ; просмотров: 10857 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Основная формула дифракционной решетки

Одними из известных эффектов, которые подтверждают волновую природу света, являются дифракция и интерференция. Главная область их применения — спектроскопия, в которой для анализа спектрального состава электромагнитного излучения используют дифракционные решетки. Формула, которая описывает положение главных максимумов, даваемых этой решеткой, рассматривается в данной статье.

В чем заключаются явления дифракции и интерференции?

Прежде чем рассматривать вывод формулы дифракционной решетки, следует познакомиться с явлениями, благодаря которым это решетка оказывается полезной, то есть с дифракцией и интерференцией.

Вам будет интересно: Пополняем словарный запас: факир — это.

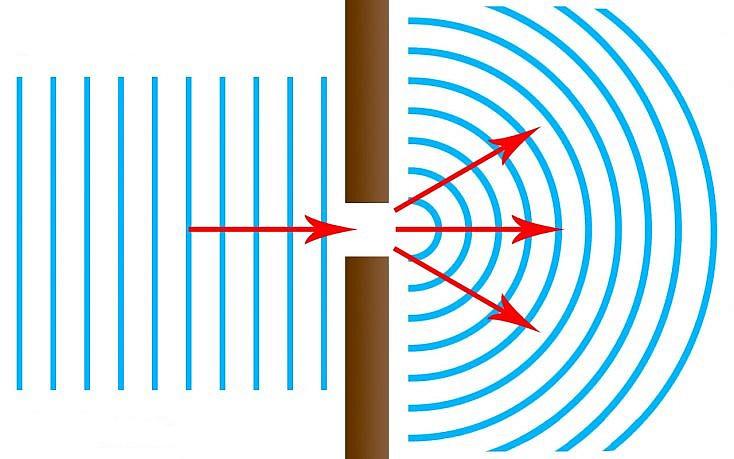
Дифракция — это процесс изменения движения волнового фронта, когда на своем пути он встречает непрозрачное препятствие, размеры которого сравнимы с длиной волны. Например, если через маленькое отверстие пропустить солнечный свет, то на стене можно наблюдать не маленькую светящуюся точку (что должно было произойти, если бы свет распространялся по прямой линии), а светящееся пятно некоторых размеров. Этот факт свидетельствует о волновой природе света.

Интерференция — еще одно явление, которое характерно исключительно для волн. Его суть заключается в наложении волн друг на друга. Если волновые колебания от нескольких источников согласованы (являются когерентными), тогда можно наблюдать устойчивую картину из чередующихся светлых и темных областей на экране. Минимумы на такой картине объясняются приходом волн в данную точку в противофазе (pi и -pi), а максимумы являются результатом попадания в рассматриваемую точку волн в одной фазе (pi и pi).

Оба описанных явления впервые объяснил англичанин Томас Юнг, когда исследовал дифракцию монохроматического света на двух тонких щелях в 1801 году.

Принцип Гюйгенса-Френеля и приближения дальнего и ближнего полей

Математическое описание явлений дифракции и интерференции является нетривиальной задачей. Нахождение точного ее решения требует выполнение сложных расчетов с привлечением максвелловской теории электромагнитных волн. Тем не менее в 20-е годы XIX века француз Огюстен Френель показал, что, используя представления Гюйгенса о вторичных источниках волн, можно с успехом описывать эти явления. Эта идея привела к формулировке принципа Гюйгенса-Френеля, который в настоящее время лежит в основе вывода всех формул для дифракции на препятствиях произвольной формы.

Тем не менее даже с помощью принципа Гюйгенса-Френеля решить задачу дифракции в общем виде не удается, поэтому при получении формул прибегают к некоторым приближениям. Главным из них является плоский волновой фронт. Именно такая форма волны должна падать на препятствие, чтобы можно было упростить ряд математических выкладок.

Следующее приближение заключается в положении экрана, куда проецируется дифракционная картина, относительно препятствия. Это положение описывается числом Френеля. Оно вычисляется так:

Где a — геометрические размеры препятствия (например, щели или круглого отверстия), λ — длина волны, D — дистанция между экраном и препятствием. Если для конкретного эксперимента F 1, тогда имеет место приближение ближнего поля или дифракция Френеля.

Разница между дифракциями Фраунгофера и Френеля заключается в различных условиях для явления интерференции на маленьком и большом расстояниях от препятствия.

Вывод формулы главных максимумов дифракционной решетки, который будет приведен далее в статье, предполагает рассмотрение дифракции Фраунгофера.

Дифракционная решетка и ее виды

Эта решетка представляет собой пластинку из стекла или прозрачного пластика размером в несколько сантиметров, на которую нанесены непрозрачные штрихи одинаковой толщины. Штрихи расположены на постоянном расстоянии d друг от друга. Это расстояние носит название периода решетки. Две других важных характеристики прибора — это постоянная решетки a и число прозрачных щелей N. Величина a определяет количество щелей на 1 мм длины, поэтому она обратно пропорциональна периоду d.

Существует два типа дифракционных решеток:

• Прозрачная, которая описана выше. Дифракционная картина от такой решетки возникает в результате прохождения через нее волнового фронта.
• Отражающая. Она изготавливается с помощью нанесения маленьких бороздок на гладкую поверхность. Дифракция и интерференция от такой пластинки возникают за счет отражения света от вершин каждой бороздки.

Какой бы ни был тип решетки, идея ее воздействия на волновой фронт заключается в создании периодического возмущения в нем. Это приводит к образованию большого количества когерентных источников, результатом интерференции которых является дифракционная картина на экране.

Основная формула дифракционной решетки

Вывод этой формулы предполагает рассмотрение зависимости интенсивности излучения от угла его падения на экран. В приближении дальнего поля получается следующая формула для интенсивности I(θ):

I(θ) = I0*(sin(β)/β)2*[sin(N*α)/sin(α)]2, где

α = pi*d/λ*(sin(θ) — sin(θ0));

β = pi*a/λ*(sin(θ) — sin(θ0)).

В формуле ширина щели дифракционной решетки обозначается символом a. Поэтому множитель в круглых скобках отвечает за дифракцию на одной щели. Величина d — это период дифракционной решетки. Формула показывает, что множитель в квадратных скобках, где появляется этот период, описывает интерференцию от совокупности щелей решетки.

Пользуясь приведенной формулой, можно рассчитать значение интенсивности для любого угла падения света.

Если находить значение максимумов интенсивности I(θ), то можно прийти к выводу, что они появляются при условии, что α = m*pi, где m является любым целым числом. Для условия максимумов получаем:

m*pi = pi*d/λ*(sin(θm) — sin(θ0)) =>

sin(θm) — sin(θ0) = m*λ/d.

Полученное выражение называется формулой максимумов дифракционной решетки. Числа m — это порядок дифракции.

Другие способы записи основной формулы для решетки

Заметим, что в приведенной в предыдущем пункте формуле присутствует член sin(θ0). Здесь угол θ0 отражает направление падения фронта световой волны относительно плоскости решетки. Когда фронт падает параллельно этой плоскости, то θ0 = 0o. Тогда получаем выражение для максимумов:

Поскольку постоянная решетки a (не путать с шириной щели) обратно пропорциональна величине d, то через постоянную дифракционной решетки формула выше перепишется в виде:

Чтобы не возникало ошибок при подстановке конкретных чисел λ, a и d в эти формулы, следует всегда использовать соответствующие единицы СИ.

Понятие об угловой дисперсии решетки

Будем обозначать эту величину буквой D. Согласно математическому определению, она записывается следующим равенством:

Физический смысл угловой дисперсии D заключается в том, что она показывает, на какой угол dθm сместится максимум для порядка дифракции m, если изменить длину падающей волны на dλ.

Если применить это выражение для уравнения решетки, тогда получится формула:

Дисперсия угловая дифракционной решетки определяется по формуле выше. Видно, что величина D зависит от порядка m и от периода d.

Чем больше дисперсия D, тем выше разрешающая способность данной решетки.

Разрешающая способность решетки

Под разрешающей способностью понимают физическую величину, которая показывает, на какую минимальную величину могут отличаться две длины волны, чтобы их максимумы на дифракционной картине появлялись раздельно.

Разрешающая способность определяется критерием Рэлея. Он гласит: два максимума можно разделить на дифракционной картине, если расстояние между ними оказывается больше полуширины каждого из них. Угловая полуширина максимума для решетки определяется по формуле:

Разрешающая способность решетки в соответствии с критерием Рэлея равна:

Δθm>Δθ1/2 или D*Δλ>Δθ1/2.

Подставляя значения D и Δθ1/2, получаем:

Это и есть формула разрешающей способности дифракционной решетки. Чем больше число штрихов N на пластинке и чем выше порядок дифракции, тем больше разрешающая способность для данной длины волны λ.

Дифракционная решетка в спектроскопии

Выпишем еще раз основное уравнение максимумов для решетки:

Здесь видно, что чем больше длина волны падает на пластинку со штрихами, тем при больших значениях углов будут появляться максимумы на экране. Иными словами, если через пластинку пропустить немонохроматический свет (например, белый), то на экране можно видеть появление цветных максимумов. Начиная от центрального белого максимума (дифракция нулевого порядка), дальше будут появляться максимумы для более коротких волн (фиолетовый, синий), а затем для более длинных (оранжевый, красный).

Другой важный вывод из этой формулы заключается в зависимости угла θm от порядка дифракции. Чем больше m, тем больше значение θm. Это означает, что цветные линии будут сильнее разделены между собой на максимумах для высокого порядка дифракции. Этот факт уже был освящен, когда рассматривалась разрешающая способность решетки (см. предыдущий пункт).

Описанные способности дифракционной решетки позволяют использовать ее для анализа спектров излучения различных светящихся объектов, включая далекие звезды и галактики.

Пример решения задачи

Покажем, как пользоваться формулой дифракционной решетки. Длина волны света, которая падает решетку, равна 550 нм. Необходимо определить угол, при котором появляется дифракция первого порядка, если период d равен 4 мкм.

Угол θ1 легко рассчитать по формуле:

Переводим все данные в единицы СИ и подставляем в это равенство:

θ1 = arcsin(550*10-9/(4*10-6)) = 7,9o.

Если экран будет находиться на расстоянии 1 метр от решетки, то от середины центрального максимума линия первого порядка дифракции для волны 550 нм появится на расстоянии 13,8 см, что соответствует углу 7,9o.

источники:

http://helpiks.org/3-74216.html

http://1ku.ru/obrazovanie/35461-osnovnaja-formula-difrakcionnoj-reshetki/

Что такое дифракционная решетка?

   Дифракционная решетка — это оптический прибор, который используется для изучения свойств света и создания спектров. Она состоит из множества параллельных узких щелей, которые расположены на определенном расстоянии друг от друга.

Когда свет проходит через решетку, он разделяется на несколько лучей, каждый из которых имеет свой угол дифракции. Это происходит из-за интерференции световых волн, проходящих через щели.

---

Полезные статьи:

Что такое спетрометр? Принцип работы

Интерферометры, виды, принцип работы

Все статьи

Дифракционная решетка это оптическая система, состоящая из множества параллельных щелей, расположенных на определенном расстоянии друг от друга. Она используется для разделения света на отдельные цвета и используется в оптических приборах, таких как спектроскопы и спектрофотометры.

Может использоваться для измерения длины волны света, определения дисперсии материала и исследования характеристик лазерного излучения. Она также может быть использована для создания цветных изображений и создания цветных фильтров.

Виды дифракционных решеток

Дифракционные решетки могут быть классифицированы по нескольким признакам, включая материал, форму, число щелей и ориентацию. Некоторые из наиболее распространенных видов дифракционных решеток включают:

• Кристаллические: используются кристаллы, такие как кварц или кристалл алмаза, которые имеют очень регулярную структуру.
• Стеклянные: изготавливаются из стекла, которое может быть отполировано до высокой степени гладкости.
• Металлические: решетки изготавливаются из металлов, таких как золото, серебро или медь.
• Пластиковые: решетки могут быть изготовлены из пластика, который имеет регулярную структуру, например, из поликарбоната или акрила.
• Полимерные: решетки изготавливаются из полимерных материалов, таких как поликарбонат или полистирол.
• Многощелевые: решетки имеют несколько щелей, которые могут быть расположены на разных расстояниях друг от друга.
• Однощелевые: имеют только одну щель.
• Круговые: имеют форму круга и используются для исследования поляризации света.
• Линейные: имеют форму линии и используются для изучения дифракции Френеля.

Каждый тип имеет свои преимущества и недостатки, которые зависят от конкретной области применения.

Характеристики и свойства дифракционной решетки

Длина дифракционной решетки

Длина дифракционной решетки — это расстояние между двумя соседними щелями в решетке. Она может быть разной в зависимости от типа решетки и ее назначения. Например, для обычных дифракционных решеток длина щелей обычно составляет от 100 до 200 микрометров.

Она может варьироваться в зависимости от ее конструкции и назначения. Некоторые из них могут иметь длину до нескольких метров, а другие — всего несколько сантиметров. В целом, длина является важным параметром, который влияет на точность и качество измерения света.

Длина волны дифракционной решётки определяется формулой Брэгга:

λ = d * sin(θ) / m,

• где λ — длина волны света,
• d — период дифракционной решётки,
• θ — угол дифракции,
• m — порядок дифракционного порядка.

Если мы знаем период дифракционной решётки, угол дифракции и порядок дифракционного максимума, то мы можем рассчитать длину волны света, которая будет соответствовать этому максимуму.

Период дифракционной решетки

Период дифракционной решетки — это расстояние между двумя соседними линиями решетки. Он определяет ширину спектра. Чем меньше период решетки, тем больше линий в спектре и тем шире спектр можно получить.

Однако, слишком маленький период может привести к тому, что линии будут слишком близко друг к другу, и их будет трудно различить. Поэтому, оптимальный период зависит от конкретной задачи и требований к спектру.

Максимум дифракционной решетки

Максимум дифракционной решетки — это угол, под которым свет максимально рассеивается при прохождении через решетку. Этот угол зависит от длины волны света и от расстояния между щелями. Чем больше расстояние между щелями, тем больше угол рассеяния.

Решетка может использоваться в различных областях, например, в оптике для создания лазерных лучей или в спектроскопии для анализа состава вещества.

Штрихи дифракционной решетки

Дифракционная решетка — это устройство, которое используется для получения дифракционных картин, которые являются результатом дифракции света на периодической структуре. Она состоит из множества параллельных линий, расположенных на определенном расстоянии друг от друга.

Штрихи дифракционной решетки представляют собой узкие линии, которые расположены на решетке. Они могут быть вертикальными, горизонтальными или наклонными. Они могут быть выполнены как на поверхности самой решетки, так и на ее обратной стороне.

Цель штрихов заключается в том, чтобы создать интерференционную картину, которая позволяет определить длину волны света. Чем более узкие штрихи используются, тем более точный результат можно получить.

Кроме того, штрихи дифракционной решетки могут быть использованы для измерения угла падения света на решетку. Это делается путем измерения расстояния между двумя соседними максимумами или минимумами.

Таким образом, штрихи играют важную роль в оптике и используются в различных научных и технических приложениях, таких как спектроскопия, лазерная техника и другие.

Порядок дифракционной решетки

Дифракционная решетка — это оптический элемент, который используется для дисперсии света и создания цветных изображений. Она состоит из множества параллельных и близко расположенных друг к другу штрихов или щелей. Порядок дифракционной решетки — это количество штрихов на единицу длины решетки.

Порядок дифракции — это порядок дифракционного максимума, который определяется расстоянием между соседними максимумами. Порядок дифракции обозначается буквой m и равен отношению расстояния между двумя максимумами к расстоянию между первым дифракционным максимумом и центральной линией.

Для расчета порядка необходимо знать длину волны света, угол падения света на решетку и угол дифракции. Формула для расчета порядка дифракции выглядит следующим образом:

m = sin(θ)/sin(θd),

• где θ — угол дифракции,
• θd — угол падения света,
• sin(θ) — синус угла дифракции,
• sin(θd) — синус угла падения света.

Порядок может быть положительным или отрицательным в зависимости от того, в какую сторону отклоняется свет при дифракции на решетке. Положительный порядок соответствует отклонению света вправо, а отрицательный — влево.

Спектр дифракционной решетки

Состоит из нескольких основных элементов:

1. Центральная полоса: Это самая яркая часть спектра, которая находится в центре. Она содержит все длины волн света, которые проходят через решетку без изменения своей частоты.

2. Краевые полосы: Они расположены по обе стороны от центральной полосы и содержат длины волн, которые были отклонены. Каждая краевая полоса соответствует определенной длине волны света.

3. Интерференционные полосы: Они появляются в спектре, когда свет проходит через дифракционную решетку несколько раз. Эти полосы имеют разную яркость и ширину в зависимости от угла падения света на решетку.

4. Полосы поглощения: Они возникают, когда свет взаимодействует с молекулами вещества, расположенного за решеткой. Эти полосы могут быть использованы для определения состава вещества.

В целом, спектр дифракционной решетки позволяет изучить свойства света и определить его частоту. Он широко используется в научных исследованиях, медицине, промышленности и других областях.

Угол дифракционной решетки

Угол дифракции — это угол между направлением распространения света и направлением, в котором свет отклоняется от своего первоначального направления. При прохождении через дифракционную решетку свет испытывает дифракцию на каждой из ее щелей, что приводит к отклонению света под углом, который зависит от длины волны света, ширины щелей и расстояния между ними.

Для расчета угла дифракции можно использовать формулу Брэгга-Френеля:

sin(θ) = λ/d * sin(φ/2),

• где θ — угол дифракции,
• λ — длина волны света,
• d — расстояние между щелями,
• φ — угол между нормалью к решетке и направлением распространения света.

Эта формула показывает, что угол дифракции зависит от длины волны, ширины щелей и угла между нормалью и направлением света. Чем больше расстояние между щелями и чем меньше ширина щелей, тем меньше угол дифракции.

Расстояние дифракционной решетки

Дифракционная решетка — это устройство, которое используется для разделения света на отдельные цвета или длины волн. Она состоит из множества параллельных узких линий, разделенных промежутками. Расстояние между линиями определяет частоту, на которую будет разбит свет.

Если расстояние между линиями меньше длины волны света, то свет будет разделен на отдельные цвета, каждый из которых будет иметь свою длину волны. Если же расстояние между линиями больше длины волны, то свет пройдет через решетку без изменения.

Таким образом, расстояние между линиями в дифракционной решетке является важным параметром, который определяет ее способность разделять свет на отдельные цвета.

Постоянная дифракционной решетки

Постоянная дифракционной решетки — это постоянная, которая определяет ее способность рассеивать свет. Формула для постоянной выглядит следующим образом:

d = λ/sin(θ),

• где d — постоянная дифракционной решетки,
• λ — длина волны света,
• θ — угол дифракции.

Плоская дифракционная решетка

Плоская дифракционная решетка представляет собой тонкую пластину, состоящую из множества параллельных линий, нанесенных на ее поверхность. Каждая линия имеет определенную ширину и угол наклона относительно нормали к поверхности решетки.

При прохождения света через плоскую дифракционную решетку, свет разделяется на различные цвета и напрвления. Это зависит от направления в зависимости от длины волнысвета и угла падения на решетку.

Это явление называется дифракцией Френеля и является результатом интеференции волн, которые отразились от каждой линии решетки.

Применения дифракционных решеток

Дифракционные решетки широко используются в различных областях науки и техники, включая:

• Оптика — используются для измерения длины волны света, определения дисперсии света и исследования других оптических явлений.
• Лазеры — для создания лазера с высокой стабильностью частоты и генерации узкополосного света.
• Астрономия — дифракция света от звездных объектов позволяет астрономам изучать структуру и свойства космических объектов.
• Медицина — анализ биологических образцов может использоваться для определения молекулярной структуры и состава клеток.
• Наука о материалах — дифракционное рассеяние света позволяет изучать структуру материалов и их свойства, такие как оптические и электронные свойства.
• Квантовая оптика — дифракция Френеля используется для генерации и управления фотонами в квантовых системах.
• Оптическая связь — элементы могут использоваться в качестве оптических фильтров и модуляторов для передачи данных в оптических системах связи.
• Оптический контроль — дифракционные методы используются для контроля качества поверхностей, измерения геометрических параметров и анализа других оптических сигналов.
• Оптика для медицины — элементы используются для диагностики и лечения офтальмологических заболеваний, таких как катаракта и глаукома.

Это только некоторые из областей применения. Они широко используются в научных исследованиях и технологиях, а также в повседневной жизни, например, в оптических приборах для просмотра изображений и в лазерных системах.

Производство дифракционных решеток

Дифракционные решетки могут быть изготовлены из различных материалов, включая кристаллы, стекло, металлы и другие материалы. Процесс производства включает в себя следующие этапы:

Подготовка материала 

Для изготовления дифракционной решетки необходимо выбрать подходящий материал, который должен иметь высокую прозрачность и однородность.

Формирование полос

На поверхность материала наносится тонкий слой материала, который будет использоваться для формирования полос. Этот слой может быть нанесен с помощью лазера, плазменного напыления или других методов.

Очистка поверхности

После нанесения слоя материала необходимо очистить поверхность от загрязнений и неровностей. Это можно сделать с помощью механической обработки или химических методов.

Обработка поверхности

На этом этапе происходит формирование полос с помощью лазерной обработки или плазменного напыления. В результате получаются узкие и параллельные полосы на поверхности материала.

Проверка качества

После формирования полос необходимо проверить качество. Это может быть сделано с помощью оптических методов, таких как измерение спектра или интерференционных картин.

В результате производства дифракционной решетки получается оптический элемент с высокой точностью и качеством, который может использоваться в различных оптических системах и устройствах.

Дифракционная решетка часто используется для определения спектра падающего на нее света, поскольку она позволяет расщеплять его на отдельные цвета. В данной статье рассмотрим, что такое дифракционная решетка, постоянная и период ее, и приведем пример решения задачи с использованием этого оптического прибора.

Явление дифракции

Суть его заключается в изменении направления распространения волны, когда она встречает на своем пути препятствие. Результат дифракции хорошо различим, если размеры препятствия сравнимы с длиной волны или меньше нее. Дифрагированная волна способна проникать в области за препятствием, куда она не смогла бы попасть, если бы двигалась вдоль прямой.

Вам будет интересно:Корневая система. Как образуются придаточные корни

На рисунке ниже приведен пример дифракции морской волны.

Видно, как прямой фронт волны после прохождения препятствия приобретает форму окружности.

Математическое описание дифракции осуществляется с использованием принципа Гюйгенса-Френеля, который гласит, что каждая точка волнового фронта является источником вторичной волны некоторой интенсивности.

Дифракция часто сопровождается интерференцией. Благодаря этим двум явлениям можно наблюдать так называемые дифракционные картины.

Дифракционная решетка

Это решетка представляет собой прозрачную пластинку, на которую нанесены непрозрачные штрихи с определенным периодом. Когда свет проходит через такую пластинку, то она вносит периодическое возмущение в его волновой фронт. В результате возникает ряд вторичных источников, которые испускают когерентные волны. В результате интерференции когерентные волны образуют на экране совокупность максимумов и минимумов, то есть дифракционную картину.

Важной характеристикой решетки является число штрихов N, нанесенных на 1 мм ее длины. Эта величина N называется постоянной дифракционной решетки, d — период решетки, который равен обратному значению от N. Период обычно выражают в мкм. Геометрический смысл величины d простой — это расстояние между двумя соседними штрихами на решетке. Период d является параметром уравнения решетки, которое будет приведено в следующем пункте.

Описанная выше решетка называется проходящей или прозрачной. Существует также отраженная дифракционная решетка, которая представляет собой совокупность периодических бороздок, нанесенных на гладкую поверхность материала. Примером этого вида решетки является DVD-диск.

Уравнение решетки

В приближении дальнего поля (дифракция Фраунгофера) уравнение для решетки выглядит следующим образом:

sin(θm) = m*λ/d.

Это выражение показывает, при каких углах θm будут возникать максимумы (яркие полосы) на экране. Здесь m = 0, ±1, 2, 3, … Эти числа называются порядком дифракции. Величина λ — это длина волны, которая дифрагирует на решетке, d — период, то есть величина, обратная постоянной дифракционной решетки. Длина самой решетки, как видно из формулы, никакой роли не играет. Углы θm измеряются между двумя прямыми: перпендикуляром, восстановленным к центру решетки, и прямой, направленной от центра к максимуму порядка m.

Приведенная формула непосредственно следует из условия интерференционного максимума. В лабораторных работах ее используют для определения либо постоянной дифракционной решетки, когда λ известна, либо длины волны, когда d известен.

Использование дифракционной решетки в спектроскопии

Приведенное выше уравнение решетки позволяет сделать вывод, что углы θm, в которых появляются максимумы, зависят от длины волны. Чем больше она, тем больше эти углы (длинные волны лучше дифрагируют, чем короткие). Это означает, что если на решетку направить белый свет, то она его разложит на ряд цветов подобно дисперсионной призме. Причем последовательность цветов, начиная от центра (m=0), будет идти от фиолетового к красному.

Каждый максимум для соответствующего порядка дифракции и белого света будет представлять собой «радугу». Единственным максимумом, который всегда будет белым, является центральный или нулевой (m=0).

Явление разложения белого света на отдельные составляющие позволяет использовать дифракционную решетку в спектроскопии. Например, пропуская свет от далекой галактики через решетку, а затем анализируя полученный спектр, можно с достоверностью сказать, какие элементы присутствуют в галактике, какая у них температура, с какой скоростью движется эта галактика относительно нас (в последнем случае учитывается эффект Доплера).

Пример решения задачи

Покажем, как пользоваться уравнением решетки, на примере решения простой задачи. Пусть постоянная дифракционной решетки равна 300 штрихов на 1 мм. Необходимо определить, при каком угле будет наблюдаться максимум первого порядка для фиолетовой (400 нм) и для красной (700 нм) волн.

Учитывая, что число штрихов N обратно пропорционально периоду d, перепишем уравнение решетки в виде:

sin(θm) = m*λ*N.

Угол для первого максимума равен:

θ1 = arcsin(λ*N).

Подставляем данные в единицах СИ в это выражение, получаем:

Для фиолетового: θ1 = arcsin(400*10-9*300*103) = 6,89o.

Для красного: θ1 = arcsin(700*10-9*300*103) = 12,12o.

Если экран поставить на расстоянии 1 метра от решетки, тогда на нем красная и фиолетовая полосы для первого порядка дифракции будут находиться на расстоянии около 9 см друг от друга.