Определение
постоянных интегрирования производится
на заключительном этапе расчета
переходного процесса, когда остальные
составляющие решения уже найдены.
Постоянные интегрирования определяются
путем подстановки в решение для искомой
функции соответствующих начальных
условий.
Пусть
решение для искомой функции i(t) содержит
только одну постоянную интегрирования:
Постоянная
интегрирования находится путем
подстановки в решение начального условия
для самой функции, т.е. i(0):
Пусть
решение для искомой функции i(t) содержит
две постоянных интегрирования и имеет
вид:
Постоянные
интегрирования в этом случае находятся
путем подстановки в решение начальных
условий для самой функции i(0) и для ее
первой производной di/dt(0):
В
результате совместного решения этой
системы уравнений определяют искомые
постоянные интегрирования А1 и А2 .
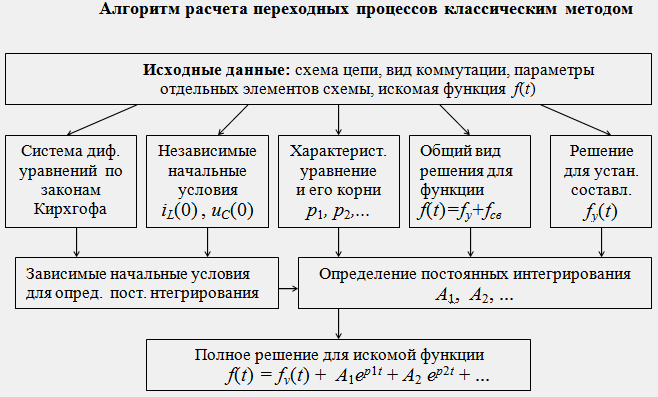
Последовательность
выполнения отдельных этапов расчета
переходных процессов классическим
методом показана ниже в виде диаграммы
в следующей лекции .
Лекции по тоэ/ №8 Алгоритм расчета переходных процессов классическим методом.
Примечания:
1.
Выполнение всех этапов, обозначенных
в диаграмме клетками, является обязательным
и необходимым.
2. Выполнение первых
пяти этапов, находящихся в верхнем
горизонтальном ряду диаграммы, может
производиться в любой последовательности,
так как они не зависят друг от друга.
Пример. Для
схемы рис. 60.1 с заданными параметрами
элементов: Е=100 В, R=50 Ом, R1=20 Ом, R2=30 Ом,
С=83,5 мкФ, определить ток i1 после
коммутации.
1)Общий
вид решения для искомой функции:
2)Определение
установившейся составляющей из расчета
схемы после коммутации:
3)Характеристическое
уравнение и его корень:
4)Независимое
начальное условие uс(0)
из расчета схемы до коммутации:
5)Система
дифференциальных уравнений по законам
Кирхгофа для схемы после коммутации:
6)Начальное
условие i1(0),
необходимое для определения постоянной
интегрирования из уравнения (1):
7)Определение
постоянной интегрирования:
8)Решение
для искомой функции:
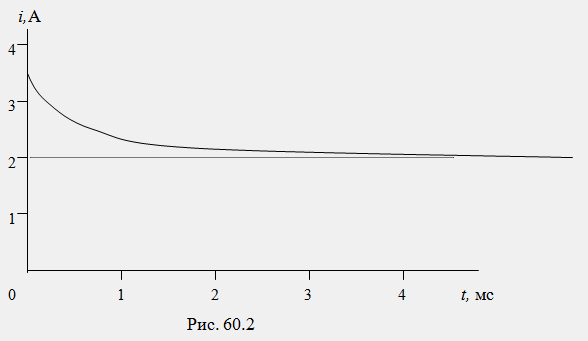
9)Графическая
диаграмма искомой функции i1(t)
показана на рис. 60.2:
Лекции по тоэ/ №9 Операторный метод расчета переходных процессов.
Если
система дифференциальных уравнений,
которыми описывается переходной процесс
в схеме, решается операционным методом,
то и сам метод расчета переходного
процесса также называется операционным
или операторным.
Сущность
операторного метода состоит в том, что
на 1-ом этапе действительные функции
времени i(t), u(t), называемые оригиналами,
заменяются некоторыми новыми функциями
I(p),U(p), называемыми операторными
изображениями. Соответствие между
оригиналом функции f(t) и ее операторным
изобра¬жением F(p) устанавливается на
основе прямого преобразования интеграла
Лапласа:
где
↔ — знак соответствия; p=δ+jω — комплексный
оператор Лапласа.
Если
δ=0, то p=jω, и преобразование Лапласа
превращается в преобразование Фурье,
которое лежит в основе комплексного
метода расчета цепей переменного тока.
Преобразование
Лапласа позволяет заменить операции
2-го рода над оригиналами функций
(дифференцирование и интегрирование)
на операции 1-го рода (умножение и деление)
над операторными изображениями этих
функций.
Расчет
переходных процессов операторным
методом условно выполняется в 3 этапа.
На
1-м этапе расчета система дифференциальных
уравнений, составленная по законам
Кирхгофа для оригиналов функций, после
применения преобразования Лапласа
превращается в систему алгебраических
уравнений для операторных изображений
этих функций.
На
2-ом этапе выполняется решение системы
алгебраических операторных уравнений
относительно искомой функции, в результате
чего получают выражение искомой функции
в операторной форме F(p).
На
заключительном 3-м этапе выполняется
обратный переход от найденного
операторного решения для искомой функции
F(p) к соответствующей ей функции времени
f(t), т. е. Выполняется переход от изображения
функции F(p) к ее оригиналу f(t).
Теоретически
обратный переход от операторного
изображения функции F(p) к ее оригиналу
f(t) устанавливается на основе обратного
преобразования Лапласа:
На
практике для обратного перехода
используются более простые и удобные
методы, а именно: формула разложения и
таблицы соответствия.
Содержание
- Обратное свойство
- Неопределенный интеграл
- Другие значения постоянной интеграции
- Как рассчитывается постоянная интегрирования?
- Примеры
- Пример 1
- Пример 2
- Пример 3
- Предлагаемые упражнения
- Упражнение 1
- Упражнение 2.
- Упражнение 3.
- Упражнение 4.
- Ссылки
В постоянная интеграции Это дополнительная ценность для вычисления первообразных или интегралов, она служит для представления решений, составляющих примитив функции. Он выражает внутреннюю неоднозначность, когда любая функция имеет бесконечное количество примитивов.
Например, если мы возьмем функцию: f (x) = 2x + 1 и получим ее первообразную:
∫ (2x + 1) dx = х2 + х + C ; куда C это постоянная интеграции и графически представляет вертикальный переход между бесконечными возможностями примитива. Правильно сказать, что (x2 + x) есть а примитивов f (x).
Таким же образом вы можете определить (x2 + х + C ) как примитив f (x).
Обратное свойство
Можно отметить, что при выводе выражения (x2 + x), мы получаем функцию f (x) = 2x + 1. Это связано с обратным свойством, существующим между выводом и интегрированием функций. Это свойство позволяет получать формулы интегрирования, начиная с дифференцирования. Это позволяет проверять интегралы через те же производные.
Однако (x2 + x) — не единственная функция, производная которой равна (2x + 1).
- d (Икс2 + х) / dx = 2x + 1
- d (Икс2 + х + 1) / dx = 2x + 1
- d (Икс2 + х + 2) / dx = 2x + 1
- d (Икс2 + х + 3) / dx = 2x + 1
- d (Икс2 + х + C) / dx = 2x + 1
Где 1, 2, 3 и 4 представляют конкретные примитивы f (x) = 2x + 1. В то время как 5 представляет неопределенный или примитивный интеграл f (x) = 2x + 1.
Примитивы функции получаются посредством первичного или интегрального процесса. Где F будет примитивом f, если верно следующее
- у = ∫ f (x) dx= F (х) + С; C = постоянная интеграции
- F ’(x) = f (x)
Можно видеть, что функция имеет единственную производную, в отличие от ее бесконечных примитивов, полученных в результате интегрирования.
Неопределенный интеграл
∫ f (x) dx = F (x) + C
Он соответствует семейству кривых с одинаковым рисунком, которые испытывают несоответствие в значениях изображений каждой точки (x, y). Каждая функция, отвечающая этому шаблону, будет отдельным примитивом, а набор всех функций известен как неопределенный интеграл.
Ценность постоянная интеграции именно он отличает каждую функцию на практике.
В постоянная интеграции предлагает вертикальный сдвиг на всех графиках, которые представляют примитивы функции. Где наблюдается параллелизм между ними, и то, что C это значение смещения.
Согласно общепринятой практике постоянная интеграции он обозначается буквой «C» после добавления, хотя на практике не имеет значения, добавляется или вычитается константа. Его реальную ценность можно найти разными способами в зависимости от первоначальные условия.
Другие значения постоянной интеграции
Уже говорилось о том, как постоянная интеграции применяется в отрасли интегральное исчисление; Представление семейства кривых, определяющих неопределенный интеграл. Но многие другие науки и отрасли приписывают очень интересные и практические ценности постоянная интегрирования, которые способствовали развитию множества исследований.
в физический константа интегрирования может принимать несколько значений в зависимости от характера данных. Очень распространенный пример — знание функции V (т) который представляет собой скорость частицы в зависимости от времени t. Известно, что при вычислении примитива V (t) функция получается R (t) который представляет собой позиция частицы против времени.
В постоянная интеграции он будет представлять значение начальной позиции, то есть в момент t = 0.
Аналогично, если функция известна В) который представляет собой ускорение частицы против времени. Примитив A (t) приведет к функции V (t), где постоянная интеграции будет значением начальной скорости V0.
в экономия, получая посредством интегрирования примитив функции стоимости. В постоянная интеграции будут представлять собой постоянные затраты. И так много других приложений, заслуживающих дифференциального и интегрального исчисления.
Как рассчитывается постоянная интегрирования?
Для расчета постоянная интегрирования, всегда будет необходимо знать первоначальные условия. Которые отвечают за определение того, какой из возможных примитивов является соответствующим.
Во многих приложениях он рассматривается как независимая переменная в момент времени (t), где постоянная C принимает значения, которые определяют первоначальные условия конкретного случая.
Если взять исходный пример: ∫ (2x + 1) dx = x2 + х + C
Допустимое начальное условие может заключаться в том, что график проходит через определенную координату. Например, известно, что примитив (x2 + х + C) проходит через точку (1, 2)
F (х) = х2 + х + C; это общее решение
F (1) = 2
Подставим в это равенство общее решение
F (1) = (1)2 + (1) + С = 2
Отсюда легко следует, что C = 0
Таким образом, соответствующий примитив для этого случая есть F (х) = х2 + х
Есть несколько типов числовых упражнений, которые работают с константы интегрирования. Фактически, дифференциальное и интегральное исчисление не перестают применяться в современных исследованиях. Их можно найти на разных академических уровнях; от первоначального расчета, через физику, химию, биологию, экономику и другие.
Это также видно при изучении дифференциальные уравнения, где постоянная интеграции Он может принимать разные значения и решения, это связано с многочисленными производными и интеграциями, которые выполняются в этом вопросе.
Примеры
Пример 1
- Пушка высотой 30 метров стреляет вертикально вверх. Известно, что начальная скорость снаряда составляет 25 м / с. Принимать решение:
- Функция, определяющая положение снаряда по времени.
- Время полета или момент, когда частица падает на землю.
Известно, что при прямолинейном движении, равномерно изменяющемся, ускорение является постоянной величиной. Это случай запуска снаряда, где ускорение будет равным гравитации.
g = — 10 м / с2
Также известно, что ускорение — это вторая производная от положения, что указывает на двойное интегрирование в разрешении упражнения, таким образом, получая два константы интегрирования.
А (т) = -10
V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C1
Начальные условия упражнения указывают на то, что начальная скорость равна V0 = 25 м / с. Это скорость в момент времени t = 0. Таким образом выполняется следующее:
V (0) = 25 = -10 (0) + C1 Y C1= 25
С определенной функцией скорости
V (t) = -10t + 25; Сходство с формулой MRUV (VF = V0 + а х т)
Аналогичным образом мы продолжаем интегрировать функцию скорости, чтобы получить выражение, определяющее положение:
R (t) = ∫V (t) dt = ∫ (-10t + 25) dt = -5t2 + 25т + C2
R (t) = -5t2 + 25т + C2 (примитив позиции)
Начальное положение R (0) = 30 м известно. Затем вычисляется конкретный примитив снаряда.
R (0) = 30 м = -5 (0)2 + 25(0) + C2 . куда C2 = 30
Первый раздел разрешен, так как R (t) = -5t2 + 25т + 30 ; Это выражение гомологично формуле смещения в MRUV R (t) = R0 + V0т — гт2/2
Для второго раздела необходимо решить квадратное уравнение: -5t2 + 25т + 30 = 0
Поскольку это заставляет частицу достигнуть земли (позиция = 0)
Фактически, уравнение 2-й степени дает нам 2 решения T: {6, -1}. Значение t = -1 игнорируется, потому что это единицы времени, домен которых не включает отрицательные числа.
Таким образом решается второй участок, где время полета равно 6 секундам.
Пример 2
- Найдите примитив f (x), удовлетворяющий начальным условиям:
- f » (x) = 4; f ‘(2) = 2; f (0) = 7
Когда информация о второй производной f ’’ (x) = 4, начинается процесс антидеривации.
f ’(x) = ∫f’ ’(x) dx
∫4 dx = 4x + C1
Затем, зная условие f ‘(2) = 2, переходим:
4 (2) + С1 = 2
C1 = -6 и f ’(x) = 4x — 8
Проделайте то же самое для второго постоянная интеграции
f (x) = ∫f ’(x) dx
∫ (4x — 
Начальное условие f (0) = 7 известно и приступаем:
2(0)2 — 8 (0) + С2 = 7
C2 = 7 и f (x) = 2x2 — 8x + 7
- f ’’ (x) = x2 ; f ‘(0) = 6; f (0) = 3
Аналогично предыдущей задаче мы определяем первые производные и исходную функцию из начальных условий.
f ’(x) = ∫f’ ’(x) dx
∫ (х2) dx = (x3/ 3) + С1
При условии f ‘(0) = 6 переходим:
( 03/ 3) + С1 = 6; куда1 = 6 и f ’(x) = (x3/3 ) + 6
Затем второй постоянная интеграции
f (x) = ∫f ’(x) dx
∫ [(x3/ 3) + 6] dx = (x4/ 12) + 6x + С2
Начальное условие f (0) = 3 известно и приступаем:
[(0)4/ 12] + 6 (0) + C2 = 3; куда2 = 3
Таким образом, мы получаем примитивное частное
f (x) = (Икс4/ 12) + 6x + 3
Пример 3
- Определите примитивные функции с учетом производных и точки на графике:
- dy / dx = 2x — 2, который проходит через точку (3, 2)
Важно помнить, что производные относятся к наклону линии, касательной к кривой в данной точке. Где некорректно предполагать, что график производной касается указанной точки, поскольку она принадлежит графику примитивной функции.
Таким образом, мы выражаем дифференциальное уравнение следующим образом:
dy = (2х — 2) дх ; тогда при применении критериев предотвращения вывода мы имеем:
∫dy = ∫ (2x — 2) dx
у = х2 — 2x + C
Применение начального условия:
2 = (3)2 — 2 (3) + С
С = -1
Получается: f (х) = х2 — 2х — 1
- dy / dx = 3x2 — 1, который проходит через точку (0, 2)
Выразим дифференциальное уравнение следующим образом:
dy = (3x2 — 1) дх ; тогда при применении критериев предотвращения вывода мы имеем:
∫dy = ∫ (3x2 — 1) дх
у = х3 — х + С
Применение начального условия:
2 = (0)2 — 2 (0) + С
С = 2
Получается: f (х) = х3 — х + 2
Предлагаемые упражнения
Упражнение 1
- Найдите примитив f (x), удовлетворяющий начальным условиям:
- f » (х) = х; f ‘(3) = 1; f (2) = 5
- е » (х) = х + 1; f ‘(2) = 2; f (0) = 1
- f » (x) = 1; f ‘(2) = 3; f (1) = 10
- е » (х) = -х; f ‘(5) = 1; f (1) = -8
Упражнение 2.
- Воздушный шар, поднимающийся со скоростью 16 футов / с, сбрасывает мешок с песком с высоты 64 футов над уровнем земли.
- Определите время полета
- Что будет вектор VF когда я упаду на пол?
Упражнение 3.
- На рисунке показан график ускорения-времени автомобиля, движущегося в положительном направлении оси x. Автомобиль двигался с постоянной скоростью 54 км / ч, когда водитель нажал на тормоза и остановился за 10 секунд. Определите:
- Начальный разгон автомобиля
- Скорость автомобиля при t = 5с
- Смещение автомобиля при торможении
Упражнение 4.
- Определите примитивные функции с учетом производных и точки на графике:
- dy / dx = x, проходящий через точку (-1, 4)
- dy / dx = -x2 +1, который проходит через точку (0, 0)
- dy / dx = -x + 1, который проходит через точку (-2, 2)
Ссылки
- Интегральное исчисление. Неопределенный интеграл и методы интегрирования. Уилсон, Веласкес Бастидас. Университет Магдалены 2014
- Стюарт, Дж. (2001). Расчет переменной. Ранние трансцендентальные. Мексика: Thomson Learning.
- Хименес, Р. (2011). Математика VI. Интегральное исчисление. Мексика: Pearson Education.
- Физика И. Мак Гроу Хилл
Определение постоянных интегрирования в классическом методе
Определение констант интегрирования классическим способом. Как известно из предыдущего, свободный ток или свободное напряжение могут быть выражены в виде суммы экспоненциальных членов. Количество полных слагаемых равно числу корней в характеристическом уравнении.
- Таким образом, для двух действительных неравных корней трех действительных неравных корней <ce = 4 «. Для любой схемы, мы можем видеть, что: 1) при t = 0+ Требуемое значение свободного тока льда представляет собой первую производную льда (0+) 2) первое число и, необязательно, свободную производную, взятую при f ~ 0 +.
используя уравнение Кирхгофа и закон переключения
Людмила Фирмаль
Значение первой производной тока обозначено как i’ce (0,.). Значение второй производной свободного тока при t = 0+ обозначено как & (0+) и т. Д. Подумайте, как определить интегральную константу A, …, Zce (0+), <^ (0+) и & (0+), и известное уравнение характеристики цепочки установки значения корня p19 представляет собой линейное уравнение
В случае ice = Aept постоянная интегрирования A определяется значением свободного тока efe (0+): Л = / „(0+). (10.15) Если характеристическое уравнение является квадратичным, а его корни не равны действительному числу, + ЛЧ (Ю.16) Это уравнение во времени: ice = PtA ^ + p2L2 ^.
- Запишите уравнения (10.16) и (10.16 ‘) для (10.16’) / = 0 (учитывая случай t-0-eM = 1). = (10.17) ice (0+) = pxAx + p2L2. (10.17 ‘) В этой системе уравнений известны 1 £ B (0+), 4D0D p ± и p2. Неизвестно Lh и Ay. Совместное решение (10.17) и (10.17 ‘) выглядит следующим образом: l (Qf) P ^ ce (0-b) • (10.17 «) 1
Если корень характеристического уравнения Pl-Pr является комплексно сопряженным, свободный ток имеет вид: = Ae ~, если sin (q + v (10.18) Угловая частота ω0 и коэффициент ослабления b известны из решения характеристического уравнения, где
два неизвестных A и v имеют значения ife (0- ») и * <* (0 +).
Людмила Фирмаль
Время Дифференцируем с уравнением (10.18), получим: ice — A6e ~ ts в (uot + v) -j-A ^ ~ h cos (nJ-fv). (10.18 ‘) уравнение (10.18’) для / == 0+: i ‘<x (04) = — / b sin v + cos v. Итак, есть два уравнения для определения двух неизвестных A и v: лед (° +) = 4sinv; Ice (0 +) — Lb sin v + <b0L cos v. Для цепей с характеристическими кубическими уравнениями свободный ток льда = A ^ 1 * + LU + A ^ 1. (10.20)
Найти первую и вторую производные левой и правой частей (10.20): ice = PyA ^ 4 — p2A2eVit 4-; (10.21) (10.22) (10.23) Cb = Pi A / * + plA2epj + plA ^. т = 0р1св (0J = А + Л.24 «Л3; 4 (0 +) = рхЛг + р2Л2 + р3Л3; ■ лед (0 +) = PiЛ x + P2 A 2 4″ Rz l 8. Уравнение одновременности (10.23) имеет вид , Система из трех линейных алгебраических уравнений с тремя неизвестными Lx, L2 и L8, включая все другие величины [px, p2, p8, <^ (0+), C (0+)
Обратите внимание, что в сложных ветвях с большим запасом энергии и определенными взаимосвязями между параметрами начальное значение одного или нескольких свободных токов или напряжений может быть равно нулю.
В этом случае количество свободных компонентов конкретного тока или напряжения будет меньше количества корней характеристического уравнения и не будет равно количеству свободных компонентов других токов, например, угловой частоты b)
Собственная угловая частота последовательного или параллельного резонансного контура, которая может возникнуть, если одна свободная вибрация равна 0, в этом случае доступна r цепь На этой частоте, до свободных компонентов, резонансный контур серии на самом деле более короткие участки цепи соединены с зажимом, параллельная схема будет резать цепь для этого. I: $ *
Теперь рассмотрим некоторые численные примеры расчета переходных процессов классическими методами в цепях первого и второго порядка с постоянными и синусоидальными источниками. d.s с нулевыми и ненулевыми начальными условиями.
Пример 128. На рисунке 309 до того, как автоматический выключатель был замкнут, начальное состояние было нулевым. E = 210 В. /? г = 1000 Ом, /? 2 = 2000 Ом. С = 50 микрофарад. 1) Найти начальные значения полной, принудительной и свободной составляющих всех токов и напряжений на емкости. 2) Определить закон изменения во времени всех ветвей тока и емкостного напряжения.
Выберите положительное направление для тока ветвления в соответствии со схемой решения в первой части проблемы. 309. Принимает положительное направление относительно напряжения, как это обычно делается, в соответствии с током.
Перед замыканием автоматического выключателя напряжение на конденсаторе равно нулю: M0-) = Согласно второму закону переключения оно остается равным нулю сразу после переключения при t-0 +.
Построить уравнение в соответствии с законом Кирхгофа. + «c = W? 2» = / 2 + «3- t = 0, переписать в /. M <> +) == W /? 2; h (0 +) = / 2 (0+) + i3 (0+), ns (0 +) = 0, поэтому h (0 +) = 7Γ = S = 0,21 (a) и (0 +) = 0: «3 (0 +) = h (0+) -i2 (0+) = 0,21 a. Независимое начальное значение схемы равно 1. «c (0+) = 0 — все остальные начальные значения являются зависимыми.
Найти текущее значение форсировки. Схема Тогда источником постоянной е., А в случае постоянного тока емкость является разомкнутой цепью, поэтому • -i = E = ΛW lW k1 + ı2zooo = 0,07 (а) Напряжение на конденсаторе является напряжением на сопротивлении Равно напряжению /? 2: IS —UR «- ^ pr 2pr ER * R1A-R2 140 В.
Найдите свободные составляющие тока, для этого каждый ток при t = 0+ является принудительным и свободным Может быть выражена как сумма: отсюда (0J = ((° +) ™ imp (0J = 0,21-0,07 = 0,14 (o);) == <2 (0 +) — <2lr (0, ..) = 0-0,07-—0,0 7 (а); он, (0+) — h (0 +) — (0J = 0, 21-0 = 0,21 (а); «ere (0+) = UC (0 +) — и Spr (0+) = 0-140 = -140 (c).
Решение второй части проблемы стр. См. 365): «T + ^ 2-0 имеет один маршрут: Ri 4- R2 RtRzC-30 сек 1. Поскольку в характеристическом уравнении существует только один маршрут, Ae & (с тем же индексом, что и у постоянной A желаемого тока): = = ‘W + = 0,07 + 0,146- ^ a; Ri_r Kb 4 = <2, ,, P + = ~~ + = 0,07-0,07e «® ° za»; z = i3np + «S» = 0 + ^ ept = 0,2 л. К SOf a; «a =« c »₽ +« a . = + A ^ ‘= 140-140e ~ ^ c.
График тока и напряжения u как функции времени качественно показан на рисунке 310. Константа интегрирования 7 ^ является током при / = 0+ Значение свободного компонента ilce равно A = ‘1 «(0+) = 0,14 a. Константа интегрирования A = * 2 «(0+) = -0,07 a; L =» s ™ (0+) = 0,21 a; L4 = ISB (0+) = -140 дюймов.
Выше решение описывается в числовой форме Напишите решение в буквальной форме: L = MO +) — <1lR (o +) = A__ | _; L2 = i, (0 +) — i2np (0+) = 0 — A-; ‘T * 2 A-4 (0 +) — ianp (0+) = A — o = A; К1Д4 = is (0,.) АСпр (0+) = 0- /? 2 * I’ <1 Как правило, требуемое количество описывается следующим образом: ЕRi + R> Е — ^ — и Ri + R *
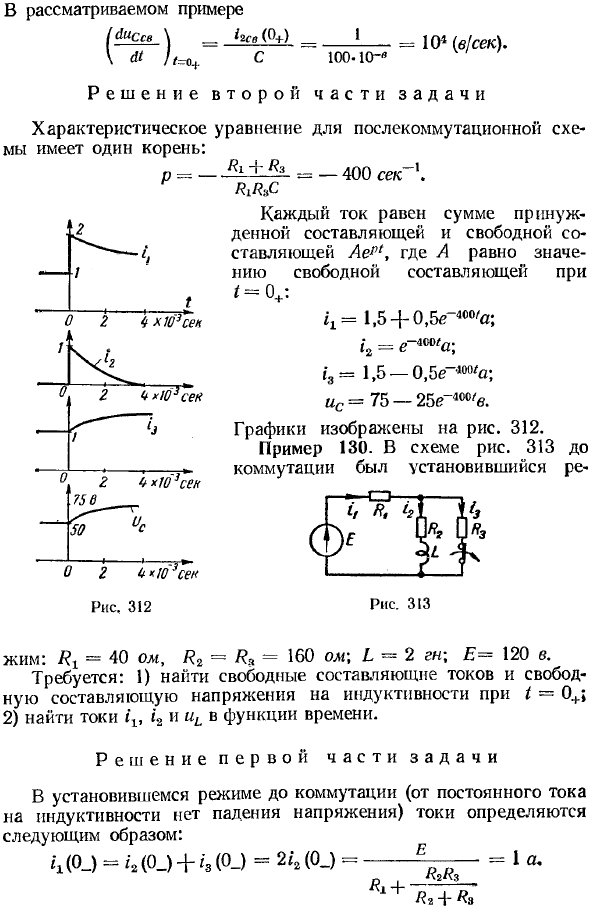
Пример 129 Рисунок 312 До того, как автоматический выключатель был замкнут, существовало устойчивое состояние: / ?! = /?} = -50 Ом C = 100 микрофарад, E = 150 дюймов Требования к рисунку 310: 1) Ток и напряжение конденсатора заполнены, принудительные и свободные компоненты и напряжение на конденсаторе отсутствуют
Найти начальное значение производной 2) Определить ток t2, t3 и напряжение u как функцию времени Решение первой части задачи i2 (0_) = 0 и «1 (0_) = i, до переключения (0_) = = — = 1 (a) n H1 + H1 + H3 150 Вт конденсатора Соответствует ли напряжение напряжению резистора? 3: (0-) == H (0-) = 1 • 50 = 50 (c).
Определить принудительное значение после переключения: -Chlr- + 100 “* «Слр (° +) = ‘zpr (° +) /? Z = 1,5 • 50 = 75 (c). Согласно второму закону Кирхгофа, образованному первой и второй ветвями t = 0+ Построить уравнение контура: H (° +) + «c (O.,.) = £, но есть (0 +) = есть (0 отсюда» 1 (0 +) = уравнение E — к (0- ) = 150-50 = 2, Ri 50 L найдено: / 3 (0+) = M ^ = 1a.
Согласно первому закону Кирхгофа «1 (0 +) =» 2 (0 +) — H3 (0+), поэтому ‘2 (0 J = h (0 +) — i3 (0+) = 2-1 = 1 (a). Общие и принудительные значения: (0 *) = 50-75 = -25 (е); (0+) = 2-1,5 = 0,5 (а);, (0 +) = 1-0 = 1 (а); 1 .5 = -0,5 ()) • сгcg (0+) = сc (0 +) — СC /, C s (^ 1) = C 1) C pr 1 C c (® +) = H (O «) H pr H c sv (° +) = H (0+) -h pr (° +) = 1-1 b; / — »^ is st dt ‘, тогда из-за st _ Che dtС
В этом примере / dt ^ Cce _ ^ 2Св (фу) 1 = 10 * (в! сек). # // m> + С100.1О ~ * Решение второй части задачи Существует один путь к характеристическому уравнению схемы после переключения. p = -A ± 2k _ 400 с ‘ RiR.fi Каждый ток равен сумме форсирующего компонента и свободного компонента Aept, A равно / = 0 +: 1,54-0,5 0’a; t2 = e “40Wa; r3 = 1,5-0,5 54 a.
Таким образом, i = inp + ice = 35,2 sinˆ-20′) 8,54e ~ 2 | 0 / a. Свободный ток, кривая 4 — общий ток после переключения (ордината кривой 4 при ω / 0 — кривая 2 и 5 Она равна сумме координат). Пример 132. На рисунке 317 замыкает переключатель на третьей ветви.
До этого было устойчивое состояние. e (t) = E = 120 дюймов 1) w, .. ‘»c ^)„. ! Найти принудительный ток и напряжение конденсатора после переключения f1 (0J = i2 (0_) = 120 50 4-10 перед включением выключателя, чтобы решить первую часть проблемы, чтобы найти: H pr ^ 2 Pr DC * 3lr = 0 *
Отсутствует падение напряжения от постоянного тока на индуктивности, поскольку ток не течет в конденсатор, поэтому вынужденное напряжение на конденсаторе от 1Lpr до падения напряжения с резистора /? 2 от тока u = 2.10 = 20 (c)
Первый закон выпрямления Z2 (0J = 4 (0+) = 2a, где (0+) = h pr (^ 4) + 12 sv (0 +)>, где 12 sv (° +) = «2 (0 +) -» 2 pr (0t) = 2-2 = 0 «i (0+) = i2 (0+) + z3 (0+),» i (0+) = 2 + равен (0 +), который строит уравнение по закону Кирхгофа о второй замкнутой цепи, образованной первой и третьей ветвями: 4 (0 +) + 4 GM * s + равно (0-J- это (0+) = 0 и 4 (0+) = 2-H3 (0J, тогда E-21 Ri + Dz 120-2-50 50 -f-50 = 0,2 (а) r3ge (0+): это (0-3 = есть (<М к пр (0+) = 0,2-0 = 0,2 (а).
Определяется ULc (/ (0 ^)) Создайте уравнение свободной компоненты, чтобы 4 ev (0+) + 4 sv (0+) + ul sv (0+) = 0 вдоль контура, образованного первой и второй ветвями -i2 sv (0 +) /? 2 = -0,2 • 50 + 0 = -10 (c), но поэтому (^ sv =, csv (M = _ 5 (a / s). L = 0 + ^ 2
Найти свободное напряжение конденсатора при t = 0+ согласно второму закону переключения .ic (0_) = «s (° +);» c (0+) = ■ использовать pr (° +) + «C cn (0+); 0 = 20+» cn (0+), следовательно, «Csv (° +) ^ -20 e- Z-0 + определяет скорость изменения свободного напряжения конденсатора.
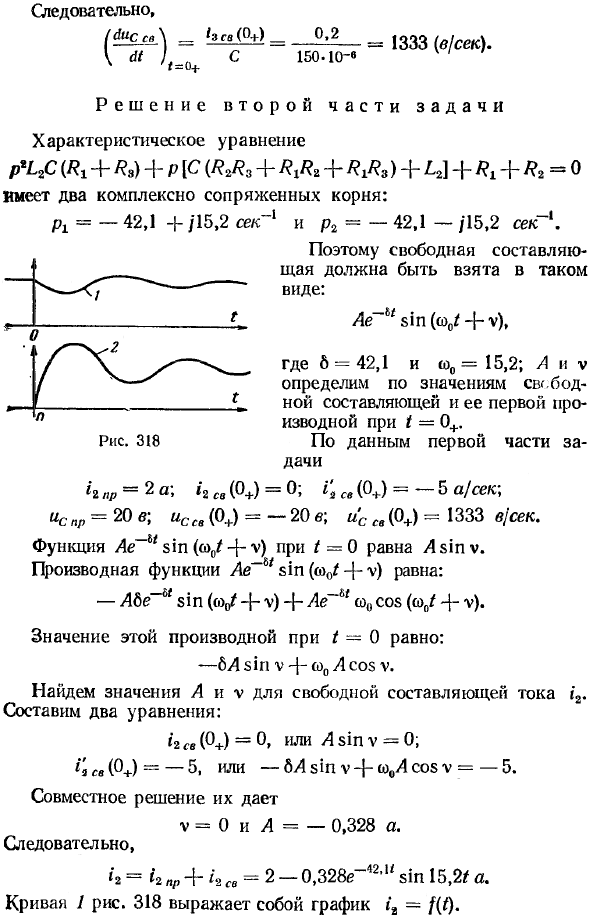
По этой причине решение для второй части задачи составляет 0,2 150,10-6 «1333 (в / с). Характеристическое уравнение имеет вид p ^ L2c (/ ?! + /? S) + p [C (?? 2 / ? S + R & + / r ^ s) + Л2] + /? х + /? 2 = 0 имеет два комплексных сопряженных корня: Pi = -42, 1 + / 15,2 с «1 и p2 = -42,1- / 15,2 с» 1.
Таким образом, свободный компонент необходимо получить в следующем формате Существует: 4e ”6z sin (coo / + v), где 6 = 42,1 и ω0 = 15,2. Данные первой части задачи G pr% a ,, <2 sv (0 +) — 0, ^ 2 sv ( 0 *) 5 и / s ssp = 20 e; ssb (0+) = -20 e; ss sv (0+) = 1333 v / s. / = 0 функция Le ”6 * sin (co0 / 4 ~ v) 4sinv.
Производная функции Ae от bi sin (. Кривая 2 на рисунке 318 показывает uc = f (t). Пример 133. 317 e (t ) = 127 sin (314 / 4-40 °) C. Параметры схемы такие же, как в Примере 132. До включения автоматического выключателя цепь находилась в устойчивом состоянии: «c (0_) = 0.
Требуется: 1) «Cr (° +) и 2) Определить i2 (t) и uc (t). Решение первой части проблемы — до переключения / определение принудительного тока и напряжения конденсатора после переключения Входной импеданс цепи номер 4-1 ^ 2) zex = /?, + ~ ^ ~ = 104,8e — jSS0 ‘; -F / <о ^ + ^ зт. 127е / 4О ° 104,8- / 9 ° м’ Ir pr (° +) == 1,213 sin 49 ° 50 ‘= 0,923 a.Подключено параллельно 1,2! 3? 49е50’а
Мгновенное значение вынужденного тока после переключения ilnp => 1,213 sinˆ + 49 ° 50′); 2-й и 3-й ответвления комплексного сопротивления = bO.Zv-‘18035; ^ rz-; Kg 4 «4-х напряжения в комплексе в параллельном сечении = = 1,2 1 Ze’49’50 ‘.56.3 ^ «‘ ® ‘= 68.2е’31’15’ in; j U23t-68,2 ^ 31 Q 10OCr- / 58 ° 45 ‘S ^ m-z2-io- | j628“ U ‘1Wee 1/3 w = 68’2g / — = 1,253е’54 ° 20’.
Мгновенные значения вынужденных токов i2 и i8 после переключения: i2 = 0,1085 sin (w / -58 ° 45 ‘), i8 = 1,253 sin (o / + 54 ° 2 (В); i2 pr (0+) = OD 085 sin (-58 ° 45 ‘) = -0,0928 a Szpr (0 +) == 1,253 sin 54 ° 20’ = 1,016 A. Принудительное напряжение на конденсаторе UCm = 1,253е / 54 ° 20 ‘.21, З- / 80 ° = 26,7y- / ^ «‘.
Мгновенное значение вынужденного напряжения, приложенного к емкости после переключения, составляет pr-26,7 sin (co / -35 ° 40′);» pr (° +) = 26> 7 sin (-35 ° 40 ‘) = -15,57 дюйма. Найти f2re (0+). Закон переключения: «2 (0 ) = <2 (0+) = -0,1415 =» 2 „p (0+) ) 4-12sv (0+); ”■ 2pr (0+) = -0,0928 a;» 2 «(0+) = -0,1415 4-0,0928 = -0,0487 a.
Согласно второму закону переключения конденсатор» Найти свободное напряжение ssv (0+). «S (0 ) =» s pr (0+) 4- и С (в (0+); «сev (0 <) = (0 _) — isp (0 +) = 0 — (- 15,57) = 15,57 (в) / 1-й и 3-й бюстгальтер для определения 3gv (0+) Настройка уравнения вдоль контура, образованного с помощью переключателя.
Заменить в нем / найти 1sv (0+) ~ 1-0.0487 4- £ 3 „(0+) 1 и sSv (® +) =, 5” 57 6-: ”’8” (0+) = ~ 10 + 1 ° ‘~ = ~ 0,1314 (а); G зв (0-J = <2 зв (0+) + rs зв (0+) ~ -0,18 А. «дн (0 +) = £ ( Для определения- ^ построим уравнение первого сформированного контура второй ветви: <1 Зв (° +) + * 2 Зв (0-i) + UL св ОМ-0 »Зв ( 0 *) * s-0,1314 150-10 «6 = -876 (в; с).
Решение второй части задачи Согласно данным, полученным при решении первой части, / 2lr = 0,1085 sin (w / -58g45 ‘), / 2sv (0+) = -0,0487 a; (0+) = 4,74 a / 7 sin (co / -35c40’), ccb (0+) = 15,57 в , Cb (0J-in / sec.
Создать два уравнения для определения корней i2ce A и v характеристического уравнения: equationsin v = -0.0487; -бЛsin v + co0 / cos v == 4.74, wh = L = 0, 184 a и v = -15с20 So G-12 „₽ +« 2 »= О, 1085 sin А-58 ° 45 ‘) + 4- 0,184e ~ 4i!’ L’s в (1512 / -15 ° 2 (D) а.
Построить два уравнения для определения констант A и v в iCw: A sin v = 15,57; -M sin v + v0A, потому что v = -876 Совместное решение: A = 21,3 и v = 136 ° 5 (G, «c = ^ SpR +» c = 26 «7 sin, А-35 ° 40 ‘) + _ [_ 21,3e ~ 42’, f sin ( 15.2Z + 136 ° 50 ‘) в. ♦
* * Здесь мы возвращаемся к основам операторного метода, который является вторым методом для расчета переходных процессов линейных электрических цепей. Я помню несколько
Смотрите также:
- Решение задач по электротехнике
В исчислении , то константа интегрирования , часто обозначается , является термин константы добавляется к первообразной функции , чтобы указать , что неопределенный интеграл от (то есть, в совокупности всех первообразных в ), на связную области , определяется только до к аддитивной константе. Эта константа выражает неоднозначность, присущую конструкции первообразных.
Более конкретно, если функция определена на интервале и является первообразной от , то набор всех первообразных задается функциями , где — произвольная константа (что означает, что любое значение будет составлять действительную первообразную). По этой причине неопределенный интеграл часто записывается как , хотя константа интегрирования может иногда опускаться в списках интегралов для простоты.
Источник
Производная любой функции постоянной равна нулю. После того, как кто-то нашел одну первообразную для функции , добавление или вычитание любой константы даст нам другую первообразную, потому что . Константа — это способ выразить, что каждая функция, по крайней мере, с одной первообразной, будет иметь их бесконечное количество.
Позвольте и быть двумя всюду дифференцируемыми функциями. Предположим, что для каждого действительного числа x . Тогда существует действительное число такое, что для любого действительного числа x .
Чтобы доказать это, обратите внимание на это . So может быть заменен на и на постоянную функцию , чтобы доказать, что всюду дифференцируемая функция, производная которой всегда равна нулю, должна быть постоянной:
Выбери реальное число , и пусть . Для любого х , в основной теоремы исчисления , вместе с предположением , что производная обращается в нуль, следует , что
тем самым показывая, что это постоянная функция.
Два факта имеют решающее значение в этом доказательстве. Сначала подключается настоящая линия . Если бы реальная линия не была подключена, мы не всегда могли бы интегрировать от фиксированного a до любого заданного x . Например, если бы мы попросили функции, определенные на объединении интервалов [0,1] и [2,3], и если бы a было равно 0, то было бы невозможно интегрировать от 0 до 3, потому что функция не определен между 1 и 2. здесь будет две константы, по одному для каждого подключенного компонента в домене . В общем, заменяя константы локально постоянными функциями , мы можем распространить эту теорему на несвязные области. Например, есть две постоянные интегрирования для и бесконечно много для , поэтому, например, общая форма интеграла от 1 / x такова:
Во-вторых, и предполагалось, что они всюду дифференцируемы. Если и не дифференцируемы хотя бы в одной точке, то теорема может потерпеть неудачу. В качестве примера, пусть будет ступенчатая функция Хевисайда , которая равна нулю для отрицательных значений x и единице для неотрицательных значений x , и let . Тогда производная от равна нулю там, где она определена, и производная от всегда равна нулю. Однако ясно, что и не отличаются на константу, даже если предположить, что и всюду непрерывны и почти всюду дифференцируемы, теорема все равно неверна. В качестве примера возьмем быть функция Кантора и снова пусть .
Например, предположим, что кто-то хочет найти первообразные . Одним из таких первообразных является . Еще один . Третий . У каждого из них есть производные , поэтому все они являются первообразными .
Оказывается, сложение и вычитание констант — единственная гибкость, которая у нас есть при нахождении различных первообразных одной и той же функции. То есть все первообразные с точностью до константы одинаковы. Чтобы выразить этот факт , мы пишем:
Замена на номер даст первообразную. Однако записывая вместо числа, можно получить компактное описание всех возможных первообразных . называется постоянной интегрирования . Легко определить, что все эти функции действительно являются первообразными :
Необходимость
На первый взгляд может показаться, что константа не нужна, так как ее можно обнулить. Более того, при вычислении определенных интегралов с использованием основной теоремы исчисления константа всегда сокращается сама с собой.
Однако попытка установить константу равной нулю не всегда имеет смысл. Например, может быть интегрирован как минимум тремя различными способами:
Таким образом, установка на ноль может оставить константу. Это означает, что для данной функции не существует «простейшей первообразной».
Другая проблема с установкой равного нулю состоит в том, что иногда мы хотим найти первообразную, которая имеет заданное значение в данной точке (как в задаче начального значения ). Например, чтобы получить первообразную , имеющую значение 100 при x = π, тогда будет работать только одно значение (в данном случае ).
Это ограничение можно перефразировать на языке дифференциальных уравнений . Нахождение неопределенного интеграла функции аналогично решению дифференциального уравнения . Любое дифференциальное уравнение будет иметь множество решений, и каждая константа представляет собой уникальное решение корректной задачи с начальным значением . Наложение условия, что наша первообразная принимает значение 100 при x = π, является начальным условием. Каждому начальному условию соответствует одно и только одно значение , поэтому без него решить задачу было бы невозможно.
Есть еще одно оправдание, исходящее из абстрактной алгебры . Пространство всех (подходящих) действительных функций на действительных числах является векторным пространством , а дифференциальный оператор — линейным оператором . Оператор переводит функцию в ноль тогда и только тогда, когда эта функция постоянна. Следовательно, ядро из пространства всех функций постоянных. Процесс неопределенного интегрирования сводится к поиску прообраза заданной функции. Для данной функции нет канонического прообраза, но набор всех таких прообразов формирует смежный класс . Выбор константы аналогичен выбору элемента смежного класса. В этом контексте решение задачи начального значения интерпретируется как лежащее в гиперплоскости, заданной начальными условиями .





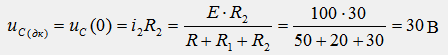


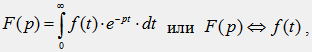
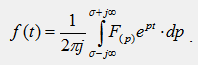










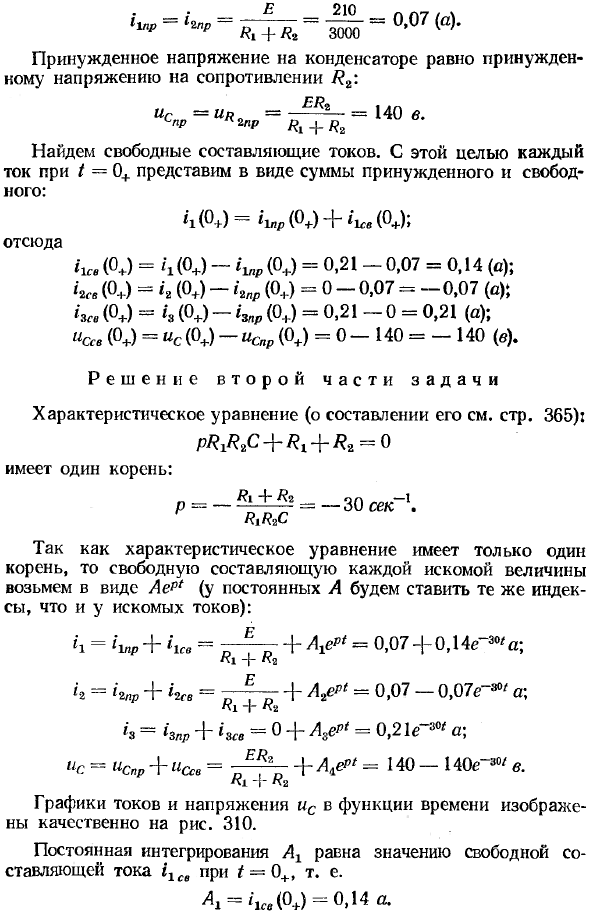























![[F (x) -G (x)] '= 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf7a4d471877352525d86a56c595661d3061ae30)

















![{ displaystyle { begin {align} { frac {d} {dx}} [ sin (x) + C] & = { frac {d} {dx}} sin (x) + { frac { d} {dx}} C \ & = cos (x) +0 \ & = cos (x) end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57a1f94e2f3c827cbd77d0648f1d7532f57f3a35)




