Как найти постоянную ридберга формула - Исправление недочетов и поиск решений вместе с Examum.ru

Экспериментальное определение постоянной Ридберга

Согласно
эмпирической формуле (501.2), постоянную
Ридберга можно определить, зная длину
волны излучения для соответствующего
перехода.

Например, в видимом спектре излучения
(серия Бальмера) атом водорода испускает
свет с длиной волны λ_кр,
соответствующей красному цвету. Эта
первая видимая линия отвечает переходу
атома с третьего на второй энергетический
уровень. Таким образом, постоянная
Ридберга может быть определена, как

. (501.12)

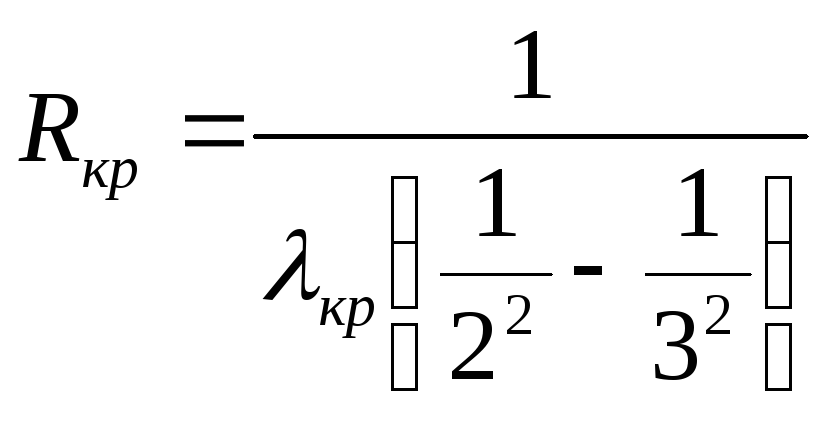
Вторая линия видимого спектра с длиной
волны λ_гол, соответствующей
голубому цвету, возникает при переходе
атома с четвертого на второй энергетический
уровень, и постоянная Ридберга определяется
так:

. (501.13)

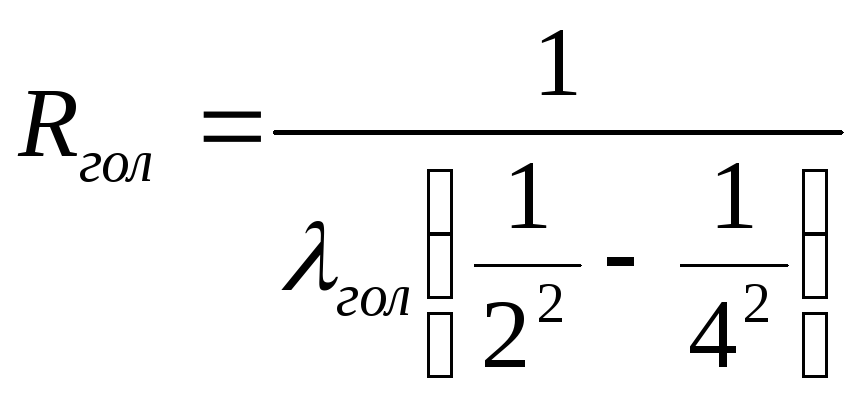
Переход со
следующего (с пятого) энергетического
уровня на второй сопровождается
излучением с длиной волны λ_син,
соответствующей синему цвету, и постоянную
Ридберга находим, как:

. (501.14)

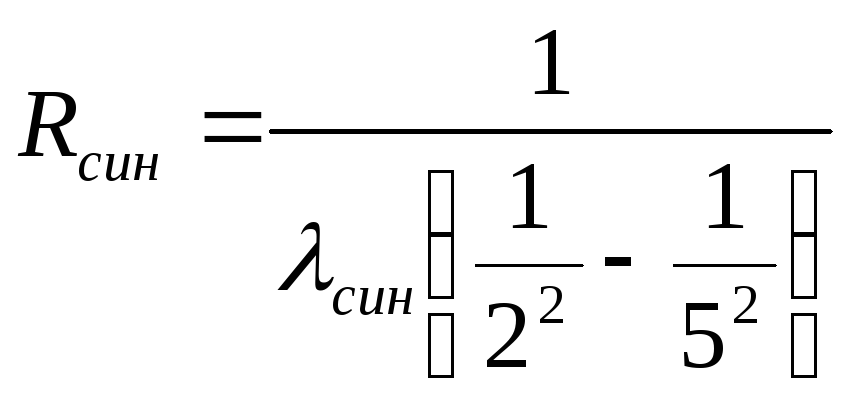
При достаточно точном определении
соответствующих длин волн все три
значения постоянной Ридберга должны
быть одинаковыми.

Пример выполнения эксперимента

Цель
эксперимента: определить значение
постоянной Ридберга.

Задача эксперимента:найти при
помощи монохроматора длины волн,
соответствующие красной, голубой и,
возможно, синей линиям спектра излучения
атомарного водорода.

Подготавливаем Таблицу №1 для
экспериментальных данных и результатов
их обработки.

Таблица №1. Экспериментальные данные
и результаты их обработки

Длина волны λ, м	№ уровня, с которого происходит переход	Постоянная Ридберга R, м^-1
	3
	4
	5

Глядя в окуляр монохроматора и вращая
регулятор длины волны, находим красную
полосу, отчетливо выделяющуюся на общем
фоне спектра и добиваемся, чтобы она
находилась в середине области обзора.
Соответствующая длина волны (в нм) будет
отображаться на счетчике монохроматора.
Ее мы записываем в первую строку Таблицы
№1 столбца «Длина волны», переведя
значение в метры.
Аналогичным образом пытаемся отыскать
в спектре голубую и синюю линии и
записываем в Таблицу №1 значения длин
их волн в метрах.
По формулам (501.12), (501.13) и (501.14) рассчитываем
значения постоянной Ридберга и записываем
их в соответствующие ячейки Таблицы
№1 (в м^-1).
Вычисляем среднее арифметическое
значение постоянной Ридберга

. (501.15)

Находим среднеквадратическую абсолютную
погрешность определения постоянной
Ридберга:

. (501.16)

где 4,3 –
коэффициент Стьюдента для трех измерений
с доверительной вероятностью Р = 0,95

Записываем окончательный результат:

м^-1.

Проверка результатов

Относительная
разность теоретического значения
постоянной Ридберга, вычисленного по
формуле (501.3), и среднего экспериментального
ее значения не должна превышать 10%:

. (501.17)

Если это так,
то эксперимент выполнен успешно.

ВОПРОСЫ
ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО ФИЗИКЕ
КУРС II,
ЧАСТЬ 3

Волны
в упругих средах. Продольные и поперечные
волны Уравнение гармонической бегущей
волны, ее график, фазовая скорость,
длина волны, волновое число (1.1, 1.3).
Фронт
волны, волновые поверхности, фазовая
скорость, волновое уравнение (1.3, 1.4).
Принцип
суперпозиции волн. Групповая скорость.
Энергия бегущей волны. Вектор плотности
потока энергии – вектор Умова (1.5, 1.6).
Электромагнитные
волны. Волновые уравнения. Уравнение
плоской гармонической волны (2, 2.1, 2.2).
Энергия
электромагнитной волны. Поток энергии.
Вектор плотности потока энергии –
вектор Пойнтинга (2.3).
Излучение
электрического диполя. Шкала
электромагнитных волн (2.4, 2.5).
Интерференция
света. Монохроматичность и когерентность
волн. Расчет интерференции двух волн
(3.1.1 – 3.1.3).
Методы
получения когерентных волн (3.2).
Оптическая
длина пути и оптическая разность хода
(3.3).
Интерференция
света в тонких пленках. Просветление
оптики. Интерферометры (3.4, 3.5).
Дифракция
света. Принцип Гюйгенса-Френеля. Метод
зон Френеля (4.1, 4.2).
Дифракция
Френеля на круглом отверстии и диске
(4.3).
Дифракция
Фраунгофера на одной щели (4.4).
Дифракционная
решетка (4.5).
Дифракция
на пространственной решетке. Формула
Вульфа-Брэгга (4.6).
Разрешающая
способность оптических приборов.
Понятие голографии (4.7, 4.8).
Взаимодействие
света с веществом. Поглощение света.
Закон Бугера. Рассеяние света. Закон
Релея (6.1 – 6.3).
Дисперсия
света. Электронная дисперсия света.
Нормальная и аномальная дисперсия
(6.4).
Поляризация
света. Естественный и поляризованный
свет. Закон Малюса (6.5).
Поляризация
света при отражении и преломлении.
Закон Брюстера (6.6).
Двойное
лучепреломление. Искусственная
оптическая анизотропия. Вращение
плоскости поляризации (6.7, 6.8).
Тепловое
излучение. Характеристики теплового
излучения. Абсолютно черное тело. Закон
Кирхгофа (7.1 – 7.3).
Распределение
энергии в спектре абсолютно черного
тела. Законы Стефана-Больцмана и Вина
(7.4 – 7.6).
Формула
Релея-Джинса. «Ультрафиолетовая
катастрофа». Гипотеза Планка. Формула
Планка. Связь формулы Планка с законами
Стефана-Больцмана и Вина (7.7).
Фотон.
Энергия, масса и импульс фотона. Давление
света (8.1, 8.2).
Фотоэффект.
Уравнение Эйнштейна для внешнего
фотоэффекта (8.3).
Эффект
Комптона. Корпускулярно-волновой
дуализм электромагнитного излучения
(8.4, 8.5).
Гипотеза
де Бройля. Опытное обоснование
корпускулярно-волнового дуализма
материи. Опыт Девиссона-Джермера (9.1).
Соотношение
неопределенностей Гейзенберга.
Невозможность классического задания
состояния микрочастиц (9.2).
Волновая
функция и ее статистический смысл
(9.3).
Уравнение
Шредингера для стационарных состояний.
Собственные функции и собственные
значения. Свободная частица (9.4, 9.5).
Частица
в одномерной прямоугольной «потенциальной
яме» (9.6).
Классический
и квантовый осцилляторы (9.7).
Модель
атома Резерфорда (11.1).
Постулаты
Бора (11.2).
Линейчатый
спектр атома водорода (11.3).
Атом
водорода согласно квантовой механики.
Квантовые числа электрона в атоме
(11.4).
Принцип
Паули (11.5).
Поглощение,
спектральное и вынужденное излучение
(12.1).
Принцип
работы лазера (12.2).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
29.08.2019122.88 Кб0M4.doc
#
#
#
#

Источник

From Wikipedia, the free encyclopedia

In spectroscopy, the Rydberg constant, symbol ${displaystyle R_{infty }}$ for
heavy atoms or $R_{text{H}}$ for hydrogen, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to the electromagnetic spectra of an atom. The constant first arose as an empirical fitting parameter in the Rydberg formula for the hydrogen spectral series, but Niels Bohr later showed that its value could be calculated from more fundamental constants according to his model of the atom.

Before the 2019 redefinition of the SI base units, ${displaystyle R_{infty }}$ and the electron spin g-factor were the most accurately measured physical constants.^[1]

The constant is expressed for either hydrogen as $R_{text{H}}$ , or at the limit of infinite nuclear mass as ${displaystyle R_{infty }}$ . In either case, the constant is used to express the limiting value of the highest wavenumber (inverse wavelength) of any photon that can be emitted from a hydrogen atom, or, alternatively, the wavenumber of the lowest-energy photon capable of ionizing a hydrogen atom from its ground state. The hydrogen spectral series can be expressed simply in terms of the Rydberg constant for hydrogen $R_{text{H}}$ and the Rydberg formula.

In atomic physics, Rydberg unit of energy, symbol Ry, corresponds to the energy of the photon whose wavenumber is the Rydberg constant, i.e. the ionization energy of the hydrogen atom in a simplified Bohr model.^{[citation needed]}

Value[edit]

Rydberg constant[edit]

The CODATA value is^[2]

${displaystyle R_{infty }={frac {m_{text{e}}e^{4}}{8varepsilon _{0}^{2}h^{3}c}}}$

or,

${displaystyle R_{infty }=109737,{text{cm}}^{-1}}$

where

The Rydberg constant for hydrogen may be calculated from the reduced mass of the electron:

${displaystyle R_{text{H}}=R_{infty }{frac {m_{text{p}}}{m_{text{e}}+m_{text{p}}}}approx 1.09678times 10^{7}{text{ m}}^{-1},}$

where

Rydberg unit of energy[edit]

The Rydberg unit of energy is equivalent to joules^[3] and electronvolts^[4] in the following manner:

${displaystyle 1 {text{Ry}}equiv hcR_{infty }={frac {m_{text{e}}e^{4}}{8varepsilon _{0}^{2}h^{2}}}={frac {e^{2}}{8pi varepsilon _{0}a_{0}}}=2.179;872;361;1035(42)times 10^{-18} {text{J}} =13.605;693;122;994(26) {text{eV}}.}$

Rydberg frequency[edit]

${displaystyle cR_{infty }=3.289;841;960;2508(64)times 10^{15} {text{Hz}}.}$

^[5]

Rydberg wavelength[edit]

${displaystyle {frac {1}{R_{infty }}}=9.112;670;505;824(17)times 10^{-8} {text{m}}}$

The angular wavelength is

${displaystyle {frac {1}{2pi R_{infty }}}=1.450;326;555;7696(28)times 10^{-8} {text{m}}}$

Occurrence in Bohr model[edit]

The Bohr model explains the atomic spectrum of hydrogen (see hydrogen spectral series) as well as various other atoms and ions. It is not perfectly accurate, but is a remarkably good approximation in many cases, and historically played an important role in the development of quantum mechanics. The Bohr model posits that electrons revolve around the atomic nucleus in a manner analogous to planets revolving around the sun.

In the simplest version of the Bohr model, the mass of the atomic nucleus is considered to be infinite compared to the mass of the electron,^[6] so that the center of mass of the system, the barycenter, lies at the center of the nucleus. This infinite mass approximation is what is alluded to with the infty subscript. The Bohr model then predicts that the wavelengths of hydrogen atomic transitions are (see Rydberg formula):

${displaystyle {frac {1}{lambda }}=mathrm {Ry} cdot {1 over hc}left({frac {1}{n_{1}^{2}}}-{frac {1}{n_{2}^{2}}}right)={frac {m_{text{e}}e^{4}}{8varepsilon _{0}^{2}h^{3}c}}left({frac {1}{n_{1}^{2}}}-{frac {1}{n_{2}^{2}}}right)}$

where n₁ and n₂ are any two different positive integers (1, 2, 3, …), and lambda is the wavelength (in vacuum) of the emitted or absorbed light.

${displaystyle {frac {1}{lambda }}=R_{M}left({frac {1}{n_{1}^{2}}}-{frac {1}{n_{2}^{2}}}right)}$

where ${displaystyle R_{M}={frac {R_{infty }}{1+{frac {m_{text{e}}}{M}}}},}$ and M is the total mass of the nucleus. This formula comes from substituting the reduced mass of the electron.

Precision measurement[edit]

The Rydberg constant is one of the most precisely determined physical constants, with a relative standard uncertainty of under 2 parts in 10¹².^[2] This precision constrains the values of the other physical constants that define it.^[7]

Since the Bohr model is not perfectly accurate, due to fine structure, hyperfine splitting, and other such effects, the Rydberg constant $R_{{infty }}$ cannot be directly measured at very high accuracy from the atomic transition frequencies of hydrogen alone. Instead, the Rydberg constant is inferred from measurements of atomic transition frequencies in three different atoms (hydrogen, deuterium, and antiprotonic helium). Detailed theoretical calculations in the framework of quantum electrodynamics are used to account for the effects of finite nuclear mass, fine structure, hyperfine splitting, and so on. Finally, the value of $R_{{infty }}$ is determined from the best fit of the measurements to the theory.^[8]

Alternative expressions[edit]

The Rydberg constant can also be expressed as in the following equations.

$R_{infty }={frac {alpha ^{2}m_{{text{e}}}c}{4pi hbar }}={frac {alpha ^{2}}{2lambda _{{{text{e}}}}}}={frac {alpha }{4pi a_{0}}}$

and in energy units

${displaystyle {text{Ry}}=hcR_{infty }={frac {1}{2}}m_{text{e}}c^{2}alpha ^{2}={frac {1}{2}}{frac {e^{4}m_{text{e}}}{(4pi varepsilon _{0})^{2}hbar ^{2}}}={frac {1}{2}}{frac {m_{text{e}}c^{2}r_{text{e}}}{a_{0}}}={frac {1}{2}}{frac {hcalpha ^{2}}{lambda _{text{e}}}}={frac {1}{2}}hf_{text{C}}alpha ^{2}={frac {1}{2}}hbar omega _{text{C}}alpha ^{2}={frac {1}{2m_{text{e}}}}left({dfrac {hbar }{a_{0}}}right)^{2}={frac {1}{2}}{frac {e^{2}}{(4pi varepsilon _{0})a_{0}}}.}$

where

$m_{text{e}}$ is the electron rest mass,
is the electric charge of the electron,
is the Planck constant,
is the reduced Planck constant,
is the speed of light in vacuum,
$varepsilon _{0}$ is the electrical field constant (permittivity) of free space,
${displaystyle alpha ={frac {1}{4pi varepsilon _{0}}}{frac {e^{2}}{hbar c}}}$ is the fine-structure constant,
$lambda _{{{text{e}}}}=h/m_{{text{e}}}c$ is the Compton wavelength of the electron,
$f_{{{text{C}}}}=m_{{{text{e}}}}c^{2}/h$ is the Compton frequency of the electron,
$omega _{{{text{C}}}}=2pi f_{{{text{C}}}}$ is the Compton angular frequency of the electron,
$a_{0}={frac {4pi varepsilon _{0}hbar ^{2}}{e^{2}m_{{{text{e}}}}}}$ is the Bohr radius,
$r_{{mathrm {e}}}={frac {1}{4pi varepsilon _{0}}}{frac {e^{2}}{m_{{{mathrm {e}}}}c^{2}}}$ is the classical electron radius.

The last expression in the first equation shows that the wavelength of light needed to ionize a hydrogen atom is 4π/α times the Bohr radius of the atom.

The second equation is relevant because its value is the coefficient for the energy of the atomic orbitals of a hydrogen atom: $E_{n}=-hcR_{infty }/n^{2}$ .

References[edit]

^ Pohl, Randolf; Antognini, Aldo; Nez, François; Amaro, Fernando D.; Biraben, François; Cardoso, João M. R.; Covita, Daniel S.; Dax, Andreas; Dhawan, Satish; Fernandes, Luis M. P.; Giesen, Adolf; Graf, Thomas; Hänsch, Theodor W.; Indelicato, Paul; Julien, Lucile; Kao, Cheng-Yang; Knowles, Paul; Le Bigot, Eric-Olivier; Liu, Yi-Wei; Lopes, José A. M.; Ludhova, Livia; Monteiro, Cristina M. B.; Mulhauser, Françoise; Nebel, Tobias; Rabinowitz, Paul; Dos Santos, Joaquim M. F.; Schaller, Lukas A.; Schuhmann, Karsten; Schwob, Catherine; Taqqu, David (2010). «The size of the proton». Nature. 466 (7303): 213–216. Bibcode:2010Natur.466..213P. doi:10.1038/nature09250. PMID 20613837. S2CID 4424731.
^ ^a ^b «2018 CODATA Value: Rydberg constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
^ «2018 CODATA Value: Rydberg constant times hc in J». NIST. The NIST Reference on Constants, Units, and Uncertainty. Retrieved 2020-02-06.
^ «2018 CODATA Value: Rydberg constant times hc in eV». NIST. The NIST Reference on Constants, Units, and Uncertainty. Retrieved 2020-02-06.
^ «2018 CODATA Value: Rydberg constant times c in Hz». NIST. The NIST Reference on Constants, Units, and Uncertainty. Retrieved 2020-02-05.
^ Coffman, Moody L. (1965). «Correction to the Rydberg Constant for Finite Nuclear Mass». American Journal of Physics. 33 (10): 820–823. Bibcode:1965AmJPh..33..820C. doi:10.1119/1.1970992.
^ P.J. Mohr, B.N. Taylor, and D.B. Newell (2015), «The 2014 CODATA Recommended Values of the Fundamental Physical Constants» (Web Version 7.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants. National Institute of Standards and Technology, Gaithersburg, MD 20899. Link to R_∞, Link to hcR_∞. Published in Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). «CODATA recommended values of the fundamental physical constants: 2010». Reviews of Modern Physics. 84 (4): 1527–1605. arXiv:1203.5425. Bibcode:2012RvMP…84.1527M. doi:10.1103/RevModPhys.84.1527. S2CID 103378639″»{{cite journal}}: CS1 maint: postscript (link) and Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). «CODATA Recommended Values of the Fundamental Physical Constants: 2010». Journal of Physical and Chemical Reference Data. 41 (4): 043109. arXiv:1507.07956. Bibcode:2012JPCRD..41d3109M. doi:10.1063/1.4724320″»{{cite journal}}: CS1 maint: postscript (link).
^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). «CODATA recommended values of the fundamental physical constants: 2006». Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP…80..633M. doi:10.1103/RevModPhys.80.633.

Источник

Введение

Квантовая теория позволила понять такие проблемы как характер взаимодействия атомов при образовании стабильных молекул, происхождение периодической системы элементов и наличие характерных электрических, магнитных, механических и оптических свойств у твёрдых тел. Однако первым шагом на этом пути было решение задачи водорода.

При рассмотрении этой задачи результаты точного квантовомеханического расчёта оказываются очень близки к результатам боровской теории водородоподобных атомов. В рамках боровской теории оптические закономерности спектров поглощения и излучения атомарного водорода имеют особенно простую и наглядную форму.

В начале кратко изложу подход к задаче водорода на основе уравнения Шредингера. Далее приведу боровское решение для движения электрона в центральном кулоновском поле атомного ядра и вытекающий из него энергетический спектр водородоподбного атома. Значительное внимание уделю принципам работы дифракционных спектральных приборов, которые отличаются от принципов работы оптических приборов, в которых в качестве диспергирующего элемента используется призма из прозрачного материала.

Цель работы состоит в освоении принципов работы дифракционного спектрометра, измерении спектра излучения дейтериевой лампы и, самое главное, определении постоянной Ридберга.

Результатом работы является вычисление постоянной Ридберга, путем исследования спектра атомарного водорода.

1.Квантовая теория атома водорода

Квантовомеханическая теория атома, стала фундаментальным вкладом в наши знания о мире. Наряду с коренной ломкой взглядов на атомные явления эта теория позволила понять такие близкие проблемы, как характер взаимодействия атомов при образовании стабильных молекул, происхождение периодической системы элементов и наличие характерных электрических, магнитных, механических и оптических свойств у твёрдых тел. Однако первым продуктивным шагом на этом пути было решение задачи водорода. Атом водорода состоит из протона с электрическим зарядом +e, в котором сосредоточена практически вся масса атома, и электрона — частицы с массой в 1836 раз меньшей и с зарядом –e, который удерживается вблизи протона электрическим полем. При таком соотношении масс можно полагать ядро совершенно неподвижным, однако, если потребуется учесть его движение, то это легко будет сделать, как и в теории Бора, путём замены массы электрона m на приведённую массу:

Потенциальная энергия электрона в водородоподобном атоме — системе с зарядом ядра Ze и движущимся вокруг него электроном — равна

где r — расстояние между неподвижным точечным ядром, расположенным в начале отсчета, и электроном.

Общий вид уравнения Шредингера для стационарных состояний имеет вид

Очевидно, что сформулированная задача имеет сферическую симметрию, поэтому решать ее целесообразно в сферических координатах, которые связаны с декартовыми координатами частицы следующими соотношениями:

Уравнение Шредингера в таком случае записывается как

Его решение стандартно, но довольно громоздко и приводит в нашем случае к результатам, близким к выводам, следующим из боровской теории.

2.Теория Бора

Для простоты Бор принял, что в атоме водорода электроны вращаются вокруг протона по окружности радиусом r с циклической частотой ω. Согласно второму закону Ньютона, мы имеем:

Бор положил, что стационарным состояниям электрона в атоме соответствует модуль механического момента, кратный постоянной Планка:

Решение уравнений (3), (4) дает выражение для радиусов круговых орбит электронов в атоме водорода:

Полная энергия электрона в атоме есть сумма кинетической и отрицательной потенциальной энергий:

Подставляя в (6) rn , получаем формулу, выражающую полную энергию электрона в атоме водорода на n‑ой стационарной орбите:

Формула (5), полученная с помощью постулатов Бора, совпадает с формулой (2), полученной с помощью решения уравнения Шредингера для атома водорода.

Однако, к сожалению, теория Бора, достаточно правильно описывая закономерности в атоме водорода и водородоподобных ионах (содержащих один электрон), даёт неправильные результаты уже для атома гелия, следующего за водородом и содержащем всего два электрона. Таким образом, теорию Бора можно рассматривать лишь как промежуточный этап на пути поиска верной теории — квантовой механики, точно описывающий закономерности микромира.

При переходе атома водорода из состояния n2 с энергией Е2 в состояние n1 с энергией Е1 излучается квант света с частотой ω, равной

Подставляя значение энергии E2 и E1 из формул (2) или (5), имеем:

Далее, вспоминая, что E2 -E1=hw, можем записать:

Формулу (10) называют обобщённой формулой Бальмера, а константу R — постоянной Ридберга.

Совокупность спектральных линий, закономерно меняющих свою интенсивность, называют спектральной серией. Предельное волновое число при называется границей серии. В видимой области спектра для водорода мы можем наблюдать только серию Бальмера: n1 = 2, n2 = 3, 4, 5, … .

В спектре излучения водорода существуют и другие серии. Это, например, серия Лаймана, все линии которой лежат в ультрафиолетовой области спектра. Для этой серии n1=1. Линии остальных серий (Пашена, Брэкета, Пфунда и др.) лежат в инфракрасной области спектра. Набор уровней энергии и возможные переходы в атоме принято показывать на энергетической диаграмме (см. рис. 2). Еn=Wn- полная энергия электрона в атоме на уровне с главным квантовым числом равном n.

Состояние атома, в котором электрон находится на низшем энергетическом уровне (для атома водорода это состояние с энергией Е1 = –13,6 эВ), называется основным. Атом без внешних возмущений может находиться в этом состоянии неопределённо долго. Энергетический уровень Е1, соответственно, является бесконечно тонким. Этот вывод вытекает непосредственно из соотношения неопределённостей:

-неопределённость значения энергии,- неопределенность времени пребывания атома в этом состоянии.

Остальные энергетические уровни являются возбужденными, так как возникают под действием внешних воздействий и могут существовать ограниченное время.

3. Описание установки и методики эксперимента

Для изучения спектра атома водорода используется спектроскоп на основе призменного монохроматора УМ-2. Схема экспериментальной установки приведена на рисунке

1- источник света, 2- входная щель спектроскопа, 3- входной объектив, 4- сложная спектральная призма, 5- микрометрический винт с отсчетным барабаном, 6- входной объектив, 7- указатель, 8- окуляр.

Свет от источника 1 через входную щель 2 и объектив 3 параллельным пучком падает на спектральную призму с высокой дисперсией 4. Призмой свет разлагается в спектр и через объектив 6 направляется в окуляр 8. При повороте призмы в центре поля зрения появляются различные участки спектра. Призму поворачивают при помощи барабана 5, на которой нанесена шкала в градусах. Вращением барабана спектральную линию подводят к стрелке указателя 7, расположенного в окуляре, и фиксируют отсчет по шкале барабана.

В работе наблюдают спектры газов в видимой области.

1. Градуируют спектроскоп по известному спектру ртути.

2. Измеряют длины волн в спектре атома водорода.

3. По измеренным длинам волн в спектре водорода определяют уровни энергии электронов, при переходах между которыми испускаются кванты света. Определяются соответствующие этим уровням квантовые числа ???????? и ????????, далее вычисляют постоянную Ридберга.

4. Основные расчетные формулы

Постоянная Ридберга (угловой коэффициент), расчёт по графику:

, где

λ – длина волны спектральных линий;

n – главное квантовое число.

Вспомогательные формулы для расчёта абсолютной погрешности постоянной Ридберга:

Угловой коэффициент прямой k= n*S3-S1S2/D

Абсолютная погрешность постоянной Ридберга, как абсолютная погрешность углового коэффициента прямой k:

, где

n – количество точек.

5. Результаты работы и их анализ

Данные градуировки спектроскопа по спектру ртути:

Градуировочный график φ(λ):

Значения длин волн λ спектральных линий водорода определяются по градуировочному графику: на оси Y откладываются значения φ, а соответствующие им значения на оси X подбираются так, чтобы точка совпала с линией. Используя график, определяем значения длин волн линий спектра водорода.

Экспериментальные данные спектра атома водорода:

Проверим справедливость формулы Бальмера. Для этого нужно построить график зависимости 1/λ(1/n2).

Данные для построения зависимости 1/λ(1/n2):

График линейной зависимости 1/λ(1/n2):

5.1 Определение постоянной Ридберга

Определяем по графику постоянную Ридберга, как угловой коэффициент линейной зависимости 1/λ(1/n2) по формуле

R = (2,445*10-6– 1,517*10-6)/( 0,111– 0,028) = 1,108*107 (м-1)

Оцениваем абсолютную погрешность R по ранее данным формулам

Ошибка определения постоянной Ридберга составила 0,98%.

Используя полученные из опыта значения длин волн построим фрагмент энергетического спектра атома водорода.

Фрагмент энергетического спектра атома водорода:

Переходы, наблюдаемые в опыте: 6s → 2p, 5s → 2p, 4s → 2p, 3s → 2p.

Заключение

В ходе работы был изучен спектр излучения атомов водорода. Был построен график линейной зависимости 1/λ(1/n2), по которому удалось определить постоянную Ридберга (R). Погрешность экспериментального определения R составила

Ошибка определения постоянной Ридберга составила 0,98%.

Постоянную Ридберга можно найти с помощью обобщенной формулы Бальмера, определив экспериментальным путем длины волн в какой-либо серии. Наиболее удобно это сделать в видимой области спектра, то есть для серии Бальмера.

В настоящей работе определяются длины волн первых четырех наиболее ярких спектральных линий этой серии, для которой i принимает значения: 3 (красная линия), 4 (голубая), 5 (фиолетовая), 6 (тёмно-фиолетовая, слаборазличимая).

Источник