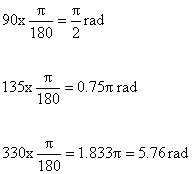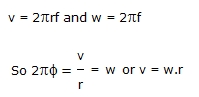В этой статье обсуждается, как найти постоянную скорость. Когда скорость постоянна, ускорение тела равно нулю.
Когда мы рассматриваем скорость объекта, а также его направление, комбинация скорости и направления формирует скорость объекта. Проще говоря, можно сказать, что скорость объекта — это скорость, с которой он изменяет свое перемещение во время движения. В этой статье обсуждается постоянная скорость, формула постоянной скорости и другие связанные темы.
Что такое скорость?
Как мы обсуждали выше, скорость определяется как скорость, с которой объект движется по прямой или угловое движение меняет свое смещение. Для линейного движения это называется линейной скоростью, а для углового движения — угловой. скорость.
Это можно назвать скоростью объекта с его направлением движения. Следует отметить, что величина как скорости, так и скорости может быть одинаковой, несмотря на то, что их значения различны. Один из них — скаляр, с которым не связано направление, а другой — вектор. Мы будем изучать скалярные и векторные величины в последующих разделах этой статьи.
Что такое ускорение?
Ускорение объекта определяется как скорость, с которой он изменяет свою скорость во время движения. Проще говоря, это величина, которая говорит нам, насколько быстро увеличивается скорость объекта. Единицы ускорение Рад/с^2.
Вход в музей Мадам Тюссо важно знать об ускорении объекта, чтобы мы могли рассчитать общее время, которое потребуется объекту, чтобы достичь определенного пункта назначения. В случае торможения замедление (отрицательное ускорение) помогает нам рассчитать, сколько времени потребуется транспортному средству, чтобы остановиться. Это необходимо для предотвращения аварий на дорогах.
Что такое скалярные и векторные величины?
Скалярные и векторные величины могут быть одинаковыми по величине. Эти величины являются мерой определенного свойства движущегося объекта.
Единственное различие между ними состоит в том, что скалярные величины не имеют направления, они имеют только числовые значения, например температуру. Принимая во внимание, что к векторным величинам прикреплен член направления. Примером векторной величины является скорость.
Что вы имеете в виду под смещением?
Перемещение – это кратчайший путь между двумя рассматриваемыми точками. Перемещение и расстояние, пройденное объектом, — две полные вещи, а не одно и то же.
Расстояние является мерой общего пути, пройденного объектом, и кратчайший путь между двумя рассматриваемыми точками называется смещением. Численно значение смещения может быть меньше или равно пройденному расстоянию. Если расстояние является кратчайшим возможным путем, то можно сказать, что перемещение и расстояние равны.
Как найти постоянную скорость на графике?
График, построенный с помощью значений смещения и времени, можно использовать для нахождения скорости объекта. Наклон этого графика дает скорость объекта.
Когда наклон постоянен, то есть смещение увеличивается линейно по прямой линии со временем, можно сказать, что объект движется с постоянной скоростью. Величину постоянной скорости можно рассчитать, вычислив тангенс угла, образуемого линией на графике с горизонталью. Это можно показать ниже-
Время представлено по оси x, а положение объекта указано по оси Y. Вычисление тангенса угла от образовавшегося треугольника. Мы получаем скорость, равную тангенсу (тета).
Как найти постоянную скорость из ускорения?
Он определяется как скорость, с которой скорость объекта изменяется во время движения. Поскольку скорость изменяется со временем, значение ускорения также изменяется. С другой стороны, мы можем сказать, что если есть ускорение, то скорость объекта непрерывно изменяется.
Если мы хотим найти значение постоянной скорости, то ускорение должно быть равно нулю. Что означает термин dv/dt=0. Следовательно, мы можем сказать, что изменение скорости равно нулю, поэтому ускорение равно нулю. Поскольку ускорение отсутствует, мы не можем найти значение постоянной скорости по ускорению.
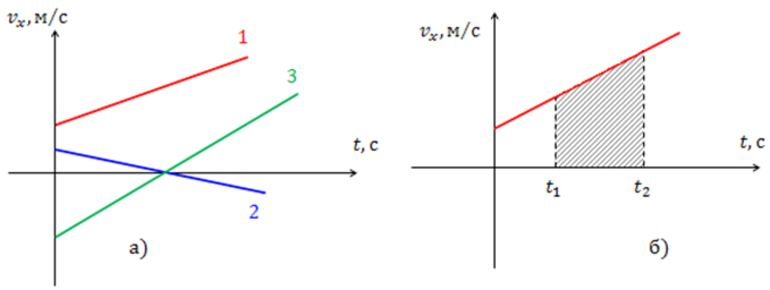
График скорости-времени
График скорость-время — это график между скоростью и временем, который помогает нам понять различные характеристики движения объекта.
Вертикальная ось представляет скорость, а горизонтальная ось представляет время. Мы можем использовать этот график для определения различных величин, таких как смещение (площадь под кривой), средняя скорость и ускорение.
Как найти постоянную скорость на графике скорость-время?
Постоянная скорость представлена в виде прямой горизонтальной линии на графике скорость-время. Все, кроме прямой горизонтальной линии на графике скорость-время, представляет собой движение с переменным скорость.
Его величину можно найти, просто наблюдая за значением, при котором проводится прямая горизонтальная линия. Это значение является значением постоянной скорости. Значение скорости не меняется при движении с постоянной скоростью. Площадь, лежащая под этой кривой, представляет собой смещение объекта.
Пример постоянной скорости
Ниже приведены некоторые примеры объектов, движущихся с постоянной скоростью. Эти примеры очень распространены и уже известны нам.
- человек ходьба с одинаковой длиной шагов- Человек, преодолевающий равные перемещения за равные промежутки времени, является пример постоянной скорости движение.
- Предмет, падающий с предельной скоростью- После достижения конечной скорости объект не достигает какой-либо значительной скорости, и значение ускорения становится равным нулю. Этот случай можно рассматривать как случай движения с постоянной скоростью.
- Поезд, проходящий равные перемещения за равные промежутки времени– Чистое изменение скорости равно нулю, так как поезд проходит равные перемещения за равные промежутки времени.
- Самолет, летящий с той же скоростью, Самолет, движущийся с одной и той же скоростью в крейсерском режиме, совершает равные перемещения за равные промежутки времени, следовательно, это также пример движения с постоянной скоростью.
- Вентилятор, вращающийся с одинаковой скоростью– Когда регулятор вентилятора остается нетронутым, скорость вентилятора не меняется, это случай углового движения и лопасти вентилятора движутся с постоянной угловой скоростью.
- Обращение Земли вокруг Солнца– Вращение Земли вокруг Солнца также является примером углового движения с постоянной скоростью. Чтобы совершить один оборот вокруг Солнца, требуется ровно 365 дней.
- Спутник на орбите Земли– Каждому спутнику необходимо достичь определенного значения скорости, чтобы поддерживать свою орбиту. Значение изменяется во время коррекции курса, но это изменение незначительно. Это подпадает под лозунг углового движения с постоянной угловой скоростью.
- Автомобиль, мчащийся на полной скорости — Когда автомобиль достигает полной скорости, значение ускорения становится равным нулю, что приводит к движению с постоянной скоростью.
- Скорость света— Скорость света постоянна в вакууме и не меняется, если не происходит изменения в среде.
- Скорость звука– Скорость звука в воздухе при стандартных температуре и давлении постоянна. Это изменяется при изменении плотности среднего.
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
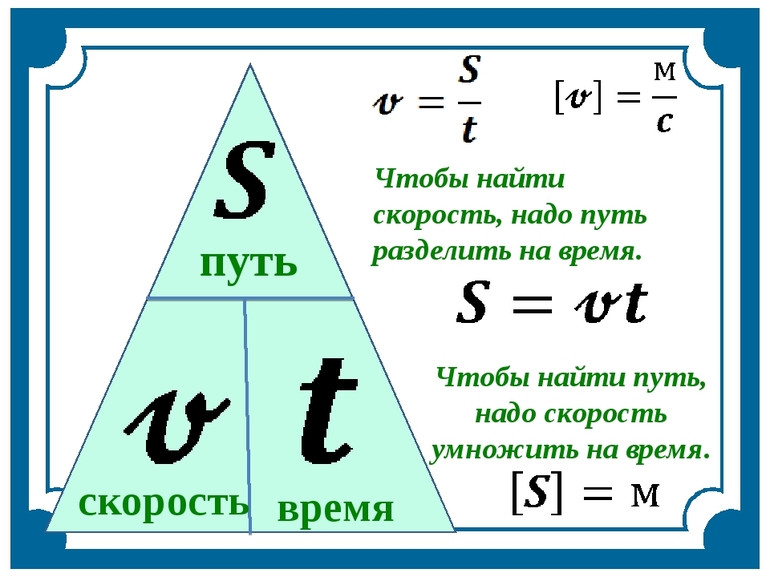
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
- S — расстояние (путь), пройденное материальной точкой или телом (м);
- T — время за которое она преодолела путь (с).
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
- неравномерную;
- среднюю;
- равномерно-переменную;
- поступательную;
- вращательную;
- ускоренную.
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
- V0 — начальная скорость;
- A — ускорение (имеет постоянное значение);
- t — время движения.
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r-1(t). То есть, с математической точки зрения, это первая производная.
Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t2/2 = (V2 — V20) /2*A.
Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V20 — 2* A * s)½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)½.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
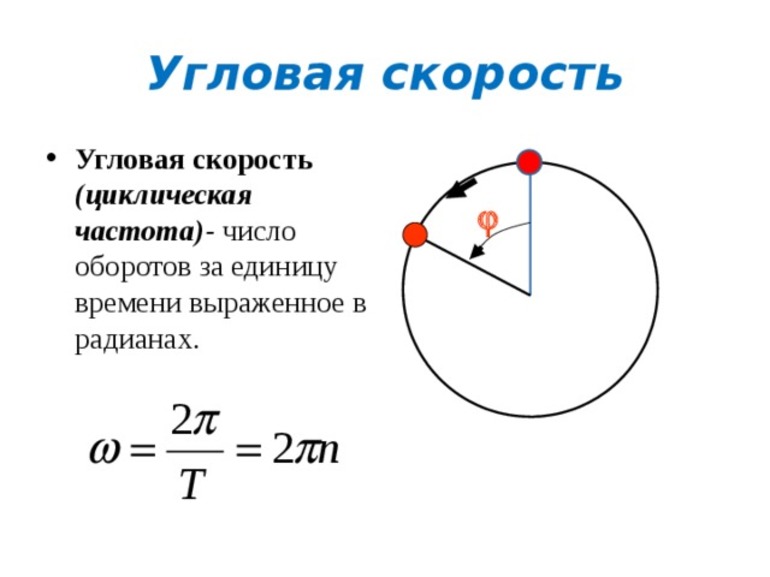
Угловая скорость
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
- Справочный портал «Калькулятор».
- Allcalc.
- Fxyz.
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Прежде чем начать говорить о равномерном прямолинейном движении необходимо уяснить следующие определения:
- равномерное движение — это движение тела с постоянной (не меняющейся) скоростью. Т. е. скорость при таком движении является константой,
- прямолинейное движение — это такое движение, траектория которого — прямая линия. Другими словами это движение по прямой,
- равномерное прямолинейное движение в таком случае — это движение по прямой с постоянной скоростью. При таком движении тело за равные промежутки времени проходит одинаковые расстояния.
Скорость при прямолинейном движении — величина постоянная. Для того, чтобы найти скорость, необходимо пройденный путь разделить на время, за которое он был пройден.
Формула скорости равномерного прямолинейного движения
{vec V=frac {vec S}{t}}
V — скорость тела
S — перемещение при прямолинейном равномерном движении (путь)
t — время движения
Найти скорость равномерного прямолинейного движения онлайн
Применительно к равномерному движению можно сказать, что скорость показывает перемещение, которое совершает тело за единицу времени
Из формулы скорости легко выразить формулу для нахождения перемещения тела:
Формула перемещения тела при равномерном прямолинейном движении
{vec S=vec V cdot t}
S — перемещение при прямолинейном равномерном движении (путь)
V — скорость тела
t — время движения
Найти перемещение при прямолинейном равномерном движении онлайн
Координату тела при прямолинейном равномерном движении легко найти по формуле:
Формула координаты тела при равномерном прямолинейном движении
{x=x_0+ V cdot t}
x — координата тела в текущий момент времени
x0 — координата тела в начальный момент времени
V — скорость тела
t — время движения
Найти координату тела при равномерном прямолинейном движении онлайн
Примеры равномерного прямолинейного движения
- автомобиль, движущийся с неизменной скоростью по прямой автомагистрали,
- самолет, который летит не меняя курса и высоты с постоянной скоростью,
- человек, идущий по прямой дороге с одной скоростью.
Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.
Скорость
Что же такое «скорость»? Можно наблюдать, как одна машина едет быстрее, другая -медленее; один человек идет быстрым шагом, другой — не торопится. Велосипедисты тоже едут с разной скоростью. Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то Допустим, что 5 км/ч. То есть за 1 час он прошел 5 километров.
Более решительные примеры по скорости, расстоянию и времени
Скорость вниз по течению = 3 1 = 4 мили в час. Какова скорость самолета и ветер? Выражение одной неизвестной переменной с точки зрения другой облегчает ее решение, что означает. Мальчик путешествовал поездом, который двигался со скоростью 30 миль в час. Затем он сел на автобус, который двигался со скоростью 40 миль в час и добрался до места назначения. Вся пройденная дистанция составляла 100 миль, а продолжительность путешествия составляла 3 часа.
Найдите расстояние, которое он проехал на автобусе. Все пройденное расстояние было 100 миль. В качестве альтернативы мы можем добавить время и приравнять его к 3 часам, что непосредственно дает расстояние. Самолет преодолел расстояние 630 миль за 6 часов.
Время, расстояние? Начнем со скорости. Посмотрите внимательно, в чем она измеряется? Естественно, км/ч, м/с. Существуют и другие единицы измерения, например, км/с (в космонавтике), мм/ч (в биохимии). Обратите внимание на то, что стоит перед знаком «/» и после. Во-первых, он означает «дробь», а значит, в числителе — мм, км, м, в знаменателе — ч, с, мин. Во-вторых, кажется это напоминает формулу, не правда ли? Километры, метры — расстояние, длина, а час, секунда, минута — время. Вот вам и подсказка. Чтобы проще было запомнить, как находить скорость, посмотрите не единицы измерения (км/ч, м/с). Одними словами:
Для первой части поездки средняя скорость была 100 миль в час, а для второй части поездки средняя скорость составляла 110 миль в час. какое время он летал с каждой скоростью? Этот калькулятор вычисляет, как быстро вы двигаетесь после падения на определенное расстояние — ваша скорость свободного падения. Он игнорирует трения и релятивистские эффекты: мы надеемся, что вы не достигнете достаточно большого уровня, чтобы иметь любой из этих изменений! Однако, если вы выпадали из самолета, вам нужно будет прокрутить вниз.
Движение в противоположных направлениях
Мы не защищаем попытки эмпирически подтвердить эти результаты с помощью вашего тела. Вставьте стандартную опровержение здесь. Если вы заполните высоту, вы получите время и скорость в конце вашего падения. Как видно, чем выше вы, тем труднее вы приземляетесь.
Время
Что из себя представляет время? Разумеется, оно зависит от скорости. Например, вы ждете у порога дома маму и старшего брата. Они идут из магазина. Брат дошел намного раньше. Маму пришлось ждать еще минут 5. Почему? Потому что они шли с разной скоростью. Разумеется, чтобы быстрее добраться до места назначения, нужно прибавить скорость: ускорить шаг, надавить на «газ» в авто посильнее, разогнаться на велосипеде. Только при спешке будьте осторожны и бдительны, чтобы не врезаться в кого-то или во что-то.
Игнорирование трения в воздухе: скорость контакта
Эта точка называется конечной скоростью. Это сильно зависит от вашего положения — что-то в форме пули будет иметь более высокую конечную скорость, чем нечто похожее на плоский блин, параллельный земле, потому что последний имеет большую площадь поверхности, подверженную трению.
Как вы можете видеть из графика выше, вам нужно упасть с высоты более 50 метров над землей, чтобы это действительно имело большое значение, и в этот момент у вас будет достаточно проблем, чтобы не волновать много. Здесь вы можете увидеть исходный код. Мы обычно измеряем углы в градусах.
У скорости есть подсказка — км/ч. А как быть со временем? Во-первых, время измеряется в минутах, секундах, часах. Формула «скорость, время, расстояние» здесь преображается следующим образом:
время t[сек., мин., ч]=S[м, мм, км]/v[м/с, мм/мин, км/ч].
Если преобразовать дробь по всем правилам математики, сократить параметр расстояния (длины), то останется только секунда, минута или час.
Но это не самый удобный способ измерения углов в круговом движении. Таким образом, коэффициент, который позволяет конвертировать из окружности в радиус, равен 2π. Таким образом, 2π описывает целый круг, так же как 360 ° описывает весь круг. Фактически, пока вы используете углы в радианах, вы можете написать это общее уравнение.
Преобразуйте следующие углы со степеней в радианы. Поэтому умножьте любой угол в градусах, чтобы найти тот же угол в радианах.
Какой угол в градусах имеет автомобиль, проходящий по круговой дорожке, если трасса имеет радиус 100 м, а расстояние, покрываемое автомобилем, составляет 470 м?
Расстояние, длина пройденного пути
Здесь будет легче сориентироваться, скорее всего, автомобилистам, у которых есть счетчик пробега в машине. Они смогут определить, сколько километров проехали, а еще и скорость знают. Но так как движение неравномерное, то установить тоное время перемещения не получится, если только мы возьмем
Нам пришлось превратить конверсионный коэффициент вверх дном, чтобы конвертировать из радианов в градусы. При линейном или прямолинейном движении мы измеряем скорость, просматривая, сколько расстояний покрывается каждую секунду. Вы можете сделать это и в круговом движении, но часто лучше использовать угловую скорость, ω.
Угловая скорость измеряет угол полного круга, покрываемого в секунду. Θ = угол поворота в радианах. Потому что 2π — это угол, охваченный, когда вы делаете полный круг. Помня, что вы также можете написать это как.
Старый проигрыватель воспроизводит записи со скоростью 45 оборотов в минуту. Для точки на окружности вычислить угловую скорость в рад с -1.
Формула пути (расстояния) — произведение скорости и времени. Конечно же, самый удобный и доступный параметр — это время. Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности. Обратите внимание, какой масштаб. Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».
Колесо автомобиля вращается со скоростью 10 оборотов в секунду при движении автомобиля. Эти уравнения позволяют связать угловую и линейную скорость.
Стреляющий выстрел крутится со скоростью 1 оборот в секунду. Эти вопросы могут быть сложными, если вы не практиковали их решение, потому что наиболее очевидным выбором ответа является ловушка. Чтобы понять, почему, попробуйте следующую проблему.
Джо управляет 120 милями со скоростью 60 миль в час, а затем он проезжает следующие 120 миль со скоростью 40 миль в час. Какова его средняя скорость для всей поездки в милях в час? Каков правильный подход к вопросам средней скорости? Обычно мы находим среднее значение двух значений, добавляя числа и делим общее на два, но это не работает, когда мы говорим о скорости. Скорость представляет общее расстояние, деленное на общее время, и этот факт полностью меняет наш подход к проблеме средней скорости.
Не упустите!
Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:
Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.
Еще до того, как мы начнем математику, давайте остановимся и рассмотрим данную информацию. Время должно учитывать наше решение. Давайте подробнее рассмотрим формулу средней скорости. Нам придется рассчитать общее расстояние и общее время, чтобы решить среднюю скорость.
Несмотря на то, что нам нужно сделать несколько расчетов, все, что нам нужно, — это текст вопроса. Общее расстояние легко вычислить: первые 120 миль, а затем еще 120 миль, что дает нам полное расстояние 240 миль. Общее время займет еще несколько шагов.
Где упоминается скорость тела?
Джо ездит на двух разных скоростях: 60 миль в час и 40 миль в час. Как мы сказали в начале проблемы, потребуется меньше времени, чтобы проехать 120 миль со скоростью 60 миль в час, чем это будет, чтобы проехать на том же расстоянии со скоростью 40 миль в час, и мы были правы. Потребовалось 2 часа, чтобы проехать 120 миль со скоростью 60 миль в час, и потребовалось 3 часа со скоростью 40 миль в час, давая нам общее время 5 часов.
Вот так легко запоминается формула «скорость, время, расстояние». Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено.
Однажды случайный прохожий спросил Эзопа: «Как скоро я доберусь до города?» Эзоп ответил: «Не знаю». Прохожему ничего не оставалось, как только пойти дальше своей дорогой – и тогда Эзоп крикнул ему вслед: «Ты дойдёшь до города к полудню!» Прохожий удивился: «Почему же ты не ответил мне сразу, если знал ответ?» И Эзоп сказал: «Как же я мог сказать это, не зная, как ты ходишь?»
В приведенных выше шагах мы рассчитали общее расстояние, и мы просто нашли общее время. Прежде чем выбрать этот ответ, полезно проверить наличие ошибок. Поскольку проблемы со средней скоростью связаны с несколькими скоростями, временем и расстояниями, тестировщики должны убедиться, что они не перепутали какие-либо значения и что их ответ кажется разумным. Выполнение быстрой проверки поможет устранить глупые ошибки.
В начале проблемы мы сделали вывод, что Джо потратил меньше времени на поездку со скоростью 60 миль в час, чем у 40 миль в час. Скорость в том, как быстро что-то растет, меняется или выполняется. Общая формула ставки. Когда скорость равна скорости, это упрощает привычную формулу.
Действительно, о том, что время, расстояние и скорость – величины взаимосвязанные, известно давно. Из этого логически следует, что зная две из них, можно вычислить третью. Формула тоже представляется предельно логичной: если скорость равна, например, 60 км/ч (возьмём для примера разрешённую скорость автомобиля в городе) – т.е. за час он проезжает 60 километров, то для нахождения расстояния, которое он преодолеет за два часа, нам надо всего лишь умножить шестьдесят на два – в результате мы получаем 120 километров.
В вопросах о скорости, особенно когда объект перемещается с одной скоростью на некоторое время, затем с другой скоростью помните, что вы никогда не найдете числовое среднее двух разных скоростей. Если вопрос задает среднюю скорость для всего путешествия, то вы добавляете расстояния от обеих частей поездки, чтобы найти общее расстояние, и добавьте время обеих частей поездки, чтобы найти общее время, и используйте те и формулу выше, чтобы вычислить скорость.
Когда ставка является нормой выполняемой работы, тогда, когда два человека работают вместе, их комбинированная ставка представляет собой сумму их соответствующих индивидуальных ставок. Убедитесь, что вы добавляете тарифы, а не что-то еще. Когда Лиза присоединяется к Мэри, и они работают вместе, им требуется всего 3 часа, чтобы нарисовать дом того же размера. Сколько времени потребуется, чтобы Лиза сама по себе нарисовала дом того же размера?
Представим это в виде формулы. Расстояние в физике принято обозначать латинской буквой S – почему так, с точностью сказать нельзя, это связывают и с немецким словом «Spur», что переводится как «колея» или «след», и с латинскими словами «sulcus» – что значит «борозда» – и «semita», переводимом как «тропинка» или «путь». Яснее происхождение обозначений для других составляющих этой формулы. Время обозначается латинской буквой t – от латинского слова «tempus», которое, собственно и означает – «время» (к нему же восходит музыкальный термин «темп» – хотя в этом можно усмотреть некоторую «путаницу»: темп в музыке – это всё-таки ближе к понятию скорости, чем времени). Время же – латинская буква v – что опять же связано с латынью: «скорость» на этом языке именуется «velocitas».
В фазе № 2 поездки автомобиль проехал 180 миль со скоростью 60 миль в час. Общее расстояние поездки = 40 миль 180 миль = 220 миль. Общее время поездки = 2 часа 3 часа = 5 часов. Средняя скорость поездки определяется. Когда Мэри рисует дом, ей требуется 4 часа.
Чтобы найти комбинированную ставку, мы добавляем индивидуальные тарифы. Знак равно. Как вы находите ускорение при заданной скорости и расстоянии? — Анонимная Малайзия. Основным уравнением для решения этого является. Это дает вам расстояние, пройденное за определенное количество времени.
Если вы знаете какие-либо 3 из этих вещей, вы можете подключить их к решению для 4-го. Ответ на этот вопрос неверен. Первоначальный ответ, по-видимому, предполагал, что скорость, которую вы знали, была только начальной. В этом случае этот ответ правильный, как стенд. Вы, кажется, предполагаете, что знаем как начальную, так и конечную скорости. Так что, конечно, если вы знаете две скорости, которые вы знаете больше, чем если бы вы их знали.
Итак, формула расстояния выглядит следующим образом: v×t=s
Исходя из этого – и зная правила умножения и деления, разумеется, которые изучают во втором классе, когда и начинают решать такие задачи – мы легко можем найти и другие составляющие. Как мы помним из начальной школы, чтобы вычислить один из множителей, необходимо разделить произведение (т.е. результат умножения) на другой из них. Иными словами, делим расстояние (s) на время (t) – получаем скорость (v), если же нам нужно вычислить время(v) – поступаем наоборот, т.е. делим расстояние на время.
Последующее наблюдение № 2: ускорение, ограничение скорости, расстояние
Вы должны указать это немного больше, прежде чем мы сможем ответить. Существует ли постоянное ускорение до достижения этой скорости, тогда ускорение прекращается? Или есть, более правдоподобно, одна из этих других ситуаций, которые также приводят к предельным скоростям.
Последующее наблюдение № 3: максимальная скорость?
Ускорение, уменьшаемое силой трения, линейной по скорости? Ускорение, уменьшаемое силой трения, квадратичной по скорости? Какой-то другой эффект нет в списке? Или время, если дано расстояние, но не время? Вот что: если ускорение остается постоянным, вы не можете иметь максимальную скорость. Скорость будет только больше и больше в направлении ускорения. Поэтому должно быть какое-то правило о том, как ускорение останавливается или сужается, чтобы дать эту максимальную скорость.
Ничего сложного в таких вычислениях нет – так что с ними с лёгкостью справляются уже второклассники… правда, такая формула предполагает, что объект, с которым мы имеем дело, постоянно движется с одной и той же скоростью (такое движение в физике называется равномерным) – что далеко не всегда имеет место в реальности. Что делать, если скорость движущегося тела изменяется – как бывает, например, когда автомобиль трогается с места?
Тут мы уже имеем дело с более сложной формулой – а именно, с формулой равноускоренного движения, для которого приходится ввести новую величину – ускорение, традиционно обозначаемое латинской буквой a. Чтобы вычислить расстояние при равноускоренном движении (при условии, что тело стартует из состояния покоя), нам придётся умножить ускорение на возведённое в квадрат время, а результат разделить на два.
Остаётся один вопрос – как вычислить ускорение? Для этого надо знать начальную скорость и конечную, соотношение между которыми характеризуется такой формулой:
(v – это конечная скорость, а v0 – начальная). «Вытащить» ускорение из этой формулы – не проблема: из конечной скорости вычитаем начальную и делим результат на время.
Остаётся только добавить, что формулами, характеризующими равноускоренное движение, мы обязаны Г.Галилею, который изучал это явление на примере ускорения при свободном падении.
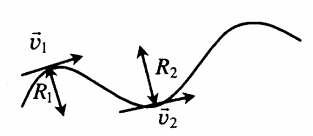
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22k