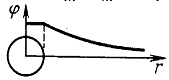
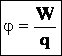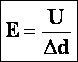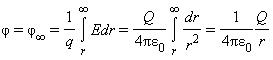Потенциал. Эквипотенциальные поверхности.
В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W1 — W2 на заряд q, получим
Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.
Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:
Единица потенциала — вольт:
Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.
С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде
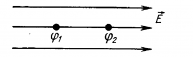
Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ1 — φ2 )> 0, то потенциал φ1 больше чем потенциал φ2 . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.
Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ∞ ). Поскольку φ∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,
Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле
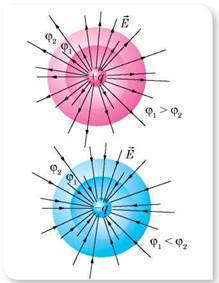
По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.
Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.
Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.
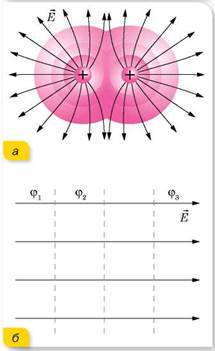
В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ1 + φ2 + φ3 . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.
Разность потенциалов
Практическое значение имеет не сам потенциал в точке, а изменение (разница) потенциала φ1 — φ2 , которое не зависит от выбора нулевого уровня отсчета потенциала. Разность потенциалов φ1 — φ2 еще называют напряжением и обозначают латинской буквой U. Тогда формула для работы по перемещению заряда приобретает вид
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля,
Единица разности потенциалов (напряжения), как и потенциала, — вольт,
Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то в случае перемещения заряда с первой эквипотенциальной поверхности на другую (потенциалы которых соответственно φ1 и φ2 ) выполненная полем работа не зависит от траектории этого движения.
Связь напряженности электрического поля с напряжением
Из формул A = Eqd и A = qU можно установить связь между напряженностью и напряжением электрического поля: Ed = U. С этой формулы следует:
- чем меньше меняется потенциал на расстоянии d, тем меньше есть напряженность электрического поля;
- если потенциал не меняется, то напряженность равна нулю;
- напряженность электрического поля направлена в сторону уменьшения потенциала.
Поскольку
то именно из этой формулы и выводится еще одна единица напряженности — вольт на метр,
|
Потенциал. Разность потенциалов. Напряжение. |
|
|
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
|
— следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
|
Разность потенциалов |
|
|
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
|
Связь между напряженностью и напряжением. |
|
|
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
|
Из этого соотношения видно:
|
|
|
Эквипотенциальные поверхности. ЭПП — поверхности равного потенциала. Свойства ЭПП: — работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; — вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
|
|
Потенциал поля точечного заряда |
|
|
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |

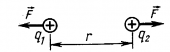
Сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на заряд каждый из зарядов системы в отдельности (принцип суперпозиции).
Тогда
A = ∑Ai
Здесь каждое слагаемое не зависит от формы пути и, следовательно не зависит от формы пути и сумма.
Итак электростатическое поле потенциально.
Работу сил электростатического поля можно выразить через убыль
|
потенциальной энергии – разность двух функций состояния: |
|||||||||
|
A12 = Eп1 – Eп2 |
(3.2.2) |
||||||||
|
Тогда выражение (3.2.2) можно переписать в виде: |
|||||||||
|
A12 = |
qq‘ |
− |
qq‘ |
(3.2.3) |
|||||
|
4πεε r |
4πεε r |
||||||||
|
0 |
1 |
0 |
2 |
||||||
|
Сопоставляя формулу (3.2.2) и (3.2.3) получим выражение для потенциальной |
|||||||||
|
энергии заряда q’ в поле заряда q: |
1 |
qq‘ |
|||||||
|
En = |
+const |
(3.2.4) |
|||||||
|
4πεε0 |
r |
||||||||
Потенциальную энергию определяют с точностью до постоянной интегрирования. Значение константы в выражении Eпот. выбирают таким образом, чтобы при удалении заряда на бесконечность (т. е. при r = ∞), потенциальная энергия обращалась
|
в нуль. Выражение (3.2.4.) – для одного заряда. Для системы зарядов |
|
|
EnΣ = ∑Eni |
(3.2.5) |
Разные пробные заряды q’,q»,… будут обладать в одной и той же точке поля разными энергиями En‘, En» и так далее. Однако отношение En/q’пр. будет для всех зарядов одним и тем же. Поэтому ввели скалярную величину, являющуюся
|
энергетической характеристикой собственно поля – потенциал. |
||||
|
φ= |
En |
(3.3.1) |
||
|
q‘ |
||||
Из этого выражения следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Подставив в (3.3.1.) значение потенциальной энергии (3.2.3), получим для
|
потенциала точечного заряда следующее выражение: |
||||
|
φ= |
1 |
q |
(3.3.2) |
|
|
4πεε0 |
r |
|||
Потенциал, как и потенциальная энергия, определяют с точностью до постоянной интегрирования. Договорились считать, что потенциал точки удаленной в бесконечность равен нулю. Поэтому когда говорят «потенциал такой-то точки» – имеют в виду разность потенциалов между этой точкой и точкой, удаленной в бесконечность. Другое определение потенциала:
φ = Aq∞ или A∞ = qφ,
т.е. потенциал числено равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность
28
dA = Fl dl = El qdl
(наоборот – такую же работу нужно совершить, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.
Если поле создается системой зарядов, то, используя принцип суперпозиции, получим:
|
1 |
N |
qi q‘ |
|||||||
|
En = |
∑= |
(3.3.3) |
|||||||
|
4πεε |
r |
||||||||
|
0 |
i 1 |
i |
|||||||
|
Тогда: |
1 |
qi |
|||||||
|
φ= ∑φi φ= |
∑ |
(3.3.4) |
|||||||
|
4πεε |
r |
||||||||
|
0 |
i |
т.е. потенциал поля, создаваемый системой зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. А вот напряженности, как вы помните, складываются при наложении полей – векторно.
По этой причине потенциалы полей считать проще, чем напряженности.
Вернемся к работе сил электростатического поля над зарядом q’. Выразим работу
|
через разность потенциалов: |
|
|
A12 = En1 − En2 = φ1q′−φ2 q′ = q′(φ1 −φ2 ) |
(3.3.5) |
|
Т.о., работа над зарядом q’ равна произведению заряда на убыль потенциала. То |
|
|
есть: |
|
|
A = q‘(φ1 −φ2 )= q‘U , |
|
|
A = qU , |
(3.3.6) |
где U – разность потенциалов или еще называют напряжение. Между прочим, хорошая аналогия:
A12 = mgh1 −mgh2 = m(gh1 − gh2 )
gh – имеет смысл потенциала гравитационного поля, а m – заряд.
Итак потенциал – скалярная величина, поэтому пользоваться и вычислять φ
проще, чем E . Приборы для измерения разности потенциалов широко распространены. Формулу A∞=qφ можно использовать для установления единиц потенциала: за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из ∞ единичного положительного заряда необходимо совершить работу равную единице.
Так в СИ – единица потенциала 1В = 1Дж/1Кл, в СГСЭ 1ед.пот. = 300В.
В физике часто используется единица энергии и работы, называемой эВ – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1В, то есть:
1эВ =1,6 10−19 Кл В =1,6 10−19 Дж
3.4. Связь между напряженностью и потенциалом.
Итак электростатическое поле можно описать либо с помощью векторной
величины E , либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:
Изобразим перемещение заряда q по произвольному пути l.
Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl можно найти так:
(3.4.1)
El – проекция E на drl ; dl – произвольное направление перемещения заряда.
29
С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl.
|
dA = −qdφ; El qdl = −qdφ |
(3.4.2) |
|||
|
El = − |
dφ |
(3.4.3) |
||
|
dl |
||||
Вот отсюда размерность напряженности поля В/м.
Для ориентации dl – (направление перемещения) в пространстве, надо знать проекции E на оси координат:
|
Ex = − |
∂φ |
; Ey = − ∂φ |
; Ez = − |
∂φ |
; |
(3.4.4) |
||||||
|
∂x |
∂y |
∂z |
||||||||||
|
r |
∂φr |
− |
∂φr |
∂φ r |
(3.4.5) |
|||||||
|
E = − |
∂x |
i |
∂y |
j − |
∂z |
k |
||||||
где i, j,k – орты осей – единичные вектора.
По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции, то есть:
gradφ = ∂∂φx ri + ∂∂φy rj + ∂∂φz kr
|
Тогда коротко записывается так: |
|
|
E = −gradφ |
(3.4.6) |
|
gradφ – вектор, показывающий направление наибыстрейшего |
увеличения |
функции. Знак минус говорит о том, что E направлен в сторону уменьшения потенциала электрического поля.
3.5. Силовые линии и эквипотенциальные поверхности.
Как мы с вами уже знаем, направление силовой линии (линии напряженности) в
каждой точке совпадает с направлением E . Отсюда следует, что напряженность E
равна разности потенциалов на единицу длины силовой линии.
Именно вдоль силовой линии происходит максимальное изменение потенциала.
Поэтому всегда можно определить E между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые
линии – прямые. Поэтому здесь определение E наиболее просто:
|
E = |
U |
В |
||
|
(3.5.1) |
||||
|
l |
||||
|
м |
Теперь запишем определение эквипотенциальной поверхности. Воображаемая поверхность все точки, которой имеют одинаковый потенциал, называют
|
эквипотенциальной поверхностью. Уравнение этой поверхности |
|
|
φ =φ (x,y,z) = const. |
(3.5.2) |
30

Рис. 3.4
При перемещении по этой поверхности на dl, потенциал не изменится: dφ = 0. Следовательно, проекция вектора E на dl равна 0, то есть El = 0. Отсюда
следует, что E в каждой точке направлена по нормали к эквипотенциальной поверхности.
Эквипотенциальных поверхностей можно провести сколько угодно много. По
густоте эквипотенциальных поверхностей можно судить о величине E , это будет при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине. На одной из лабораторных работах мы с вами будем моделировать электрическое поле и находить эквипотенциальные поверхности и силовые линии от электродов различной формы – очень наглядно вы увидите как могут располагаться эквипотенциальные поверхности.
Формула E = −gradφ – выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в каждой точке. Можно решить и
обратную задачу, т.е. по известным значениям E в каждой точке поля найти разность φ между двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть, вычислена как:
2 r r
A12 = ∫qEdl
1
С другой стороны работу можно представить в виде:
A12 = q(φ1 −φ2 )
тогда
|
2 |
r r |
|
|
φ1 −φ2 = ∫Edl |
(3.5.3) |
|
|
1 |
Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля не зависит от пути. Для обхода по замкнутому контуру φ1 = φ2 получим:
т.е. пришли к известной нам теореме о циркуляции вектора напряженности.
Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее этим
свойством, называется потенциальным. Из обращения в нуль циркуляции вектора E ,
следует, что линии E электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах и на отрицательных зарядах заканчиваются или уходят в бесконечность.
31
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Потенциал φ является энергетической характеристикой электростатического поля.
Во многих задачах электростатики при вычислении потенциалов за начальную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов: φ = φ1 + φ2 + φ3 + …
Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям.
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рисунке представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
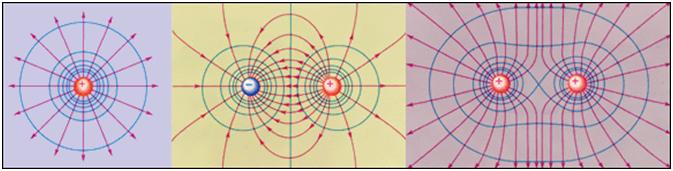
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Свойства эквипотенциальных поверхностей:
- В каждой точке эквипотенциальной поверхности вектор напряженности поля перпендикулярен ей и направлен в сторону убывания потенциала.
- Работа сил поля при перемещению заряда по эквипотенциальной поверхности равна нулю.
Эквипотенциальные поверхности
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
Электрический потенциал можно представить графически, изображая эквипотенциальные линии или в трех измерениях — эквипотенциальные поверхности. Всем точкам эквипотенциальной поверхности соответствует один и тот же потенциал. Иначе говоря, разность потенциалов между любыми двумя точками этой поверхности равна нулю, и при перемещении заряда из одной точки в другую работа не совершается.
Эквипотенциальная поверхность в любой точке должна быть перпендикулярна направлению напряженности электрического поля. Если бы это было не
так (т. е. если бы существовала компонента Е, параллельная поверхности), то для перемещения заряда вдоль поверхности в направлении, противоположном этой компоненте Е, приходилось бы совершать работу, что противоречит предположению об эквипотенциальности поверхности.
Тот факт, что силовые линии электрического поля перпендикулярны эквипотенциальным поверхностям, помогает построению эквипотенциальных поверхностей,
если известно расположение силовых линий.

Рис. 24.2. Эквипотенциальные линии (штриховые) между двумя заряженными параллельными пластинами, перпендикулярные силовым
линиям поля (сплошные линии).
На рис. 24.2 изображено несколько эквипотенциальных линий (штриховые линии) для поля между параллельными
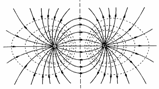
пластинами, разность потенциалов которых составляет 20 В. Эти линии принадлежат эквипотенциальным поверхностям, которые пересекают рисунок перпендикулярно плоскости книжной страницы. Потенциал отрицательной пластины условно принят за нулевой; указан соответствующий потенциал каждой эквипотенциальной линии. Эквипотенциальные линии для случая двух равных по величине и противоположных по знаку зарядов показаны штриховыми линиями на рис. 24.3.

Рис. 24.3. Эквипотенциальные линии (штриховые) и силовые линии электрического поля (сплошные линии) вблизи двух противоположно заряженных частиц.
В одном из разделов ранее мы видели, что в статическом случае внутри проводника не существует электрическое поле, так как в противном случае на свободные электроны действовала бы сила и они пришли бы в движение. Иными словами, в статическом случае проводник должен находиться целиком под одним и тем же потенциалом, и поверхность проводника является, таким образом, эквипотенциальной. (Иначе свободные электроны на поверхности пришли бы в движение.) Это полностью согласуется с уже отмеченным выше фактом, что электрическое поле у поверхности проводника перпендикулярно поверхности.
Продолжение следует. Коротко о следующей публикации:
Электрон-вольт, единица энергии.
Один электрон-вольт равен энергии, которую приобретает электрон, проходя разность потенциалов 1 В.
Альтернативные статьи:
Электрический ток,
Закон Ома.
Замечания и предложения принимаются и приветствуются!