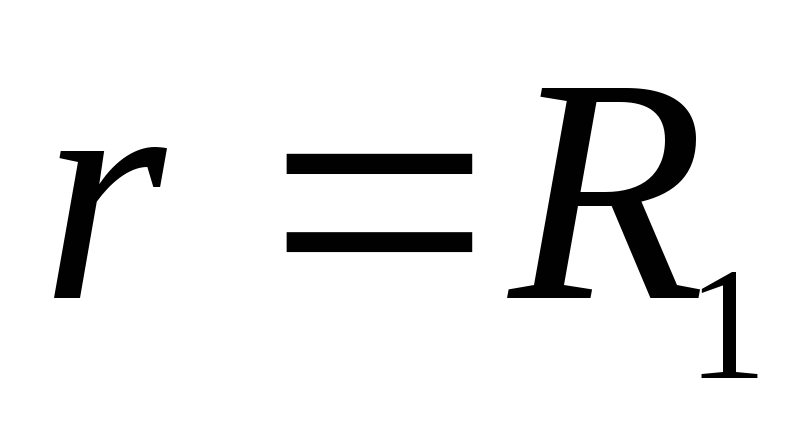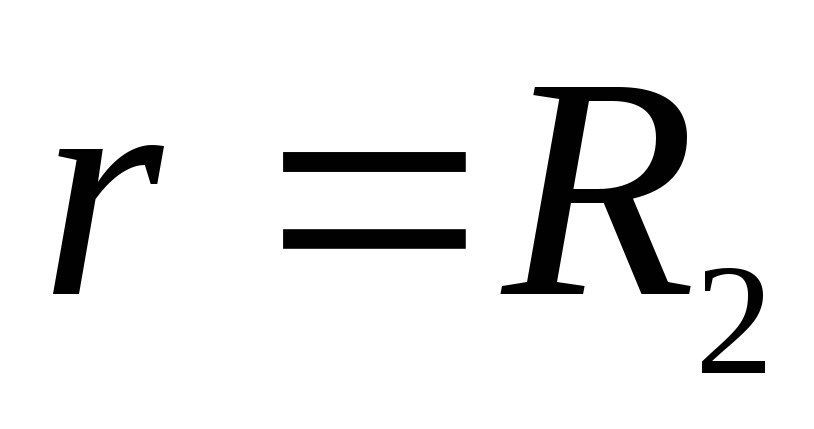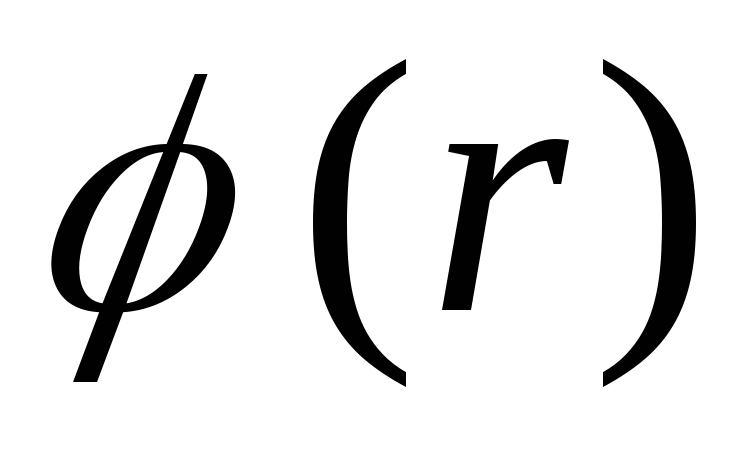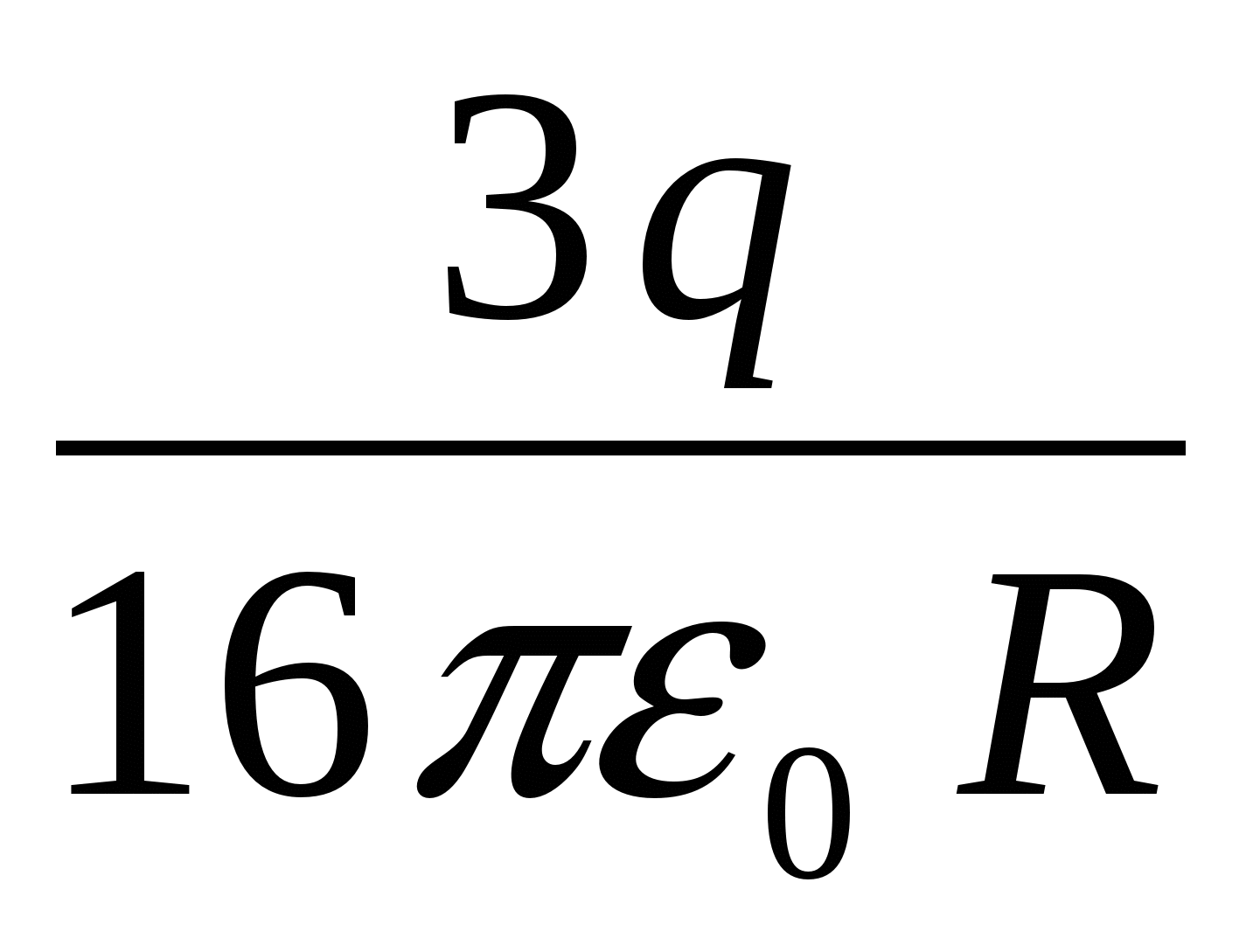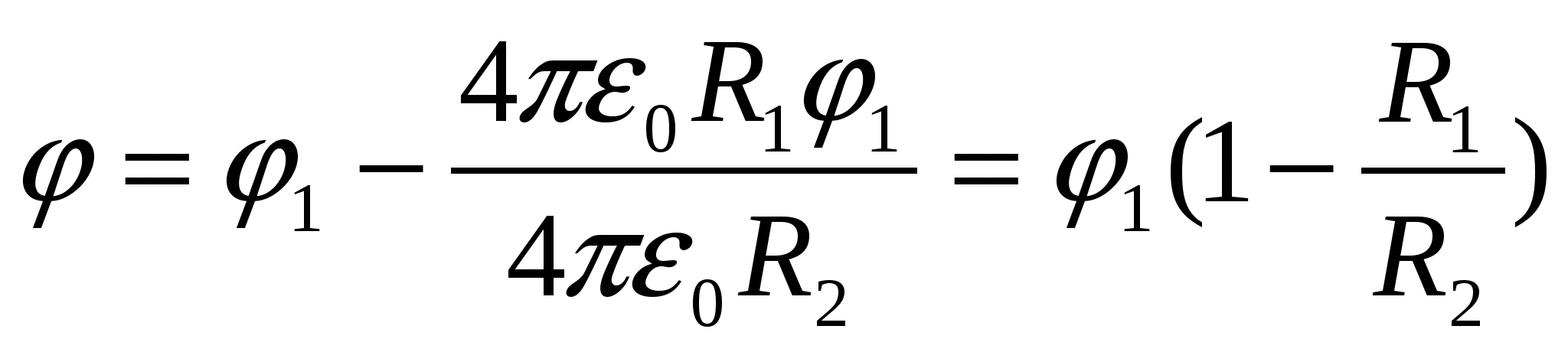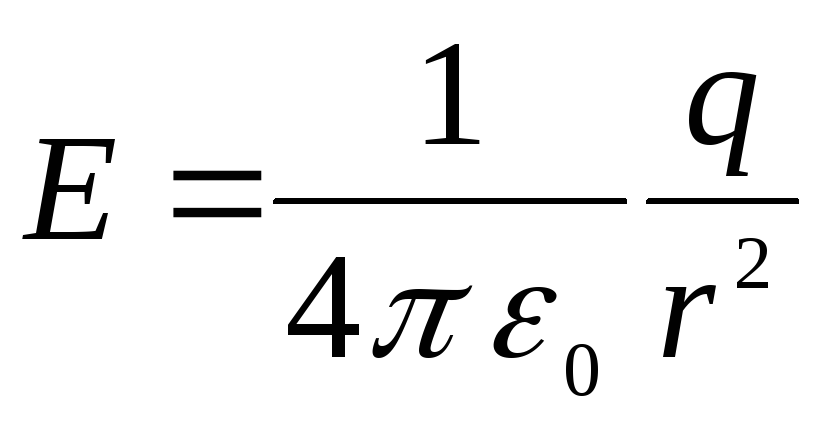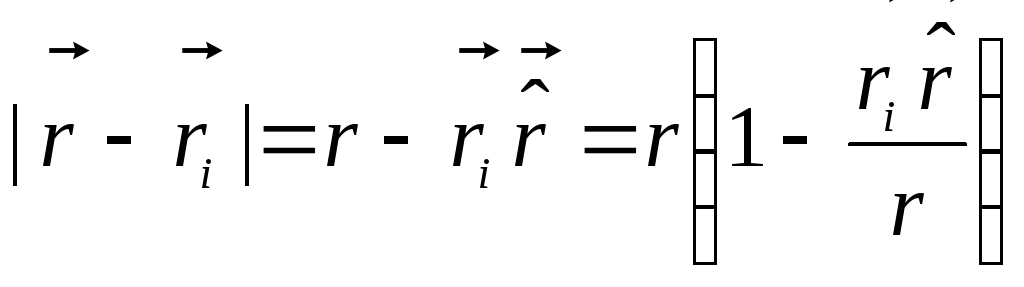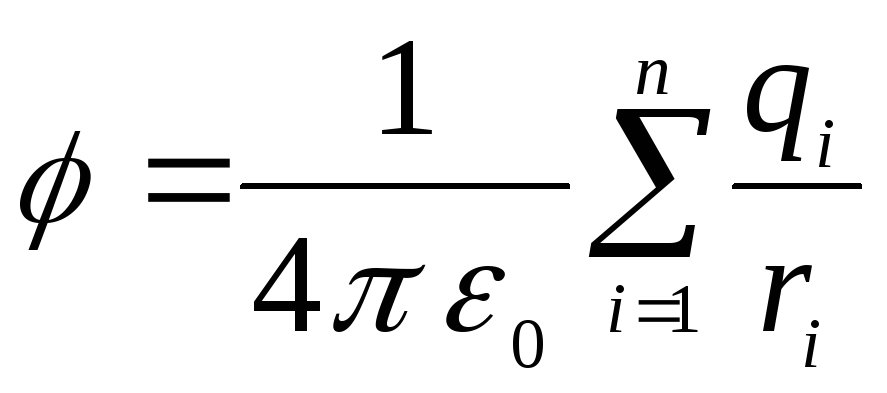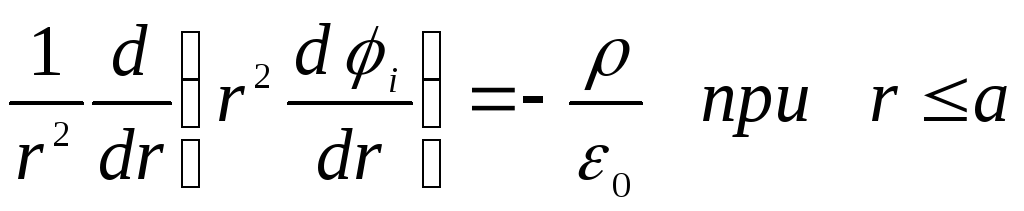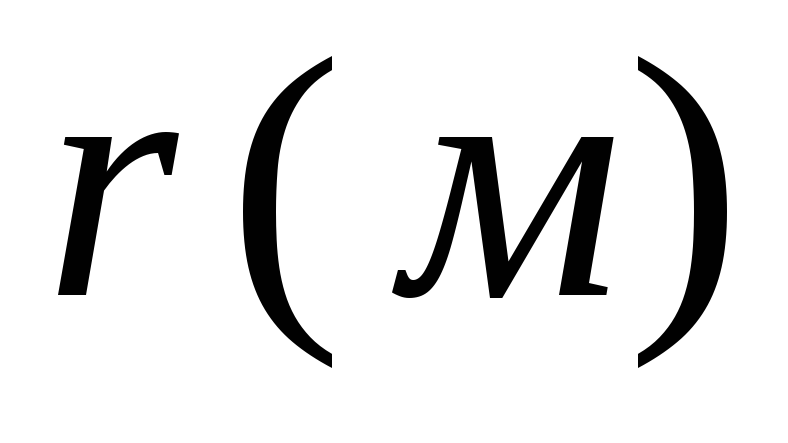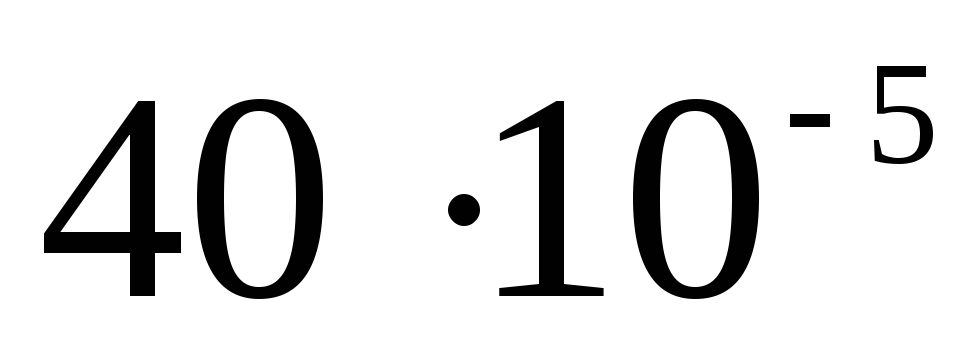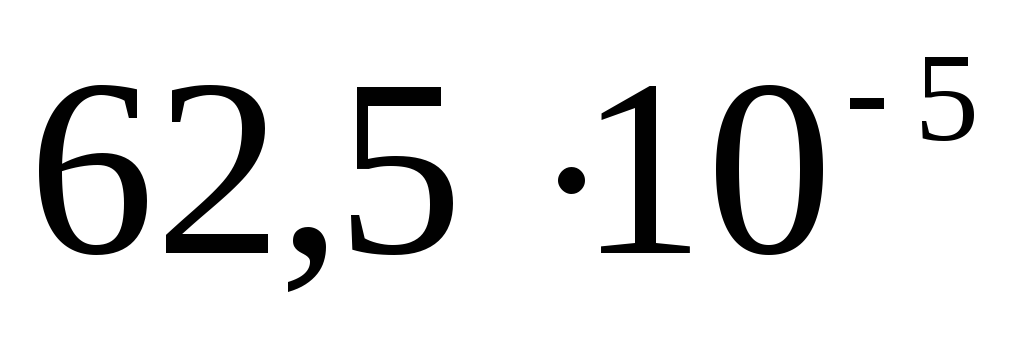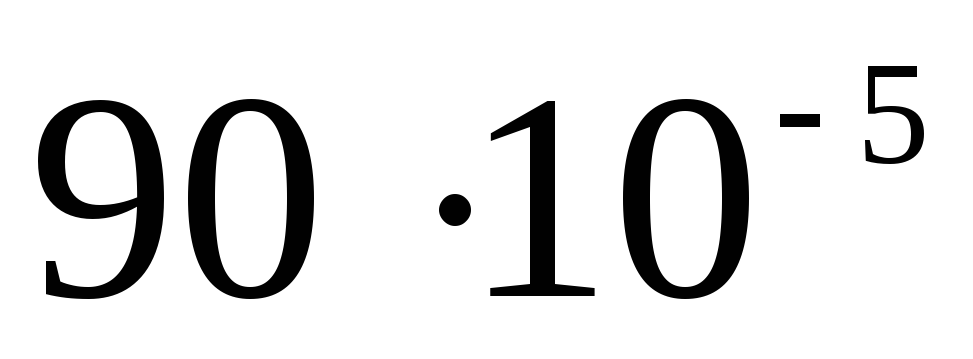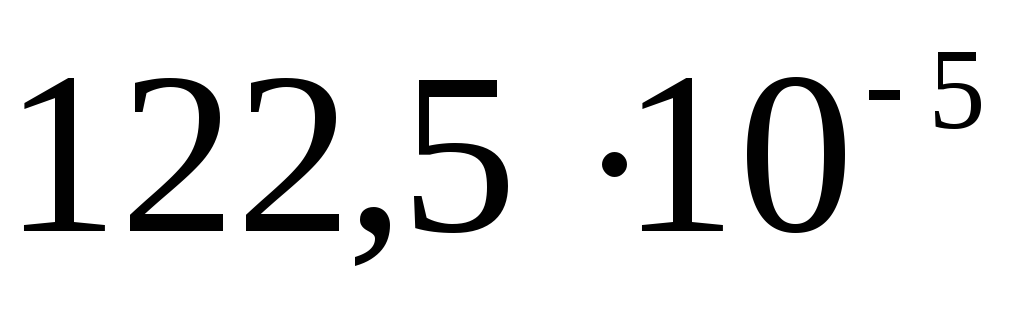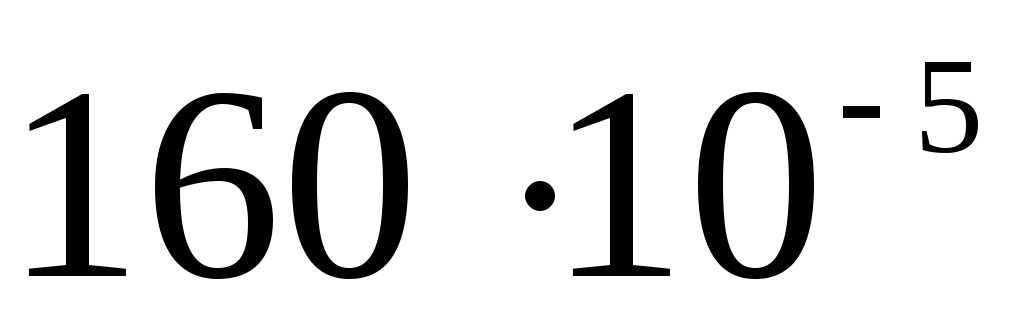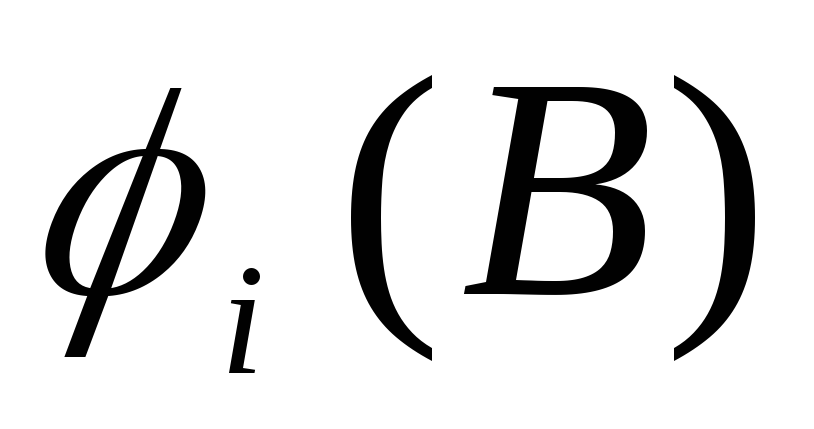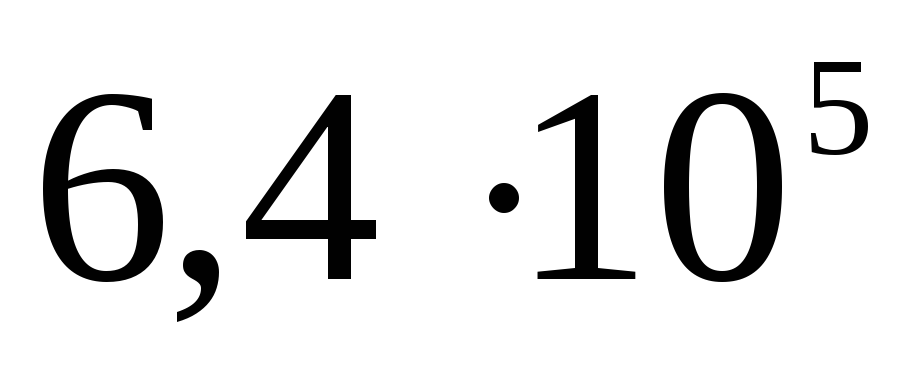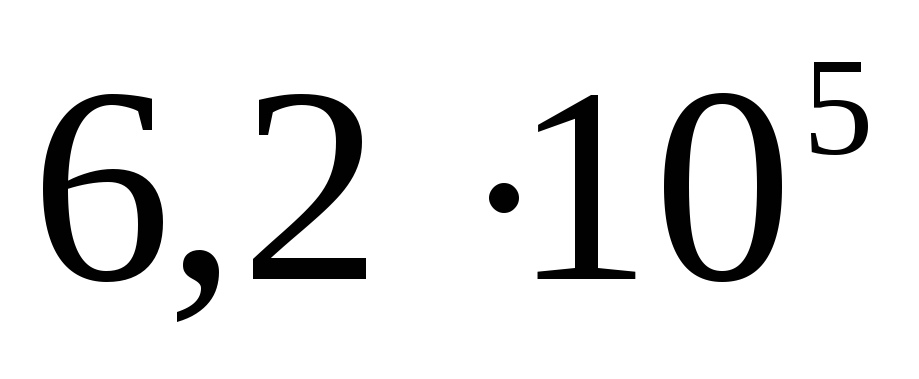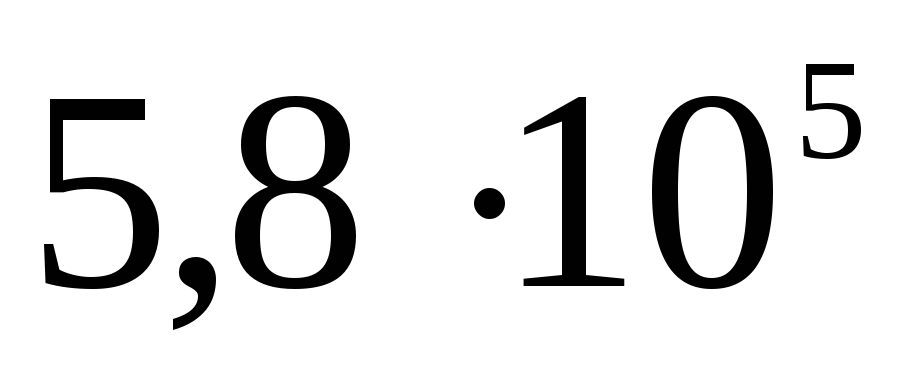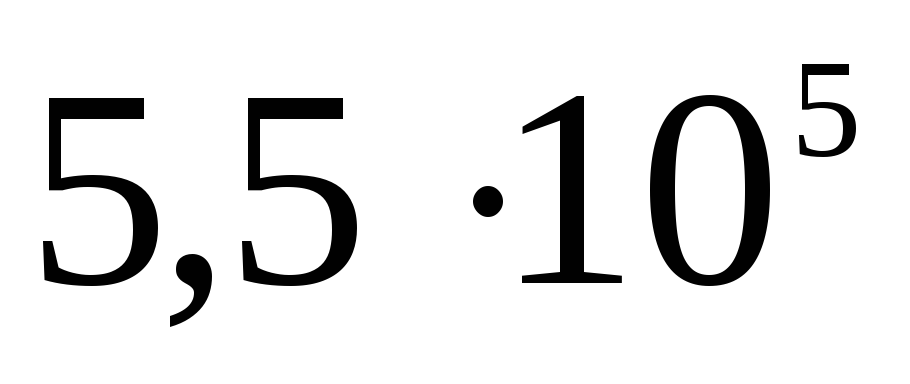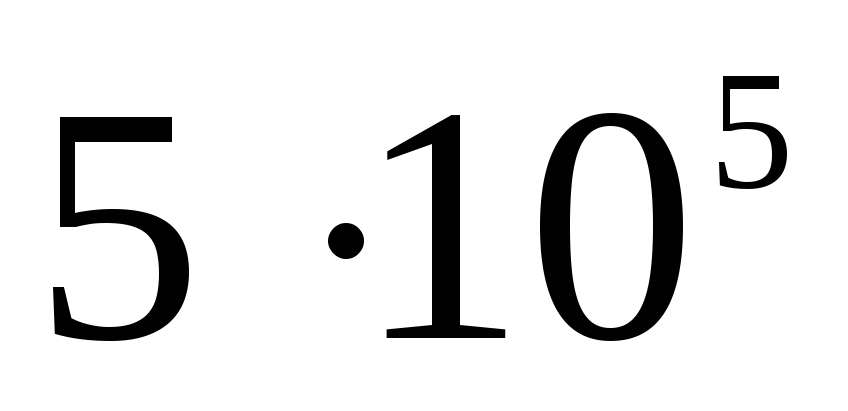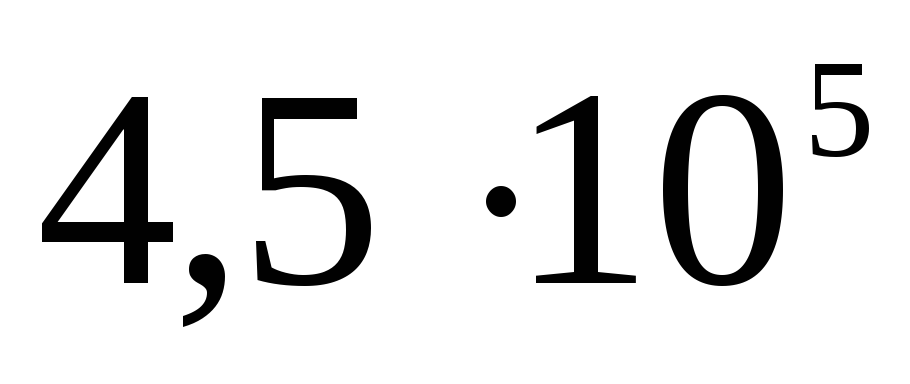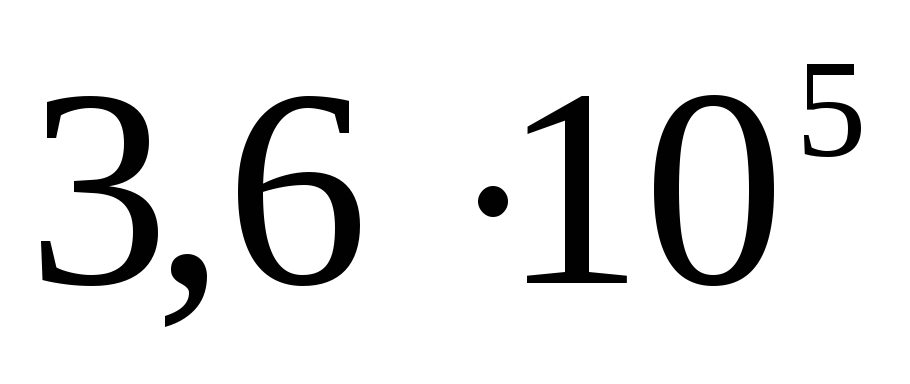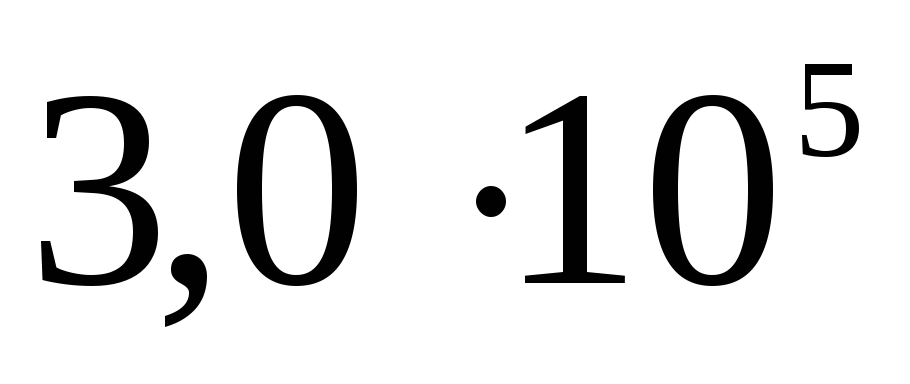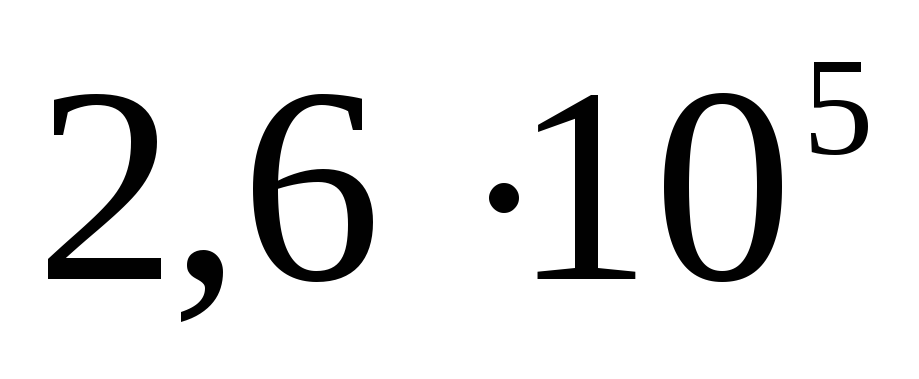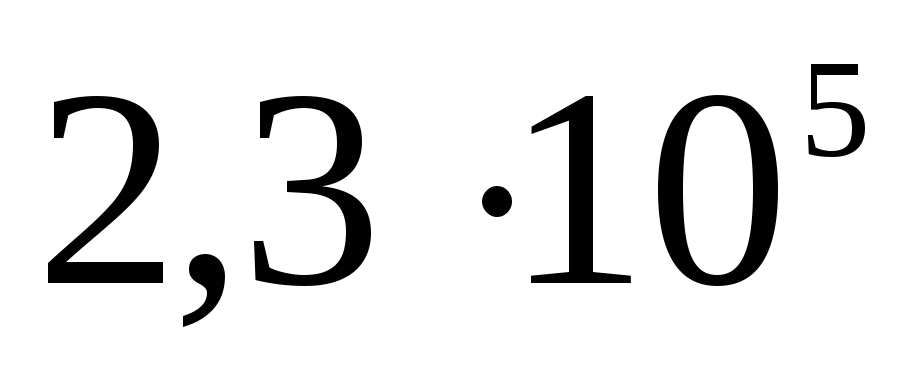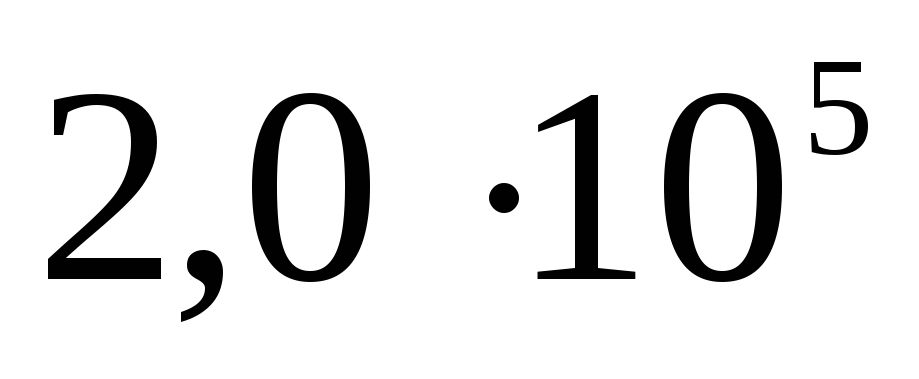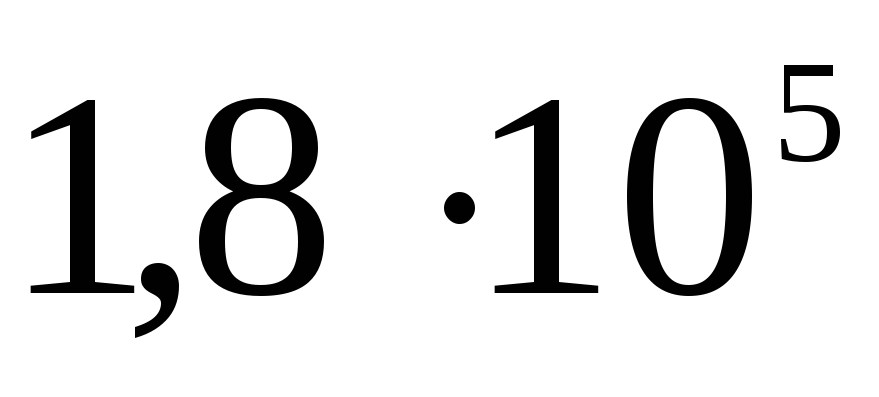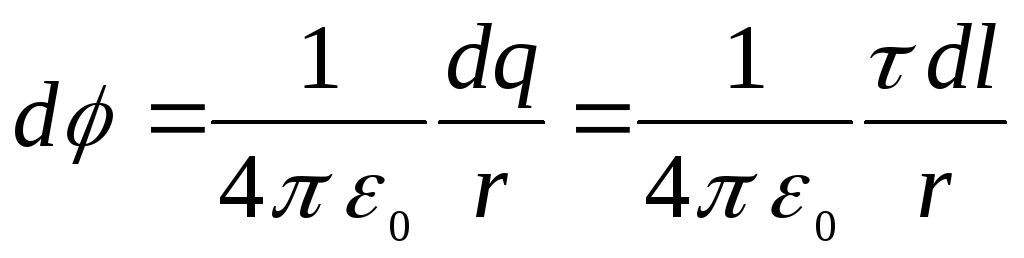Примеры решения задач по физике — концентрические проводящие сферы
Суббота, 25 февраля, 2012
Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.
Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.
Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φin (внутренней) и φex (внешней).
Решение. Потенциал на поверхности внутренней сферы φex складывается из двух потенциалов: внешней сферы φ1 и собственно внутренней сферы φ2.
Потенциал внешней сферы φ1 в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):
Потенциал внутренней сферы φ2 определяется известным соотношением:
Тогда общий потенциал φin на поверхности внутренней сферы равен:
Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’1 и собственно внешней сферы φ’2.
Потенциал внутренней сферы φ’1 на расстоянии R от ее центра определяется известным соотношением:
Формула, определяющая потенциал внешней сферы φ’2 на ее поверхности, также хорошо известна:
Тогда общий потенциал на поверхности внешней сферы равен:
Задача 2. Металлический шар радиуса R1, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R2. Определите потенциал шара φ1 после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают.
Решение. До соединения сфер проводником заряд первой был равен:
После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:
где q1 и q2 — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q1 + q2. После несложных преобразований получаем:
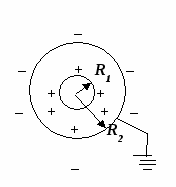
Задача 3. Металлический шар радиуса R1, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R2. Чему станет равен потенциал шара φ‘, если заземлить оболочку?
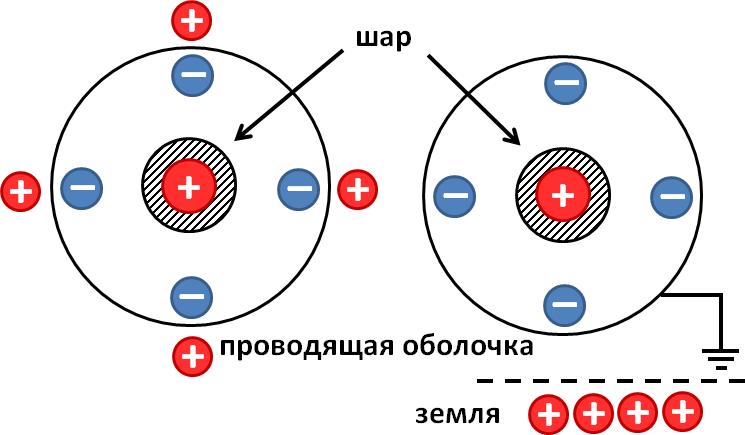
Начнем с рисунка к решению задачи:
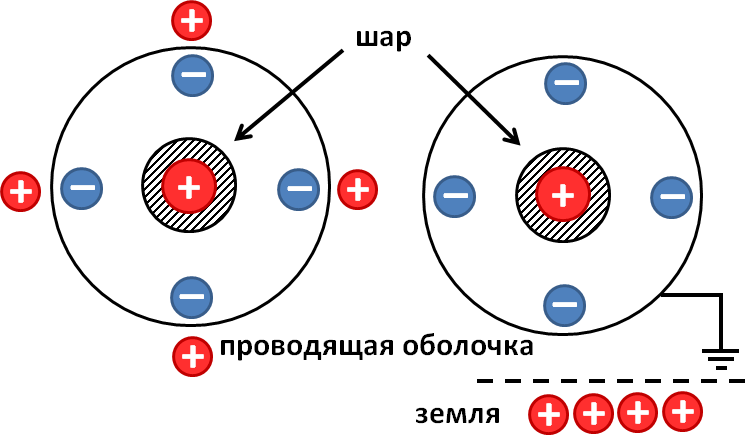
После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы
Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:
Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.
В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q2, поскольку он притягивается к положительному заряду q1 внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:
Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:
Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.
Репетитор по физике и математике
Сергей Валерьевич
Учителя только открывают двери, дальше вы идете сами.
© Китайская пословица
Три заряженные концентрические сферы
Продолжаю серию задач с проводящими сферами. Вот несложная задача.
Три проводящие концентрические сферы радиусов ,
и
имеют заряды
,
и
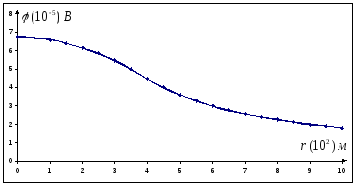
соответственно. Определите потенциал каждой из сфер и постройте график зависимости
.
Решение. Рассмотрим внутреннюю сферу. Ее потенциал будет складываться из потенциалов всех трех сфер, причем потенциал поверхности будет равен потенциалу любой точки внутри нее:
Если рассмотреть пространство между внутренней и второй сферами, то потенциал каждой точки здесь зависит от ее расстояния от центра сферы и определяется по формуле:
На поверхности это величина , а при удалении от центра потенциал падает — это гипербола.
Теперь рассмотрим вторую сферу. Он также является суммой трех потенциалов:
Первое слагаемое — потенциал внутренней сферы на расстоянии , второе — потенциал самой этой сферы, третье — потенциал внешней сферы.
При удалении от поверхности этой сферы потенциал тоже будет падать, так как он будет определяться выражением:
Теперь переходим ко внешней сфере: ее потенциал складывается из потенциалов двух первых при , и потенциала самой третьей сферы.
Значит, во внешнем пространстве тоже будет нулевой потенциал.
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
What is the potential between 2 concentric spheres?
-
Thread starter
Red -
Start date
Aug 19, 2014 -
-
Tags -
Potential
Spheres
-
- Aug 19, 2014
- #1
Homework Statement
Consider two concentric spherical conducting shell. The inner sphere has radius r1, potential V1, while the outer sphere has radius r2, potential V2. Find the potential at the center of these two sphere, at r0=(r1+r2)/2.
2. The attempt at a solution
I tried to use method of images, by modelling there to be a charge q1 at the center of the inner sphere and q2 at the center of the outer sphere. Since both sphere are concentric, q1 and q2 are at the same location. So I attempt to add up q1 and q2 (which I now know is wrong), and then find the potential at r0. My answer is double the correct answer.
Answers and Replies
- Aug 19, 2014
- #2
You have to add the potentials at the point to get the net potential. Could you show your working for ##V_1## and ##V_2##?
- Aug 19, 2014
- #3
- Aug 19, 2014
- #4
How far away is the inner point charge from the point?
How far away is the outer point charge? Those are the radial distances you should be concerned with.
Then sum ##V_{net} = V_1 + V_2##.
- Aug 19, 2014
- #5
You can treat each concentric sphere like a point charge and calculate the potential of each one using ##V = k frac{q}{r}##.
Not so fast — you cannot treat a uniform shell of charge as a point charge for calculating potentials inside the shell.
I let V1=-kq1/r1, V2=-kq2/r2.
The potential at the outer shell is not solely due to the charge on the outer shell. There is a contribution from the inner shell.
- Aug 19, 2014
- #6
- Aug 19, 2014
- #7
Yes exactly, the potential at the outer shell is related to the charge that contribute to the inner shell. Haruspex how can I find the mean potential at the center of the two shells?
There may be a quicker way, but this way looks safe:
Suppose the charges are q1, q2. Compute the potentials that should result. What equations does that give you?
- Aug 19, 2014
- #8
- Aug 20, 2014
- #9
Remember that the electric field is gradient of the potential: you get the potential difference between two points if you integrate -E(r) between those points. Choose V(∞)=0 and integrate E2 between r2 and infinity. Integrate also E1 between r1 and r2. You get two equations which relate the unknown charges to the potentials V1 and V2. If you know the charges it is easy to get the potential at r=(r1+r2)/2
ehild
- Aug 20, 2014
- #10
- Aug 20, 2014
- #11
I don’t quite get you. If I sum up q1 and q2 then I get V0=(r1V1+r2V2)/r0.
No, I mean compute the potentials that ought to result at the two shells. Equating those to the given potentials allows you to deduce the charges.
Note that the two potentials are not simply q1/r1 and q2/r2, which you seem to be assuming.
- Aug 20, 2014
- #12
Hi ehild, thank you for your response, however the charge on the shells are not known. What is known is that the outer shell has potential V2 and the inner shell has potential V1. How do I find the potential at the center between these two shells?
Find the relation between the charges and the potentials. From those, you can determine the charges.
Supposing the inner shell has q1 charge. What is the electric field around it in terms of q1 if r1<r<r2? Apply Gauss’ Law.
ehild
- Aug 20, 2014
- #13
- Aug 20, 2014
- #14
If you have an expression for the potential given the two charges, then you can apply the boundary conditions to this, i.e., the potential at the outer shell has to be ##V_2## and the inner ##V_1##. This gives you two equations and two unknowns, so you will be able to deduce the charges and thus the potential. After this you should be able to simply plug in whatever ##r## you want into this.
- Aug 20, 2014
- #15
Thank for your responses. I think there is an misunderstanding. Maybe I should ask the question in a slightly different way: A potential VH is applied between 2 spherical conducting shell.
It doesn’t matter how the shells have the given potentials. It might as well be via an applied charge, so you can solve it the way ehild, Orodruin and I are suggesting. We’re all telling you the same method, so how about trying it?
- Aug 20, 2014
- #16
Thank for your responses. I think there is an misunderstanding. Maybe I should ask the question in a slightly different way: A potential VH is applied between 2 spherical conducting shell. The inner sphere has radius r1, while the outer sphere has radius r2. What is the potential at the center of these two sphere, at r0=(r1+r2)/2?
You misunderstand the problem. The two shells are concentric, the radii are given, r1 and r2. The potential is given for both spheres; V1 and V2 . The problem asks the potential at distance ro=(r1+r2)/2 from the common centre of the spheres. In the centre, the potential is the same as on the inner sphere, that is V1.
If you do not want to use charges, remember that the electric potential U obeys the Laplace equation at points where the charge density is zero. Because of the spherical symmetry of the problem, U depends only on the radius r, and [tex]frac{1}{r^2}frac {partial }{partial r}left(r^2 frac {partial U}{partial r}right)=0[/tex] with the boundary conditions U(r1)=V1, U(r2)=V2.
See http://en.wikipedia.org/wiki/Laplace_operator
What is the solution for U(r) between the shells r1<r<r2?
ehild
- Aug 20, 2014
- #17
It doesn’t matter how the shells have the given potentials.
Or, put in another way, as long as you are not putting charges between the shells, any charge configuration that fulfills the boundary conditions is going to give you the same potential. You might as well select a surface charge on the shells. Or you could assume a point charge in the common center of the spheres and a surface charge on a shell with radius ##R gg r_2##. Both approaches will give you the same form for the potential between the shells, which can then be adjusted to accommodate the boundary conditions.
The alternative is to do what ehild suggests and bite into the Laplace equation with spherical symmetry in spherical coordinates. This requires at least some knowledge about differential equations and how to solve them (in particular differential equations of Euler type).
Note to self: You have been spending too much time on PF when you start writing ## instead of $ in your LaTeX source …
- Aug 20, 2014
- #18
Answer is…Potential in between spear is only due to inner spar…outer spear effect is zero…But outside of whole spear there is net potential occur… So
Answer:
(1).inside the inner spear,potential is zero.
(2).between two spear, potential is only due to inner spear.
(3).outside the whole spear there is potential present due to both spears.
- Aug 20, 2014
- #19
Potential in inner part of spear is always zero due to equal distribution of charge. ..Right?…but outside of spear there is net potential …okey so.
The potential inside a conductor is constant.
And what do you mean on spear? The problem is about concentric spherical shells.
ehild
- Aug 20, 2014
- #20
The potential inside a conductor is constant.
And what do you mean on spear? The problem is about concentric spherical shells.
If I am going to attempt a translation of DRU’s post, I do believe «spear = sphere» and «potential = field» …
- Aug 20, 2014
- #21
Homework Statement
A potential VH is applied between 2 spherical conducting shell. The inner sphere has radius r1, while the outer sphere has radius r2. Find the potential at the center of these two sphere, at r0=(r1+r2)/2.
2. The attempt at a solution
I tried to use method of images, by modelling there to be a charge q1 at the center of the inner sphere and q2 at the center of the outer sphere. Since both sphere are concentric, q1 and q2 are at the same location. So I attempt to add up q1 and q2 (which I now know is wrong), and then find the potential V0 at r0. I get (r1V1+r2V2)/r0. My answer is double the correct answer.
Since you reposted this in the Advanced forum, let me bring it back here.
Your main problem seems to be that you are assuming that the potential of both charged shells behave as ##q/r##. This is only true as long as you are outside of the shell and the only shell you are outside of is the smaller one. Inside a spherical shell, the potential is constant (see http://en.wikipedia.org/wiki/Shell_theorem — it is described for gravity but applies just as well to electrostatics) and proportional to ##q/R##, where ##R## is the (constant) shell radius and not the coordinate ##r##
What does this tell you about the potential between the two shells?
- Aug 20, 2014
- #22
- Aug 20, 2014
- #23
1. Compute the ##rho## needed to give a single shell potential ##V_1##.
2. Use that to get the field.
3. Attempted to use that field to get to the potential you want.
The above procedure fails because your setup is not a single shell. The potential at r1 is also going to have a contribution from the outer shell so in order to get the correct potential of the inner shell you need to account for this.
However, it is true that the field between the shells is going to be given by the inner charge only. Let this charge be an unknown and integrate to get the potential at an arbitrary r between the shells. What is the result? (Do not assume the potential goes to zero at infinity, infinity is not part of your domain.)
- Aug 20, 2014
- #24
You know what the potential of a point charge in the center is. What is the resulting potential difference between r1 and r2? Can you think of any way of changing the potential without changing the fields? (And thus without changing the potential difference between r1 and r2.)
- Aug 20, 2014
- #25
The potential inside a conductor is constant.
And what do you mean on spear? The problem is about concentric spherical shells.ehild[/QUOT
sorry for English…there is potential difference and sphere…
- Aug 20, 2014
- #26
- Aug 20, 2014
- #27
Potential at center of both sphere is (v1 + v2)…
Where v1= potential incide outer sphere and v2 for inner sphere.
- Aug 20, 2014
- #28
Potential at center of both sphere is (v1 + v2)…
Where v1= potential incide outer sphere and v2 for inner sphere.
This is not the answer to the intended problem. He wants to compute the potential at ##r = (r_1+r_2)/2##, i.e., halfway between the shells.
Furthermore, the potential inside of the inner shell is just ##V_1##, assuming there inner shell at ##r=r_1## is kept at this potential and there are no charges inside. If the potential was ##V_1+V_2##, the potential would not be continuous at ##r=r_1## …
Also, this is the homework forum, we are here to try to help people solve problems, not solve the problems for them.
- Aug 20, 2014
- #29
Thank for all of your responses, I really appreciate them. I am quite confused now. I let the inner shell has a surface charge density of ρ and using Gauss Law I found the electric field between the shells. The electric field is E(r)=r12ρ/ε0r2. How should I continue to find the potential at r0? I attempted to take an integration from r1 to r0 but I cannot get the answer.
Take the integral of E(r) from r1 to a general r, to get the potential function U(r).
As ##-nabla U = E(r)##
[tex]-int_{r_1}^{r} nabla U(r’) dr’ =V_1-V(r) =int_{r_1}^{r}E(r’)dr'[/tex]
and use the condition that [tex]V_1-V_2 =int_{r_1}^{r_2}E(r’)dr'[/tex]
to get the unknown ρ.
- Aug 20, 2014
- #30
Thank for all of your responses, I really appreciate them. I am quite confused now. I let the inner shell has a surface charge density of ρ and using Gauss Law I found the electric field between the shells. The electric field is E(r)=r12ρ/ε0r2. How should I continue to find the potential at r0? I attempted to take an integration from r1 to r0 but I cannot get the answer.
Introducing charge densities is an unnecessary complication. It isn’t a hard problem once you get the concepts straight.
There are standard formulae for the potential at a given distance from a uniformly charged spherical shell, which I assume you know. It falls into two cases, according to whether the point is inside or outside the shell.
Let the charges on the spheres be q1, q2. You have four resulting potentials to calculate:
— the potential at r1 resulting from q1
— the potential at r2 resulting from q1
— the potential at r1 resulting from q2
— the potential at r2 resulting from q2
From the above potentials, find
— the total potential at r1 (which equals V1)
— the total potential at r2 (which equals V2)
That gives you two equations with two unknowns. From these you can express q1, q2 as functions of V1, V2.
- Aug 20, 2014
- #31
If you have not yet solved it, since you seem to be at least somewhat familiar with integration and therefore should be with differentiation, I would suggest going back to ehild’s post #16. You may or may not prefer the differential equation on the form
$$
r^2 U»(r) + 2r U'(r) = 0,
$$
with boundary conditions ##U(r_1)=V_1##, ##U(r_2)=V_2##. Once done it will be easier to discuss the solution and the interpretation of it.
- Aug 20, 2014
- #32
It never ceases to amaze me how you can say a relatively basic thing in so many ways.If you have not yet solved it, since you seem to be at least somewhat familiar with integration and therefore should be with differentiation, I would suggest going back to ehild’s post #16. You may or may not prefer the differential equation on the form
$$
r^2 U»(r) + 2r U'(r) = 0,
$$
with boundary conditions ##U(r_1)=V_1##, ##U(r_2)=V_2##. Once done it will be easier to discuss the solution and the interpretation of it.
The S.I. unit system and the concepts of mathematics are a privilege to learn, and to apply.
That differential equation solution is quite interesting, but the simplicity of haruspex’s post would probably be the elementary way of visualizing this.
- Aug 20, 2014
- #33
- Aug 22, 2014
- #34
It never ceases to amaze me how you can say a relatively basic thing in so many ways.If you have not yet solved it, since you seem to be at least somewhat familiar with integration and therefore should be with differentiation, I would suggest going back to ehild’s post #16. You may or may not prefer the differential equation on the form
$$
r^2 U»(r) + 2r U'(r) = 0,
$$
with boundary conditions ##U(r_1)=V_1##, ##U(r_2)=V_2##. Once done it will be easier to discuss the solution and the interpretation of it.
The equation in Post #16 is easier to solve for r1<r<r2:
##frac{1}{r^2}frac {partial }{partial r}left(r^2 frac {partial U}{partial r}right)=0##
Multiply by r2:
##frac {partial }{partial r}left(r^2 frac {partial U}{partial r}right)=0##
Integrate once, the right side is a constant: ##r^2 frac {partial U}{partial r}=Arightarrow frac {partial U}{partial r}=frac{A}{r^2}##
Integrate again :##U=-frac{A}{r}+B##.
Use the boundary conditions:
##V_1=-frac{A}{r_1}+B##
##V_2=-frac{A}{r_2}+B##
It is two equations for the constant A and B. Solve, substitute into the equation for U(r): ##U=-frac{A}{r}+B##. You can calculate the potential at any point between the shells.
ehild
- Aug 22, 2014
- #35
The equation in Post #16 is easier to solve for r1<r<r2:
I guess this depends on your definition of «easy» and pre-knowledge. Recognizing it as an ODE of Euler type, it is just about insering ##r^k## and solving the resulting ##k(k+1)=0##.
That said, neither method is really hard.
Suggested for: What is the potential between 2 concentric spheres?
- Jan 31, 2023
- Feb 19, 2023
- Dec 20, 2022
- Mar 21, 2023
- Feb 10, 2023
- May 19, 2023
- Jan 8, 2023
- Aug 3, 2021
- Oct 31, 2021
- Feb 16, 2023
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.
Потенциал внутренней сферы φ
2 определяется известным соотношением:
Тогда общий потенциал φ
in на поверхности внутренней сферы равен:
Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’
1 и собственно внешней сферы φ’
2 .
Потенциал внутренней сферы φ’
1 на расстоянии R
от ее центра определяется известным соотношением:
Формула, определяющая потенциал внешней сферы φ’
2 на ее поверхности, также хорошо известна:
Тогда общий потенциал на поверхности внешней сферы равен:
Решение.
До соединения сфер проводником заряд первой был равен:
После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:
где q
1 и q
2 — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q
= q
1 + q
2 . После несложных преобразований получаем:
Начнем с рисунка к решению задачи:
После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы
Решение.
Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:
Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.
В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q
2 , поскольку он притягивается к положительному заряду q
1 внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:
Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:
Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.
Сергей Валерьевич
ЭЛЕКТРОДИНАМИКА
Электростатика
1
(ЦТ 2001 г.Тест 9. А19). Проводящий шар радиуса R
имеет положительный заряд +
q
. Если на расстоянии 2R
от центра шара поместить точечный отрицательный заряд –2q
, то потенциал в центре шара
Типичная ошибка
при решении происходит из неверного толкования формулировки: «поле внутри проводящего шара отсутствует». Из этого утверждения делается ошибочный вывод: обе характеристики поля: и напряженность, и потенциал – равны нулю. В действительности в этом случае нулю равна лишь напряженность поля, т.к. свободные заряды перестают перемещаться по поверхности проводника тогда, когда вектор 
Решение
Потенциал, создаваемый сферически симметрично распределенным зарядом q
в центре шара, такой же, как на его поверхности и равен φ
1
=
q
/4
πε
0
R
; потенциал, создаваемый в этой же точке точечным зарядом –2q
, расположенным вне сферы на расстоянии 2R
от ее центра, равен φ
2
= – 2
q
/4
πε
0
2
R
; потенциал в центре шара – результат суперпозиции двух полей, т.е. φ =
φ
1
+
φ
2
= q
/4
πε
0
R
–2
q
/4
πε
0
2
R
= 0
.
При выполнении тестовых заданий удобно сделать запись как можно более короткой. Например, в данном случае достаточно одного общего уравнения φ
=
q
/4
πε
0
r
.
Т.к. точечный отрицательный заряд вдвое больше заряда, распределенного на сфере и находится от центра сферы вдвое дальше, из записанного уравнения видно, что потенциалы обоих зарядов равны по величине и противоположны по знаку, следовательно, результирующий потенциал равен 0.
2
(ЦТ 2001 г. Тест 11. А 19).
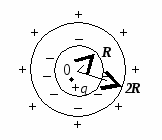
и 2
R
,
на расстоянии R/
2
q
.
Потенциал в центре сферы равен…
Решение
Затруднения
вызывает построение картины распределения зарядов на поверхностях шарового слоя.
Благодаря электростатической индукции на внутренней поверхности сферы появляется заряд –
q
, а на наружной +q
.
Потенциал в центре сферы
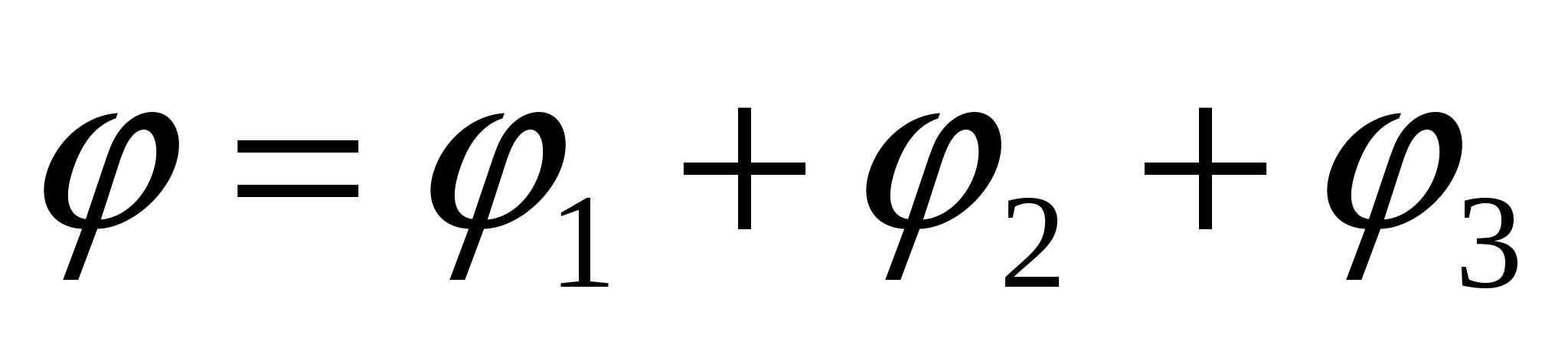
Подобная же задача – А 19 в тесте № 12, 2001 г. :
Внутри шарового металлического слоя, внутренний и внешний радиусы которого соответственно равны 2R
и 4R
,
на расстоянии R
от центра находится точечный положительный заряд q
. Потенциал в центре сферы равен ….
Ответ:
3
(ЦТ 2000 г.Тест… А19). Металлический шар радиусом R
1
, имеющий потенциал φ
1
, окружают незаряженной сферической проводящей оболочкой радиусом R
2
. Найдите потенциал шара после того, как он будет на некоторое время соединен с оболочкой?
Решение
Потенциал заряженного шара
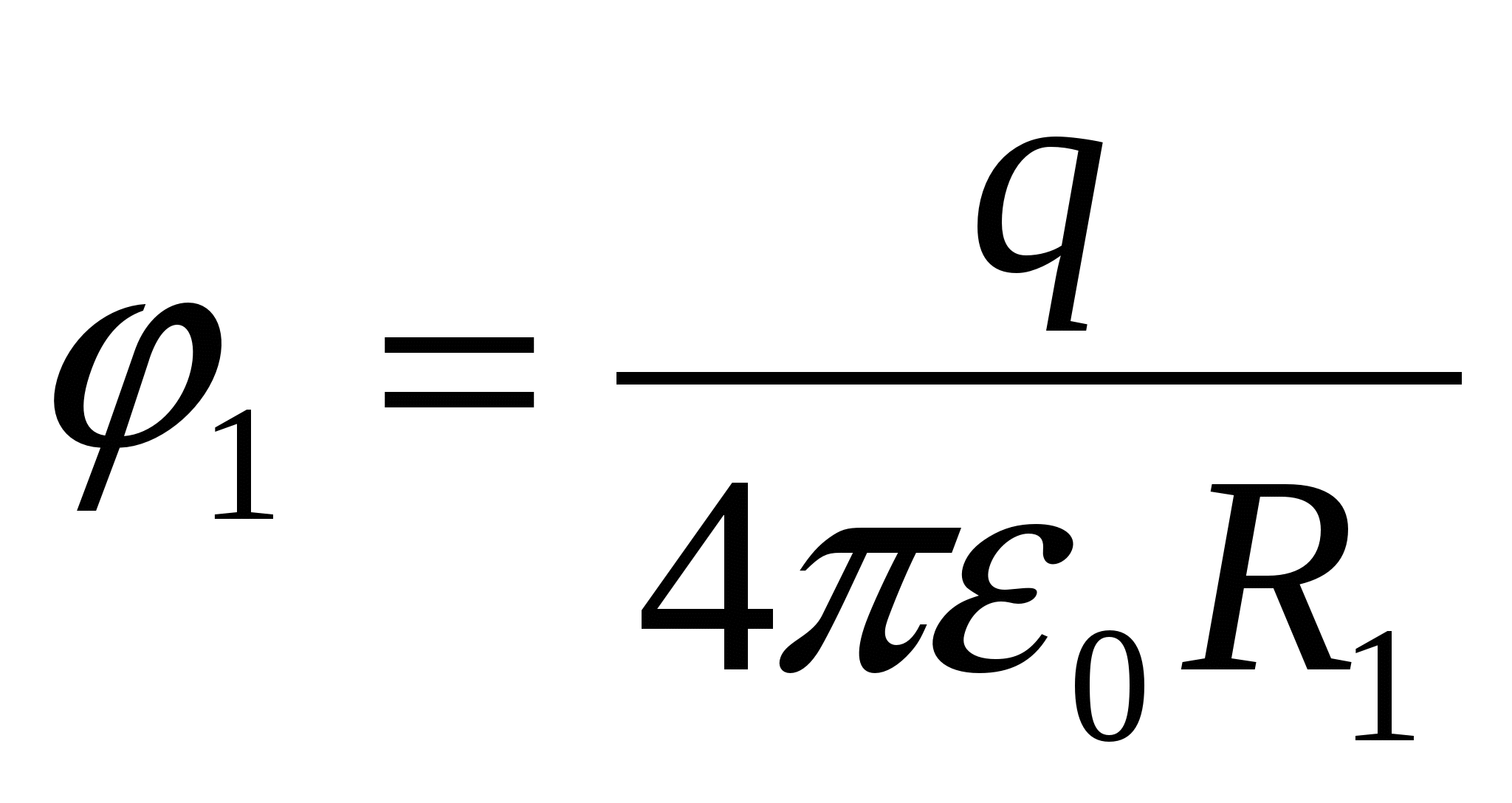
Если заряженный шар касается внутренней поверхности оболочки, заряды, стремясь расположиться на возможно больших расстояниях друг от друга, переходят на оболочку. Напряженность поля внутри оболочки становится равной 0, потенциал поля в точках оболочки и внутри нее равен
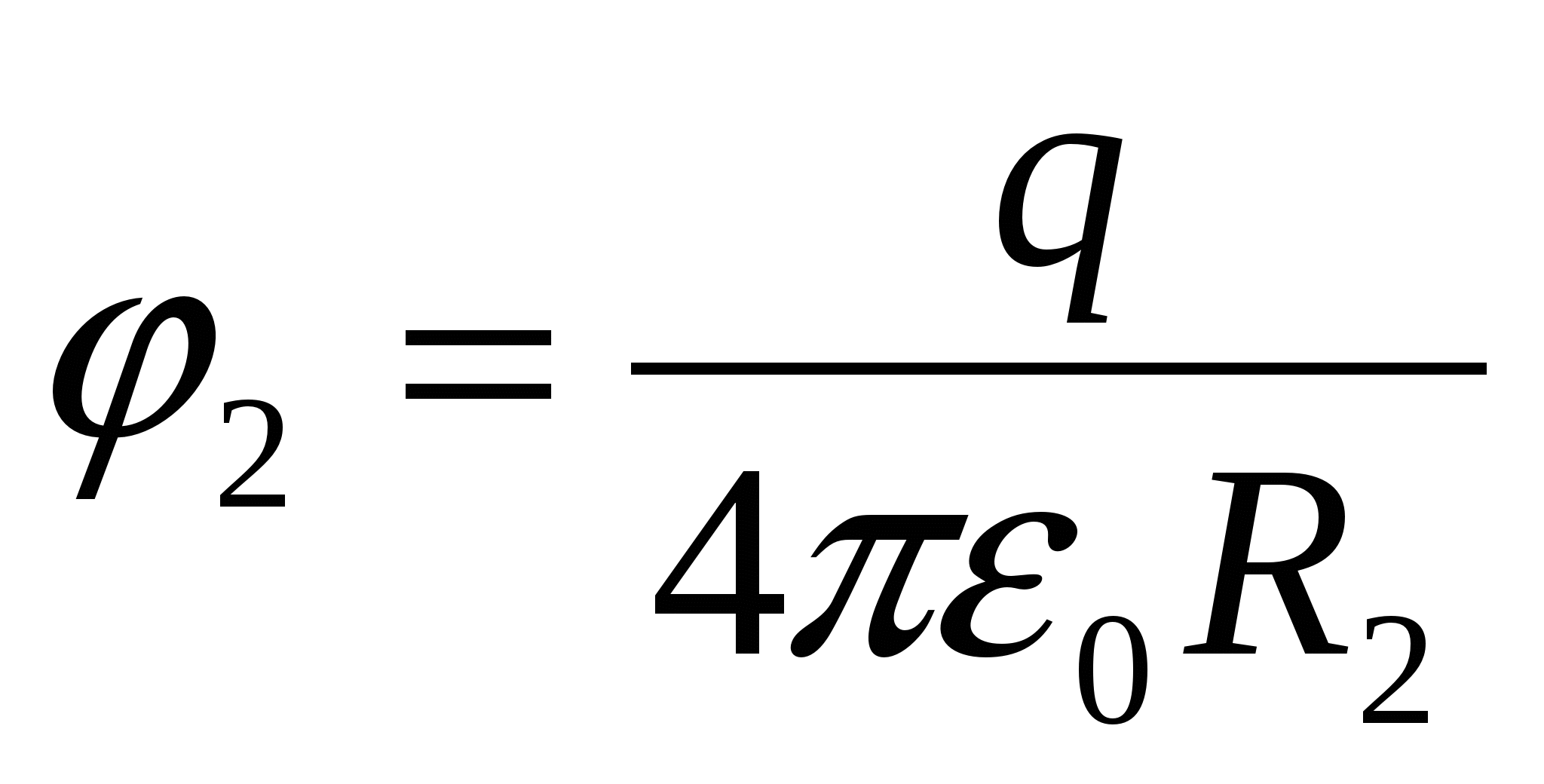
См. предыдущую задачу), где

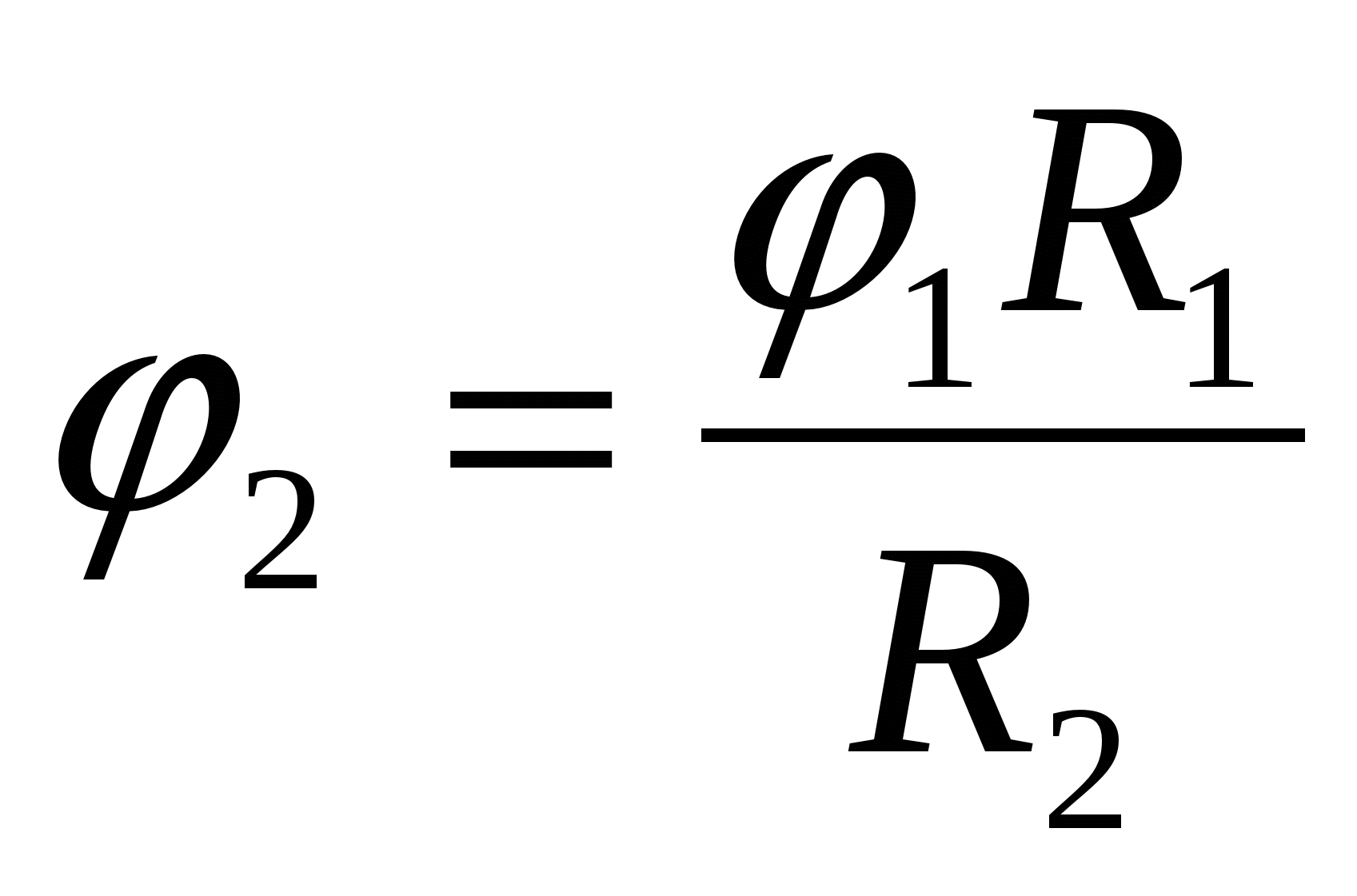
Правильный ответ –1
.
4
(ЦТ 2000 г. Тест… А19). Металлический шар радиуса R
1
, имеющий потенциал φ
1
, окружают сферической проводящей оболочкой радиуса R
2
. Чему будет равен потенциал шара, если заземлить оболочку?
Решение
Наиболее частая ошибка
состоит в том, что не учитывается потенциал поля, созданного зарядами, наведенными на оболочке при ее заземлении.
Первый вариант
решения
. Потенциал на поверхности шара, созданный зарядом шара
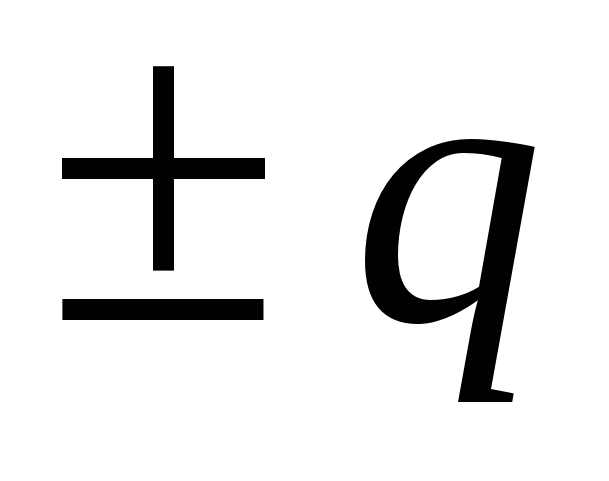
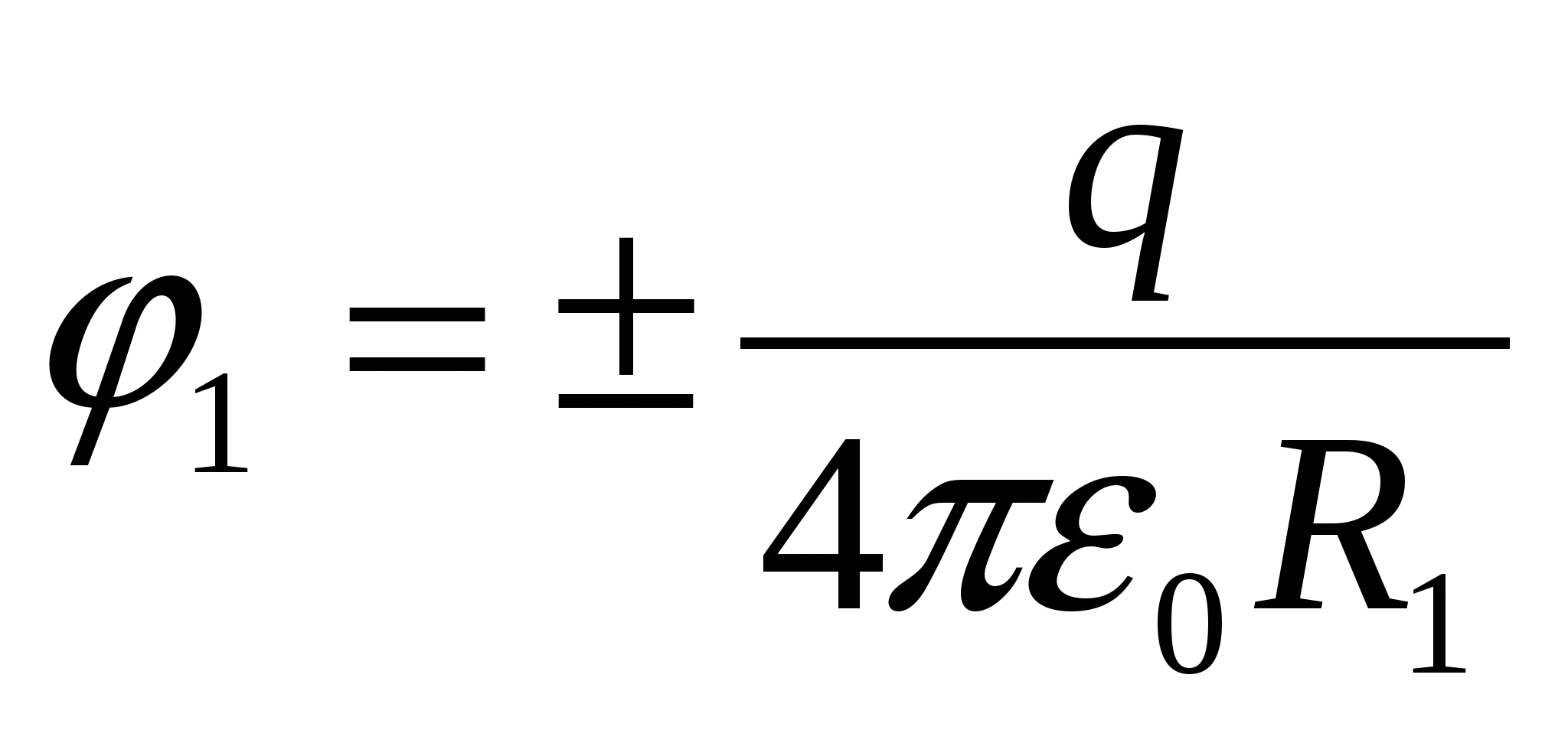
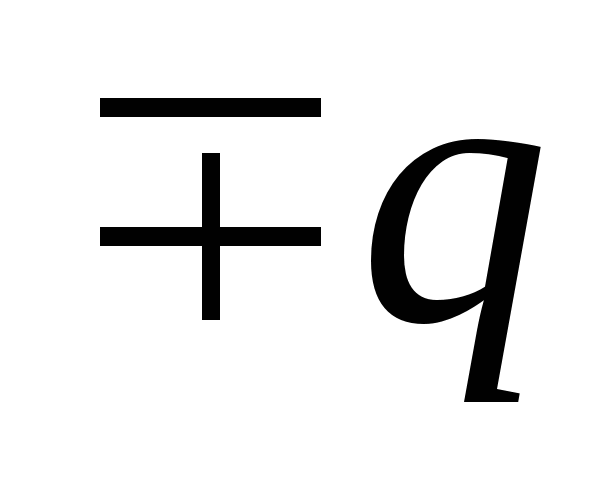
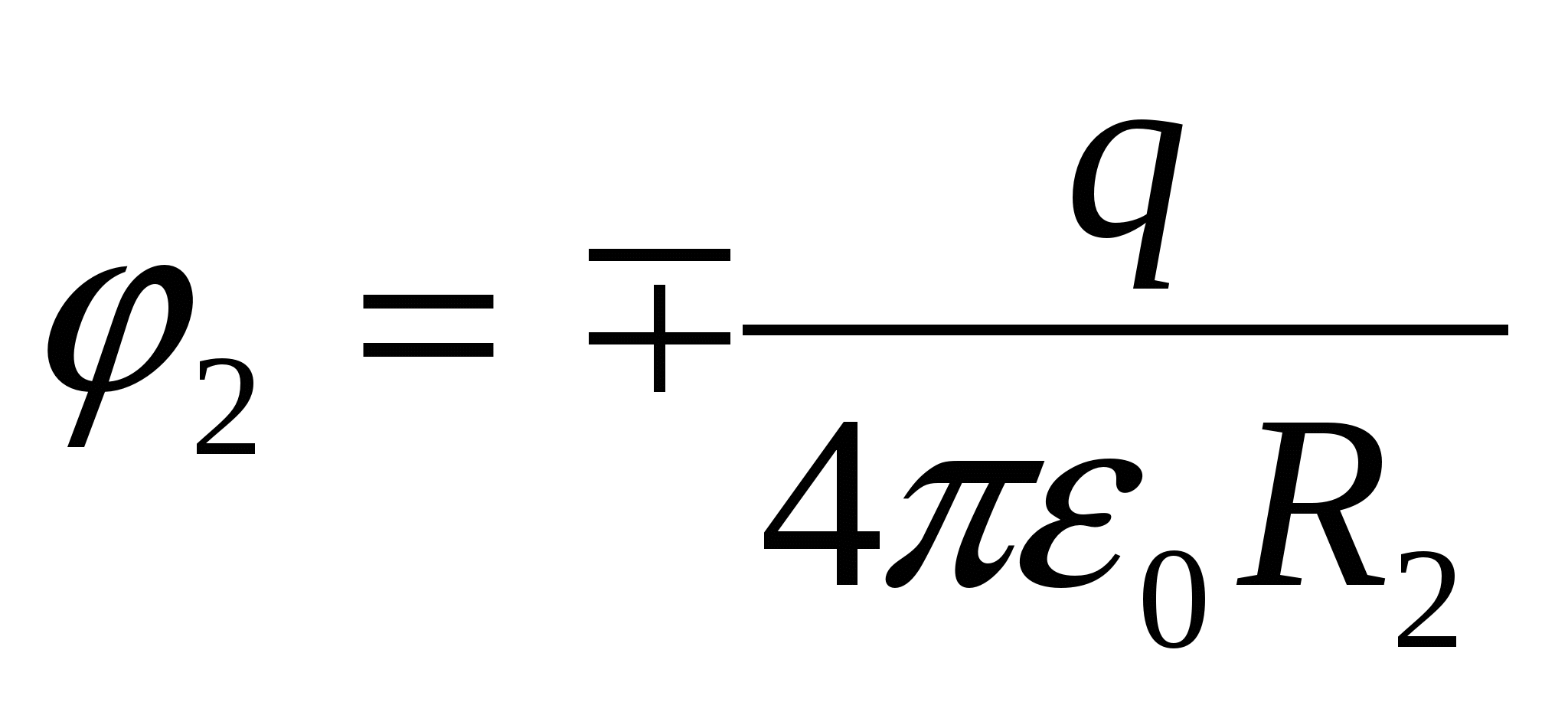
Суперпозиция исходного поля шара и поля, созданного наведенным зарядом оболочки, дает на поверхности шара потенциал
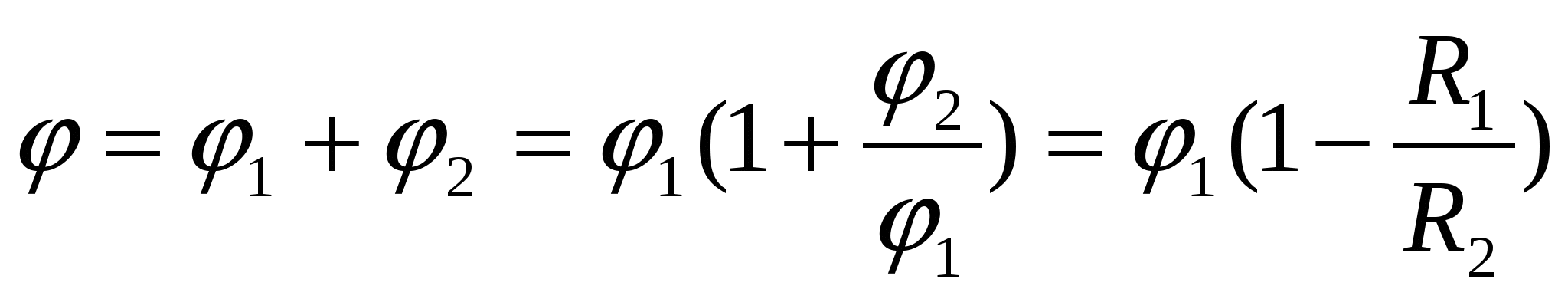
.
Второй вариант
решения
. Можно в рассуждениях исходить из того, что потенциал оболочки после заземления равен 0,
как этопринято в технике (заземленная оболочка принимается за начало отсчета потенциальной энергии), из этого условия находится величина и знак наведенного заряда. Потенциал оболочки φ
2 складывается из потенциала, обусловленного наведенным на ней зарядом q
2
и потенциалом поля шара φ
1
:
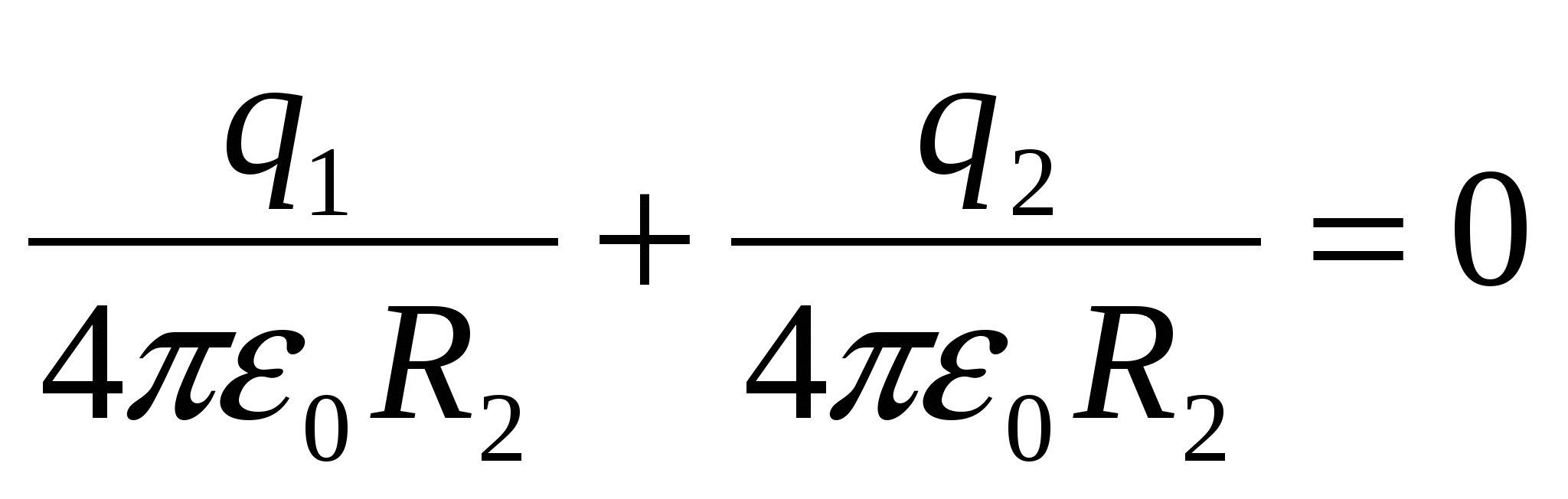

1
= –
q
2.
.
Находим потенциал шара после заземления оболочки:
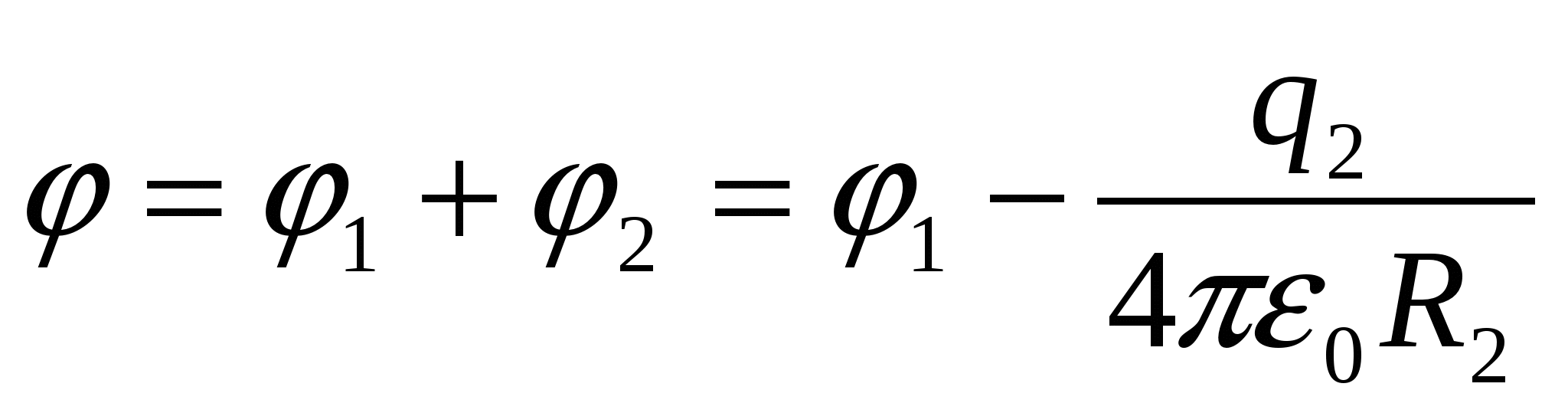
Из
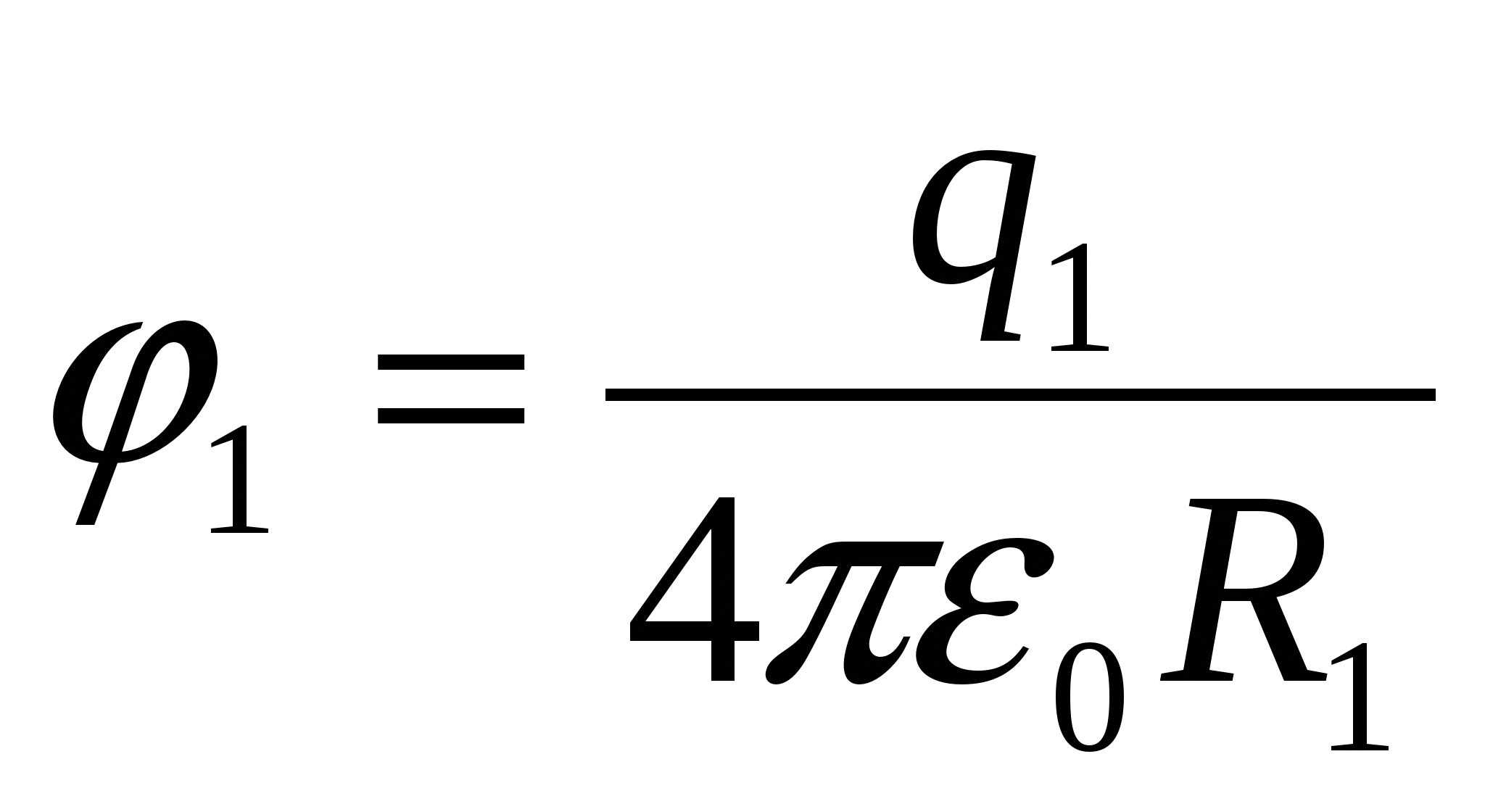
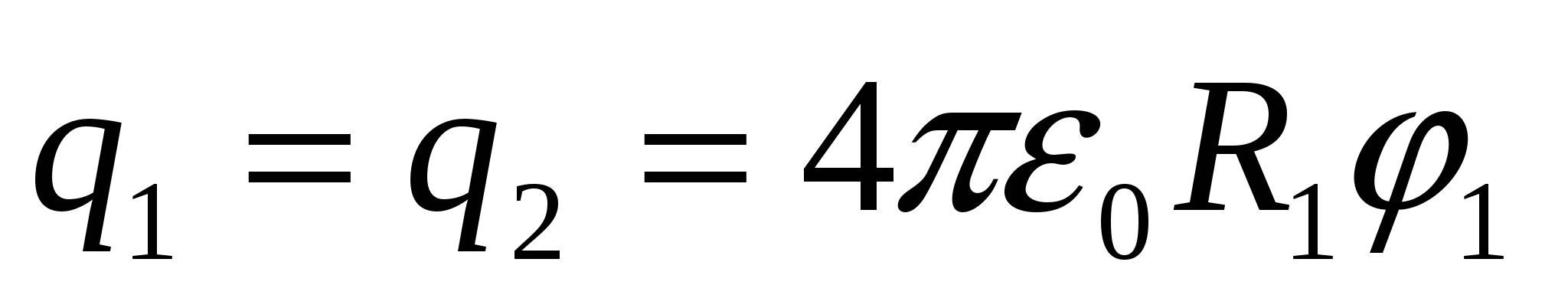
:
.
У этого варианта решения есть минусы:
– в ранее решенных задачах отсчитывали потенциал (потенциальную энергию) от точки, бесконечно удаленной от заряда, что имеет ясный физический смысл; логично всегда использовать одно и тоже начало отсчета;
– решение получилось более громоздким.
5
(ЦТ 2001 г. Тест 3. А19). Тонкое закрепленное кольцо радиуса R
равномерно заряжено так, что на единицу длины кольца приходится заряд +γ .
В вакууме на оси кольца на растоянии l
от его центра помещен маленький шарик, имеющий заряд +q
. Если шарик освободить, то в процессе движения он приобретет максимальную кинетическую энергию, равную
Р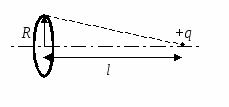
По закону сохране-ния энергии E
=
U
,
где U
– энергия взаимодей-ствия точечного заряда и кольца.
Типичная ошибка:
при решении этой задачи считают, что в силу симметричности распределения заряда по кольцу можно «стянуть» его в центр кольца и находить потенциал поля, созданного кольцом в месте нахождения заряда, как потенциал поля точечного заряда:
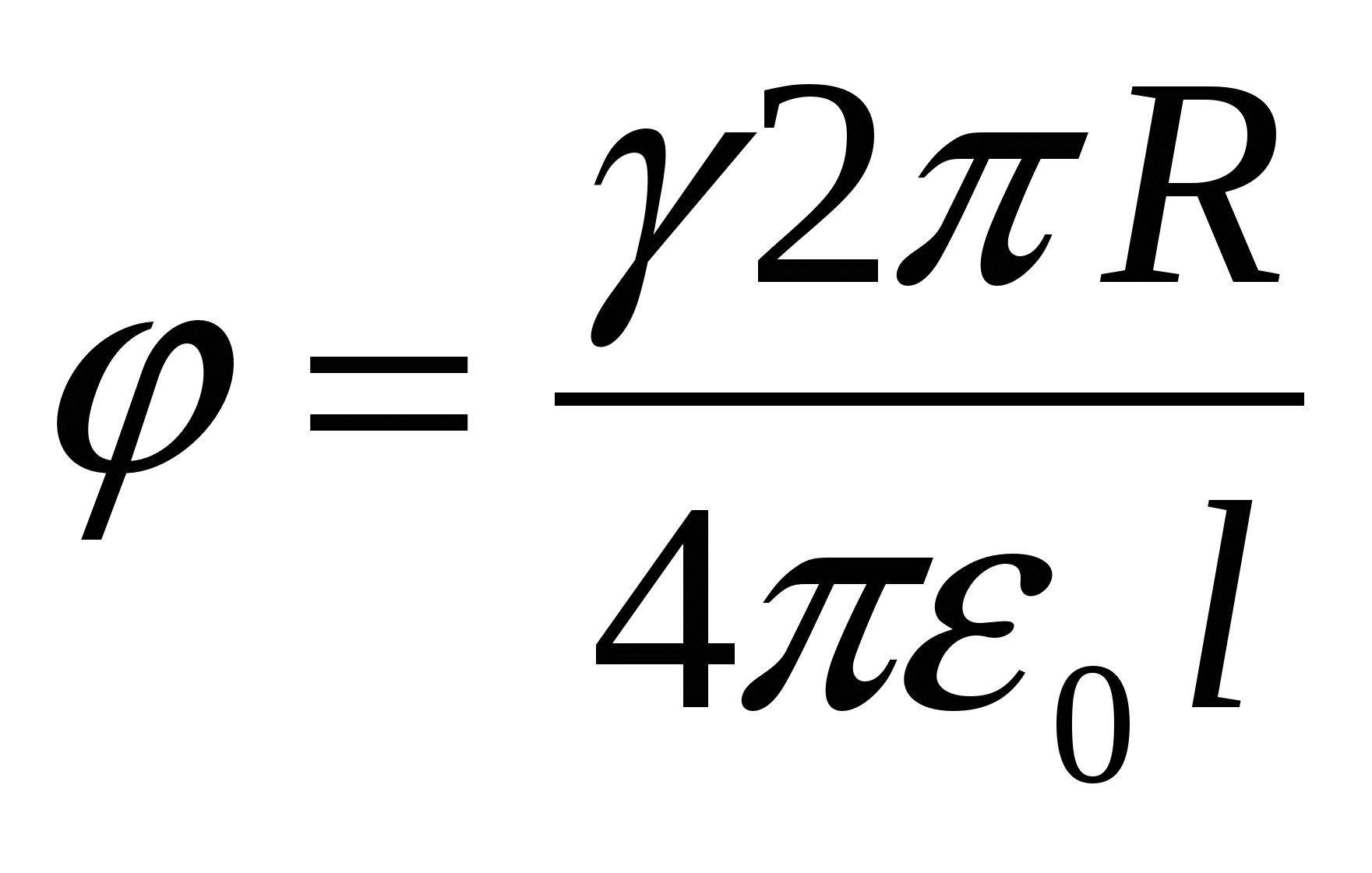
и просуммировать результаты:
Энергия взаимодействия кольца с зарядом и максимальная кинетическая энергия заряда равны, согласно закону сохранения энергии:
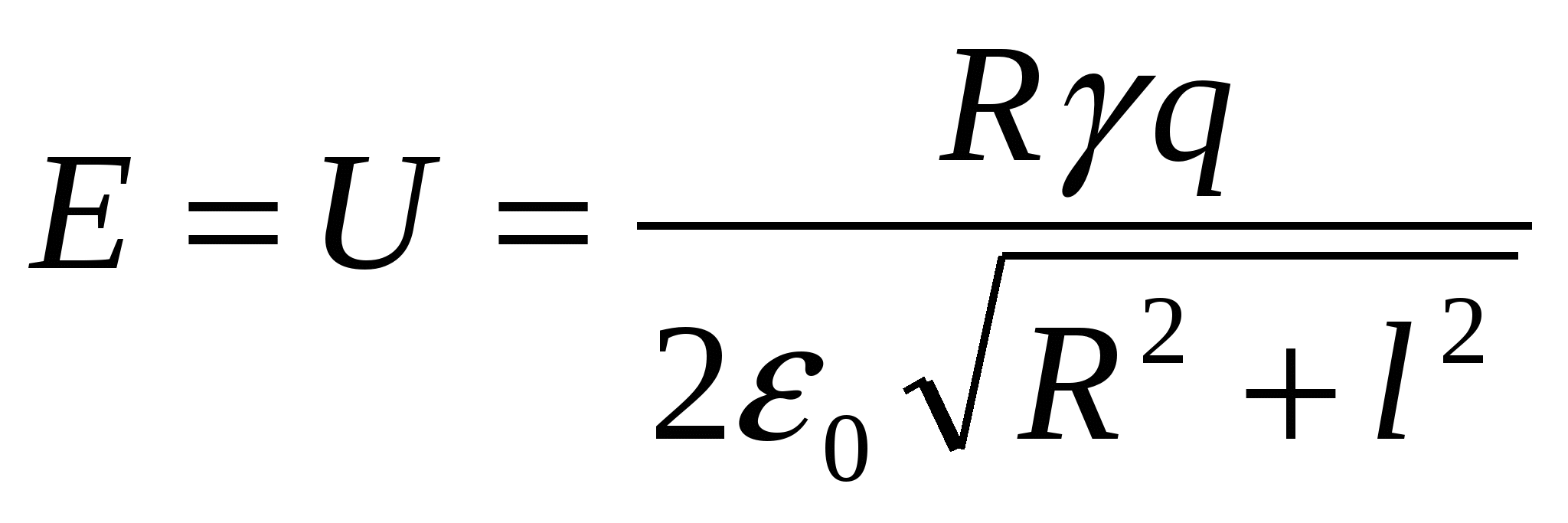
Подобным же образом находится потенциал при решении задачи А 19 из теста № 8 ЦТ 2001 г.:по тонкому проволочному кольцу радиуса 3 см равномерно распределен заряд 10 –9 Кл. Определите разность потенциалов между центром кольца и точкой, находящейся на оси кольца на расстоянии 4 см от центра. Ответ
: 120 В.
6
(ЦТ 2000 г. Тест 3. А 20).Если металлический шар радиуса R
1
, заряженный до потенциала φ
1
, соединить тонкой
проволокой с незаряженным металлическим шаром радиуса R
2 , то общий потенциал соединения окажется равным
7
(ЦТ 2001г. Тест 2. А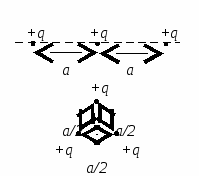
, находящихся в вакууме вдоль одной прямой на расстоянии a
друг от друга, расположить в вершинах равностороннего треугольника со стороной a
/2.
7.1. Имеются два
электрода в виде концентрических сфер
с радиусами a
(внутренняя) и b
(внешняя). Такая система называется
шаровым конденсатором. Найдите потенциал
любой точки поля между электродами.
7.2. Вычислите
потенциал электрического поля диполя.
7.3. Найдите потенциал
поля системы зарядов, находящихся в
объеме с линейными размерами l
,
на расстояниях
.
7.4. Изобразите
потенциальную диаграмму системы из
двух заряженных сфер.
7.5. Вычислите
потенциал поля шара радиусом a
,
равномерно заряженного по объему: а)
внутри шара; б) вне шара. Изобразите
график
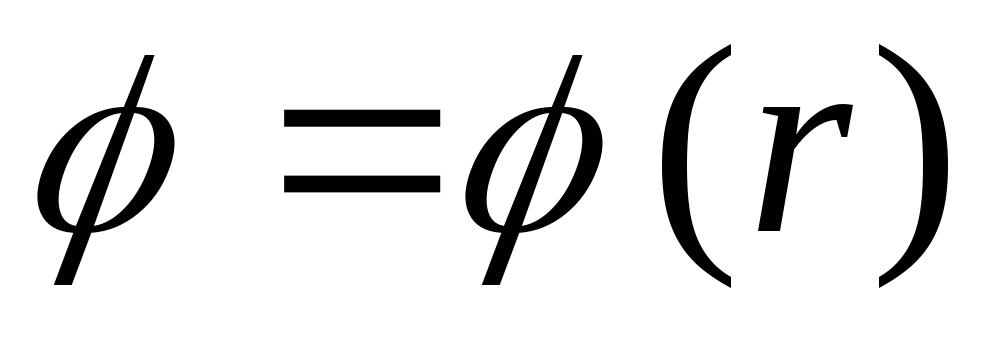
гдеr
– расстояние от центра шара. Решите
задачу путем интегрирования уравнения
Пуассона в сферических координатах, а
также используя связь между напряженностью
поля и потенциалом.
7.6. По тонкому
проволочному кольцу радиуса R
равномерно распределен заряд q
.
Исследовать зависимость потенциала
электрического поля на оси кольца от
расстояния до его центра. Найти
напряженность как градиент потенциала.
7.7. Сфера радиуса

равномерно заряженная зарядом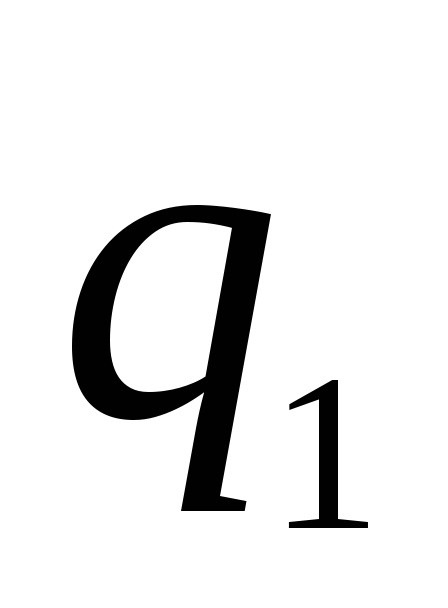
окружена тонкой концентрической сферой
радиуса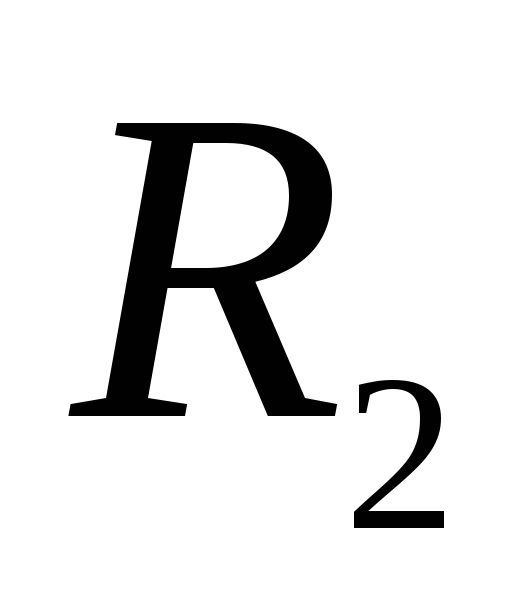
Какой заряд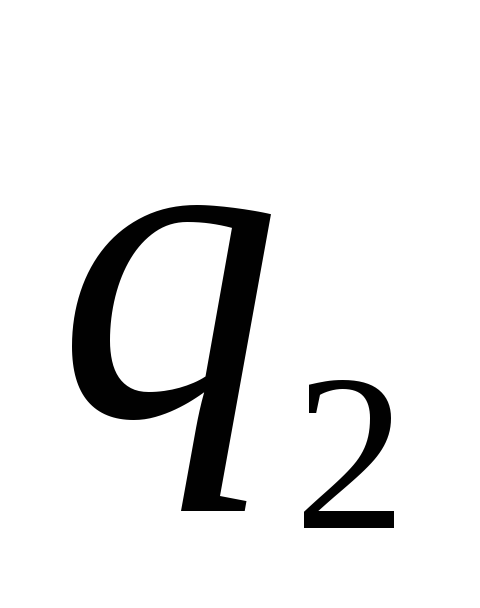
потенциал внутренней сферы относительно
бесконечности обратился в нуль? Заряд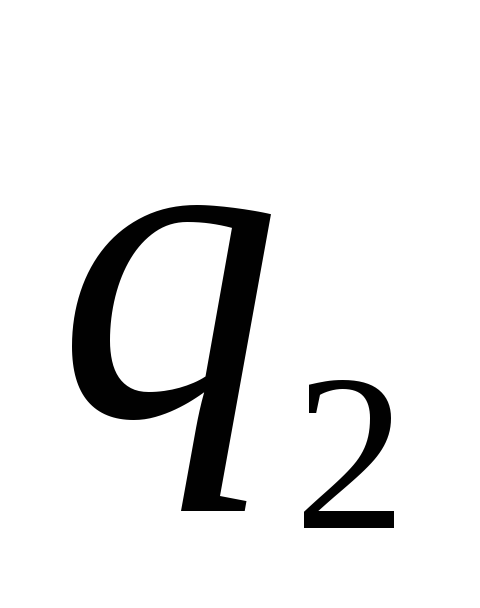
поверхности.
Решение задач
и, следовательно,
изменяется в пространстве так же, как
и в случае поля точечного заряда, откуда
следует, что разность потенциалов между
внутренней сферой и какой – либо точкой
поля, удаленной на расстояние r
от центра конденсатора, равна
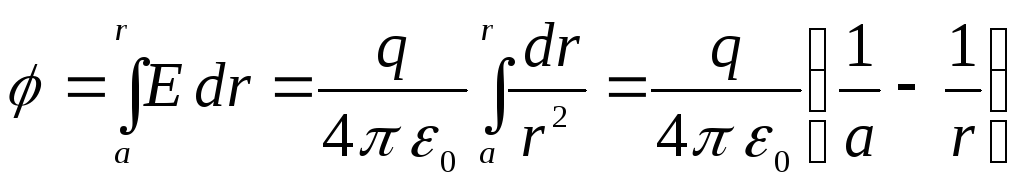
Разность потенциалов
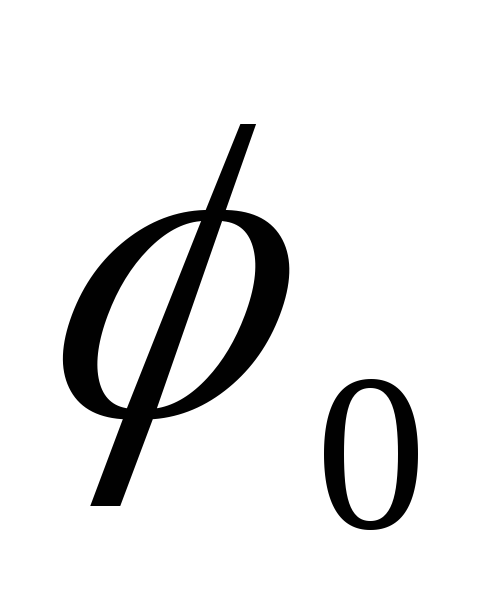
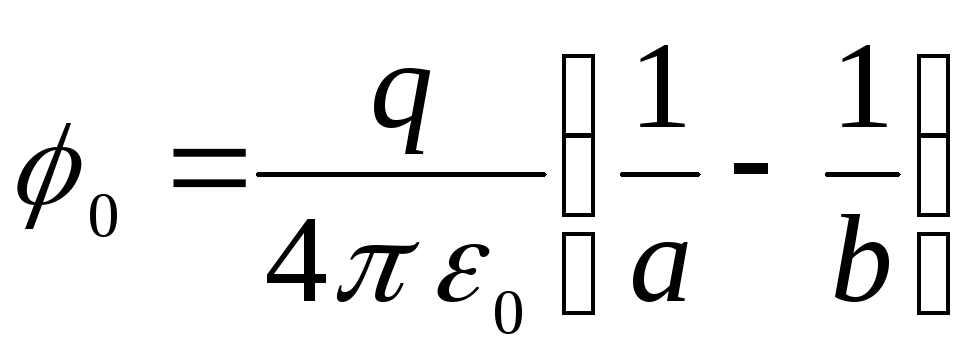
Из этих двух формул
следует
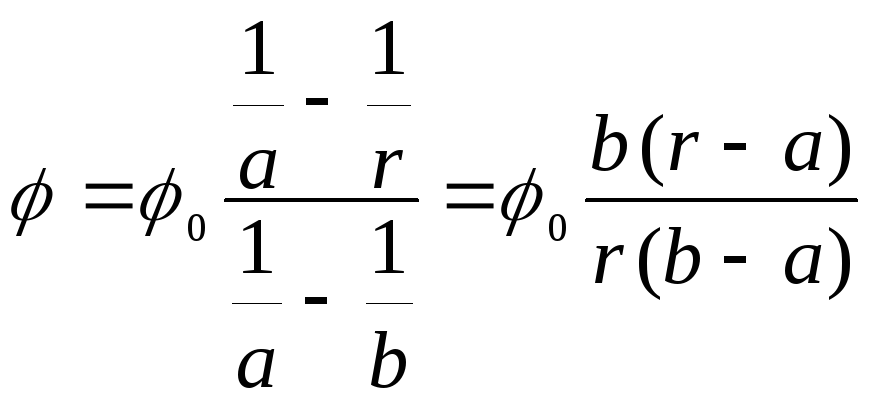
Измерив
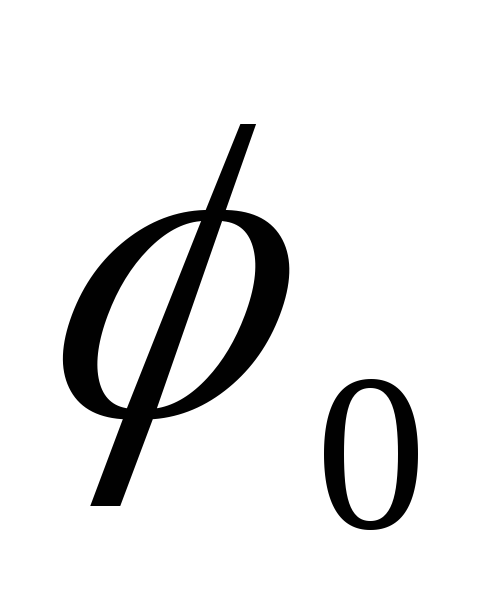
потенциал любой точки поля.
7.2. Пусть система
зарядов
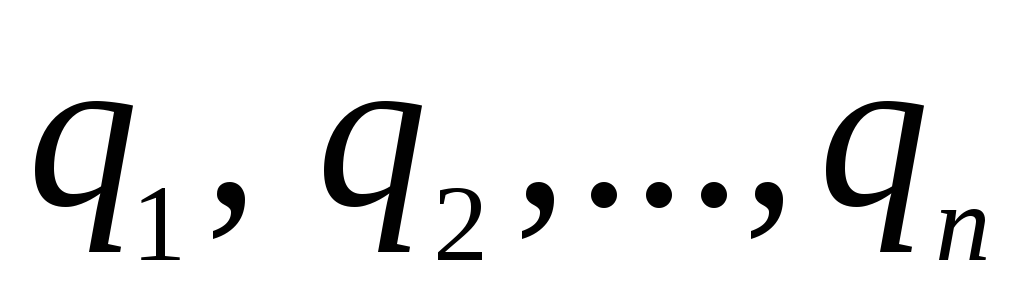
l. Найдем потенциал поля, создаваемого
этой системой зарядов на расстояниях
r, больших по сравнению с l. Выберем начало
координат O внутри объема, который
занимает система зарядов, и определим
положение зарядов с помощью радиусов
– векторов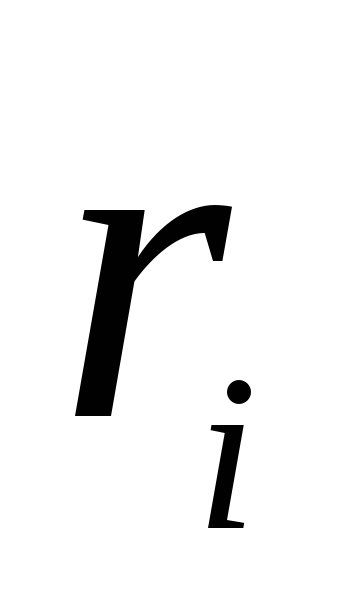
векторов
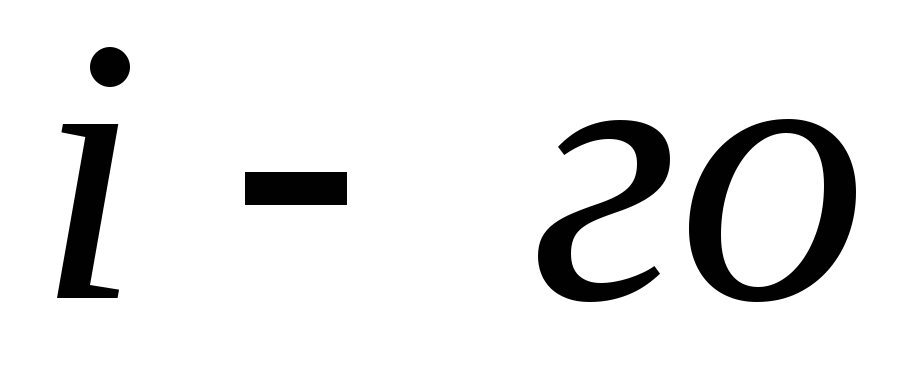
радиус – вектором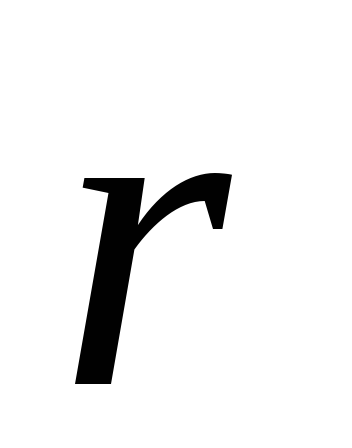
равен
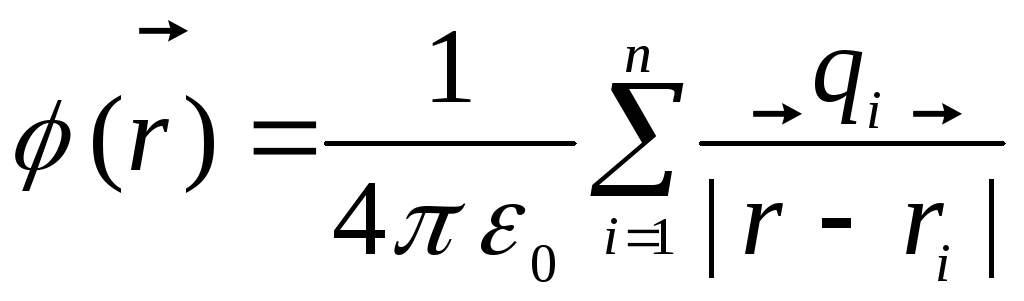
Так как
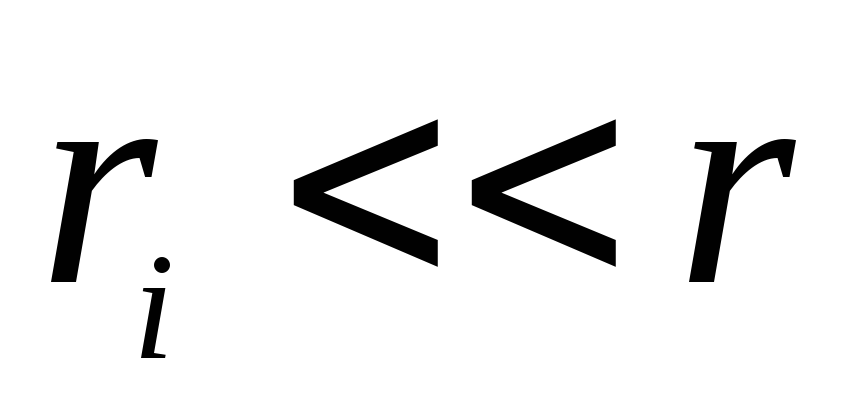
то можно положить, что
(символом
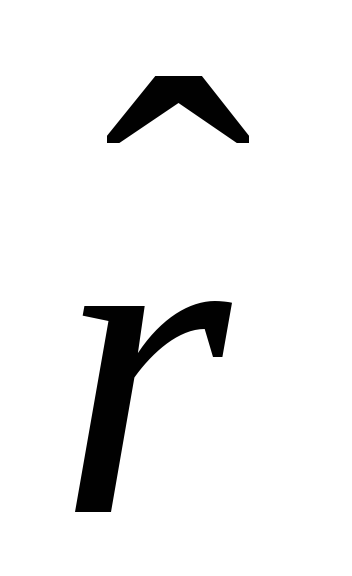
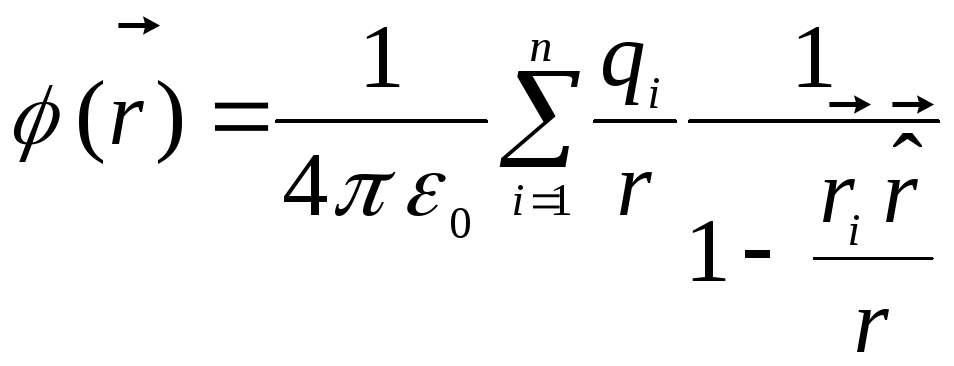
Воспользуемся
формулой
при
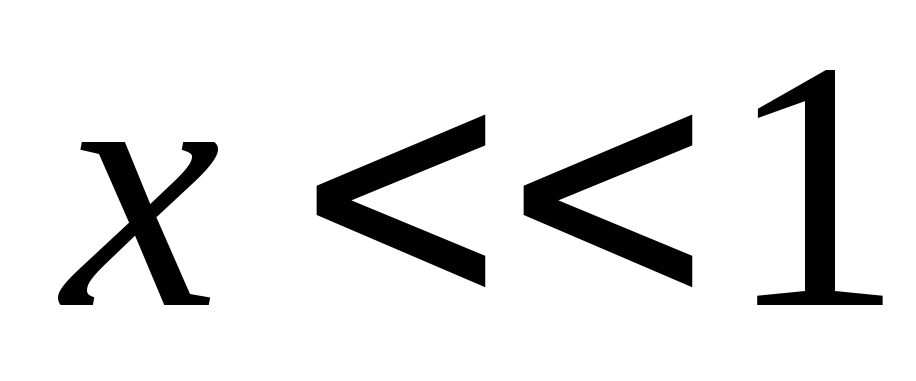
Теперь мы можем
записать
Первый член этого
выражения есть потенциал поля точечного
заряда величиной
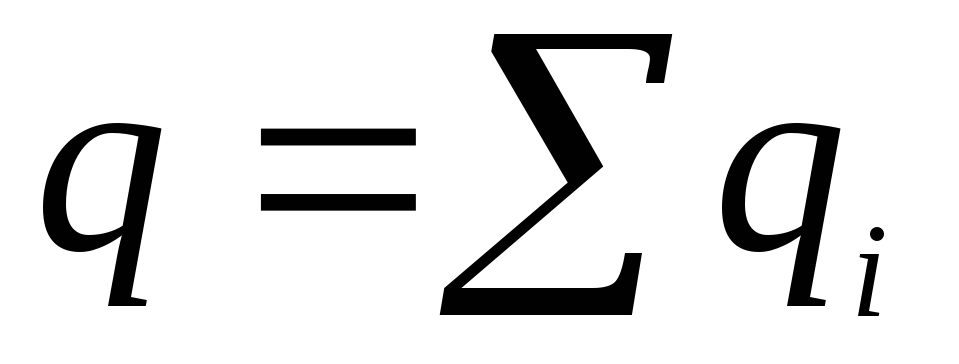
Второй член такого же вида, как выражение,
определяющее потенциал поля диполя.
Роль электрического момента диполя
играет величина
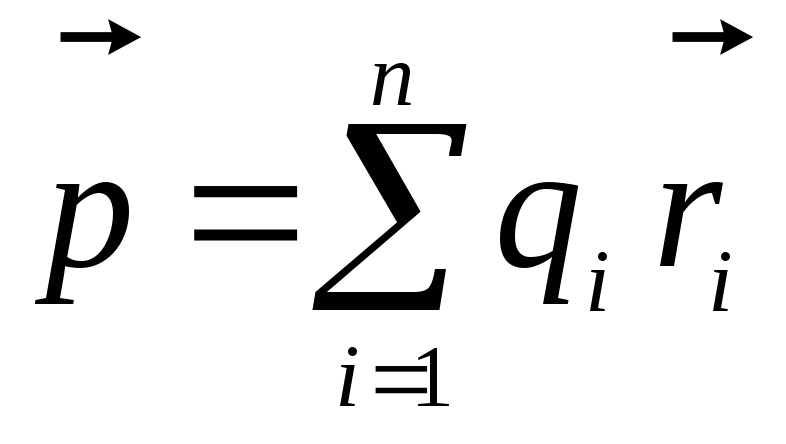
которую называют
дипольным электрическим моментом
системы зарядов.
7.3. Если поле создано
несколькими зарядами, то потенциал
этого поля равен сумме потенциалов
полей, созданных отдельными зарядами
Здесь

рассматриваемой точке относительно
бесконечности,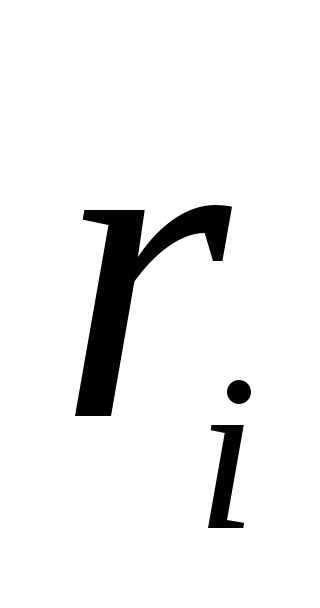
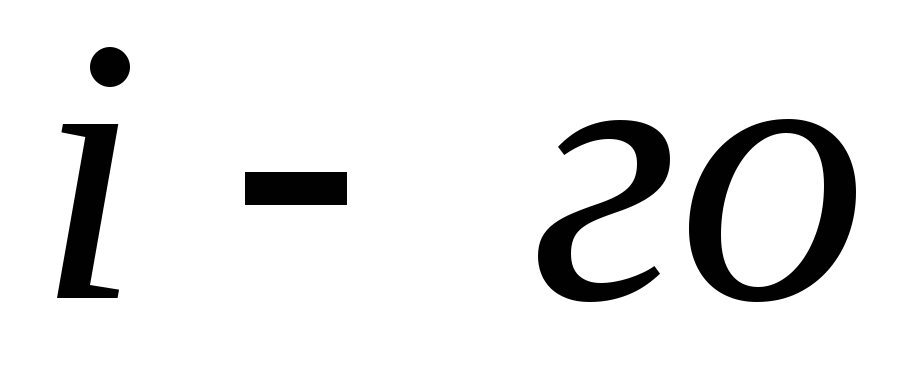
всем точечным зарядам.
Рассматриваемое
поле обладает осевой симметрией, поэтому
картина поля в любой плоскости, проходящей
через ось диполя, будет одной и той же,
а вектор

M относительно диполя будем характеризовать
с помощью радиус – вектора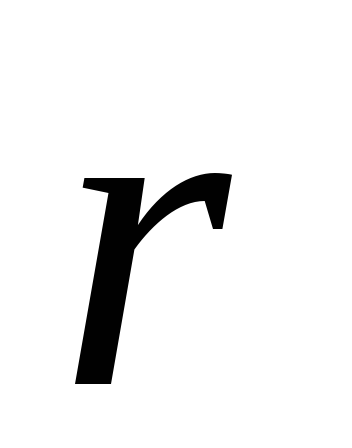
либо с помощью полярных координат r и

Положение заряда
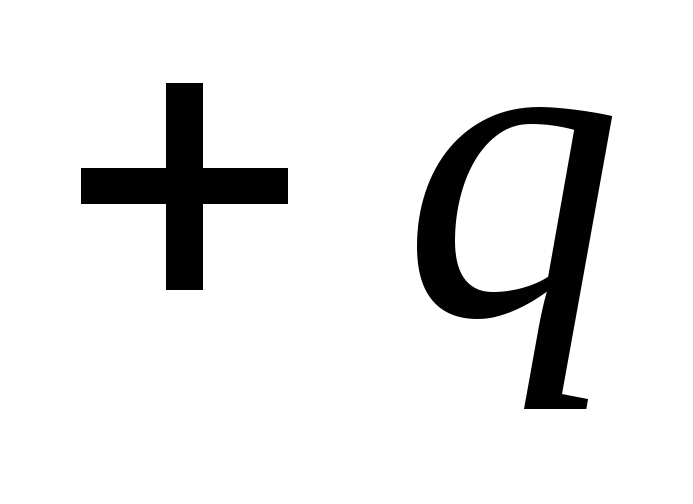
вектором
а заряда

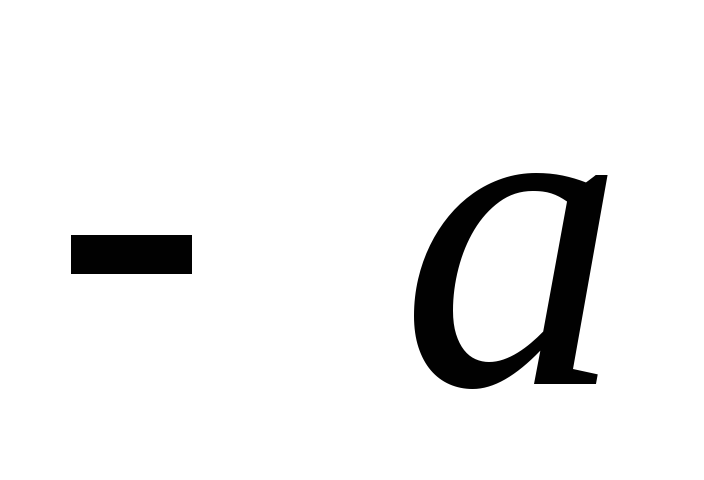
Очевидно, что
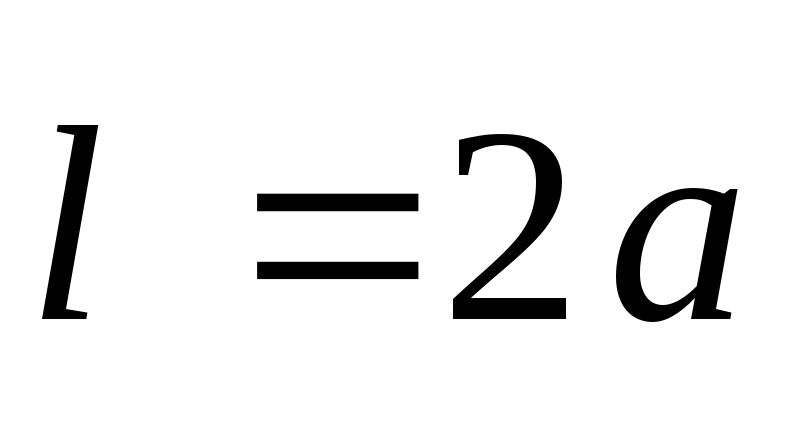
где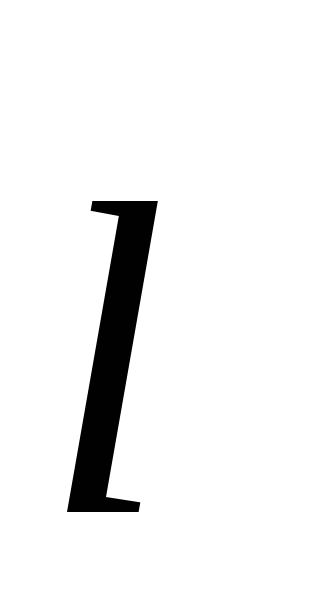

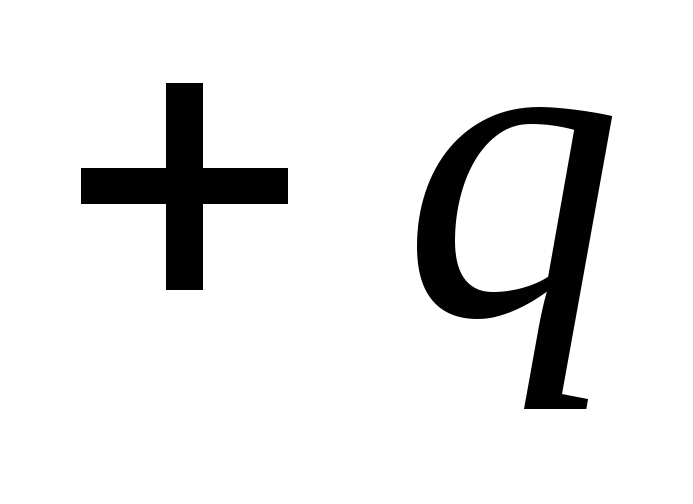
соответственно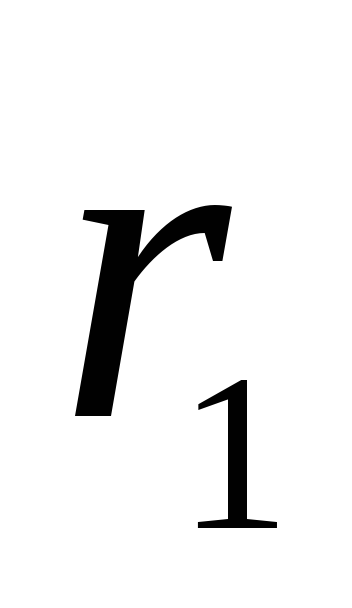
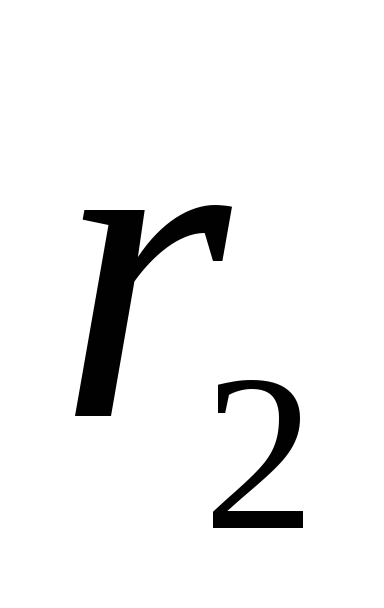
Так как
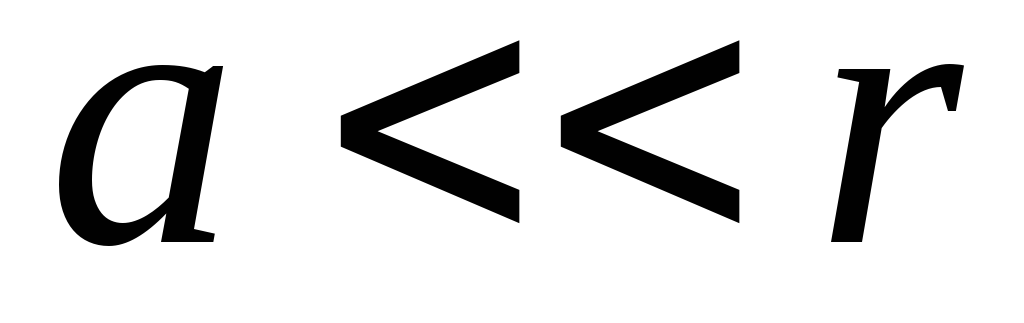
то можно положить, что
Потенциал в точке,
определяемой радиус – вектором
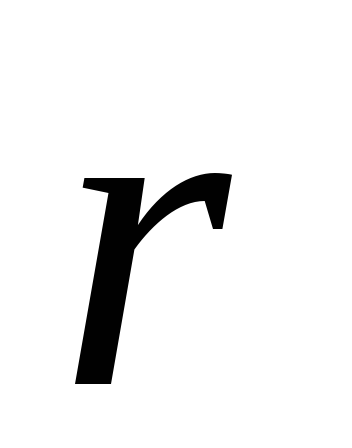
равен
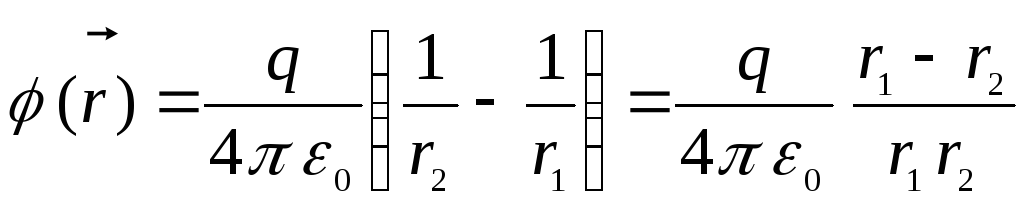
Произведение
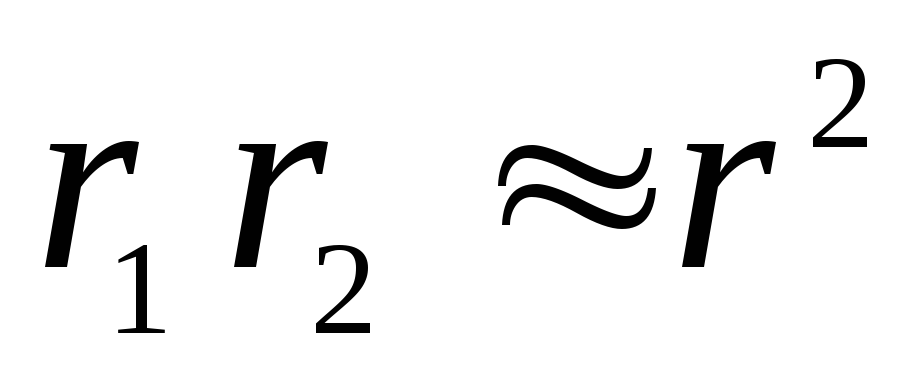
разность
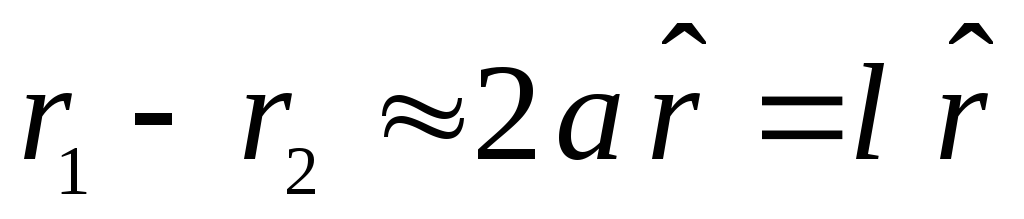
Следовательно,
,
где
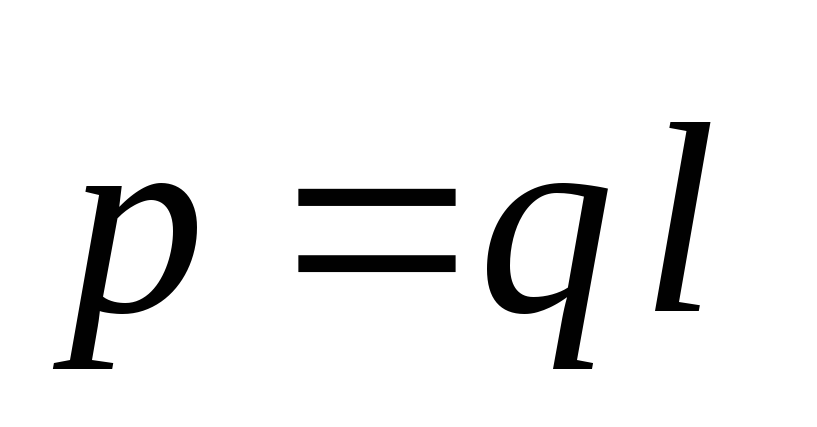
Из этой формулы
видно, что потенциал поля диполя
определяется его электрическим моментом.
Сравнивая потенциал поля диполя с
потенциалом поля точечного заряда,
видно, что потенциал поля диполя убывает
с расстоянием быстрее
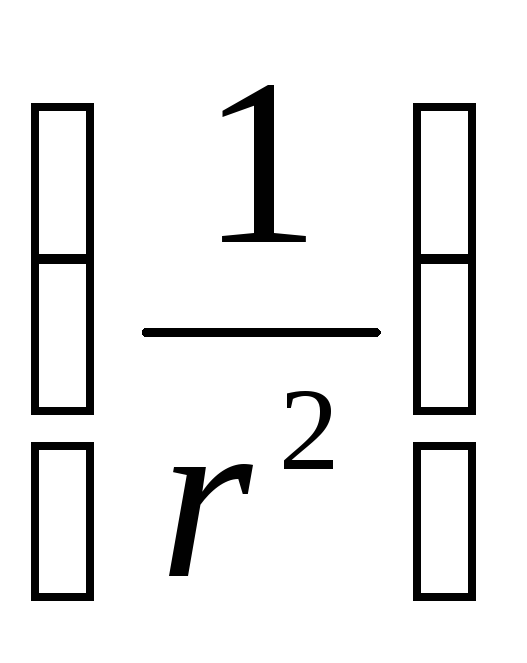
чем потенциал поля точечного заряда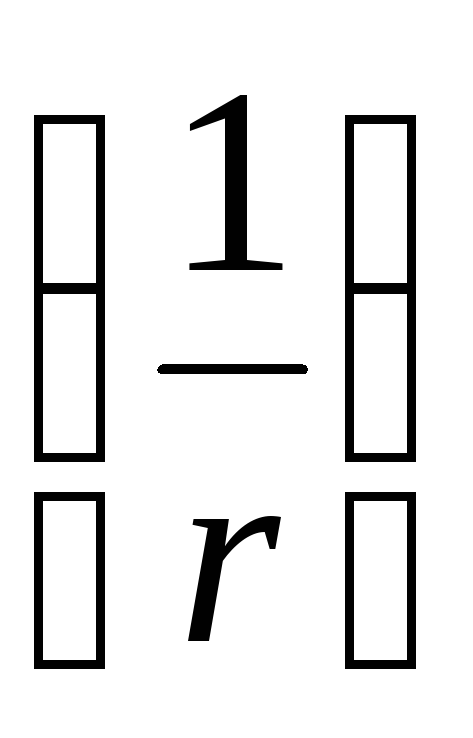
Из рисунка ___ видно,
что
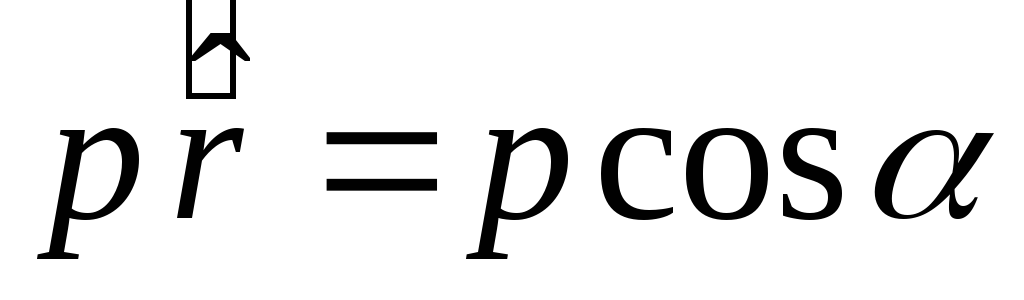
Поэтому
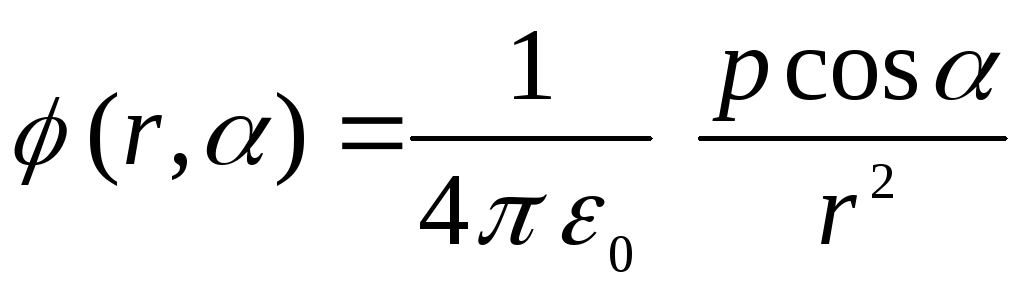
7.4. Пусть внутренняя
сфера, радиус которой

имеет положительный заряд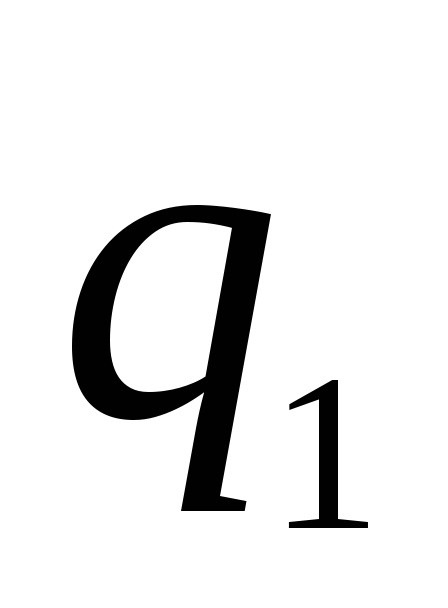
а внешняя с радиусом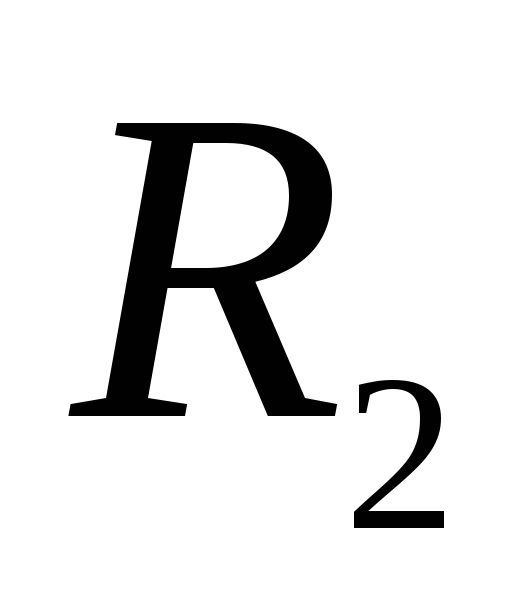
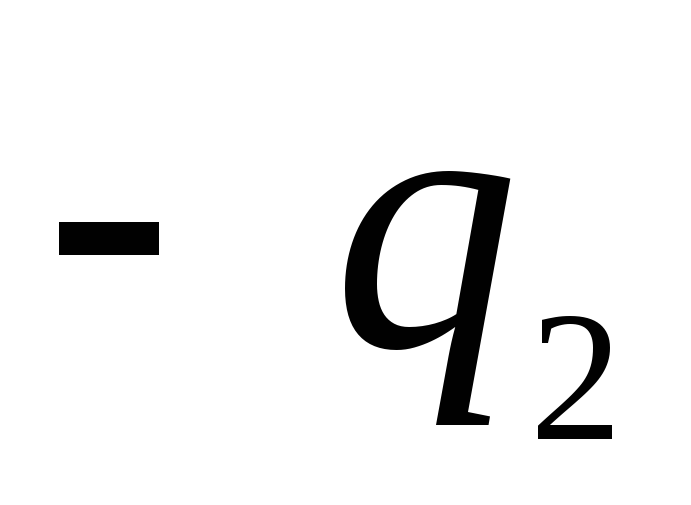
причем
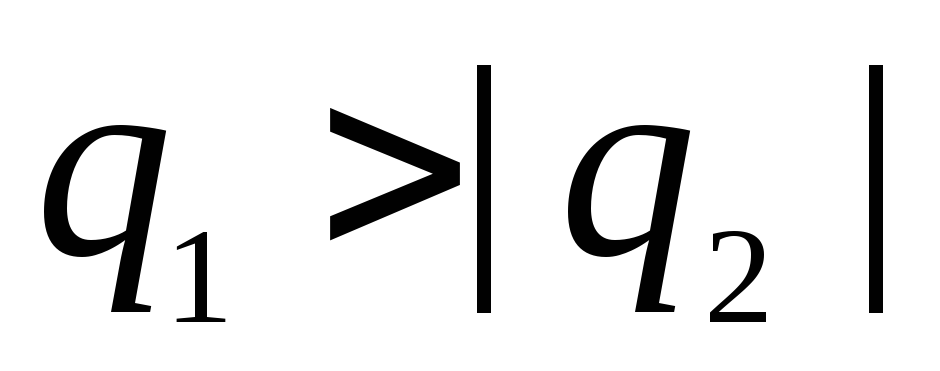
Вне сфер потенциал
будет равен
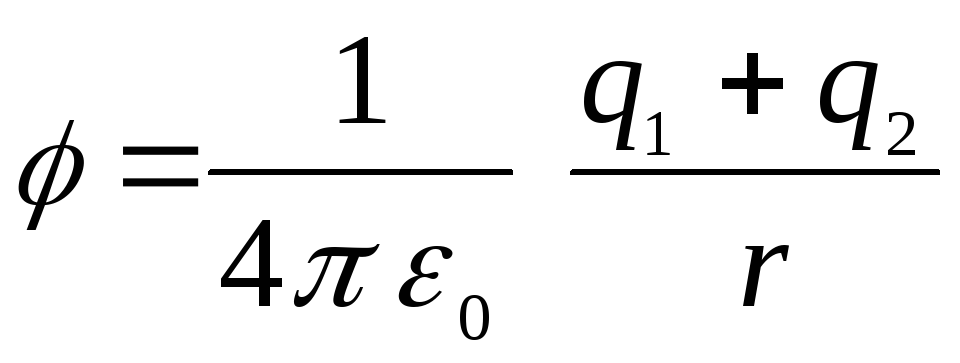
так как его создают
совместно обе сферы (потенциал есть
работа внешних сил, совершаемая при
перемещении единичного положительного
заряда из бесконечности в данную точку
поля). Работа по перемещению единичного
положительного заряда из бесконечности
в область между сферами будет равна
сумме двух работ:
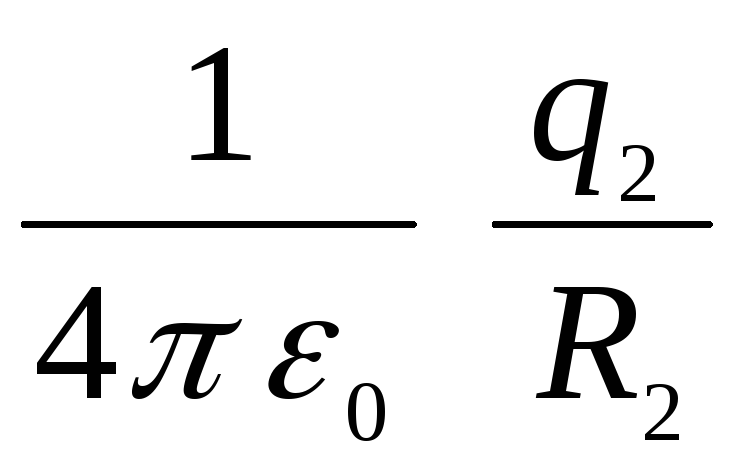
стороны внешней сферы на пути из
бесконечности до ее поверхности) и
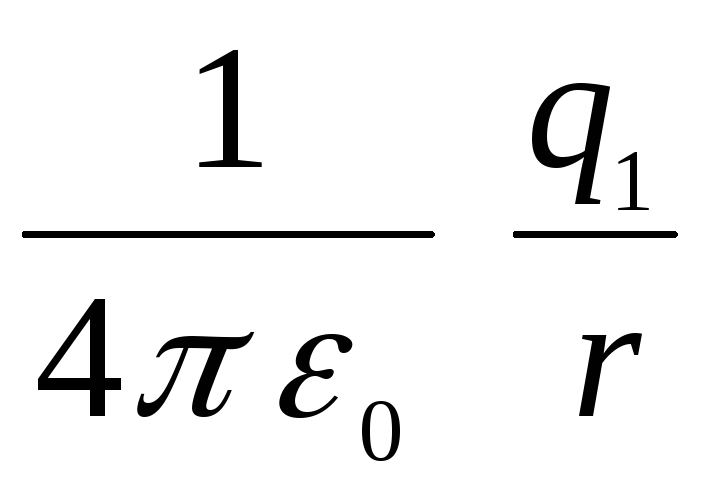
т.е.
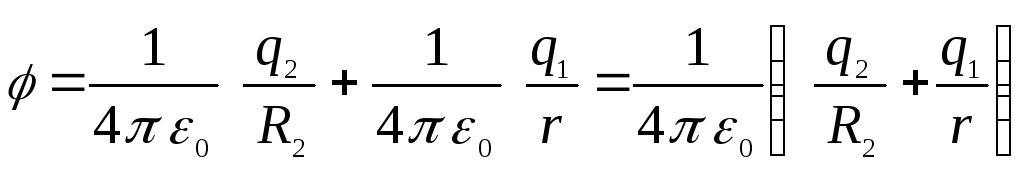
Внутри меньшей
сферы потенциал будет постоянен и равен
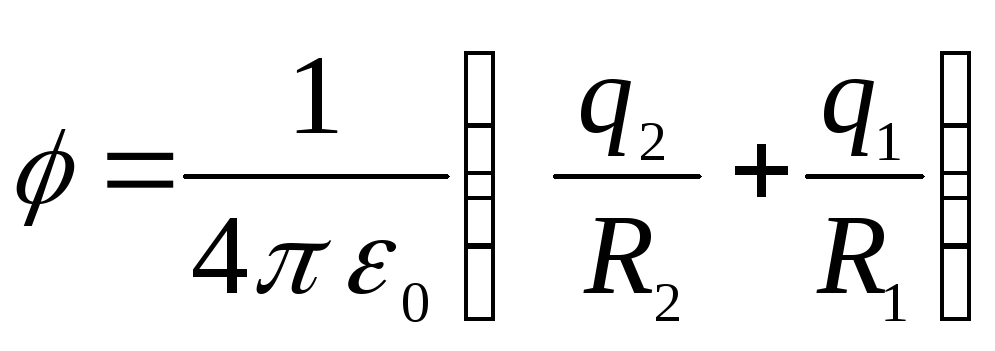
График, построенный
по первой и второй формулам, изображен
на рисунке ____1.
Если заряды сфер
будут равны по величине и противоположны
по знаку, т.е.
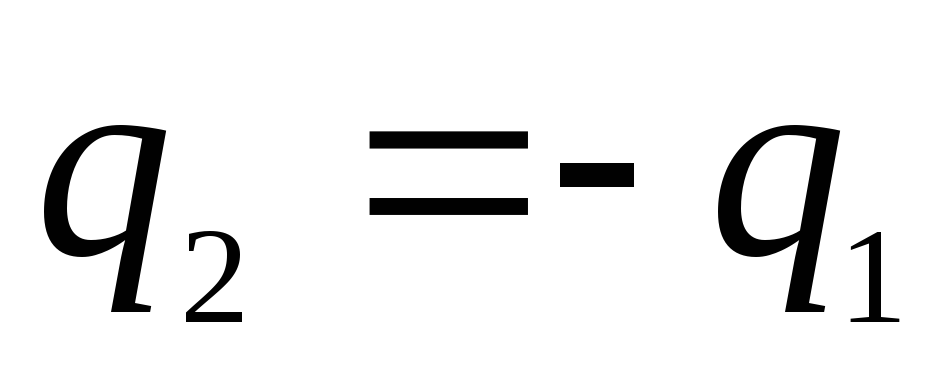
конденсатором), то потенциал во внешней
области обращается в нуль, а между
обкладками равен
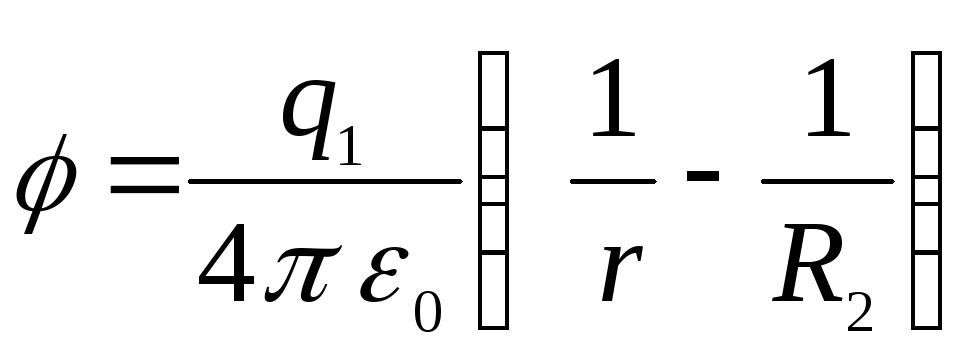
Получается график,
изображенный на рисунке ___2.
Если внутренняя
сфера имеет отрицательный заряд, а
внешняя – положительный, то график
переворачивается и выглядит так, как
изображено на рисунке ____3.
7.5. Интегрирование
уравнения Пуассона в сферических
координатах. Введем сферическую систему
координат
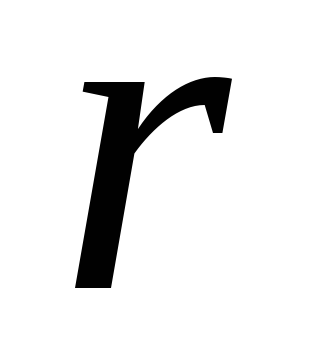


приняв за начало отсчета центр шара.
Уравнение Гаусса в дифференциальной
форме (уравнение Пуассона), определяющее
потенциал поля, принимает вид
где
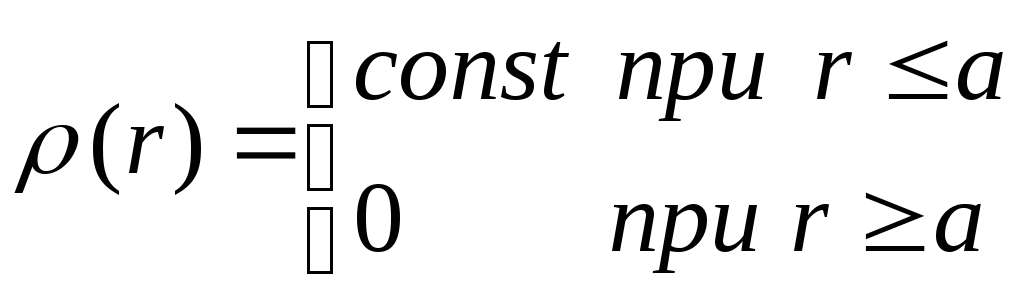
Вследствие
сферически симметричного распределения
зарядов, потенциал

зависит от углов

т.е.
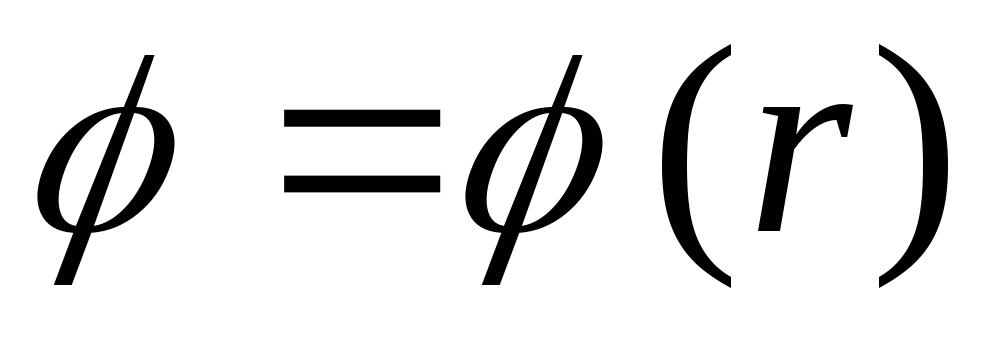
Поэтому уравнение Пуассона упрощатся
и принимает вид
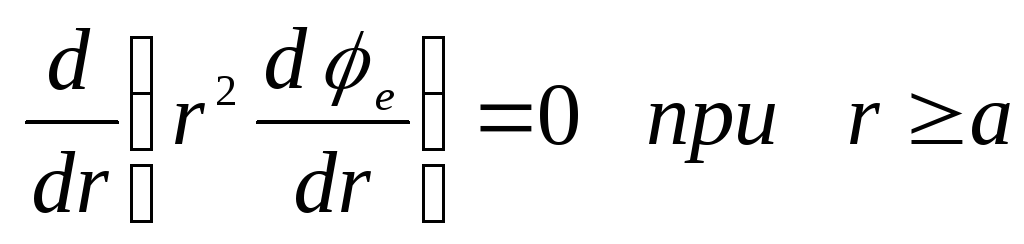
Здесь через
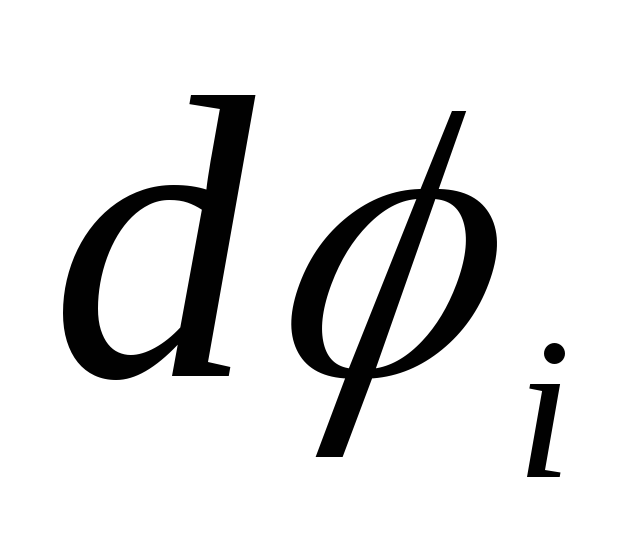
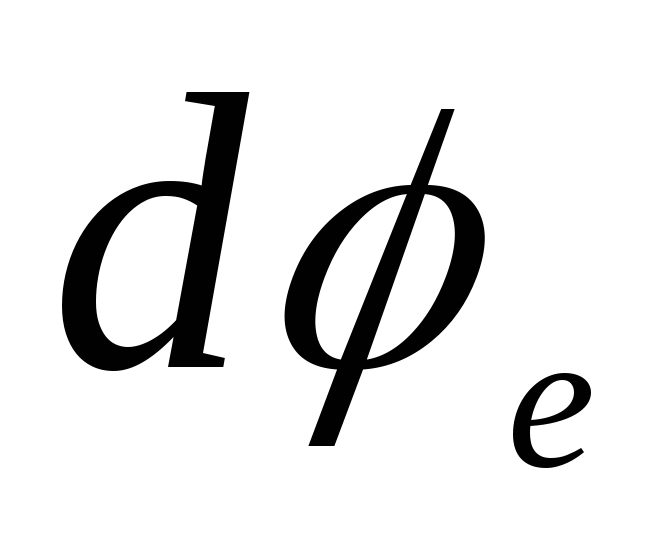
находим
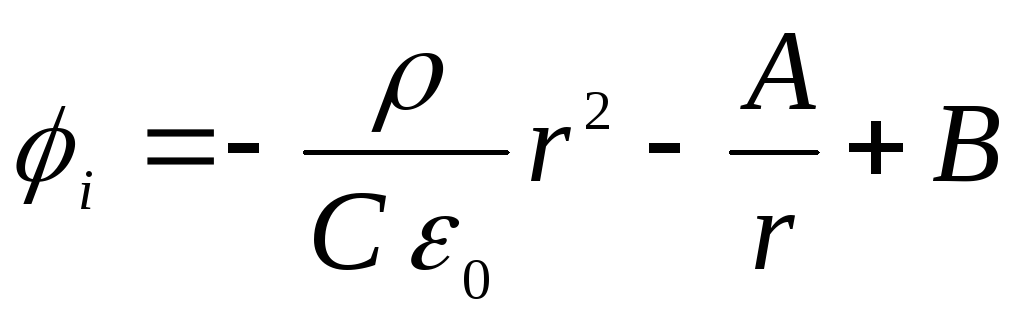
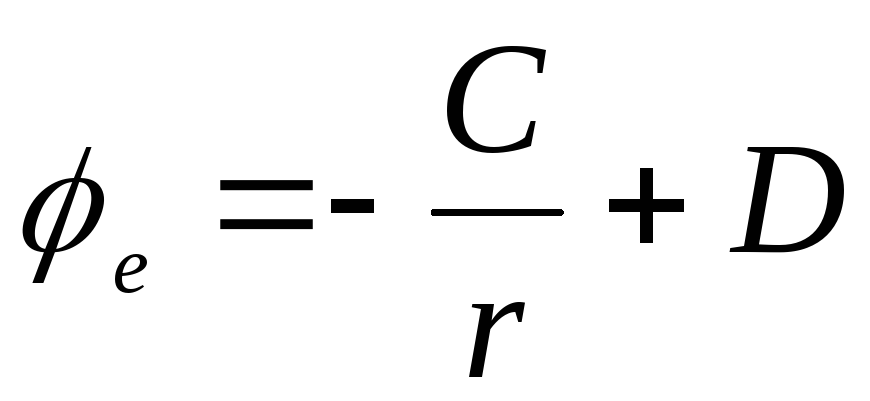
Постоянные A, B, C,
D должны быть определены из следующих
граничных условий.
1) Потенциал

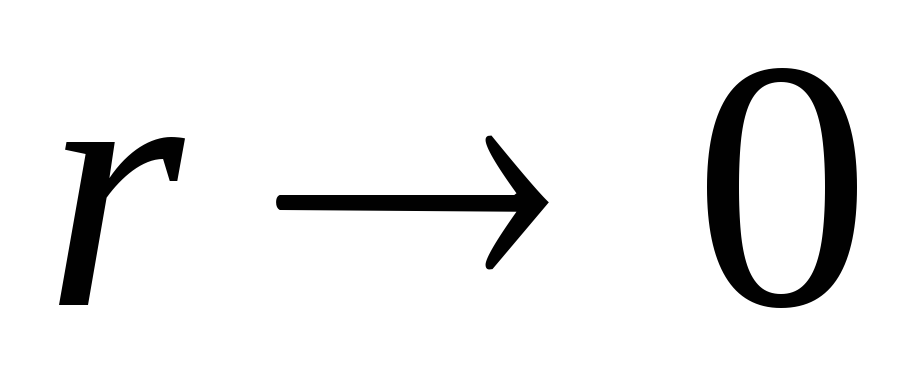
откуда непосредственно следует, что
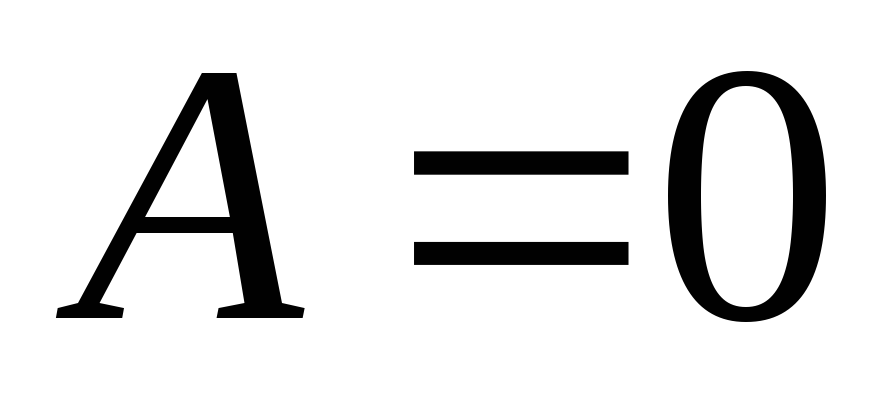
2)
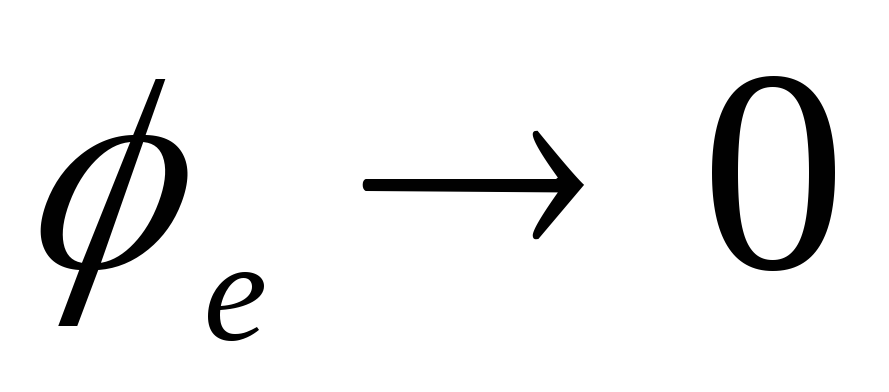

откуда следует, что
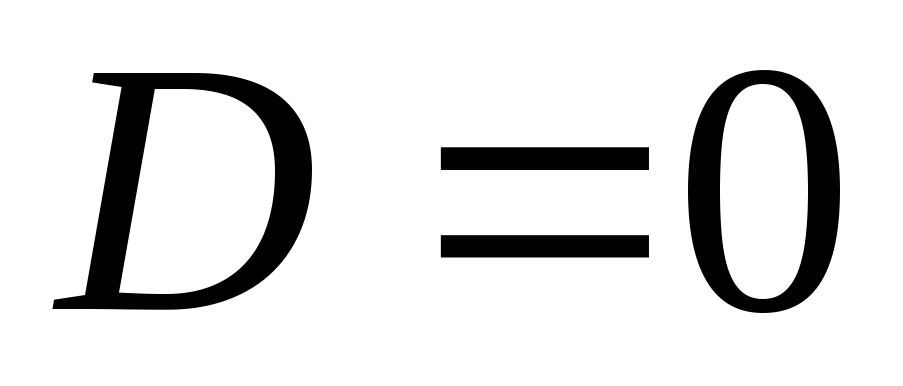
3) Потенциал
электростатического поля является
непрерывной функцией координат, поэтому
необходимо, чтобы
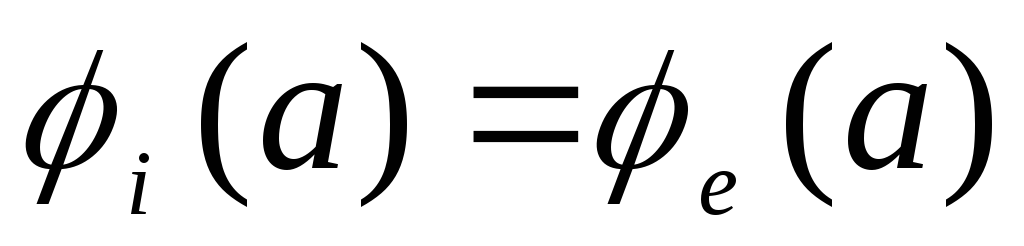
4) Нормальная
составляющая вектора

прохождении через поверхность шара,
т.е.
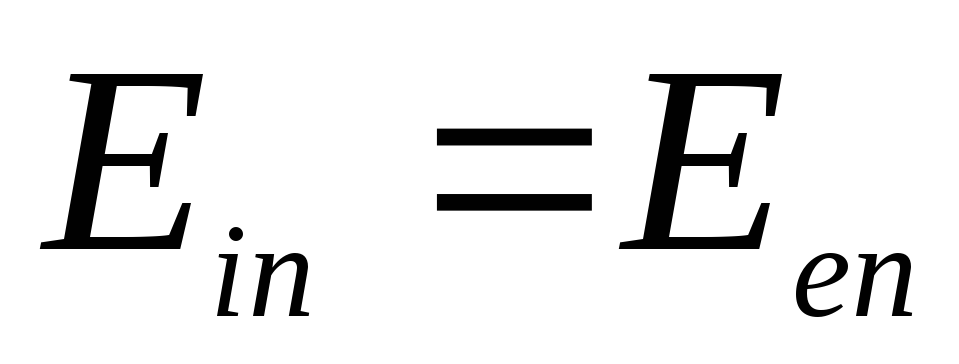
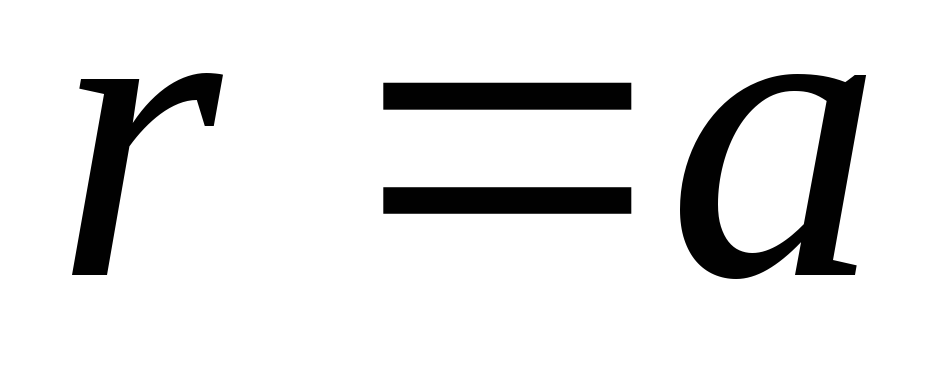
так как поверхностная плотность заряда
на поверхности шара равна нулю. Последнее
условие эквивалентно требованию
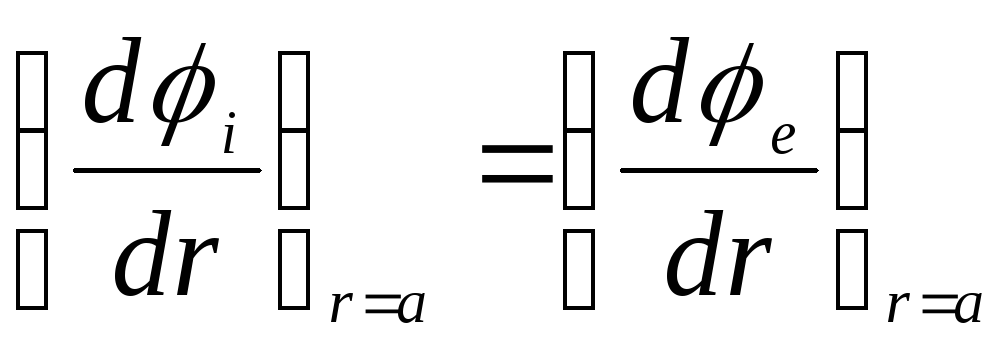
Из последних двух
условий находим
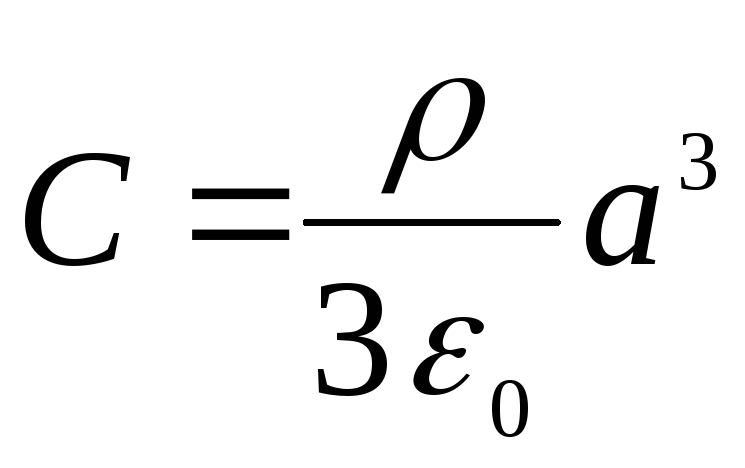
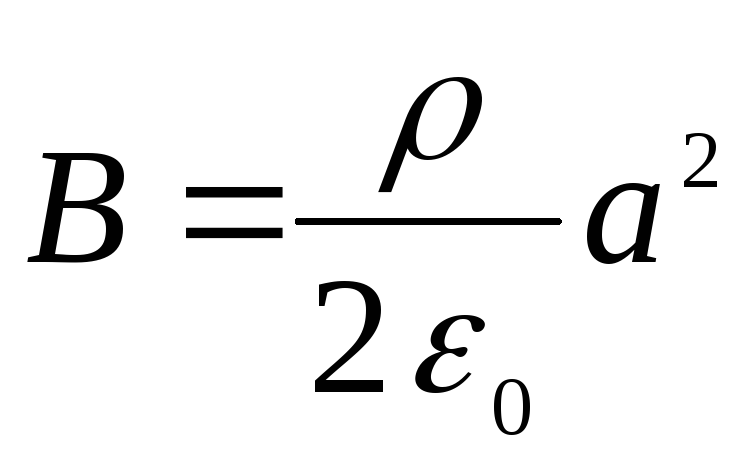
Искомые потенциалы
окончательно запишем в виде
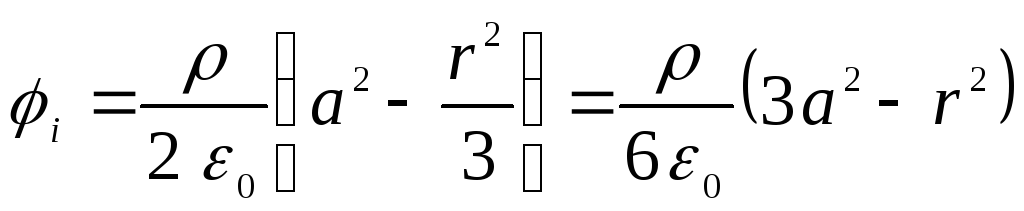
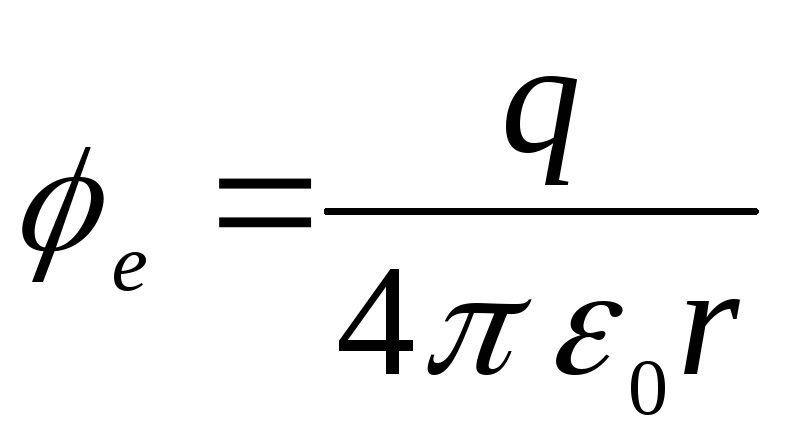
Из этих формул
видно, что вне шара потенциал поля
аналогичен полю точечного заряда.
Изобразим график
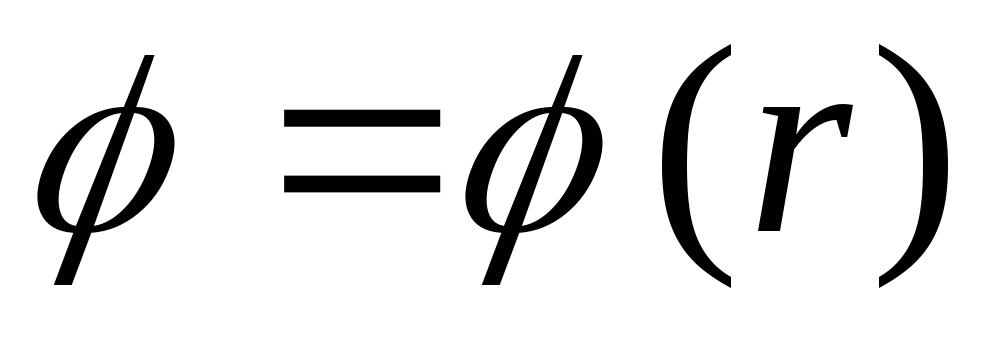
Пусть
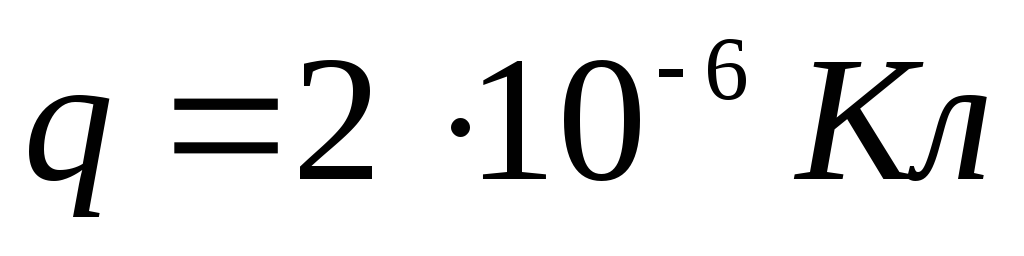
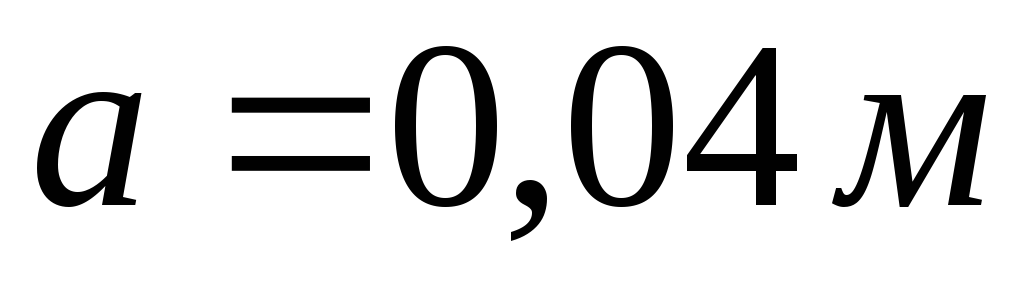
Найдем объемную плотность заряда
и отношение
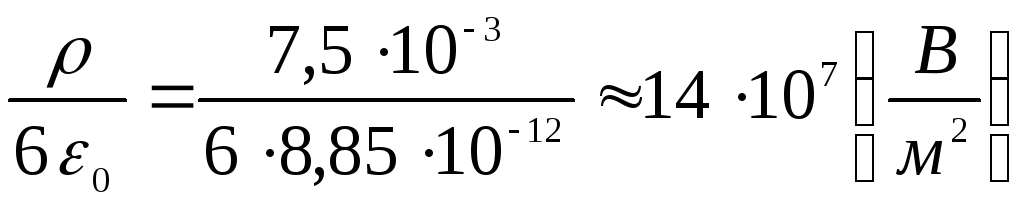
Теперь можно
записать, что потенциал внутри сферы
Составим таблицу
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потенциал вне
сферы
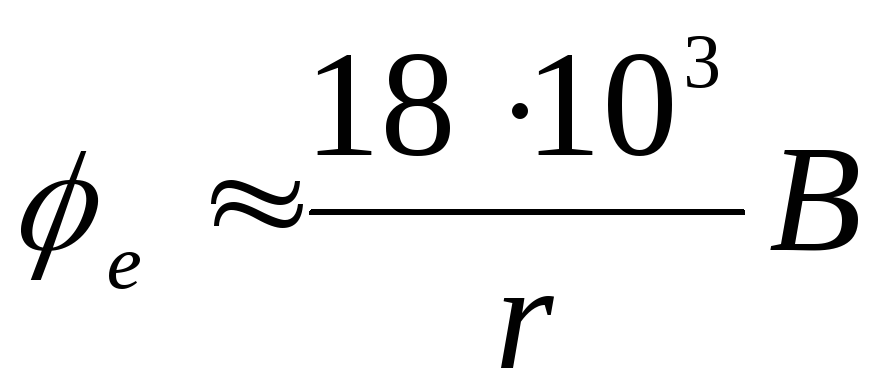
|
|
|||||||
|
|
|
|
|
|
|
|
|
Теперь строим
график
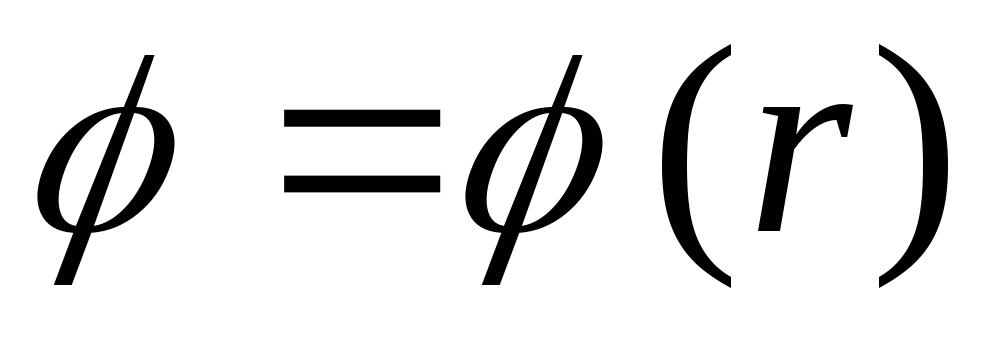
Связь между
напряженностью и потенциалом.
Зависимость
напряженности электростатиического
поля от расстояния до центра шара внутри
шара имеет вид (см. решение задачи 1.5.4.)
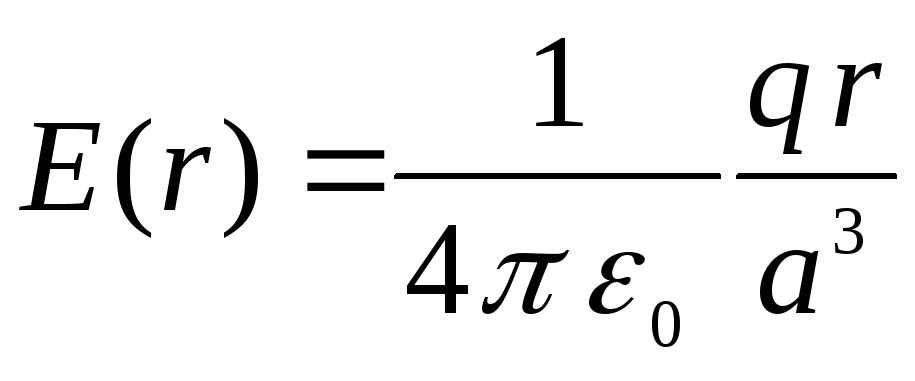
т.е. внутри шара
напряженность поля растет линейно с
расстоянием от центра. При
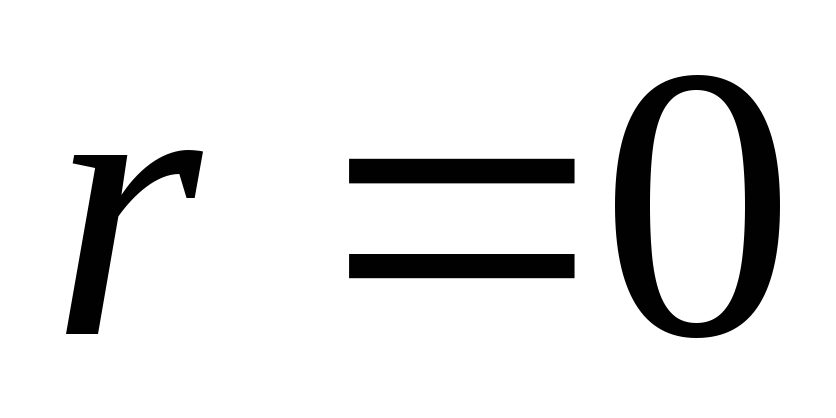
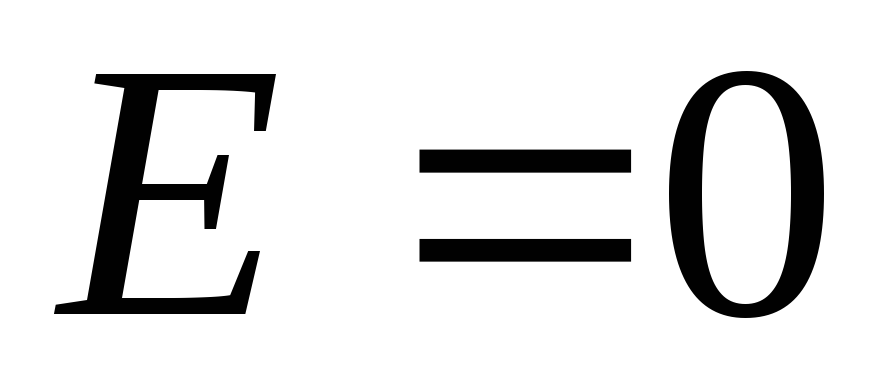
при
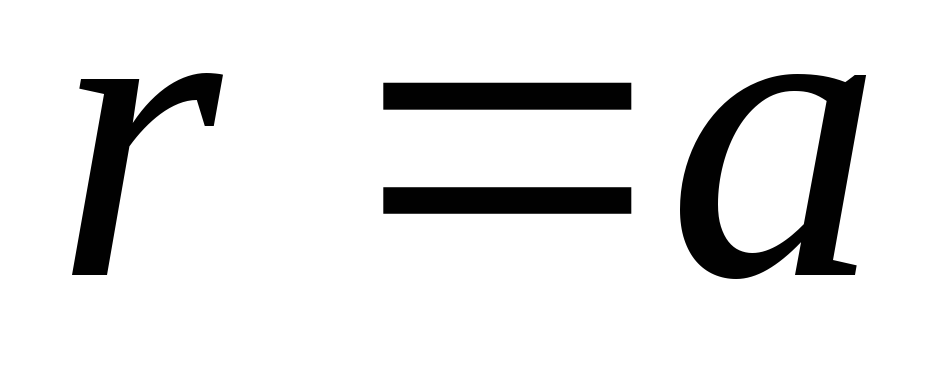
равной
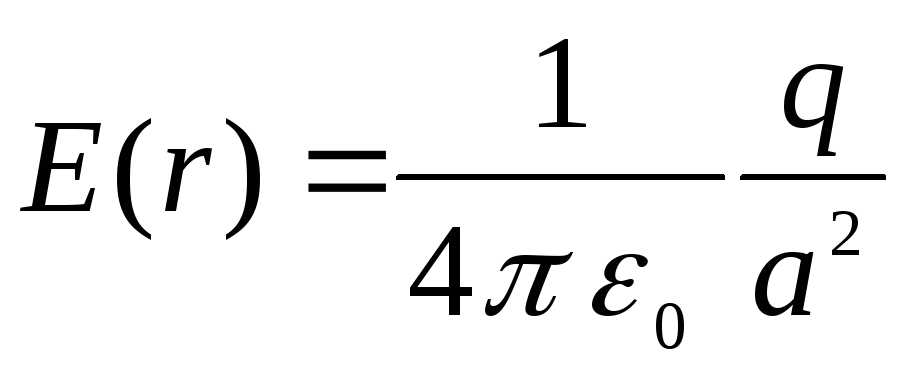
При

как напряженность поля точечного заряда.
Изменение потенциала
в поле заряженного шара
Потенциал поля
внутри шара
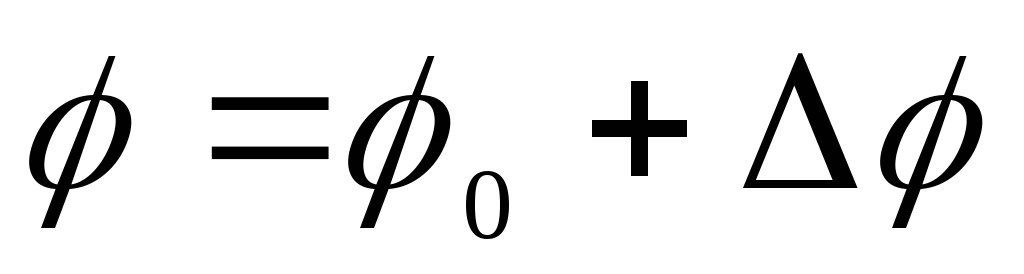
где
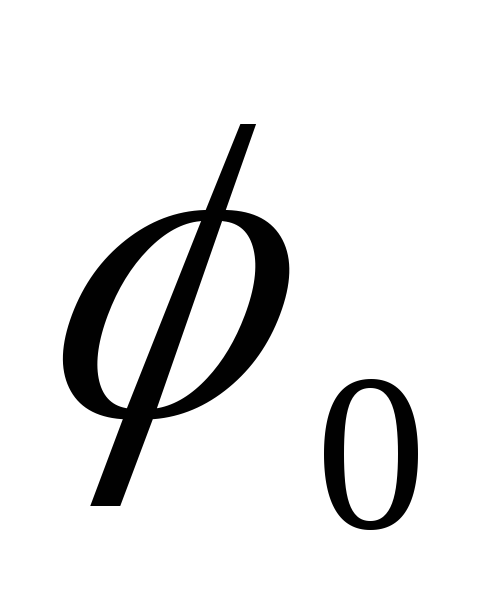
(потенциал поля точечного заряда), равный
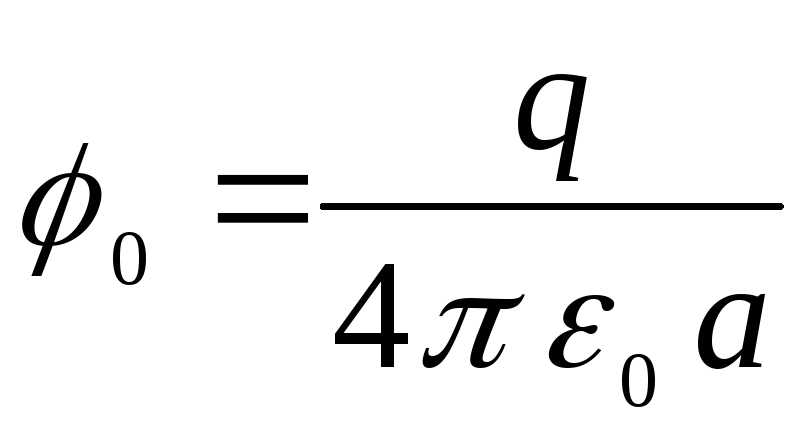
Окончательно
получим
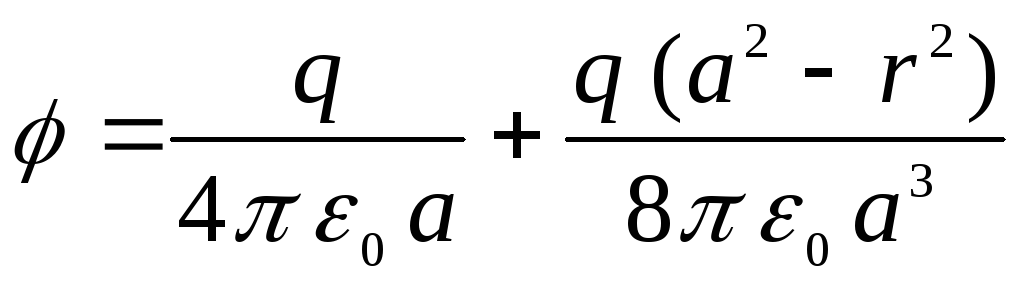
Учитывая, что
объемная плотность заряда
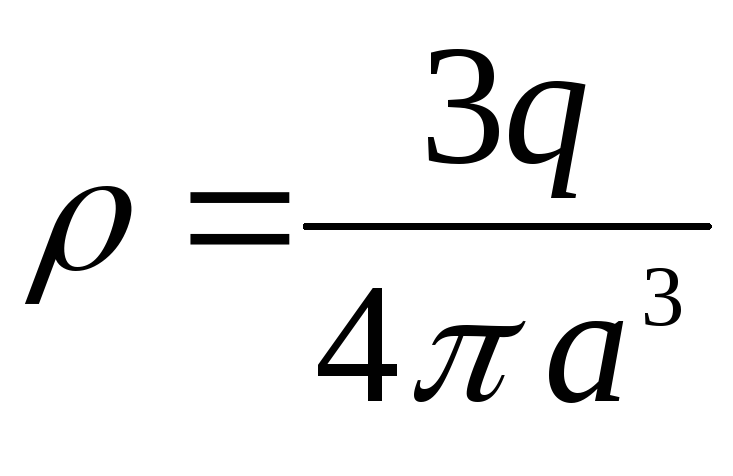
можно записать
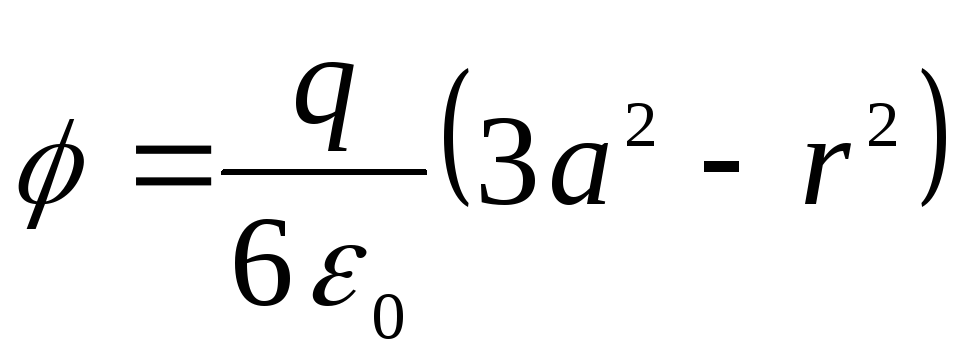
т.е. мы пришли к
той же формуле, что и при решении задачи
путем интегрирования уравнения Пуассона.
1.7.6. Потенциал
результирующего поля в точке A
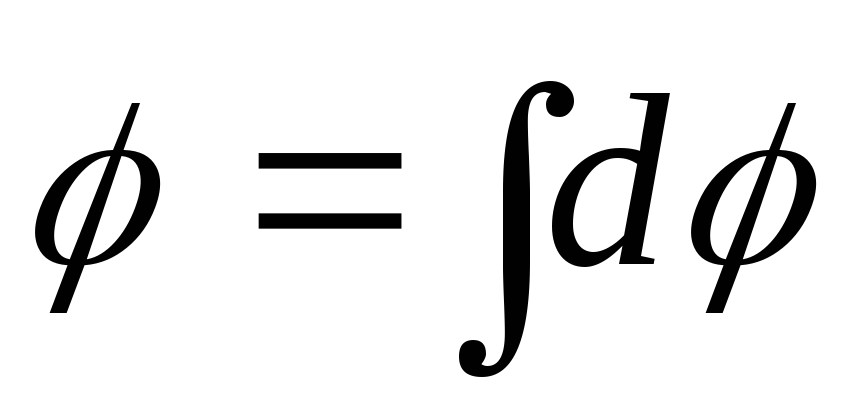
есть потенциал
поля, созданного зарядом
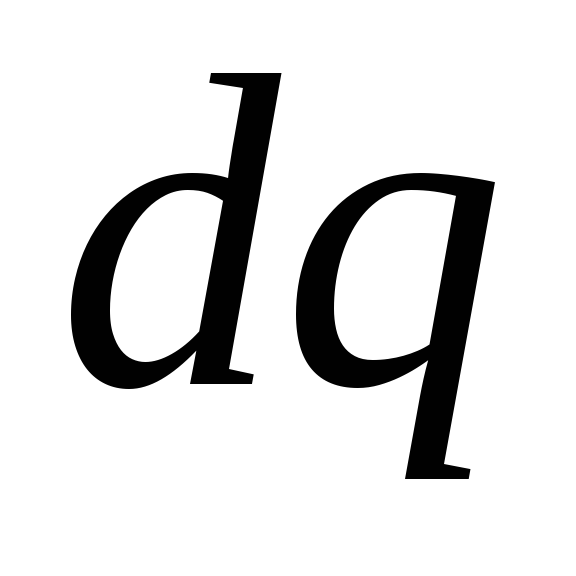

есть линейная
плотность заряда, r – расстояние от
элемента

формул имеем
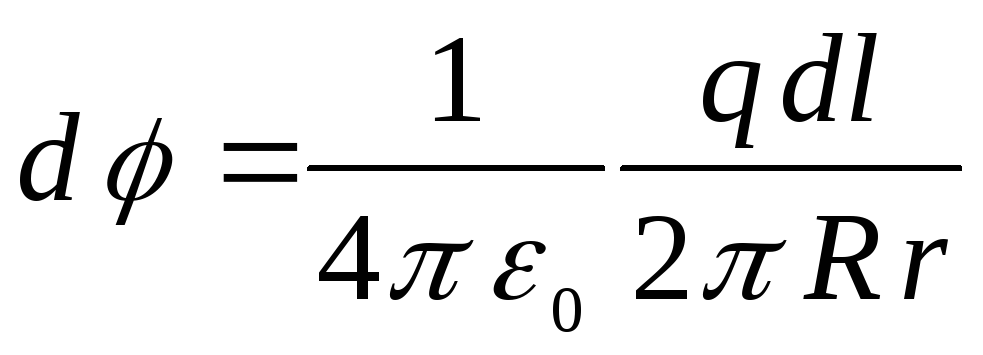
Результирующий
потенциал
Из геометрических
соображений следует, что
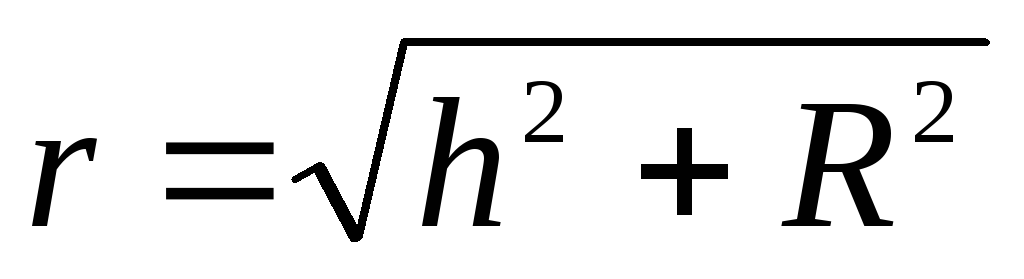
Следовательно,
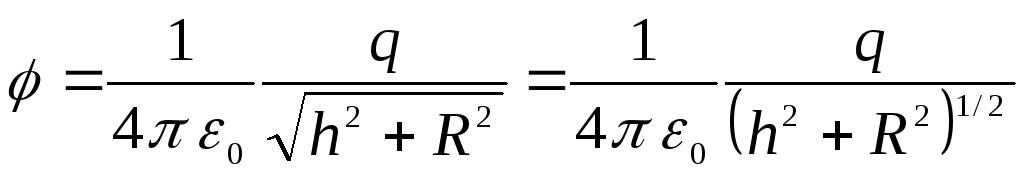
Напряженность
поля
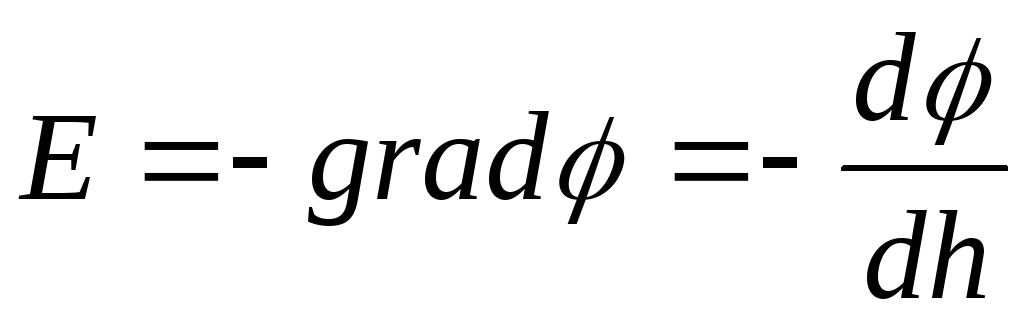
Анализ выражений
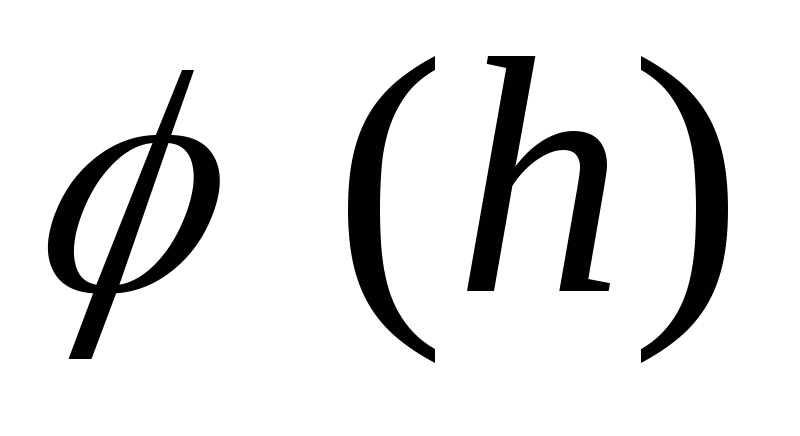
показывает, что в центре кольца (
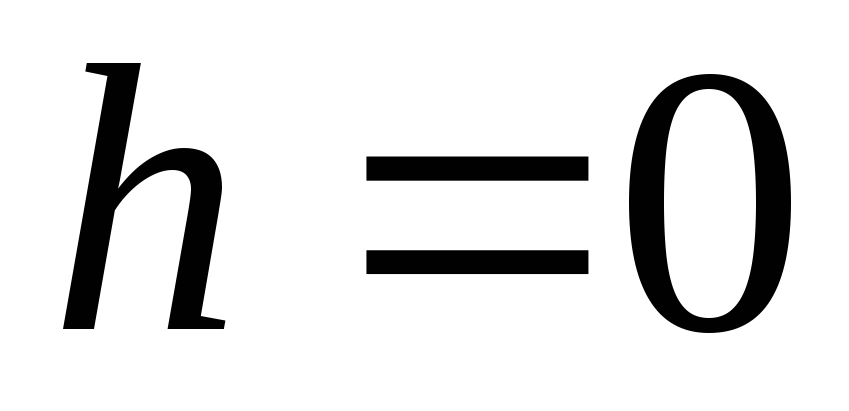
потенциал имеет максимальное значение,
а напряженность поля обращается в нуль.
При
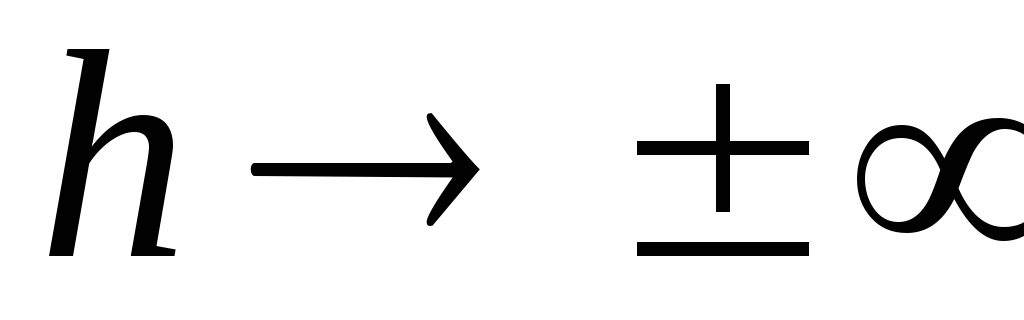
к нулю.
При
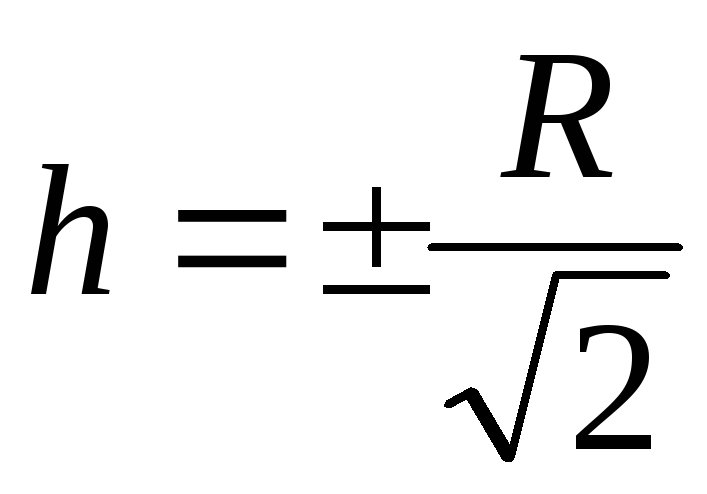
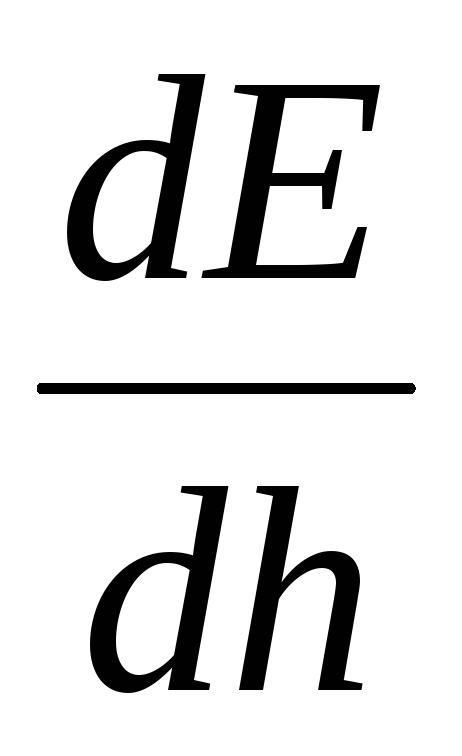
точке напряженность поля максимальна,
а на графике
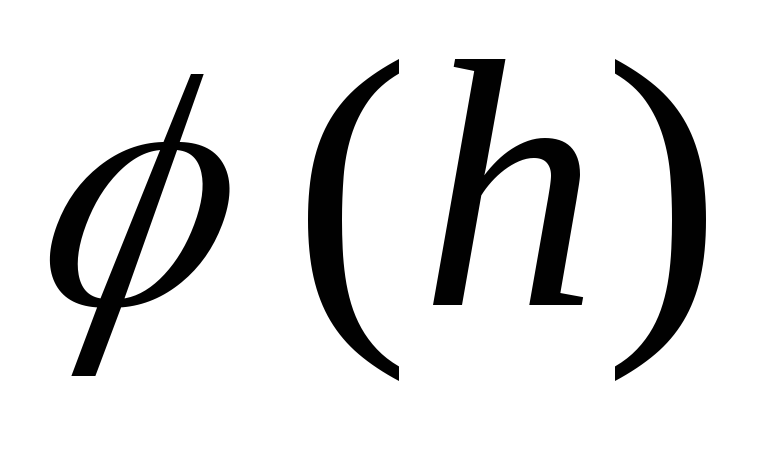
расположен в 1-й и 3-й четвертях, т.е.
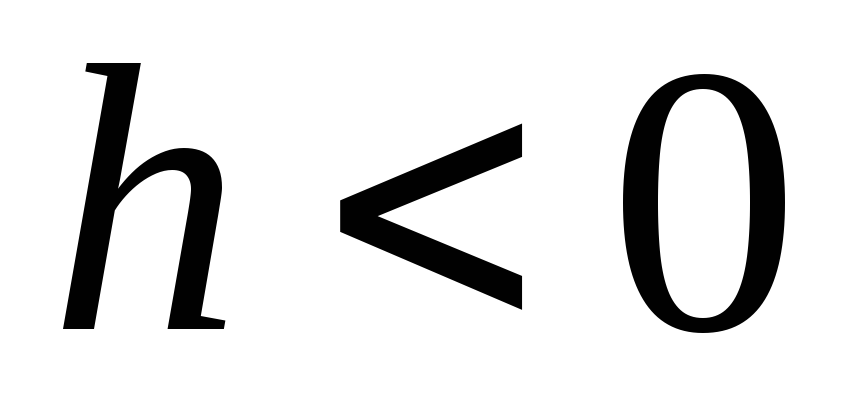
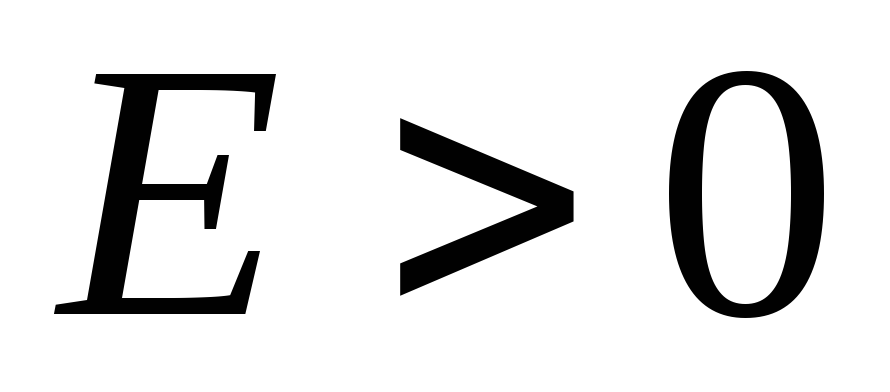
Это значит, что при переходе через центр
кольца (
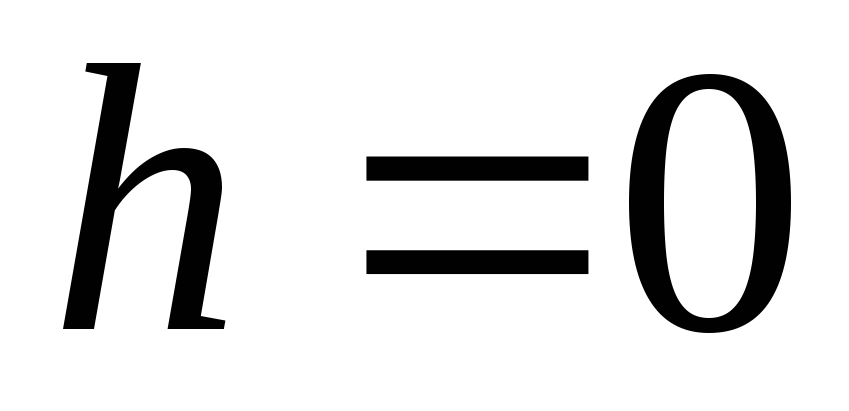
вектор
График
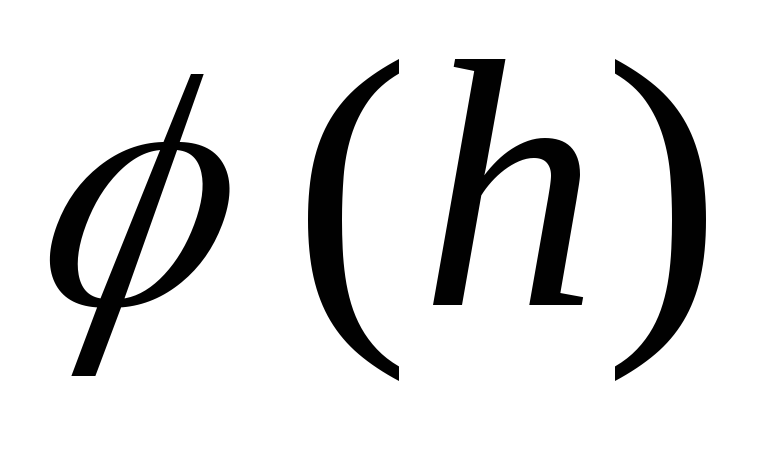
обе стороны от кольца в точках, лежащих
на его оси, потенциал положителен.
На примере решения
этой задачи можно убедиться, что при
изменении начала отсчета потенциала
разность потенциалов между двумя любыми
точками не меняется. Не меняется и весь
характер зависимости потенциала от
расстояния. Например, если выбрать
начало отсчета в центре кольца, т.е. если
предположить, что
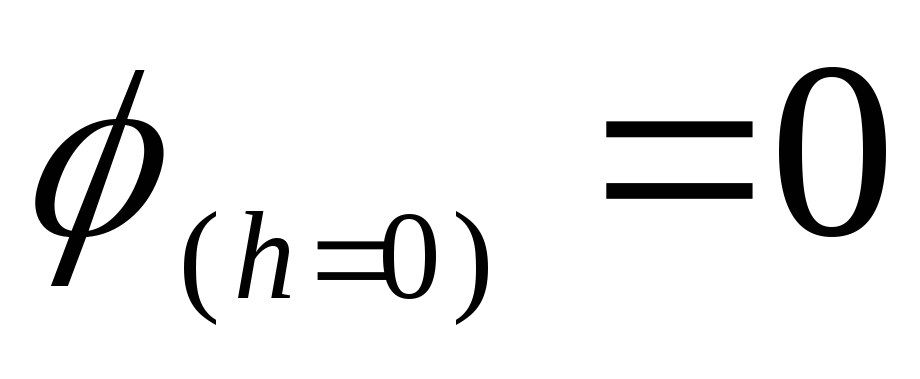
то потенциал любой точки, лежащий на
оси кольца, равен
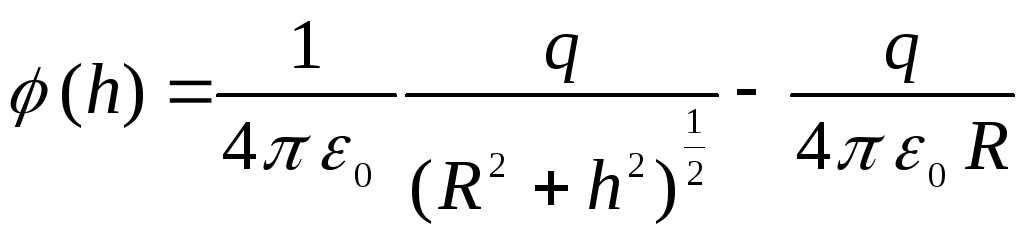
Эта формула может
быть легко получена на основании принципа
суперпозиции.
Если начало отсчета
потенциала выбрано в центре кольца, то
потенциал поля, созданного элементарным
зарядом
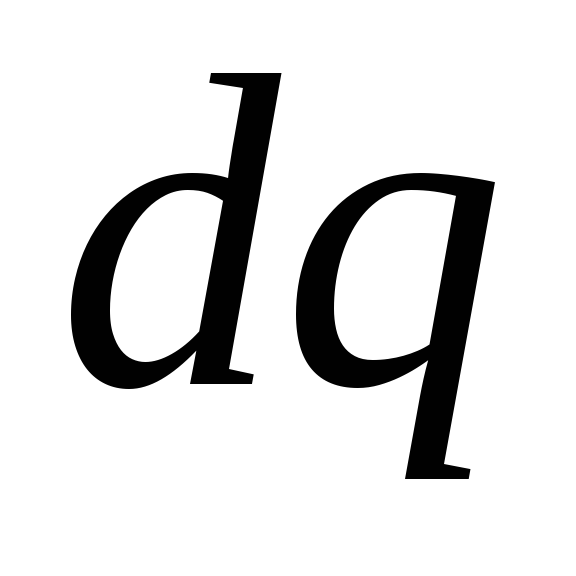
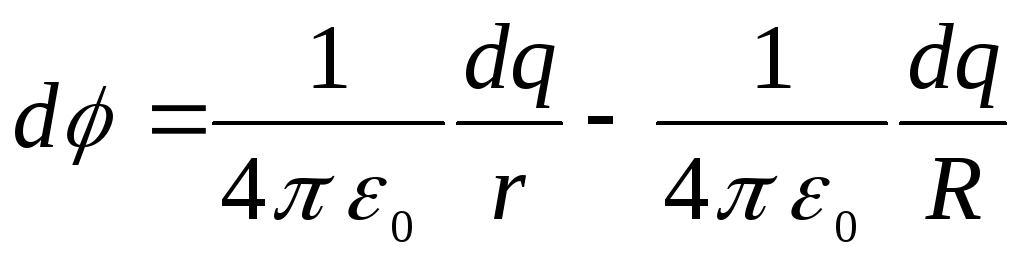
Интегрируя это
выражение по всему кольцу, получим
формулу
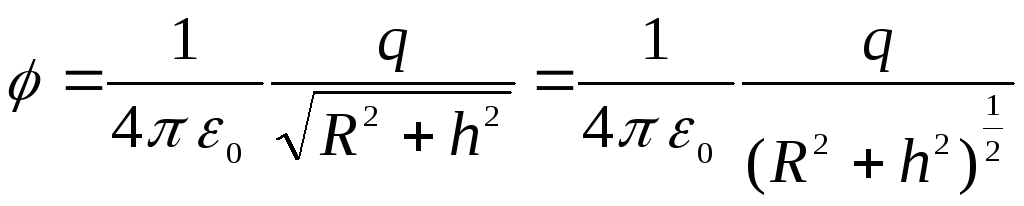
График зависимости
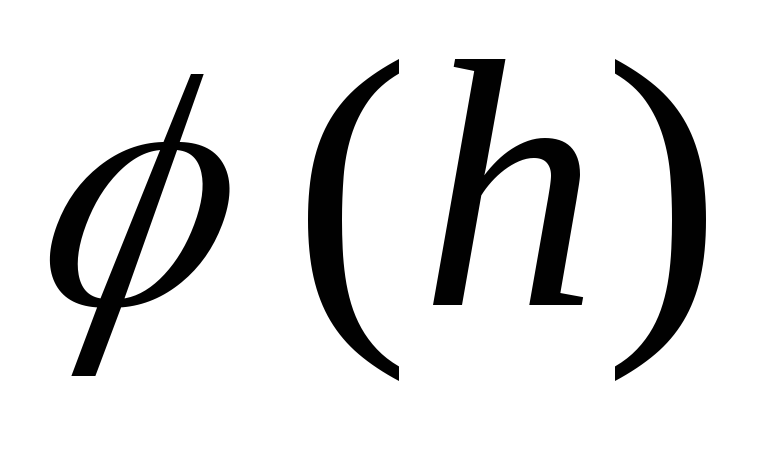
не меняя своего характера, смещается
вниз параллельно самому себе на величину
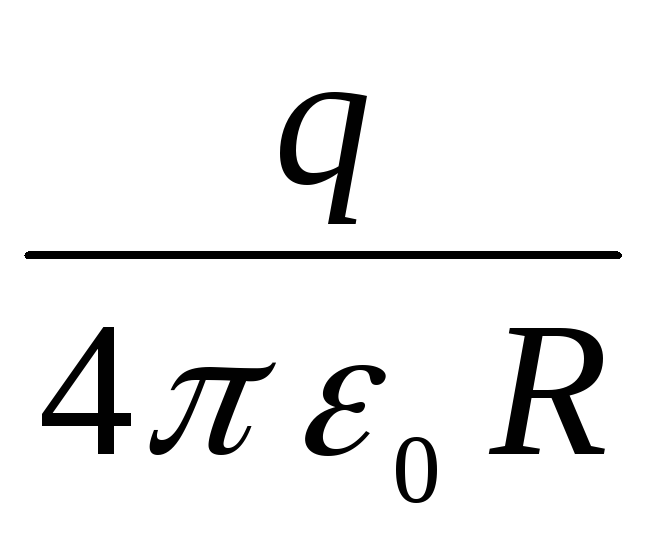
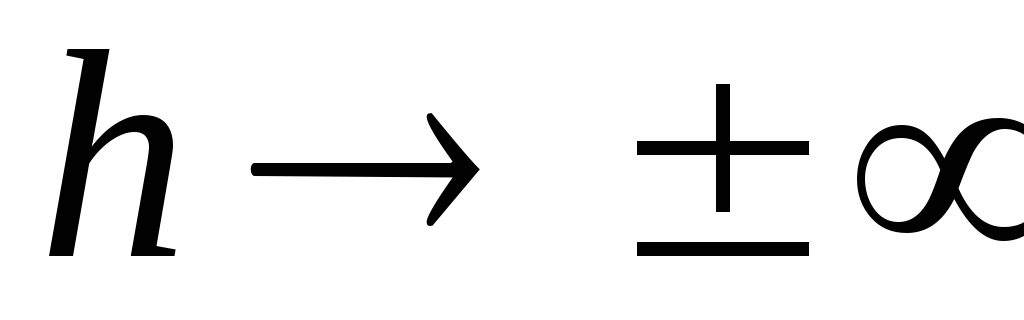
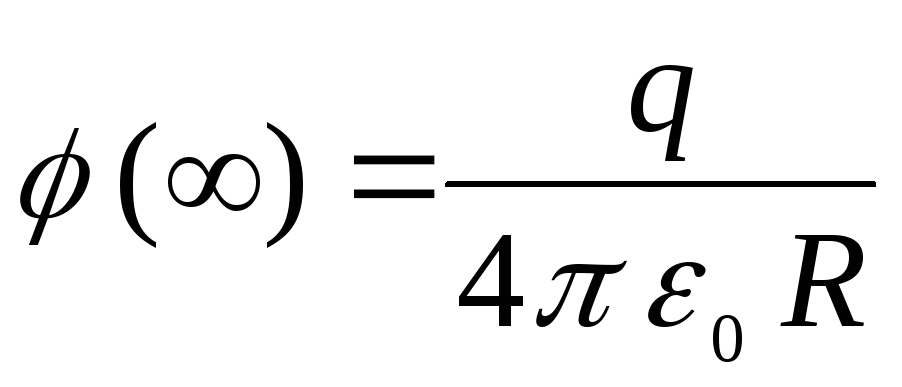
7.7. Потенциал
численно равен работе, совершаемой
силами электрического поля при перемещении
единичного положительного заряда из
данной точки поля (в нашем случае, с
поверхности внутренней сферы) в
бесконечность, т.е.
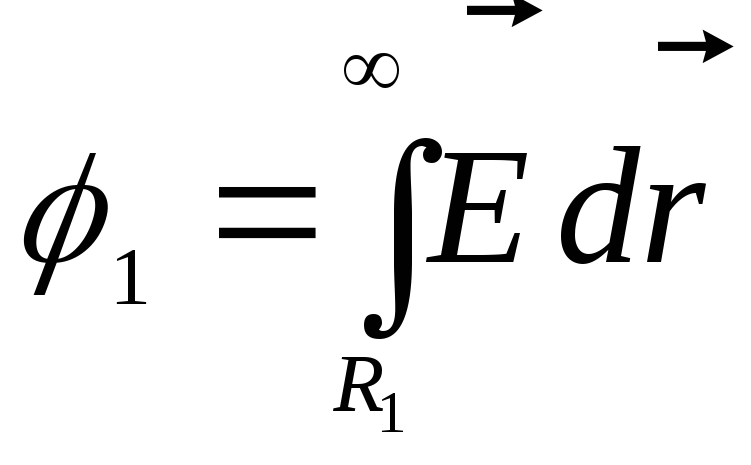
где

во всех точках интервала интегрирования.
В интервале
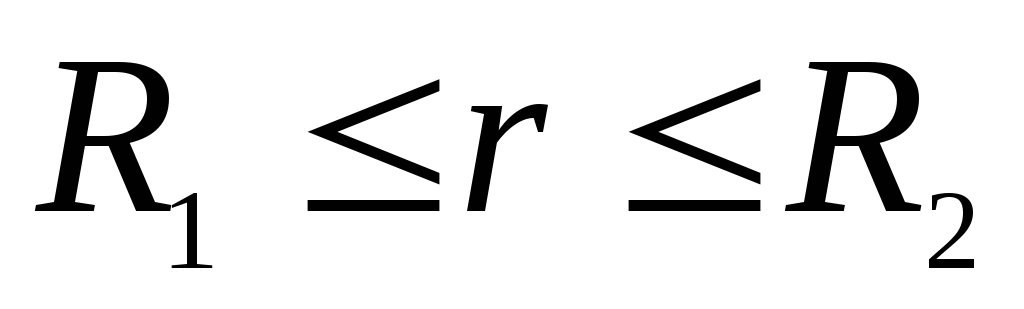
сферы. Вектор
независимо от величины и знака заряда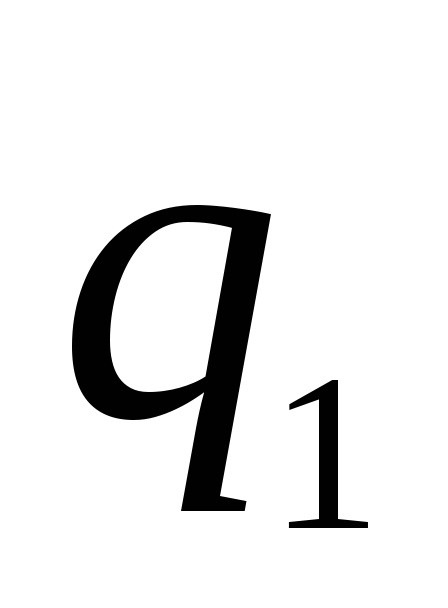
направлен по радиусу от центра. При
перемещении единичного положительного
заряда от
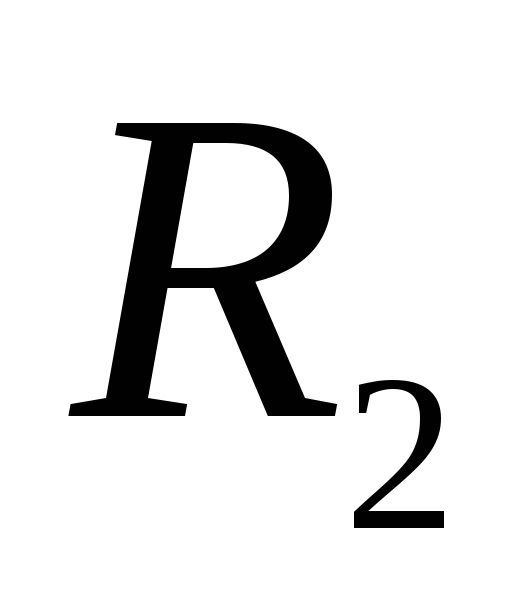
работу. При
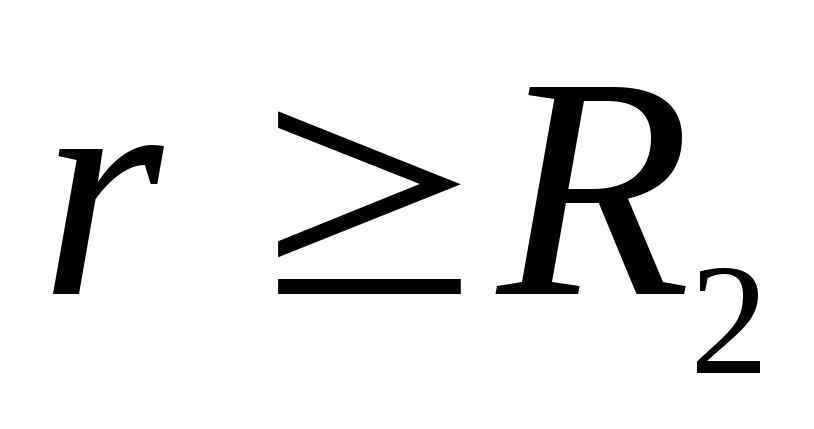
т.е. за пределами второй сферы работа
сил поля отрицательна и, следовательно,
вектор
точках
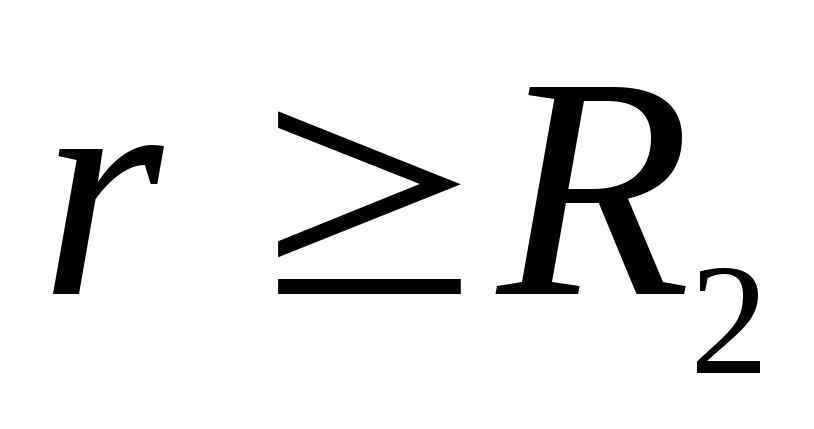
зарядов на обеих сферах. Заряд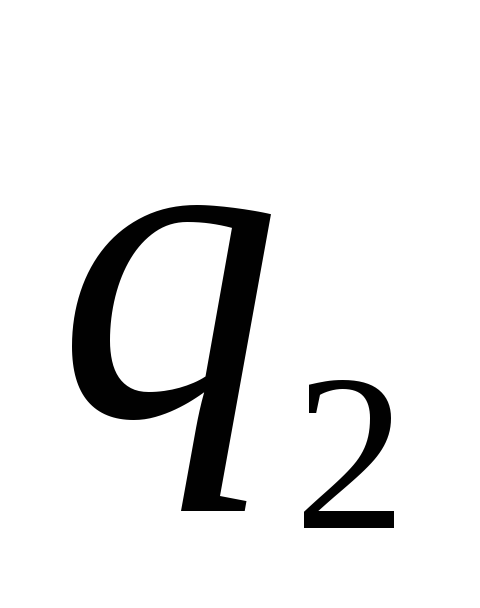
должен быть больше заряда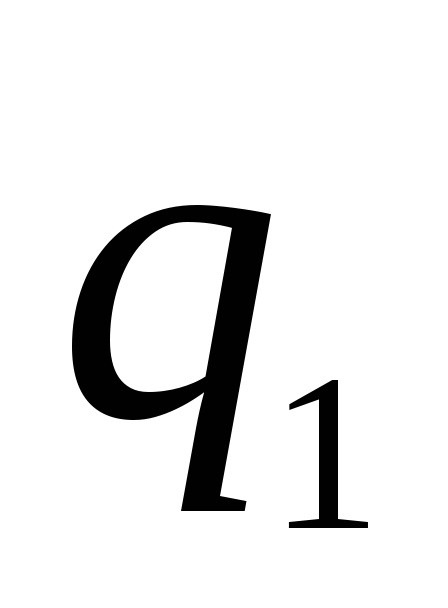
Так как векторы
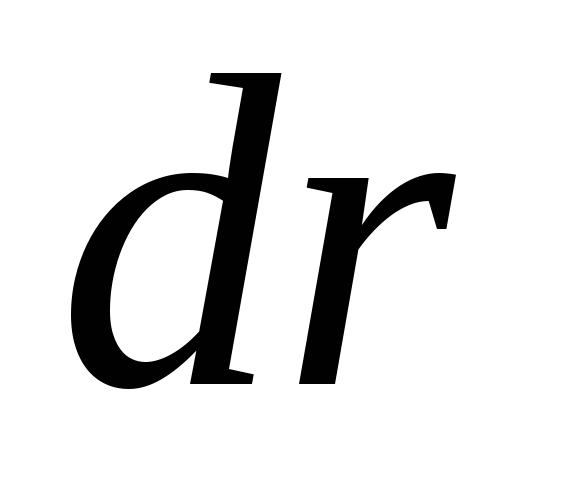
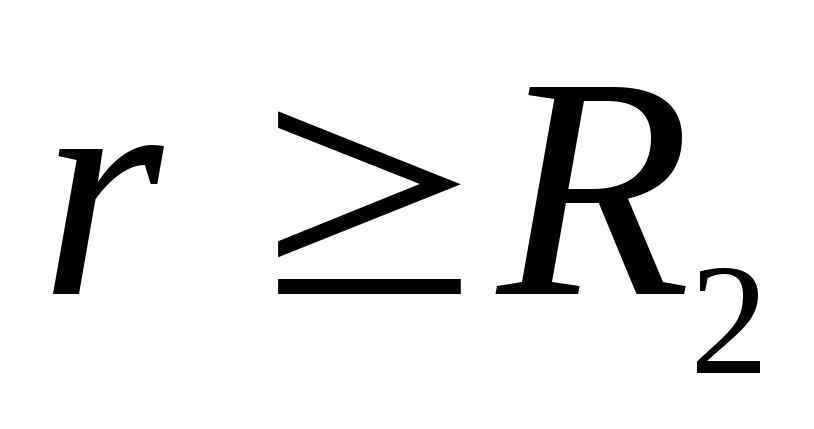
то скалярное произведение
можно заменить произведением
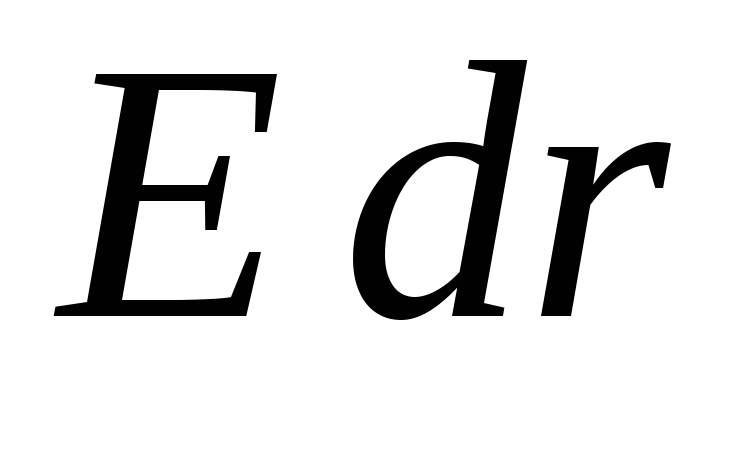
противоположно, напряженность поля
должна считаться отрицательной). В
формуле
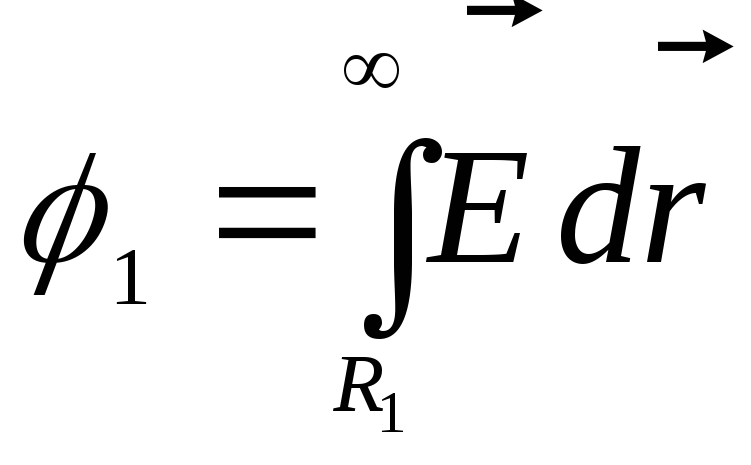
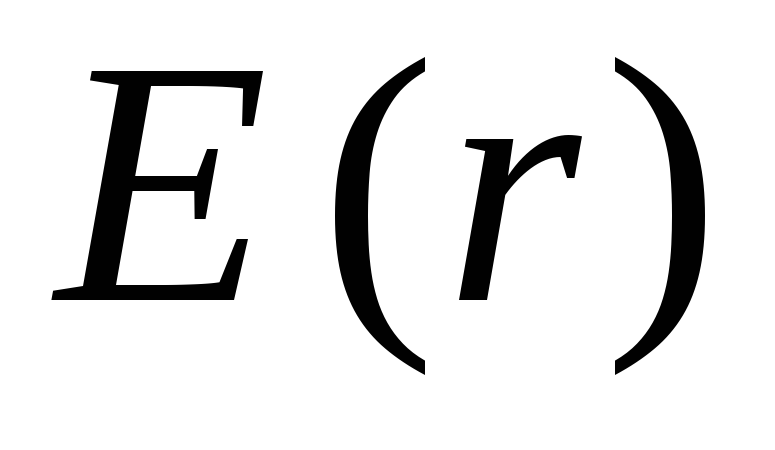
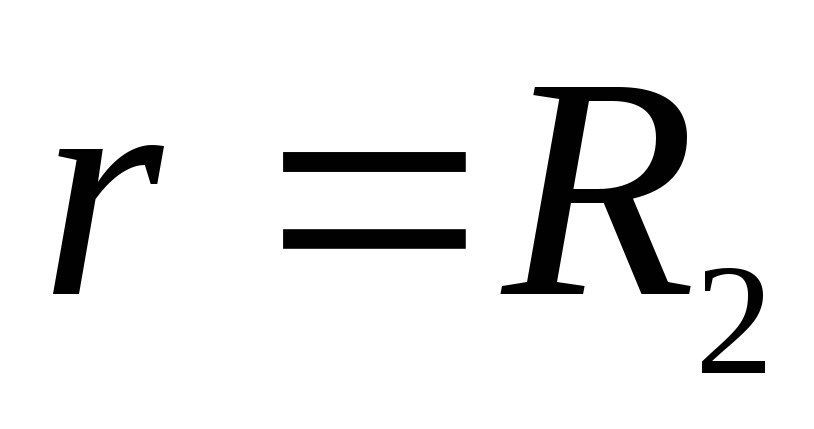
Поэтому интеграл нужно разбить на два
интеграла в пределах от
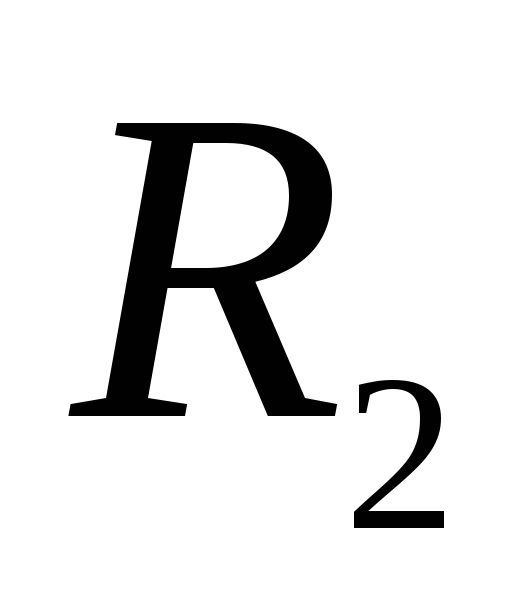
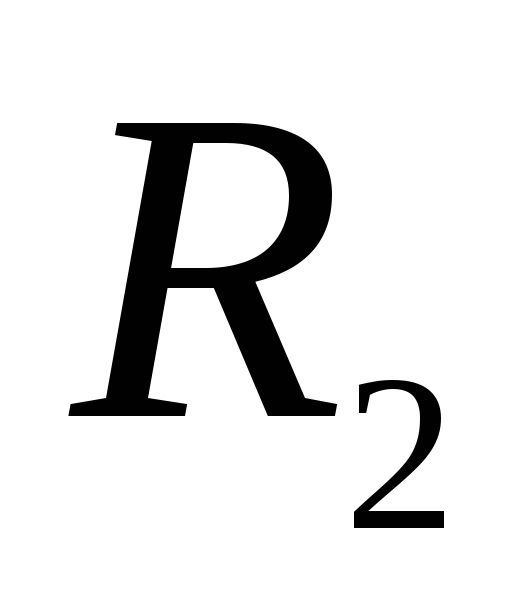

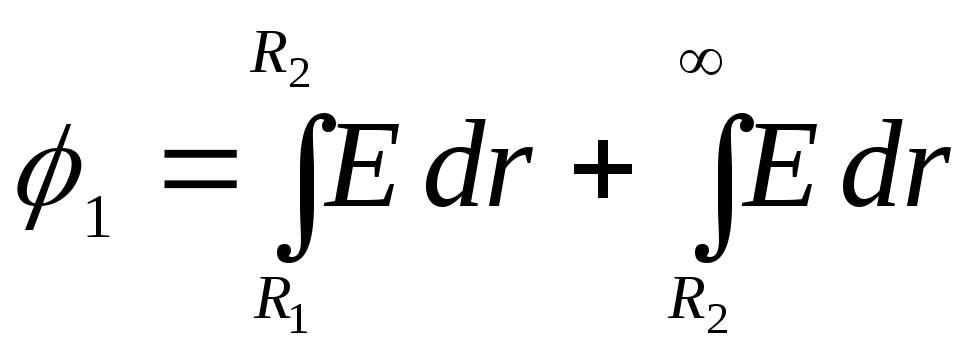
При
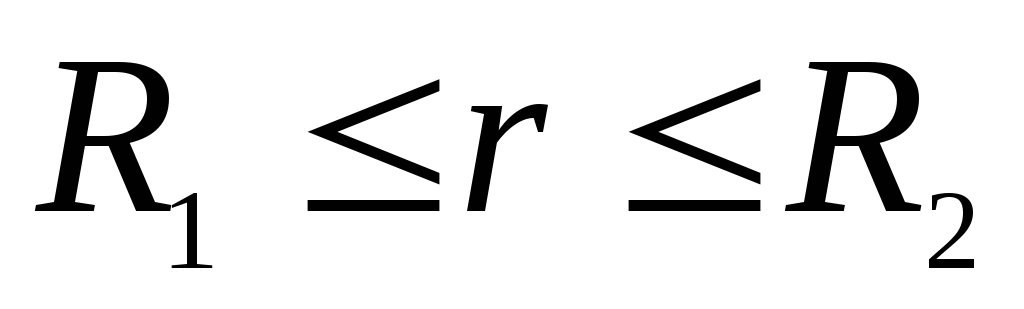
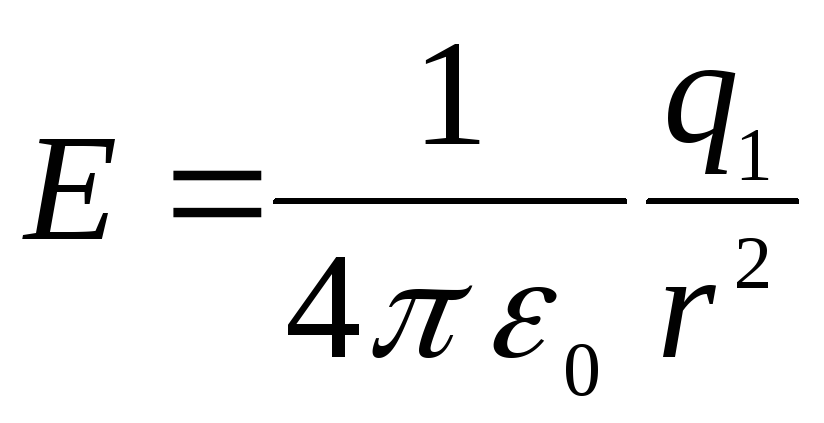
а при
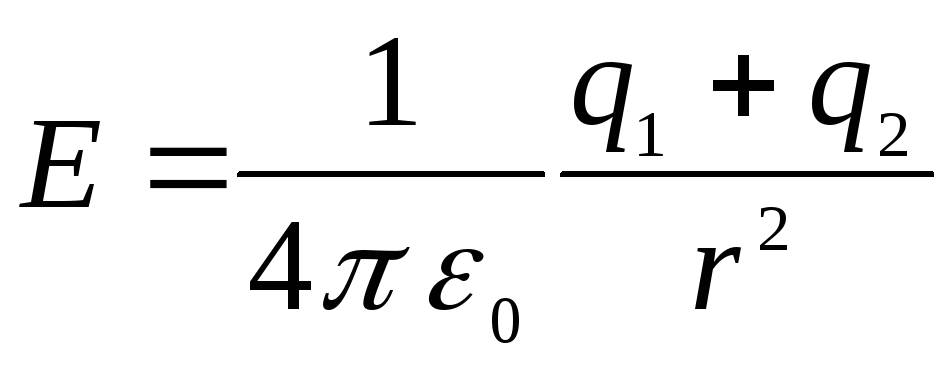
Подставив эти
выражения в соответствующие интегралы,
получим
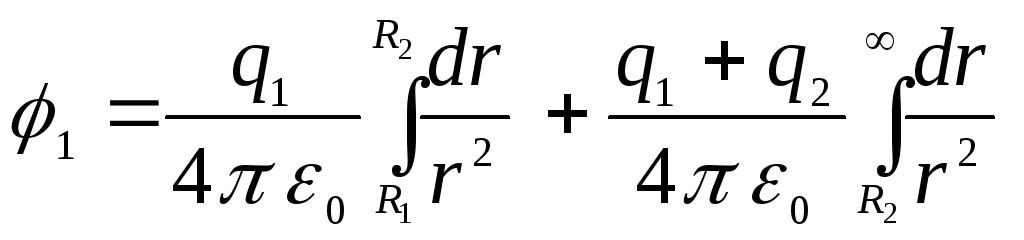
Интегрируя и
приводя подобные члены, получим
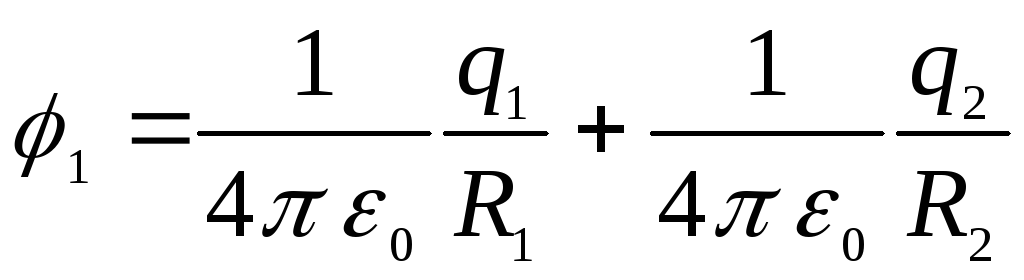
Так как по условию
задачи
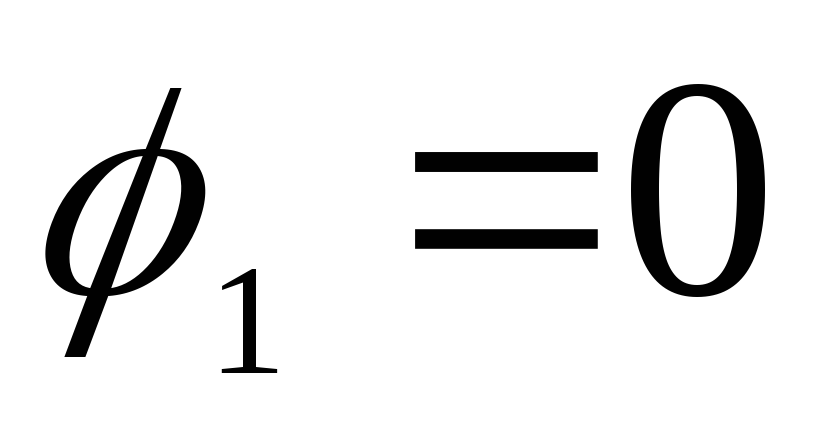
то
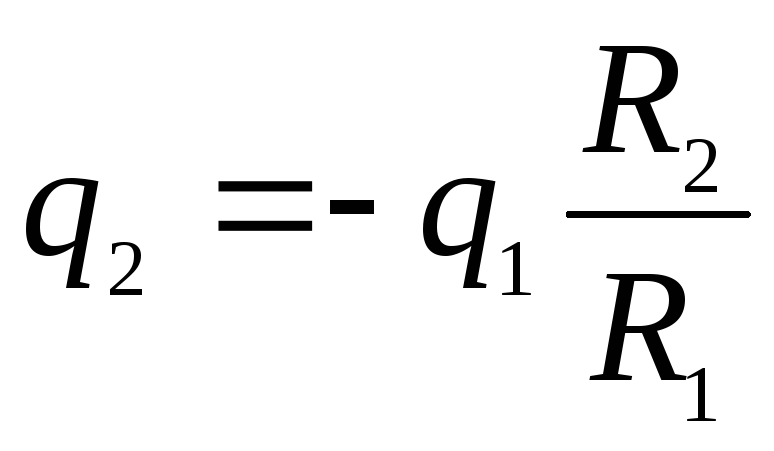
График зависимости
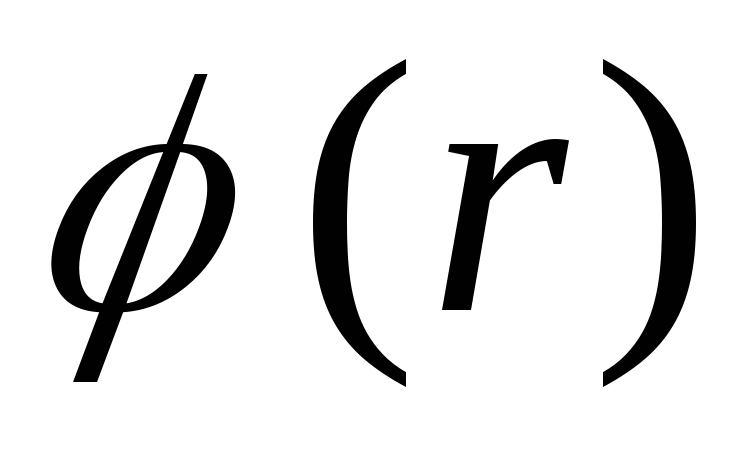
Проанализируем
полученный график.
Согласно условию
задачи, при заданном значении
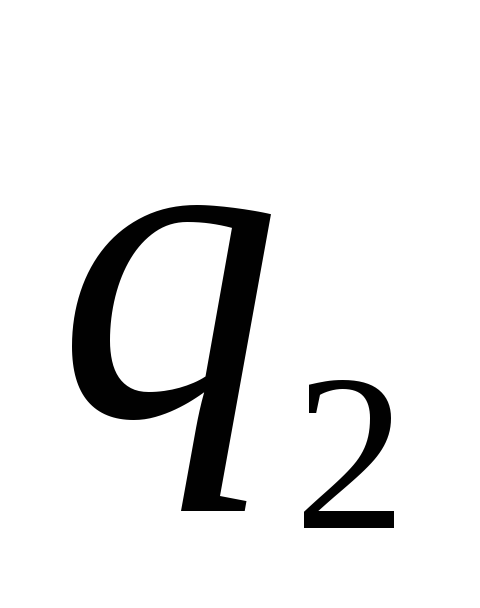
сферы
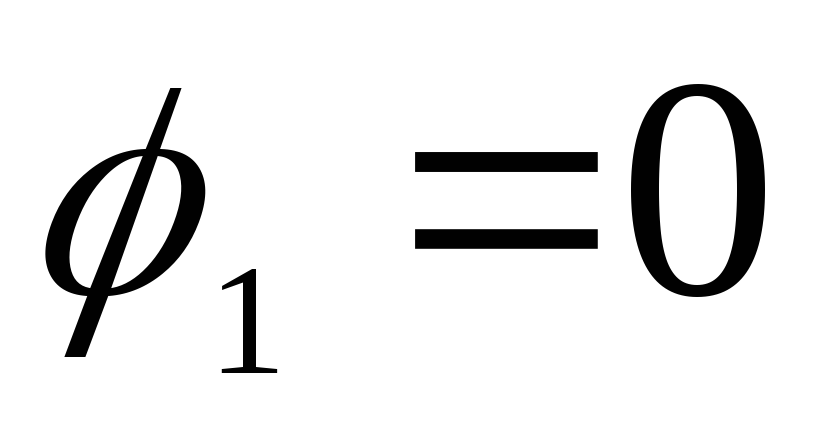
При
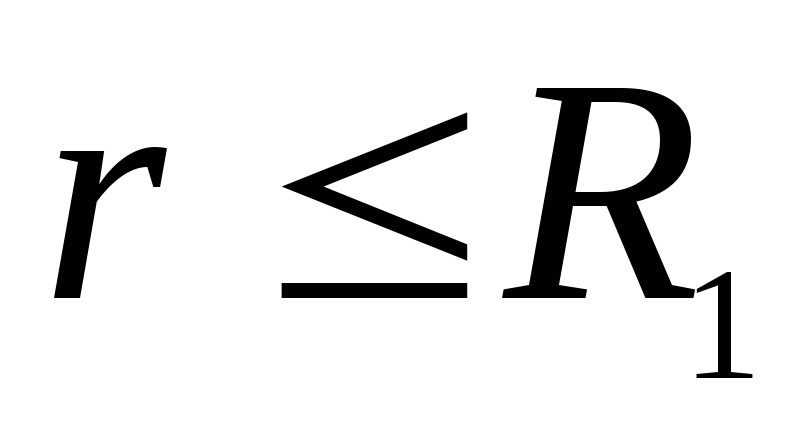
на поверхности, следовательно, графиком
на участке от
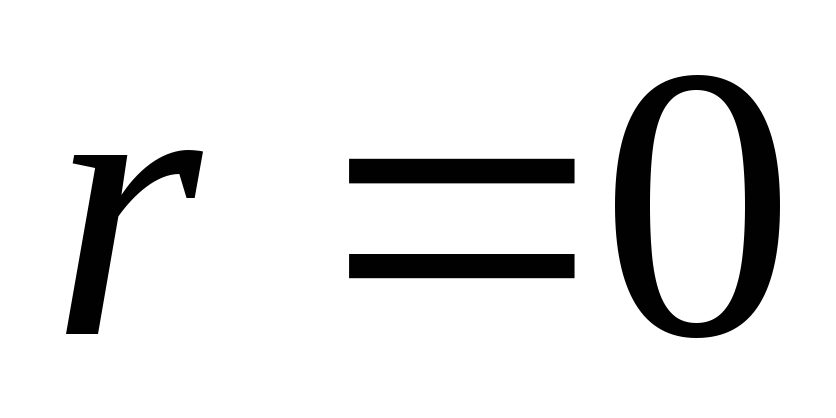
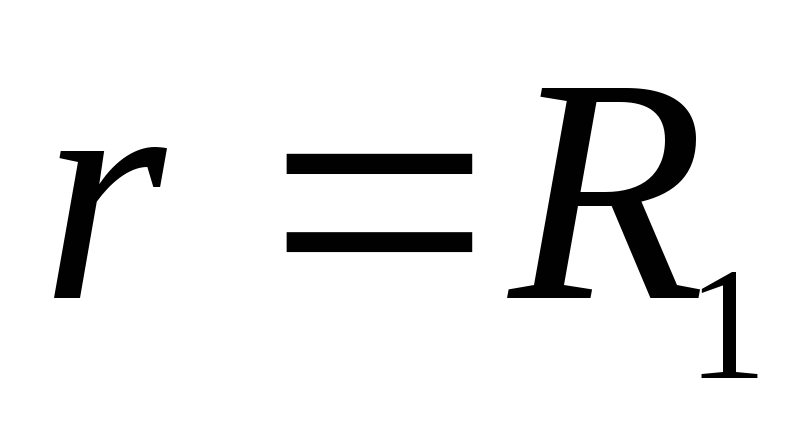
осью абсцисс. При
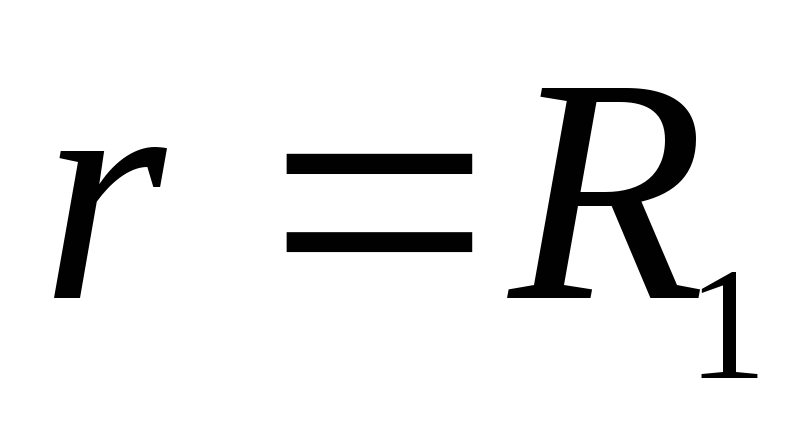

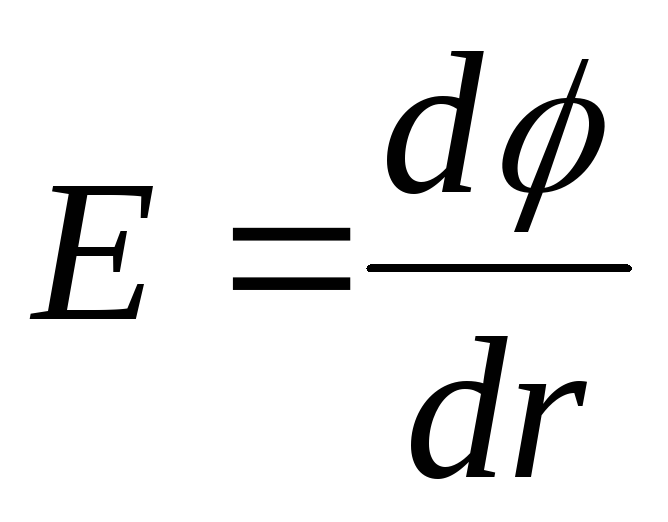
то на графике точка
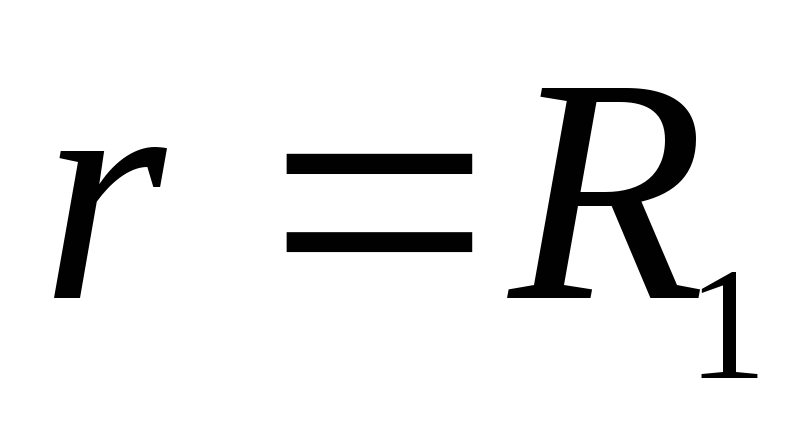
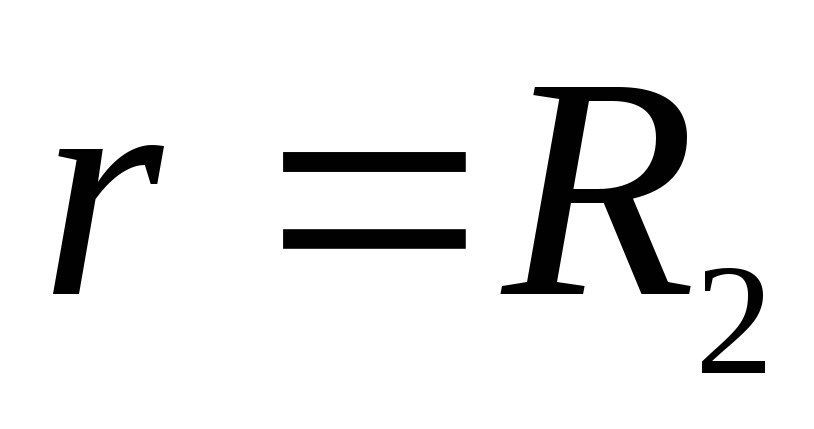
представляют особые точки. На участке
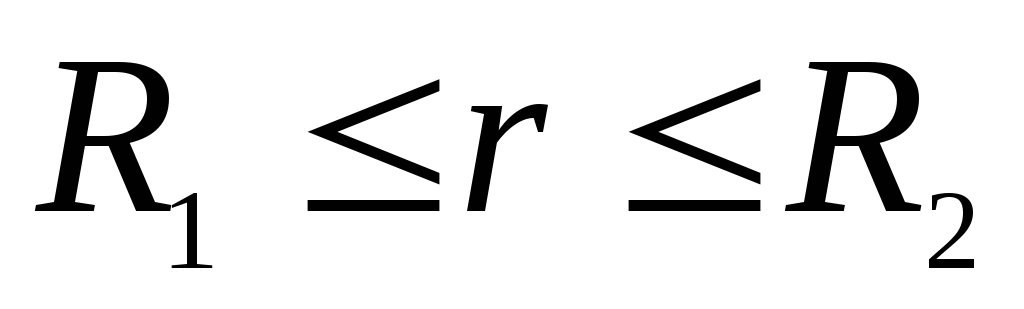

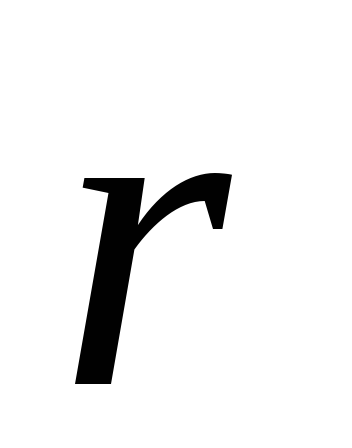
Поэтому, по мере удаления от поверхности
внутренней сферы потенциал убывает до
некоторого значения
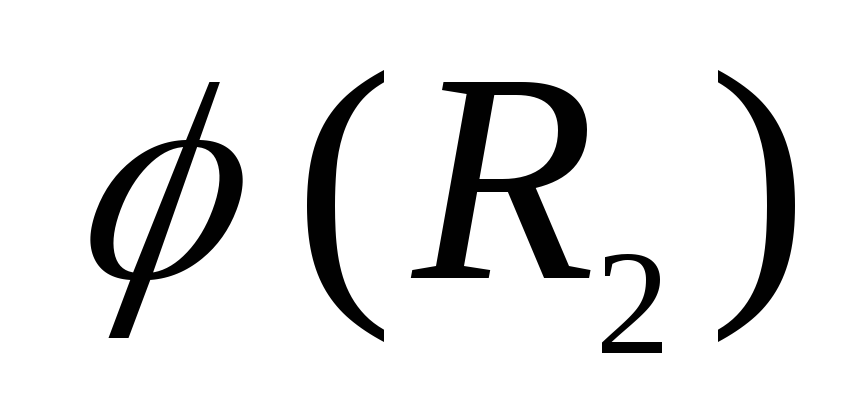
На участке
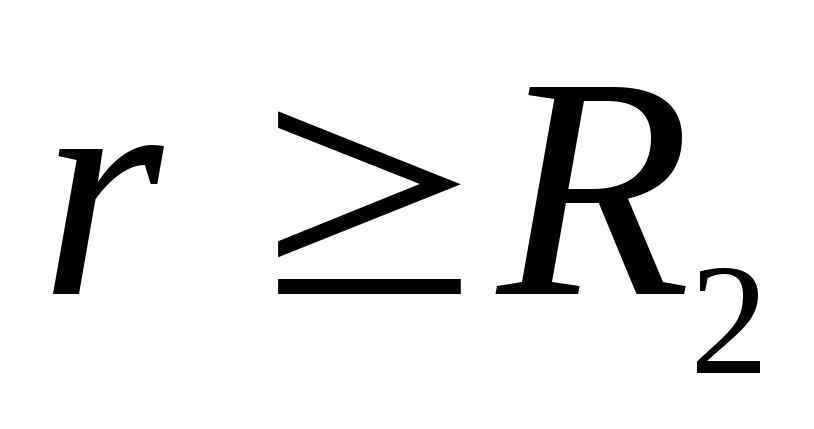

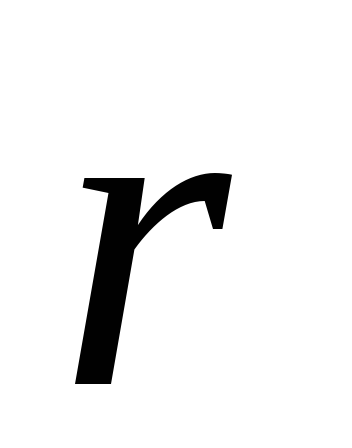
поэтому, по мере удаления от поверхности
внешней сферы потенциал возрастает, и
при
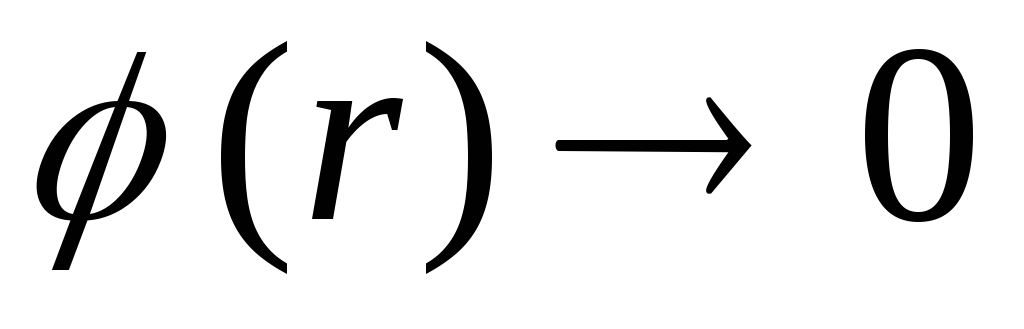
Несмотря на то, что в точках