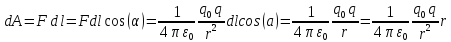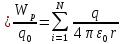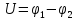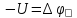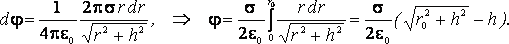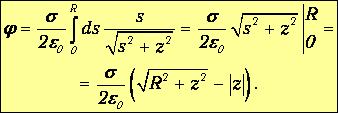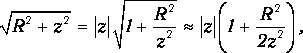Как найти потенциал полусферы - Исправление недочетов и поиск решений вместе с Examum.ru

2018-05-14

Найти потенциал и напряженность электрического поля в центре полусферы радиуса $R$, заряженной равномерно с поверхностной плотностью $sigma$.

Решение:

Рассмотрим кольцевой элемент, как показано на рисунке. Тогда заряд, элемента, $dq = (2 pi R sin theta) R d theta sigma$,

Следовательно, потенциал, обусловленный рассматриваемым элементом в центре полушария,

$d phi = frac{1}{4 pi epsilon_{0} } frac{dq}{R} = frac{2 pi sigma R sin theta d theta }{4 pi epsilon_{0} } = frac{ sigma R}{2 epsilon_{0} } sin theta d theta$

Таким образом, потенциал от всего полушария

$phi = frac{R sigma}{2 epsilon_{0} } int_{0}^{ pi /2} sin theta d theta = frac{ sigma R}{2 epsilon_{0} }$

Тогда из симметрии задачи электрическое поле полусферы направлено к отрицательной оси у. Получаем

$dE_{y} = frac{1}{4 pi epsilon_{0} } frac{dq cos theta}{R^{2} } = frac{ sigma}{2 epsilon_{0} } sin theta cos theta d theta$

Таким образом, $E = E_{y}^{ prime} = frac{ sigma}{2 epsilon_{0} } int_{0}^{ pi /2} sin theta cos theta d theta = frac{ sigma }{4 epsilon_{0} } int_{0}^{ pi /2} sin 2 theta d theta = frac{ sigma}{4 epsilon_{0} }$ вдоль YO

Источник

Потенциал электростатического поля. Циркуляция напряженности электрического поля. Работа перемещения заряда в электрическом поле. Энергия системы электрических зарядов.

На
заряд, помещенный в эл. поле действует
сила, следовательно, его перемещение
сопровождается работой:

Если
работа совершается силами поля, то dA>0

Если
внешними силами, то dA<0

Если
перемещение заряда конечно

Если
работа совершается внешними силами

Эл.
поле потенциально. Работа по перемещению
заряда не зависит от пути, по которому
он перемещается, а определяется только
конечным и начальным значениями.

Тело,
находящееся в потенциальном поле сил
обладает потенциальной энергией,
расходуемой на совершение работы силами

Cледовательно,
потенциальная энергия в данной точке
поля зависит от величины пробного
заряда, переносимого в данном поле.

Отношение W_pк величине
зависит
только от его местоположения, значит
данное отношение может служить
энергетической характеристикой э л.
поля.

Из
равенства

следует,

поля – физическая величина, равная
отношению работы, которую совершают
силы поля над единичным положительным
зарядом к величине этого заряда при
удалении его из этой точки на бесконечность.

Потенциал-
величина скалярная.

Потенциал
суммарного эл. поля есть алгебраическая
сумма потенциалов, всех налагаемых
полей.

Циркуляцией вектора
напряженности называется работа, которую
совершают электрические силы при
перемещении единичного положительного
заряда по замкнутому пути LТак
как работа сил электростатического
поля по замкнутому контуру равна нулю
(работа сил потенциального поля),
следовательно циркуляция напряженности
электростатического поля по замкнутому
контуру равна нулю.

Примеры расчета потенциала электрического поля распределенных зарядов.

Потенциал
электрического поля на оси равномерно
заряженного кольца

Чтобы
найти потенциал в точке А,
надо применить принцип суперпозиции
полей. Разобьем диск на элементарные
кольца толщиной dr.
Площадь кольца радиуса r равна 2rdr,
а заряд кольца — 2rdr.
Потенциал поля кольца равен сумме
потенциалов, созданных всеми его
точечными элементами. Так как последние
равноудалены от точки А,
то, заменив заряд кольца точечным зарядом
той же величины, удаленным на расстояние
от точки А,
найдем потенциал кольца:

Потенциал
электрического поля на оси равномерно
заряженного диска

Найдем
для примера потенциал электрического
поля, создаваемого на оси диска радиусом
R, равномерно заряженного с поверхностной
плотностью заряда s
(рис. 1.28).

Рис.
1.28. Вычисление потенциала на оси
заряженного диска

Выделим
на диске кольцо радиусом s и шириной ds
(заштриховано на рис.). Площадь кольца
равна 2psds
и потому на нем сосредоточен заряд

Поскольку
все элементы кольца находятся на
одинаковом расстоянии

от
точки наблюдения А, то потенциал dj,
создаваемый кольцом в точке А, дается
все той же формулой (10.30):

Полный
же потенциал
поля,
создаваемый
всем диском
в точке A, равен сумме потенциалов dj
от всех возможных колец с радиусами s,
где 0<s<R

(1.44)

В
пределе больших расстояний от центра
диска z>>R имеем разложение

и
формула для потенциала переходит в

где
мы ввели полный заряд диска

Потенциал
электрического поля равномерно
заряженной полусферы

Найдем
потенциал равномерно заряженной сферы.
Чтобы найти потенциал полусферы,
требуется радиус, используемый в
формулах, делить на 2.

Пусть
дан шар радиусом R и ему сообщен заряд
Q, равномерно распределенный по объему.
Вследствие симметрии поле направлено
по радиусам шара. Вне шара (r>R) оно
совпадает с полем точечного заряда.
Проведем мысленно сферу радиусом r<R
внутри шара. По теореме Остроградского-Гаусса
напряженность поля на поверхности сферы
дается выражением

где
q(r) —
заряд внутри сферы. Объемная плотность
r
заряда равна отношению полного заряда
Q к объему шара

Заряд
q(r) находим как произведение плотности
заряда на объем, ограниченный воображаемой
сферой

Подставляя
q(r) в выражение E(r), находим поле на
расстоянии r<R от центра шара. В итоге
получаем следующее выражение для
напряженности
поля равномерно заряженного шара

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

2.32. Заземленная проводящая плоскость имеет выступ в форме полусферы радиуса $a$. Центр полусферы лежит на плоскости. На оси симметрии системы на расстоянии $b>a$ от плоскости находится точечный заряд $q$. Найти потенциал электрического поля, а также заряд $Q,$ индуцированный на выступе?

Для того чтобы вся сфера была эквипотенциальной с $varphi =0$ поместим заряд $q’=-qfrac ab$ как в задаче 2.27 в точку $x=b’=frac{a^2}{b}.$ Теперь, что бы добиться эквипотенциальности плоской границы, как в задаче 2.22, поместим заряды $-q$ и $-q’$ в точки $x=-b$ и $x=-b’$. Теперь поверхность плоскости с выступом у нас будет иметь потенциал $varphi =0$, тогда приходим к тому, что в полупространстве потенциал описывается решением уравнения $Delta varphi = -4pi qdelta(vec r — vec b)$, где $vec b$ — вектор проведённый из начала координат к точке с зарядом $q$, с нулевым граничным условием на плоскости с выступом. В силу единственности решения, такое решение можно получить добавив три виртуальных заряда в соответствующие точки, тогда
$$varphi = frac q{r_1} — frac q{r_2} + frac{q’}{r_3} — frac{q’}{r_4},$$
где
$r_i$ показаны на рисунке.

Расписав расстояния $r_i$ через расстояние $r$ и угол $theta :$
$$
r_1=sqrt{r^{2}+b^{2}-2rbcdotcos(theta)}, hspace{7pt} r_2=sqrt{r^{2}+b^{2}+2rbcdotcos(theta)},
$$
$$
r_3=sqrt{r^{2}+(frac{a^{2}}{b})^{2}-2rfrac{a^{2}}{b}cdotcos(theta)}, hspace{7pt}
r_4=sqrt{r^{2}+(frac{a^{2}}{b})^{2}+2rfrac{a^{2}}{b}cdotcos(theta)}
$$
и взяв производную по $r$ — найдём нормальную составляющую электрического поля и поверхностную плотность зарядов:
$$
sigma=qfrac{b^{2}-a^{2}}{4pi a}left(frac{1}{left(b^{2}+a^{2}+2abcdotcos(theta)right)^{frac{3}{2}}}-frac{1}{left(a^{2}+b^{2}-2abcdotcos(theta)right)^{frac{3}{2}}}right)
$$
Что бы получить заряд осталось проинтегрировать
$$
Q=intop_{0}^{frac{pi}{2}}sigma,dS=intop_{0}^{frac{pi}{2}}sigma2pi a^{2}sintheta,dtheta .
$$
Подставив полученную поверхностную плотность зарядов, проинтегрируем и придём к выражению:
$$
Q=-qleft(1-frac{b^{2}-a^{2}}{bsqrt{b^{2}+a^{2}}}right).
$$

Источник

Задача.
Одна половина сферы радиуса $R$ покрыта зарядом с плотностью , другая — зарядом с плотностью . Необходимо найти потенциал системы зарядов на большом расстоянии от центра сферы .

Пытался начать с рассмотрения одной полусферы и найти напряжённость в её центре:
(Данный вопрос обсуждался, в частности, здесь: http://dxdy.ru/topic15843.html)
Далее перейти к заряду ( $E=frac{q}{R^2}$ ):
Тогда потенциал: $phi_1,=,frac{q}{r},=,frac{sigmapi R^2}{r}$
После чего нужно учесть, что мы работаем не с симметричным объектом и потенциал будет меняться в зависимости от угла. Как точно учесть эту зависимость не знаю, но предполагаю, что через , если считать, что нулевой угол совпадает с плоскостью среза полусферы:
$phi_2,=,phi_1cosalpha,=,frac{q}{r},=,frac{sigmapi R^2}{r}sinalpha$
Тогда для второй полусферы в потенциале ничего менять не надо, потому что синус даст верный знак, который должен появиться из-за противоположного заряда.
И значит в итоге нужно взять сумму потенциалов в точке:

Под вопросом 2 момента:
1) переход от полусферы к рассмотрению заряда в центре (всё же это не целая сфера);
2) учёт зависимости значения потенциала от угла.

В чём не верны рассуждения?

Источник

Найти потенциал поля в центре окружности

2018-05-14
Найти потенциал и напряженность электрического поля в центре полусферы радиуса $R$, заряженной равномерно с поверхностной плотностью $sigma$.

Рассмотрим кольцевой элемент, как показано на рисунке. Тогда заряд, элемента, $dq = (2 pi R sin theta) R d theta sigma$,

Следовательно, потенциал, обусловленный рассматриваемым элементом в центре полушария,

Таким образом, потенциал от всего полушария

Тогда из симметрии задачи электрическое поле полусферы направлено к отрицательной оси у. Получаем

Таким образом, $E = E_^ < prime>= frac< sigma> <2 epsilon_<0>> int_<0>^ < pi /2>sin theta cos theta d theta = frac< sigma > <4 epsilon_<0>> int_<0>^ < pi /2>sin 2 theta d theta = frac< sigma> <4 epsilon_<0>>$ вдоль YO

Задача 2: потенциал электрического поля в центре кольца

По тонкому проволочному кольцу равномерно распределен заряд с линейной плотностью τ = 100 пКл/м. Определить потенциал Φ электрического поля в центре кольца.

Эта задача была размещена посетителями в разделе Решаем вместе 8 октября 2007 года.

Потенциал в центре проволочного кольца определим по принципу суперпозиции, разбив кольцо на элементарные участки с зарядом q_i. Получим формулу (на рисунке слева), в которой:

i — количество разбиений,

потенциал Φ_i, создаваемый в центре кольца элементарным зарядом q_i, равен:

Из формулы линейной плотности заряда кольца

выразим:

Произведем суммирование Φ:

Φ = 1 • q_iN = 1 • q = 2πτR = τ .

4πε_o R 4πε_o R 4πε_oR 2ε_o

Выполнив расчеты, получим: Φ = 5.65 В.

Потенциальность электростатического поля

Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.

Что такое потенциальное поле

Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).

Поле называется потенциальным, если при перемещении по любому замкнутому контуру работа сил поля равняется 0 .

Известно, что сила гравитации F G

1 r 2 , которая убывает обратно пропорционально квадрату расстояния, является потенциальной, при этом ее потенциальность обусловлена именно обратно пропорциональной зависимостью от расстояния. Сила Кулона тоже обратно пропорциональна квадрату расстояния. Напомним закон Кулона F E

1 r 2 . Все математическое описание потенциала создавалось при изучении сил гравитации. Понятие о потенциале появилось в работах Ж. Л. Лагранжа в 1777 году. Определение «потенциал» было введено в науку намного позже Дж. Грином и К. Ф. Гауссом.

На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.

Легко докажем это математически. Циркуляция вектора напряженности поля точечного заряда E i → по любому замкнутому контуру равняется 0 :

Если поле создает N точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:

∮ L E → d s → = ∮ L ∑ i E i → d s → = ∑ i ∮ L E i → d s → = ∑ i 0 = 0 .

Приведенный выше критерий потенциальности поля не дифференциален, поэтому его трудно применять. Нужно проверять равенство 0 работы по замкнутому контуру. А это означает, что необходимо анализировать бесконечное число циклов, что, в конечном итоге, невозможно. Критерий потенциальности применим лишь в случае, когда известна аналитическая формула работы, что не всегда возможно. Поэтому нужно отыскать другой критерий потенциальности поля, который был бы прост в применении. Данным критерием является дифференциальная формулировка. Она определяется при помощи понятия ротор вектора r o t A → .

Что такое ротор. Практические задачи

Ротор − это вектор, проекция которого на направление единичного вектора n → определяется таким образом:

r o t n A → = lim ∆ S → 0 ∮ A → · d s → ∆ S ,

где ∆ S − это площадь, которая лежит в плоскости перпендикулярной к n → , ограниченная малым контуром L , на контуре L − это направление положительного обхода связано с n → правилом правого винта.

Обращаем внимание, что в формуле большой буквой S обозначена площадь, а маленькой буквой s − линейное перемещение.

Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:

r o t A → = ∇ × A → = i → j → k → ∂ ∂ x ∂ ∂ y ∂ ∂ z A x A y A k .

Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:

∫ A L 1 B E → · d s → = ∫ A L 2 B E → · d s → .

где L 1 и L 2 − это различные пути между точками А и В . При замене местами пределов интегрирования получаем:

∫ A L 2 B E → · d s → = — ∫ B L 2 A E → · d s → .

Выражение ∫ A L 1 B E → · d s → = ∫ A L 2 B E → · d s → представим в виде:

∫ A L 1 B E → · d s → = ∫ B L 2 A E → · d s → = ∮ L E → · d s → = 0 .

где L = L 1 + L 2 . Применяем формулу Стокса:

∫ S r o t A → · d S → = ∮ L A → · d s → ,

к уравнению выше, получаем:

∮ L E → · d s → = ∫ S r o t E → · d S → = 0 ,

где S − это поверхность, ограниченная контуром L . Поскольку поверхность произвольная, то интеграл в выражении ∮ L E → · d s → = ∫ S r o t E → · d S → = 0 может равняться 0 , только если равняется 0 подынтегральное выражение, а поскольку d S → ≠ 0 то есть:

Это дифференциальная формулировка потенциальности электростатического поля.

Необходимо найти r o t n υ → для точек оси вращения, если υ → − это вектор скорости точек твердого тела, вращающегося с угловой скоростью ω вокруг оси коллинеарной n →

Решение

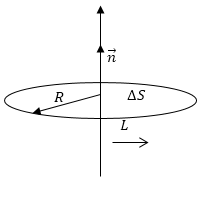
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок 1 ). Известно, что:

υ = ω R , ∆ S = π R 2 .

Обозначим υ d s . d s как скалярное значение элемента окружности. Для этого используем формулу определения ротора, получаем:

r o t n υ → = lim R → 0 ∮ ω R → · d s → π R 2 = lim R → 0 ω R 2 π R π R 2 = 2 ω ,

где ∮ d s = 2 π R − это длина окружности.

Ответ: Ротор линейной скорости точек вращающегося тела равняется r o t n υ → = 2 ω .

Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.

Решение

Поскольку электростатическое поле потенциально, тогда выполняется равенство:

A = ∮ L E → d s → = 0 .

Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.

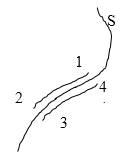
Допустим обратное. Пускай вдоль поверхности S (рисунок 2 ) непрерывности нет. Это означает, что если 1 , 2 и 3 , 4 разделенные поверхностью S , но бесконечно близкие друг к другу точки, тогда работа электростатических сил на пути 1 → 2 отличается на конечную величину от работы тех же сил на пути 3 → 4 . Так как мы считаем, что отрезки 1 → 2 и 3 → 4 бесконечно малы, силы конечны, значит, и работа, которую выполняют электрические силы на заданных отрезках, бесконечно малая величина. Выходит, что работа на пути 1 → 2 → 3 → 4 → 1 не должна равняться 0 . То есть работа сил по перемещению пробного заряда по замкнутому контуру не равняется 0 . Это невозможно, поскольку электростатическое поле потенциально. Мы показали, что тангенциальные составляющие напряженности электростатического поля не непрерывны.

источники:

http://www.afportal.ru/physics/task/electrostatics/field-intensity/2

http://zaochnik.com/spravochnik/fizika/elektricheskoe-pole/potentsialnost-elektrostaticheskogo-polja/

Источник

Примеры расчета потенциала электрического поля распределенных зарядов.

Найти потенциал поля в центре окружности

Задача 2: потенциал электрического поля в центре кольца

Потенциальность электростатического поля

Что такое потенциальное поле

Что такое ротор. Практические задачи