Нахождение потенциала
В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля $bar { a } (mathbf { textit { M } } )$, то $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $, где $M_0 in V$ — фиксированная точка. Обычно, если в точке $mathbf { textit { O } } (0,0,0)$ поле не имеет особенностей, то в качестве точки $M_0 (x_0 ,y_0 ,z_0 )$ берётся именно эта точка, если в этой точке поле не определено, берётся другая точка.
Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим $varphi (M)=intlimits_ { x_0 } ^x { P(x,y_0 ,z_0 )dx } +intlimits_ { y_0 } ^y { Q(x,y,z_0 )dy } +intlimits_ { z_0 } ^z { R(x,y,z)dz } $.
Пример 1
Доказать, что поле $bar { a } (x,y,z)=frac { ycos (xy) } { z } bar { i } +frac { xcos (xy) } { z } bar { j } -frac { sin (xy) } { z^2 } bar { k } $ потенциально и найти потенциал этого поля.
Решение
Мы будем доказывать, что это поле потенциально в любой односвязной области $mathbf { textit { V } } $, не содержащей точку $mathbf { textit { O } } (0,0,0)$. Условие безвихревости поля $bar { a } $:
$rotbar { a } (M)=left| { begin{array} { l } ,bar { i } ,,,,bar { j } ,,,bar { k } \ frac { partial } { partial x } ,,frac { partial } { partial y } ,,frac { partial } { partial z } \ ,P,,Q,,,R \ end{array} }right|=left( { frac { partial R } { partial y } -frac { partial Q } { partial z } }right)bar { i } +left( { frac { partial P } { partial z } -frac { partial R } { partial x } }right)bar { j } +left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)bar { k } =0$ в координатной форме сводится к равенствам $frac { partial R } { partial y } =frac { partial Q } { partial z } , frac { partial P } { partial z } =frac { partial R } { partial x } , frac { partial Q } { partial x } =frac { partial P } { partial y } $.
В нашем поле $P(x,y,z)=frac { ycos (xy) } { z } , Q(x,y,z)=frac { xcos (xy) } { z } ,R(x,y,z)=-frac { sin (xy) } { z^2 } $. Находим производные:
$frac { partial R } { partial y } =-frac { xcos (xy) } { z^2 } $,
$frac { partial Q } { partial z } =-frac { xcos (xy) } { z^2 } =frac { partial R } { partial y } $,
$frac { partial P } { partial z } =-frac { ycos (xy) } { z^2 } $,
$frac { partial R } { partial x } =-frac { ycos (xy) } { z^2 } =frac { partial P } { partial z } $,
$frac { partial Q } { partial x } =frac { cos (xy)-xysin (xy) } { z } $,
$frac { partial P } { partial y } =frac { cos (xy)-xysin (xy) } { z } =frac { partial Q } { partial x } $ Потенциальность поля доказана.
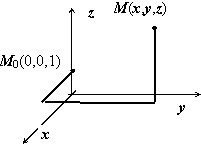
Ищем потенциал. Интеграл $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $ вычисляем по изображённому на рисунке пути, отправляясь от точки $mathbf { textit { M } } _ { 0 } $(0,0,1). $varphi (x,y,z)=intlimits_0^x { frac { 0cdot cos (xcdot 0) } { 1 } dx } +intlimits_0^y { frac { xcdot cos (xy) } { 1 } dy } -intlimits_1^z { frac { sin (xy) } { z^2 } dz } = =left. { sin (xy) }right|_0^y +left. { frac { sin (xy) } { z } }right|_1^z =sin (xy)+left[ { frac { sin (xy) } { z } -sin (xy) }right]=frac { sin (xy) } { z } $.
Если бы мы взяли в качестве точки $mathbf { textit { M } } _ { 0 } $ другую точку $mathbf { textit { M } } _ { 1 } $, то получили бы выражение, отличающееся на некоторую постоянную { более точно, на $C=intlimits_ { mathop { M_0 M_1 } limits^cup } { bar { a } dbar { r } } )$, поэтому $varphi (x,y,z)= frac { sin (xy) } { z } +C$.
Потенциал. Разность потенциалов. ЗАДАЧИ с решениями
Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.
Задача № 2.
Потенциал заряженного шара φ1 = 300 В. Чему равен потенциал φ2 электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?
Смотреть решение и ответ

Задача № 3.
Определить потенциал φ точки поля, находящейся на расстоянии а = 9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10–11 Кл/см2. Среда — воздух.
Задача № 4.
В точке 1 поля точечного заряда-источника потенциал φ1 = 40 В, а в точке 2 φ2 = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6).
Задача № 5.
В трех вершинах квадрата со стороной а = 20 см находятся заряды q1 = 1 • 10–8 Кл, q2 = 2 • 10–8 Кл и q3 = 2 • 10–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине.
Задача № 6.
Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.
Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух.
Задача № 8.
В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔWп и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.
Смотреть решение и ответ
Задача № 9.
Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ.
Задача № 10.
На пластине М поддерживается потенциал φ1 = +80 В, а на пластине N – φ2 = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d1 = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ1 поля на участке МР и изменение напряженности поля ΔЕ2 на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами.
Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
§ 6. Потенциал поля точечного заряда и заряда, равномерно распределённого по сферической поверхности
Примем потенциал бесконечности равным нулю. Тогда, используя (5.2), можно вывести, что на расстоянии $$ r$$ от точечного заряда $$ Q$$ потенциал электростатического поля:
| $$ varphi =k{displaystyle frac{Q}{r}}$$. | (6.1) |
 |
| Рис. 6.1 |
Возьмём теперь заряд $$ Q$$, равномерно распределённый по сфере радиуса $$ R$$ (рис. 6.1).
Для нахождения потенциала на расстоянии $$ r$$ от центра сферы перенесём мысленно пробный заряд $$ q$$ из исследуемой точки в бесконечность и применим формулу (5.2). Для произвольной точки $$ K$$ вне сферы $$ {varphi }_{K}={A}_{Kinfty }/q$$, где $$ {A}_{Kinfty }$$ – работа сил поля над $$ q$$ при его перемещении из т. $$ K$$ в бесконечность. Эта работа не изменится, если весь заряд $$ Q$$ сферы поместить в центр сферы, т. к. поля обоих зарядов $$ Q$$ при $$ r>R$$ совпадают (см. §3). Для точечного заряда $$ Q$$ отношение $$ {A}_{Kinfty }/q$$ есть потенциал его поля в т. $$ K$$, который находится по формуле (6.1). Итак, для сферы $$ {varphi }_{K}=kQ/r$$. В предельном случае при $$ r=R$$ получим потенциал сферы, равный `kQ//R`.
Для произвольной точки $$ B$$ внутри сферы $$ {varphi }_{B}={A}_{BCinfty }/q={A}_{BC}+{A}_{Cinfty }/q$$.
Здесь $$ {A}_{Binfty }$$, $$ {A}_{BC}$$ и $$ {A}_{Cinfty }$$ – работа сил поля над зарядом $$ q$$ на участках $$ BCinfty $$, `BC` и $$ Cinfty .$$ Внутри сферы поля нет, сила на $$ q$$ со стороны поля не действует и $$ {A}_{BC}=0$$. Тогда $$ {varphi }_{B}={A}_{Cinfty }/q$$. Но правая часть последнего равенства есть потенциал т. $$ C$$, т. е. потенциал сферы, равный `kQ//R`. Значит, потенциал любой точки внутри сферы равен потенциалу сферы: $$ {varphi }_{B}=kQ/R$$.
Итак, для заряда $$ Q$$, равномерно распределённого по сфере радиуса $$ R$$ потенциал поля вне сферы равен потенциалу точечного заряда, равного заряду сферы и помещённого в центре сферы (как и для напряжённости), а потенциал внутри сферы один и тот же и равен потенциалу сферы:
$$ varphi =k{displaystyle frac{Q}{r}}$$ при $$ r>R, varphi =k{displaystyle frac{Q}{R}}$$ при $$ rle R$$.
В двух вершинах прямоугольника со сторонами $$ a$$ и $$ 2a$$ (рис. 6.2) закреплены точечные заряды $$ Q$$ и $$ 3Q$$. Какую минимальную работу надо совершить, чтобы переместить точечный заряд $$ 4Q$$ из состояния покоя из вершины $$ B$$ в вершину $$ C$$?
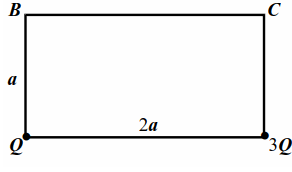 |
| Рис. 6.2 |
Здесь идёт речь о работе $$ A$$, которую необходимо совершить нам против электрических сил при переносе заряда $$ 4Q$$. Работа $$ A$$ в сумме с работой $$ {A}_{1}$$ сил электростатического поля над зарядом $$ 4Q$$ равна изменению кинетической энергии перемещаемого заряда:
$$ A+{A}_{1}=∆K$$
Отсюда $$ A=-{A}_{1}+∆K$$.
Работа $$ A$$ будет минимальной, если величина $$ ∆K$$ минимальна, т. е. заряд $$ 4Q$$ придёт в вершину $$ C$$ с нулевой скоростью, т. е. $$ ∆K=0.$$ Итак, $$ A=-{A}_{1}.$$ Работа сил поля над зарядом $$ {A}_{1}=4Q({varphi }_{B}-{varphi }_{C}), $$ где
$$ {varphi }_{B}=k{displaystyle frac{Q}{a}}+k{displaystyle frac{3Q}{asqrt{5}}}, {varphi }_{C}=k{displaystyle frac{Q}{asqrt{5}}}+k{displaystyle frac{3Q}{a}}$$
— потенциалы результирующего поля, созданного зарядами $$ Q$$ и $$ 3Q$$ в вершинах $$ B$$ и $$ C$$.
Окончательно
$$ A={displaystyle frac{8(sqrt{5}-1)}{sqrt{5}}}{displaystyle frac{k{Q}^{2}}{a}}>0$$.
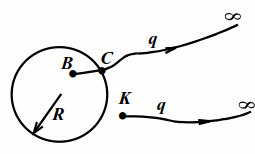
В центре сферы радиусом $$ R$$ находится точечный заряд $$ Q>0$$. По сфере равномерно распределён заряд $$-4Q<0$$. Найти потенциалы $$ {varphi }_{A}, {varphi }_{C}$$ на расстояниях $$ R/2$$ и $$ 2R$$ от центра сферы (рис. 6.3).
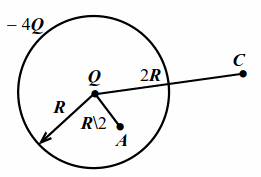 |
| Рис. 6.3 |
Потенциал в любой точке равен сумме потенциалов полей, созданных в этой точке зарядами $$ Q$$ и $$ -4Q$$. Для точек $$ A$$ и $$ C$$ :
$$ {varphi }_{A}=k{displaystyle frac{Q}{R/2}}+k{displaystyle frac{-4Q}{R}}=-2k{displaystyle frac{Q}{R}}$$,
$$ {varphi }_{C}=k{displaystyle frac{Q}{2R}}+k{displaystyle frac{-4Q}{2R}}=-{displaystyle frac{3}{2}}k{displaystyle frac{Q}{R}}$$.
§
15. ПОТЕНЦИАЛ. ЭНЕРГИЯ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ
ЗАРЯДОВ. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА
В ПОЛЕ
Основные
формулы
Потенциал
электрического поля есть величина,
равная отношению потенциальной энергии
точечного положительного заряда,
помещенную в данную точку поля, к этому
заряду;
=П/Q,
или
потенциал электрического поля есть
величина, равная отношению работы сил
поля по перемещению точечного
положительного заряда из данной точки
поля в бесконечность к этому заряду:
=A/Q.
Потенциал
электрического поля в бесконечности
условно принят равным нулю.
Отметим, что при
перемещении заряда в электрическом
поле работа Aв.с
внешних сил равна по модулю работе Aс.п
сил поля и противоположна ей по знаку:
Aв.с=
– Aс.п.
Потенциал
электрического поля, создаваемый
точечным зарядом Q на
расстоянии r от заряда,
.
Потенциал
электрического поля, создаваемого
металлической, несущей заряд Q сферой
радиусом R, на расстоянии
гот центра сферы:
внутри сферы
(r<R) ;
на поверхности
сферы (r=R)
;
вне сферы (r>R) .
Во всех приведенных
для потенциала заряженной сферы формулах
есть диэлектрическая
проницаемость однородного безграничного
диэлектрика, окружающего сферу.
Потенциал
электрического поля, созданного системой
п точечных зарядов, в данной точке
в соответствии с принципом суперпозиции
электрических полей равен алгебраической
сумме потенциалов 1,
2, … , n,
создаваемых отдельными точечными
зарядами Q1,
Q2, …, Qn:
Энергия W
взаимодействия системы точечных зарядов
Q1, Q2,
…, Qn
определяется работой, которую эта
система зарядов может совершить при
удалении их относительно друг друга
в бесконечность, и выражается формулой
,
где i
— потенциал поля, создаваемого всеми
п–1 зарядами (за исключением 1-го) в
точке, где расположен заряд Qi.
Потенциал связан
с напряженностью электрического поля
соотношением
Е= –grad.
В случае электрического
поля, обладающего сферической симметрией,
эта связь выражается формулой

или в скалярной
форме
,
а
в случае однородного поля, т. е. поля,
напряженность которого в каждой точке
его одинакова как по модулю, так и по
направлению,
E=(1–2,)/d,
где 1
и 2
— потенциалы точек двух эквипотенциальных
поверхностей; d —
расстояние между этими поверхностями
вдоль электрической силовой линии.
Работа, совершаемая
электрическим полем при перемещении
точечного заряда Q из
одной точки поля, имеющей потенциал 1,
в другую, имеющую потенциал 2,
A=Q(1—2),
или
,
где El
— проекция вектора напряженности Е
на направление перемещения; dl
— перемещение.
В случае однородного
поля последняя формула принимает вид
A=QElcos,
где l
— перемещение; —
угол между направлениями вектора Е
и перемещения l.
Примеры
решения задач
Пример 1.
Положительные заряды Q1=3
мкКл и Q2=20
нКл находятся в вакууме на расстоянии
r1=l,5
м друг от друга. Определить работу A,
которую надо совершить, чтобы сблизить
заряды до расстояния r2=1
м.
Решение.
Положим, что первый заряд Q1
остается неподвижным, а второй Q2
под действием внешних сил перемещается
в поле, созданном зарядом Q1,
приближаясь к нему с расстояния r1=t,5
м до r2=1 м.
Работа А’
внешней силы по перемещению заряда Q
из одной точки поля с потенциалом
1
в другую, потенциал которой 2,
равна по модулю и противоположна по
знаку работе А сил поля по перемещению
заряда между теми же точками:
А’= —А.
Работа А сил
поля по перемещению заряда A=Q(1—2).
Тогда работа А’ внешних сил может
быть записана в виде
A‘=
–Q(1—2)=Q(2—1). (1)
Потенциалы точек
начала и конца пути выразятся формулами
;
.
Подставляя выражения
1
и 2 в
формулу (1) и учитывая, что для данного
случая переносимый заряд Q=Q2,
получим
. (2)
Если
учесть, что 1/(40)=9109
м/Ф, то после подстановки значений
величин в формулу (2) и вычисления найдем
A‘=180 мкДж.
Пример 2. Найти
работу А поля по перемещению заряда
Q=10 нКл из точки 1
в точку 2 (рис. 15.1), находящиеся между
двумя разноименно заряженными с
поверхностной плотностью =0,4
мкКл/м2 бесконечными параллельными
плоскостями, расстояние l
между которыми равно 3 см.
Р
Возможны два способа решения задачи.
1-й способ.
Работу сил поля по перемещению заряда
Q из точки 1 поля с потенциалом 1
в точку 2 поля с потенциалом 2
найдем по формуле
A=Q(1—2). (1)
Для определения
потенциалов в точках 1 и 2 проведем
через эти точки эквипотенциальные
поверхности I и II.
Эти поверхности будут плоскостями, так
как поле между двумя равномерно
заряженными бесконечными параллельными
плоскостями однородно. Для такого поля
справедливо соотношение
1—2=El, (2)
где Е —
напряженность поля; l
— расстояние между эквипотенциальными
поверхностями.
Напряженность
поля между параллельными бесконечными
разноименно заряженными плоскостями
E=/0.
Подставив это выражение Е в формулу
(2) и затем выражение 1—2
в формулу (1), получим
A=Q(/0)l.
2-й способ. Так
как поле однородно, то сила, действующая
на заряд Q, при его перемещении
постоянна. Поэтому работу перемещения
заряда из точки 1 в точку 2 можно
подсчитать по формуле
A=Fr
cos, (3)
где F
— сила, действующая на заряд; r
— модуль перемещения заряда Q
из точки 1 в точку 2;
— угол между направлениями перемещения
и силы. Но F=QE=Q(/0).
Подставив это выражение F в равенство
(3), а также заметив, что rcos=l,
получим
A=Q(/0)l. (4)
Таким образом, оба
решения приводят к одному и тому же
результату.
Подставив в
выражение (4) значение величин Q,
, 0
и l, найдем
A=13,6
мкДж.
Пример 3. По
тонкой нити, изогнутой по дуге окружности
радиусом R,
равномерно распределен заряд с линейной
плотностью =10 нКл/м.
Определить напряженность Е и
потенциал
электрического поля, создаваемого таким
р
зарядом в точке О, совпадающей с
центром кривизны дуги. Длина l
нити составляет 1/3 длины окружности и
равна 15 см.
Решение. Выберем
оси координат так, чтобы начало координат
совпадало с центром кривизны дуги, а
ось у была симметрично расположена
относительно концов дуги (рис. 15.2). На
нити выделим элемент длины dl.
Заряд dQ=dl,
находящийся на выделенном участке,
можно считать точечным.
Определим
напряженность электрического поля в
точке О. Для этого найдем сначала
напряженность dE
поля, создаваемого зарядом dQ:
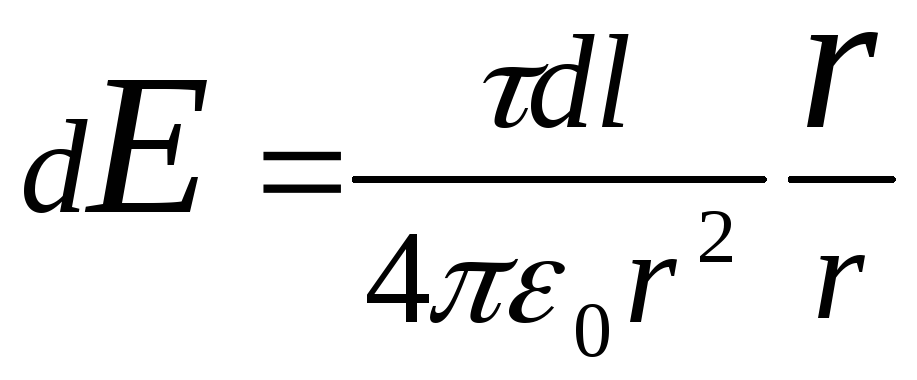
где r
—радиус-вектор, направленный от элемента
dl к
точке, напряженность в которой вычисляется.
Выразим вектор dE через проекции dEx
c и dEy
на оси координат:
,
где i
и j — единичные векторы
направлений (орты).
Напряженность Е
найдем интегрированием:
.
Интегрирование
ведется вдоль дуги длины l.
В силу симметрии интеграл
равен нулю. Тогда

где
.
Так как r=R=const
и dl=Rd.
то
Подставим найденное
выражение dEy
в (1) и, приняв во внимание симметричное
расположение дуги относительно оси Оу,
пределы интегрирования возьмем от 0 до
/3, а результат
удвоим;

Подставив указанные
пределы и выразив R
через длину дуги (3l=2r),
получим

Из этой формулы
видно, что вектор Е совпадает с
положительным направлением оси Оу
Подставив значение
и l в последнюю формулу и сделав
вычисления, найдем
E=2,18
кВ/м.
Определим потенциал
электрического поля в точке О. Найдем
сначала потенциал d,
создаваемый точечным зарядом dQ
в точке О:
Заменим r
на R и произведем
интегрирование:
.Так
как l=2R/3,
то
=/(60).
Произведя вычисления
по этой формуле, получим
=188 В.
Пример 4.
Электрическое поле создана длинным
цилиндром радиусом R=1
см, равномерно заряженным с
линейной плотностью =20
нКл/м. Определить разность потенциалов
двух точек этого поля, находящихся на
расстояниях a1=0,5
см и а2=2 см от поверхности
цилиндра, в средней его части.
Решение. Для
определения разности потенциалов
воспользуемся соотношением между
напряженностью поля и изменением
потенциала Е= —grad.
Для поля с осевой симметрией, каким
является поле цилиндра, это соотношение
можно записать в виде
Е= –(d/dr),
или d=
—Еdr.
Интегрируя последнее
выражение, найдем разность потенциалов
двух точек, отстоящих на r1
и r2 от оси
цилиндра;
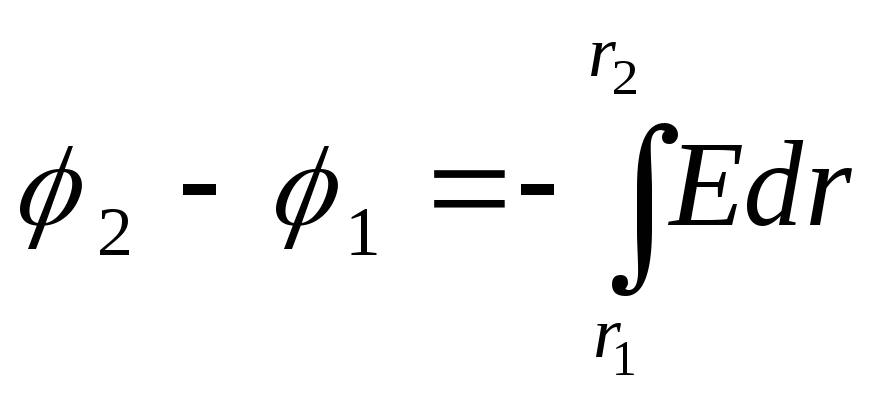
Так как цилиндр
длинный и точки взяты вблизи его средней
части, то для выражения напряженности
поля можно воспользоваться формулой
.
Подставив это выражение Е в равенство
(1), получим

Так как величины
r2 и r1
входят в формулу в виде отношения, то
их можно выразить в любых, но только
одинаковых единицах:
r1=R+a1=1,5
см; r2=R+a2=3
см.
Подставив значения
величия , 0,
r1 и r2
в формулу (2) и вычислив, найдем
1—2=250
В.
Пример 5.
Электрическое поле создано тонким
стержнем, несущим равномерно распределенный
по длине заряд =0,1
мкКл/м. Определить потенциал
поля в точке, удаленной от концов стержня
на расстояние, равное длине стержня.
Решение. Заряд,
находящийся на стержне, нельзя считать
точечным, поэтому непосредственно
применить для вычисления потенциала
формулу
, (1)
справедливую
только для точечных зарядов, нельзя. Но
если разбить стержень на элементарные
отрезки dl,
то заряд dl,
находящийся на каждом из них, можно
рассматривать как точечный и тогда
формула (1) будет справедлива. Применив
эту формулу, получим
, (2)
где r
— расстояние точки, в которой
определяется потенциал, до элемента
стержня.
Из рис. 15.3 следует,
что dl=(rd/cos).
Подставив это выражение dl
в формулу (2), найдем.
Интегрируя
полученное выражение в пределах от 1
да 2,
получим потенциал, создаваемый всем
зарядом, распределенным на стержне:
В
силу симметрии расположения точки А
относительно концов стержня имеем 2=1
и поэтому
Следовательно,

как
Рис 15.3
(см. табл. 2), то.
Подставляя пределы
интегрирования, получим
Сделав вычисления
по этой формуле, найдем
=990 В.
Пример 6.
Электрон со скоростью v=1,83106
м/с влетел в однородное электрическое
поле в направлении, противоположном
вектору напряженности поля. Какую
разность потенциалов U
должен пройти электрон, чтобы обладать
энергией Ei=13,6
эВ*? (Обладая такой энергией, электрон
при столкновении с атомом водорода
может ионизировать его. Энергия 13,6 эВ
называется энергией ионизации водорода.)
Решение.
Электрон должен пройти такую разность
потенциалов U, чтобы приобретенная
при этом энергия W в
сумме с кинетической энергией T,
которой обладал электрон перед вхождением
в поле, составила энергию, равную энергии
ионизации Ei,
т. е. W+T=Ei.
Выразив в этой формуле W=eU
и Т =(mv2/2),
получим eU+(mv2/2)=Ei.
Отсюда.
___________________
* Электрон-вольт
(эВ) — энергия, которую приобретает
частица, имеющая заряд, равный заряду
электрона, прошедшая разность потенциалов
1 В. Эта внесистемная единица энергии в
настоящее время допущена к применению
в физике.
Произведем
вычисления в единицах СИ:
U=4,15 В.
Пример 7. Определить
начальную скорость υ0
сближения протонов, находящихся
на достаточно большом расстоянии друг
от друга, если минимальное расстояние
rmin, на которое
они могут сблизиться, равно 10-11
см.
Р е ш е н и е. Между
двумя протонами действуют силы
отталкивания, вследствие чего
движение протонов будет замедленным.
Поэтому задачу можно решить как в
инерциальной системе координат
(связанной с центром масс двух протонов),
так и в неинерциальной (связанной с
одним из ускоренно движущихся
протонов). Во втором случае законы
Ньютона не имеют места. Применение
же принципа Даламбера затруднительно
из-за того, что ускорение системы будет
переменным. Поэтому удобно рассмотреть
задачу в инерциальной системе отсчета.
Поместим начало
координат в центр масс двух протонов.
Поскольку мы имеем дело с одинаковыми
частицами, то центр масс будет находиться
в точке, делящей пополам отрезок,
соединяющий частицы. Относительно
центра масс частицы будут иметь в любой
момент времени одинаковые по модулю
скорости. Когда частицы находятся
на достаточно большом расстоянии друг
от друга, скорость υ1 каждой
частицы равна половине υ0,
т. е. υ1 =υ0/2.
Для решения задачи
применим закон сохранения энергии,
согласно которому полная механическая
энергия Е изолированной системы
постоянна, т. е.
Е=Т+П,
где Т — сумма
кинетических энергий обоих протонов
относительно центра масс; П — потенциальная
энергия системы зарядов.
Выразим потенциальную
энергию в начальный П1 и конечный
П2 моменты движения.
В начальный момент,
согласно условию задачи, протоны
находились на большом расстоянии,
поэтому потенциальной энергией можно
пренебречь (П1=0). Следовательно,
для начального момента полная энергия
будет равна кинетической энергии T1
протонов, т. е.
E=Tl.
(1)
В конечный момент,
когда протоны максимально сблизятся,
скорость и кинетическая энергия
равны нулю, а полная энергия будет равна
потенциальной энергии П2, т. е.
Е=П2.
(2)
Приравняв правые
части равенств (1) и (2), получим
T1=П2.
(3)
Кинетическая
энергия равна сумме кинетических энергий
протонов:
(4)
Потенциальная
энергия системы двух зарядов Q1
и Q2, находящихся
в вакууме, определяется по формуле
,
где r — расстояние
между зарядами. Воспользовавшись этой
формулой, получим
(5)
С учетом равенств
(4) и (5) формула (3) примет вид
откуда
Выполнив вычисления
по полученной формуле, найдем υ0=2,35
Мм/с.

8. Электрон без начальной скорости
прошел разность потенциалов U0=10
кВ и влетел в пространство между
пластинами плоского конденсатора,
заряженного до разности потенциалов
Ul=100 В, по линии АВ,
параллельной пластинам (рис. 15.4).
Расстояние d между пластинами
равно 2 см. Длина l1
пластин конденсатора в направлении
полета электрона, равна 20 cм.
Определить расстояние ВС на
экране Р, отстоящем от конденсатора
на l2=1 м.
Р е ш е н и е. Движение
электрона внутри конденсатора
складывается из двух движений: 1)
по инерции вдоль линии АВ с постоянной
скоростью υ0, приобретенной
под действием разности потенциалов U0,
которую электрон прошел до
конденсатора; 2) равномерно ускоренного
движения в вертикальном направлении
к положительно заряженной пластине
под действием постоянной силы поля
конденсатора. По выходе из конденсатора
электрон будет двигаться равномерно
со скоростью υ, которую он имел
в точке М в момент вылета из
конденсатора.
Из рис. 15.4 видно,
что искомое расстояние |BC|=h1+h2,
где с h1 — расстояние, на
которое сместится электрон в вертикальном
направлении во время движения в
конденсаторе; h2 — расстояние
между точкой D на экране, в которую
электрон попал бы, двигаясь по выходе
из конденсатора по направлению
начальной скорости υ0, и точкой
С, в которую электрон попадет в
действительности.
Выразим отдельно
h1 и h2. Пользуясь
формулой длины пути равномерно
ускоренного движения, найдем
.
(1)
где а — ускорение,
полученное электроном под действием
поля конденсатора; t- время полета
электрона внутри конденсатора.
По второму закону
Ньютона a=F/m, где F — сила, с которой
поле действует на электрон; т- его
масса. В свою очередь, F
=eE=eU1/d, где е — заряд
электрона; U1 — разность
потенциалов между пластинами конденсатора;
d — расстояние между ними. Время
полета электрона внутри конденсатора
найдем из формулы пути равномерного
движения
,
откуда
где l1
— длина конденсатора в направлении
полета электрона. Выражение скорости
найдем из условия равенства работы,
совершенной полем при перемещении
электрона, и приобретенной им кинетической
энергии:.
Отсюда
(2)
Подставляя в
формулу (1) последовательно значения а,
F, t и υ02
из соответствующих выражений,
получим
Длину отрезка h2
найдем из подобия треугольников MDC
и векторного:
(3)
где υ1
— скорость электрона в вертикальном
направлении в точке М; l2—
расстояние от конденсатора до экрана.
Скорость υ1
найдем по формуле υ1=at, которая
с учетом выражений для а, F и t
примет вид
Подставив выражение
υ1 в формулу (3), получим
,
или, заменив υ02 по
формуле (3), найдем
Окончательно для
искомого расстояния |BC|
будем иметь
|BC|=
Подставив
значения величин U1, U0,
d, l1 и l2
в последнее выражение и произведя
вычисления, получим |BC|=5,5cм.
Задачи
Потенциальная
энергия и потенциал поля точечных
зарядов
15.1. Точечный
заряд Q = 10 нКл, находясь в некоторой
точке поля, обладает потенциальной
энергией П = 10 мкДж. Найти потенциал φ
этой точки поля.
5.2. При перемещении
заряда Q=20 нКл между двумя точками
поля внешними силами была совершена
работа А=4 мкДж. Определить работу
A1 сил поля и разность Δφ
потенциалов этих точек поля.
15.3. Электрическое
поле создано точечным положительным
зарядом Q1=6 нКл. Положительный
заряд Q2 переносится из точки
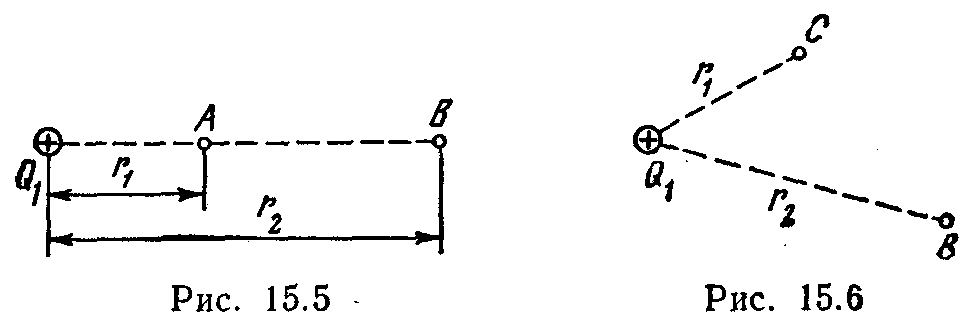
А этого поля в точку В (рис. 15.5).
Каково изменение потенциальной
энергии ΔП, приходящееся на единицу
переносимого заряда, если r1=20
см и r2=50 см?
15.4. Электрическое
поле создано точечным зарядом Ql=50
нКл. Не пользуясь понятием потенциала,
вычислить работу А в
нешних
сил по перемещению точечного заряда
Q2= -2 нКл из точки С в точку
В
(рис. 15.6), если r1=10
см, r2=20 см.
Определить также изменение ΔП
потенциальной энергии системы
зарядов.
15.5. Поле создано
точечным зарядом Q=1 нКл. Определить
потенциал φ поля в точке, удаленной
от заряда на расстояние r=20
см.
15.6. Определить
потенциал φ электрического поля в точке,
,удаленной от зарядов Q1= -0,2
мкКл и Q2=0,5 мкКл соответственно
на r1=15 см и r2=25
см. Определить также минимальное и
максимальное расстояния между
зарядами, при которых возможно решение.
15.7. Заряды Q1=1
мкКл и Q2= -1 мкКл находятся
на расстоянии d=10 см. Определить
напряженность Е и потенциал φ поля
в точке, удаленной на расстояние
r= 10 см от первого
заряда и лежащей на линии, проходящей
через первый заряд перпендикулярно
направлению от Q1 к Q2.
15.8. Вычислить
потенциальную энергию П системы двух
точечных зарядов Q1=100 нКл
и Q2=10 нКл, находящихся на
расстоянии d=10 см друг от друга.
15.9. Найти
потенциальную энергию П системы трех
точечных зарядов Q1=10 нКл,
Q2=20 нКл и Q3= -30
нКл, расположенных в вершинах
равностороннего треугольника со стороной
длиной a=10 см.
15.10. Какова
потенциальная энергия П системы четырех
одинаковых точечных зарядов Q=10
нКл, расположенных в вершинах квадрата
со стороной длиной а=10 см? .
15.11. Определить
потенциальную энергию П системы четырех
точечных зарядов, расположенных в
вершинах квадрата со стороной длиной
a=10 см. Заряды одинаковы по модулю
Q=10 нКл,но два из них отрицательны.
Рассмотреть два возможных случая
расположения зарядов.

Поле создано двумя точечными зарядами
+2Q и -Q, находящимися на
расстоянии d=12 см друг от друга.
Определить геометрическое место точек
на плоскости, для которых потенциал
равен нулю (написать уравнение линии
нулевого потенциала).
5.13. Система
состоит из трех зарядов — двух одинаковых
по величине Q1=|Q2|=1
мкКл и противоположных по знаку и заряда
Q=20 нКл, расположенного точке 1
посередине между двумя другими зарядами
системы (рис. 15.7). Определить изменение
потенциальной энергии ΔП системы при
переносе заряда Q из точки 1 в
точку 2. Эти точки удалены от отрицательного
заряда Q1 на расстояние а=0,2
м.