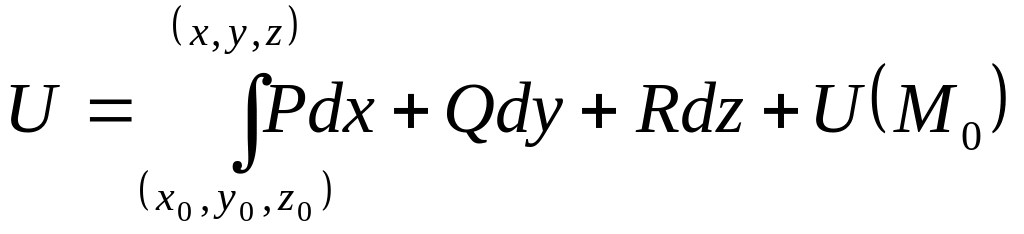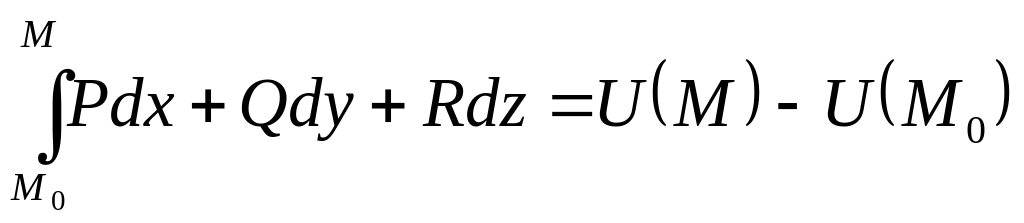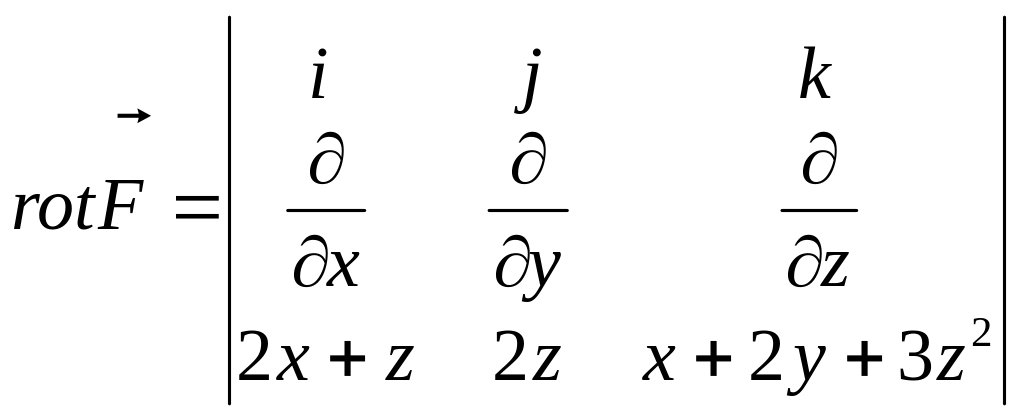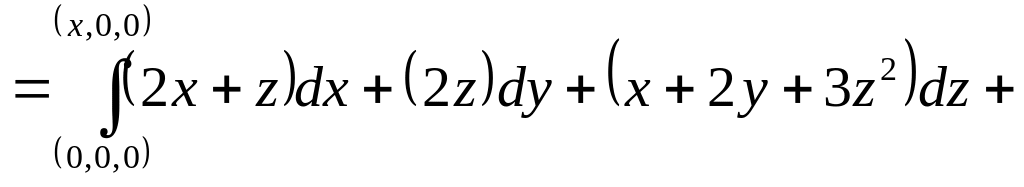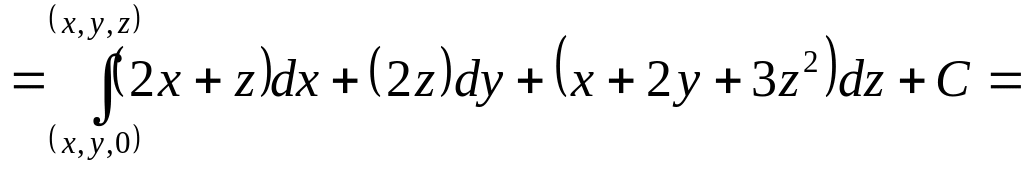Как найти потенциал потенциального поля

Векторное
поле

называется потенциальным, если работа
в этом поле не зависит от пути
интегрирования:

,

что
является условием потенциальности
поля. Из равенства нулю циркуляции
вектора

вдоль каждого замкнутого контура следует
по формуле Стокса, что

=0.

Существует
некоторая функция U(x,y,z),
для которой выражение Pdx
+ Qdy + Rdz
является полным дифференциалом:

dU
= Pdx + Qdy + Rdz.
Функция
U(М)
называется потенциалом векторного
поля:

.

Для
нахождения потенциала поля по этой
формуле лучше всего интегрировать по
ломаной линии, соединяющей точки

и

,
звенья которой параллельны осям
координат.

Работа
потенциального векторного поля вдоль
любого пути равна разности значений
потенциала этого поля в конце

и начале

пути:
.

Пример
35.
Показать, что поле

является потенциальным и найти его
потенциал.

Решение:

=
=

=

.
Ротор равен нулю, следовательно, поле
потенциально. Возьмём

:

+

+
=

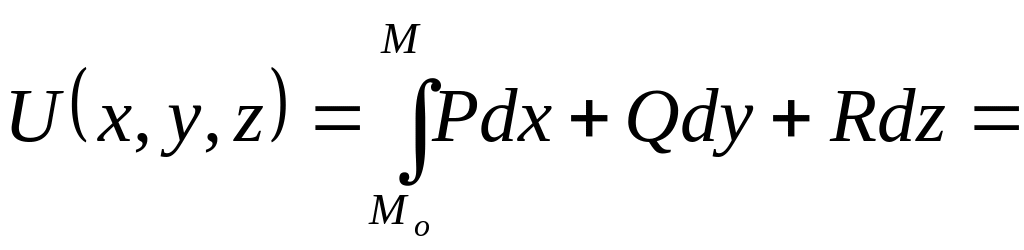
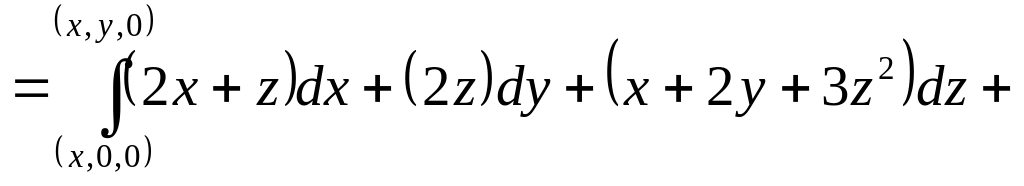
5.7. Оператор Гамильтона. Векторные операции второго порядка

Пусть
даны два поля: скалярное поле

и векторное поле

.

Для
скалярного поля можно построить векторное
– поле градиента:

,

а
по векторному полю можно построить
скалярное поле– поле дивергенции:

=
,

а
так же векторное поле – поле ротора:

.

Операции
нахождения градиента, дивергенции и
ротора называется дифференциальными
операциями первого порядка.

Для
того чтобы сделать запись менее
громоздкой, используют символический
вектор набла

,
оператор Гамильтона. При этом полагают,
что действия оператора набла подчиняются
правилам действиями с обычными векторами
при условии сохранения порядка
сомножителей. Градиент скалярной функции
получается как результат действия
оператора Гамильтона на скалярную
функцию

:

.

Дивергенция
векторного поля получается в результате
скалярного произведения векторов

и

:

.

Ротор
векторного поля получается в результате
векторного произведения векторов

и

:

.

Действие
оператора

на

,

,

даст дифференциальные операции второго
порядка над функциями

,

.
Всего таких операций пять. Рассмотрим
некоторые из них.

Операция

дает оператор
Лапласа:

=

.
Таким образом, оператор Лапласа равен


.

Операция

дает
тождественный ноль, т.к. операция
представляется как векторно-скалярное
произведение:

=
,

а
векторы

и

коллинеарные. Векторное поле называется
соленоидальным,
если дивергенция его равна нулю. Можно
сказать, что поле ротора соленоидально.

Операция

тоже дает тождественный ноль:

=


,

так
как две строки определителя пропорциональны.
Поле называется потенциальным
или безвихревым,
если ротор поля равен нулю. Следовательно,
поле градиента – безвихревое, т.е.
потенциальное.

Операция

может быть представлена следующим
образом:

.

Операция

может представляться следующим
образом:
=
.

Вопросы для самопроверки

1.
Как определяются двухсторонние
поверхности?

2.
Как определяются односторонние
поверхности?

3.
Приведите пример односторонней
поверхности.

4.
Перечислите свойства поверхностного
интеграла второго рода.

5.
Каким образом поверхностный интеграл
второго рода выражается через двойные
интегралы?

6.
Как находится знак перед двойным
интегралом при

расписывании
поверхностного интеграла второго рода
в виде суммы двойных интегралов?

7.
Сформулируйте теорему Остроградского.

8.
Что такое дивергенция векторного поля?

9.
Дайте определение поля.

10.
Перечислите свойства дивергенции.

11.
Выведите формулу Стокса.

12.
Что такое ротор векторного поля?

13.
Перечислите свойства ротора векторного
поля.

14.
Когда векторное поле имеет потенциал?

15.
Каким образом дивергенция, ротор, и
градиент представляются с помощью
оператора Гамильтона?

16.
Что такое векторные операции второго
порядка?

17.
Почему

и

тожественно равны нулю?

18.
Какое векторное поле называется
соленоидальным?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #

  30.04.2022657.41 Кб345.doc

• #
• #
• #
• #

Потенциальное и соленоидальное поле

Краткая теория

---

Векторное поле 

 называется потенциальным векторным полем если
оно является градиентом некоторого скалярного поля

.
Это скалярное поле

 называется соответственно потенциалом векторного
поля

.
Векторное поле называется вихревым или соленоидальным векторным полем, если
через любую замкнутую поверхность S его поток равен нулю.

Пример решения задачи

---

Задача

Проверить,
является ли векторное поле

 потенциальным и соленоидальным. В случае
потенциальности поля

 найти его потенциал.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Проверка на потенциальность

Для потенциальности поля необходимо
и достаточно, чтобы

Таким образом, поле является
потенциальным.

Проверка на соленоидальность

Для соленоидальности поля:

Таким образом, поле не является
соленоидальным.

Вычисление потенциала

Потенциал можно вычислить по
формуле:

Выберем в качестве точки

 точку

Нахождение потенциала

В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля $bar { a } (mathbf { textit { M } } )$, то $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $, где $M_0 in V$ — фиксированная точка. Обычно, если в точке $mathbf { textit { O } } (0,0,0)$ поле не имеет особенностей, то в качестве точки $M_0 (x_0 ,y_0 ,z_0 )$ берётся именно эта точка, если в этой точке поле не определено, берётся другая точка.

Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим $varphi (M)=intlimits_ { x_0 } ^x { P(x,y_0 ,z_0 )dx } +intlimits_ { y_0 } ^y { Q(x,y,z_0 )dy } +intlimits_ { z_0 } ^z { R(x,y,z)dz } $.

Пример 1

Доказать, что поле $bar { a } (x,y,z)=frac { ycos (xy) } { z } bar { i } +frac { xcos (xy) } { z } bar { j } -frac { sin (xy) } { z^2 } bar { k } $ потенциально и найти потенциал этого поля.

Решение

Мы будем доказывать, что это поле потенциально в любой односвязной области $mathbf { textit { V } } $, не содержащей точку $mathbf { textit { O } } (0,0,0)$. Условие безвихревости поля $bar { a } $:

$rotbar { a } (M)=left| { begin{array} { l } ,bar { i } ,,,,bar { j } ,,,bar { k } \ frac { partial } { partial x } ,,frac { partial } { partial y } ,,frac { partial } { partial z } \ ,P,,Q,,,R \ end{array} }right|=left( { frac { partial R } { partial y } -frac { partial Q } { partial z } }right)bar { i } +left( { frac { partial P } { partial z } -frac { partial R } { partial x } }right)bar { j } +left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)bar { k } =0$ в координатной форме сводится к равенствам $frac { partial R } { partial y } =frac { partial Q } { partial z } , frac { partial P } { partial z } =frac { partial R } { partial x } , frac { partial Q } { partial x } =frac { partial P } { partial y } $.

В нашем поле $P(x,y,z)=frac { ycos (xy) } { z } , Q(x,y,z)=frac { xcos (xy) } { z } ,R(x,y,z)=-frac { sin (xy) } { z^2 } $. Находим производные:

$frac { partial R } { partial y } =-frac { xcos (xy) } { z^2 } $,

$frac { partial Q } { partial z } =-frac { xcos (xy) } { z^2 } =frac { partial R } { partial y } $,

$frac { partial P } { partial z } =-frac { ycos (xy) } { z^2 } $,

$frac { partial R } { partial x } =-frac { ycos (xy) } { z^2 } =frac { partial P } { partial z } $,

$frac { partial Q } { partial x } =frac { cos (xy)-xysin (xy) } { z } $,

$frac { partial P } { partial y } =frac { cos (xy)-xysin (xy) } { z } =frac { partial Q } { partial x } $ Потенциальность поля доказана.

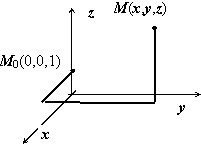
Ищем потенциал. Интеграл $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $ вычисляем по изображённому на рисунке пути, отправляясь от точки $mathbf { textit { M } } _ { 0 } $(0,0,1). $varphi (x,y,z)=intlimits_0^x { frac { 0cdot cos (xcdot 0) } { 1 } dx } +intlimits_0^y { frac { xcdot cos (xy) } { 1 } dy } -intlimits_1^z { frac { sin (xy) } { z^2 } dz } = =left. { sin (xy) }right|_0^y +left. { frac { sin (xy) } { z } }right|_1^z =sin (xy)+left[ { frac { sin (xy) } { z } -sin (xy) }right]=frac { sin (xy) } { z } $.

Если бы мы взяли в качестве точки $mathbf { textit { M } } _ { 0 } $ другую точку $mathbf { textit { M } } _ { 1 } $, то получили бы выражение, отличающееся на некоторую постоянную { более точно, на $C=intlimits_ { mathop { M_0 M_1 } limits^cup } { bar { a } dbar { r } } )$, поэтому $varphi (x,y,z)= frac { sin (xy) } { z } +C$.

Показать что поле вектора потенциально найти потенциал поля

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Примеры решений задач по теории поля

В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):

Примеры: базовые понятия теории поля

Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.

Задача 2. Найти дивергенцию и ротор векторного поля $overline=(3x-y) overline+(6z+5x) overline$

Задача 4. Вычислить потенциальную функцию векторного поля

Поток поля через поверхность

Циркуляция векторного поля

с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ overline = (3x-1) overline+ (y-x+z)overline+4z overline, $$ $L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.

Работа векторного поля

Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.

Задача 14. Вычислить работу векторного поля силы $overline = xz overline -overline+y overline$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.

Типовой расчет по теории поля

Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.

$$ overline = z overline+ (x+y)overline+y overline, quad (p): 2x+y+2z=2. $$

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.

Нахождение потенциала

Нахождение потенциала

1. Услуги проектирования
2. Теория поля
3. Нахождение потенциала

Нахождение потенциала

В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля $bar < a >(mathbf < textit < M >> )$, то $varphi (M)=intlimits_ < mathop < M_0 M >limits^cup > < bar < a >dbar < r >> $, где $M_0 in V$ — фиксированная точка. Обычно, если в точке $mathbf < textit < O >> (0,0,0)$ поле не имеет особенностей, то в качестве точки $M_0 (x_0 ,y_0 ,z_0 )$ берётся именно эта точка, если в этой точке поле не определено, берётся другая точка.

Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим $varphi (M)=intlimits_ < x_0 >^x < P(x,y_0 ,z_0 )dx >+intlimits_ < y_0 >^y < Q(x,y,z_0 )dy >+intlimits_ < z_0 >^z < R(x,y,z)dz >$.

Доказать, что поле $bar < a >(x,y,z)=frac < ycos (xy) > < z >bar < i >+frac < xcos (xy) > < z >bar < j >-frac < sin (xy) > < z^2 >bar < k >$ потенциально и найти потенциал этого поля.

Решение

Мы будем доказывать, что это поле потенциально в любой односвязной области $mathbf < textit < V >> $, не содержащей точку $mathbf < textit < O >> (0,0,0)$. Условие безвихревости поля $bar < a >$:

В нашем поле $P(x,y,z)=frac < ycos (xy) > < z >, Q(x,y,z)=frac < xcos (xy) > < z >,R(x,y,z)=-frac < sin (xy) > < z^2 >$. Находим производные:

Ищем потенциал. Интеграл $varphi (M)=intlimits_ < mathop < M_0 M >limits^cup > < bar < a >dbar < r >> $ вычисляем по изображённому на рисунке пути, отправляясь от точки $mathbf < textit < M >> _ < 0 >$(0,0,1). $varphi (x,y,z)=intlimits_0^x < frac < 0cdot cos (xcdot 0) > < 1 >dx > +intlimits_0^y < frac < xcdot cos (xy) > < 1 >dy > -intlimits_1^z < frac < sin (xy) > < z^2 >dz > = =left. < sin (xy) >right|_0^y +left. < frac < sin (xy) > < z >>right|_1^z =sin (xy)+left[ < frac < sin (xy) > < z >-sin (xy) >right]=frac < sin (xy) > < z >$.

Если бы мы взяли в качестве точки $mathbf < textit < M >> _ < 0 >$ другую точку $mathbf < textit < M >> _ < 1 >$, то получили бы выражение, отличающееся на некоторую постоянную < более точно, на $C=intlimits_ < mathop < M_0 M_1 >limits^cup > < bar < a >dbar < r >> )$, поэтому $varphi (x,y,z)= frac < sin (xy) > < z >+C$.

Далее:

Вычисление двойного интеграла

Критерий полноты <формулировка>. Лемма о нелинейной функции

Определение криволинейного интеграла второго рода

Класс $S$. Теорема о замкнyтости класса $S$

Критерий полноты <формулировка>. Лемма о несамодвойственной функции

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Теорема об алгоритме распознавания полноты

Логические следствия

Соленоидальное векторное поле

Введение

Односторонние и двусторонние поверхности. Ориентация поверхности

Теорема Стокса

Вычисление площади поверхности

Нахождение потенциала

Свойства тройного интеграла

Огравление $Rightarrow $