Как найти потенциал заземленной сферы

Примеры решения задач по физике — концентрические проводящие сферы

Суббота, 25 февраля, 2012

Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.

Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.

Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φ_in (внутренней) и φ_ex (внешней).

Решение. Потенциал на поверхности внутренней сферы φ_ex складывается из двух потенциалов: внешней сферы φ₁ и собственно внутренней сферы φ₂.

Потенциал внешней сферы φ₁ в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):

   

Потенциал внутренней сферы φ₂ определяется известным соотношением:

   

Тогда общий потенциал φ_in на поверхности внутренней сферы равен:

   

Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’₁ и собственно внешней сферы φ’₂.

Потенциал внутренней сферы φ’₁ на расстоянии R от ее центра определяется известным соотношением:

   

Формула, определяющая потенциал внешней сферы φ’₂ на ее поверхности, также хорошо известна:

   

Тогда общий потенциал на поверхности внешней сферы равен:

   

Задача 2. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R₂. Определите потенциал шара φ₁ после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают.

Решение. До соединения сфер проводником заряд первой был равен:

   

После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:

   

где q₁ и q₂ — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q₁ + q₂. После несложных преобразований получаем:

   

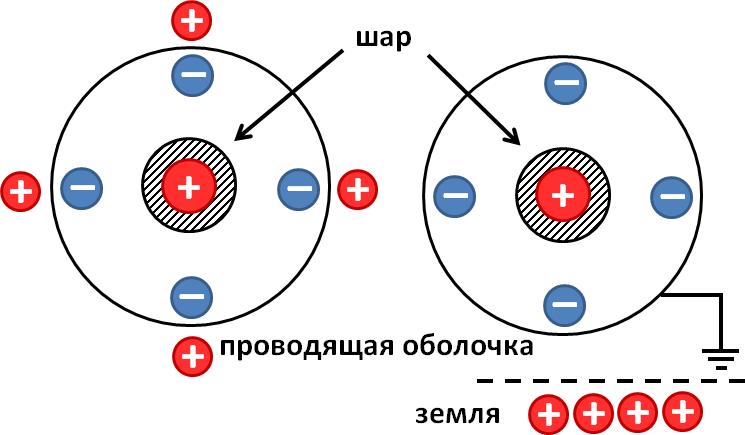
Задача 3. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R₂. Чему станет равен потенциал шара φ‘, если заземлить оболочку?

Начнем с рисунка к решению задачи:

Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:

   

Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.

В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q₂, поскольку он притягивается к положительному заряду q₁ внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:

   

Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:

   

   

Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.

Репетитор по физике и математике
Сергей Валерьевич

(1), где и — поверхностная плотность заряда на правой и левой сторонах пластины, которая возникает после внесения пластины в поле .

В силу закона сохранения заряда, суммарный заряд пластины не изменится, поэтому (2). Решая систему (1)-(2), получим

Слева от пластины . Справа — .

35. Задача на самостоятельное решение. Металлический шар радиуса помещён в однородное электрическое поле. Изобразить качественно картину силовых линий поля и эквипотенциальных поверхностей.

2.8.5.Тема 4. Модели электростатики: «Одиночные диэлектрики в электростатическом поле»

36. В некоторой точке изотропного диэлектрика с проницаемостью вектор электрического смещения имеет значение . Чему равна поляризованность в этой точке?

Используя соотношения и , находим .

37. Внутри диэлектрика известны и

, где .

а) Определить — плотность связанных зарядов и плотность — свободных зарядов внутри диэлектриков.

б) Чему равна диэлектрическая проницаемость ?

Используем формальные выражения для нахождения и :

38. Показать, что на границе раздела двух диэлектриков силовые линии испытывают преломление (рис. 38).

На границе двух диэлектриков для вектора выполняются условия: (тангенциальные компоненты вектора непрерывны) (нормальные компоненты вектора испытывают скачок) .

Таким образом .

39. Диэлектрическая пластина ширины с проницаемостью , помещена в однородное электрическое поле напряжённости , линии которого перпендикулярны пластине.

а) изобразить линии и .

б) построить качественные графики зависимостей , и потенциала (где — перпендикулярна к пластине).

Вектор направлен вдоль оси , точка находится на середине ширины пластины.

в
) определить поверхностную плотность связанных зарядов на той стороне, в которую входят линии поля из вакуума (рис. 39).

40. Длинная тонкая диэлектрическая палочка помещена в однородное электрическое поле, как показано на рис. 40а. Изобразить качественную картину линий поля и график зависимости от (см. рис. 40б).

41.Показать, что напряжённость поля в средней части длинной и узкой щели, продырявленной в диэлектрике, равна напряжённости поля в диэлектрике, если эта щель расположена параллельно вектору и что равна индукции в диэлектрике, если щель перпендикулярна (рис. 41).

П ерпендикулярная щель.

При отсутствии свободных зарядов в диэлектрике из следует, что или , так как в щели, где находится вакуум (или воздух) , то получаем .

Узкая параллельная щель.

Поскольку тангенциальные составляющие вектора при переходе из одной среды в другую не изменяются, то имеем или .

2.8.6.Тема 5. Модели электростатики: «Комбинации моделей»

Используя базовые модели, можно составить множество различных комбинаций (комбинированных моделей). Поведение и параметры большей части таких комбинированных моделей можно определить только прямым решением составленных для них систем дифференциальных уравнений с соответствующими граничными условиями. Делать выводы относительно конкретного поведения таких моделей на основе качественных рассуждений, опирающихся на фундаментальные законы, общие принципы или физические аналогии не представляется возможным. С другой стороны, далеко не во всех случаях удаётся решить систему уравнений аналитическим способом, что обусловлено математической сложностью. В этих случаях используют численные методы, методы качественной математики и т.п. — в общем, всё, что выходит за рамки курса общей физики. Однако существуют и простые комбинации моделей, поведение которых можно определить прямым использованием готовых формул или специальными методами, работающими в рамках готовых формул. Для таких моделей на основе фундаментальных законов, общих принципов и готовых формул можно предсказать их поведение в конкретных случаях без обращения к дифференциальным уравнениям и их решениям.

Рассмотрим некоторые из таких моделей.

2.8.6.1.Модель: «точечный заряд и сфера».

42. Чему равен заряд заземленной металлической сферы радиуса , если на расстоянии от её центра находится точечный заряд ?

(Рис.43). Найдём свойства, на которые будем опираться. В электростатике проводников это условия ил . Так как сфера заземлена, то потенциал её равен потенциалу Земли и равен нулю. Заряд , помещённый на расстоянии от центра сферы «притянет» к себе на ближайшую к нему часть поверхности сферы отрицательные заряды. На дальнем конце Земли возникнет положительный заряд, но никакой роли в силу его малости и размеров Земли он играть не будет, и мы им пренебрежём. Что касается отрицательного заряда, то величина этого заряда и распределение его по поверхности сферы будут такими, чтобы потенциал поля в каждой точке сферы был равен нулю. Потенциал поля в данной точке в силу принципа суперпозиций равен сумме потенциалов, создаваемых в данной точке зарядом и отрицательными зарядами на поверхности сферы :

(1)

Это уравнение выполняется для всех точек сферы, в том числе и для её центра. Заряд на сфере распределён неравномерно, однако можно разбить поверхность сферы на такие малые кусочки, что по отношению к центру сферы их можно считать точечными и тогда (1) будет иметь вид

или

Так как — одинаково, то имеем , где — полный заряд, наведённый на сферу. Окончательно получаем .

43.Чему равен потенциал изолированного незаряженного металлического шара радиуса , если на расстоянии от его центра находится точечный заряд .

Потенциалы всех точек шара равны. Для центра шара .

По закону сохранения заряда, сумма наведённых положительных зарядов равна сумме наведённых отрицательных зарядов

.

П оэтому .

44.Точечный заряд помещён внутрь проводящей сферы радиуса и находится на расстоянии от его центра. Сфера заземлена. Какие заряды будут индуцированы на внутренней и наружной поверхности сферы, если: а) шар заземлён; б) шар изолирован и не заряжен. (Рис.44).

При помещении вовнутрь полости сферы заряда он начинает притягивать заряды другого знака и отталкивать заряды того же знака, который имеет сам. В результате на внутренней поверхности сферы возникнет индуцированный заряд другого знака, неравномерно распределённый по поверхности. Индуцированные заряды взаимодействуют между собой силами отталкивания, но силы притяжения со стороны заряда удерживают их на месте. Возникшие заряды того же знака, что и , будут отталкиваться как зарядом, так и друг другом. В результате они начнут разбегаться, занимая такие места, чтобы как можно дальше находиться друг от друга и заряда . В результате они попадут на поверхность сферы. Однако условие электростатики для проводников — равенство нулю напряжённости электрического поля внутри проводника. Это значит, что когда электрические заряды попадут на поверхность и «остановятся», то заряды, расположенные на внутренней стороне сферы, и заряд никакого действия уже на них оказывать не будут.

Распределение зарядов на поверхности будет, таким образом, определяться не положением заряда , а условиями, в которые заряды попадут на поверхности. Если поверхность сферическая, то распределение зарядов будет равномерное. Однако, если сфера заземлена, то заряды получат возможность «убежать» на Землю с поверхности сферы, чтобы быть как можно дальше друг от друга.

Таким образом, в случае заземлённой сферы индуцированный заряд на её поверхности будет равен нулю. Внутри поверхности мы можем использовать теорему Гаусса:

, так как, , то .

т.е. индуцированный на внутренней сфере заряд равен по величине помещённому внутрь сферы заряду и противоположен ему по знаку.

Если сфера изолирована, то индуцированные заряды остаются на поверхности сферы. В силу закона сохранения заряда, величина общего индуцированного заряда равна нулю. Значит, заряд на внешней поверхности будет равен заряду на внутренней поверхности сферы, а значит, равен заряду и по величине, и по знаку. При этом для сферы распределение заряда будет равномерным и не будет зависеть от положения заряда внутри полости сферы.

45. Задача для самостоятельного решения. Точечный заряд находится между двумя заземлёнными проводящими концентрическими сферами с радиусами и на расстоянии от центра ( ). Найти величину индуцированных на сферах зарядах.

Итак, заряды, помещённые на сферическую поверхность, равномерно распределяются по ней. А что будет, если проводник не обладает сферической симметрией. Вообще говоря, вопрос распределения зарядов на поверхности проводника очень сложный, поэтому мы можем рассмотреть (в рамках наших средств) только самую простую модель и сделать самые общие выводы.

46. Система проводников состоит из двух сфер, радиусами и , соединённых проводом. Сферы расположены друг от друга далеко и электрически не влияют друг на друга. Определим отношения напряжённостей поля у поверхности каждой из сфер при сообщении системе некоторого заряда.

При помещении зарядов, они будут перемещаться и распределяться так, чтобы потенциалы сфер стали одинаковыми. При этом на одной сфере будет заряд , на другой — общему заряду, помещённому в систему). Поскольку сферы электрически не влияют друг на друга, то заряды на них распределены равномерно. Тогда, отношение напряжённостей каждой из сфер .

2018-02-18   

Внутри сферы радиуса $R$, заряд которой равен $q$, находится заземленная проводящая сфера радиуса $r$. Центры сфер совпадают. Найти напряженность электрического поля вне большой сферы на расстоянии $l$ oт ее центра.

Решение:

Электрическое поле в данном случае сферически симметрично. Внутри заземленной сферы поле равно нулю, значит, потенциал в этой области (В частности, в центре) одинаков й такой же, как и на поверхности внутренней сферы, т. е. равен нулю. Учтем, что этот потенциал создается зарядами на внешней и внутренней сферах. Потенциалы складываются алгебраически, поэтому, разбивая заряды, находящиеся на поверхности сфер, на малые доли так, чтобы можно было для каждой доли пользоваться формулой потенциала точечного заряда, имеем для центра сфер

$frac{ Delta q_{1} }{R} + cdots + frac{ Delta q_{n} }{R } + frac{ Delta Q_{1} }{ r} + cdots + frac{ Delta Q_{N} }{r} = 0$,

$Delta q_{1} + cdots + Delta q_{n} = q, Delta Q_{1} + cdots + Delta Q_{N} = Q$,

т. е. $q/R + Q/r = 0, Q = — qr/R$, где $Q$ — заряд на внутренней сфере.

Напряженность поля на внешней сфере создается обоими зарядами $q$ и $Q$ так, как если бы они были точечными и были помещены в центр системы. Это можно увидеть, например, с помощью картины линий напряженности электрического поля. Таким образом, на расстоянии $l$ от центра

$E = frac{q+Q}{4 pi epsilon_{0}l^{2} } = frac{q}{ 4 pi epsilon_{0}l^{2} } left ( 1 — frac{r}{R} right )$.

Содержание книги

Предыдующая страница

§10. Проводники и диэлектрики в электростатическом поле

10.4 Расчет поля в присутствии проводников. Метод изображений.

Мы уже подчеркивали, что основная проблема расчета полей в присутствии проводников заключается в появлении индуцированных зарядов, распределение которых заранее не известно. В связи с этим рассмотренные ранее методы, основанные на законе Кулона и принципе суперпозиции, в данном случае оказываются непригодными. Принципиально иной подход к решению данной задачи заключается в расчете распределения потенциала электростатического поля. Действительно, на поверхности проводника распределение заряда не известно, но ведь потенциал проводника постоянен!

Сам метод основан на решении уравнений ^[1] для потенциала поля. Сами эти уравнения довольно сложны и рассматриваются в курсе физики высшей школы, однако, их физический смысл основывается на законе Кулона и связи потенциала с напряженностью поля.

Однако в некоторых случаях можно рассчитать электрическое поле и распределение индуцированных на поверхности проводника зарядов, используя искусственный прием, который называется метод изображений.

Изложим кратко суть и дадим обоснование этого метода.

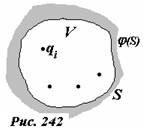
Пусть в некоторой области пространства V, ограниченной поверхностью S (в частном случае граница области может простираться до бесконечности), задано распределение зарядов q_i (рис. 242).

Электрическое поле в выделенной области определяется однозначно, если

— задано распределение зарядов внутри этой области;

— задано распределение потенциала на границе области.

Заметим, что на границе области могут существовать заряды, однако даже при неизвестном их распределении, задание потенциала на границе однозначно определяет поле внутри области. Поэтому две различные задачи, но с одинаковыми распределениями зарядов внутри области и одинаковыми потенциалами на границе имеют внутри области одинаковые решения. Иногда при неизвестном распределении индуцированных зарядов на границе удается подобрать такое распределение зарядов вне рассматриваемой области, что для нового распределения выполненяются граничные условия исходной задачи. В этом случае дополнительные заряды называются зарядами-изображениями. Поиск изображений имеет смысл вести тогда, когда новая задача оказывается проще исходной и имеет простое решение.

Помимо задания распределения потенциала, в качестве граничных условий могут использоваться и некоторые другие, например, значение напряженности поля. Формулировке граничных условий, по этой причине уделяется серьезное внимание в курсе электродинамики.

Точечный заряд над плоской проводящей поверхностью.

Рассмотрим простейшую задачу, допускающую решение с помощью метода изображений.

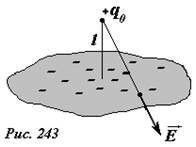
Пусть точечный заряд +q₀ находится на расстоянии l от бесконечной металлической пластины (рис. 243).

Очередной раз мы пользуемся моделями – в данном случае под бесконечной, понимается пластина, размеры которой значительно больше расстояния до заряда. Кроме того, можно считать, что пластина заземлена, так как она «касается бесконечности».

Под действием электрического поля заряда +q₀ электроны пластины придут в движения и начнут скапливаться под точечным зарядом, создавая отрицательный индуцированный заряд.

Если пластина реально заземлена, то эти заряды натекут из заземления. На большой незаземленной пластине возникнут положительные заряды на краях пластины, но так как эти края находятся далеко, то их полем в рассматриваемой области можно пренебречь.

Распределение поверхностной плотности индуцированных зарядов на пластине σ не известно, но известно, что ее потенциал постоянен и равен нулю.

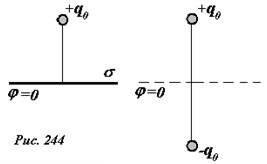
Легко придумать другую задачу, для которой будет выполнено такое же граничное условие. Действительно, рассмотрим поле, создаваемое двумя точечными зарядами q = +q₀ и q’ = —q₀ , находящимися на расстоянии 2l друг от друга (рис. 244). Во всех точках плоскости, перпендикулярной отрезку, соединяющими заряды и проходящей через ее середину, потенциал равен нулю, так как эти точки находятся на равном расстоянии от двух зарядов равных по величине и противоположных по направлению.

Сравним данную простую задачу (два точечных заряда) с исходной (точечный заряд и индуцированные им заряды σ на проводящей пластине): в полупространстве над пластиной распределения зарядов одинаковы (в обоих случаях – один точечный заряд), на граничной плоскости потенциалы равны; следовательно, в этом полупространстве электрические поля также одинаковы.

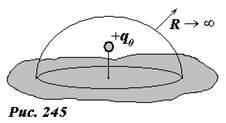
Строго говоря, мы должны рассматривать замкнутую область пространства, поэтому мысленно накроем заряд +q₀ полусферой, опирающейся на плоскость, положим ее потенциал равным нулю и устремим ее радиус к бесконечности, и таким образом придем к рассматриваемому полупространству (рис. 245).

Таким образом, в верхнем полупространстве задачи эквивалентны – заряды и поле распределены одинаково. Следовательно, можно утверждать, что индуцированные на металлической пластине заряды σ создают в верхнем полупространстве такое же электрическое поле как заряд q’ = —q₀, расположенный симметрично относительно верхней поверхности пластины. Следовательно, для расчета электрического поля следует зеркально симметрично под пластиной расположить заряд-изображение q’ = —q₀. Подчеркнем, что реально никакого такого заряда не возникает, его роль – описать поле, создаваемое реальными индуцированными зарядами на поверхности пластины. Ввиду явной симметрии такое же поле возникает и в нижнем полупространстве (то есть поле заряда q’, расположенного в той же точке, что и исходный заряд +q₀). Это поле индуцированных зарядов складывается с полем исходного заряда, поэтому и оказывается, что в нижнем полупространстве поле равно нулю, как и должно быть внутри проводника.

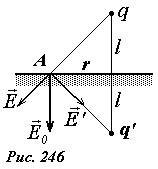
Напряженность суммарного поля у границы (~vec E_0) можно рассчитать по принципу суперпозиции как сумму полей, создаваемых исходным зарядом (~vec E)и его изображением (~vec E’) (рис. 246):

(~vec E_0 = vec E’ + vec E) .

Суммарный вектор направлен перпендикулярно границе и равен

(~E = 2 frac{q}{4 pi varepsilon_0 (l^2 + r^2)} cos alpha = frac{ql}{2 pi varepsilon_0 (l^2 + r^2)^{frac{3}{2}}}) ,

здесь r расстояние от основания перпендикуляра из заряда на плоскость пластины до рассматриваемой точки. Поверхностная плотность заряда у поверхности проводника связана с напряженностью поля соотношением (sigma = varepsilon_0 E) , поэтому распределение поверхностной плотности индуцированных зарядов на пластине осесимметрично и имеет вид

(~sigma = frac{ql}{2 pi (l^2 + r^2)^{frac{3}{2}}}) ,

Сила притяжения заряда к пластине определяется полем, создаваемым индуцированными зарядами, которое в свою очередь эквивалентно полю заряда изображения, поэтому равно силе взаимодействия двух точечных зарядов q и q’

(~F = -frac{q^2}{4 pi varepsilon_0 (2l)^2} = -frac{q^2}{16 pi varepsilon_0 l^2}) .

Энергия взаимодействия исходного и индуцированных зарядов равна только половине (!) энергии взаимодействия зарядов q и q’. Заметьте, что две задачи (заряд и пластина — два заряда) эквивалентны только в верхнем полупространстве. Реально поле существует только в верхней половине пространства. Так энергия взаимодействия есть энергия поля, то и энергия взаимодействия будет в два раза меньше. Поэтому

(~W = — frac{1}{2} frac{q^2}{4 pi varepsilon_0 (2l)} = -frac{q^2}{16 pi varepsilon_0 l}) .

Этот вывод можно пояснить следующим образом: при двух реальных точечных зарядах при перемещении одного из них второй остается неподвижным. Если же уносить заряд от проводящей границы, то его изображение также удаляется, поэтому совершаемая работа будет меньше.

Картина силовых линий также может быть рассчитана, как поле двух точечных зарядов (рис. 247). Обратите внимание, что во всех точках плоскости силовые линии перпендикулярны поверхности.

Продолжим развитие идей построения зарядов-изображений.

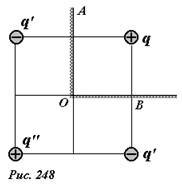
Пусть точечный заряд q находится на биссектрисе прямого двугранного угла AOB, образованного двумя бесконечными проводящими плоскостями (рис. 248). Попытаемся построить набор зарядов изображений так, чтобы удовлетворить граничным условиям — на гранях угла потенциал должен быть равен нулю. Прежде всего, зеркально отобразим исходный заряд в двух плоскостях — получим два изображения q’. Но эти три заряда не обеспечивают равенство нулю потенциала на гранях угла. Необходимо еще один раз отобразить изображения в другой грани — тем самым появляется еще один заряд-изображение q’’. Отметим, что этот заряд является одновременно изображением обоих зарядов q’. Однако его величина также равна q (а не 2q), так как единственное и основное правило построения — удовлетворение граничных условий. Легко проверить, что поле четырех зарядов имеет нулевой потенциал, как на плоскости OA, так и на плоскости OB. Таким образом, поле, образованное зарядом q и индуцированными на плоскостях зарядами эквивалентно полю четырех точечных зарядов, причем эта эквивалентность выполняется только в одной четверти угла, содержащей исходный заряд. В оставшихся четвертях поле отсутствует. Но картина силовых линий получается достаточно симпатичной, если построить поле четырех зарядов, подразумевая, что реально поле только в одной четверти, поэтому в остальных четвертях оно заштриховано (рис. 249).

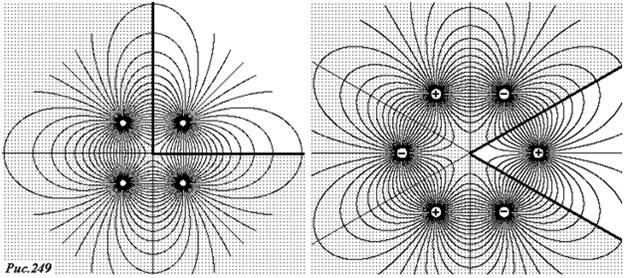
Совершенно аналогично можно построить поле заряда, помещенного на биссектрису двугранного угла, величина которого целое число раз укладывается в полном угле, например, в угле 60°. Шесть зарядов, знаки которых чередуются, расположенных в вершинах правильного шестиугольника, обеспечивают равенство нулю потенциала на гранях угла.

Изображение заряда в сфере.

Прежде, чем приступить к рассмотрению следующей группы задач, связанных с описанием взаимодействия точечного заряда и проводящей сферы, решим одну вспомогательную задачу.

Пусть электростатическое поле создается двумя точечными зарядами, находящимися на расстоянии l друг от друга. Величины и знаки зарядов различны и равны q₁ и q₂. Покажем, что поверхность нулевого потенциала этого поля представляет собой сферу.

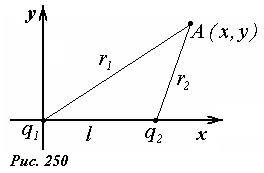
Выберем систему координат, так чтобы заряд q₁ находился в начале координат, а заряд q₂ на оси Ox (рис. 250). Так задача обладает осевой симметрией, то достаточно показать, что в плоскости xOy линия нулевого потенциала является окружностью. Запишем выражение для потенциала электростатического поля в произвольной точке A с координатами (x,y)

(~varphi = frac{q_1}{4 pi varepsilon_0 r_1} + frac{q_2}{4 pi varepsilon_0 r_2} = frac{1}{4 pi varepsilon_0} left (frac{q_1}{sqrt{x^2 + y^2}} + frac{q_2}{sqrt{(x — l)^2 + y^2}}right )) .

Полагая φ = 0, получим уравнение, определяющее линию нулевого потенциала. Обозначим (~frac{q_2}{q_1} = k) , и преобразуем это уравнение к виду:

(~left ( x + frac{l}{k^2 — 1} right )^2 + y^2 = frac{k^2 l^2}{(k^2 — 1)^2}) .

А это есть уравнение окружности радиуса (~R = frac{k l}{k^2 — 1}) с центром, лежащим на оси X в точке с координатой (~x_c = — frac{l}{k^2 — 1}). В пространстве, с учетом осевой симметрии (вращая вокруг оси X) эта линии образует сферу.

Итак, запомним – в поле создаваемом двумя точечными зарядами разными по знаку и величине, поверхность нулевого потенциала представляет собой сферу.

Рассмотрим теперь такую систему: точечный заряд q расположен на расстоянии l от центра металлической заземленной сферы радиуса R. Исследуем электрическое поле в этом случае.

На поверхности металлической заземленной сферы возникнут индуцированные заряды, распределение которых заранее не известно, однако потенциал сферы равен нулю. Мы показали, что поле двух точечных зарядов имеет в качестве поверхности нулевого потенциала сферу. Теперь мы можем использовать этот результат.

Для этого необходимо внутри сферы можно построить заряд изображение q’, такой, чтобы поле двух точечных зарядов имело нулевой потенциал на поверхности сферы. В этом случае вне сферы поле двух точечных зарядов q, q’ и поле, создаваемое зарядом q и зарядами, индуцированными на поверхности металлической сферы, будут одинаковыми. (Вне сферы распределения зарядов одинаковы, на границе — одинаковые граничные условия – поэтому поля вне сферы будут одинаковыми).

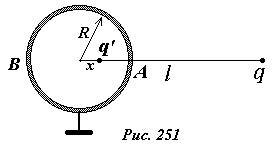
Для определения величины заряда-изображения q’ и его положения можно потребовать выполнения условия φ = 0 в двух точках сферы, например, A и B (рис. 251):

(~left{begin{matrix} frac{1}{4 pi varepsilon_0} frac{q}{l — R} + frac{1}{4 pi varepsilon_0} frac{q’}{R — x} = 0 \ frac{1}{4 pi varepsilon_0} frac{q}{l + R} + frac{1}{4 pi varepsilon_0} frac{q’}{R + x} = 0 end{matrix}right. ) .

Решив эту систему относительно неизвестных q’ и x, получим

(~left{begin{matrix} q’ = -q frac{R}{l} \ x = frac{R^2}{l} end{matrix}right. ) .

Таким образом, вне сферы поле эквивалентно полю двух точечных зарядов исходного q и найденного заряда изображения q’. Внутри сферы эти поля, конечно же, различаются — внутри реальной проводящей сферы поле отсутствует.

Для определения суммарного индуцированного заряда воспользуемся теоремой Гаусса. Окружим сферу замкнутой поверхностью. По теореме Гаусса, поток вектора напряженности электрического поля через эту поверхность равен суммарному заряду внутри поверхности, деленному на ε₀. Так поле индуцированных зарядов эквивалентно полю заряда изображения, то и суммарный индуцированный заряд равен величине заряда-изображения (~q’ = -q frac{R}{l}) .

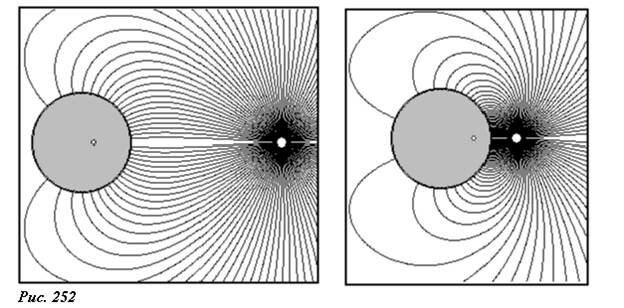
На рисунке 252 показаны силовые линии поля, при двух различных значениях расстояниях до точечного заряда. Обратите внимание, что при увеличении расстояния между зарядом и сферой искажения поля точечного заряда уменьшаются. Как всегда, у поверхности проводника силовые линии перпендикулярны границе, что соответствует условию равновесия индуцированных зарядов на поверхности проводника.

Еще раз подчеркнем — вне сферы поля эквивалентны, но это не значит, что индуцированные заряды концентрируются в одной точке — они распределены по поверхности сферы.

Силу взаимодействия между сферой и точечным зарядом можно найти как силу взаимодействия между двумя точечными зарядами q, q’ :

(~F = frac{q q’}{4 pi varepsilon_0 (l — x)^2} = -frac{q^2}{4 pi varepsilon_0} frac{Rl}{(l^2 — R^2)^2}) .

Заметим, что при l >> R сила взаимодействия становится равной

(~F = -frac{q^2}{4 pi varepsilon_0} frac{R}{l^3}) ,

то есть сила убывает обратно пропорционально кубу расстояния. Такая зависимость может быть качественно объяснена: величина заряда, индуцированного на сфере обратно пропорциональна расстоянию до исходного заряда, а сила взаимодействия между точечными зарядами обратно пропорциональна квадрату расстояния — следовательно, сила взаимодействия сферы и заряда обратно пропорциональна кубу расстояния.

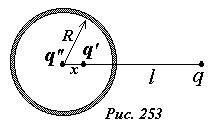
Рассмотрим, как изменится картина поля, если сфера не заземлена. Потенциал незаземленной сферы отличен от нуля, но по-прежнему постоянен, но величина его заранее не известна. Но для изолированной сферы суммарный индуцированный заряд равен нулю — в поле точечного заряда произойдет только перераспределение зарядов по поверхности сферы. Мы можем добиться выполнения граничных условий, поместив в центр шара еще один заряд-изображение q’’ = —q’ (рис. 253). Действительно, заряды q, q’ создают поле, потенциал которого на поверхности сферы равен нулю, а заряд, помещенный в центре сферы, на ее поверхности создает постоянный (но не равный нулю) потенциал, поэтому эквипотенциальность сферы не нарушится. Из теоремы Гаусса следует, что суммарный индуцированный заряд сферы равен сумме зарядов изображений, поэтому при выполнении условия q’’ = —q’, этот заряд окажется равным нулю.

Итак, вне сферы поле, создаваемое точечным зарядом q и индуцированными зарядами на поверхности, эквивалентно полю трех точечных зарядов q, q’, q’’.

Обратите внимание, число зарядов изображений определяется только необходимостью выполнения граничных условий.

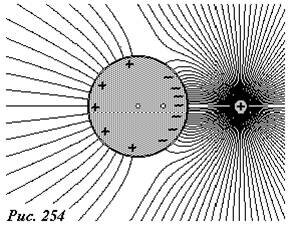
На рисунке 254 показана картина силовых линий электрического поля рассматриваемой системы зарядов. Обратите внимание, что имеются силовые линии, начинающиеся на положительных зарядах сферы. Незаземленная сфера гораздо меньше возмущает поле точечного заряда, чем заземленная. Действительно, на ней происходит только перераспределение зарядов.

Сила, действующая на заряд q, вычисляется как сумма сил, действующих со стороны двух изображений

(~F = frac{q q’}{4 pi varepsilon_0 (l — x)^2} + frac{q q»}{4 pi varepsilon_0 l^2}= -frac{q^2}{4 pi varepsilon_0} frac{R^3 (2l^2 — R^2)}{l^3 (l^2 — R^2)^2}) .

При l >> R сила взаимодействия

(~F = -frac{q^2}{2 pi varepsilon_0} frac{R^3}{l^5}) ,

убывает обратно пропорционально пятой степени расстояния, что также легко объяснимо: величина индуцированного дипольного момента пропорциональна величине внешнего поля (которое убывает обратно пропорционально квадрату расстояния), а величина поля диполя убывает обратно пропорционально кубу расстояния.

Заметим, что в данном случае можно вычислить потенциал сферы, не рассчитывая распределения зарядов на поверхности. По принципу суперпозиции, потенциал центра сферы равен сумме потенциалов заряда q и индуцированных зарядов на поверхности сферы. Все индуцированные заряды находятся на одном и том же расстоянии от центра и их сумма равна нулю, следовательно, равен нулю и потенциал, создаваемый ими в центре сферы. Поэтому потенциал в центре сферы, следовательно, и в любой ее точке, равен потенциалу поля точечного заряда (~varphi = frac{q}{4 pi varepsilon_0 l}) .

Суммарный заряд сферы остается равным нулю, но сфера приобретает индуцированный дипольный момент, который равен дипольному моменту двух зарядов-изображений

(~p = q’ x = q frac{R^3}{l^2}) .

Перепишем эту формулу в виде

(~p = q frac{R^3}{l^2} = frac{q}{4 pi varepsilon_0 l^2} varepsilon_0 (4 pi R^3) = 3V varepsilon_0 E_0) ,

где (~V = frac{4}{3} pi R^3) — объем сферы, (~E_0 = frac{q}{4 pi varepsilon_0 l^2}) — напряженность поля, создаваемого точечным зарядом в центре сферы. Таким образом, мы видим, что индуцированный дипольный момент сферы пропорционален напряженности внешнего поля. В общем случае связь между напряженностью внешнего поля и величиной индуцированного заряда записывают виде

(~p = alpha varepsilon_0 E) ,

где E — напряженность внешнего электрического поля, коэффициент пропорциональности α имеет размерность объема и называется поляризуемостью тела. Мы показали, что для проводящей сферы (аналогично шара), поляризуемость равна ее утроенному объему. В общем случае поляризуемость зависит от формы тела и его электрических свойств, однако по порядку величины она равна объему тела.

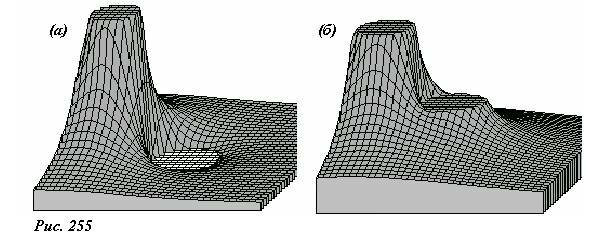
Достаточно интересно рассмотреть распределение потенциала в плоскости, проходящей через точечный заряд и центр сферы. Эти потенциальные функции для заземленной (а) и незаземленной (б) сфер изображены на рисунке 255. Функция, описывающая потенциал поля, вне сферы совпадает с потенциалом поля точечных зарядов (исходного и изображений), а внутри сферы равна нулю в случае (а) и постоянна в случае (б) – круглые горизонтальные площадки совпадает с сечением сферы. Резкое «возвышение» есть потенциал поля точечного заряда, который стремится к бесконечности, здесь, как и на других рисунках, он «обрезан».

Проводящий шар в однородном поле.

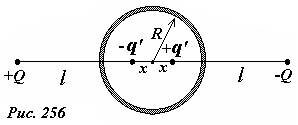
Посмотрим, какие изменения внесет проводящий шар, помещенный в однородное электрическое поле. Данная задача весьма популярна, известно несколько принципиально различных методов ее решения. Мы же воспользуемся уже полученными нами результатами. Поместим шар посредине между двумя одинаковыми по величине, но противоположными по знаку точечными зарядами +Q и —Q (рис. 256). Обозначим расстояния от зарядов до центра шара l.

Построим изображения каждого заряда в шаре — два заряда, величины которых равны (~q’ = Q frac{R}{l}) , и расположены на расстоянии (~x = frac{R^2}{l}) от центра шара. Теперь мысленно начнем уносить заряды Q на бесконечность (~l to infty) . При этом заряды-изображения будут приближаться к центру шара, образуя точечный диполь с дипольным моментом

(~p = 2q’ x = 2 frac{Q R^3}{l^2}) .

При увеличении расстояния между зарядами поле в области шара становится практически однородным с напряженностью

(~E = 2 frac{Q}{4 pi varepsilon_0 l^2}) .

Выразим индуцированный дипольный момент шара через напряженность поля

(~p = 4 pi varepsilon_0 R^3 E) .

как видите, этот дипольный момент не зависит от «придуманных» зарядов Q и расстояния l, поэтому и в однородном поле шар будет иметь такой же дипольный момент. Обратите внимание, что и в данном случае поляризуемость шара равна его утроенному объему.

Таким образом, поле индуцированных на поверхности шара зарядов эквивалентно полю точечного диполя, находящегося в центре шара. Картину силовых линий такого поля мы уже использовали ранее.

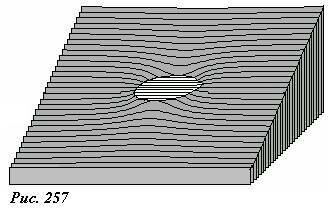
Неплохо также смотрится и распределение потенциала (рис. 257).

Заметим, что потенциал однородного поля изменяется по линейному закону, поэтому распределение потенциала в таком поле изображается наклонной плоскостью. При помещении в это поле проводящего шара на наклонной плоскости появляется горизонтальная площадка, постоянного потенциала на проводнике.

Задание для самостоятельной работы.

1. Найдите распределение поверхностной плотности индуцированных зарядов на поверхности металлического шара, помещенного во внешнее электрическое поле.

Примечания

1. ↑ Эти уравнения называются уравнениями С. Пуассона, или в частных случаях уравнениями П. Лапласа. С математической точки зрения они являются уравнениями в частных производных, поэтому их изучение далеко выходит за рамки наших возможностей.

Следующая страница